数据降维的方法:
- 特征选择
- PCA(主成分分析)
- LDA(线性判别分析)
这里,我们只讨论前两种方法。
特征选择
首先,我们讨论特征选择。
特征选择的目的
- 去除冗余特征,冗余特征之间的相关度较高,会浪费计算性能。
- 去除噪声特征,噪声特征会对预测结果有影响。
特征选择的方法
对于特征选择,我们可以从专业知识技能或业务的角度进行选择,比如,在研究A股的时候,我们可以根据自身对金融市场的理解,把日本股市的特征排除在外。
对于不同的应用场景,根据其技术和业务特点,均有不同的特征选择方法。
但这个不是我们这份笔记的讨论重点。
这份笔记主要从数理统计的角度,进行特征选择。
主要有四种方法:
- Filter(过滤式):VarianceThreshold
- Embedded(嵌入式):正则化、决策树
- Wrapper(包裹式)
- 神经网络
对于Embedded(嵌入式)和神经网络,我们放在后面讲具体的算法的时候再讨论。而Wrapper(包裹式)这种其实并不常见。
这里主要讨论Filter(过滤式)。
Filter(过滤式):VarianceThreshold
正如VarianceThreshold的字面含义,是从方差大小的角度来考虑,把方差小的特征过滤掉。即,认为方差小的特征,在每个样本中差异不大,不足以作为样本的特征。
我们用scikit-learn进行特征选择。
1 | from sklearn.feature_selection import VarianceThreshold |
参数:
threshold的默认值是0。- 训练集方差低于此阈值的特征将被删除。默认情况是保持所有特性的方差为非零,即去除所有样本中具有相同值的特征。
- 具体情况需要具体分析
threshold的取值,一般情况下在[0,10]之间。
示例代码:
1 | from sklearn.feature_selection import VarianceThreshold |
运行结果:
1 | [[0, 2, 0, 3], [0, 1, 4, 3], [0, 1, 1, 3]] |
PCA
PCA是Principal Components Analysis的缩写,即主成分分析。
PCA的介绍
我们首先从这四张图片开始,以此对PCA有一个最简单的认识。
如这四张二维图片,分别从不同的角度描述了一辆三维的宝马汽车。

很直观的感受,右下角的图像能最好的描述该三维的宝马汽车。
PCA是降低原数据的维数,并同时只损失少量的信息。是一种分析简化数据集的技术。
关于该方法的数学解释,大家可以参考本文的最后一部分。实际上从数学角度能给大家更好的解释,而且实话实说,这个解释并不晦涩难懂。
PCA的特点
- 只有当特征数量超过100的时候,才可能有PCA。
- 原因是高维度数据容易
特征之间通常是相关的。 - 这个特点也是特征选择和PCA的主要区别。
- 原因是高维度数据容易
- PCA在减少特征数量的时候,数据也会被改变。
PCA的实现
我们用scikit-learn实现PCA。
1 | from sklearn.decomposition import PCA |
其中,有一个参数要特别注意。n_components,在取不同类别的参数时,有不同的含义。
- 当
n_components是0到1之间的小数时,代表保留百分之多少的信息。- 经验而言,该值通常90%到95%。
- 当
n_components是整数时,代表保留多少个特征。 - 当
n_components取'mle'时,代表指定在mle算法(极大似然估计)下,让PCA自动选取维数。 - 上述三种方法,一般用第一种。
示例代码:
1 | from sklearn.decomposition import PCA |
运行结果:
1 | [[0, 2, 0, 3], [0, 1, 4, 3], [0, 1, 1, 3]] |
当然,我们也可以令n_components取'mle'。
示例代码:
1 | from sklearn.decomposition import PCA |
运行结果:
1 | ValueError: n_components='mle' is only supported if n_samples >= n_features |
如运行结果所示,要求样本数大于或等于特征数。
我们修改X,使其行数大于或等于列数,再试一下。
示例代码:
1 | from sklearn.decomposition import PCA |
运行结果:
1 | [[1, 2, 3], [2, 3, 4], [4, 5, 6]] |
专题:PCA的数学解释
PCA的数学例子
一维
假设存在数据如下:
| S1 | S2 | S3 | S4 | S5 | S6 | |
|---|---|---|---|---|---|---|
| X | 10 | 11 | 8 | 3 | 2 | 1 |
我们可以很轻松的画出图形:
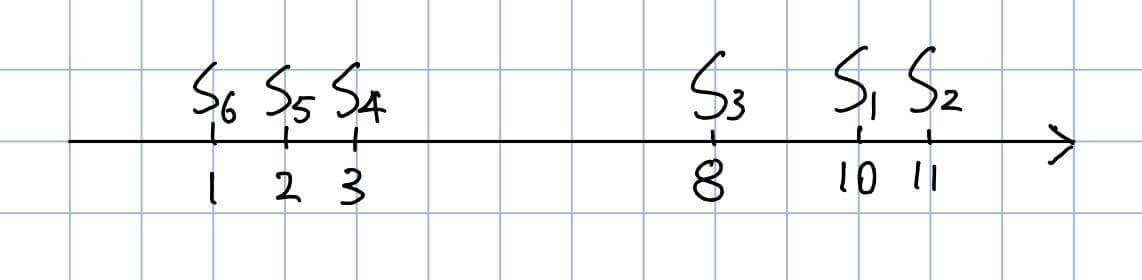
也很容易的得出结论:
S1、S2和S3有相对较大的值,S4、S5和S6有相对较小的值。S1与S2、S3之间的相似性,比S1与S4、S5、S6之间的相似性大。
二维
假设存在数据如下:
| S1 | S2 | S3 | S4 | S5 | S6 | |
|---|---|---|---|---|---|---|
| X | 10 | 11 | 8 | 3 | 2 | 1 |
| Y | 6 | 4 | 5 | 3 | 2.5 | 1 |
我们可以很轻松的画出图形
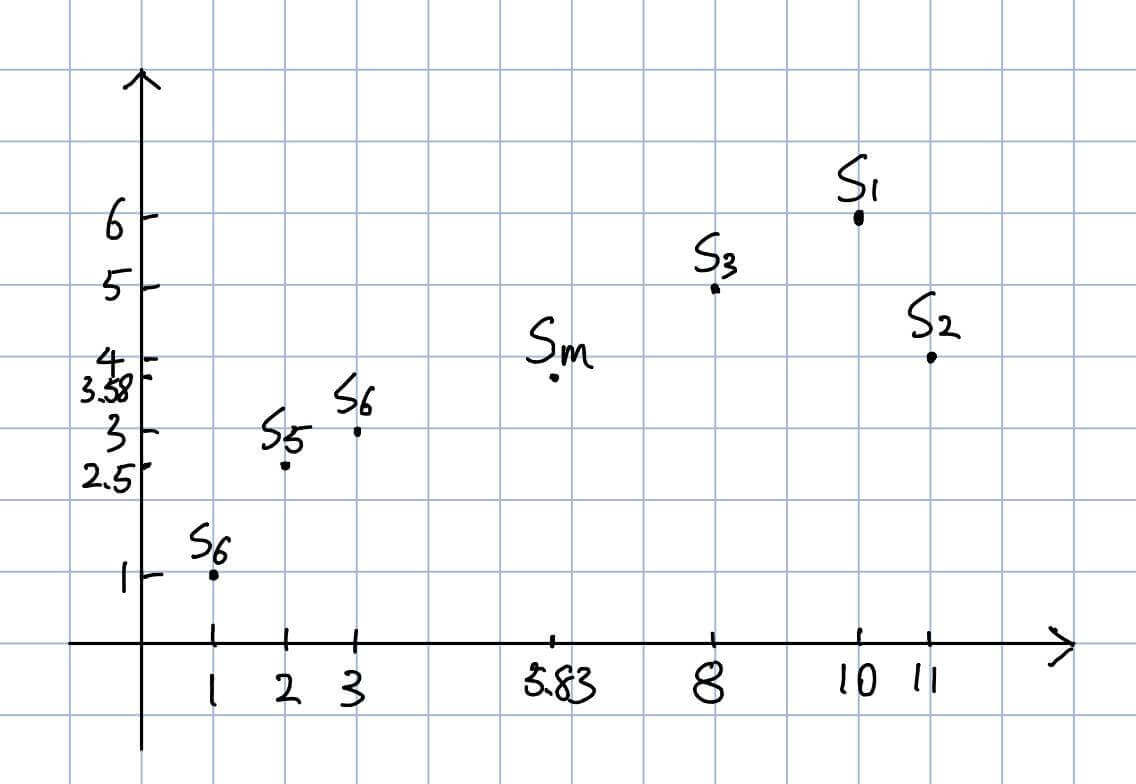
其中Sm的横坐标为6个点横坐标的平均值,Sm的纵坐标为6个点纵坐标的平均值。
也很容易的得出结论:
S1、S2和S3在右上方聚集,S4、S5和S6在左下方聚集。
平移所有的点
然后我们对二维情况所有的点进行平移,至Sm恰好处于(0,0)。
同时,我们试图寻找一条直线PC1,使得该直线最能拟合这6个点。
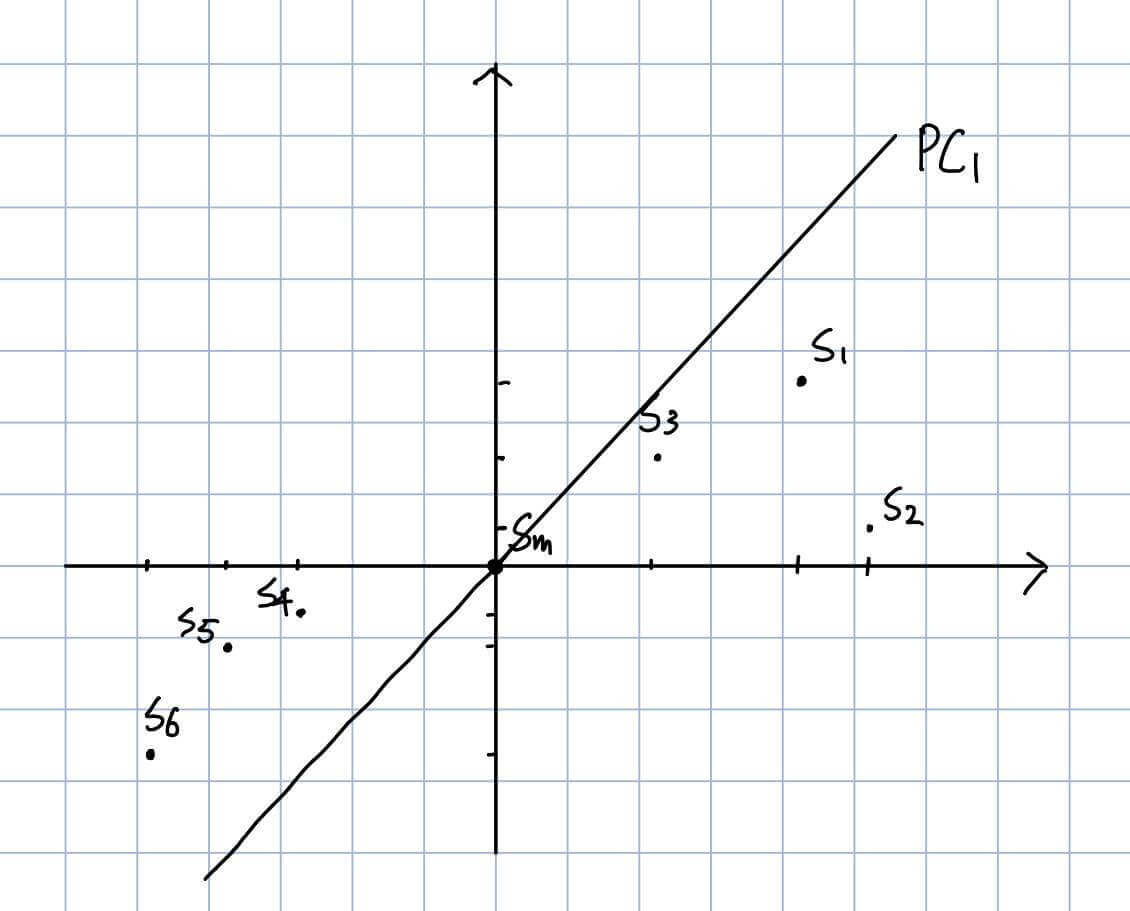
在求得PC1之后,我们作PC1的垂线PC2。同时我们抹去X轴和Y轴,旋转PC1至水平,PC2至竖直。
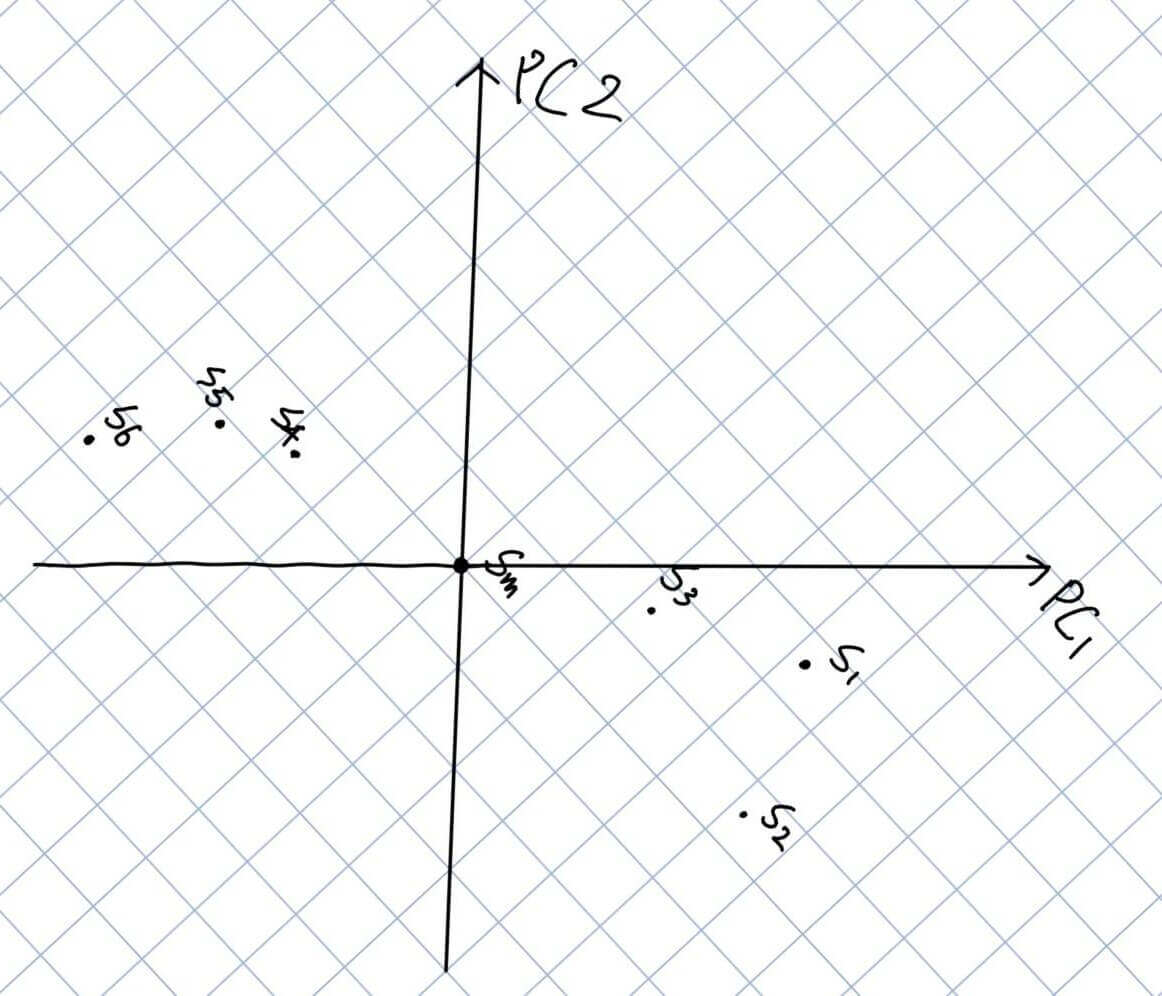
我们可以看到大部分点的在PC1上的坐标远远大于在PC2上的坐标,即在PC2上的值都趋于0,所以,我们可以考虑舍弃PC2的坐标。
因此,这时候我们便实现了主成分分析,将二维特征用一维进行了表示。
多维的情况与这里类似,不再赘述。
PCA的数学总结
通过上述例子,我们可以得出结论。
PCA的思路是,保持空间中每个点的位置不变,通过旋转坐标轴,使得某些点在某个坐标轴上的值足够大,而在某个坐标轴上值足够小,从而舍弃值足够小的坐标,以此舍弃某些特征,实现主成分分析。