常用模型

机器学习的常用模型可分为如下几类

监督学习
- 分类
  - kNN
  - 贝叶斯
  - 决策树和随机森林
  - 逻辑回归
- 回归
  - 线性回归
  - 岭回归
无监督学习
- 聚类
  - KMeans
强化学习

不同的模型对于数据的要求也不一样。
其中监督学习要求数据拥有特征值和目标值，无监督学习只要求有特征值。
而在监督学习中，分类问题要求目标值是离散型数据，回归问题则要求目标是连续型数据。

关于强化学习，在《强化学习浅谈及其Python实现》中，有专门的一个系列进行讨论。

常用函数

在机器学习中，有两种函数。

假设函数
损失函数

我们举一个例子来讨论两种函数。
假设存在数据如下，我们要求寻找一个最能拟合所有点的模型。

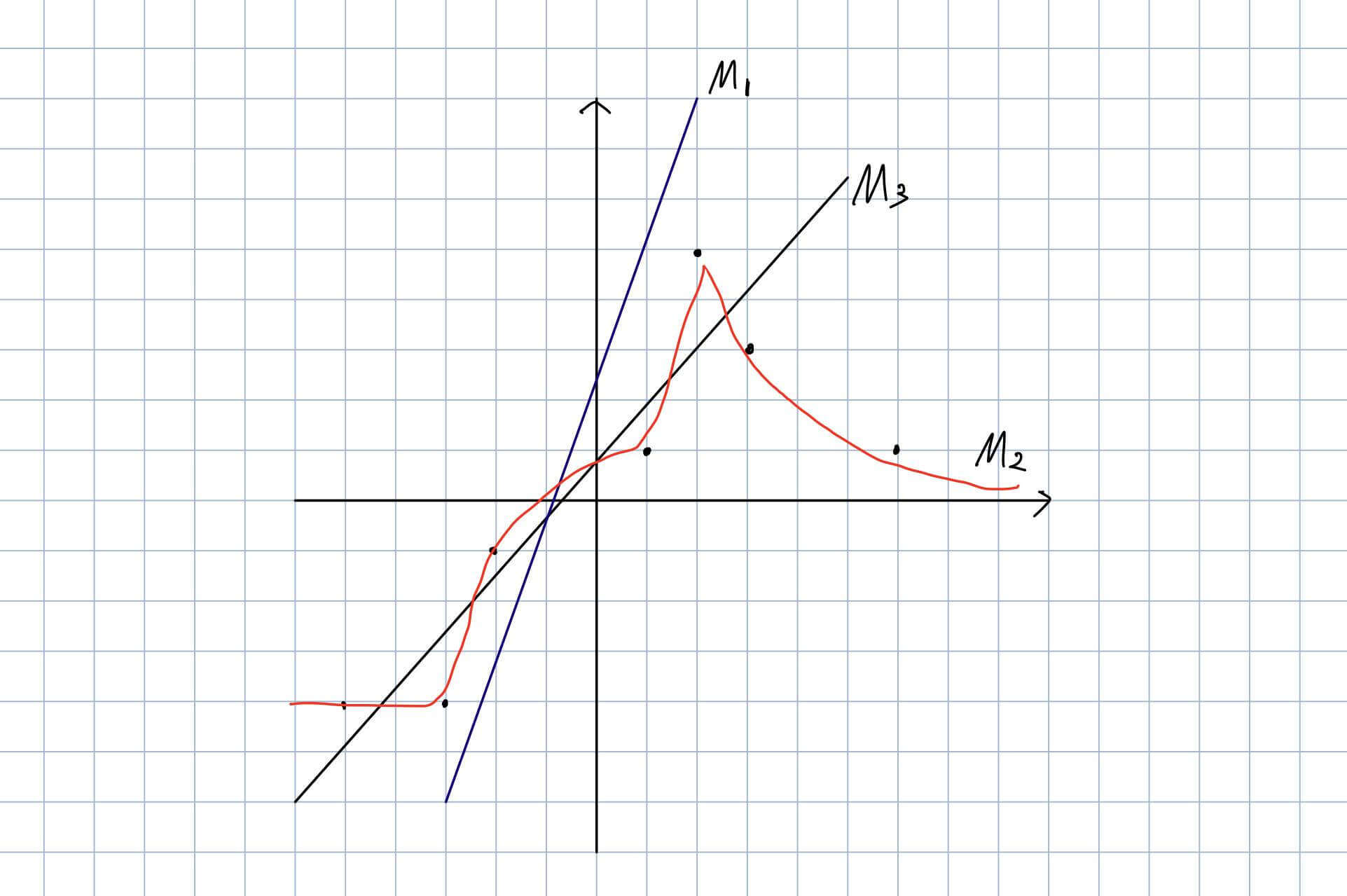
假设函数

假设函数通常记作 $H(x)$ ，其中 $x$ 是需要传入的参数，当然这里的 $x$ 不一定代表一个数字，可以有多种形式，可能是一个向量、也可能是一个矩阵等。在传入参数之后， $H(x)$ 能够得到一个结果，这个结果便是我们模型的预测值。

损失函数

那么，我们怎么知道这个预测值与真实值到底有多么拟合呢？损失函数。
损失函数通常计作 $L(x)$ ， $L$ 代表 $Loss$ 。
在上面的例子，我们可以用每个点到模型的距离平方来评估。
但是，只有每个点到模型的距离的平方，还不够，这时候不足以评价模型的好与不好。
我们还需要对所有的距离进行平方再求和，这就是损失函数。

有极少数的资料，还会有成本函数的概念。认为：损失函数针对单个样本，成本函数针对整体数据集。

模型评估

分类模型评估

常用的分类模型评估方法有

准确率
精确率和召回率
平衡F分数

准确率

即：预测结果与事实相符的百分比

精确率和召回率

以二分类为例：预测结果与真实标记之间存在四种不同的组合

	预测为正	预测为负
真实为正	真正例 TP	伪反例 FN
真实为负	伪正例 FP	真反例 TN

TP：True Positive，预测结果为正，真实为正。这时候与事实相符。
FP：False Positive，预测结果为正，真实为负。这时候与事实不符。
FN：False Negative，预测结果为负，真实为正。这时候与事实不符。
TN：True Negative，预测结果为负，真实为负。这时候与事实相符。

精确率与召回率

精确率：预测为正的样本中，真实为正的比例。（查的准）
- 比如100人进行新冠肺炎的核算检测，核酸检测认为其中10人感染了新冠，实际上这10人中只有9人感染了新冠。那么精确率为90%。
召回率：真实为正的样本中，预测为正的比例。（查的全）
- 比如100人进行新冠肺炎的核算检测，其中有15人是感染了新冠的，核酸检测这15人中只有10人感染了新冠。那么召回率为66.66%

精确率的公式

$\text{精确率} = \frac{TP}{TP + FP}$

$TP + FP$ ：预测为正
$TP$ ：真实为正

召回率的公式

$\text{召回率} = \frac{TP}{TP + FN}$

$TP + FN$ ：真实为正
$TP$ ：预测为正

平衡F分数

上面我们讲了精确率和召回率，而平衡F分数就是兼顾精确率和召回率的公式。
$F_\beta$ 的公式

$F_\beta = (1+\beta^2) * \frac{\text{精确率} * \text{召回率}}{\beta^2 * \text{精确率} + \text{召回率}}$

例如：

$F_1 = 2 * \frac{\text{精确率} * \text{召回率}}{\text{精确率} + \text{召回率}}$

另外还有 $F_{0.5}$ 和 $F_2$ 。

$F_1$ 认为精确率和召回率同等重要。
$F_{0.5}$ 认为精确率比召回率重要。
$F_2$ 认为召回率比精确率重要。

分类模型评估的实现

1	from sklearn.metrics import classification_report

传入的参数有

y_true：真实目标值
y_pred：估计器预测目标值
target_name：目标类别名称

返回每个类别的精确率和召回率

回归模型评估

常见的回归模型评估方法有

平均绝对误差
平均方差
R平方

平均绝对误差

$fi$ 是预测值， $yi$ 是真实值， $ei=|fi-yi|$ 就是绝对误差，那么很多 $ei$ 的平均就是平均绝对误差。

实现方式

1 2	from sklearn.metrics import mean_absolute_error mean_absolute_error(y_test, y_pred)

平均方差

与平均绝对误差类似，很多方差的平均就是平均方差。

实现方式

1 2	from sklearn.metrics import mean_squared_error mean_squared_error(y_test, y_pred)

R平方

R平方定义

我们先定义这些符号。

$y_i$ 是目标值的真实值
$\hat{y_i}$ 是目标值的真实值的预测值
$\bar{y_i}$ 是目标值的真实值的平均值

ESS(Explained Sum of Squares)是回归平方和

$ESS = \sum_{i=1}^n(\hat{y_i} - \bar{y_i})^2$

RSS(Residual Sum of Squares)是残差平方和

$RSS = \sum_{i=1}^n(y_i - \hat{y_i})^2$

TSS(Toatl Sum of Squares of Deviations)是总离差平方和

$TSS = \sum_{i=1}^n(y_i - \bar{y_i})^2$

R平方

$R^2 = \frac{ESS}{TSS} = \frac{TSS-RSS}{TSS} = 1 - \frac{RSS}{TSS}$

ESS，RSS，TSS之间还存在关系，我们举例来说明。

假设 $Y$ 是关于 $X_1$ ， $X_2$ ， $X_3$ ， $X_4$ 的线性回归，且

方差来源	平方和	自由度
$\text{回归平方和}ESS$	$67965$	$4$
$\text{残差平方和}RSS$	$3080$	$16$
$\text{总平方和}TSS$	$71045$	$20$

$\text{样本总数}T - 1 = TSS\text{的自由度}$ ，即 $\text{样本总数}T=21$
$TSS = ESS + RSS$
$ESS$ 的自由度是自变量的个数
$RSS\text{的自由度} = T - K = 21 - 5 = 16$ $R S S 的自由度 = T - K = 21 - 5 = 16$
- $T$ 是样本个数
- $K$ 是参数个数，在这里是 $\text{自变量个数}+1$ 。（因为回归模型中还有一个常数）

R平方缺陷

R平方的缺陷有

如果有更多的回归变量加入回归方程中， $R^2$ 只会增大不会减少，容易误解。
对于时间序列回归， $R^2$ 通常很大，此时难以判断模型的优劣。

所以有了有调整的 $R^2$ ，记作 $Adj\ R^2$

$Adj\ R^2 = 1 - \frac{RSS/(T-K)}{TSS/(T-1)} = 1 - \frac{T-1}{T-K}(1-R^2)$

其中

$T$ 是样本个数
$K$ 是参数个数

R平方的实现

1 2	from sklearn.metrics import r2_score r2_score(y_test, y_pred)

两个问题

一、为什么不把损失函数作为模型的评估方法？
因为损失函数并不能很好的作为从业务角度去评价模型。比如，在分类问题中，有时候我们需要的查的准，在预测为正的样本实际为正的比例要高，所以我们用精准率。但是有时候我们需要实际为正中预测为正的比例，召回率。此外，我们还可能会平衡F分数，兼顾准确率和召回率等。此外，在分类问题中，即使准确率也有交叉熵损失更利于从业务角度去评估模型。而在回归模型评估方法中，平均绝对误差和平均方差，其实和回归问题的损失函数均方误差非常相似。而R平方是决定系数，可以反应因变量的变化对自变量的影响力。

二、为什么不把模型评估方法做为目标函数？
因为大多数模型评估方法没法通过梯度进行优化，比如准确率、精准率和召回率等。

文章作者: Kaka Wan Yifan

文章链接: https://kakawanyifan.com/10204

留言板