近朱者赤,近墨者黑。(出自:晋·傅玄《太子少傅箴》)
这是kNN算法的核心思想。
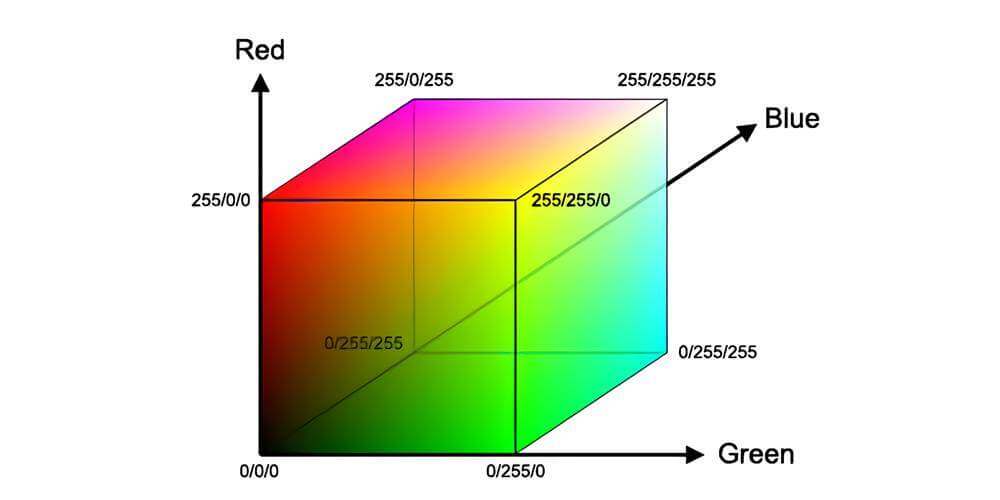
例如,计算机中的RGB颜色空间,就是最直接最明显的近朱者赤,近墨者黑。

kNN,英文全称为K-nearst neighbor,中文名称为K近邻算法,它是由Cover和Hart在1968年提出来的。
kNN的距离
近朱者赤,近墨者黑。那么,我们首先需要确定远和近。
常见的描述距离的有:
- 欧式距离
- 余弦距离
欧式距离
欧式距离就是两点之间距离
假设,存在两个点:A(Xa,Ya,Za),B(Xb,Yb,Zb)
则,A和B之间的距离为
(Xa−Xb)2+(Ya−Yb)2+(Za−Zb)2
余弦距离
余弦距离就是两个向量之间的夹角的余弦值
假设,存在两个向量。A(Xa,Ya,Za),B(Xb,Yb,Zb)
则,A和B之间夹角的余弦值为
cos<A,B>=∣A∣∣B∣A∗B
cos<A,B>=(Xa+Ya+Za)2+(Xb+Yb+Zb)2XaXb+YaYb+ZaZb
两个距离的比较
- 欧氏距离体现数值上的绝对差异
- 余弦距离体现方向上的相对差异
假设有这么一个场景。RGB值,理论上有2563种颜色,但是其中有名字的颜色只有136种。
比如
苍白的紫罗兰红色 219,112,147
熏衣草花的淡紫色 230,230,250
矢车菊的蓝色 100,149,237
现在,我们任意给定一组RGB值,这一组RGB值,很可能不在这136种有颜色的RGB中。要求找出最接近的颜色名称。
那么这个时候,余弦距离可能会认为和 (1,0,0) 最接近的颜色是 (255,0,0) 。
但,显然不是这样。
这时候应该用欧氏距离。欧氏距离可能会认为和 (1,0,0) 最接近的颜色是 (2,0,0) 。
scikit-learn中的默认距离
在scikit-learn的官方文档,是这么表述的:
The default metric is minkowski, and with p=2 is equivalent to the standard Euclidean metric.
这里提到了p=2时的闵可夫斯基距离。
闵可夫斯基距离的公式如下
d=pk=1∑n∣x1k−x2k∣p
其中p是一个参数。
- 当p=1时,称为是曼哈顿距离
- 当p=2时,称为欧氏距离
- 当p→∞时,就是切比雪夫距离
kNN的实现
我们以《充电桩故障分类与检测》为例。这也是百度曾经举办的一个比赛,但是比赛的数据已经不提供下载了。不过我的GitHub中还有数据。
赛题介绍:https://dianshi.bce.baidu.com/competition/19/question
数据下载:https://github.com/KakaWanYifan/BaiduPower
实现方式也很简单。
1
| from sklearn.neighbors import KNeighborsClassifier
|
示例代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler
import pandas as pd
data = pd.read_csv('../data/data_train.csv',names = ['id','k1k2','lock','stop','gate','thdv','thdi','label'])
print(data.head(10))
y = data['label']
x = data.drop(['label','id'],axis=1)
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.25)
knn = KNeighborsClassifier(n_neighbors=5)
knn.fit(x_train,y_train)
y_predict = knn.predict(x_test)
print(y_predict)
knn.score(x_test,y_test)
|
运行结果:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| id k1k2 lock stop gate thdv thdi label
0 1 11.802741 12.122681 -0.057440 12.089629 11.809618 11.468398 1
1 2 11.818357 12.135362 -0.055879 12.056373 11.671259 38.840074 1
2 3 11.802741 12.121097 -0.060561 12.038968 12.163057 14.761536 1
3 4 11.844897 12.157545 -0.094915 12.059551 10.682868 16.772367 1
4 5 11.818357 12.121097 -0.087113 12.054791 9.838321 141.752642 1
5 6 11.818357 12.140113 -0.083992 12.064298 11.396249 19.982123 1
6 7 11.821478 12.130612 -0.105850 12.059551 10.694349 12.984901 1
7 8 11.819918 12.121097 -0.085552 12.062716 10.686139 197.598946 1
8 9 11.849578 12.125861 -0.090233 12.043715 11.513550 14.365037 1
9 10 11.773081 12.105262 -0.071496 12.053209 10.545958 24.675184 1
[0 1 0 ... 1 0 1]
15
0.8856140350877193
|
完整的代码已经PUSH到了我的GitHub上
https://github.com/KakaWanYifan/BaiduPower
kNN的优缺点
-
优点
- 简单
- 无需迭代训练
-
缺点
- 容易受k值的影响
- k太小,容易受异常点影响。
- k太大,容易受样本数量的影响。
- 性能缺陷
- 算法时间复杂太高(所以kNN一般只适合小数据场景)