3.栈、队列

双向链表的四个方法

在正式开始这一章的讨论之前，我们来做一件事情，实现一个双向链表的四个方法：

1. 在头部添加
2. 在尾部添加
3. 在头部删除
4. 在尾部删除

如果继续用单向链表的话，为了删除尾部节点，我们需要一个一个指针的指下去，直到倒数第一个节点，然后把其和最后一个节点的指针断开。为了提高效率，我们用空间换时间，采用双向链表。

• Java
• Python

示例代码：

package ch03;

/**
 * 双向链表
 */
public class DoubleLink {

    /**
     * 双向节点
     */
    public static class DoubleNode{

        // 节点的值
        int data;
        // next 节点
        DoubleNode next;
        // prev 节点
        DoubleNode prev;

        /**
         * 构造方法
         * @param data 节点的值
         */
        DoubleNode(int data){
            this.data = data;
        }
    }

    // head 节点
    public DoubleNode head;
    // tail 节点
    public DoubleNode tail;

    /**
     * 在头部添加节点
     * @param data
     */
    public void addAtHead(int data){
        // 当前操作的节点
        DoubleNode curr = new DoubleNode(data);

        // 如果头节点是NULL，说明整个链表都是NULL
        if (null == head){
            head = curr;
            tail = curr;
        }else {
            // 当前节点的next指向头节点
            curr.next = head;
            // 头节点的prev指向当前节点
            head.prev = curr;
            // 把当前节点作为头节点
            head = curr;
        }
    }

    /**
     * 移除头部节点，并返回
     * @return
     */
    public DoubleNode removeAtHead(){
        // 如果头节点是NULL，说明整个链表都是NULL
        if (null == head){
            return null;
        }

        // 如果上面的都没有命中
        // 当前要操作的节点就是头节点
        DoubleNode curr = head;
        // 设置新的头节点
        head = head.next;
        // 当前节点就是以前的头节点，next指向空
        curr.next = null;
        // 新的头节点的指针，也指向空。
        head.prev = null;
        return curr;
    }


    /**
     * 在尾部添加节点
     * @param data
     */
    public void addAtTail(int data){
        // 当前操作的节点
        DoubleNode curr = new DoubleNode(data);

        // 如果尾节点是NULL，说明整个链表都是NULL
        if (null == tail){
            tail = curr;
            head = curr;
        }else{
            // 尾节点的next 指向当前节点
            tail.next = curr;
            // 当前节点的prev 指向尾节点
            curr.prev = tail;
            // 把当前节点作为尾节点
            tail = curr;
        }
    }

    /**
     * 移除尾部节点，并返回
     * @return
     */
    public DoubleNode removeAtTail(){
        // 如果尾节点是null，说明真个链表都是空的
        if (null == tail){
            return null;
        }
        // 当前操作的节点
        DoubleNode curr = tail;
        // 把尾节点的前一个节点，作为新的尾节点
        tail = tail.prev;
        // 新的尾节点的next指向null
        tail.next = null;
        // 当前节点的前一个节点指向null
        curr.prev = null;

        return curr;
    }

    /**
     * 输出链表
     */
    public void output(){
        String rnt = "";
        DoubleLink.DoubleNode temp = head;
        while (temp!=null) {
            rnt = rnt + temp.data + " ";
            temp = temp.next;
        }
        System.out.println(rnt);
    }

    public static void main(String[] args) {
        DoubleLink doubleLink = new DoubleLink();
        for (int i = 0; i < 10; i++) {
            doubleLink.addAtHead(9-i);
        }
        doubleLink.output();
        System.out.println(doubleLink.removeAtHead().data);
        System.out.println(doubleLink.removeAtTail().data);
        doubleLink.output();
        doubleLink.addAtTail(10);
        doubleLink.addAtTail(11);
        doubleLink.addAtTail(12);
        doubleLink.output();
    }
}

运行结果：

0 1 2 3 4 5 6 7 8 9 
0
9
1 2 3 4 5 6 7 8 
1 2 3 4 5 6 7 8 10 11 12

示例代码：

class DoubleNode:
    def __init__(self, data):
        """

        :param data:
        """
        self.data = data
        self.next = None
        self.prev = None


class DoubleLink:
    def __init__(self):
        self.head = None
        self.tail = None

    def addAtHead(self, data):
        """

        :param data:
        :return:
        """
        curr = DoubleNode(data)

        if self.head is None:
            self.head = curr
            self.tail = curr
        else:
            curr.next = self.head
            self.head.prev = curr
            self.head = curr

    def removeAtHead(self):
        """

        :return:
        """
        if self.head is None:
            return None
        curr = self.head
        self.head = self.head.next
        self.head.prev = None
        curr.next = None
        return curr

    def addAtTail(self, data):
        """

        :param data:
        :return:
        """
        curr = DoubleNode(data)

        if self.tail is None:
            self.tail = curr
            self.head = curr
        else:
            self.tail.next = curr
            curr.prev = self.tail
            self.tail = curr

    def removeAtTail(self):
        """

        :return:
        """
        if self.tail is None:
            return None

        curr = self.tail
        self.tail = self.tail.prev
        self.tail.next = None
        curr.prev = None

        return curr

    def output(self):
        rnt = ""
        temp = self.head;
        while temp is not None:
            rnt = rnt + str(temp.data) + " "
            temp = temp.next

        print(rnt)


if __name__ == '__main__':
    doubleLink = DoubleLink()
    for i in range(10):
        doubleLink.addAtHead(9 - i)

    doubleLink.output()
    print(doubleLink.removeAtHead().data)
    print(doubleLink.removeAtTail().data)
    doubleLink.output()
    doubleLink.addAtTail(10)
    doubleLink.addAtTail(11)
    doubleLink.addAtTail(12)
    doubleLink.output()

运行结果：

0 1 2 3 4 5 6 7 8 9 
0
9
1 2 3 4 5 6 7 8 
1 2 3 4 5 6 7 8 10 11 12

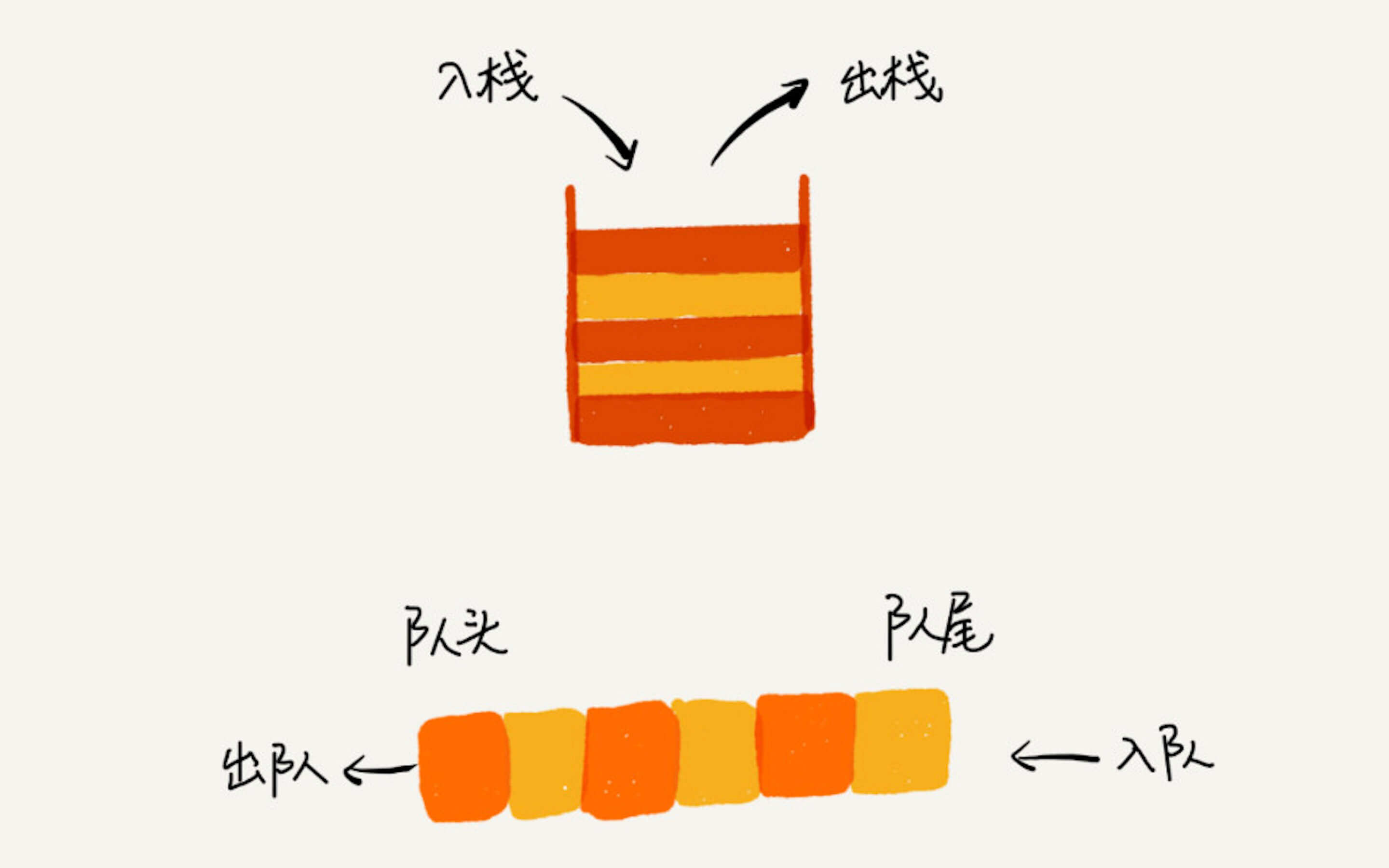
栈和队列

关于栈和队列的特点，我想大家都很清楚了。
栈：先进后出
队列：先进先出

我们把刚刚讨论的双向链表的在头部添加和在头部删除两个组合起来，是不是先进后出？栈。
其中在头部添加对应入栈push()，在头部删除对应出栈pop()。
这种通过链表实现的栈被称为链式栈。

把在头部添加和在尾部删除两个组合起来，是不是先进先出？队列。
其中在头部添加对应入队enqueue()，在尾部删除对应出队dequeue()。
通过链表实现的队列是链式队列。

在《Redis应用实践与原理解析：1.基础》，会看到类似的思路。Redis提供了双向链表，然后我们在基础上，实现了栈和队列的效果。

除了通过链表实现，我们还可以通过数组实现。
通过数组实现的栈被称为顺序栈。
通过数组实现的队列被称为顺序队列。

接下来我们通过数组再实现一遍。

基于数组的栈

我们每次入栈，都插入在数组的尾部。每次出栈，都从数组的尾部取值。这样最方便，入栈和出栈都不用移动数组中的元素。时间复杂度是$O(1)$。

• Java
• Python

示例代码：

package ch03;

/**
 * 顺序栈
 */
public class ArrayStack {

    // 用来存储容器中的元素
    private int[] array;
    // 容器中元素的个数
    private int size;

    /**
     * 构造方法
     * @param capacity 初始化大小
     */
    public ArrayStack(int capacity) {
        this.array = new int[capacity];
        size = 0;
    }

    /**
     * 数组扩容
     */
    public void resize(){
        // 扩大到原来大小的两倍
        int[] arrayNew = new int[array.length*2];
        //从旧数组拷贝到新数组
        System.arraycopy(array, 0, arrayNew, 0, array.length);
        array = arrayNew;
    }

    /**
     * 入栈
     * @param data
     */
    public void push(int data){
        //如果实际元素达到数组容量上线，数组扩容
        if(size >= array.length){
            resize();
        }
        array[size] = data;
        size++;
    }

    /**
     * 出栈
     */
    public Integer pop(){
        if (size <= 0){
            return null;
        }
        int index = size - 1;
        int rnt = array[index];
        size--;
        return rnt;
    }

    /**
     * 输出数组
     */
    public void output(){
        String rnt = "";
        for (int i = 0; i < size; i++) {
            rnt = rnt + array[i] + " ";
        }
        System.out.println(rnt);
    }

    public static void main(String[] args) {
        ArrayStack arrayStack = new ArrayStack(3);
        System.out.println(arrayStack.pop());
        arrayStack.push(1);
        arrayStack.push(2);
        arrayStack.push(3);
        arrayStack.output();
        arrayStack.push(4);
        arrayStack.push(5);
        arrayStack.push(6);
        arrayStack.output();
        System.out.println(arrayStack.pop());
        System.out.println(arrayStack.pop());
        System.out.println(arrayStack.pop());
        arrayStack.output();
        System.out.println(arrayStack.pop());
        System.out.println(arrayStack.pop());
        System.out.println(arrayStack.pop());
        System.out.println(arrayStack.pop());
    }

}

运行结果：

null
1 2 3 
1 2 3 4 5 6 
6
5
4
1 2 3 
3
2
1
null

示例代码：

class ArrayStack:
    def __init__(self, capacity):
        """

        :param capacity: 长度
        """
        self.array = [None] * capacity
        self.size = 0

    def resize(self):
        """
        数组扩容
        :return:
        """
        array_new = [None] * len(self.array) * 2
        # 从旧数组拷贝到新数组
        for i in range(self.size):
            array_new[i] = self.array[i]
        self.array = array_new

    def push(self, data):
        """
        在尾部放入新元素
        :param data:
        :return:
        """
        # 如果实际元素达到数组容量上线，数组扩容
        if self.size >= len(self.array):
            self.resize()
        # 在尾部放入新元素
        self.array[self.size] = data
        self.size = self.size + 1

    def pop(self):
        if self.size <= 0:
            return None
        index = self.size - 1
        self.size = self.size - 1
        return self.array[index]

    def output(self):
        """
        输出数组
        :return:
        """
        print(self.array[:self.size])


if __name__ == '__main__':
    arrayStack = ArrayStack(3)
    print(arrayStack.pop())
    arrayStack.push(1)
    arrayStack.push(2)
    arrayStack.push(3)
    arrayStack.output()
    arrayStack.push(4)
    arrayStack.push(5)
    arrayStack.push(6)
    arrayStack.output()
    print(arrayStack.pop())
    print(arrayStack.pop())
    print(arrayStack.pop())
    arrayStack.output()
    print(arrayStack.pop())
    print(arrayStack.pop())
    print(arrayStack.pop())
    print(arrayStack.pop())

运行结果：

None
[1, 2, 3]
[1, 2, 3, 4, 5, 6]
6
5
4
[1, 2, 3]
3
2
1
None

基于数组的队列

对于基于数组的队列，如果我们入队插入在数组尾部，出队从数组头部出队，这样每次出队的时间复杂度是$O(n)$，如果出队从尾部出队，入队从头部入队，每次入队的时间复杂度是$O(n)$。
有没有办法让入队和出队的时间复杂度都是$O(1)$呢？

$$\begin{aligned} & \text{扇子别动，脑袋动。} \\ & \text{数组别动，指针动。} \end{aligned}$$

数组别动，指针动。

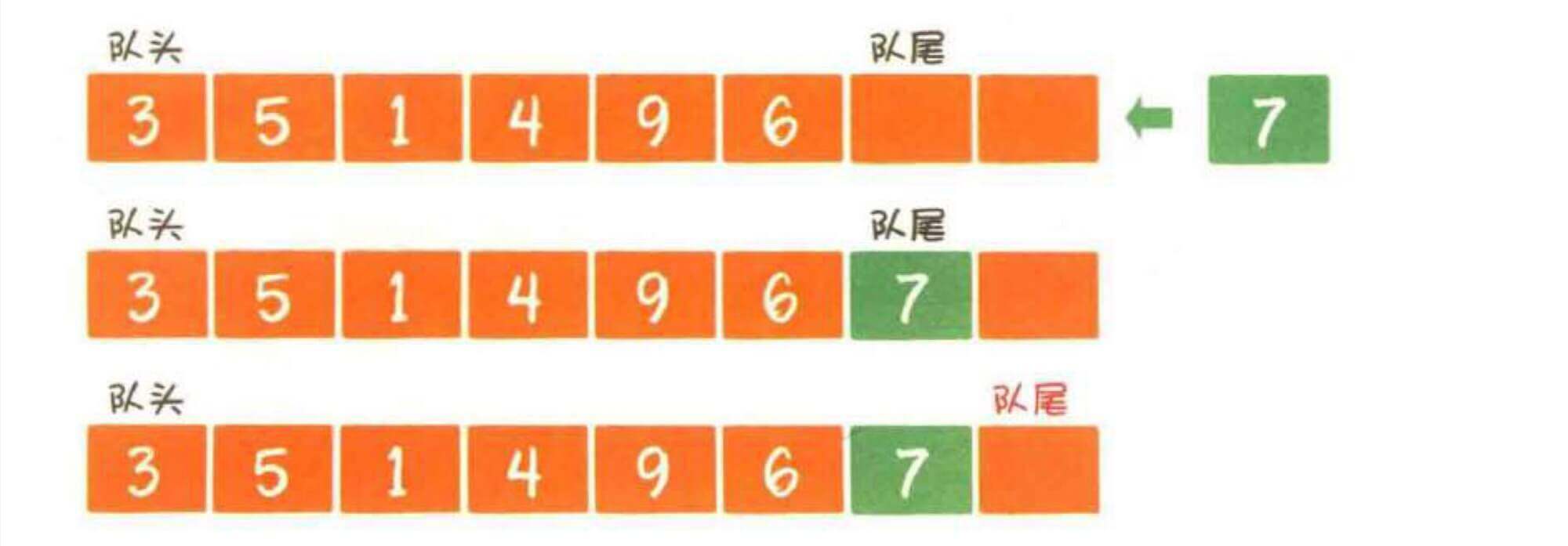
我们在一个数组上定义两个指针，一个是队头，一个是队尾。

所有的入队，都是从队尾入队，队尾指针往后移动。

所有的出队，都是从对头出队，队头指针往后移动。

这样做，入队和出队，时间复杂度都是$O(1)$了。
但是，这样，队列的空间会越来越小。

如图，此时队列的空间是2，已经无法再塞进任何元素了。

那怎么办呢？

循环数组

我们队头指针与队尾指针在移动到数组最后之后，再回到数组的头部。

那？什么时候说明队列满了呢？

$$\begin{aligned} & \text{直到} \\ & \text{(队尾下标 + 1) 除以 数组长度 的余数} = \text{队头下标} \\ & \text{队列真的满了} \end{aligned}$$

用计算机语言描述

• Java
• Python

示例代码：

package ch03;

public class ArrayQueue {

    // 数组
    private int[] array;
    // 队头
    private int head;
    // 队尾
    private int tail;

    public ArrayQueue(int capacity) {
        this.array = new int[capacity];
    }


    /**
     * 出队
     * @return 出队的元素
     * @throws Exception 队列是空的
     */
    public int deQueue() throws Exception {
        if (tail == head){
            throw new Exception("队列是空的");
        }
        // 即将出队的元素
        int data = array[head];
        // head指针后移
        head = (head + 1) % array.length;
        return data;
    }

    /**
     * 入队
     * @param data 入队的元素
     * @throws Exception 队列是满的
     */
    public void enQueue(int data) throws Exception {
        if ((tail + 1) % array.length == head){
            throw new Exception("队列是满的");
        }
        array[tail] = data;
        tail =(tail+1)%array.length;
    }


    /**
     * 输出队列
     */
    public void output(){
        String rnt = "";
        for(int i=head; i!=tail; i=(i+1)%array.length){
            rnt = rnt + array[i] + " ";
        }
        System.out.println(rnt);
    }

    public static void main(String[] args) throws Exception {
        ArrayQueue arrayQueue = new ArrayQueue(6);
        arrayQueue.enQueue(1);
        arrayQueue.enQueue(2);
        arrayQueue.enQueue(3);
        arrayQueue.enQueue(4);
        arrayQueue.enQueue(5);
        arrayQueue.deQueue();
        arrayQueue.deQueue();
        arrayQueue.deQueue();
        arrayQueue.enQueue(6);
        arrayQueue.enQueue(7);
        arrayQueue.enQueue(8);
        arrayQueue.output();
    }

}

运行结果：

4 5 6 7 8

示例代码：

class ArrayQueue:
    array = []
    head = 0
    tail = 0

    def __init__(self, capacity):
        self.array = [None] * capacity
        self.head = 0
        self.tail = 0

    def deQueue(self):
        """
        出队
        :return: 出队的元素
        """
        if self.tail == self.head:
            raise Exception('队列是空的')
        data = self.array[self.head]
        self.head = (self.head + 1) % len(self.array)
        return data

    def enQueue(self, data):
        """
        入队
        :param data: 进入队伍的元素
        :return:
        """
        if (self.tail + 1) % len(self.array) == self.head:
            raise Exception('队列是满的')
        self.array[self.tail] = data
        self.tail = (self.tail + 1) % len(self.array)

    def output(self):
        """
        输出
        :return:
        """
        rnt = ""
        i = self.head
        while i != self.tail:
            rnt = rnt + str(self.array[i]) + " "
            i = (i + 1) % len(self.array)
        print(rnt)


if __name__ == '__main__':
    arrayQueue = ArrayQueue(6)
    arrayQueue.enQueue(1)
    arrayQueue.enQueue(2)
    arrayQueue.enQueue(3)
    arrayQueue.enQueue(4)
    arrayQueue.enQueue(5)
    arrayQueue.deQueue()
    arrayQueue.deQueue()
    arrayQueue.deQueue()
    arrayQueue.enQueue(6)
    arrayQueue.enQueue(7)
    arrayQueue.enQueue(8)
    arrayQueue.output()

运行结果：

4 5 6 7 8

关于栈和队列，有很多的应用。例如：

1. 深度优先遍历和栈有关
2. 广度优先遍历和队列有关
3. 递归，和栈有关。