9.决策树

决策树的思想

下班顺路买一斤包子带回来，如果看到卖西瓜的，就买一个。
这是一个最简单的决策树，其结构如下

if (没看见卖西瓜的) 
   买一斤包子
else
   买一只包子

决策树的思想来源非常朴素。最早的决策树就是利用"if-else"分支结构的一种学习方法。

回到上面那个我们看到卖西瓜的就买一个的故事。这时候，我们已经看到了卖西瓜的，准备买一个。
这是我们挑选西瓜的决策树。

graph LR wenli{纹理=?} gendi{根蒂=?} chugan{触感=?} seze{色泽=?} huaigua-1(坏瓜) huaigua-2(坏瓜) huaigua-3(坏瓜) huaigua-4(坏瓜) haogua-1(好瓜) haogua-2(好瓜) haogua-3(好瓜) haogua-4(好瓜) wenli -- 清晰 --> gendi wenli -- 稍糊 --> chugan wenli -- 模糊 --> huaigua-1(坏瓜) gendi -- 蜷缩 --> haogua-1 gendi -- 稍蜷 --> seze gendi -- 硬挺 --> huaigua-2 chugan -- 硬滑 --> haogua-2 chugan -- 软粘 --> huaigua-3 seze -- 青绿 --> haogua-3 seze -- 乌黑 --> huaigua-4 seze -- 浅白 --> haogua-4

那么

• 整个决策树是怎么来的呢？
• 买西瓜为什么先看纹理？
• 为什纹理模糊的直接认为是坏瓜？

这就涉及到决策树的构建。

决策树的构建

决策树的构建方法和信息论有关。
我们这里介绍和信息论有关的两个知识点

1. 信息熵
2. 信息增益

信息熵

假设，现在有8个西瓜，而且8个西瓜中只有一个是好瓜。而我们对西瓜完全不了解，只能猜。这时候卖西瓜的和我们玩一个游戏，猜一次一块钱。
那么，成本最小的方式是：

graph LR 1-4{在1-4中?} 1-2{在1-2中?} 5-6{在5-6中?} 1{1?} 3{3?} 5{5?} 7{7?} g1(瓜-1) g2(瓜-2) g3(瓜-3) g4(瓜-4) g5(瓜-5) g6(瓜-6) g7(瓜-7) g8(瓜-8) 1-4 -- 是 --> 1-2 1-4 -- 否 --> 5-6 1-2 -- 是 --> 1 1-2 -- 否 --> 3 5-6 -- 是 --> 5 5-6 -- 否 --> 7 1 -- 是 --> g1 1 -- 否 --> g2 3 -- 是 --> g3 3 -- 否 --> g4 5 -- 是 --> g5 5 -- 否 --> g6 7 -- 是 --> g7 7 -- 否 --> g8

按照这个策略，我们只需要猜三次，就可以选中最好的西瓜。即我们只需要猜三次，就可以让不确定变成确定。

那么，我们还会发现。
有8个西瓜，只有1个好瓜，且8个西瓜是好瓜的概率相等的时候

$$\log_2 8 = 3\text{比特}$$

而且

$$-\bigg (\sum_{i=1}^{8} \frac{1}{8} * \log_2 \frac{1}{8} \bigg ) = 3$$

这就是信息熵的公式。
信息熵计作$H$，单位是比特

$$H(X) = \sum_{i\in X} P(i) * \log_2 P(i)$$

信息熵越大，不确定性也越大。

信息增益

信息增益的公式

特征$A$对训练数据集$D$的信息增益，计作$g(D,A)$。
其含义是训练数据集$D$的信息熵$H(D)$与给定A条件下信息熵$H(D|A)$的差。
公式为

$$g(D,A) = H(D) - H(D|A)$$

其中，$H(D|A)$的公式为

$$\begin{aligned} H(D|A) & = \sum_{i=1}^n \frac{D_i}{D} * H(D_i) \\ H(D|A) & = \sum_{i=1}^n \frac{D_i}{D} \sum_{i=1}^K \frac{D_{ik}}{D_i} * \log_2 \frac{D_{ik}}{D_i} \end{aligned}$$

即，信息增益是指在已知特征$X_1$的信息，而使目标$Y$的信息不确定性的减少程度。

信息增益的计算

我们继续以西瓜为例。
假设，存在数据如下：

ID	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
纹理	清晰	清晰	清晰	清晰	清晰	稍糊	稍糊	稍糊	稍糊	稍糊	模糊	模糊	模糊	模糊	模糊
根蒂	蜷缩	稍蜷	稍蜷	蜷缩	蜷缩	蜷缩	稍蜷	稍蜷	硬挺	硬挺	硬挺	稍蜷	稍蜷	硬挺	蜷缩
触感	硬滑	硬滑	硬滑	软粘	硬滑	硬滑	硬滑	软粘	软粘	软粘	软粘	软粘	硬滑	硬滑	硬滑
色泽	青绿	乌黑	青绿	青绿	乌黑	乌黑	浅白	浅白	乌黑	浅白	乌黑	浅白	乌黑	浅白	青绿
好坏	坏	坏	好	好	坏	坏	坏	好	好	好	好	好	好	好	坏

则有
信息熵

$$\begin{aligned} H(D) & = -\bigg (\frac{\text{好}}{\text{好 + 坏}} * \log_2 \frac{\text{好}}{\text{好 + 坏}} + \frac{\text{坏}}{\text{好 + 坏}} * \log_2 \frac{\text{坏}}{\text{好 + 坏}} \bigg ) \\ & = -\bigg (\frac{9}{9 + 6} * \log_2 \frac{9}{9 + 6} + \frac{6}{9+6} * \log_2 \frac{6}{9+6} \bigg ) \\ & \approx 0.97095 \end{aligned}$$

信息增益

我们以纹理为例

$$\begin{aligned} g(D,\text{纹理}) & = H(D) - H(D'|\text{纹理}) \\ & = H(D) - \frac{\text{清晰}}{\text{清晰 + 稍糊 + 模糊}} * H(\text{清晰}) + \frac{\text{稍糊}}{\text{清晰 + 稍糊 + 模糊}} * H(\text{稍糊}) + \frac{\text{模糊}}{\text{清晰 + 稍糊 + 模糊}} * H(\text{模糊}) \\ & = 0.97095 - \frac{5}{5 + 5 + 5} * H(\text{清晰}) + \frac{5}{5 + 5 + 5} * H(\text{稍糊}) + \frac{5}{5 + 5 + 5} * H(\text{模糊}) \end{aligned}$$

当纹理为清晰的时候，有

ID	1	2	3	4	5
纹理	清晰	清晰	清晰	清晰	清晰
根蒂	蜷缩	稍蜷	稍蜷	蜷缩	蜷缩
触感	硬滑	硬滑	硬滑	软粘	硬滑
色泽	青绿	乌黑	青绿	青绿	乌黑
好坏	坏	坏	好	好	坏

即

$$\begin{aligned} H(\text{清晰}) & = -\bigg (\frac{\text{好}}{\text{好 + 坏}} * \log_2 \frac{\text{好}}{\text{好 + 坏}} + \frac{\text{坏}}{\text{好 + 坏}} * \log_2 \frac{\text{坏}}{\text{好 + 坏}} \bigg ) \\ & = -\bigg (\frac{2}{2 + 3} * \log_2 \frac{2}{2 + 3} + \frac{3}{2 + 3} * \log_2 \frac{3}{2 + 3} \bigg ) \\ & = 0.97095 \end{aligned}$$

$H(\text{稍糊})$ 和 $H(\text{模糊})$ 的计算过程略。

$$\begin{aligned} H(\text{稍糊}) & = 0.97095 \\ H(\text{模糊}) & = 0.72193 \end{aligned}$$

即

$$\begin{aligned} g(D,\text{纹理}) & = 0.97095 - \frac{5}{5 + 5 + 5} * H(\text{清晰}) + \frac{5}{5 + 5 + 5} * H(\text{稍糊}) + \frac{5}{5 + 5 + 5} * H(\text{模糊}) \\ & = 0.97095 - \frac{5}{5 + 5 + 5} * 0.97095 + \frac{5}{5 + 5 + 5} * 0.97095 + \frac{5}{5 + 5 + 5} * 0.72193) \\ & \approx 0.08301 \end{aligned}$$

通过这个计算过程，我们可以找出信息增益最大的一个特征。
把信息增益最大的特征，作为第一个判断标准。

根据这个规则，即可构建决策树

常见决策数算法

除了

• ID3：信息增益，最大准则

决策树的构建方法还有

• C4.5：信息增益率，最大准则
• CART：
  • 回归树：平方误差，最小准则
  • 分类树：基尼系数，最小准则

在《集成学习概览及其Python实现：1.决策树》，我们对这三种决策树，以及决策树构建方法的更多内容，都有更详细的讨论。

决策树的实现

我们以泰坦尼克号旅客的生存状况预测这个场景为例。

数据
http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic.txt

from sklearn.tree import DecisionTreeClassifier

参数：

• criterion：默认是基尼系数，也可以用信息增益entropy
• max_depth：树的深度
• random_state：随机数的种子

方法：

• decision_path：决策树的路径

示例代码：

from sklearn.tree import DecisionTreeClassifier
from sklearn.feature_extraction import DictVectorizer
from sklearn.model_selection import train_test_split
import pandas as pd

# 获取数据
titan = pd.read_csv('http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic.txt')

# 处理数据
x = titan[['pclass','age','sex',]]

# 缺失值处理
x['age'].fillna(x['age'].mean(),inplace=True)

y = titan['survived']

# 分割数据到训练集
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.25)

# 特征工程
# 类别用 One-Hot编码
dict = DictVectorizer(sparse=False)
# to_dict
x_train = dict.fit_transform(x_train.to_dict(orient='records'))
print(dict.get_feature_names())
x_test = dict.transform(x_test.to_dict(orient='records'))

print(x_train)
print(x_test)

dec = DecisionTreeClassifier()
dec.fit(x_train,y_train)
print(dec.score(x_test,y_test))

运行结果：

['age', 'pclass=1st', 'pclass=2nd', 'pclass=3rd', 'sex=female', 'sex=male']
[[31.19418104  0.          0.          1.          1.          0.        ]
 [34.          0.          1.          0.          0.          1.        ]
 [31.19418104  0.          0.          1.          1.          0.        ]
 ...
 [31.19418104  0.          0.          1.          0.          1.        ]
 [31.19418104  1.          0.          0.          1.          0.        ]
 [25.          0.          1.          0.          1.          0.        ]]
[[31.19418104  0.          0.          1.          0.          1.        ]
 [31.19418104  0.          1.          0.          0.          1.        ]
 [23.          0.          0.          1.          0.          1.        ]
 ...
 [31.19418104  1.          0.          0.          0.          1.        ]
 [50.          1.          0.          0.          1.          0.        ]
 [46.          1.          0.          0.          0.          1.        ]]
0.7993920972644377

决策树的可视化

决策树信息的获取

决策树的一个主要优点就是过程的可视化。

from sklearn.tree import export_graphviz

示例代码

from sklearn.tree import export_graphviz
# 格式必须dot
export_graphviz(dec,out_file='tree.dot',feature_names=dict.get_feature_names())
print('FINISH')

决策树信息的可视化查看

通过上一步，我们获取了dot文件。现在，我们想可视化查看dot文件

在macOS下

1. 下载Homebrew
   在控制台输入命令

   /bin/bash -c "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/master/install.sh)"

2. brew install graphviz
3. VSCODE安装插件Graphviz Preview。
4. 这时候可以查看或者导出文件了。

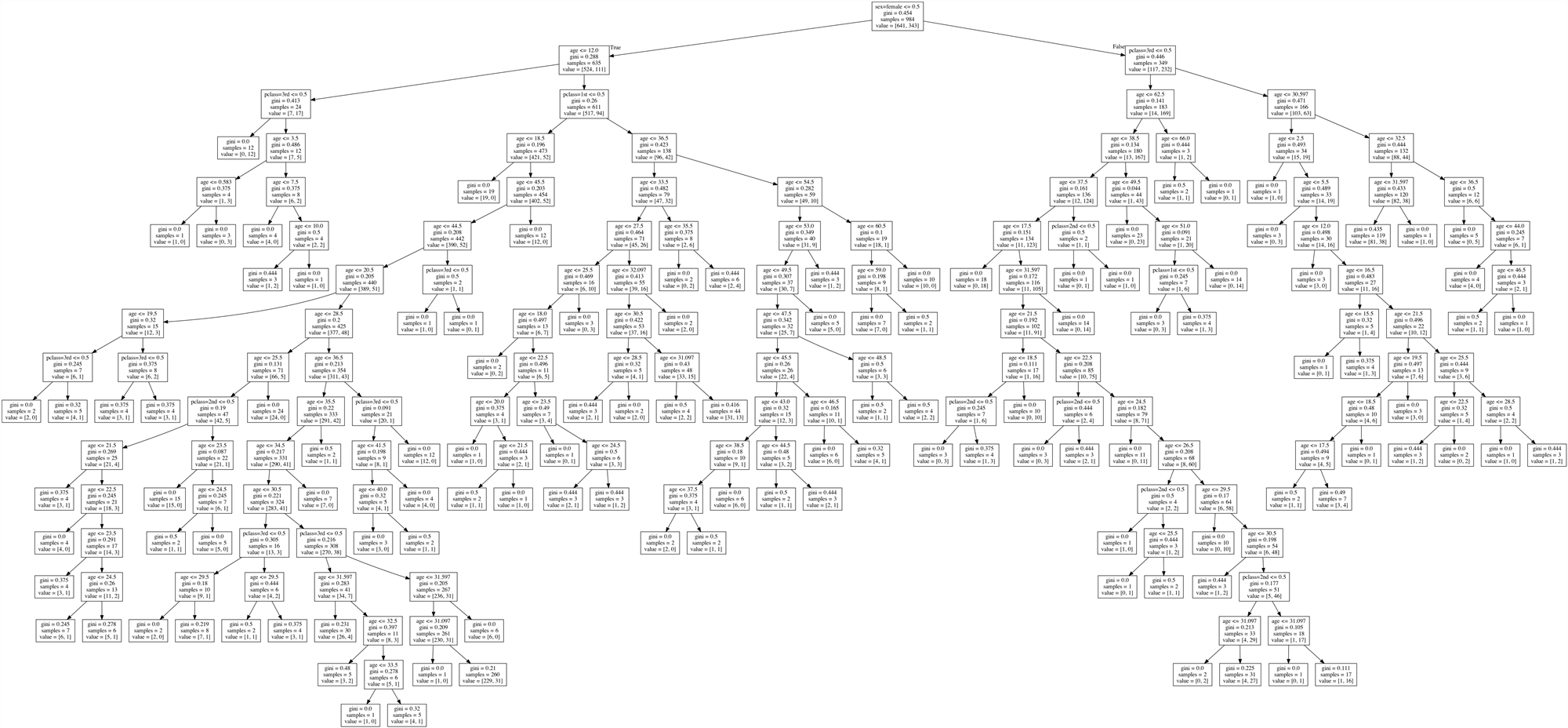
比如，刚刚我们的决策树是这样的。

在Windows系统下

1. 下载并安装Windows版本的
   http://www.graphviz.org/
2. 用所安装的软件打开dot文件

决策树的优缺点

1. 优点

   • 可视化，易于解释
   • 数据无需进行归一化或标准化

2. 缺点

   • 容易过拟合。

决策树的改进

决策树的缺点是容易过拟合。
改进方法有两种

1. 剪枝
2. 随机森林

我们先介绍剪枝。
如上我们所构建的决策树的图片所示，决策树的有些枝只有极少数个样本。

依据两个参数来进行剪枝。

1. min_samples_split
   内部节点再划分所需最小样本数
   这个值限制了子树继续划分的条件，如果某节点的样本数少于min_samples_split，则不会继续再尝试选择最优特征来进行划分。 默认是2。
   如果样本量不大，不需要管这个值。如果样本量数量级非常大，则推荐增大这个值。

2. min_samples_leaf
   叶子节点最少样本数
   这个值限制了叶子节点最少的样本数，如果某叶子节点数目小于样本数，则会和兄弟节点一起被剪枝。 默认是1。
   如果样本量不大，不需要管这个值。如果样本量数量级非常大，则推荐增大这个值。

这两种方法其实都是前剪枝方法，在《集成学习概览及其Python实现：1.决策树》，我们对剪枝方法有更翔实的讨论。