这一系列的笔记，我们讨论集成学习。其实这个话题在《经典机器学习及其Python实现：10.集成学习和随机森林》中，我们已经讨论过了，但是当时的讨论非常非常的浅显。这一系列的笔记，我们会用三章的篇幅较深刻的讨论集成学习。

如果要讨论集成学习的话，就不得不先讨论决策树。

决策树是一种有监督的机器学习方法，模仿的是人类做决策的过程，在早期人工智能模型中有很多应用。但是，现在，决策树更多的作为集成学习的基础。这一章，我们试图把集成学习的基础梳理清楚，有利于我们讨论集成学习。

同样，在《经典机器学习及其Python实现：9.决策树》，我们对决策树进行了一个非常简单的讨论。这次重新讨论。

决策树的决策和构建

决策树的决策方法

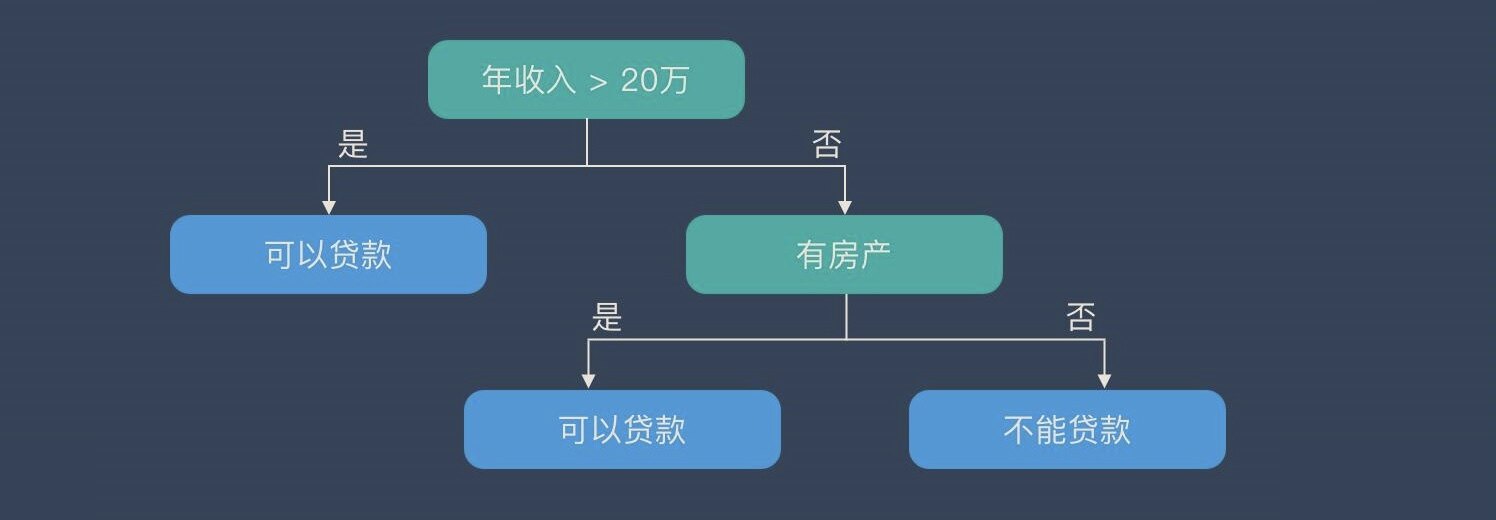
这里有一张动图，非常直观的描绘了决策树的决策方法。来了一条新数据，按照生成好的树的标准，落到某一个节点上，这个节点的标签是哪个类别就属于哪个类别。

决策树的特点有：

可以处理非线性的问题。
可解释性强。
没有所谓的模型的参数 $\theta$ ，与之不同的是神经网络、线性回归等都有 $\theta$ 。
模型简单"if-else/switch"，模型预测效率高。
这里提一个问题，决策树需要一直做"if-else/switch"，就像"买西瓜"的那个例子，首先要判断纹理是清晰、稍糊还是模糊？是三种纹理的哪一种？那么是不是就要求决策树中样本的特征都必须是离散的？
不是，连续的也可以处理，稍后我们讨论经典决策树算法C4.5和CART的时候，就可以看到对连续值的处理。
不可导。
虽然在《集成学习概览及其Python实现：2.GBDT》和《集成学习概览及其Python实现：3.XGBoost》中，我们讨论的GBDT和XGBoost都是有办法可导的，但是决策树本身是不可导的。

接下来，我们尝试用数学式子来描述决策树。

比如，有这么一颗决策树。

整体描述方式：

$G(x) = \sum_{t=1}^T q_t(x) \cdot g_t(x)$

$T$ 是叶子节点数，也就是路径数。在这里， $T=3$ 。
$q_t(x)$ 是条件函数，其含义是样本 $x$ 是否落在叶子节点 $t$ 上，"是"表示为 $1$ ，"否"表示为 $0$ 。
$g_t(x)$ 是叶子节点的函数，输出是一个常数。在这里输出的就是"可以贷款"和"不能贷款"。

这种描述方式，我们会在《集成学习概览及其Python实现：3.XGBoost》中用到。

递归描述方式：

$G(x) = \sum_{c=1}^C [b(x) = c] \cdot G_c(x)$

$C$ 是每一个节点的分支数
$[b(x)=c]$ 输出是否属于当前分支，"是"表示为 $1$ ，"否"表示为 $0$ 。
$G(x)$ 是父树
$G_c(x)$ 是子树

在这里，从根结点出发的话， $G(x)$ 是整棵树， $C=2$ ，分别代表"年收入大于20万"的"是"和"否"，子树是以"有房产"为根节点的那颗树。

决策树的构建方法

接下来，我们来讨论如何构建决策树，就以我们刚刚的递归描述为例。

函数： $\text{DecisionTree}(data: \mathcal{D} = \{(x_n,y_n)\}_{n=1}^N)$
如果不再划分：
返回 $g_t(x)$ (可以是落在这个节点上的样本的标签的的众数，也可以是平均数)。
否则：
寻找分支方法 $b(x)$
从数据 $\mathcal{D}$ 中分出 $\mathcal{D}_c = \{(x_n,y_n);b(x_n) = c\}$
构建子树 $G_c \leftarrow \text{DecisionTree}(\mathcal{D}_c)$
返回 $G(x) = \sum_{c=1}^C[b(x) = c]G_c(x)$

这个算法就是递归算法，在《算法入门经典(Java与Python描述)：4.递归》中，我们对递归算法有过专门的讨论。

总之，决策时的构建过程就是数据不断分裂的递归过程，每一次分裂，尽可能让类别一样的数据在树的一侧，当树的叶子节点的数据都是一类的时候(或满足了停止分裂条件)，停止分裂。

再看看上面的构建方法，“寻找分支方法 $b(x)$ ”，“如果不再划分”，把话说清楚啊。

$\begin{aligned} & \text{根据什么条件划分？} \\ & \text{什么时候不再划分？} \end{aligned}$

这就是接下来，我们要讨论的内容了。

分裂指标

首先，我们回答第一个问题，根据什么条件划分？
根据分裂指标。
那么什么是分裂指标呢？
常见的分裂指标有：

信息增益
信息增益率
基尼系数
均方误差

接下来。我们分别讨论。

信息增益

如果要讨论分类，又不得不提到信息熵这个概念。这个，其实我们已经讨论过很多次了。
熵这个名词的由来，还有一个故事，在Peter Harrington写的《机器学习实战》中有记录。

信息熵是用来衡量信息不确定性的指标。

$H(X) = - \sum_{i=1}^{N} p_i * \log_2 p_i$

题外话

与之相关的概念，还有一个是交叉熵，常用作分类问题的损失函数。
交叉熵的公式：

$H(\bold{p}||\bold{q}) = - \sum_{i=1}^{N} p_i \log_2 q_i$

从交叉熵出发，我们还可以讨论KL散度，讨论不对称性，讨论在One-Hot中的特别情况。但，在这里，我们不做展开，具体可以参考《深度学习初步及其Python实现：2.神经网络基础》。

我们以一款很经典的游戏《热血足球》为例，来讨论信息熵。

下面的表格，是风雨球场中的风和雨对进球的影响。
(我们假设玩家的水平等变量都是一致的，即除了风雨，其他变量都是一致的。在"控制变量法"的前提下，风雨是影响进球与否的唯一因素。这样我们的讨论才更有意义。)

序号	1	2	3	4	5	6	7	8	9	10	11	12	13	14
风	没风	有风	没风	没风	没风	有风	有风	没风	没风	没风	有风	有风	没风	有风
雨	雨天	雨天	晴天	晴天	晴天	晴天	晴天	雨天	雨天	晴天	雨天	晴天	晴天	晴天
球	没进	没进	进了	进了	进了	没进	进了	没进	进了	进了	进了	进了	进了	没进

我们一共有14个样本，其中9个样本进了，5个样本没进。所以信息熵为：

$-\Big(\frac{9}{14} \log_2 \frac{9}{14}\Big) - \Big(\frac{5}{14} \log_2 \frac{5}{14}\Big) = 0.9402$

如果，我们根据有风和没风进行划分的话，则有：

风	进了	没进	合计	进了的概率
没风	6	2	8	0.75
有风	3	3	6	0.50

$\begin{aligned} \text{没风：} - \Big(\frac{6}{8} \log_2 \frac{6}{8}\Big) - \Big(\frac{2}{8} \log_2 \frac{2}{8}\Big) &= 0.3113 \\ \text{有风：} - \Big(\frac{3}{6} \log_2 \frac{3}{6}\Big) - \Big(\frac{3}{6} \log_2 \frac{3}{6}\Big) &= 1.0 \end{aligned}$

再乘以比例并相加，这就是分裂后的信息熵，这个也被称为条件熵：

$\frac{8}{14} * 0.3113 + \frac{6}{14} * 1.0 = 0.6065$

分裂前的信息熵减去分裂后的信息熵，就是信息增益，代表给定一个条件下，信息不确定性减少的程度。

$0.9402 - 0.6065 = 0.3337$

那么，我们怎么根据信息增益去划分呢？
把信息增益最大的特征，作为判断标准。

信息增益有一个缺点，会导致决策树倾向于选择特征数量多的特征，即倾向于多分叉。
因为，当特征的取值较多时，根据此特征划分更容易得到熵更小的子集，又因为划分前的熵是固定的；所以，信息增益更大。因此信息增益会导致决策树倾向于选择特征数量多的特征，即倾向于多分叉。

信息增益率

为了克服信息增益的缺点，我们引入一个新的概念，信息增益率。

$\text{信息增益率} = \frac{\text{信息增益}}{\text{类别特征本身的熵}}$

需要注意的概念是类别特征本身的熵。
继续以《热血足球》为例，风这个特征把数据分成了两份， $8$ 份没风， $6$ 份有风。那么，风这个类别特征本身的熵是

$-\bigg(\frac{8}{14} \log_2 \frac{8}{14} + \frac{6}{14} \log_2 \frac{6}{14} \bigg) = 0.9852$

信息增益率是

$\frac{0.3337}{0.9852} = 0.3387$

即在信息增益的基础上乘上一个惩罚因子，特征个数越多，惩罚因子越小，特征个数越少，惩罚因子越大。
到这里我们或许会又疑虑了，特征少，怎么还惩罚大？因为我们是乘以惩罚因子。
这个惩罚因子也被称为分裂信息(Split information)。
通过这种方法，克服了采用信息增益会导致决策时倾向于多分叉的缺点。

基尼系数

基尼系数，也被成为基尼指数。这个在经济学中经常见到，是衡量一个国家或地区居民收入差距的常用指标。
基尼系数最大为 $1$ ，最小为 $0$ ，基尼系数越小，表明收入分配越平等。

基尼系数的计算公式：

$\text{Gini}(p) = \sum_{k=1}^{K}p_k(1-p_k) = 1 - \sum_{k=1}^{K} p_k^2$

$p_k$ 为样本点属于第 $k$ 个的概率。

特别的如果是两个类别的话，则有：

$\begin{aligned} \text{Gini}(p) & = p(1-p) + (1-p)p \\ & = 2p(1-p) \end{aligned}$

在经典决策树算法CART中，我们会大量用到这个两个类别的计算。

继续以《热血足球》为例。

我们一共有14个样本，其中9个样本进了，5个样本没进。所以

$\text{Gini} = 1 - \sum_{k=1}^{K} p_k^2 = 1 - \Big(\frac{9}{14}\Big)^2 - \Big(\frac{5}{14}\Big)^2 = 0.459$

如果按照某个维度对数据集进行划分后，可以计算多个节点的基尼系数：

$\text{Gini} = \frac{|D_1|}{|D|} \text{Gini}(D_1) + \frac{|D_2|}{|D|} \text{Gini}(D_2)$

$|D|$ 、 $|D_1|$ 、 $|D_2|$ 代表数据集的样本数

比如，按照风这个维度划分。

风	进了	没进	合计	进了的概率
没风	6	2	8	0.75
有风	3	3	6	0.50

$\begin{aligned} \text{Gini} & = \frac{8}{14}\text{Gini}(6,2) + \frac{6}{14}\text{Gini}(3,3) \\ & = \frac{8}{14} * \Big(1 - \Big(\frac{6}{8}\Big)^2 - \Big(\frac{2}{8}\Big)^2 \Big) + \frac{6}{14} * \Big(1 - \Big(\frac{3}{6}\Big)^2 - \Big(\frac{3}{6}\Big)^2 \Big) \\ & = 0.4386 \end{aligned}$

那么，风的基尼增益是多少呢？

$0.459 - 0.4286 = 0.0304$

不过，需要注意的是，在CART中，其实我们用的是特征的基尼系数，而不是基尼增益。
即，更多的时候，我们采用这种

$\text{Gini} = \frac{|D_1|}{|D|} \text{Gini}(D_1) + \frac{|D_2|}{|D|} \text{Gini}(D_2)$

基尼系数和信息熵的关系

在上文，我们讨论了基尼系数和信息熵。现在，我们来讨论一下两者之间的关系。但，在这之前，我们要先复习一下一个常见的幂级数展开式。

$\begin{aligned} \ln(1+x) & = \sum_{n=1}^{\infty} (-1)^{n-1} \frac{x^n}{n} \\ & = x - \frac{x^2}{x} + \frac{x^3}{3} - \frac{x^4}{4} + \cdots + (-1)^{n-1} \frac{x^n}{n} + \cdots \end{aligned}$

注意： $-1 < x \leq 1$

所以呢，我们也有：

$\begin{aligned} \ln(x) & = \sum_{n=1}^{\infty} (-1)^{n-1} \frac{(x-1)^n}{n} \\ & \approx (x-1) \end{aligned}$

注意： $0 < x \leq 2$

再来看看我们熵的计算公式
在上文是

$H(X) = - \sum_{i=1}^{n} p_i * \log_2 p_i$

我们把底数改成自然对数 $e$ ，即写作

$H(X) = - \sum_{i=1}^{n} p_i * \ln p_i$

其中， $p_i$ 是我们用频率来表示的概率，但是毫无疑问， $p_i \in (0,2]$ 。所以

$\ln p_i \approx p_i - 1$

所以，我们有

$\begin{aligned} H(X) & = - \sum_{i=1}^{n} p_i * \ln p_i \\ & = \sum_{i=1}^{n} p_i (- \ln p_i) \\ & \approx \sum_{i=1}^{n} p_i (1 - p_i) \end{aligned}$

再看看基尼系数的公式

$\text{Gini}(p) = \sum_{k=1}^{K}p_k(1-p_k)$

所以，基尼系数是以自然对数 $e$ 为底的信息熵的一阶泰勒展开。

均方误差

均方误差的公式：

$\text{MSE}(\hat{y},y) = \frac{1}{n}\sum_{i=1}^{n}(\hat{y}_i - y_i)^2$

关于均方误差误差的划分标准，我们放在讨论经典决策树算法CART的回归树的时候再讨论。因为只有在那时候才用的上。

剪枝

接下来，我们讨论第二个问题，什么时候停止？

第一种方法，直到每一个叶子节点的样本的标签都是一样的时候，才停止。这个当然没问题，完全可以做到，但是容易过拟合。

既然提到了过拟合，我们就会想到，我们曾经用一章的内容，专门讨论这个话题，《深度学习初步及其Python实现：5.过拟合》。
过拟合是一个模型在训练数据上能获得比较好的拟合，但是在训练数据外的数据集上却不能很好地拟合数据。过拟合是因为模型过于复杂。
解决方法是让模型不那么复杂。
那么，有哪些方法可以处理过拟合呢？
当时的方法有学习率衰减，可惜这个不可以，决策树中就没有学习率。
当时的方法还有动量，这个也不可以，动量是在梯度上做文章，决策树中没有梯度。
当时的方法还有Dropout，这个当然也不可以，Dropout是随机断开神经网络的连接，决策树中就没有所谓的神经连接。
提前停止可以吗？这个可以。

前剪枝

提前停止，就是前剪枝方法。
我们可以设置树的最大深度，每个叶子节上的最小样本数，每个分支上的最小样本数等等各种方法。这些在sklearn中都有专门的参数，直接配置即可。

至此，我们其实已经回答了什么时候停止。第一种是直到每一个叶子节点的样本的标签都是一样的时候，第二种是满足前剪枝的条件。

但，既然提到了前剪枝，就不得不提一下后剪枝。

后剪枝

与前剪枝不同的是，前剪枝是在决策树构建过程中，提前停止。后剪枝是在决策树构建好后，开始裁剪。

实际上，在决策树和集成学习中，我们说的剪枝一般都是指后剪枝。

常见的三种后剪枝方法：

降低错误剪枝(REP)
悲观错误剪枝(PEP)
代价复杂度剪枝(CCP)

除了这三种，还有最小误差剪枝(MEP)、基于错误剪枝(EBP)。
我们主要讨论前三种。

降低错误剪枝(REP)

在该方法中，可用的数据被分成两个样例集合：一个训练集用来构建学习到的决策树，一个分离的验证集用来评估修剪这个决策树的影响。如果剪枝有利于降低错误率(包括错误率不变)，则认为该子树是可以修剪的。

悲观错误剪枝(PEP)

悲观剪枝认为如果决策树的精度在剪枝前后没有影响的话，则进行剪枝。与降低错误剪枝不同的是，只需要训练集，不用验证集。

步骤如下：

1、计算剪枝前目标子树每个叶子节点的误差，并进行连续修正：

$\text{Error}(Leaf_i) = \frac{\text{error}(\text{Leaf}_i) + 0.5}{N(T)}$

$\text{error}(\text{Leaf}_i)$ 是第 $i$ 个叶子上，犯错的样本个数。
$N(T)$ ，目标子树的总样本个数。
$+0.5$ 是为了修正。

2、计算剪枝前目标子数的修正误差：

$\text{Error}(T) = \sum_{i=1}^L \text{Error}(\text{Leaf}_i) = \frac{\sum_{i=1}^L \text{error}(\text{Leaf}_i)+0.5*L}{N(T)}$

$L$ 是叶子节点的个数。

3、计算剪枝前目标子树误判个数的期望值：

$E(T) = N(T) * \text{Error}(T) = \sum_{i=1}^T \text{error}(\text{Leaf}_i) + 0.5 * L$

4、计算剪枝前目标子树误判个数的标准差：

$\text{std}(T) = \sqrt{N(T) * \text{Error}(T) * (1 - \text{Error}(T))}$

5、计算剪枝前误判上限(即悲观误差)：

$E(T) + \text{std}(T)$

6、剪枝后，原来的目标子树成为了一个叶子节点。计算剪枝后该节点的修正误差：

$\text{Error}(\text{Leaf}) = \frac{\text{error}(\text{Leaf}) + 0.5}{N(T)}$

7、计算剪枝后该节点误判个数的期望值：

$E(\text{Leaf}) = \text{error}(\text{Leaf}) + 0.5$

8、比较剪枝前后的误判个数，如果满足以下不等式，则剪枝；否则，不剪枝：

$E(\text{Leaf}) < E(T) + \text{std}(T)$

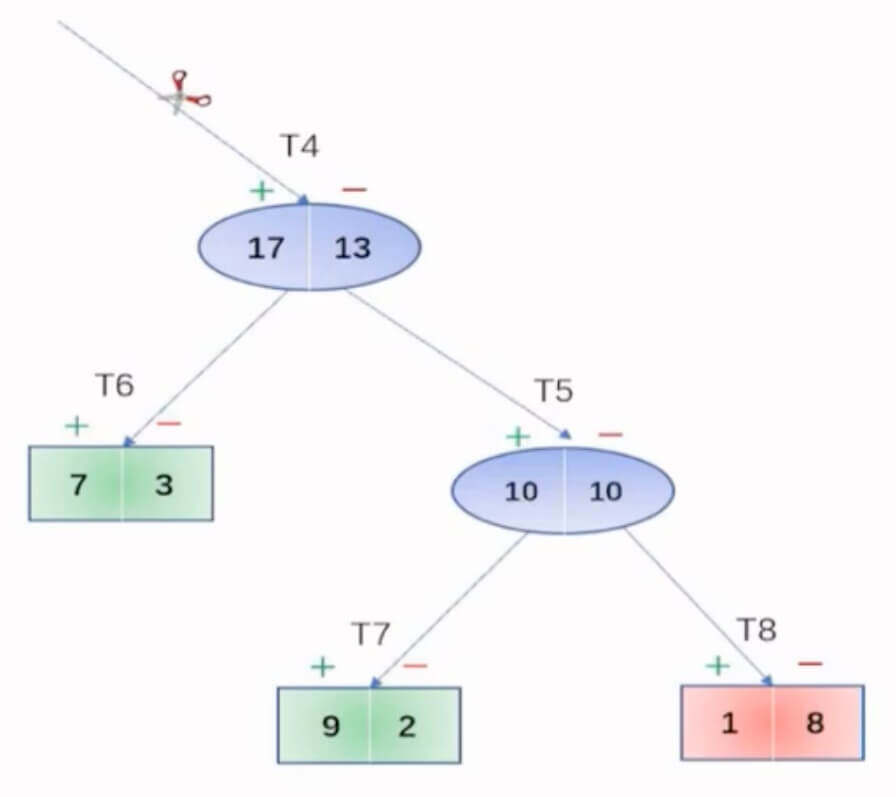
举个例子。

T4、T5、T6、T7、T8，代表节点。
+、-，代表正类和负类。

先计算剪枝前。
T6有 $7$ 个正类， $3$ 个负类，所有T6是正类。同理，T7代表正类，T8代表负类。
T6上误判个数是3、T7上误判个数是2，T8上误判个数是1。
即
剪枝前目标子数的修正误差：

$\text{Error}(T) = \frac{3 + 2 + 1 + 0.5*3}{30} = \frac{7.5}{30}$

剪枝前目标子树误判个数的期望值：

$E(T) = 30 * \frac{7.5}{30} = 7.5$

剪枝前目标子树误判个数的标准差：

$\text{std}(T) = \sqrt{30 * \frac{7.5}{30} * \bigg(1 - \frac{7.5}{30}\bigg)} \approx 2.37$

所以，剪枝前误判上限(即悲观误差)：

$E(T) + \text{std}(T) = 9.87$

在计算剪枝后，T4属于正类，13个误判。

剪枝后该节点的修正误差：

$\text{Error}(\text{Leaf}) = \frac{13 + 0.5}{30} = \frac{13.5}{30}$

剪枝后该节点误判个数的期望值：

$E(\text{Leaf}) = 30 * \frac{13.5}{30} = 13.5$

再进行比较。

$13.5 > 9.87$

即

$E(\text{Leaf}) > E(T) + \text{std}(T)$

即，剪枝条件不满足。
综上所述，不剪枝。

代价复杂度剪枝(CCP)

代价复杂度剪枝(CCP)，第一个C是Cost，代价；第二个C是Complexity，复杂度。
是根据剪枝前后的损失函数来决定是否剪枝。

损失函数：

$C_\alpha (T) = C(T) + \alpha |T|$

$T$ ：决策树
$C_\alpha(T)$ ：损失函数
$C(T)$ ：预测误差
$|T|$ ：叶子节点的个数，反映树的复杂度
$\alpha$ ：惩罚参数

预测误差有多种形式，比如：经验熵、基尼系数。
基尼系数，我们在上文已经讨论过了，这里讨论一下经验熵。

$C(T) = \sum_{t=1}^{|T|} N_t H_t(T) = - \sum_{t=1}^{|T|} \sum_{k=1}^K N_{tk} \log \frac{N_{tk}}{N_t}$

$t$ ：叶子节点，共有 $|T|$ 个叶子节点
这个式子的含义其实是经验熵的加权，权重是 $\frac{N_t}{N}$ ， $N_t$ 是叶子节点的样本数， $N$ 是所有的样本，即树上所有叶子节点的样本。因为 $N$ 是常数，所以这里把 $N$ 省略了。

特别的，这个带惩罚项的损失函数，容易让我们想到正则化，其一般形式如下：

$\min_{f \in \mathcal{F}} \frac{1}{N} \sum_{i=1}^N L(y_i,f(x_i)) + \lambda J(f)$

其实就是一种正则化方法。

步骤如下：

1、剪枝前的决策树记做 $T_A$ ，计算每个叶子节点 $t$ 的经验熵：

$H_t = - \sum_{k=1}^K \frac{N_{tk}}{N_t} \log \frac{N_{tk}}{N_t}$

2、剪枝前决策树的损失函数为：

$C_{\alpha}(T_A) = C(T_A) + \alpha|T_A|$

3、剪枝后的决策树记做 $T_B$ ，损失函数为：

$C_{\alpha}(T_B) = C(T_B) + \alpha|T_B|$

4、比较剪枝前后的损失函数，如果满足以下不等式，则剪枝；否则，不剪枝：

$C_{\alpha}(T_B) \leq C_{\alpha}(T_A)$

经典决策树算法

我们讨论三种经典决策树算法：

ID3
C4.5
CART

ID3

ID3(Iterative Dichotomiser 3,迭代二叉树3代)，以信息增益为划分标准。
特别需要注意的是，dichotomiser，这个词的意思不是二叉树，而是变形者，即迭代变形3代，但是却通常把ID3翻译成迭代二叉树3代。
其实这个名字特别容易误导大家，ID3的树结构就不是二叉树。

构建方法也很简单。
输入：训练数据集、特征集、阈值
输出：决策树
终止条件(满足之一则终止)：

条件一：子数据集中的所有类标签完全相同。
条件二：使用完了所有特征仍然不能将数据集划分为唯一类别的分组，用多数表决。
否则，依此执行下述步骤：
第一步：使用分裂准则(信息增益最大)指定分裂特征和分裂点，划分数据集。若划分的数据集信息增益小于某个阈值，停止划分，用多数表决。
第二步：删除已用特征，并递归产生子树。

提一个问题，ID3处理的是分类问题还是回归问题？当然是分类问题，我们看构建过程"多数表决"。
那么，ID3可以处理回归问题吗？不可以，因为ID3的划分标准是信息增益。

C4.5

C4.5和ID3相比，改进的方法有：

划分标准
连续值的处理
缺失值的处理
后剪枝

划分标准

在上文我们讨论的ID3，其划分标准是信息增益，而C4.5的划分标准是信息增益率。在上文我们讨论过，信息增益会导致决策树倾向于多分叉，信息增益率通过引进分裂信息(Split information)惩罚项，以克服信息增益导致决策时倾向于多分叉的缺点。

在具体实践上，还有一种方法。先从候选特征中找出信息增益高于平均水平的属性，再从中选择信息增益率最高的。而不是直接选择信息增益率最高的特征。

连续值的处理

ID3只能处理离散值，但是C4.5可以处理连续值。
具体处理步骤如下：

把需要处理的样本(对应根节点)或样本子集(对应子树)按照连续变量的大小从小到大进行排序。
假设该特征对应的不同的特征值一共有 $N$ 个，那么总共有 $N-1$ 个可能的候选分割阈值点，每个候选的分割阈值点的值为上述排序后的属性值中两两前后连续元素的中点。那么接下来呢？遍历扫描 $N-1$ 个分割点？不，二分法。

不过，即使我们用二分法了，如果连续特征值比较多的话，C4.5的性能还是会下降。

缺失值的处理

ID3不能处理缺失值，但是C4.5可以处理缺失值。
有这么几种情况。

一、选最佳划分特征时，某些样本缺某些特征值，该如何计算各个信息增益率？（构建树选特征）
两个方法：

忽略缺失特征值的样本
将该特征中出现频率最高的特征值赋予缺失该特征值的样本。

二、已选择最佳划分特征，某些样本缺该属性值，该把这些样本划分到哪个类？（继续构建树分类）
两个方法：

忽略缺失特征值的样本
将该特征中出现频率最高的特征值赋予缺失该特征值的样本。

三、决策树已生成，待分类数据缺失某些特征值，如何对这些数据分类？（树已经构建，决策使用过程）
两个方法，一、忽略？
不，是待分类的，这个样本要进入模型了，无论如何，需要一个交代，要给一个分类结果。
两个方法：

缺失特征值的样本在到达该特征时结束分类过程，把这些样本划分为特征A的子树中概率最大的类别。
将该特征中出现频率最高的特征值赋予缺失该特征值的样本，继续分类。

后剪枝

C4.5还有一个特点，有后剪枝方法，具体是悲观错误剪枝(PEP)。

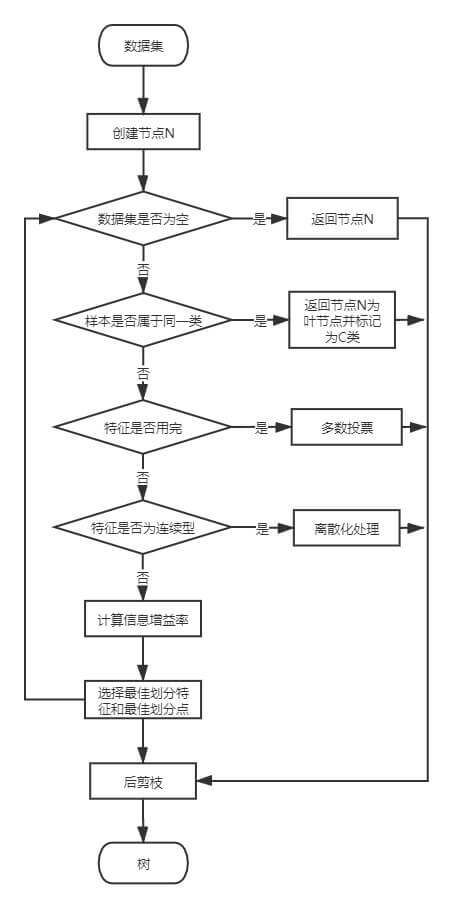
树的构建过程

最后，总结以下树的构建过程。

CART

CART，全称是Classification And Regression Tree，也正如这个名字，Classification And Regression，这个算法解决的是分类和回归问题，那么，怎么解决呢？Tree。

之前我们讨论过，ID3虽然翻译成了迭代二叉树3代，但其实不是二叉树，那个D是dichotomiser，是变形者的意思。但是这里我们的CART是一颗正儿八经的二叉树。

那么，如果就是有三个特征怎么办？比如西瓜的纹理，就是有清晰、稍模糊和模糊三种，怎么办？那就分为清晰和不清晰，然后不清晰再分为模糊和不模糊。

构建

CART的分类树和回归树的构建方法略有不同，主要是分裂指标(划分标准)不一样。我们分开讨论。
先讨论分类树。

分类树

有了上文的基础，我想我们现在讨论CART的决策树的构建就很简单了，只需要提一点，是根据基尼系数来划分。
构建过程如图：

满足三个条件中的一个则进行后剪枝，然后输出树。

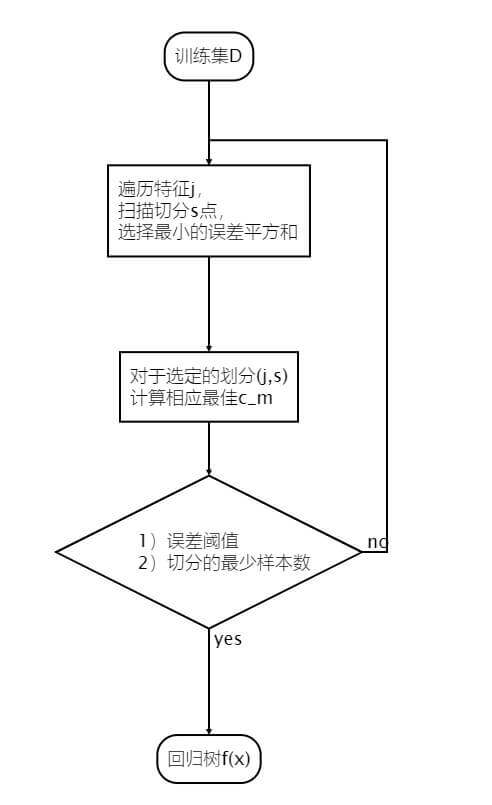
回归树

顾名思义，分类树输出离散值、回归树输出连续值。
预测方式：分类树，采用叶子节点里概率最大的类别作为当前节点的预测类别；回归树，采用叶子的均值。

回归树的划分标准如下：

$\min_{j,s}\bigg[ \min \sum_{x_i \in R_1(j,s)} (y_i - c_1)^2 + \min \sum_{x_i \in R_2(j,s)} (y_i - c_2)^2 \bigg]$

$R_1(j,s)$ 表示在该划分的左区域。
$R_2(j,s)$ 表示在该划分的右区域。
$j,s$ 表示第 $j$ 个变量的划分点 $s$ 。
$c_m = \frac{1}{N_m} \sum_{x_i \in R_m(j,s)} y_i,\quad m=1,2$
左边最小且右边也最小的时候，整体自然最小。

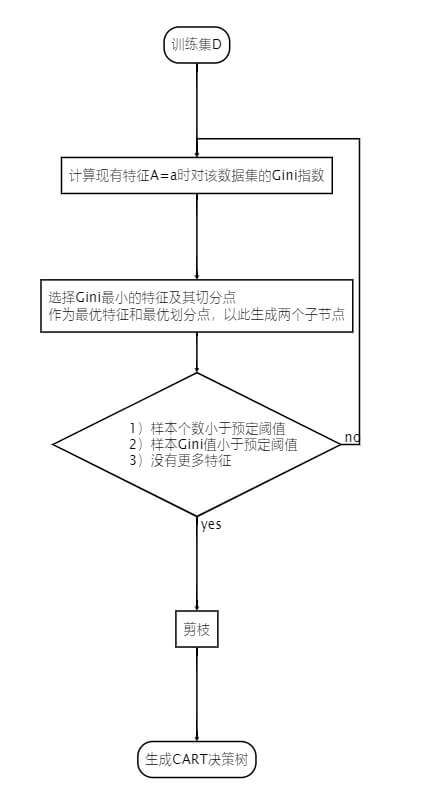
构建方法如图：

后剪枝

CART的后剪枝方法为代价复杂度剪枝(CCP)。

比较

模型	处理的问题	树结构	划分标准	连续值处理	缺失值处理	剪枝
ID3	分类	多叉树	信息增益	不支持	不支持	无
C4.5	分类	多叉树	信息增益率	支持	支持	有
CART	分类、回归	二叉树	基尼系数、均方误差	支持	支持	有

特征选择

最后，还有一个惊喜。

通过上述我们对决策树的讨论，我们不断的根据特征来划分数据，如果某个特征多次被用到？或者某个特征的划分效果特别好？是不是能忽然领悟到了什么？好像决策树可以用来做特征选择？
是的。
在sklearn中，我们可以打印决策树中特征重要性评分。

1	print(tree.feature_importances_)

关于决策树的实现，可以参考《经典机器学习及其Python实现：9.决策树》

文章作者: Kaka Wan Yifan

文章链接: https://kakawanyifan.com/10701