最后一章，我们讨论XGBoost。这是一个特别振奋人心的模型，被誉为神器。
G是gradient，梯度；Boost是提升；X是extremely。XGBoost的含义就是特别好的梯度提升模型。

其实这个名字还有一个特点，上文我们讨论的GBDT，DT是Decision Tree，决策树。在取名字的时候，专门强调了基学习器是决策树，而且根据我们上文的讨论，还是回归树。
但我们这个模型是XGBoost，而不是XGBDT，因为，基学习器不仅可以是决策树，还可以是多种。

目标函数的结构

通过之前的讨论，我们知道在Boosting中，我们的目标函数是

$\text{Obj} = \sum_{i=1}^n L(y_i,\hat{y}_i) + \sum_{m=1}^M \Omega(f_m),\quad f_m \in \mathcal{F}$

$\hat{y}_i = \sum_{m=1}^M \beta_m f_m(x_i),\quad f_m \in \mathcal{F}$
$\sum_{i=1}^n L(y_i,\hat{y}_i)$ 是损失部分
$\sum_{m=1}^M \Omega(f_m)$ 是复杂度惩罚项，即正则部分。
$n$ 是样本数

这个目标函数与其他的目标函数不同的是，我们不能通过随机梯度下降法求解，因为我们要找的不是最优的向量，而是最优函数，要通过Boosting的方法。
比如，我们从一个常数函数出发，然后每次增加一个新的函数。

$\begin{aligned} \hat{y}_i^{(0)} & = 0 \\ \hat{y}_i^{(1)} & = f_1(x_i) = \hat{y}_i^{(0)} + f_1(x_i) \\ \hat{y}_i^{(2)} & = f_1(x_i) + f_2(x_i) = \hat{y}_i^{(1)} + f_2(x_i) \\ & \cdots \\ \hat{y}_i^{(k)} & = \sum_{m=1}^k f_m(x_i) = \hat{y}_i^{(k-1)} + f_k(x_i) \end{aligned}$

$\hat{y}_i^{(k)}$ 是在第 $k$ 轮的模型
$\hat{y}_{i}^{(k-1)}$ 是上一轮已经确定的模型
$f_k(x_i)$ 是新函数

所以现在的问题是，我们如何找到我们需要在每一轮新加的函数。

我们试图改写我们的目标函数，让其和我们每一轮新加的函数有关。
在第 $k$ 轮，我们的目标函数是

$\begin{aligned} \text{Obj}^{(k)} & = \sum_{i=1}^n L(y_i,\hat{y}_i^{(k)}) + \sum_{i=1}^k \Omega(f_i) \\ & = \sum_{i=1}^n L\bigg(y_i,\hat{y}_i^{(k-1)} + f_k(x_i)\bigg) + \Omega(f_k) + \text{constant} \end{aligned}$

$\text{constant}$ 是一个常量，代表的是 $k-1$ 轮及 $k-1$ 轮之前的树复杂度惩罚项之和
在第 $k$ 轮的时候，实际上 $\hat{y}_i^{(k-1)}$ 也是常数，因为在之前就已经确定了
只有 $f_k$ 是未知的，我们要做的就是找到一个 $f_k$ 最小化目标函数。

接下来，就是XGBoost的一个妙招了，泰勒展开。
我们先来复习一下泰勒展开

$f(x + \Delta x) \approx f(x) + f'(x) \Delta x + \frac{1}{2} f''(x) \Delta x^2$

那么，我们的目标函数里，谁是 $x$ ，谁是 $\Delta x$ ？
肯定不是 $y_i$ ，这个是样本标签的真实值，是常数。也不是 $\hat{y}_i^{(k-1)}$ ，这个在第 $k$ 轮的时候也是常数。
$f_k(x_i)$ ，这个是 $\Delta x$ ，也就是我们每次要新增的那一颗"小树"。

然后，我们把我们的目标函数中的损失部分进行泰勒展开，则有：

$\text{Obj}^{(k)} \approx \sum_{i=1}^{n}\bigg[L(y_i,\hat{y}_i^{(k-1)}) + g_i f_k(x_i) + \frac{1}{2}h_if_k^2(x_i)\bigg] + \Omega(f_k) + \text{constant}$

$L(y_i,\hat{y}_i^{(k-1)})$ 对应泰勒展开式的 $f(x)$
$g_i f_k(x_i)$ 对应泰勒展开式的 $f'(x) \Delta x$
$\frac{1}{2}h_if_k^2(x_i)$ 对应泰勒展开式的 $\frac{1}{2} f''(x) \Delta x^2$

其中

$\begin{aligned} g_i & = \frac{\partial L(y_i,\hat{y}_i^{(k-1)})}{\partial \hat{y}_i^{(k-1)}} \\ h_i & = \frac{\partial^2 L(y_i,\hat{y}_i^{(k-1)})}{\partial {\big(\hat{y}_i^{(k-1)}}\big)^2} \end{aligned}$

现在，我们把我们的目标函数中无关紧要的内容都移除掉。
什么是无关紧要的？过去的，历史的，我们无法改变，无法优化的。因为我要做好现在。

根据这个准则，有哪些要移除掉？

$\text{constant}$ ，这个肯定是要移除的，代表的是 $k-1$ 轮及 $k-1$ 轮之前的树的复杂度惩罚之和。
$L(y_i,\hat{y}_i^{(k-1)})$ ，这个也是要移除的，这个是 $k-1$ 的损失部分。

因此，我们新的目标函数是

$\text{Obj}^{(k)} \approx \sum_{i=1}^{n}\bigg[g_i f_k(x_i) + \frac{1}{2}h_if_k^2(x_i)\bigg] + \Omega(f_k)$

其中

目标函数的详情

通过上文的讨论，我们得到的其实只是目标函数的结构，我们甚至完全没法优化这个函数。
所以，我们需要目标函数的详情。

g_i和h_i

在这个目标函数中， $g_i$ 和 $h_i$ 直接来源于我们的损失函数。

树

那么， $f_k(x_i)$ 是什么呢，是树。
在第一章，我们讨论过用数学式子来描述树的方式，第一种是整体描述方式，而且我们还说我们会在《集成学习概览及其Python实现：3.XGBoost》中用到，就在这里。

我们用一个向量来描述我们的树，这个向量的元素就是有分数的叶子节点。同时，我们还有一个函数，这个函数描述的是某个样本会落在哪一个叶子节点上，即样本映射到叶子节点的关系。
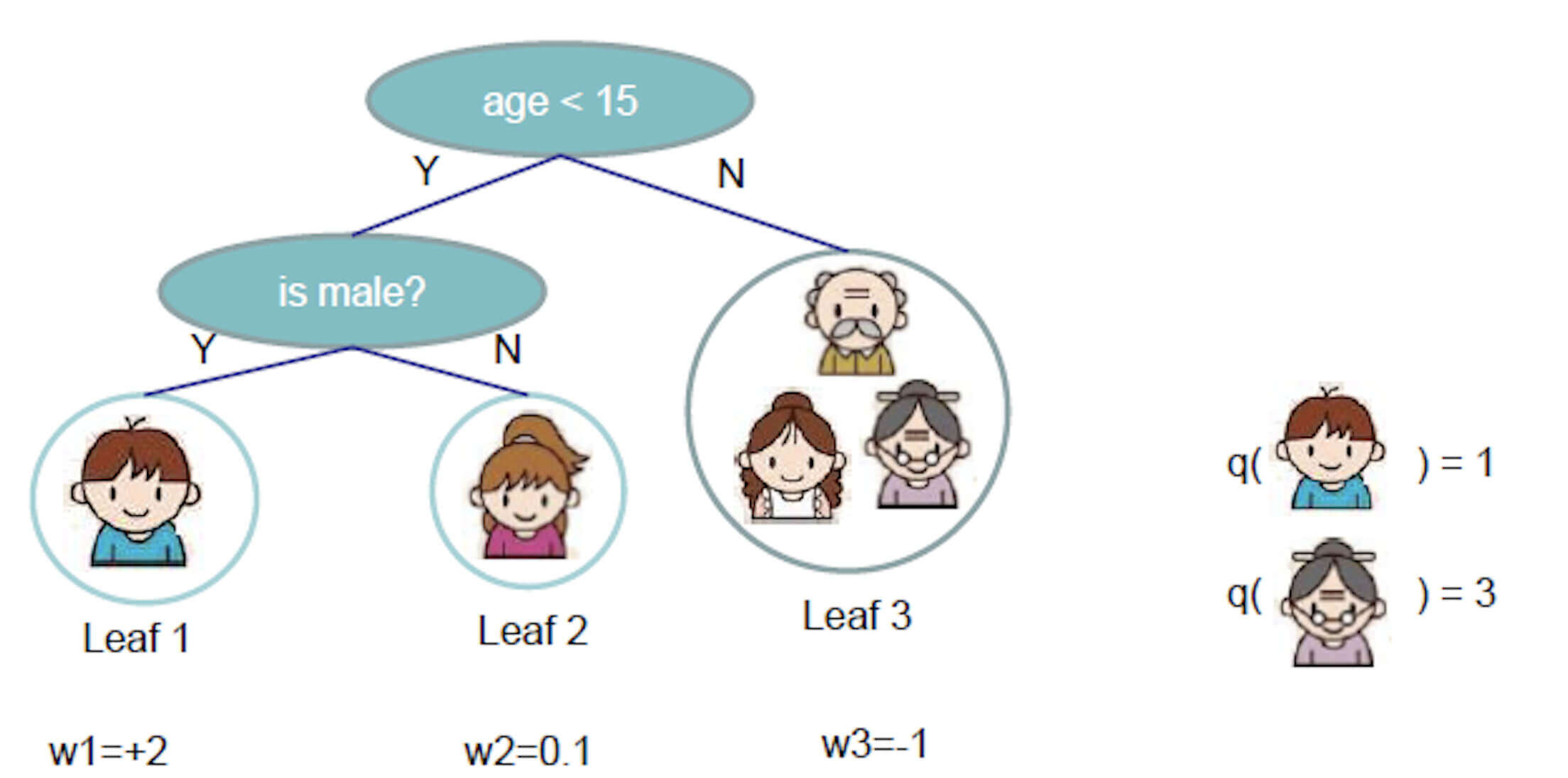
举个例子：

我们有三个叶子节点"Leaf1"、“Leaf2"和"Leaf3”，每个叶子节点也都有一个分数，分别是"w1"、“w2"和"w3”。同时，我们有一个映射函数 $q(x)$ ，比如小男孩会落在index为 $1$ 的叶子节点上。

这就是我们的树，用数学表达就是

$f_k(x) = \omega_{q(x)}$

$\omega$ 就是节点的分数
$q$ 实际代表树的结构

树的复杂度惩罚

再来看看我们的目标函数，还有一个不知道的， $\Omega(f_k)$ 。这个其实可以是多种多样的，在这里是

$\Omega(f_k) = \gamma T + \frac{1}{2} \lambda \sum_{j=1}^T \omega_j^2$

$\gamma$ 和 $\lambda$ 是超参数
$T$ 是叶子节点个数

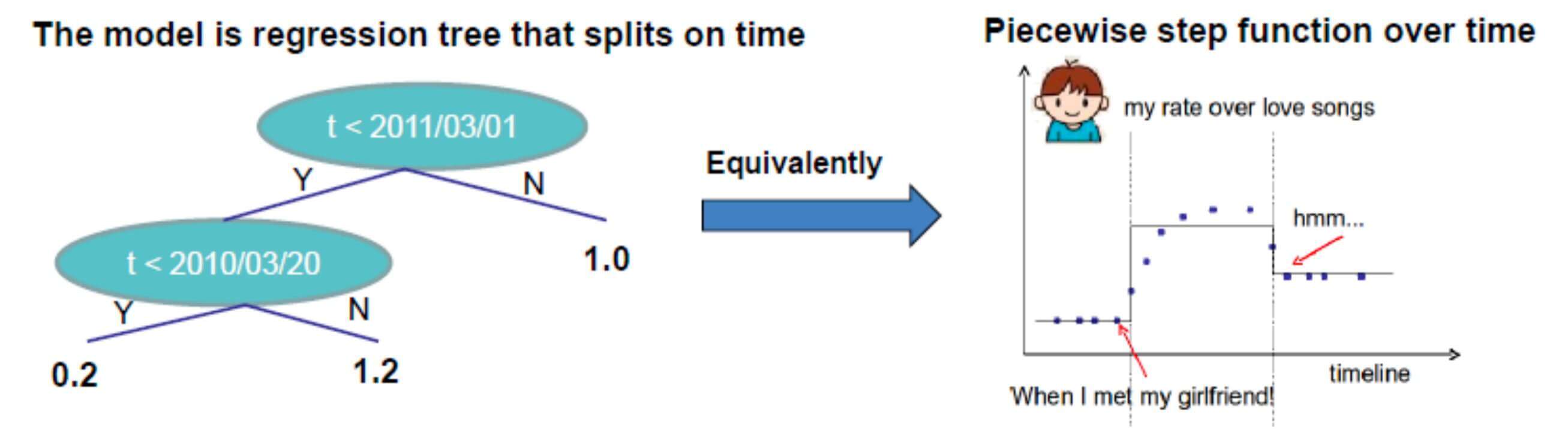
题外话，这里有大写的 $\Omega$ ，又有小写的 $\omega$ ，这个来自XGBoost作者陈天奇的PPT。其实，如果仔细看他的那份PPT的话，会发现里面还隐藏着他的恋爱时间。所以，我也比较怀疑，陈天奇用大写的 $\Omega$ ，又用小写的 $\omega$ ，或许是有意为之。

注意"when I met my girlfriend"和"Hmmm"。

好了，题外话就聊到这里。

回到主题，在刚刚的例子中，树的复杂度惩罚

$\Omega = \gamma 3 + \frac{1}{2} \lambda (2^2 + 0.1^2 + (-1)^2)$

目标函数

现在，我们终于有完整的详细的目标函数了。

$\begin{aligned} \text{Obj}^{(k)} & \approx \sum_{i=1}^{n}\bigg[g_i f_k(x_i) + \frac{1}{2}h_if_k^2(x_i)\bigg] + \Omega(f_k) \\ & \approx \sum_{i=1}^n \bigg[g_i \omega_q(x_i) + \frac{1}{2}h_i\omega_{q(x_i)}^2 \bigg] + \gamma T + \lambda \frac{1}{2} \sum_{j=1}^T \omega_j^2 \\ & \approx \sum_{j=1}^T \bigg[(\sum_{i \in I_j} g_j) \omega_j + \frac{1}{2} (\sum_{i \in I_j} h_i + \lambda) \omega_j^2 \bigg] + \gamma T \end{aligned}$

$I_j$ 是第 $j$ 个叶子节点的样本个数
从第二行折腾到第三行的原因是为了整合 $\sum$ ，便于后续的优化

目标函数的优化

我们终于得到了完整的详细的目标函数，而且为了便于优化，而且我们还把 $\sum$ 进行了整合。
在正式对目标函数进行优化之前，我们来看一个很简单的问题。
假设存在一个函数 $f(x)$

$f(x) = Gx + \frac{1}{2}Hx^2 \quad H > 0$

现在问，这个函数的在 $x$ 为何值时取得最小值，最小值是多少？
令 $f'(x) = 0$ ，求 $x$ 。
$x = - \frac{G}{H}$ 。
即

$\begin{aligned} \argmin_x Gx + \frac{1}{2}Hx^2 & = - \frac{G}{H} \\ \min_x Gx + \frac{1}{2}Hx^2 & = -\frac{1}{2} \frac{G^2}{H} \end{aligned}$

然后，我们假设

$\begin{aligned} G_j & = \sum_{i \in I_j} g_j \\ H_j & = \sum_{i \in I_j} h_j \end{aligned}$

则有

$\begin{aligned} \text{Obj}^{(k)} & \approx \sum_{j=1}^T \bigg[(\sum_{i \in I_j} g_j) \omega_j + \frac{1}{2} (\sum_{i \in I_j} h_i + \lambda) \omega_j^2 \bigg] + \gamma T \\ & \approx \sum_{j=1}^T \bigg[G_j \omega_j + \frac{1}{2} (H_j + \lambda) \omega_j^2 \bigg] + \gamma T \end{aligned}$

现在，我们把上式的 $G_j$ 、 $H_j$ 、 $T$ 都看成是常量。所以我们很容易得到最优的 $\omega$ 和最优 $\omega$ 时候的最小 $\text{Obj}$ 。

$\begin{aligned} \argmin_{\omega_j} \text{Obj} & = - \frac{G_j}{H_j + \lambda} \\ \min \text{Obj} & = - \frac{1}{2} \sum_{j=1}^T \frac{G_j^2}{H_j + \lambda} + \gamma T \end{aligned}$

上文我们讨论过，一棵树由两部分组成，一部分是各叶子节点的分数，一部分是样本映射到节点的关系，即树的结构 $q(x)$ 。看成常量，就意味着 $q(x)$ 是固定的。

所以，上述我们的 $\min \text{Obj}$ 反映的是这个 $q(x)$ 有多么好，即这个树结构有多么好。
而我们的 $\argmin_{\omega_j} \text{Obj}$ 反映的是在树固定的前提下，如何给叶子节点最佳的分数。【注意！这时候不再是利用众树或者平均数了】

那么？树的每一次分裂怎么分呢？
$\text{Obj}$ 的收益最大原则。

我们从根节点出发，每一次分裂计算收益

$\text{Gain} = \frac{G_L^2}{H_L + \lambda} + \frac{G_R^2}{H_R + \lambda} - \frac{(G_L + G_R)^2}{H_L + H_R + \lambda} - \gamma$

$\frac{G_L^2}{H_L + \lambda}$ 是左侧的 $\text{Obj}$
$\frac{G_R^2}{H_R + \lambda}$ 是右侧的 $\text{Obj}$

我们遵循每次收益最大的原则，那么，如果某次所有的收益都是负数，怎么办？我们可以提前停止，都是负收益就不再分裂了。可是，万一有更大的收益在后面等着我们呢？
所以，第二种方案，后剪枝。我们先直接分到我们设置的最大深度，这时候，每一次分裂的收益以及该分裂之后的所有的分裂的收益，我们都知道了，然后再慢慢进行剪枝。

最后一点，我们上述所有的内容，其实都是在寻找我们每一轮要新增的那个 $f(x)$ 。但更多的时候，我们不会直接加进去，而是会乘以一个学习率。这样是为了给后面的轮次的优化保留一点机会，也能防止过拟合。

调参

关于XGBoost的参数，更详细的可以参考官方文档：https://xgboost.readthedocs.io/en/latest/parameter.html

XGBoost中的参数有三种。

General Parameters，普通参数
Booster Parameters，分类器参数
Learning Task Parameters，学习目标参数

我们分别讨论

General Parameters

booster [default: gbtree]
基学习器的类型。
可选的有：

gbtree：树模型
gblinear：线性模型
dart：树模型的一种，特点是每次训练新树的时候，随机从前m轮的树中扔掉一些，来避免过拟合。

silent [default: 0]
是否打印running messages：

0：运行时打印running messages
1：运行时不打印running messages

不推荐使用，因为有更好的参数：verbosity。

verbosity [default: 1]
训练过程中打印的日志等级：

0：silent
1：warning
2：info
3：debug

nthread [default: 当前计算机的最大可用线程]
因为默认值就是最大可用线程，所以如果我们希望以最大速度运行，不建议设置这个参数。

Booster Parameters

eta [default: 0.3]
学习率

gamma [default: 0]
叶子节点分裂时所需要的最小的损失减少量，这个值越大，叶子节点越难分裂。
其实就是如下式子的 $\gamma$

$\text{Gain} = \frac{G_L^2}{H_L + \lambda} + \frac{G_R^2}{H_R + \lambda} - \frac{(G_L + G_R)^2}{H_L + H_R + \lambda} - \gamma$

$\frac{G_L^2}{H_L + \lambda}$ 是左侧的 $\text{Obj}$
$\frac{G_R^2}{H_R + \lambda}$ 是右侧的 $\text{Obj}$

max_depth [default: 6]
树的最大深度
用来控制过拟合，一般在3-10之间。树的深度越大，则对数据的拟合程度越高，同时过拟合可能性也越大。

min_child_weight [default: 1]
最小的叶子节点权重，越小越没有限制。太小容易过拟合，太大容易欠拟合。

其实就是： $H_j$

$H_j = \sum_{i \in I_j} h_j$

其中

$h_i = \frac{\partial^2 L(y_i,\hat{y}_i^{(k-1)})}{\partial {\big(\hat{y}_i^{(k-1)}}\big)^2}$

如果我们的损失函数是均方差的话，二阶导之后， $h_i = 1$ 。那么，此时，min_child_weight其实就是叶子节点中的样本个数。

subsample [default: 1]
样本抽样比例，在每次训练的随机选取sub_sample比例的样本来作为训练样本。

colsample_bytree [default: 1]
每棵树的特征抽样比例。
与这个参数相似的参数还有：

colsample_bylevel：每一层深度的树特征抽样比例。
colsample_bynode：每一个节点的特征抽样比例。

lambda [default: 1]
L2 正则的惩罚系数

alpha [default: 0]
L1 正则的惩罚系数

Learning Task Parameters

objective [default: reg:squarederror(均方误差)]
目标函数的选择

reg:squarederror：均方误差。
reg:logistic：对数几率损失，参考对数几率回归(逻辑回归)。
binary:logistic：二分类的逻辑回归问题，输出为概率。
binary:hinge：二分类合页损失，此时不输出概率值，而是0或1。
multi:softmax：使用softmax的多分类，输出类别。(同时需要设置参数类别个数，num_class)。

eval_metric [default: 根据objective而定]
模型性能度量方法

rmse：均方误差开根号
mae：平均绝对误差
logloss：负对数近似函数值
error：二分类错误率
merror：多分类错误率
mlogloss：多分类的logloss
auc：roc曲线下面积
aucpr：pr曲线下面积

Q&A

XGBoost与GBDT有什么不同

基学习器

正如GBDT的名字中的DT，Decision Tree，决策树。GBDT中的基学习器必须是决策树，而且是回归树(这是因为GBDT需要用残差来拟合梯度)。而在XGBoost中，基学习器除了是决策树，还可以是线性分类器。

目标函数

XGBoost的目标函数结构如下

$\text{Obj}^{(k)} \approx \sum_{i=1}^{n}\bigg[g_i f_k(x_i) + \frac{1}{2}h_if_k^2(x_i)\bigg] + \Omega(f_k)$

其中

XGBoost的目标函数加了正则项，相当于预剪枝，使得学习出来的模型更加不容易过拟合。但在GBDT中没有。
XGBoost利用泰勒展开，相当于对目标函数的损失部分求二阶导。而GBDT只有一阶导。相比之下，XGBoost逼近的更接近，所以也更快。
XGBoost的目标函数的损失部分还可以自定义，但是GBDT必须是均方误差。

列抽样

XGBoost支持列采样，与随机森林类似，用于防止过拟合。但GBDT没有。

缺失值处理

对树中的每个非叶子结点，XGBoost可以自动学习出它的默认分裂方向。如果某个样本该特征值缺失，会将其划入默认分支。但GBDT没有。

XGBoost泰勒二阶展开有哪些好处

精准性

相对于GBDT的一阶泰勒展开，XGBoost采用二阶泰勒展开，可以更为精准的逼近真实的损失。

可扩展性

损失函数支持自定义，只需要该损失函数二阶可导即可，毕竟需要二阶泰勒展开。

XGBoost是如何防止过拟合的

在目标函数添加正则部分，即复杂度惩罚项。
列抽样：训练的时候只用一部分特征。
子采样：每轮计算可以不使用全部样本。
设置学习率。我们在得到要新增的那个 $f(x)$ 后，不直接加进去，而是乘以一个学习率。这样是为了给后面的轮次的优化保留一点机会，防止过拟合。

XGBoost模型如果过拟合了怎么解决

减小学习率
直接控制模型的复杂度。包括max_depth,min_child_weight等参数

XGBoost是如何处理缺失值

在遍历的时候。比如在某个特征上寻找最佳分位点时，不会对该列特征缺失的样本进行遍历，而只对该列特征不缺失的样本上对应的特征值进行遍历，通过这个技巧来减少了寻找分位点的时间开销。

此外，XGBoost会将该特征缺失的样本分别分配到左叶子结点和右叶子结点，两种情形都计算一遍后，选择分裂后收益最大的那个方向(左分支或是右分支)，作为预测时特征值缺失样本的默认分支方向。

但，如果在训练中没有缺失值而在预测中出现缺失，那么会自动将缺失值的划分方向放到右子结点。

XGBoost中叶子结点的分数如何计算出来

与GBDT以及其他传统的集成学习方法不同，不是众数，也不是平均数。

我们从XGBoost的目标函数开始讨论

$G_j=\sum_{i \in I_j}g_j$
$H_j=\sum_{i \in I_j}h_j$

我们把 $G_j$ 、 $H_j$ 、 $T$ 都看成是常量。求导，令导函数的值为 $0$ ，则有：

$\argmin_{\omega_j} \text{Obj} = - \frac{G_j}{H_j + \lambda}$

这样就找到了叶子节点的分数 $\omega$ 。

需要注意的是，我们在把 $G_j$ 、 $H_j$ 、 $T$ 都看成是常量的同时，也意味着这时候样本映射到节点的关系，即树的结构 $q(x)$ 是固定的。

XGBoost中的一棵树的停止生长条件

逻辑严密的话，有三种。
第一种是出现负收益就提前停止。我们遵循每次收益最大的原则，如果某次所有的收益都是负数，那我们提前停止。
但这样做有一个问题，如果有更大的收益在后面呢？所以，第二种，直接分裂到我们设置的最大分裂次数，然后进行后剪枝。即停止生长条件是到达最大分裂次数。
最后一种，如果数据确实比较好的话，的确可能会出现XGBoost的某棵树成功的做到了每个叶子节点的样本的标签都是一样的，这时候会自动停止树的生长。