2.GBDT

这一章，我们的主题是一种集成学习算法的代表，GBDT，Gradient Boosting Decision Tree，梯度提升决策树，也简称梯度提升树。
但在正式开始讨论GBDT之前，我们要讨论一下三种集成学习的方法。

还是那句话，在《经典机器学习及其Python实现：10.集成学习和随机森林》中，我们已经讨论过"集成学习"以及一种集成学习的方法的代表"随机森林"，但当时我们的讨论的太浅显了。这一章，我们重新讨论。

集成学习方法

三种集成学习方法

集成学习是通过构建并组合多个基学习器来完成学习任务的算法，常见的集成学习方法有三种：

1. Bagging：对训练集进行抽样，将抽样的结果用于训练基学习器。特点是并行，独立训练，各个基学习器之间互相不影响。
   代表是随机森林。
2. Boosting：利用训练集训练出的模型，根据本次模型的预测结果，调整训练集，然后利用调整后的训练集训练下一个模型。特点是串行，需要首先有第一个模型。
   代表有Adaboost、GBDT、XGBoost、LightGBM。
3. Stacking：Bagging和Boosting都有一个共同点，基学习器是同一类(不一定都是决策树，但都是同一类)。而Stacking中基学习器可以是不同的类别。

Stacking

例如，下图就是一种Stacking的结构。

graph LR lr{逻辑回归} svm{支持向量机} dt{决策树} 3rd{又一个基学习器} o(输出) lr -- w1 --> 3rd svm -- w2 --> 3rd dt -- w3 --> 3rd 3rd --> o

• 不同的基学习器以不同的权重，输入到又一个基学习器中，然后输出。这个结构，非常的类似于神经网络。
• Stacking至少要有两层，一层的不算Stacking。就像Stacking这个单词一样，堆叠。
• 实际上也是一种多模型的融合方法。

关于Stacking，在本章的最后，我们会讨论GBDT+LR，这就是一种典型的Stacking方法。

并行与串行

Bagging和Boosting，除了对训练集的处理不一样，Boosting会去调整训练集，但Bagging不会。还有一个区别。
Bagging是并行，独立训练，基学习器之间互相不影响。基于这个特点，我们就可以多线程，甚至上集群了。
Boosting是串行的，但是在具体实现中，我们能让局部并行。比如，对于决策树的训练，我们有一个操作是选择最佳的分裂指标，这时候可并行。

Bagging

关于Bagging及其代表算法随机森林，我们在《经典机器学习及其Python实现：10.集成学习和随机森林》中已经讨论过了，这里不再赘述。
唯一需要补充的两点是：

1. 除了用众数(投票)的方法，对于回归树，可以用求平均的方法。
2. 随机森林的随机性体现在每颗树的训练样本是随机的，树中每个节点的分裂属性集合也是随机选择确定的。即随机性体现在随机选取子集和随机选取特征。

Boosting

上文，我们讨论了，Boosting是利用训练集训练出的模型，根据本次模型的预测结果，调整训练集，然后利用调整后的训练集训练下一个模型，而且是串行。
那么在这个过程中，主要涉及两个东西，加法模型和前向分步。

加法模型是指，强学习器由一系列弱学习器线性相加而成。组合形式如下：

$$F_M(x;P) = \sum_{m=1}^{n}\beta_mh(x;a_m)$$

• $h(x;a_m)$是弱学习器。
• $a_m$是弱学习器学习到的最优参数。
• $\beta_m$是弱学习器在强学习器中所占的比重。
• $P$是所有的$a_m$和$\beta_m$的组合。

前向分步是指，在训练过程中，下一轮迭代产生的分类器是在上一轮的基础上训练得来的。即

$$F_{m}(x) = F_{m-1}(x) + \beta_m h_m(x;a_m)$$

在《深度学习初步及其Python实现》中，我们多次提到了前向计算。注意前向计算和前向分步不一样。前向计算中，传递的是输出值；前向分步中，传递的是模型。

Adaboost

接下来，我们讨论Boosting的一个代表，Adaboost，这个模型用于处理二分类问题。

Adaboost的原理

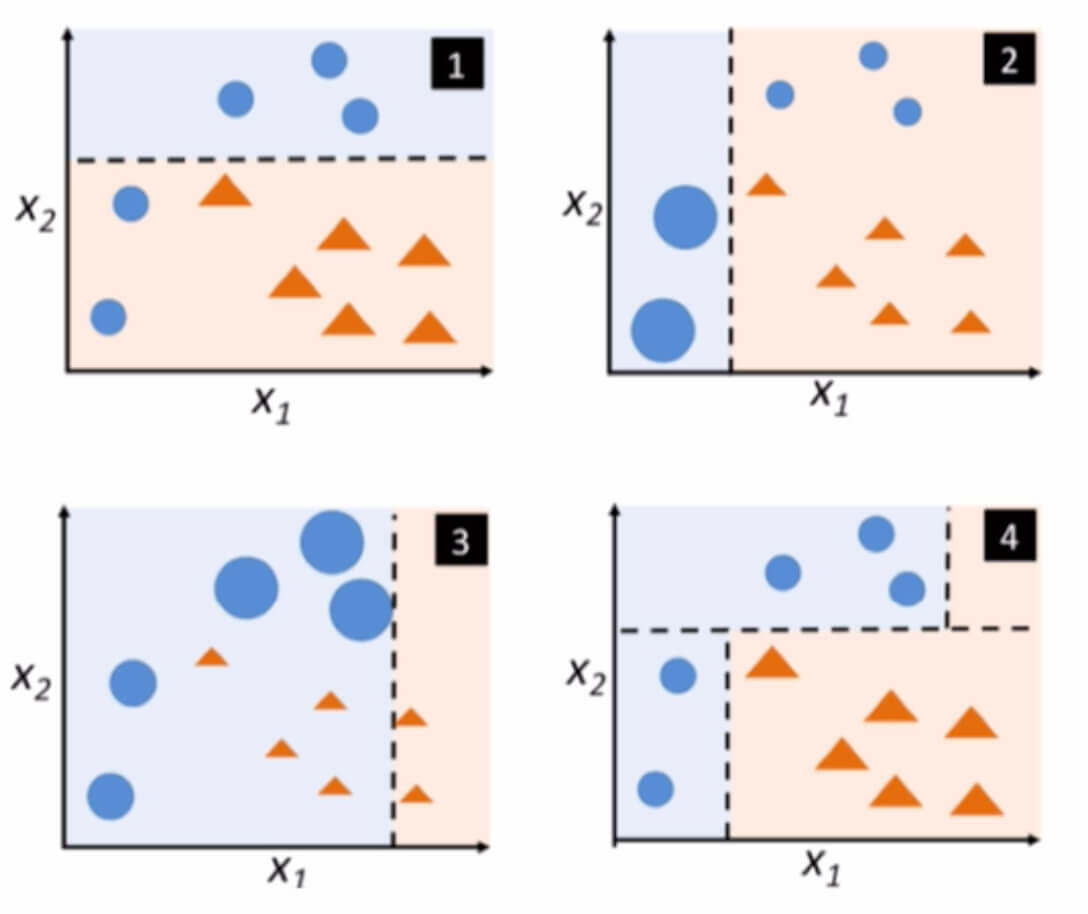
我们知道Boosting做的事情是调整训练集。
作为Boosting的代表Adaboost，其调整训练集的方法是在样本的权重上做文章，将关注点放在被错误分类的样本上，降低上一轮被正确分类的样本权值，提高被错误分类的样本权值。让模型在下一次要把注意力放在没有分类正确的样本上。

如图所示：

1. 首先对圆形和三角形进行分类，这时候左下角的圆被错误分类了。
2. 提高左下角圆的权值，降低被正确分类的右下方三角形的权值，重新分类。这时候右上角的圆被错误分类了。
3. 提高右上角圆的权值，降低被正确分类的样本权值，重新分类。
4. 将上述三个分类器加起来，得到新的分类器。

Adaboost采用加权投票的方法，分类误差小的弱分类器权重大，而分类误差大的弱分类器权重小。
这也是与随机森林的一个区别，随机森林是"同股同权"，Adaboost是"同股不同权"。

Adaboost的算法

假设输入训练数据为：

$$T = \{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\}$$

• $x_i \in \bold{X}$，为实数空间。
• $y_i \in \bold{Y}$，只有$-1$和$1$两个取值。

第一步 初始化训练样本的权值。

$$D_1 = (w_{1,1},w_{1,2},\cdots,w_{1,i}),\quad w_{1,i} = \frac{1}{N},\quad i=1,2,\cdots,N$$

• 其中$w_{1,1}$的第一个$1$代表第一个分类器，第二个$1$代表第一个样本。

第二步 循环$M$次，得到所有的$M$个弱分类器。
比如，现在我们拿到了$m-1$个弱分类器，现在我们来训练第$m$个弱分类器。

1、使用具有权值分布$D_m$的训练数据集进行训练，得到弱分类器$G_m(x)$。

• 训练过程也是上一章的决策树构建过程。
• $D_m$已经进行了加权，在$m-1$步时，分对的权值变大，分错的权值变小。

2、计算$G_m(x)$在训练数据集上的分类错误率：

$$e_m = \sum_{i=1}^{N} w_{m,i} * I(G_m(x_i) \neq y_i)$$

• $I(\cdot)$是指示函数，返回$1$和$0$
• 这个式子的含义是把分错的权重叠加。

3、计算$G_m(x)$在强分类器(整体)中所占的权重

$$\alpha_m = \frac{1}{2}\log\frac{1-e_m}{e_m}$$

• 当弱分类器的误差率$e_m \leq 0.5$时，$\alpha_m \geq 0$，并且$\alpha_m$随着$e_m$的减小而增大，即分类误差率越小的基学习器在最终集成时占比越大。所以AdaBoost能够适应各个弱分类器的训练误差率，这也是它的名称中"适应性(Adaptive)"的由来。

4、更新数据集的权值分布。

$$D_{m+1} = (w_{m+1,1},w_{m+1,2},\cdots,w_{m+1,N})$$

$$w_{m+1,i} = \frac{w_{m,i}}{z_m}\exp(-\alpha_m y_i G_m(x_i)),\quad i=1,2,\cdots,10$$

• $\alpha_m$是$G_m(x)$在强分类器(整体)中所占的权重
• $y_i$是真实值
• $G_m(x_i)$是预测值
• $y_i$只有$-1$和$1$两种取值。如果分类正确，则$y_i G_m(x_i) > 0$，反之$y_i G_m(x_i) < 0$。通过这种方法调整样本中的权值分布。
• $z_m$是归一化因子，使样本概率分布的和为$1$。
  $z_m = \sum_{i=1}^{N}w_{m,i}\exp(-\alpha_m y_i G_m(x_i))$

第三步
最后我们得到了$M$个基分类器，然后我们进行相加，构建分类器的线性组合。

$$F(x) = sign(f(x)) = sign\bigg(\sum_{i=1}^{N}\alpha_m G_m(x) \bigg)$$

GBDT的原理

GBDT，Gradient Boosting Decision Tree，梯度提升决策树。

GBDT是一种利用多棵回归树解决回归问题的方案，每一个基学习器都是回归树。虽然通过调整损失函数，也可以解决分类问题，但需要强调的是，即使用GBDT来解决分类问题了，其基学习器依旧是回归树。

那么，这时候就有一个问题了，为什么GBDT要用回归树去解决分类问题？
这是因为只能用回归树。
为什么只能用回归树？
因为我们想用回归问题的损失函数，均方误差。
为什么想用均方误差呢？
这个我们很快就会讨论。

GBDT还有一个特点，通过全部样本迭代生成多棵回归树。
那么，这时候又有问题了，基学习器必须得有所不同吧。随机森林是每次随机有放回抽样，以此来实现不同的基学习器；Adaboost是加大被错误分类的样本的权重，以此来实现不同的基学习器。那么，GBDT呢？GBDT是在样本的$y$上做文章，修改样本的$y$。让每一轮的决策树学习上一轮决策树没有学到的残差。

刚刚我们说，用回归树的目的是想用均方误差，现在就讨论。
首先，什么是均方误差。这个我们讨论太多遍了，而且我们知道，更多的时候，我们用的是非标的均方误差。

$$\frac{1}{2} \sum (y - f(x))^2$$

• 为了便于计算，不乘以$\frac{1}{N}$，而是乘以$\frac{1}{2}$。这就是非标的均方误差。

对于单个样本就是

$$\frac{1}{2}(y_i - f(x_i))^2$$

现在，我们对函数求负梯度(梯度提升)就是：

$$-\frac{\partial L(y_i,f(x_i))}{\partial f(x_i)} = y_i - f(x_i)$$

• $f(x_i)$是我们的决策树，在上一章的开篇，我们就讨论了，决策树不可导。
  所以，这里我们只能把$f(x_i)$看成一个自变量。

然后，现在有一个非常巧的事情，$y_i - f(x_i)$就等于残差。所以，我们就知道负梯度了。

GBDT的算法

输入：训练数据集$\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\}$，$y_i \in \{+1,-1\}$
输出：回归树$F_T(x)$
 
初始化：$f_0(x) = \argmin_{h_0} \sum_{i=1}^{N} L(y_i,h_0(x))$
对于需要生成$M$颗基学习器，有$m=1,2,\cdots,M$：
  计算负梯度$\tilde{y}_i = - \bigg[\frac{\partial L(y_i,F(x_i))}{\partial F(x_i)}\bigg]_{F(x) = F_{m-1}(x)},\quad i = 1,2,\cdots,N$。这里的负梯度也就是残差。
  拟合残差，得到当前最好的基学习器。$\omega_m=\argmin_{\omega_m} \sum_{i=1}^{N}(\tilde{y}_i - h_t(x;\omega_m))^2$。($\tilde{y}_i$是真实值。)
  计算基学习器的权重。$\alpha_m=\argmin_{\alpha_m}\sum_{i=1}^{N}L(y_i,f_{m-1}(x_i))+\alpha_{m}h_m(x;\omega_m)$。
  更新$F_m(x)=F_{m-1}(x) + \alpha_m h_m(x;\omega_m)$

提起GBDT，让我想起了费马大定理的证明过程，长达400年的科学家们的接力。每一位科学家在前人研究的基础上，再往前进步一点。就像每一颗决策树，在之前决策树的基础上，再进步一点。

GBDT解决分类问题

在上文我们讨论了，GBDT是一种利用多棵回归树解决回归问题的方案，每一颗回归树就是一个基学习器。
而且，我们说了通过调整损失函数，也可以解决分类问题。现在，我们就来讨论，如何用GBDT解决分类问题。

二分类

原本是解决回归问题的模型，经过简单的改造后，就成了可以解决二分类问题的模型。这个我们很容易联想到线性回归和逻辑回归。
逻辑回归是在线性回归的外面套了一层Sigmoid函数，并把损失函数改成了交叉熵损失。
现在，我们照葫芦画瓢。

Sigmoid的函数形式是

$$sigmoid(x) = \frac{1}{1 + e^{-x}}$$

那么，在原本的GBDT的外面套一层Sigmoid就是

$$P(y=1|x) = \frac{1}{1 + e^{-\sum_{m=1}^{M}h_m(x)}}$$

• $P(y=1|x)$表示为$1$的概率
• $h_m(x)$是决策树

交叉熵是

$$H(\bold{p}||\bold{q}) = - \sum_i p_i \log_2 q_i$$

二分类的交叉熵损失是

$$Loss(\hat{y}_i) = - y_i \log \hat{y}_i - (1 - y_i)\log (1 - \hat{y}_i)$$

• $\hat{y}_i$是预测值

那么，对于GBDT二分类的交叉熵损失就是

$$Loss(F(x)) = y_i \log(1 + e^{-F(x_i)}) + (1 - y_i)[F(x_i) + \log(1 + e^{-F(x_i)})]$$

• $F(x) = \sum_{m=1}^{M}h_m(x)$

与解决回归问题一样，我们求负梯度，则有：

$$\begin{aligned} -\frac{\partial Loss(F(x))}{\partial F(x)}\bigg|_{x_i,y_i} & = y_i - \frac{1}{1 + e^{-F(x_i)}} \\ & = y_i - \hat{y}_i \end{aligned}$$

$y_i - \hat{y}_i$是什么？这个我们在讨论GBDT解决回归问题的时候见过，是残差。在这里就是真实标签与预测概率的差。

所以呢，就有了下面的GBDT解决二分类的算法：

初始化：
  $F_0(x) = h_0(x) = \log\frac{p_1}{1-p_1}$，其中$p_1$是训练样本中$y=1$的比例，即用先验信息来初始化。
对于需要生成$M$颗基学习器，有$m=1,2,\cdots,M$：
  计算负梯度$\tilde{y}_i$，在这里就是残差。$\tilde{y}_i = \hat{y}_i - y_i$，$\hat{y}_i = \frac{1}{1 + e^{-F_{m-1}(x_i)}}$
  拟合残差，得到当前最好的基学习器。$\omega_m=\argmin_{\omega_m} \sum_{i=1}^{N}(\tilde{y}_i - h_m(x;\omega_m))^2$。($\tilde{y}_i$是真实值。)
  计算基学习器的权重。$\alpha_m=\argmin_{\alpha_m}\sum_{i=1}^{N}L(y_i,f_{m-1}(x_i))+\alpha_{m}h_m(x;\omega_m)$。
  更新$F_m(x)=F_{m-1}(x) + \alpha_m h_m(x;\omega_m)$
 
因为损失函数不一样，所以负梯度不一样。另外，因为是分类问题，所以初始化方法不一样。除了这两点，并没有其他区别。

多分类问题

多分类问题，不过是原本套一层Sigmoid的，现在改成套一层Softmax。另外，有几个类别，我们就需要几个GBDT。即

$$\begin{aligned} P(y=1|x) & = \frac{e^{F_1(x)}}{\sum_{i=1}^{k}e^{F_i(x)}} \\ P(y=2|x) & = \frac{e^{F_2(x)}}{\sum_{i=1}^{k}e^{F_i(x)}} \\ & \cdots \\ P(y=k|x) & = \frac{e^{F_k(x)}}{\sum_{i=1}^{k}e^{F_i(x)}} \\ \end{aligned}$$

损失函数为：

$$Loss(F_i(x)) = - \sum_{i=1}^{k} y_i \log \frac{e^{F_i(x)}}{\sum_{j=1}^k e^{F_j(x)}}$$

• $y_i$是样本标签做one-hot编码之后的值。所以在$k$个$y$中，有且只有一个为$1$，其余都是$0$。

求负梯度，则有：

$$\begin{aligned} -\frac{\partial Loss(F_q)}{\partial F_q} & = y_q - \frac{e^{F_q(x)}}{\sum_{j=1}^{k}e^{F_j(x)}} \\ & = y_q - \hat{y}_q \end{aligned}$$

后续内容略，与二分类非常相似。

GBDT和随机森林的区别

1. 集成学习方法：GBDT是Boosting方法，随机森林是Bagging方法。
2. GBDT不断的降低模型的偏差，随机森林不断降低模型的方差。
3. GBDT每次使用全部样本，随机森林则是随机有放回的抽样。
4. GBDT是加权融合，随机森林是多棵树进行多数表决(回归问题是取平均)。
5. GBDT对异常值比较敏感，随机森林对异常值不敏感。
6. GBDT容易过拟合，随机森林不容易过拟合。

GBDT+LR

GBDT+LR的原理

GBDT和LR结合后，在一个领域有重要应用，计算广告。
具体大家可以参考论文《Practical Lessons from Predicting Clicks on Ads at Facebook》

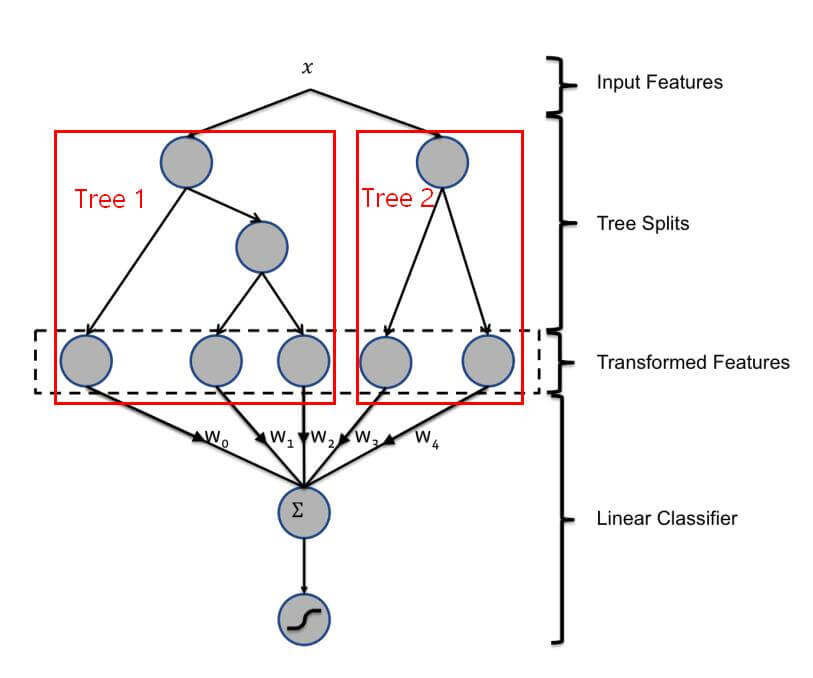
现在，我们讨论这个模型。结构如下图：

我们知道，LR，逻辑回归，其实本质上是一个线性回归，其优点是速度快，缺点是处理非线性的数据效果不好。对此，我们有一个办法是数据升维。比如我们有两个维度$X_1$和$X_2$，然后我们人为的创造新的维度$X_1 * X_2$，$X_1^2$，$X_2^2$等等。这个也叫做特征组合(特征衍生)，现在，我们把这项操作交给GBDT来做。

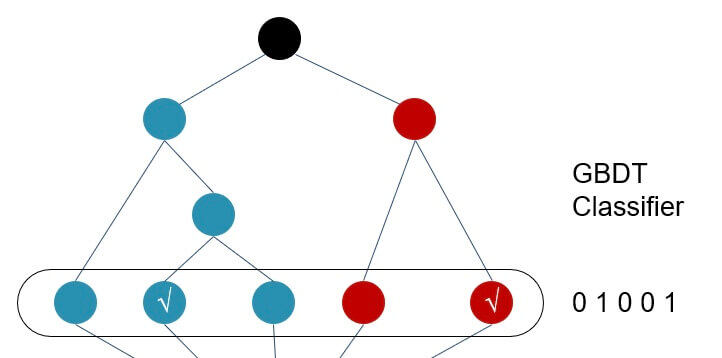
就如上面的图，一个样本在进入Tree1后，会不断的进行if-else的判断，最后落在一个叶子节点上，而叶子的含义其实也就是一个或多个特征的组合；然后这个样本再进入Tree2，同样，也会落在某一个叶子节点上，也是一个或多个特征的组合。
然后我们把所有树的叶子节点拼接起来，再进行One-Hot编码。这样就完成了特征的组合。

比如：

剩下的事情，就交给LR了。

GBDT+LR的实现

接下来，我们看看如何实现GBDT+LR。
示例代码：

import numpy as np
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_auc_score
from sklearn.preprocessing import OneHotEncoder
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split


class GradientBoostingWithLR(object):
    def __init__(self):
        self.gbdt_model = None
        self.lr_model = None
        self.gbdt_encoder = None
        self.X_train_leafs = None
        self.X_test_leafs = None
        self.X_trans = None

    def gbdt_train(self, X_train, y_train):
        """
        只训练GBDT模型
        :param X_train:
        :param y_train:
        :return:
        """
        gbdt_model = GradientBoostingClassifier(n_estimators=10, max_depth=6, verbose=0, max_features=0.5)
        # 训练学习
        gbdt_model.fit(X_train, y_train)
        return gbdt_model

    def lr_train(self, X_train, y_train):
        """
        只训练逻辑回归模型
        :param X_train:
        :param y_train:
        :return:
        """
        lr_model = LogisticRegression()
        # 预测及AUC评测
        lr_model.fit(X_train, y_train)
        return lr_model

    def gbdt_lr_train(self, X_train, y_train):
        """
        训练gbdt+lr
        :param X_train:
        :param y_train:
        :return:
        """
        # 训练GBDT模型
        self.gbdt_model = self.gbdt_train(X_train, y_train)

        # 使用GBDT的apply方法对原有特征进行编码
        self.X_train_leafs = self.gbdt_model.apply(X_train)[:, :, 0]

        # 对特征进行ont-hot编码
        self.gbdt_encoder = OneHotEncoder(sparse=False)
        self.X_trans = self.gbdt_encoder.fit_transform(self.X_train_leafs)

        # 采用LR进行训练
        self.lr_model = self.lr_train(self.X_trans, y_train)
        return self.lr_model

    def gbdt_lr_pred(self, model, X_test, y_test):
        """
        预测及AUC评估
        :param model:
        :param X_test:
        :param y_test:
        :return:
        """
        self.X_test_leafs = self.gbdt_model.apply(X_test)[:, :, 0]

        (train_rows, cols) = self.X_train_leafs.shape
        X_trans_all = self.gbdt_encoder.fit_transform(np.concatenate((self.X_train_leafs, self.X_test_leafs), axis=0))

        y_pred = model.predict_proba(X_trans_all[train_rows:])[:, 1]
        auc_score = roc_auc_score(y_test, y_pred)
        print('GBDT+LR AUC score: %.5f' % auc_score)
        return auc_score

    def model_assessment(self, model, X_test, y_test, model_name="GBDT"):
        """
        模型评估
        :param model:
        :param X_test:
        :param y_test:
        :param model_name:
        :return:
        """
        y_pred = model.predict_proba(X_test)[:, 1]
        auc_score = roc_auc_score(y_test, y_pred)
        print("%s AUC score: %.5f" % (model_name, auc_score))
        return auc_score


def load_data():
    """
    调用sklearn的iris数据集，将多类数据构造成2分类数据,同时切分训练测试数据集
    """
    iris_data = load_iris()
    X = iris_data['data']
    # 二分类，只有target为1的是true，其他都是0。
    y = iris_data['target'] == 1

    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=0)
    return X_train, X_test, y_train, y_test


if __name__ == '__main__':
    X_train, X_test, y_train, y_test = load_data()

    gblr = GradientBoostingWithLR()
    gbdt_lr_model = gblr.gbdt_lr_train(X_train, y_train)
    # 单独评估GBDT分类器
    gblr.model_assessment(gblr.gbdt_model, X_test, y_test)
    # 评估GBDT作为编码器+LR作为分类器
    gblr.gbdt_lr_pred(gbdt_lr_model, X_test, y_test)

运行结果：

GBDT AUC score: 0.98355
GBDT+LR AUC score: 0.99412