2.神经网络基础

全连接层

回到上一章我们讨论的内容。

$$\bold{h} = relu(\bold{X}*\bold{W} + \bold{b})$$

例如：

$$[o_1 \quad o_2] = relu \bigg( [x_1 \quad x_2 \quad x_3] \cdot \left[ \begin{matrix} w_{11} & w_{12} \\ w_{21} & w_{22} \\ w_{31} & w_{32} \\ \end{matrix} \right] + [ b_1 \quad b_2] \bigg)$$

$$o_{1} = relu(x_{1}w_{11} + x_{2}w_{21} + x_3w_{31} + b_{1})$$

$$o_{2} = relu(x_{1}w_{12} + x_{2}w_{22} + x_3w_{32} + b_{2})$$

上述过程我们可以画图为：

我们看到每一个$o$都和每一个$x$连接了。
这就是一个全连接层，即每一个结点都与上一层的所有结点相连。

神经网络

我们把这种由神经元相互连接而成的网络叫做神经网络。

在上一章，我们层层堆叠的全连接层，每一层的结点都和上一层的所有结点相连，即每一层都是全连接层。我们把这种的神经网络叫做全连接神经网络。

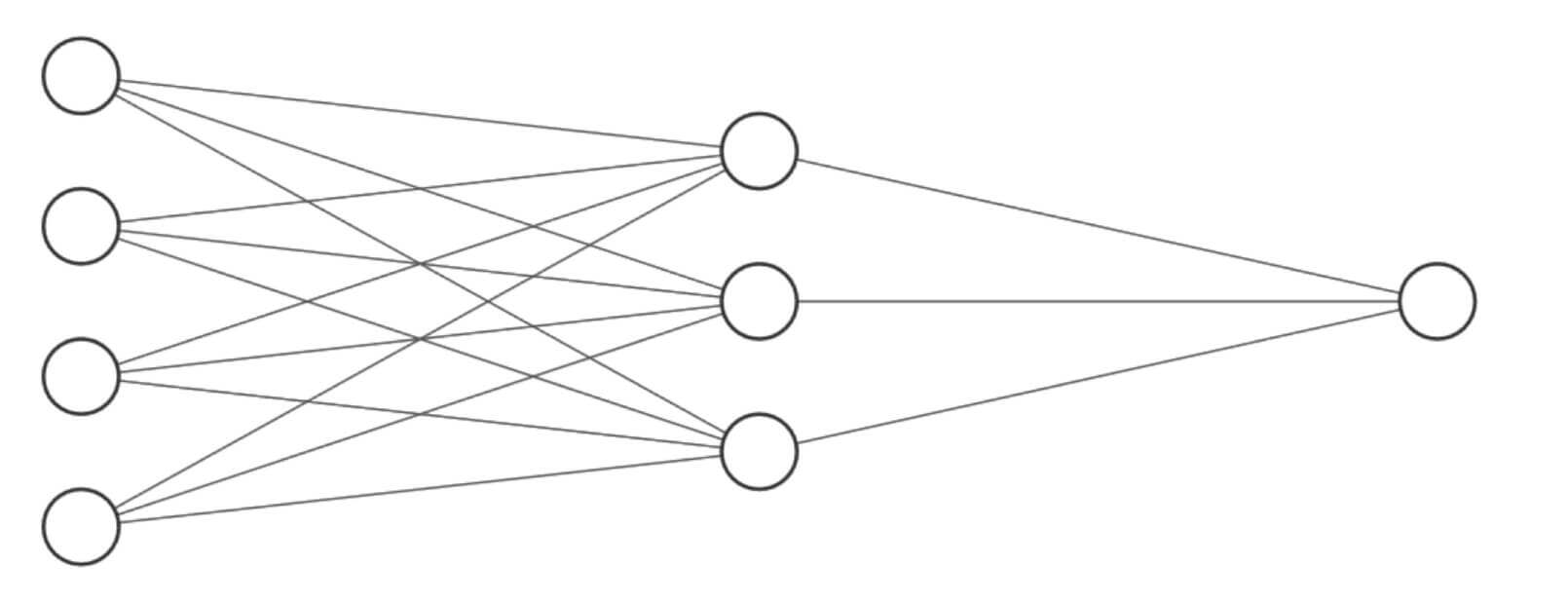
如下图所示，也是一个全连接神经网络。

从左到右，依次是：

1. 输入层
2. 隐藏层1
3. 隐藏层2
4. 隐藏层3
5. 输出层

这就是一个神经网络的结构。
其输出节点数依次是256、128、64、10，这当然不是唯一的，可以是256、256、64、10或512、64、32、10等等，都可以。网络结构是一个超参数。但是，不同的网络结构，效果是不一样。至于哪一种网络结构是最优的，这需要很多的领域经验知识和大量的实验尝试，或者可以通过所谓的AutoML搜索较优解。

输出层

我们重点讨论一下输出层。
我们的神经网络有各种各样的应用场景。有回归、有分类，有二分类、有多分类，等等。也因为多种多样的应用场景，所以我们有多种多样的输出层。其中常见的有：

1. $o_i \in R^d$：输出值属于整个实数空间或部分连续的实数空间。
2. $o_i \in [0,1]$：输出值在$[0,1]$的区间。
3. $o_i \in [0,1] \text{且} \sum o_i = 1$：输出值在$[0,1]$的区间，并且所有输出值之和为1。
4. $o_i \in [-1,1]$：输出值在$[-1,1]$之间。

输出值属于实数空间

$o_i \in R^d$
这是一个典型的回归问题，应用场景有年龄预测、股价预测等各种。

输出值在[0,1]的区间

$o_i \in [0,1]$
常见的应有场景就是二分类问题。
例如：

输出节点是$P(A|\bold{x})$，表示在输入$\bold{x}$的情况下，输出为$A$的概率。

但，这里有一个问题，输出值怎么能恰到好处的在0和1之间？我们做压缩映射。
所以，首先，我们需要一个值域是$[0,1]$的函数：sigmoid。

$$sigmoid(x) = \frac{1}{1 + e^{-x}}$$

在TensorFlow的实现方法是：

tf.sigmoid()

示例代码：

import tensorflow as tf

a = tf.linspace(-10,10,21)
print(a)
print('\n')
print(tf.sigmoid(a))

运行结果：

tf.Tensor(
[-10.  -9.  -8.  -7.  -6.  -5.  -4.  -3.  -2.  -1.   0.   1.   2.   3.
   1.   5.   6.   7.   8.   9.  10.], shape=(21,), dtype=float64)


tf.Tensor(
[4.53978687e-05 1.23394576e-04 3.35350130e-04 9.11051194e-04
 2.47262316e-03 6.69285092e-03 1.79862100e-02 4.74258732e-02
 1.19202922e-01 2.68941421e-01 5.00000000e-01 7.31058579e-01
 8.80797078e-01 9.52574127e-01 9.82013790e-01 9.93307149e-01
 9.97527377e-01 9.99088949e-01 9.99664650e-01 9.99876605e-01
 9.99954602e-01], shape=(21,), dtype=float64)

二分类问题中，除了单一输出节点，还有一种是两个输出节点。

如图所示，我们要求两个输出节点之和为1，但这个sigmoid没法做到。这是我们的第三种输出层，SoftMax。

输出值在[0,1]的区间，并且所有输出值之和为1

$o_i \in [0,1] \text{且} \sum o_i = 1$

除了输出值在$[0,1]$的区间，我们还要所有输出值的和为1。

$$Softmax(z_i) = \frac{e^{z_i}}{\sum_{1}^{j}{e^{z_j}}}$$

• 其中$e$是自然对数，$e \approx 2.718281828459$

例如：

$$S_1 = \frac{e^{2.0}}{e^{2.0} + e^{1.0} + e^{0.1}}$$

$$S_1 \approx 0.659 \approx 0.7$$

在TensorFlow的实现方法是：

tf.nn.softmax()

示例代码：

import tensorflow as tf
import numpy as np
a = tf.linspace(-10,10,21)
print(a)
print('\n')
prob = tf.nn.softmax(a)
print(prob)
print('\n')
print(np.sum(prob.numpy()))

运行结果：

tf.Tensor(
[-10.  -9.  -8.  -7.  -6.  -5.  -4.  -3.  -2.  -1.   0.   1.   2.   3.
   1.   5.   6.   7.   8.   9.  10.], shape=(21,), dtype=float64)


tf.Tensor(
[1.30289758e-09 3.54164282e-09 9.62718331e-09 2.61693975e-08
 7.11357976e-08 1.93367146e-07 5.25626399e-07 1.42880069e-06
 3.88388295e-06 1.05574884e-05 2.86982290e-05 7.80098744e-05
 2.12052824e-04 5.76419338e-04 1.56687021e-03 4.25919483e-03
 1.15776919e-02 3.14714295e-02 8.55482149e-02 2.32544158e-01
 6.32120559e-01], shape=(21,), dtype=float64)


1.0

输出值在[-1,1]之间

$o_i \in [-1,1]$

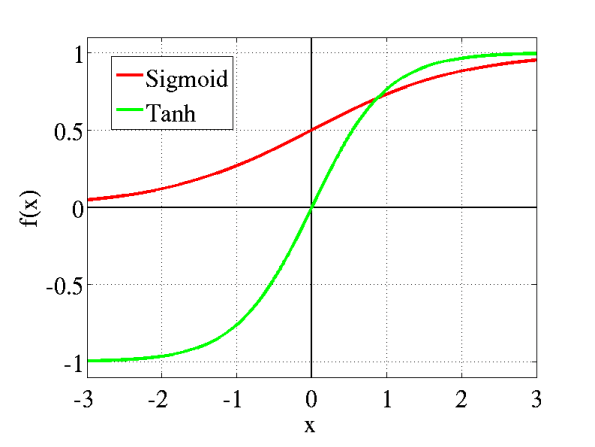
我们的压缩映射函数是双曲正切($\tanh$)。

$$tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$$

在TensorFlow的实现方法是

tf.tanh()

示例代码：

import tensorflow as tf
a = tf.linspace(-10,10,21)
print(a)
print('\n')
print(tf.tanh(a))

运行结果：

tf.Tensor(
[-10.  -9.  -8.  -7.  -6.  -5.  -4.  -3.  -2.  -1.   0.   1.   2.   3.
   1.   5.   6.   7.   8.   9.  10.], shape=(21,), dtype=float64)


tf.Tensor(
[-1.         -0.99999997 -0.99999977 -0.99999834 -0.99998771 -0.9999092
 -0.9993293  -0.99505475 -0.96402758 -0.76159416  0.          0.76159416
  0.96402758  0.99505475  0.9993293   0.9999092   0.99998771  0.99999834
  0.99999977  0.99999997  1.        ], shape=(21,), dtype=float64)

其实，刚刚我们讨论的压缩映射方法，就是几个常见的激活函数。

损失函数

刚刚我们讨论了输出层，针对不同的应用场景，我们有不同的输出方法。但是我们怎么评价输出的好坏呢？
接下来，我们讨论损失函数。
常见的损失函数有两中：

1. 均方误差(MSE)
2. 交叉熵损失(Cross Entropy Loss)

均方误差

均方误差(Mean Squared Error，简称MSE)，这个我们在《经典机器学习及其Python实现》中已经讨论过了。
均方误差的公式：

$$MSE(\bold{y},\bold{o}) = \frac{1}{d_{out}}\sum_{i=1}^{d_{out}}(y_i - o_i)^2$$

有时候，为了计算方便，我们还有不除$d_{out}$的均方误差，或者除以$2$的均方误差。但是本质还是均方误差，我们或许可以把这种称为非标的均方误差。

特别的，还有一个类似的损失，二范数。

$$L_{2-norm}(\bold{y},\bold{o}) = \sqrt{\sum_{i=1}^{d_{out}}(y_i - o_i)^2}$$

在TensorFlow中，我们可以很方便的计算这些损失。
均方误差：

tf.losses.MSE()

二范数：

tf.norm()

除了TensorFlow，在Keras中，同样有方法。

tf.keras.losses.mean_squared_error()

示例代码：

import tensorflow as tf

y = tf.constant([0,1,2,0,1,2])
y = tf.one_hot(y,depth=3)
y = tf.cast(y,dtype=tf.float32)
print(y)
out = tf.random.normal([6,3])
print(out)
loss_1 = tf.reduce_mean(tf.square(y-out))
loss_2 = tf.square(tf.norm(y-out))/(6*3)
loss_3 = tf.reduce_mean(tf.losses.MSE(y,out))

print(loss_1)
print(loss_2)
print(loss_3)

print(tf.reduce_mean(tf.keras.losses.mean_squared_error(y,out)))

运行结果：

tf.Tensor(
[[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]
 [1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]], shape=(6, 3), dtype=float32)
tf.Tensor(
[[ 1.1934481  -0.6930259   0.5534205 ]
 [-0.49817067 -0.834483    0.4182236 ]
 [ 0.90017426  1.707261   -1.1986054 ]
 [-0.04155555  0.65489596  1.0418415 ]
 [ 1.8492013   0.5265525   0.37141058]
 [-2.0288062  -0.19234754 -0.7208679 ]], shape=(6, 3), dtype=float32)
tf.Tensor(1.4814755, shape=(), dtype=float32)
tf.Tensor(1.4814756, shape=(), dtype=float32)
tf.Tensor(1.4814755, shape=(), dtype=float32)
tf.Tensor(1.4814755, shape=(), dtype=float32)

交叉熵损失

交叉熵主要用于计算分类问题的损失。既可以用于二分类问题，也可以用于多分类问题，而且通常和Softmax配合使用。

熵

首先，我们讨论一下什么是熵(Entropy)。

$$H(\bold{P}) = - \sum_{i} P_i \log_2 P_i$$

熵越大，代表不确定性越大，信息量也就越大。

例如，现在有一张图片，我们识别这张图片到底是猫还是狗。
假设，我们认为肯定是猫，肯定不是狗。则

$$H(\bold{P}) = - (1 * \log_{2}1 + 0 * \log_{2}0) = 0$$

即，我们的确定性很大，信息量很小。

假设，我们完全无法判断是猫或是狗，我们认为一半的可能是猫，一半的可能是狗。则

$$H(\bold{P}) = - (0.5 \log_{2}0.5 + 0.5 \log_{2}0.5) = 1$$

即，我们的确定性很小，信息量很大。

$\log$的底数不一定是2，可以是其他底数。

交叉熵

在讨论了熵之后，我们讨论什么是交叉熵。
交叉熵的公式：

$$H(\bold{p}||\bold{q}) = - \sum_i p_i \log_2 q_i$$

又或者：

$$H(\bold{p}||\bold{q}) = H(\bold{p}) + D_{KL}(\bold{p}||\bold{q})$$

其中$D_{KL}(\bold{p}||\bold{q})$代表$\bold{p}$和$\bold{q}$的KL散度：

$$D_{KL}(\bold{p}||\bold{q}) = \sum p_i \log\Big( \frac{p_i}{q_i} \Big)$$

即

$$H(\bold{p}||\bold{q}) = \text{p的熵} + \text{p和q的KL散度}$$

KL散度是用于衡量2个分布之间距离的指标。当$\bold{p}$和$\bold{q}$处处相等时，即$\bold{p} = \bold{q}$时，$D_{KL}(\bold{p}||\bold{q})$取得最小值，最小值为0。
根据公式，我们也可以发现

• $D_{KL}(\bold{p}||\bold{q}) \neq D_{KL}(\bold{q}||\bold{p})$
• $H(\bold{p}||\bold{q}) \neq H(\bold{q}||\bold{p})$
  这个被称为不对称性。

特别的，当$\bold{p}$采用One-Hot编码时，$H(\bold{p}) = 0$，$H(\bold{p}||\bold{q}) = D_{KL}(\bold{p}||\bold{q})$
所以，在采用One-Hot编码的分类问题中：

$$\begin{aligned} H(\bold{p}||\bold{q}) &= D_{KL}(\bold{p}||\bold{q}) &= \sum_i y_i\log\Big(\frac{y_i}{o_i}\Big) \end{aligned}$$

而，我们也知道，在$\bold{p}$中，有且仅有一个$y_j = 1$，所以

$$H(\bold{p}||\bold{q}) = - \log{o_j}$$

其中$j$为One-Hot编码中1所在的索引号。

我们再举一个例子。
金庸的武侠小说《笑傲江湖》中有一个组合"桃谷六仙"，分别是"桃根仙"、“桃干仙”、“桃枝仙”、“桃叶仙”、“桃花仙”、“桃实仙”。

现在任意给一张照片，要求识别是六人中的哪一位？假设我们真实值是[1 0 0 0 0 0]，即桃根仙，我们的输出是[0.5 0.2 0.1 0.1 0.05 0.05]。
则其交叉熵

$$H(\bold{p}||\bold{q}) = - \log{o_j} = - \log{o_1} = - \log 0.5$$

在TensorFlow中，我们可以很方便的计算交叉熵。

tf.losses.categorical_crossentropy()

示例代码：

import tensorflow as tf

loss = tf.losses.categorical_crossentropy([1,0,0,0,0,0],[0.5,0.2,0.1,0.1,0.05,0.05])
print(loss)

运行结果：

tf.Tensor(0.6931472, shape=(), dtype=float32)

• 底数是$e$。

和机器学习、深度学习的关系

最后，我们补充一下讨神经网络和机器学习、深度学习的关系。
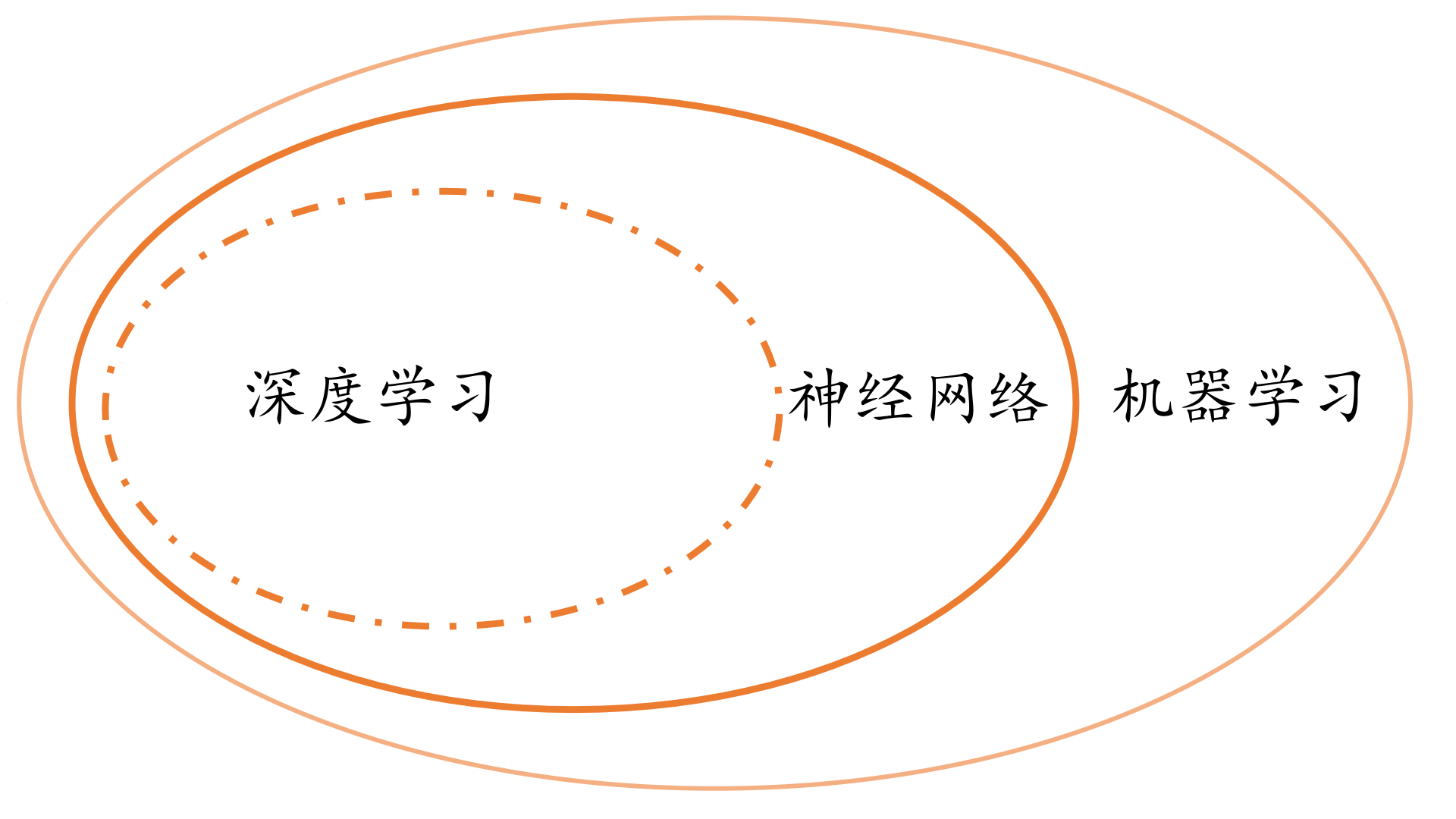
我想，用一张图，就可以说明。

其实三者之间的界限没有那么清晰。广义的机器学习包括了神经网络和深度学习，狭义的机器学习指的是机器学习和神经网络中间的那个环。广义的神经网络包括了深度学习，而深度学习特指基于深层神经网络实现的模型或算法。