3.梯度下降

上一章，我们讨论了损失函数。损失函数用以衡量模型的拟合效果。那么如何寻找一组参数，使损失函数的值最小呢？梯度下降。

梯度

首先，我们需要讨论的第一个问题，到底什么是梯度？
有很多资料一讲梯度，就拿滑雪举例子。这个例子当然是对的，但是似乎还是没讲清楚。
如果要讨论什么是梯度的话，我们可以尝试按这个框架来讨论。

$$\text{导数} \ \longrightarrow \ \text{偏导数} \ \longrightarrow \ \text{方向导数} \ \longrightarrow \ \text{梯度}$$

导数

在高中期间，我们就已经学过了导数。

$$f'(x_0) = \lim_{\Delta x \rightarrow 0}\frac{\Delta y}{\Delta x} = \frac{f(x_0+\Delta x) - f(x_0)}{\Delta x}$$

即，随着自变量$x$的变化，$y$的变化。是$y$在$x$上的变化率。

偏导数

后来，在大一的时候，我们学习了偏导数。

$$\frac{\partial f(x_0,y_0)}{\partial x} = \lim_{\Delta x \rightarrow 0}\frac{f(x_0 + \Delta x,y_0) - f(x_0,y_0)}{\Delta x}$$

即，$f(x,y)$在点$(x_0,y_0)$处对$x$的偏导数。同理，我们可以知道$f(x,y)$在点$(x_0,y_0)$处对$y$的偏导数。
函数在不同的坐标轴上的变化率就是偏导数。

方向导数

方向导数的定义

那么，函数在某点，沿着某特定方向（不一定是坐标轴）的变化率就是方向导数。

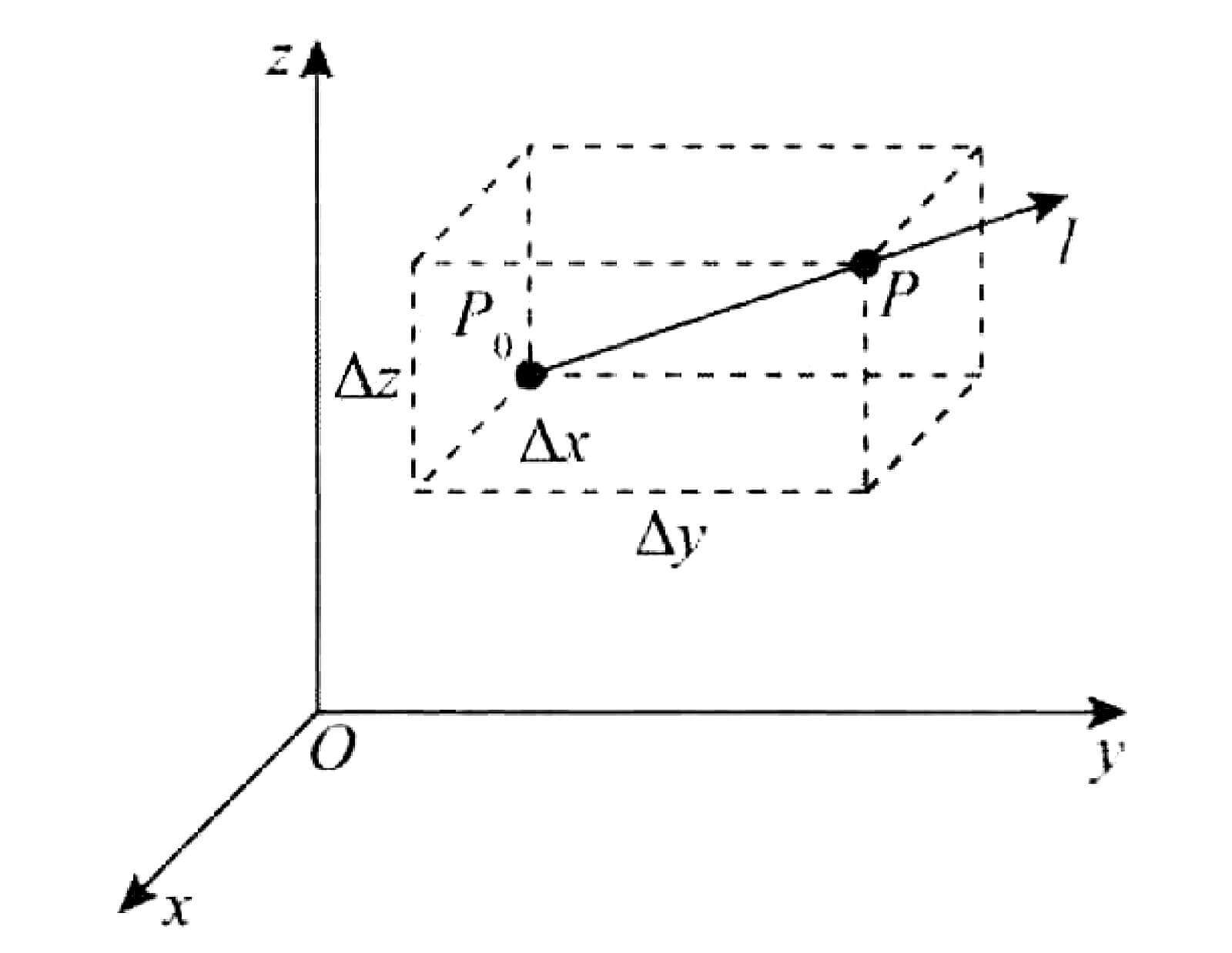
如图所示，假设存在一个三元函数$u=u(x,y,z)$在点$P_0(x_0,y_0,z_0)$的某空间领域$U\subset\bold{R}^3$内有定义，$l$为从点$P_0$出发的射线，$P(x,y,z)$为$l$上的且$U$内的任一点。则有：

$$\begin{cases} x - x_0 = \Delta x = t \cos \alpha \\ y - y_0 = \Delta y = t \cos \beta \\ z - z_0 = \Delta z = t \cos \gamma \end{cases}$$

其中$t$表示$P$到$P_0$之间的距离，$t=\sqrt{(\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2}$。

$$\lim_{t \rightarrow 0^+}\frac{u(P) - u(P_0)}{t} = \lim_{t \rightarrow 0^+}\frac{u(x_0 + t\cos\alpha,y_0 + t\cos\beta,z_0 + t\cos\gamma) - u(x_0,y_0,z_0)}{t}$$

这个极限，就是函数$u=u(x,y,z)$在$P_0$处，沿方向$l$的方向导数，记作$\frac{\partial u}{\partial l}\Big|_{p_{0}}$

方向导数的计算公式

但是有了定义还不够，根据定义，我们并不能很快的进行计算。我们还需要一个东西，计算公式。
假设存在一个三元函数$u=u(x,y,z)$在$P_0(x_0,y_0,z_0)$处可微，则有：

$$\frac{\partial u}{\partial l}\bigg|_{p_{0}} = u'_{x}(P_0)\cos\alpha + u'_{y}(P_0)\cos\beta + u'_{z}(P_0)\cos\gamma$$

其中，$\cos\alpha$、$\cos\beta$、$\cos\gamma$是方向$l$的方向余弦。
上面的公式，我们也可以写成这种形式：

$$\frac{\partial u}{\partial l}\bigg|_{p_{0}} = \left[ \begin{matrix} u'_{x}(P_0) \quad u'_{y}(P_0) \quad u'_{z}(P_0) \end{matrix} \right] \cdot \left[ \begin{matrix} \cos\alpha \\ \cos\beta \\ \cos\gamma \\ \end{matrix} \right]$$

其中，$[u'_{x}(P_0),u'_{y}(P_0),u'_{z}(P_0)]$就是$\bold{grad}\ u$，梯度。

例题

求函数$z = xe^{2y}$在点$P(1,0)$沿点$Q(2,-1)$方向的方向导数。

解：
由题意可以，方向$\overrightarrow{l}$即$\overrightarrow{PQ} = (1,-1)$，所以$x$轴到方向$\overrightarrow{l}$的转角$\alpha = - \frac{\pi}{4}$，$y$轴到方向$\overrightarrow{l}$的转角为$\beta = - \frac{3\pi}{4}$

$$\frac{\partial z}{\partial \overrightarrow{l}}\bigg|_{(1,0)} = \left[ \begin{matrix} \frac{\partial z}{\partial x}\bigg|_{(1,0)} \quad \frac{\partial z}{\partial y}\bigg|_{(1,0)} \end{matrix} \right] \cdot \left[ \begin{matrix} \cos\alpha \\ \cos\beta \end{matrix} \right] = - \frac{\sqrt{2}}{2}$$

梯度

那么，现在我们讨论第二个问题，沿着哪一个方向的方向导数最大呢？这就需要引出第二个概念，梯度。
正如我们之前讨论的，梯度的定义为：
假设存在一个三元函数$u=u(x,y,z)$在$P_0(x_0,y_0,z_0)$处具有一阶偏导数，则有：

$$\bold{grad}\ u |_{P_{0}} = (u'_x(P_0),u'_y(P_0),u'_z(P_0))$$

为函数$u = u(x,y,z)$在点$P_0$处的梯度。

那么为什么梯度的方向就是方向导数值最大的方向呢？这就不得不从方向导数和梯度的关系讲起。

方向导数和梯度的关系

正如我们之前讨论的。

$$\begin{aligned} \frac{\partial u}{\partial l}\bigg|_{p_{0}} &= \left[ \begin{matrix} u'_{x}(P_0) \quad u'_{y}(P_0) \quad u'_{z}(P_0) \end{matrix} \right] \cdot \left[ \begin{matrix} \cos\alpha \\ \cos\beta \\ \cos\gamma \\ \end{matrix} \right] \\ &= \bold{grad}\ u|_{P_0} \cdot \overrightarrow{l} \\ &= \bold{|}\bold{grad}\ u|_{P_0}\bold{|} * \bold{|}\overrightarrow{l}\bold{|} * \cos\theta \end{aligned}$$

其中，$\theta$是$\bold{grad}\ u|_{P_0}$和$\overrightarrow{l}$的夹角。而且，$\bold{|}\overrightarrow{l}\bold{|} = 1$，则有

$$\frac{\partial u}{\partial l}\bigg|_{p_{0}} = \bold{|}\bold{grad}\ u|_{P_0}\bold{|} * \cos\theta$$

显然，当$\theta = 0$时候，$\cos\theta$取得最大值，$\frac{\partial u}{\partial l}|_{p_{0}}$也取得最大值。
所以，我们得出结论。
函数在某点的梯度是一个向量，它的方向与取得最大方向导数的方向一致，而它的模为方向导数的最大值。

举例

在讨论梯度之后，我们再来举一个例子。
假设我们的损失函数为：

$$f(x,y) = x^2 + y^2$$

那么我们的目标当然是求解一组$(x,y)$使得$f(x,y)$的值最小。
根据之前的讨论，我们的更新规则是，沿着梯度的方向下降。则有：

$$x = x - lr \frac{\partial f(x,y)}{\partial x}$$

$$y = y - lr \frac{\partial f(x,y)}{\partial y}$$

其中：

$$\frac{\partial f(x,y)}{\partial x} = \frac{\partial x^2}{x} + \frac{\partial y^2}{x} = 2x$$

$$\frac{\partial f(x,y)}{\partial y} = \frac{\partial x^2}{y} + \frac{\partial y^2}{y} = 2y$$

那么，当$x=1\ y=2$时，其梯度为$(2,4)$。

求解梯度的实现方法

当然，我们不用每次都手工去求解梯度，在TensorFlow中有自动求解梯度的方法。

1. 首先，我们需要用with tf.GradientTape() as tape:把函数表达式包进去。
2. 用[w_grad] = tape.gradient(func,[w])求解梯度，传入函数和需要求解的参数。返回参数的梯度。

示例代码：

import tensorflow as tf

with tf.GradientTape() as tape:
    x = tf.Variable(1.0)
    y = tf.Variable(2.0)
    tape.watch([x,y])
    z = tf.math.pow(x,2) + tf.math.pow(y,2)

print(tape.gradient(z,[x,y]))

运行结果：

[<tf.Tensor: shape=(), dtype=float32, numpy=2.0>, <tf.Tensor: shape=(), dtype=float32, numpy=4.0>]

二阶梯度

还有一个概念是二阶梯度，这个有点像是导数的导数。

$$z = x^2 + y^2$$

则

$$\frac{\partial z}{\partial x} = 2x$$

$$\frac{\partial^2 z}{\partial x^2} = 2$$

示例代码：

import tensorflow as tf

x = tf.Variable(1.0)
y = tf.Variable(2.0)
with tf.GradientTape() as t1:
    with tf.GradientTape() as t2:
        t2.watch([x])
        z = tf.math.pow(x,2) + tf.math.pow(y,2)
    dz_dx = t2.gradient(z,[x])
    t1.watch([x])
d2z_dx2 = t1.gradient(dz_dx,[x])
print(d2z_dx2)

运行结果：

[<tf.Tensor: shape=(), dtype=float32, numpy=2.0>]

激活函数及其梯度

在上一章讨论输出层的时候，其实我们讨论的就是激活函数。这次我们会更系统的讨论一下激活函数及其梯度。
常见的激活函数有：

1. 阶跃函数
2. Sigmoid
3. Tanh
4. ReLU
5. LeakyReLu

阶跃函数

最初，人们在通过模拟青蛙的神经元，创建了第一个激活函数，阶跃函数。

$$O = \begin{cases} 1 & \text{if }\sum w_i x_i > 0 \\ 0 & \text{otherwise} \end{cases}$$

现在，我们试图对这个激活函数进行求导，其导函数非常简单：

$$O' = \begin{cases} 0 & \text{if }\sum w_i x_i \neq 0 \\ \text{不可导 } & \text{if } \sum w_i x_i = 0 \end{cases}$$

这个导函数会导致一个问题，没法梯度下降，要么是$\text{学习率} \times 0$，要么是不可导。

当时的科学家们用了一个方法，启发式搜索。

Sigmoid

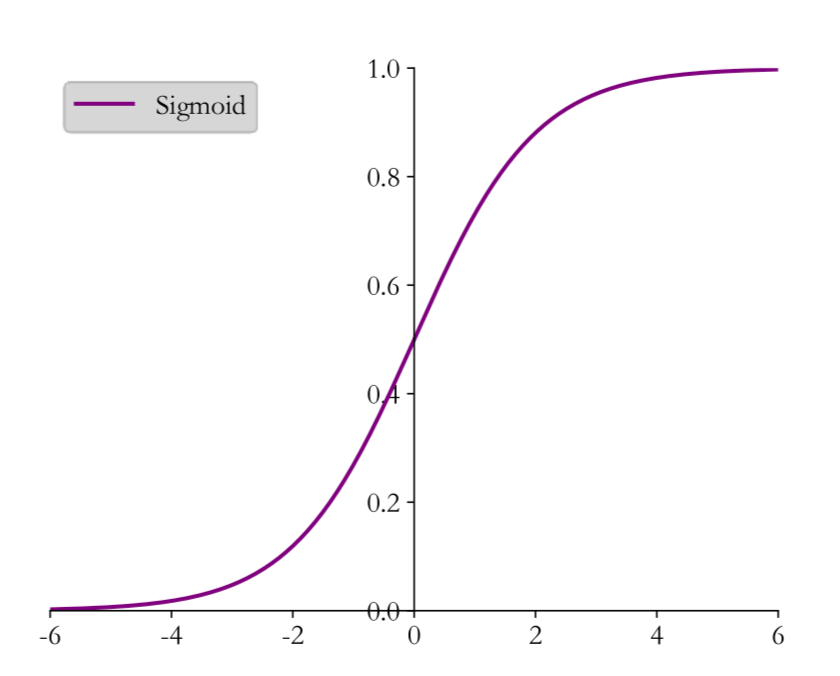
为了解决没法进行梯度下的问题，我们引入Sigmoid。

$$sigmoid(x) = \frac{1}{1 + e^{-x}}$$

Sigmoid函数处处可导，而且其值域是(0,1)。

如果我们再对Sigmoid函数进行求导，还会有惊喜发现：
Sigmoid的导函数如下：

$$sigmoid' = \frac{e^{-x}}{(1+e^{-x})^2}$$

我们对其结果进行简化。

$$\begin{aligned} \frac{e^{-x}}{(1+e^{-x})^2} &= \Big(\Big(\frac{1}{1+e^{-x}}\Big)^{-1} - 1\Big)\Big(\frac{1}{1+e^{-x}}\Big)^2 \\ &= ({sigmoid}^{-1} - 1){sigmoid}^2 \\ &= sigmoid - {sigmoid}^2 \end{aligned}$$

即

$${sigmoid}' = sigmoid - {sigmoid}^2$$

那么什么是惊喜呢？
惊喜就是求Sigmoid的导函数的值，非常方便。

在TensorFlow中，Sigmoid的实现方法是：

tf.sigmoid()

示例代码：

import tensorflow as tf

a = tf.linspace(-10,10,21)
with tf.GradientTape() as tape:
    tape.watch(a)
    y = tf.sigmoid(a)

grads = tape.gradient(y,[a])
print(grads)

运行结果：

[<tf.Tensor: shape=(21,), dtype=float64, numpy=
array([4.53958077e-05, 1.23379350e-04, 3.35237671e-04, 9.10221180e-04,
       2.46650929e-03, 6.64805667e-03, 1.76627062e-02, 4.51766597e-02,
       1.04993585e-01, 1.96611933e-01, 2.50000000e-01, 1.96611933e-01,
       1.04993585e-01, 4.51766597e-02, 1.76627062e-02, 6.64805667e-03,
       2.46650929e-03, 9.10221180e-04, 3.35237671e-04, 1.23379350e-04,
       4.53958077e-05])>]

这么看起来，Sigmoid函数似乎完美？不但可以梯度下降，求导函数的值还方便。
但，就像每一枚硬币都有正反两面。
如Sigmoid的函数图像所示，最左边一段和最右边一段，这两段，其导数值接近0。这样会导致我们用学习率去乘以一个接近与0的值，以至于参数会长时间得到不更新。这种现象被称之为梯度弥散。

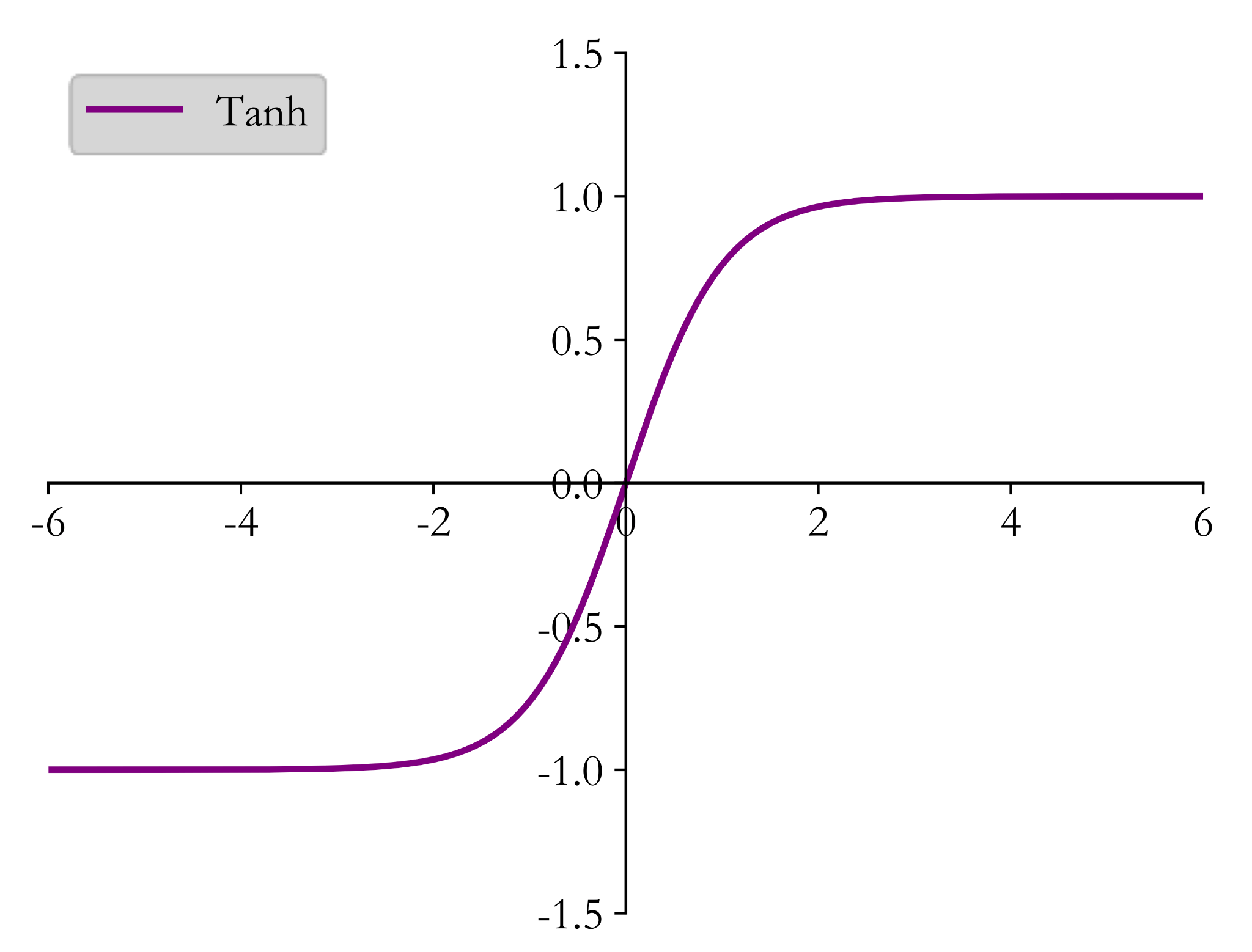
Tanh

我们再讨论一个激活函数，$\tanh$，这个激活函数在RNN中应用比较多。
不过，需要事先说明的是，这个函数不过是Sigmoid的孪生兄弟，他的优点也是求导方便，缺点也是容易导致梯度弥散。

$$tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$$

我们对其进行简单的变换，则有：

$$tanh(x) = 2 sigmoid(2x) - 1$$

我们对其进行求导，则有：

$$tanh' = 1 - tanh^2$$

在TensorFlow中，Tanh的实现方法是：

tf.tanh()

示例代码：

import tensorflow as tf

a = tf.linspace(-10,10,21)
with tf.GradientTape() as tape:
    tape.watch(a)
    y = tf.tanh(a)

grads = tape.gradient(y,[a])
print(grads)

运行结果：

[<tf.Tensor: shape=(21,), dtype=float64, numpy=
array([8.24461455e-09, 6.09199171e-08, 4.50140598e-07, 3.32610934e-06,
       2.45765474e-05, 1.81583231e-04, 1.34095068e-03, 9.86603717e-03,
       7.06508249e-02, 4.19974342e-01, 1.00000000e+00, 4.19974342e-01,
       7.06508249e-02, 9.86603717e-03, 1.34095068e-03, 1.81583231e-04,
       2.45765474e-05, 3.32610934e-06, 4.50140598e-07, 6.09199171e-08,
       8.24461455e-09])>]

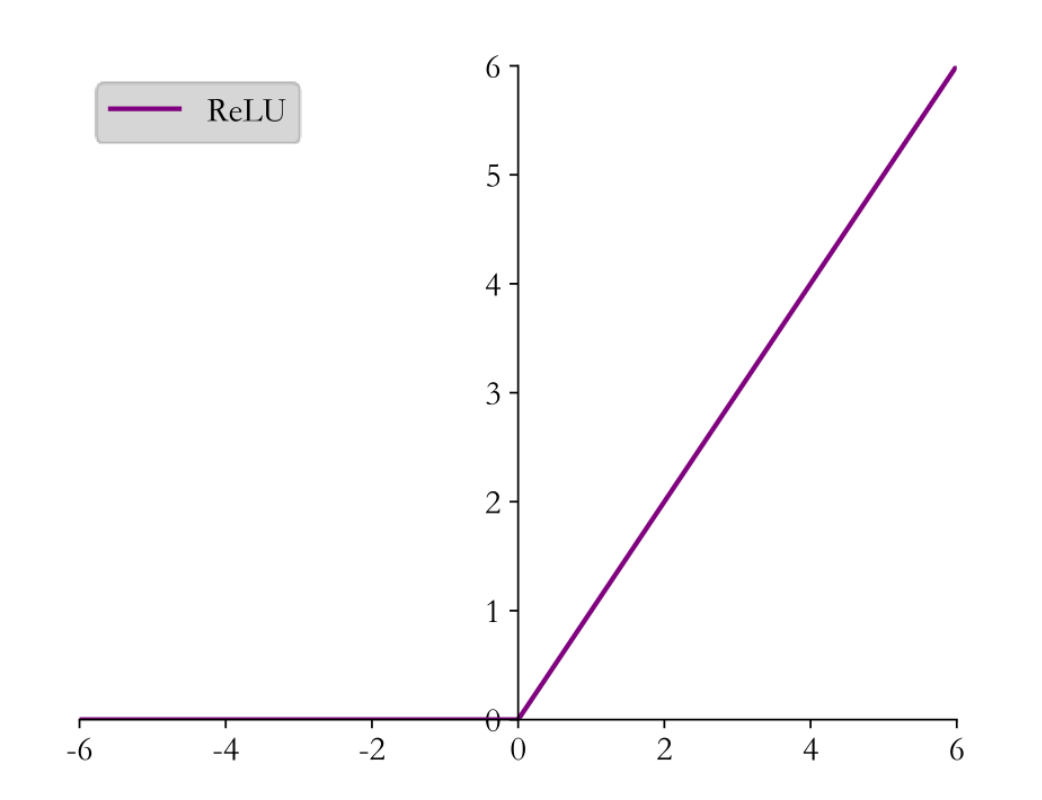
ReLU

ReLU函数，非常的简单，重剑无锋，大巧不工。
ReLU也被称为深度学习的奠基石。其全称是Rectified Linear Unit，译作线性整流函数。

$$relu(x) = \begin{cases} x & \text{for } x \ge 0 \\ 0 & \text{for } x < 0 \end{cases}$$

ReLU的导函数也非常简单。

$$relu'(x) = \begin{cases} 1 & \text{for } x \ge 0 \\ 0 & \text{for } x < 0 \end{cases}$$

在TensorFlow中，ReLU的实现方法是：

tf.nn.relu()

示例代码：

import tensorflow as tf

a = tf.linspace(-10,10,21)
with tf.GradientTape() as tape:
    tape.watch(a)
    y = tf.nn.relu(a)

grads = tape.gradient(y,[a])
print(grads)

运行结果：

[<tf.Tensor: shape=(21,), dtype=float64, numpy=
array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1.])>]

正如运行结果所示，ReLU函数的的缺点是，当$x<0$时，其导数值恒为$0$。同样会出现梯度弥散现象。

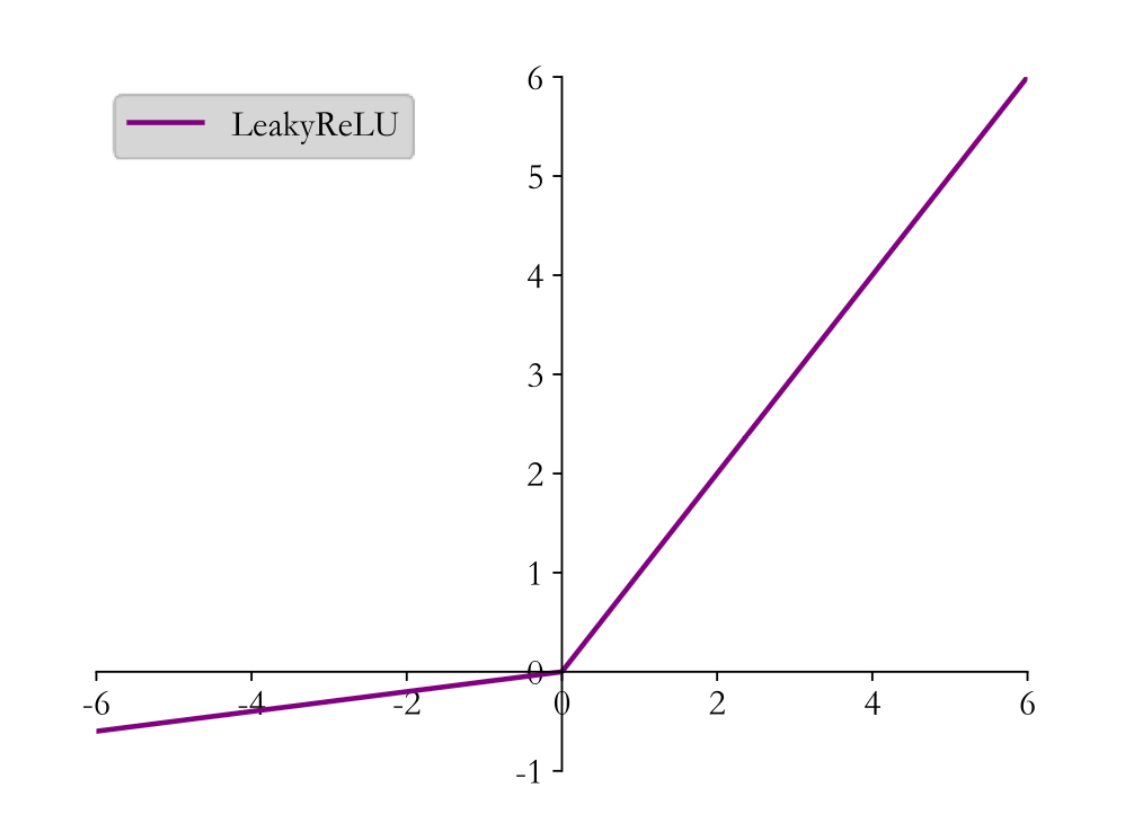
LeakyReLU

为了克服ReLU函数的梯度弥散问题，我们再引入一个激活函数，LeakyReLU。

$$leakyrelu(x) = \begin{cases} x & \text{for } x \ge 0 \\ px & \text{for } x < 0 \end{cases}$$

其中$p$是一个超参数，通常设置为一个较小的值，在TensorFlow中默认为0.2。

$$leakyrelu'(x) = \begin{cases} 1 & \text{for } x \ge 0 \\ p & \text{for } x < 0 \end{cases}$$

在TensorFlow中，LeakyReLU的实现方法是：

tf.nn.leaky_relu()

示例代码：

import tensorflow as tf

a = tf.linspace(-10,10,21)
with tf.GradientTape() as tape:
    tape.watch(a)
    y = tf.nn.leaky_relu(a,alpha=0.01)

grads = tape.gradient(y,[a])
print(grads)

运行结果：

[<tf.Tensor: shape=(21,), dtype=float64, numpy=
array([0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01,
       1.  , 1.  , 1.  , 1.  , 1.  , 1.  , 1.  , 1.  , 1.  , 1.  ])>]

如何选择激活函数

现在，我们来讨论一个问题，哪个激活函数是最好的？

我想，这个问题，金庸先生已经给出了我们答案。独孤求败在不同的情况下，用了不同的剑。每一个人要选择适合自己的剑，就像杨过，选择的是玄铁重剑。

我们选择激活函数，也要在不同的情况下，选择不同的激活函数。

几个经验总结有：

1. 如果输出是0、1值（二分类问题），则输出层选择Sigmoid函数，然后其它的所有单元都选择ReLU函数。
2. 如果在隐藏层上不确定使用哪个激活函数，那么通常会使用ReLU激活函数。有时，也会使用tanh激活函数。
3. Sigmoid激活函数：除了输出层是一个二分类问题基本不会用它。
4. ReLU激活函数：最常用的默认函数，如果不确定用哪个激活函数，就使用ReLu或者Leaky ReLU，再去尝试其他的激活函数。
5. 如果遇到了一些死的神经元，我们可以使用Leaky ReLU函数。

损失函数及其梯度

损失函数，其实在上一章，我们已经讨论过了。

1. 均方误差(MSE)
2. 交叉熵损失(Cross Entropy Loss)

这一章，我们主要讨论损失函数的梯度。

均方误差

均方误差的公式：

$$MSE(\bold{y},\bold{o}) = \frac{1}{d_{out}}\sum_{i=1}^{d_{out}}(y_i - o_i)^2$$

但是，这个公式求导计算不方便。所以，我们考虑进行缩放，因为缩放并不会改变梯度的方向。这就是我们说的非标的均方误差
缩放后的均方误差公式：

$$L = \frac{1}{2}\sum_{k=1}^K\big(y_k - o_k)^2$$

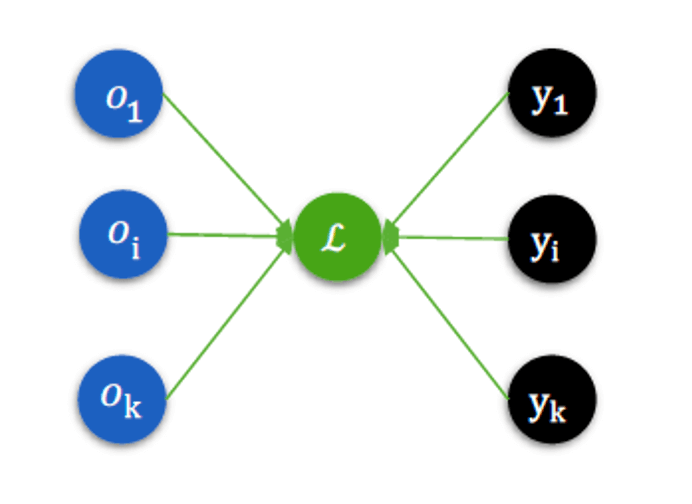
我们还可以用一张图来描述均方误差，这样有助于我们计算均方误差的梯度。

现在，我们求$\frac{\partial L}{\partial o_i}$

$$\begin{aligned} \frac{\partial L}{\partial o_i} &= \sum_{k=1}^{K}(y_k - o_k) \frac{\partial (y_k - o_k)}{\partial o_i} \\ &= \sum_{k = 1}^{K}(y_k - o_k) * -1 * \frac{\partial o_k}{\partial o_i} \end{aligned}$$

由图像，我们也可以看出，当$k \neq i$时，$o_k$和$o_i$是没有关系的，$\frac{\partial o_k}{\partial o_i} = 0$。但是，当且仅当$k=i$的时候，$\frac{\partial o_k}{\partial o_i} = 1$。
所以，我们有

$$\frac{\partial L}{\partial o_i} = (o_i - y_i)$$

示例代码：

import tensorflow as tf

y = tf.constant([1.,2.,3.])
o = tf.constant([2.,2.,3.])

with tf.GradientTape() as tape:
    tape.watch([o])
    # 因为使用的是非标的均方误差，所以自己写一个。
    loss = tf.square(y - o)/2

grads = tape.gradient(loss,[o])
print(grads)

运行结果：

[<tf.Tensor: shape=(3,), dtype=float32, numpy=array([ 1., -0., -0.], dtype=float32)>]

交叉熵损失

交叉熵损失通常和Softmax配合使用，我们先讨论Softmax。

Softmax

$$p_i = \frac{e^{z_i}}{\sum_{k=1}^{K} e^{z_k}}$$

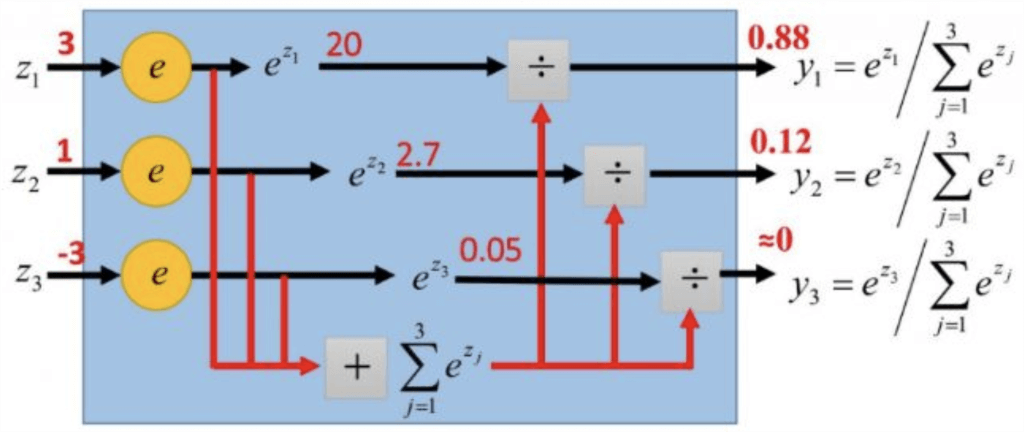
正如我们上一章所讨论的，Softmax的作用是将$K$个输出节点映射为概率，并保证概率之和为$1$。

如图所示：

$$y_1 = \frac{e^{z_1}}{e^{z_1} + e^{z_2} + e^{z_3}}$$

首先，我们讨论$\frac{\partial y_1}{\partial z_1}$，也就是$i=j$时。

$$\begin{aligned} \frac{\partial y_1}{\partial z_1} &= \frac{e^{z_1}(e^{z_1} + e^{z_2} + e^{z_3}) - e^{z_1}e^{z_1}}{(e^{z_1} + e^{z_2} + e^{z_3})^2} \\ &= \frac{e^{z_1}(e^{z_1} + e^{z_2} + e^{z_3} - e^{z_1})}{(e^{z_1} + e^{z_2} + e^{z_3})^2} \\ &= \frac{e^{z_1}}{(e^{z_1} + e^{z_2} + e^{z_3})^2} \times \frac{e^{z_1} + e^{z_2} + e^{z_3} - e^{z_1}}{e^{z_1} + e^{z_2} + e^{z_3}} \\ &= y_1(1- y_1) \end{aligned}$$

然后，我们再讨论一个，$\frac{\partial y_1}{\partial z_2}$，也就是$i\neq j$时。

$$\begin{aligned} \frac{\partial y_1}{\partial z_2} &= \frac{0 - e^{z_1}e^{z_2}}{e^{z_1} + e^{z_2} + e^{z_3}} \\ &= - y_1 y_2 \end{aligned}$$

现在，我们把这个推广到一般的形式。

$$p_i = \frac{e^{z_i}}{\sum_{k=1}^{K} e^{z_k}}$$

• 当$i=j$时，有：

$$\begin{aligned} \frac{\partial p_i}{\partial z_j} &= \frac{e^{z_i}(\sum_{k=1}^K e^{z_k}) - e^{z_i}e^{z_j}}{(\sum_{k=1}^K e^{z_k})^2} \\ &= \frac{e^{z_i}}{\sum_{k=1}^{K} e^{z_k}} \times \frac{\sum_{k=1}^{K} e^{z_k} - e^{z_j}}{\sum_{k=1}^{K} e^{z_k}} \\ &= p_i(1-p_j) \end{aligned}$$

• 当$i\neq j$时，有：

$$\begin{aligned} \frac{\partial p_i}{\partial z_j} &= \frac{- e^{z_i}e^{z_j}}{(\sum_{k=1}^K e^{z_k})^2} \\ &= - p_i p_j \end{aligned}$$

交叉熵损失

交叉熵：

$$\begin{aligned} H(\bold{p}||\bold{q}) &= D_{KL}(\bold{p}||\bold{q}) &= \sum_i y_i\log\Big(\frac{y_i}{o_i}\Big) \end{aligned}$$

如果我们用$y$表示真实值，用$p$表示预测值，用$L$表示损失函数，则有：

$$L = - \sum_{k=1}^{K} y_k \log(p_k)$$

则，损失函数对$z_i$的偏导数为：

$$\frac{\partial L}{\partial z_i} = - \sum_{k=1}^{K} y_k \frac{\partial \log(p_k)}{\partial z_i}$$

根据复合函数的求导法则，我们还有：

$$\begin{aligned} \frac{\partial L}{\partial z_i} &= - \sum_{k=1}^{K} y_k \frac{\partial \log(p_k)}{\partial p_k} \cdot \frac{\partial p_k}{\partial z_i} \\ &= - \sum_{k=1}^{K} y_k \frac{1}{p_k} \cdot \frac{\partial p_k}{\partial z_i} \end{aligned}$$

那么，$\frac{\partial p_k}{\partial z_i}$等于多少呢？回到上一步，Softmax。
上式中，$k$从$1$一直到$K$，有且仅有一次，$k=i$，所以，我们可以把上式拆开，有：

$$\begin{aligned} \frac{\partial L}{\partial z_i} &= -y_i(1-p_i) - \sum_{k \neq i}^{K} y_k \frac{1}{p_k}(- p_k p_i) \\ &= -y_i(1-p_i) + \sum_{k \neq i}^{K} y_k p_i \\ &= p_i\Big( y_i + \sum_{k \neq i}^{K} y_k) - y_i \Big) \end{aligned}$$

特别的，当$\bold{p}$采用One-Hot编码时。

$$L = - \sum_k y_k \log (P_k)$$

根据复合函数求导法则。$f(g(x))$，令$u = g(x)$，则有

$$\frac{\partial f(g(x))}{\partial x} = \frac{\partial f(u)}{\partial u} \frac{\partial g(x)}{\partial x} = f'(u) g'(x)$$

可以求得交叉熵损失的导数为

$$\frac{\partial L}{\partial z_i} = p_i \Big( y_i + \sum_{k \neq i} y_k \Big) - y_i$$

特别的，对于用One-Hot编码表示的标签y，有

$$\sum_k y_k = 1$$

$$y_i + \sum_{k \neq i}y_k = 1$$

因此有

$$\frac{\partial L}{\partial z_i} = p_i - y_i$$

示例代码：

import tensorflow as tf

# 两个样本，每个样本有4个特征
x = tf.random.normal([2,4])
# 权重
w = tf.random.normal([4,3])
# 偏置
b = tf.zeros([3])
# 两个样本的分类
y = tf.constant([2,0])
# 共有三种类别
y = tf.one_hot(y,depth=3)

with tf.GradientTape() as tape:
    tape.watch([w,b])
    logits = x@w + b
    loss = tf.reduce_mean(tf.losses.categorical_crossentropy(y,logits,from_logits=True))

grads = tape.gradient(loss,[w,b])
print(grads[0])
print(grads[1])

运行结果：

tf.Tensor(
[[ 0.14168215  0.0084892  -0.15017135]
 [-0.08154044 -0.09412258  0.17566304]
 [ 0.07595219  0.01904502 -0.0949972 ]
 [-0.03096705  0.0171328   0.01383425]], shape=(4, 3), dtype=float32)
tf.Tensor([-0.12995178  0.07289901  0.05705276], shape=(3,), dtype=float32)

全连接层及其梯度

截止目前，我们讨论了激活函数及其梯度，损失函数及其梯度。现在我们把两者串在一起，讨论全连接层及其梯度。

一个输出节点的全连接层

首先，我们从最简单的，只有一个输出节点的情况开始。

• $x_1$、$x_2$、$x_j$、$x_J$代表输入节点。
• $w^{(1)}_{j1}$代表第一层，$j1$代表第$j$个到下一层第$1$个节点的连接，上标$(1)$代表第一层，在这里只有一层。
• $o_1^{(1)}$代表输出节点，下标$1$代表第一个输出节点，上标$(1)$代表第一层。在这里只有一层一个。

我们采用均方误差作为损失函数，为了便于计算，采用的是非标的均方误差，这个我们之前已经讨论过了，不影响梯度的方向。

为了表达方便，我们把上标省略。

$$loss = \frac{1}{2}\Big( o_1^{(1)} - t \Big)^2 = \frac{1}{2}(o_1 - t)^2$$

则，$loss$对于$w_{j1}$的偏导数为：

$$\frac{\partial loss}{\partial w_{j1}} = (o_1 - t)\frac{\partial o_1}{\partial w_{j1}}$$

而$o_1 = sigmoid(z_1)$，${sigmoid}' = sigmoid - {sigmoid}^2$，则有：

$$\frac{\partial loss}{\partial w_{j1}} = (o_1 - t)(sigmoid(z_1) - sigmoid(z_1)^2)\frac{\partial z_1}{\partial w_{j1}}$$

其中$\frac{\partial z_1}{\partial w_{j1}} = x_j$，则有：

$$\frac{\partial loss}{\partial w_{j1}} = (o_1 - t)(sigmoid(z_1) - sigmoid(z_1)^2)x_j$$

我们再把$sigmoid(z_1)$写回$o_1$：

$$\frac{\partial loss}{\partial w_{j1}} = (o_1 - t)(o_1 - {o_1}^2)x_j$$

示例代码：

import tensorflow as tf

x = tf.random.normal([1,3])
w = tf.ones([3,1])
b = tf.ones([1])
y = tf.constant([1])

with tf.GradientTape() as tape:
    tape.watch([w,b])
    logits = tf.sigmoid(x@w + b)
    loss = tf.reduce_mean(tf.losses.MSE(y,logits))

grads = tape.gradient(loss,[w,b])
print(grads[0])
print(grads[1])

运行结果：

tf.Tensor(
[[-0.00134863]
 [-0.00221338]
 [-0.00171576]], shape=(3, 1), dtype=float32)
tf.Tensor([-0.00225344], shape=(1,), dtype=float32)

多个输出节点的全连接层

现在，我们把一个输出节点的全连接层扩展到多个输出节点的全连接层。

同样，我们采用非标准的均方误差作为损失函数。

$$loss = \frac{1}{2}\sum_{i=1}^{K}\Big( o_i^{(1)} - t_i \Big)^2$$

而且，如图所示，我们发现$w^{(1)}_{jk}$只会影响$z^{(1)}_k$，进而只会影响$o^{(1)}_k$。因此，我们有

$$\frac{\partial loss}{\partial w_{jk}} = (o_k - t_k)\frac{\partial o_k}{w_{jk}}$$

与之前的讨论类似。$o_k = sigmoid(z_k)$，${sigmoid}' = sigmoid - {sigmoid}^2$，则有：

$$\frac{\partial loss}{\partial w_{jk}} = (o_k - t_k)(sigmoid(z_k) - sigmoid(z_k)^2)\frac{\partial z_k}{\partial w_{jk}}$$

其中$\frac{\partial z_k}{\partial w_{jk}} = x_j$，则有：

$$\frac{\partial loss}{\partial w_{jk}} = (o_k - t_k)(sigmoid(z_k) - sigmoid(z_k)^2)x_j$$

我们再把$sigmoid(z_k)$写回$o_k$：

$$\frac{\partial loss}{\partial w_{jk}} = (o_k - t_k)(o_k - o_k^2)x_j$$

示例代码：

import tensorflow as tf

x = tf.random.normal([2,4])
w = tf.ones([4,3])
b = tf.ones([3])
y = tf.constant([2,0])
y = tf.one_hot(y,depth=3)

with tf.GradientTape() as tape:
    tape.watch([w,b])
    prob = tf.nn.softmax(x@w + b,axis=1)
    loss = tf.reduce_mean(tf.losses.MSE(y,prob))

grads = tape.gradient(loss,[w,b])
print(grads[0])
print(grads[1])

运行结果：

tf.Tensor(
[[-0.02149573 -0.02382743  0.04532316]
 [-0.00848718  0.1299872  -0.12150002]
 [ 0.16653773 -0.00511115 -0.16142657]
 [-0.11861646  0.05700291  0.06161355]], shape=(4, 3), dtype=float32)
tf.Tensor([-0.03703704  0.07407407 -0.03703704], shape=(3,), dtype=float32)