特别注意!我们整章所有涉及的反向传播都是针对多层全连接层,有且只有Sigmoid一种激活函数,并且损失函数为均方误差。对于其他类型的网络,需要重新进行推导,但是整体方法都是一样的。
链式法则
链式法则其实在上一章我们已经用过了,就是复合函数的求导法则。f ( u ) f(u) f ( u ) u u u u = g ( x ) u = g(x) u = g ( x )
∂ f ( g ( x ) ) ∂ x = ∂ f ( u ) ∂ u ∂ g ( x ) ∂ x = f ′ ( u ) g ′ ( x ) \frac{\partial f(g(x))}{\partial x} = \frac{\partial f(u)}{\partial u} \frac{\partial g(x)}{\partial x} = f'(u) g'(x)
∂ x ∂ f ( g ( x ) ) = ∂ u ∂ f ( u ) ∂ x ∂ g ( x ) = f ′ ( u ) g ′ ( x )
例:
令 y = f ( 3 x − 2 3 x + 2 ) , f ′ ( x ) = arctan ( x ) , 求 ∂ y ∂ x \text{令}y = f\Big(\frac{3x-2}{3x+2}\Big),f'(x) = \arctan(x),\text{求}\frac{\partial y}{\partial x}
令 y = f ( 3 x + 2 3 x − 2 ) , f ′ ( x ) = arctan ( x ) , 求 ∂ x ∂ y
解:
∂ y ∂ x = f ′ ( 3 x − 2 3 x + 2 ) ( 3 ( 3 x + 2 ) − ( 3 x − 2 ) 3 ( 3 x + 2 ) 2 ) = arctan ( 3 x − 2 3 x + 2 ) ( 3 ( 3 x + 2 ) − ( 3 x − 2 ) 3 ( 3 x + 2 ) 2 ) \begin{aligned}
\frac{\partial y}{\partial x} &= f'\Big(\frac{3x-2}{3x+2}\Big) \Big(\frac{3(3x+2) - (3x-2)3}{(3x+2)^2}\Big) \\
&= \arctan\Big(\frac{3x-2}{3x+2}\Big) \Big(\frac{3(3x+2) - (3x-2)3}{(3x+2)^2}\Big)
\end{aligned}
∂ x ∂ y = f ′ ( 3 x + 2 3 x − 2 ) ( ( 3 x + 2 ) 2 3 ( 3 x + 2 ) − ( 3 x − 2 ) 3 ) = arctan ( 3 x + 2 3 x − 2 ) ( ( 3 x + 2 ) 2 3 ( 3 x + 2 ) − ( 3 x − 2 ) 3 )
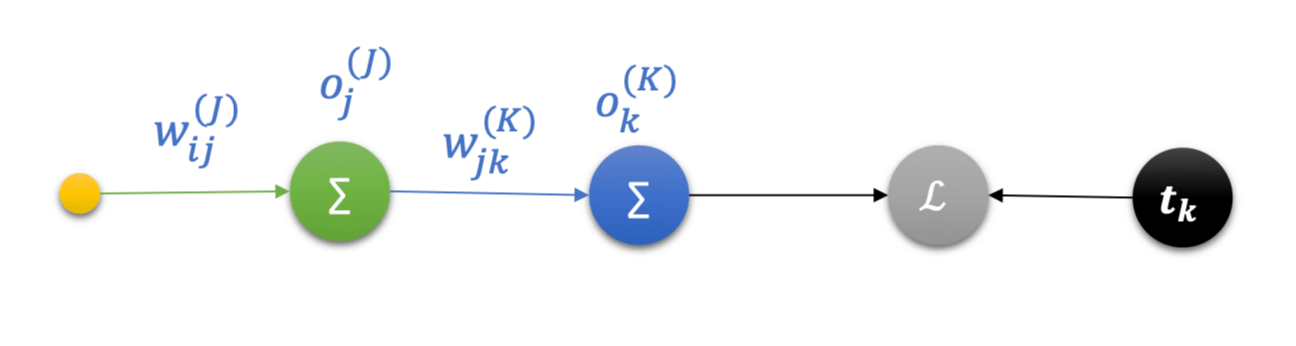
又如,存在一个模型如下:w i j ( J ) w_{ij}^{(J)} w i j ( J ) o j ( J ) o_j^{(J)} o j ( J ) w j k ( K ) w_{jk}^{(K)} w j k ( K ) o k ( K ) o_k^{(K)} o k ( K ) t k t_k t k L L L
∂ L ∂ w i j ( J ) = ∂ L ∂ o k ( K ) o k ( K ) o j ( J ) o j ( J ) w i j ( J ) \frac{\partial L}{\partial w_{ij}^{(J)}} = \frac{\partial L}{\partial o_k^{(K)}}\frac{o_k^{(K)}}{o_j^{(J)}}\frac{o_j^{(J)}}{w_{ij}^{(J)}}
∂ w i j ( J ) ∂ L = ∂ o k ( K ) ∂ L o j ( J ) o k ( K ) w i j ( J ) o j ( J )
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 import tensorflow as tfx = tf.constant(1.2 ) w1 = tf.constant(2.3 ) b1 = tf.constant(3.4 ) w2 = tf.constant(4.5 ) b2 = tf.constant(5.6 ) with tf.GradientTape(persistent=True ) as tape: tape.watch([w1,b1,w2,b2]) y1 = x * w1 + b1 y2 = y1 * w2 + b2 dy2_dy1 = tape.gradient(y2,y1) dy1_dw1 = tape.gradient(y1,w1) dy2_dw1 = tape.gradient(y2,w1) print(dy2_dy1) print(dy1_dw1) print(dy2_dy1 * dy1_dw1) print(dy2_dw1)
运行结果:
1 2 3 4 tf.Tensor(4.5, shape=(), dtype=float32) tf.Tensor(1.2, shape=(), dtype=float32) tf.Tensor(5.4, shape=(), dtype=float32) tf.Tensor(5.4, shape=(), dtype=float32)
反向传播算法
我们以红烧肉这道菜为例,来讨论反向传播算法。顾客说咸了这个信号,传递给买菜的小伙,买菜小伙以此调整他的"买菜函数"。
这就是反向传播算法,误差以某种形式在各层的表现,并以此来修正各层的权重。
推导
在上面的例子中,一开始,我们只有厨师这一层。这是单层的情况,这个问题,我们在上一章已经讨论过了。
∂ l o s s ∂ w j k = ( o k − t k ) ( o k − o k 2 ) x j \frac{\partial loss}{\partial w_{jk}} = (o_k - t_k)(o_k - o_k^2)x_j
∂ w j k ∂ l o s s = ( o k − t k ) ( o k − o k 2 ) x j
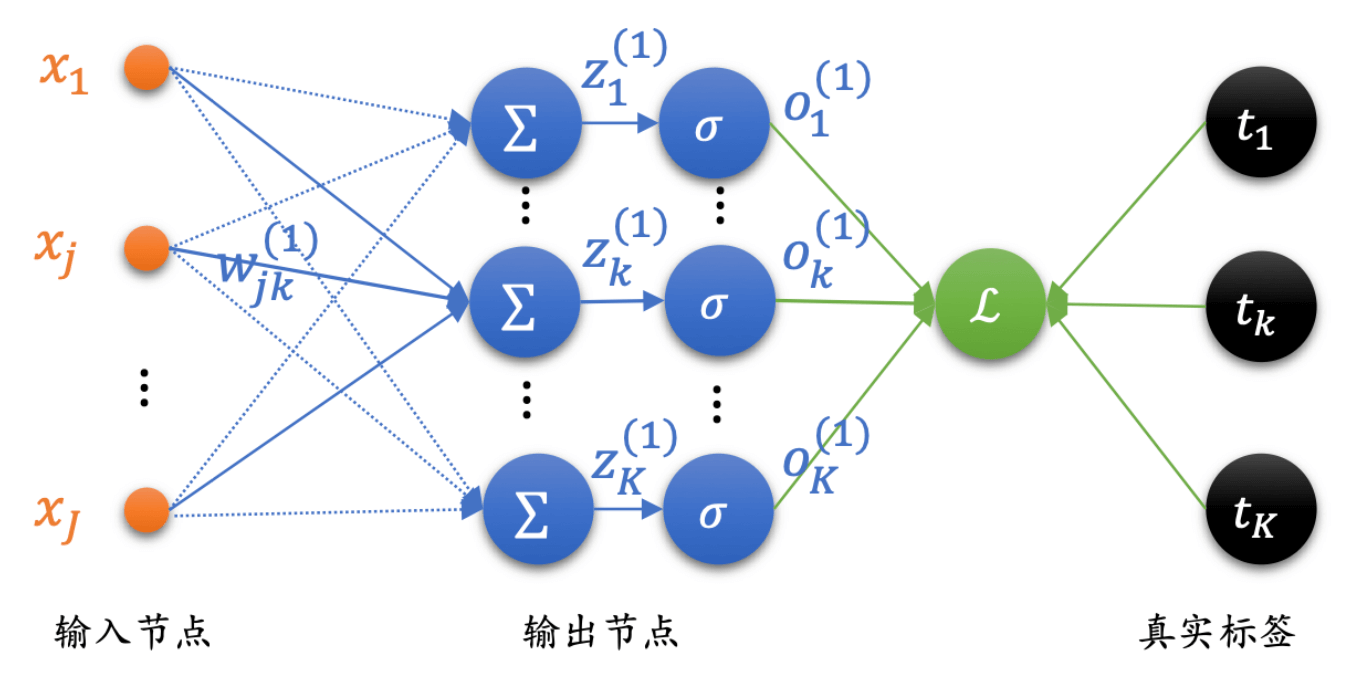
后来,我们把买菜小伙找来了,这时候就是多层。多层神经网络的结构如下:
l o s s = 1 2 ∑ k = 1 K ( o k − t k ) 2 loss = \frac{1}{2}\sum_{k = 1}^{K}\Big( o_k - t_k \Big)^2
l o s s = 2 1 k = 1 ∑ K ( o k − t k ) 2
同样,我们求损失函数的梯度,则有:
∂ l o s s ∂ w i j = ∂ ∂ w i j 1 2 ∑ k = 1 K ( o k − t k ) 2 = ∑ k = 1 K ( o k − t k ) ∂ ∂ w i j o k \begin{aligned}
\frac{\partial loss}{\partial w_{ij}} &= \frac{\partial}{\partial w_{ij}}\frac{1}{2}\sum_{k = 1}^{K}\Big(o_k - t_k\Big)^2 \\
&= \sum_{k = 1}^{K}(o_k - t_k)\frac{\partial}{\partial w_{ij}}o_k
\end{aligned}
∂ w i j ∂ l o s s = ∂ w i j ∂ 2 1 k = 1 ∑ K ( o k − t k ) 2 = k = 1 ∑ K ( o k − t k ) ∂ w i j ∂ o k
而其中,o k = s i g m o i d ( z k ) o_k = sigmoid(z_k) o k = s i g m o i d ( z k ) s i g m o i d ′ = s i g m o i d − s i g m o i d 2 {sigmoid}' = sigmoid - {sigmoid}^2 s i g m o i d ′ = s i g m o i d − s i g m o i d 2
∂ l o s s ∂ w i j = ∑ k = 1 K ( o k − t k ) ∂ ∂ w i j s i g m o i d ( z k ) = ∑ k = 1 K ( o k − t k ) ( s i g m o i d ( z k ) − s i g m o i d ( z k ) 2 ) ∂ z k ∂ w i j \begin{aligned}
\frac{\partial loss}{\partial w_{ij}} &= \sum_{k = 1}^{K}(o_k - t_k)\frac{\partial}{\partial w_{ij}}sigmoid(z_k) \\
&= \sum_{k = 1}^{K}(o_k - t_k)(sigmoid(z_k) - sigmoid(z_k)^2)\frac{\partial z_k}{\partial w_{ij}}
\end{aligned}
∂ w i j ∂ l o s s = k = 1 ∑ K ( o k − t k ) ∂ w i j ∂ s i g m o i d ( z k ) = k = 1 ∑ K ( o k − t k ) ( s i g m o i d ( z k ) − s i g m o i d ( z k ) 2 ) ∂ w i j ∂ z k
我们再把s i g m o i d ( z k ) sigmoid(z_k) s i g m o i d ( z k ) o k o_k o k
∂ l o s s ∂ w i j = ∑ k = 1 K ( o k − t k ) ( o k − o k 2 ) ∂ z k ∂ w i j \frac{\partial loss}{\partial w_{ij}} = \sum_{k = 1}^{K}(o_k - t_k)(o_k - o_k^2)\frac{\partial z_k}{\partial w_{ij}}
∂ w i j ∂ l o s s = k = 1 ∑ K ( o k − t k ) ( o k − o k 2 ) ∂ w i j ∂ z k
而,关于∂ z k ∂ w i j \frac{\partial z_k}{\partial w_{ij}} ∂ w i j ∂ z k
∂ z k ∂ w i j = ∂ z k ∂ o j ∂ o j ∂ w i j \frac{\partial z_k}{\partial w_{ij}} = \frac{\partial z_k}{\partial o_j}\frac{\partial o_j}{\partial w_{ij}}
∂ w i j ∂ z k = ∂ o j ∂ z k ∂ w i j ∂ o j
因此,有:
∂ l o s s ∂ w i j = ∑ k = 1 K ( o k − t k ) ( o k − o k 2 ) ∂ z k ∂ o j ∂ o j ∂ w i j \frac{\partial loss}{\partial w_{ij}} = \sum_{k = 1}^{K}(o_k - t_k)(o_k - o_k^2)\frac{\partial z_k}{\partial o_j}\frac{\partial o_j}{\partial w_{ij}}
∂ w i j ∂ l o s s = k = 1 ∑ K ( o k − t k ) ( o k − o k 2 ) ∂ o j ∂ z k ∂ w i j ∂ o j
而,关于∂ z k ∂ o j \frac{\partial z_k}{\partial o_j} ∂ o j ∂ z k
∂ z k ∂ o j = w j k \frac{\partial z_k}{\partial o_j} = w_{jk}
∂ o j ∂ z k = w j k
因此,有:
∂ l o s s ∂ w i j = ∑ k = 1 K ( o k − t k ) ( o k − o k 2 ) w j k ∂ o j ∂ w i j \frac{\partial loss}{\partial w_{ij}} = \sum_{k = 1}^{K}(o_k - t_k)(o_k - o_k^2)w_{jk}\frac{\partial o_j}{\partial w_{ij}}
∂ w i j ∂ l o s s = k = 1 ∑ K ( o k − t k ) ( o k − o k 2 ) w j k ∂ w i j ∂ o j
同样,o j = s i g m o i d ( z j ) o_j = sigmoid(z_j) o j = s i g m o i d ( z j ) s i g m o i d ′ = s i g m o i d − s i g m o i d 2 {sigmoid}' = sigmoid - {sigmoid}^2 s i g m o i d ′ = s i g m o i d − s i g m o i d 2
∂ l o s s ∂ w i j = ∑ k = 1 K ( o k − t k ) ( o k − o k 2 ) w j k ( o j − o j 2 ) ∂ z j ∂ w i j \frac{\partial loss}{\partial w_{ij}} = \sum_{k = 1}^{K}(o_k - t_k)(o_k - o_k^2)w_{jk}(o_j - o_j^2)\frac{\partial z_j}{\partial w_{ij}}
∂ w i j ∂ l o s s = k = 1 ∑ K ( o k − t k ) ( o k − o k 2 ) w j k ( o j − o j 2 ) ∂ w i j ∂ z j
而,关于∂ z j ∂ w i j \frac{\partial z_j}{\partial w_{ij}} ∂ w i j ∂ z j
∂ z j ∂ w i j = o i \frac{\partial z_j}{\partial w_{ij}} = o_i
∂ w i j ∂ z j = o i
因此,有:
∂ l o s s ∂ w i j = ∑ k = 1 K ( o k − t k ) ( o k − o k 2 ) w j k ( o j − o j 2 ) o i \frac{\partial loss}{\partial w_{ij}} = \sum_{k = 1}^{K}(o_k - t_k)(o_k - o_k^2)w_{jk}(o_j - o_j^2)o_i
∂ w i j ∂ l o s s = k = 1 ∑ K ( o k − t k ) ( o k − o k 2 ) w j k ( o j − o j 2 ) o i
同时,我们发现( o j − o j 2 ) o i (o_j - o_j^2)o_i ( o j − o j 2 ) o i k k k k k k ( o j − o j 2 ) o i (o_j - o_j^2)o_i ( o j − o j 2 ) o i ( o j − o j 2 ) o i (o_j - o_j^2)o_i ( o j − o j 2 ) o i
∂ l o s s ∂ w i j = ( o j − o j 2 ) o i ∑ k = 1 K ( o k − t k ) ( o k − o k 2 ) w j k \frac{\partial loss}{\partial w_{ij}} = (o_j - o_j^2)o_i\sum_{k = 1}^{K}(o_k - t_k)(o_k - o_k^2)w_{jk}
∂ w i j ∂ l o s s = ( o j − o j 2 ) o i k = 1 ∑ K ( o k − t k ) ( o k − o k 2 ) w j k
我们用δ k \delta_k δ k ( o k − t k ) ( o k − o k 2 ) (o_k - t_k)(o_k - o_k^2) ( o k − t k ) ( o k − o k 2 )
∂ l o s s ∂ w i j = ( o j − o j 2 ) o i ∑ k = 1 K δ k w j k = o i ( o j − o j 2 ) ∑ k = 1 K δ k w j k \begin{aligned}
\frac{\partial loss}{\partial w_{ij}} &= (o_j - o_j^2)o_i\sum_{k = 1}^{K}\delta_k w_{jk} \\
&= o_i(o_j - o_j^2)\sum_{k = 1}^{K}\delta_k w_{jk}
\end{aligned}
∂ w i j ∂ l o s s = ( o j − o j 2 ) o i k = 1 ∑ K δ k w j k = o i ( o j − o j 2 ) k = 1 ∑ K δ k w j k
类似的,我们用δ j \delta_j δ j ( o j − o j 2 ) ∑ k = 1 K δ k w j k (o_j - o_j^2)\sum_{k = 1}^{K}\delta_k w_{jk} ( o j − o j 2 ) ∑ k = 1 K δ k w j k
∂ l o s s ∂ w i j = o i δ j \frac{\partial loss}{\partial w_{ij}} = o_i \delta_j
∂ w i j ∂ l o s s = o i δ j
小结
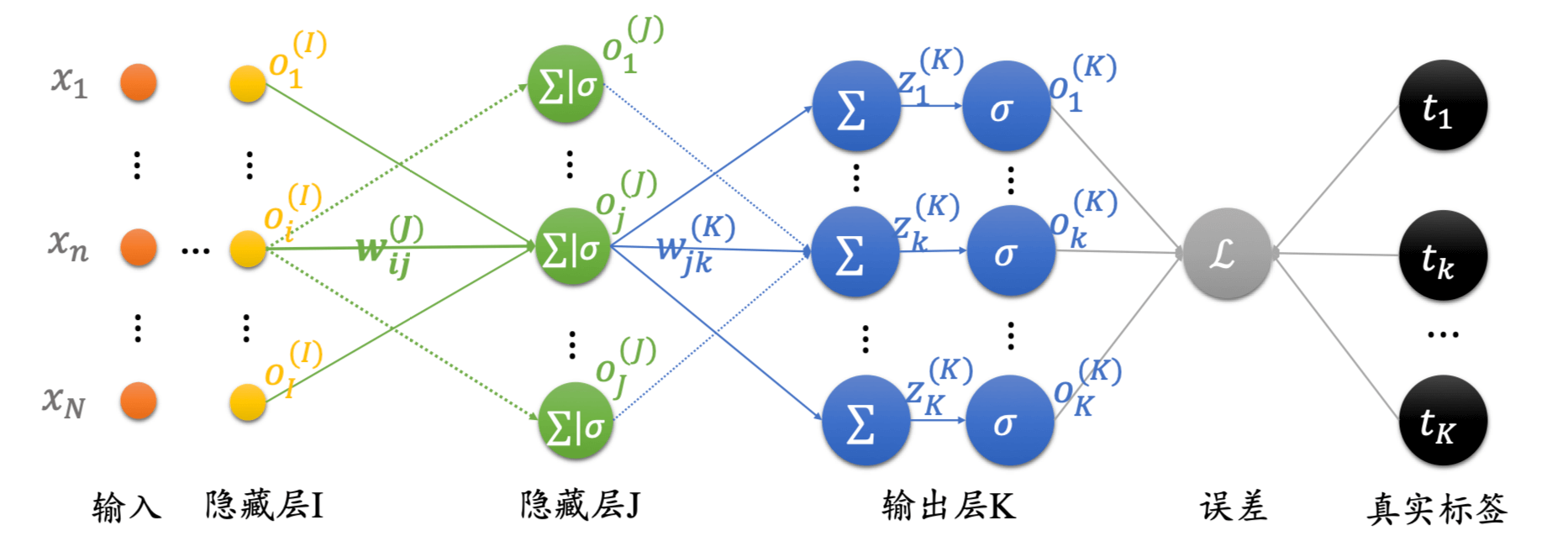
最后,我们做一个小结。k ∈ K k \in K k ∈ K
∂ l o s s ∂ w j k = o j δ k K \frac{\partial loss}{\partial w_{jk}} = o_j\delta_k^{K}
∂ w j k ∂ l o s s = o j δ k K
δ k K = ( o k − t k ) ( o k − o k 2 ) \delta_k^{K} = (o_k - t_k)(o_k - o_k^2)
δ k K = ( o k − t k ) ( o k − o k 2 )
从左往右,倒数第二层。对于该隐藏层,j ∈ J j \in J j ∈ J
∂ l o s s ∂ w i j = o i δ j J \frac{\partial loss}{\partial w_{ij}} = o_i\delta_j^J
∂ w i j ∂ l o s s = o i δ j J
δ j J = ( o j − o j 2 ) ∑ k = 1 K δ k K w j k \delta_j^J = (o_j - o_j^2)\sum_{k = 1}^{K}\delta_k^{K} w_{jk}
δ j J = ( o j − o j 2 ) k = 1 ∑ K δ k K w j k
从左往右,倒数第三层。对于该隐藏层,i ∈ I i \in I i ∈ I
∂ l o s s ∂ w n i = o n δ i I \frac{\partial loss}{\partial w_{ni}} = o_n\delta_i^{I}
∂ w n i ∂ l o s s = o n δ i I
δ i I = ( o i − o i 2 ) ∑ j = 1 J δ j I w i j \delta_i^I = (o_i - o_i^2)\sum_{j = 1}^{J}\delta_j^{I} w_{ij}
δ i I = ( o i − o i 2 ) j = 1 ∑ J δ j I w i j
其中,o n o_n o n δ k ( K ) \delta_k^{(K)} δ k ( K ) δ j ( J ) \delta_j^{(J)} δ j ( J ) δ i ( I ) \delta_i^{(I)} δ i ( I )
用法
现在,我们知道了如何求每一层每一个节点的权值的梯度。那么再结合我们的梯度下降方法,用起来。
网络初始化:对各连接权重赋一个初始值,设定误差函数,设定学习率和最大学习次数。
随机选取:随机选取第n个训练样本以及对应的期望输出。
隐藏层计算:计算隐藏层各神经元的输入和输出。
求偏导数:利用网络期望输出和实际输出,计算误差函数对输出层的各神经元的偏导数。
修正输出层权值:利用输出层各神经元的偏导数和隐藏层各神经元的输出来修正输出层的权值。
修正隐藏层权值:利用当前隐藏层各神经元的偏导数和输入层各神经元的输入修正当前隐藏层的权值。
计算误差:用修正后的权重,计算新模型的误差。
如此迭代更新。
基于numpy的实现
现在,我们基于numpy实现反向传播神经网络,以加强我们对反向传播算法的理解。
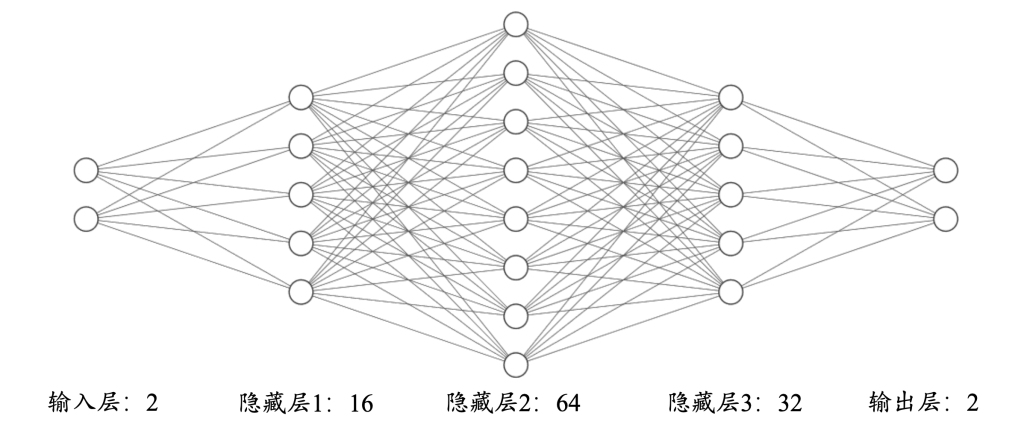
我们设计这么一个神经网络。
输出层的节点个数为2。
三个隐藏层的节点个数,从左到右,依次为:16、64、32。
输出层的节点个数为2,分别表示属于类别一和属于类别二的概率。
数据集
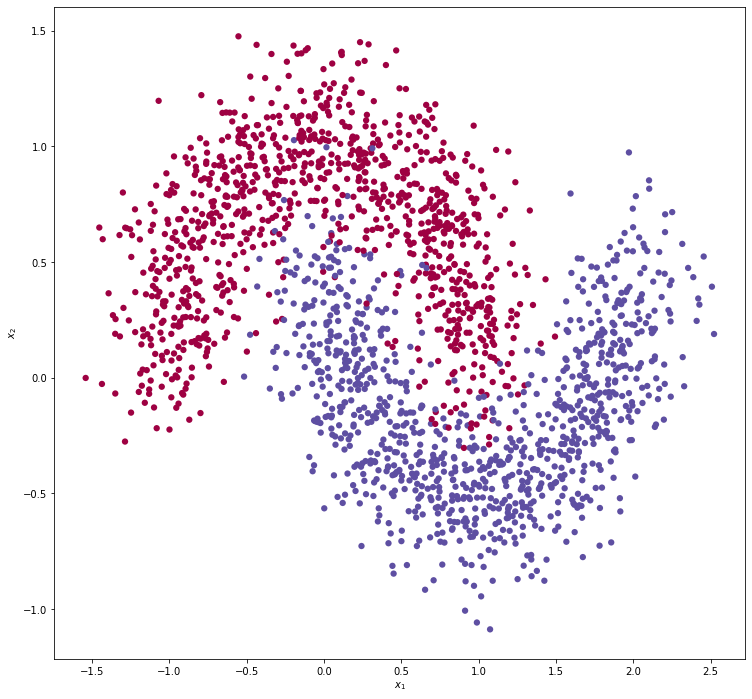
如图所示,是我们的数据集,两个对着的月牙。
我们通过scikit-learn的make_moons来生成模拟数据。样本数设置为2000,然后75%的数据用于训练,25%的数据用于测试。至于为什么是75% - 25%,这是一个经验公式。
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 from sklearn.datasets import make_moonsfrom sklearn.model_selection import train_test_splitN_SAMPLES = 2000 TEST_SIZE = 0.25 x,y = make_moons(n_samples=N_SAMPLES,noise=0.2 ) x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=TEST_SIZE) print(x_train.shape, y_train.shape) print(x_test.shape, y_test.shape)
运行结果:
1 2 (1500, 2) (1500,) (500, 2) (500,)
我们还可以把这些点的分布画出来,这样就有了我们这一小节开头的那张图片,对着的月牙。
示例代码:
1 2 3 4 5 6 7 8 9 10 from matplotlib import pyplot as pltplt.figure(figsize=(16 ,12 )) axes = plt.gca() axes.set(xlabel="$x_1$" , ylabel="$x_2$" ) plt.subplots_adjust(left=0.20 ) plt.subplots_adjust(right=0.80 ) plt.scatter(x[:, 0 ], x[:, 1 ], c=y.ravel(), s=40 , cmap=plt.cm.Spectral, edgecolors='none' ) plt.show()
网络层
现在,我们来定义一个网络层。首先我们要知道网络层的输入是什么,输出是什么,在输出之前,可能还有一个激活函数,在激活函数之前,还有还需要用输入乘以权重加上偏置。输入乘以权重加上偏置再作为激活函数的自变量。所以,我们需要的内容有:
输入节点数
输出节点数
激活函数类型
权重
偏置
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 class Layer : def __init__ (self, n_input, n_neurons, activation=None, weights=None, bias=None) : ''' :param n_input: 输入节点数 :param n_neurons: 输出节点数 :param activation: 激活函数类型 :param weights: 权重 :param bias: 偏置 ''' self.n_input = n_input self.n_neurons = n_neurons self.activation = activation self.weights = weights if weights is not None else np.random.randn(n_input, n_neurons) * np.sqrt(1 / n_neurons) self.bias = bias if bias is not None else np.random.rand(n_neurons) * 0.1 self.outputs = None self.error = None self.delta = None
如示例代码所示,除了记录我们之前讨论的那5个值,我们还让全连接层额外记录了三个值。
outputs:输出值error:用于计算当前层delta的中间变量delta:记录当前层的delta
这三个值都都需要通过计算得到,我们先讨论outputs。z = x ⋅ w + b z = \bold{x} \cdot \bold{w} + \bold{b} z = x ⋅ w + b z z z
阶跃函数
Sigmoid
Tanh
ReLU
LeakyReLU
我们知道,其中阶跃函数,连梯度下降都没法用。这里我们实现后面四种。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 def calculate_outputs (self,inputs) : ''' :param inputs: 输入值 :return: 输出值,last_activation ''' z = np.dot(x,self.weights) + self.bias if self.activation is None : self.outputs = z elif self.activation.lower() == 'sigmoid' : self.outputs = 1 / (1 + np.exp(-z)) elif self.activation.lower() == 'tanh' : self.outputs = np.tanh(z) elif self.activation.lower() == 'relu' : self.outputs = np.maximum(z, 0 ) elif self.activation.lower() == 'leakyrelU' : if z >= 0 : self.outputs = z else : self.outputs = z * 0.2 return self.outputs
当时在讨论激活函数的时候,我们还讨论了一个东西,激活函数的梯度,这个是做反向传播的时候用的。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 def activation_derivative (self, z) : ''' :param z: 激活函数的值 :return: 导函数的值 ''' if self.activation is None : return np.ones_like(z) elif self.activation.lower() == 'sigmoid' : return z * (1 - z) elif self.activation.lower() == 'tanh' : return 1 - z ** 2 elif self.activation.lower() == 'relu' : grad = np.array(z, copy=True ) grad[z > 0 ] = 1. grad[z <= 0 ] = 0. return grad elif self.activation.lower() == 'leakyrelU' : grad = np.array(z, copy=True ) grad[z > 0 ] = 1. grad[z <= 0 ] = 0.2 return grad return z
现在,我们还有当前层的delta不知道,而这个是非常依赖于整体网络模型的。所以,现在我们讨论网络模型。
网络模型
我们知道,网络模型是由一层又一层的网络层组成的。所以,首先需要一个列表,来存储网络层,最好还有一个方法,新增网络层;一个方法,删除网络层。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class NeuralNetwork : def __init__ (self) : self.layers = [] def add_layer (self, layer) : ''' :param layer: 网络层 :return: 新的网络层列表 ''' self.layers.append(layer) def remove_layer (self,layer) : ''' :param layer: 网络层 :return: 新的网络层列表 ''' self.layers.remove(layer)
我们的输入,经过一层又一层的神经网络,最后输出。即前向计算,这个代码很好写。
1 2 3 4 5 6 7 8 9 10 11 12 13 def feed_forward (self,inputs) : ''' :param inputs: 整个神经网络的输入 :return: 整个神经网络的输出 ''' X = inputs for layer in self.layers: X = layer.calculate_outputs(X) return X
反向传播的实现
反向传播的实现,估计是这里最有难度的。那怎么办呢?
计算整个神经网络的输出。
分别计算输出层的δ \delta δ δ \delta δ
寻找前一层的输出,即当前层的输入,将其与δ \delta δ
用权重减去梯度和乘以学习率的乘积。
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 def backpropagation (self,inputs,trues,lr) : ''' :param inputs: 整个神经网络的输入 :param trues: 真实值 :param lr: 学习率 :return: ''' outputs = self.feed_forward(inputs) for i in reversed(range(len(self.layers))): layer = self.layers[i] if layer == self.layers[-1 ]: layer.error = trues - outputs layer.delta = layer.error * layer.activation_derivative(outputs) else : next_layer = self.layers[i+1 ] layer.error = np.dot(next_layer.weights,next_layer.delta) layer.delta = layer.error * layer.activation_derivative(layer.outputs) for i in range(len(self.layers)): layer = self.layers[i] o_i = np.atleast_2d(inputs if i == 0 else self.layers[i-1 ].outputs) grads = layer.delta * o_i.T layer.weights = layer.weights + grads * lr
训练方法
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 def train (self, x_train, y_train, lr, max_epochs) : """ :param x_train: x 训练数据 :param y_train: y 训练数据 :param lr: 学习率 :param max_epochs: 训练机的最大循环迭代次数 :return: """ y_onehot = np.zeros((y_train.shape[0 ], 2 )) y_onehot[np.arange(y_train.shape[0 ]), y_train] = 1 for i in range(max_epochs): for j in range(len(x_train)): self.backpropagation(x_train[j], y_onehot[j], lr) if i % 10 == 0 : mse = np.mean(np.square(y_onehot - self.feed_forward(x_train))) print('Epoch: #%s, MSE: %f' % (i, float(mse)))
测试方法
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 def test (self, x_test, y_test) : """ :param x_test: x 测试数据 :param y_test: y 测试数据 :return: """ y_onehot = np.zeros((y_test.shape[0 ], 2 )) y_onehot[np.arange(y_test.shape[0 ]), y_test] = 1 mse = np.mean(np.square(y_onehot - self.feed_forward(x_test))) print('Finish!!!, MSE: %f' % float(mse))
Main方法
目前,我们整个网络都已经准备好了。然后我们示例化网络,定义结构。然后依次调用训练方法和测试方法。
1 2 3 4 5 6 7 8 9 x_data_train, x_data_test, y_data_train, y_data_test = generate_data(n_samples=2000 , test_rate=0.25 , noise=0.2 ) nn = NeuralNetwork() nn.add_layer(Layer(n_input=2 , n_neurons=16 , activation='sigmoid' )) nn.add_layer(Layer(n_input=16 , n_neurons=64 , activation='sigmoid' )) nn.add_layer(Layer(n_input=64 , n_neurons=32 , activation='sigmoid' )) nn.add_layer(Layer(n_input=32 , n_neurons=2 , activation='sigmoid' )) nn.train(x_train=x_data_train, y_train=y_data_train, lr=0.01 , max_epochs=1000 ) nn.test(x_test=x_data_test, y_test=y_data_test)
运行结果:
1 2 3 4 5 6 7 8 9 10 Epoch: #0, MSE: 0.256296 Epoch: #10, MSE: 0.143641 Epoch: #20, MSE: 0.093635 【部分运行结果略】 Epoch: #970, MSE: 0.028779 Epoch: #980, MSE: 0.028763 Epoch: #990, MSE: 0.028747 Finish!!!, MSE: 0.026823