过拟合

什么是过拟合

我们之前讨论的梯度下降也好，反向传播也好，都是在做一件事情，使损失函数的值最小。我们的损失函数用来表示模型对训练集的拟合效果，损失函数的值越小，拟合效果越好。现在，我们用一个过于复杂的模型去拟合训练集，这个模型能拟合所有的训练集，损失函数的值为 $0$ 。这么看来，我们有了一个完美的模型？但是，有时候不是这样的。

在训练集上表现很好的模型，在测试集中也会表现很好。这是基于一个假设，训练集和测试集是独立同分布的。这点没有问题，在一定的应用场景下，假设成立。

但是，会有噪音啊，上帝可能会掷骰子，我们可能会把上帝掷的骰子也学进去。

过于复杂的模型，在训练集上表现非常好，但在测试集上表现不如人意。这种现象就是过拟合。

模型的容量

在过拟合的定义中，我们提到了一词：“过于复杂的模型”。
那么，怎么衡量模型的复杂程度呢？模型的容量。
那么，什么是模型的容量呢？模型假设空间的大小。
那么，什么是假设空间呢？模型可以表示的函数集的大小。
那么，什么是函数集呢？

我们举例子，假设现在有这么几个模型。

模型一： $y = k_1x_1 + b$
模型二： $y = k_2x_2^2 + k_1x_1 + b$
模型三： $y = k_3x_3^3 + k_2x_2^2 + k_1x_1 + b$

对于模型一：当 $k_1 = 0$ ，是常数；当 $k_1 \neq 0$ ，是一次多项式。所以模型一的假设空间是[一次多项式、常数]。
对于模型二：当 $k_2 = 0$ ，是一次多项式；当 $k_1 \neq 0$ ，是二次多项式。所以模型二的假设空间是[二次多项式、一次多项式、常数]。
因此我们说模型二的假设空间比模型一的假设空间大，模型二的容量比模型一的容量大。
同理，我们知道，模型三的假设空间是[三次多项式、二次多项式、一次多项式、常数]，是三个模型中容量最大的那个。只要模型一和模型二能够表达的，模型三都能表达。这样看起来，模型三是万能的。似乎我们可以直接选择容量最大的模型。但是，模型容量越大，需要消耗的计算资源越多。而且，假设空间越大，越容易学习到噪音，产生过拟合现象。

泛化能力

现在我们已经知道什么是"过于复杂的模型"，"在训练集上表现非常好，但在测试集上表现不如人意。"这个也有个专门的名词：泛化能力。
那么通过训练集所训练出的模型在测试集上也能表现良好，这个就叫泛化能力较好。反之，则称为泛化能力较差。

那么如何去选择合适的模型容量，取得较好的泛化能力呢？

有一种方法是VC维度，这是统计学习理论中的内容，实际中很少用。很少用的原因不是说不合理，这个方法是有理论保证的。很少用的原因很难用，毕竟有些神经网络模型非常复杂。
第二种方法是"如无必要，勿增实体"，例如，如果通过两层的神经网络结构可以很好的表达，那么就不要用三层的。这个也被称为奥卡姆剃刀原理，出自《箴言书注》。那么，什么是《箴言》呢？《圣经》。

还有一个和"泛化能力"比较接近的名词，叫做"鲁棒性"，这个在一个户外群中，有过讨论。

比如说汽车司机，汽车司机在身体不适的情况下，依旧能很好的开车，就是鲁棒性强。然后汽车司机除了能开汽车，还能开飞机坦克就是说泛化能力强。
然后以户外装备来说，如果户外装备在有一定的损耗下，还很好用，就是鲁棒性强。如果这个装备除了能在雪地里用，还能在沙漠甚至水下用，就是泛化能力强。

交叉验证

接下来，我们讨论办法。

完整可运行代码见：
https://github.com/KakaWanYifan/deep-learning-for-blog/blob/master/Ch05/Ch05-1.py

关于交叉验证，我们在《经典机器学习及其Python实现：7.交叉验证和网格搜索》中也有过讨论。当时，我们把数据分为了两部分，训练集和测试集。现在我们对训练集再进行划分。划分为训练集和验证集，通过新的训练集和验证集，我们也可以得到一个准确率。

例如：把数据分成4等份，这个也被成为4折交叉验证。

第一份	第二份	第三份	第四份	结果
验证集	训练集	训练集	训练集	当前情况下，模型的准确率
训练集	验证集	训练集	训练集	当前情况下，模型的准确率
训练集	训练集	验证集	训练集	当前情况下，模型的准确率
训练集	训练集	训练集	验证集	当前情况下，模型的准确率

在每一种的训练集和验证集下，我们都可以一个得到模型的准确率，对准确率求平均。通过这种方法让模型的评估结果更加准确可信。

这种方法的思路其实是，在训练集上表现非常好，但在测试集上表现不如人意。不一定就是过拟合，也可能是"模型真的有问题"，在训练集上表现非常好只是运气好而已。而通过交叉验证，就是检查模型是真的过拟合了，还是"模型真的有问题"。就像在高考前的模拟成绩非常好，但是高考成绩不如意。可能就是水平不行，除非高考前足够多次的模拟成绩都很好，那么就要找找原因了。
我们这里非常通俗描述的"模型真的有问题"，"水平不行"就是欠拟合。

过拟合：
一个假设在训练数据上能获得比较好的拟合，但是在训练数据外的数据集上却不能很好地拟合数据，此时认为这个假设出现了过拟合的现象。
模型过于复杂
欠拟合：
一个假设在训练数据上不能获得更好的拟合，但是在训练数据外的数据集上也不能很好地拟合数据，此时认为这个假设出现了欠拟合的现象。
模型过于简单

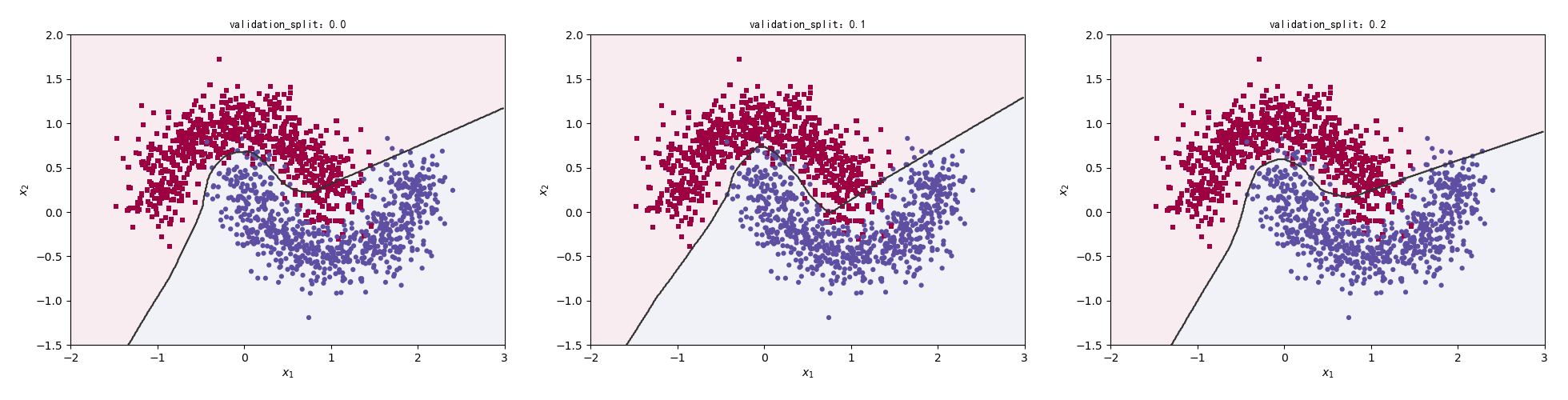
在TensorFlow要实现交叉验证，非常简单。用model.fit()中的validation_split参数进行控制即可。

1	model.fit(x_train, y_train, epochs=5,validation_split=validation_split, verbose=1)

接下来我们比较在没有交叉验证和交叉验证比例为0.1、0.2时的分类效果。

示例代码：

for n in range(3):

    validation_split = n * 0.1

    model = Sequential()
    model.add(layers.Dense(16, input_dim=2, activation='relu'))
    model.add(layers.Dense(64, activation='relu'))
    model.add(layers.Dense(128, activation='relu'))
    model.add(layers.Dense(16, activation='relu'))
    model.add(layers.Dense(1, activation='sigmoid'))
    model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
    model.fit(x_train, y_train, epochs=5,validation_split=validation_split, verbose=1)
    preds = model.predict_classes(np.c_[XX.ravel(), YY.ravel()])
    title = "validation_split：{0}".format(validation_split)
    make_plot(x_train, y_train, title, XX, YY, preds)

运行结果：

Epoch 1/5
47/47 [==============================] - 0s 1ms/step - loss: 0.4773 - accuracy: 0.8220
Epoch 2/5
47/47 [==============================] - 0s 1ms/step - loss: 0.3035 - accuracy: 0.8547
Epoch 3/5
47/47 [==============================] - 0s 979us/step - loss: 0.2711 - accuracy: 0.8867
Epoch 4/5
47/47 [==============================] - 0s 915us/step - loss: 0.2322 - accuracy: 0.9040
Epoch 5/5
47/47 [==============================] - 0s 1ms/step - loss: 0.1953 - accuracy: 0.9227

【部分运行结果略】

Epoch 1/5
38/38 [==============================] - 0s 8ms/step - loss: 0.5479 - accuracy: 0.8000 - val_loss: 0.3755 - val_accuracy: 0.8767
Epoch 2/5
38/38 [==============================] - 0s 1ms/step - loss: 0.3366 - accuracy: 0.8525 - val_loss: 0.2758 - val_accuracy: 0.8933
Epoch 3/5
38/38 [==============================] - 0s 2ms/step - loss: 0.2928 - accuracy: 0.8750 - val_loss: 0.2519 - val_accuracy: 0.8767
Epoch 4/5
38/38 [==============================] - 0s 1ms/step - loss: 0.2520 - accuracy: 0.9017 - val_loss: 0.1991 - val_accuracy: 0.9333
Epoch 5/5
38/38 [==============================] - 0s 2ms/step - loss: 0.2121 - accuracy: 0.9183 - val_loss: 0.1613 - val_accuracy: 0.9433

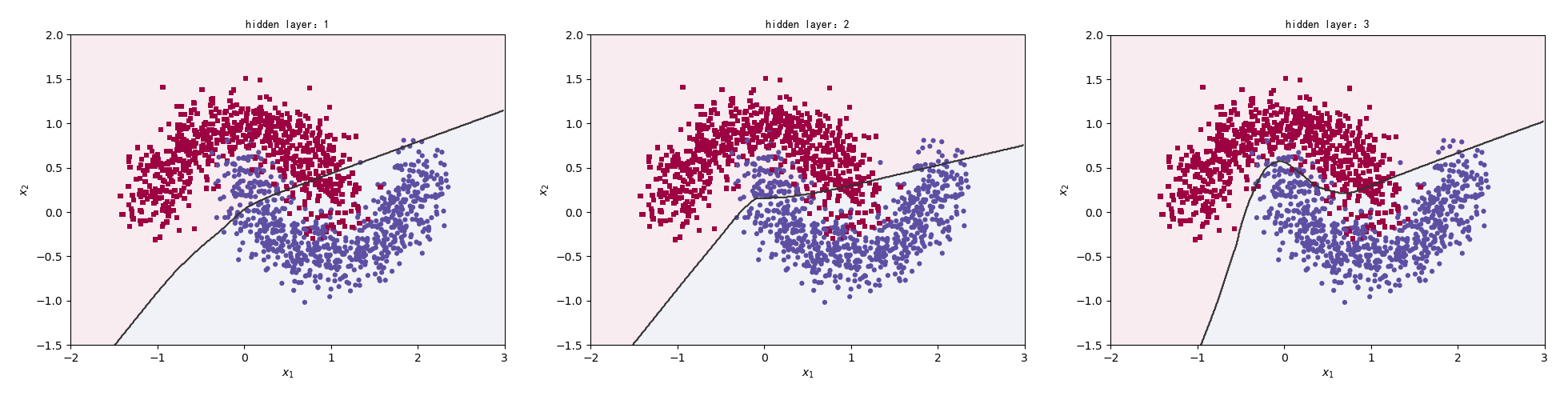
重新设计模型

完整可运行代码见：
https://github.com/KakaWanYifan/deep-learning-for-blog/blob/master/Ch05/Ch05-2.py

通过交叉验证，我们检查模型是不是真的过拟合。那么，如果真的是过拟合了，怎么办？
重新设计模型。

我们用model.add()方法来添加网络层。

1	model.add(layers.Dense(128, activation='relu'))

我们把隐藏层定为layers.Dense(64, activation='relu')。分别比较一层隐藏层、二层隐藏层、三层隐藏层的情况。

示例代码：

for n in range(3):
    model = Sequential()
    model.add(layers.Dense(64, input_dim=2, activation='relu'))
    for i in range(n):
        model.add(layers.Dense(64, activation='relu'))
    model.add(layers.Dense(1, activation='sigmoid'))
    model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
    model.fit(x_train, y_train, epochs=5, verbose=1)
    preds = model.predict_classes(np.c_[XX.ravel(), YY.ravel()])
    title = "hidden layer：{0}".format(n+1)
    make_plot(x_train, y_train, title, XX, YY, preds)

运行结果：

Epoch 1/5
47/47 [==============================] - 0s 1000us/step - loss: 0.6139 - accuracy: 0.7373
Epoch 2/5
47/47 [==============================] - 0s 1ms/step - loss: 0.4670 - accuracy: 0.8400
Epoch 3/5
47/47 [==============================] - 0s 766us/step - loss: 0.3926 - accuracy: 0.8407
Epoch 4/5
47/47 [==============================] - 0s 723us/step - loss: 0.3518 - accuracy: 0.8520
Epoch 5/5
47/47 [==============================] - 0s 745us/step - loss: 0.3281 - accuracy: 0.8620

【部分运行结果略】

Epoch 1/5
47/47 [==============================] - 0s 936us/step - loss: 0.4731 - accuracy: 0.8240
Epoch 2/5
47/47 [==============================] - 0s 979us/step - loss: 0.2935 - accuracy: 0.8627
Epoch 3/5
47/47 [==============================] - 0s 936us/step - loss: 0.2630 - accuracy: 0.8720
Epoch 4/5
47/47 [==============================] - 0s 936us/step - loss: 0.2347 - accuracy: 0.8933
Epoch 5/5
47/47 [==============================] - 0s 1ms/step - loss: 0.2045 - accuracy: 0.9140

当然重新设计模型不仅仅是说网络层数的减少。重新设计，甚至可以完全推倒重来。

关于不同层数以及每层不同节点对同一个问题的影响，谷歌有很方便的工具，可以带给我们很直观的理解。

https://playground.tensorflow.org

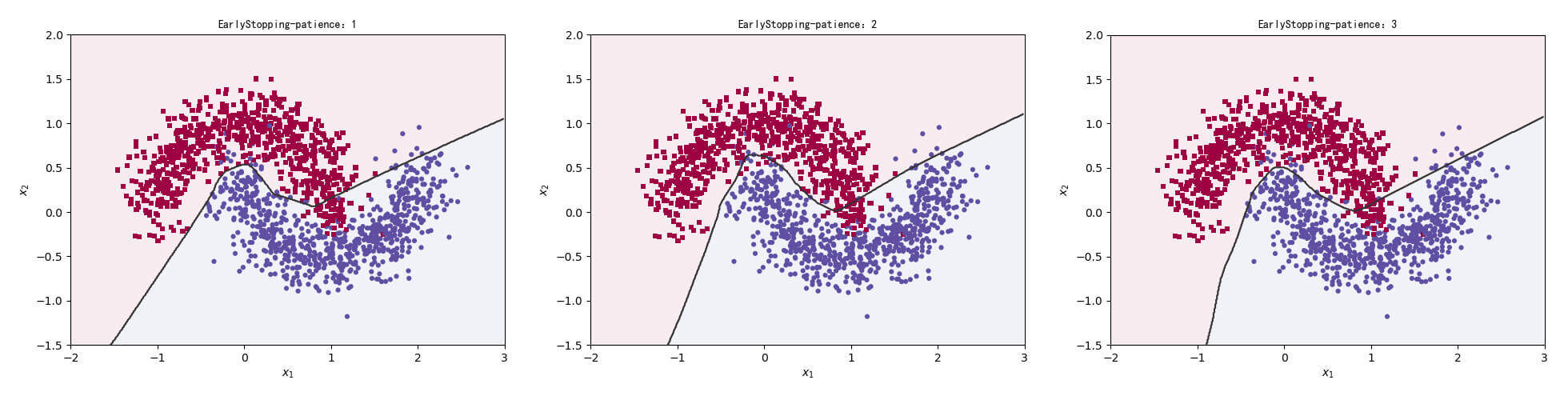
提前停止

完整可运行代码见：
https://github.com/KakaWanYifan/deep-learning-for-blog/blob/master/Ch05/Ch05-3.py

在上一小节中，我们人为的选用更简单的模型。现在我们通过程序来控制，让模型不至于太复杂。

我们把对训练集中的一个Batch运算更新一次叫做一个Step，对训练集的所有样本循环迭代一次叫做一个Epoch。在数次Step或数次Epoch后使用，用验证集进行验证。验证越频繁，越能够精准地观测模型的训练状况。但是也会增加计算的代价，一般建议在几个Epoch后进行一次验证运算。如果一定的次数后，验证性能没有提升，我们就提前停止。

伪代码：

带 Early stopping 功能的功能的网络训练网络训练算法

随机初始化参数 $\theta$
repeat
for step = 1,2,…,N do
随机采样 Batch ${(\bold{x},y)}\sim\boldsymbol{D}^{train}$
$\theta \leftarrow \theta - \eta\nabla_\theta L(f(\bold{x}),y)$
end

if 是每第n个 Epoch do
测试所有 ${(\bold{x},y)}\sim\boldsymbol{D}^{train}$ 上的验证性能
if 验证性能连续数次不提升 do
保存网络状态，提前停止训练。
end
end
until 训练达到最大回合数 Epoch
利用保存的网络测试 ${(\bold{x},y)}\sim\boldsymbol{D}^{train}$ 性能
输出：网络参数 $\theta$ 与测试性能

在TensorFlow中，我们不用手动去写上面的逻辑，有很方便的工具。

early_stopping=tf.keras.callbacks.EarlyStopping(monitor='val_loss', min_delta=0,
                              patience=0, verbose=0, mode='auto',
                              baseline=None, restore_best_weights=False)

model.fit(callbacks = [early_stopping])

参数介绍：

monitor：被监测的数据。
min_delta：在被监测的数据中被认为是提升的最小变化，例如，小于min_delta的绝对变化会被认为没有提升。
patience：没有进步的训练轮数，在这之后训练就会被停止。
verbose：详细信息模式。
mode：{auto,min,max} 其中之一。在min模式中，当被监测的数据停止下降，训练就会停止；在max模式中，当被监测的数据停止上升，训练就会停止；在 auto 模式中，方向会自动从被监测的数据的名字中判断出来。
baseline：要监控的数量的基准值。如果模型没有显示基准的改善，训练将停止。
restore_best_weights：是否从具有监测数量的最佳值的时期恢复模型权重。如果为False，则使用在训练的最后一步获得的模型权重。

我们比较patience分别为1、2、3时的结果。
示例代码：

for n in range(3):
    patience = n + 1
    early_stopping = EarlyStopping(monitor='loss', min_delta=0, patience=patience, verbose=0, mode='auto',
                                   baseline=None, restore_best_weights=False)

    model = Sequential()
    model.add(layers.Dense(16, input_dim=2, activation='relu'))
    model.add(layers.Dense(64, activation='relu'))
    model.add(layers.Dense(128, activation='relu'))
    model.add(layers.Dense(16, activation='relu'))
    model.add(layers.Dense(1, activation='sigmoid'))
    model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
    model.fit(x_train, y_train, epochs=5, verbose=1, callbacks=[early_stopping])
    
    preds = model.predict_classes(np.c_[XX.ravel(), YY.ravel()])
    title = "EarlyStopping-patience：{0}".format(patience)
    make_plot(x_train, y_train, title, XX, YY, preds)

运行结果：

Epoch 1/5
47/47 [==============================] - 0s 1ms/step - loss: 0.4638 - accuracy: 0.8373
Epoch 2/5
47/47 [==============================] - 0s 1ms/step - loss: 0.2753 - accuracy: 0.8747
Epoch 3/5
47/47 [==============================] - 0s 979us/step - loss: 0.2378 - accuracy: 0.8987
Epoch 4/5
47/47 [==============================] - 0s 1ms/step - loss: 0.2053 - accuracy: 0.9147
Epoch 5/5
47/47 [==============================] - 0s 1ms/step - loss: 0.1690 - accuracy: 0.9327

【部分运行结果略】

Epoch 1/5
47/47 [==============================] - 0s 1ms/step - loss: 0.5083 - accuracy: 0.8220
Epoch 2/5
47/47 [==============================] - 0s 1ms/step - loss: 0.3121 - accuracy: 0.8693
Epoch 3/5
47/47 [==============================] - 0s 936us/step - loss: 0.2613 - accuracy: 0.8853
Epoch 4/5
47/47 [==============================] - 0s 915us/step - loss: 0.2178 - accuracy: 0.9153
Epoch 5/5
47/47 [==============================] - 0s 1ms/step - loss: 0.1642 - accuracy: 0.9387

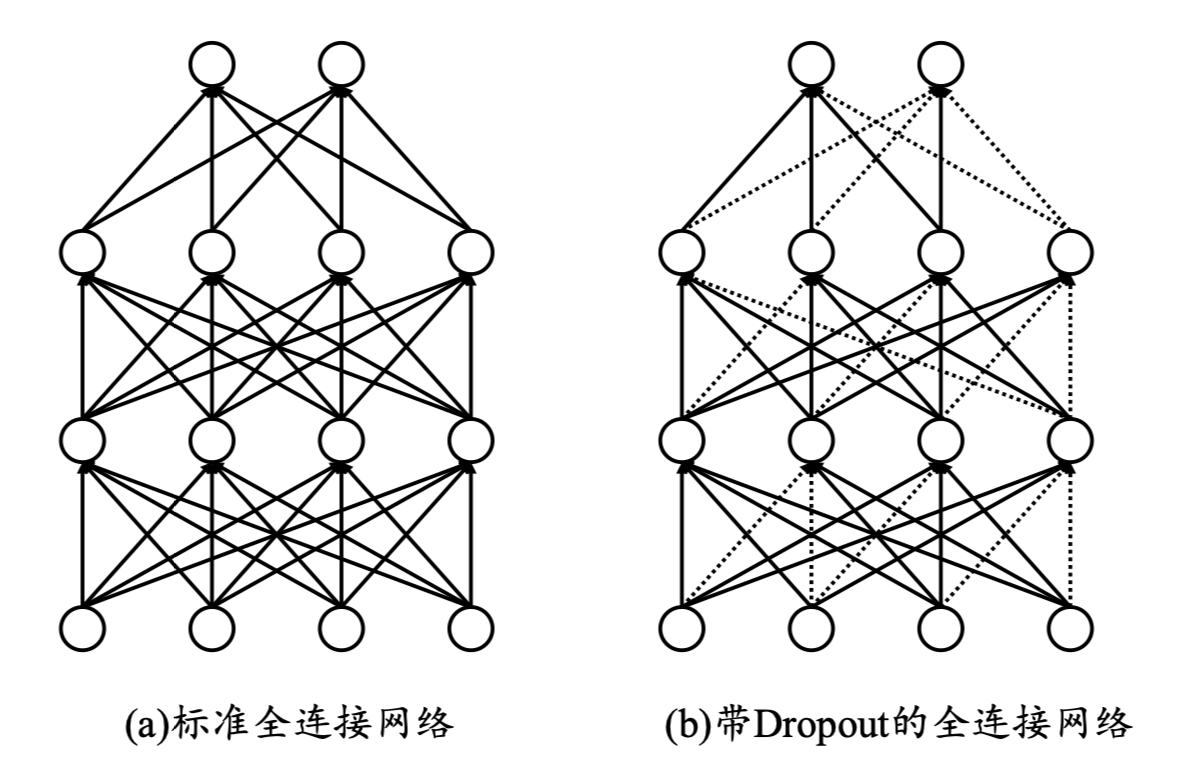
Dropout

完整可运行代码见：
https://github.com/KakaWanYifan/deep-learning-for-blog/blob/master/Ch05/Ch05-4.py

Dropout通过随机断开神经网络的连接，减少每次训练时实际参与的参数量；需要注意的是，在测试的时候，Dropout会恢复所有的连接，保证模型测试时获得最好的性能。

在TensorFlow中，Dropout的方法是

1	tf.nn.dropout(x, rate)

除此之外，我们还可以在网络中插入一个Dropout层。

1	model.add(layers.Dropout())

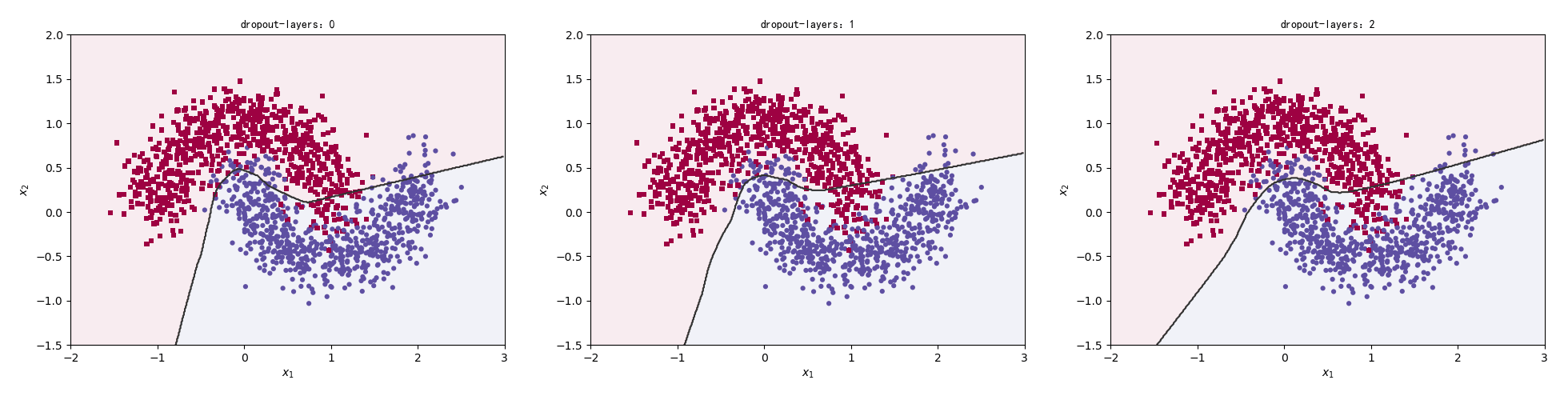
我们分别比较不加Dropout，Dropout的数量为1和2的情况。
示例代码：

for n in range(3):
    early_stopping = EarlyStopping(monitor='loss', min_delta=0, verbose=0, mode='auto',
                                   baseline=None, restore_best_weights=False)
    model = Sequential()
    model.add(layers.Dense(16, input_dim=2, activation='relu'))
    if n > 0:
        model.add(layers.Dropout(rate=0.3))
    model.add(layers.Dense(64, activation='relu'))
    if n > 1:
        model.add(layers.Dropout(rate=0.3))
    model.add(layers.Dense(128, activation='relu'))
    model.add(layers.Dense(16, activation='relu'))
    model.add(layers.Dense(1, activation='sigmoid'))
    model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
    model.fit(x_train, y_train, epochs=5, verbose=1, callbacks=[early_stopping])
    
    preds = model.predict_classes(np.c_[XX.ravel(), YY.ravel()])
    title = "dropout-layers：{0}".format(n)
    make_plot(x_train, y_train, title, XX, YY, preds)

运行结果：

Epoch 1/5
47/47 [==============================] - 0s 1ms/step - loss: 0.5210 - accuracy: 0.7933
Epoch 2/5
47/47 [==============================] - 0s 1ms/step - loss: 0.3122 - accuracy: 0.8680
Epoch 3/5
47/47 [==============================] - 0s 979us/step - loss: 0.2571 - accuracy: 0.8927
Epoch 4/5
47/47 [==============================] - 0s 894us/step - loss: 0.2254 - accuracy: 0.9067
Epoch 5/5
47/47 [==============================] - 0s 1000us/step - loss: 0.1999 - accuracy: 0.9213

【部分运行结果略】

Epoch 1/5
47/47 [==============================] - 0s 1ms/step - loss: 0.5133 - accuracy: 0.8060
Epoch 2/5
47/47 [==============================] - 0s 1ms/step - loss: 0.3414 - accuracy: 0.8487
Epoch 3/5
47/47 [==============================] - 0s 1000us/step - loss: 0.3220 - accuracy: 0.8613
Epoch 4/5
47/47 [==============================] - 0s 1ms/step - loss: 0.2905 - accuracy: 0.8853
Epoch 5/5
47/47 [==============================] - 0s 1ms/step - loss: 0.2709 - accuracy: 0.8893

正则化

正则化，这个我们在《经典机器学习及其Python实现：12.Lasso回归和岭回归》中也讨论过了。
例如，我们的模型为 $y = \beta_0 + \beta_1x + \beta_2x^2 + \beta_3x^3 + ··· + \beta_nx^n$ 。
我们用 $L(f_\theta(\bold{x},y))$ 表示损失函数，之前我们的目标是寻找一组 $\theta$ ，使得损失函数的值最小。
现在我们的不但要求损失函数的值小，还要求模型简单，两者都要兼顾。这时候我们加入一个惩罚因子，模型越复杂，惩罚因子越大。
即，新的损失函数为：

$L(f_\theta(\bold{x},y)) + \lambda \cdot \Omega(\theta)$

$\Omega(\theta) = \sum||\theta_i||_l$

其中

$\lambda$ 是正则化力度，这是一个超参数。
$||\theta_i||_l$ 表示参数 $\theta_i$ 的 $l$ 范数。

常见的有

$L1$ 正则化： $\Omega(\theta) = \sum||\theta_i||_1$ ，表示 $\theta_i$ 中非所有元素的绝对值之和。
$L2$ 正则化： $\Omega(\theta) = \sum||\theta_i||_2$ ，表示 $\theta_i$ 中非所有元素的平方和。

还有一种正则化， $L0$ 正则化： $\Omega(\theta) = \sum||\theta_i||_0$ ，表示 $\theta_i$ 中非零元素的个数。因为是非零元素的个数，所以无法剃度下降。

在TensorFlow中实现正则化的方法是：

# L1 Regularization Penalty
tf.keras.regularizers.L1(0.3)
# L2 Regularization Penalty
tf.keras.regularizers.L2(0.1)
# L1 + L2 penalties
tf.keras.regularizers.L1L2(l1=0.01, l2=0.01)

layer = tf.keras.layers.Dense(
    5, input_dim=5,
    kernel_initializer='ones',
    kernel_regularizer=tf.keras.regularizers.L1(0.01),
    activity_regularizer=tf.keras.regularizers.L2(0.01))

示例代码略，模仿前面的例子，很容易实现。

动量

动量是物理学中的一个概念。记的在高中物理中学过这个的，现在倒是忘得一干二净了。深度学习中的动量或许和高中物理中的动量有点关系，但这不是我们讨论的重点，毕竟以我现在的物理水平，是讨论不来的。

我们直接讨论深度学习中的动量。
在之前章节中，我们讨论了梯度下降。

$\bold{w}^{k+1} = \bold{w}^{k} - lr * f'(\bold{w}^k)$

现在，我们改一下梯度下降的规则。

$\bold{z}^{k+1} = \beta\bold{z}^{k} + f'(\bold{w}^k)$

$\bold{w}^{k+1} = \bold{w}^{k} - lr * \bold{z}^{k+1}$

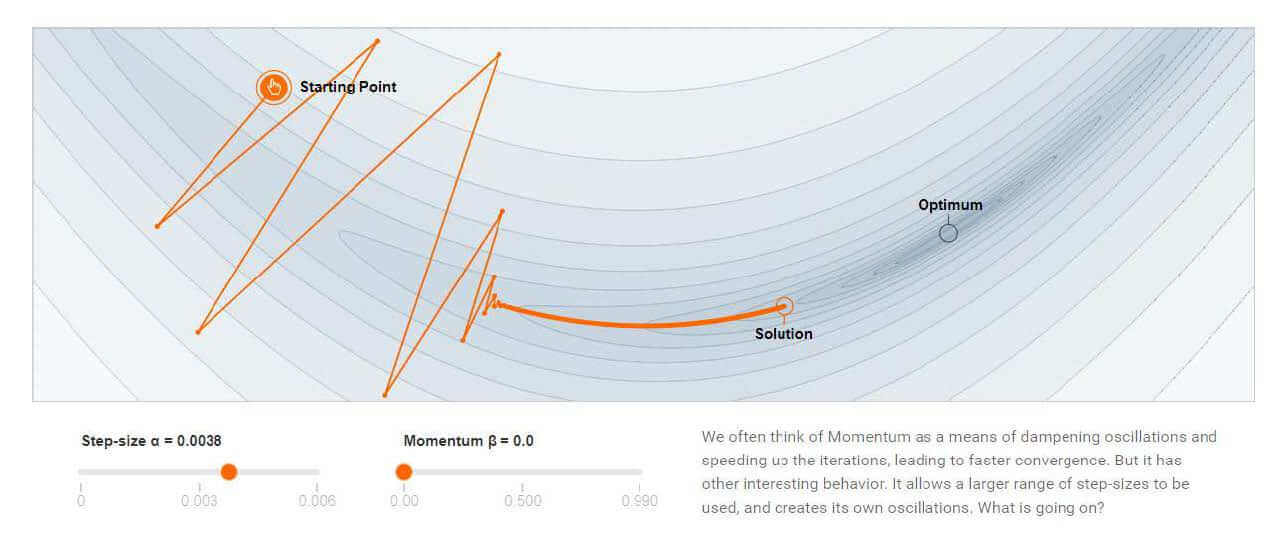
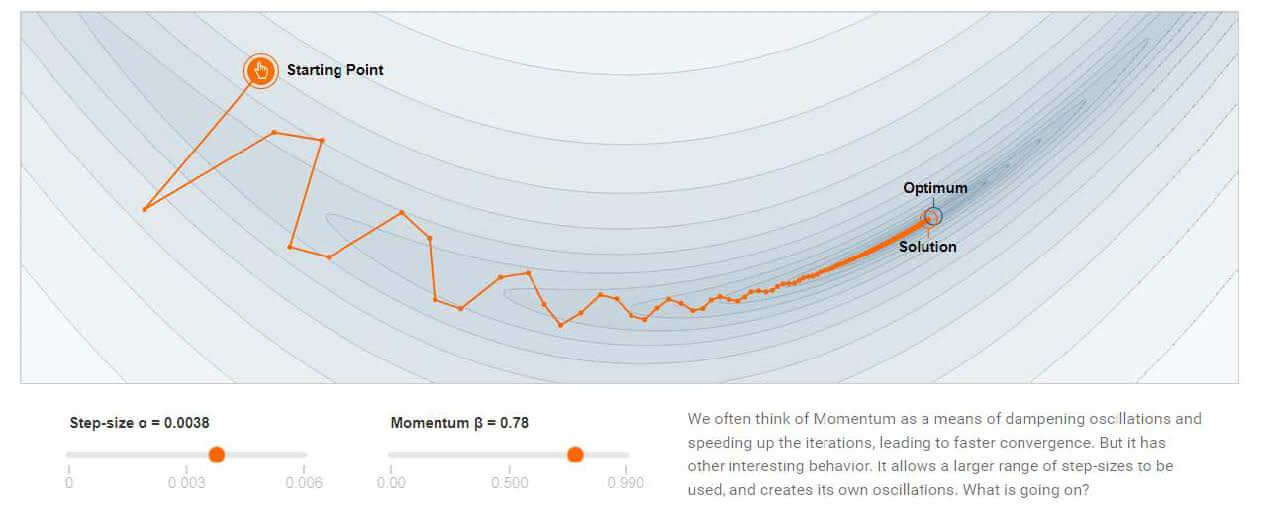
即改变了梯度的方向，避免"急转弯"。

下图分别是没有动量和有动量情况下的梯度下降。

没有动量：

有动量：

在TensorFlow中，我们可以非常方便的实现，设置momentum参数即可。

1	optimizers.SGD(learning_rate=0.02,momentum=0.9)

1	optimizers.RMSprop(learning_rate=0.01,momentum=0.02)

不过，需要注意的是，不是所有的优化方法都有momentum这个参数。比如：optimizers.Adam()。

示例代码略，模仿前面的例子，很容易实现。

学习率衰减

80！80！80！这就是学习率没有及时衰减的后果。

正如我们之前讨论的，学习率不能太大，否则效果太差。当然学习率也不能太小，否则优化的太慢。现在我们有一个折衷的办法，先快后慢。学习效率从大到小，逐步衰减。

和动量不同的是，学习率衰减的实现不是直接配置参数即可，但是也非常方便。

optimizer = optimizers.SGD(learning_rate=0.2)

for epoch in range(100):
    
    # 部分代码略

    optimizer.learning_rate = 0.2 * (100-epoch)/100
    
    # 部分代码略

示例代码略，模仿前面的例子，很容易实现。

数据增强

现在我们换一个思路。
我们过拟合的原因也可能是训练集太规范，以至于一上测试集，模型就不行。就像我们训练一只军队，每一次训练都恰好是风和日丽时，结果上战场那天，却是狂风暴雨，导致最后作战效果不好。
那么，怎么解决这个问题呢？
正所谓：有困难要上。没有困难，创造困难也要上。
现在我们创造困难。

我们以图像的旋转为例：
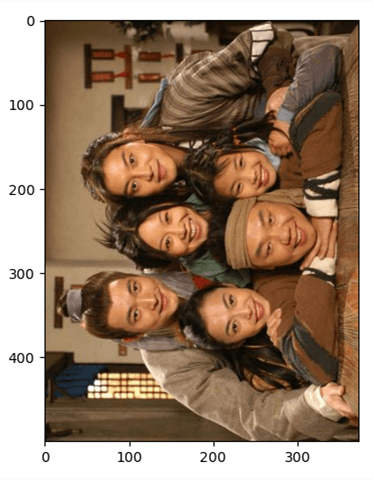
旋转方法：

1	tf.image.rot90(x)

示例代码：

import tensorflow as tf
import matplotlib.pyplot as plt

x = tf.io.read_file('img.jpg')
x = tf.image.decode_jpeg(x,channels=3)
x = tf.image.rot90(x)
plt.imshow(x)
plt.show()