12.Lasso回归和岭回归

正则化

惩罚因子

在上一章，我们定义了线性回归的损失函数。

$$J(\bold{w}) = \sum_{i=1}^m(h_w(x_i) - y_i)^2$$

现在，我们修改损失函数。

$$J(\bold{w}) = \sum_{i=1}^m\bigg((h_w(x_i) - y_i)^2 + ||w||\bigg)$$

$$\begin{aligned} \text{当}||w|| & = |w_1| + |w_2| + ··· + |w_n| \text{，称之为L1正则化} \\ \text{当}||w|| & = w_1^2 + w_2^2 + ··· + w_n^2 \text{，称之为L2正则化} \end{aligned}$$

这里的$||w||$也被称为惩罚因子。

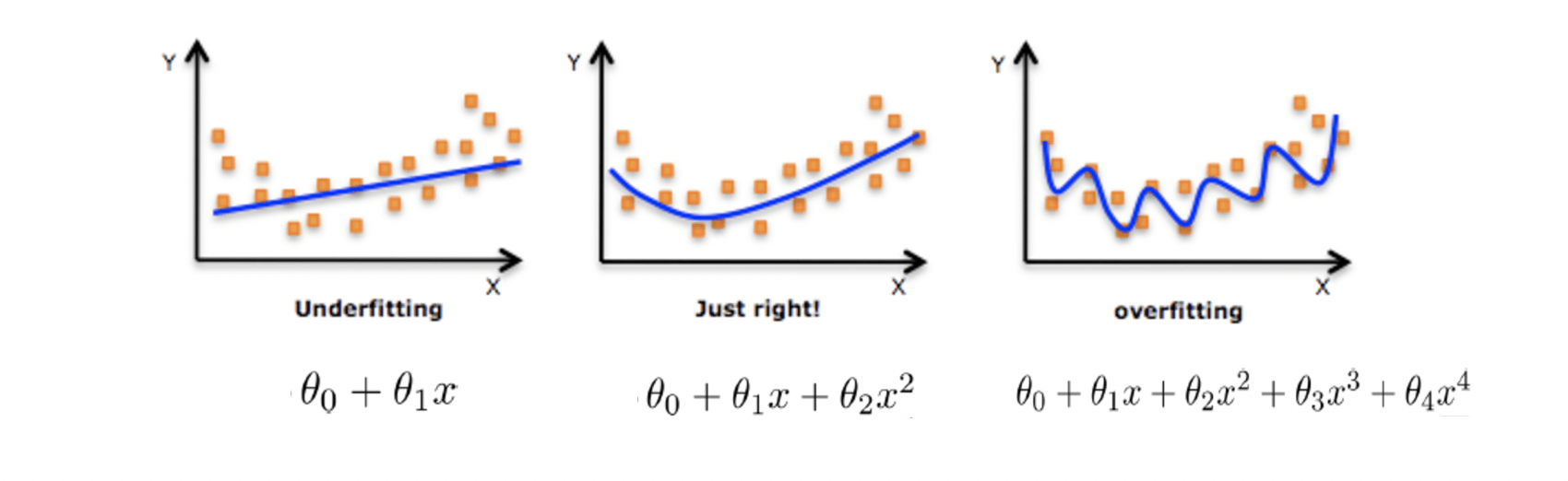
那么，为什么加上惩罚因子之后，就能避免过拟合呢？

回到这张图。
我们知道为了"覆盖"所有的点，就需要高次项。我们需要修改$w_4x^4$中的$w_4$，那么为了控制$w_4$，所以修改损失函数。

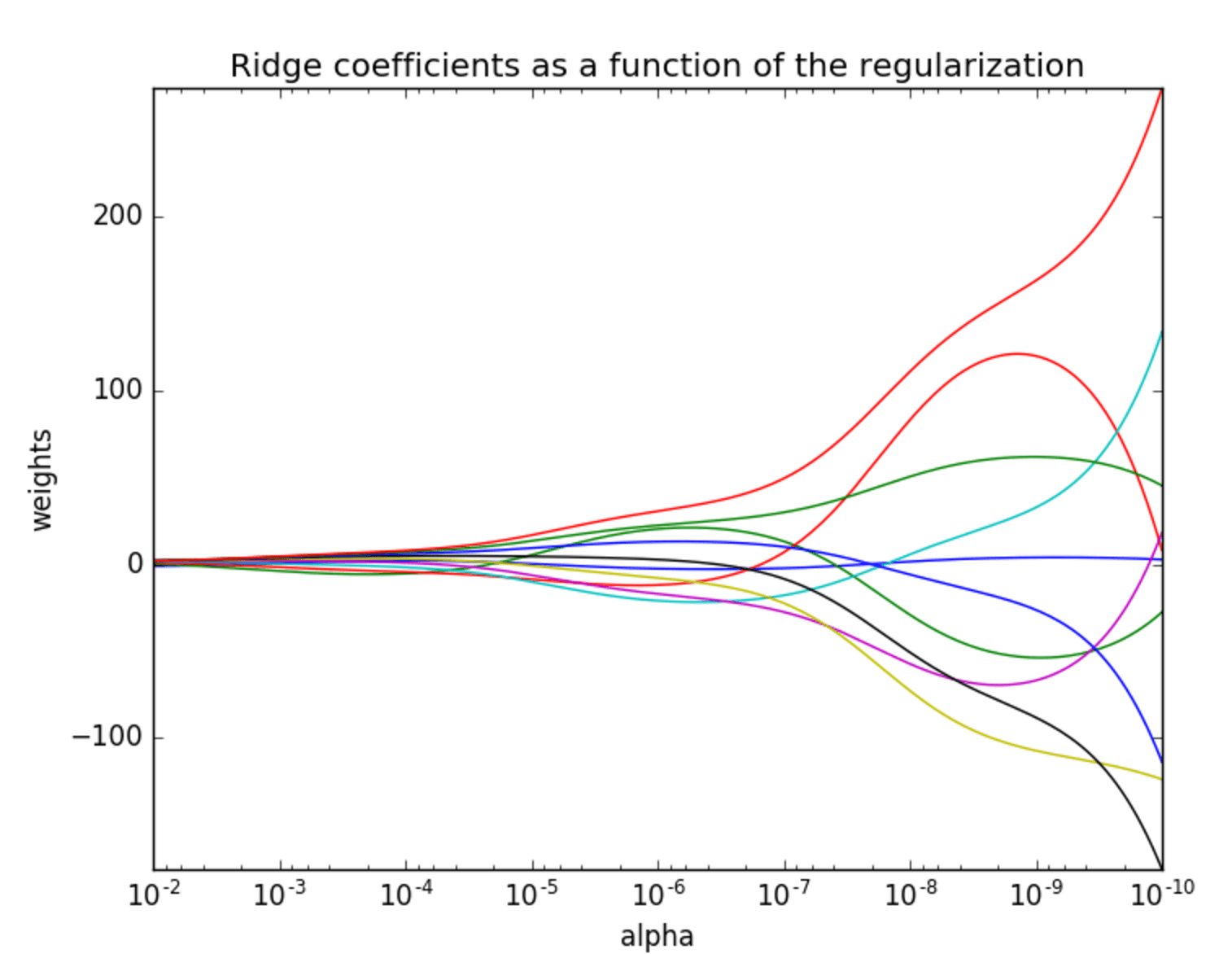
正则化力度

我们再次修改损失函数

$$J(\bold{w}) = \sum_{i=1}^m\bigg((h_w(x_i) - y_i)^2 + \lambda||w||\bigg)$$

即，我们又对惩罚因子加上了一个权重$\lambda$，这个$\lambda$就被称为正则化力度。

该参数是一个超参数，需要我们自己设定。

Lasso回归

Lasso回归的介绍

带有L1正则化的线性回归就是Lasso回归

Lasso可能会使得某一些特征的权重为0，即可能会删除一些特征。
所以。Lasso回归也可能用来做特征选择。

相比之下，岭回归会会使得某一些特征的权重趋于0，但是不等于0，因此不会删除特征。

Lasso回归的实现

from sklearn.linear_model import Lasso

示例代码：

from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Lasso
import numpy as np

# 获取数据
lb = load_boston()

# 分割数据集到训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)

# 特征值和目标值是都必须进行标准化处理, 实例化两个标准化API
std_x = StandardScaler()
x_train = std_x.fit_transform(x_train)
x_test = std_x.transform(x_test)

# 目标值
std_y = StandardScaler()
y_train = std_y.fit_transform(y_train.reshape(-1,1))
y_test = std_y.transform(y_test.reshape(-1,1))

print('Lasso回归')
l = Lasso()
l.fit(x_train,y_train)
print('系数')
print(l.coef_)
print('采用的特征数')
print(np.sum(l.coef_ != 0))
print('R2分数')
print(l.score(x_test,y_test))

运行结果：

Lasso回归
系数
[-0.  0. -0.  0. -0.  0. -0.  0. -0. -0. -0.  0. -0.]
采用的特征数
0
R2分数
-0.0008009875102807927

该模型最终没有采用任何一个特征，最后预测结果和实际差距非常大，以至于R平方是负数。
(回归函数拟合效果差于取平均值时R平方会为负数)。

岭回归

岭回归的介绍

带有L2正则化的线性回归就是岭回归

岭回归的实现

from sklearn.linear_model import Ridge

参数：

• alpha：正则化力度

如图，是正则化力度与权重的关系。我们看到力度越来越大，权重会逐渐收敛到0。

示例代码：

from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import SGDRegressor
from sklearn.linear_model import Ridge

# 获取数据
lb = load_boston()

# 分割数据集到训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)

# 特征值和目标值是都必须进行标准化处理, 实例化两个标准化API
std_x = StandardScaler()
x_train = std_x.fit_transform(x_train)
x_test = std_x.transform(x_test)

# 目标值
std_y = StandardScaler()
y_train = std_y.fit_transform(y_train.reshape(-1,1))
y_test = std_y.transform(y_test.reshape(-1,1))

print('岭回归')
r = Ridge()
r.fit(x_train,y_train)
print(r.coef_)
print(r.score(x_test,y_test))

运行结果：

岭回归
[[-0.11414664  0.13163317 -0.02079794  0.08976539 -0.19450693  0.22951016
   0.01828466 -0.34513553  0.24843382 -0.16661707 -0.20787019  0.08481452
  -0.48469022]]
0.7054521883835955

岭回归和线性回归的比较

• 岭回归得到的回归系数更符合实际，更可靠。
• 能让估计参数的波动范围变小，变的更稳定。

模型的保存与加载

from sklearn.externals import joblib

模型保存的方法

joblib.dump(r,'r.pkl')

把模型存入到本地的文件'r.pkl'。
模型加载的方法

m = joblib.load('r.pkl')

从本地的文件'r.pkl'加载模型。

示例代码：

from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Ridge
from sklearn.externals import joblib

# 获取数据
lb = load_boston()

# 分割数据集到训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)

# 特征值和目标值是都必须进行标准化处理, 实例化两个标准化API
std_x = StandardScaler()
x_train = std_x.fit_transform(x_train)
x_test = std_x.transform(x_test)

# 目标值
std_y = StandardScaler()
y_train = std_y.fit_transform(y_train.reshape(-1,1))
y_test = std_y.transform(y_test.reshape(-1,1))

print('岭回归')
r = Ridge()
r.fit(x_train,y_train)
print(r.coef_)
print(r.score(x_test,y_test))

joblib.dump(r,'r.pkl')

m = joblib.load('r.pkl')
print(m.coef_)
print(m.score(x_test,y_test))

运行结果：

岭回归
[[-0.11196121  0.14923795  0.03729775  0.0773936  -0.2776023   0.25036726
   0.05149061 -0.32467193  0.29429566 -0.19711174 -0.23929005  0.09799755
  -0.42338591]]
0.7588045809699258
[[-0.11196121  0.14923795  0.03729775  0.0773936  -0.2776023   0.25036726
   0.05149061 -0.32467193  0.29429566 -0.19711174 -0.23929005  0.09799755
  -0.42338591]]
0.7588045809699258