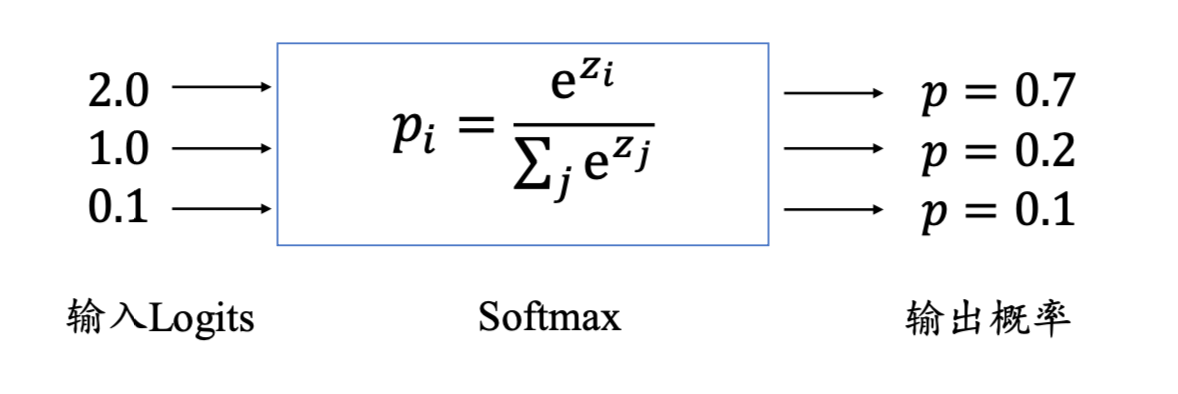13.逻辑回归

逻辑回归虽然被称为回归，但并不是用来处理回归问题。不过既然被称为回归，这里面肯定还是有故事的，这就不得不从逻辑回归和线性回归的关系讲起。

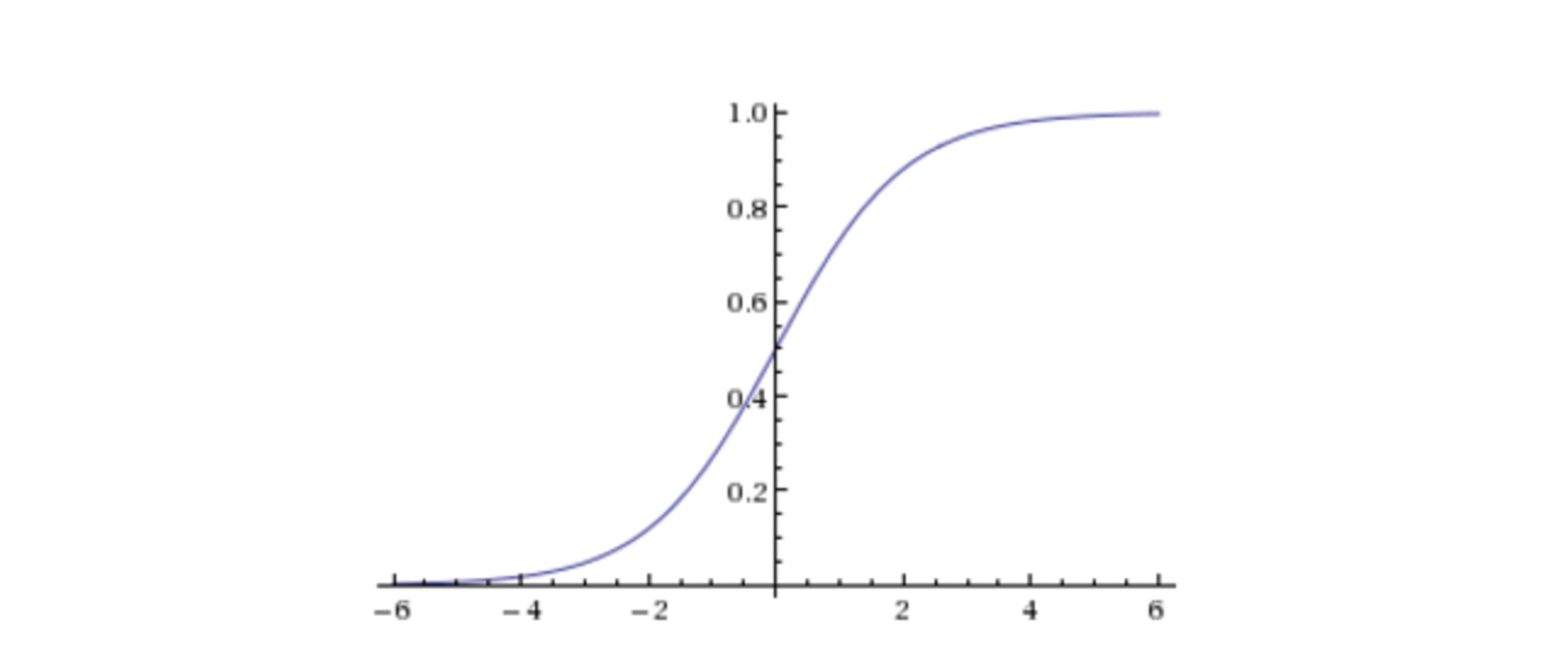
sigmoid函数

sigmoid的函数表达式

$$sigmoid(x) = \frac{1}{1 + e^x}$$

为了便于表达，我们用换元法，把$x$换成$y$。
并假设$y$是一个关于特征的线性组合

$$\begin{aligned} y = w_0 + w_1x_1 + w_2x_2 + ··· + w_dx_d = \bold{w}^T \bold{x} \end{aligned}$$

那么，我们得到整个逻辑回归的形式

$$logistics(\bold{w}) = \frac{1}{1 + e^{\bold{w}^T \bold{x}}}$$

即，逻辑回归和线性的关系是：逻辑回归是线性回归再包装了一层。

损失函数

定义
虽然逻辑回归是线性回归的包装。但是毕竟处理的问题不同，也不是简单的包装。
比如：损失函数不同。

对于单个样本，损失函数

$$j(h_w(x),y) = \Bigg\{\begin{array}{l} -\log_{10} (h_w(x)) & \text{if } y = 1,\\ -\log_{10}(1-h_w(x)) & \text{if } y = 0 \end{array}$$

其中

• $h_w(x)$是在当前模型下的预测值，也就是在(0,1)区间的sigmoid值。

将所有的样本进行求和，就是完整的损失函数

$$J(\bold{w}) = \sum_{i=1}^m -y_i\log_{10} (h_w(x)) - (1-y_i)\log_{10}(1-h_w(x))$$

计算
假设现在存在四个样本，四个样本的目标值分别是1 0 0 1。
对于四个样本预测的概率分别为0.6 0.1 0.51 0.7。
则

$$\begin{aligned} J(\bold{w}) & = (- 1 * \log_{10}0.6 - 0 * log_{10} (1-0.6) ) \\ & + ( - 0 * \log_{10}0.1 - 1 * log_{10} (1-0.1) ) \\ & + ( - 0 * \log_{10}0.51 - 1 * log_{10} (1-0.51) ) \\ & + ( - 1 * \log_{10}0.7 - 0 * log_{10} (1-0.7) ) \\ \end{aligned}$$

这个损失函数就是交叉熵损失，在《深度学习初步及其Python实现：2.神经网络基础》中，我们有关于交叉熵损失更详细的讨论。

优化

同线性回归的优化，就是寻找一个$\bold{w}$，使得损失函数的值最小。
在线性回归，我们的目标函数是均方误差，我们可以用梯度下降方法，求局部最低点。
但是在逻辑回归，我们的目标函数是对数似然损失(交叉熵损失)，可能会有多个局部最小点。

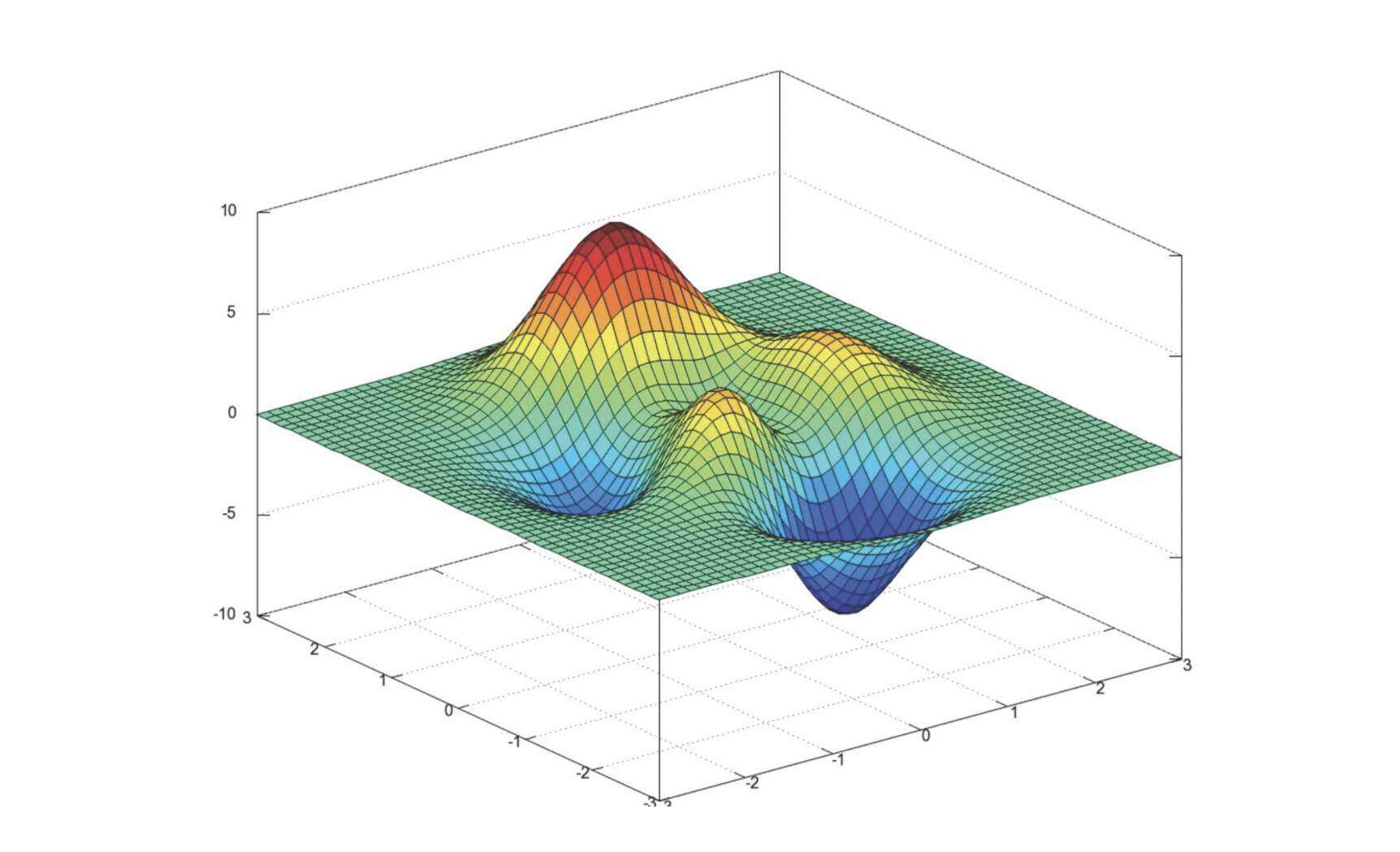
就像这张图

该问题截至目前，无解。

只有一些尽量改善的方法

1. 多次随机初始化，比较最小值结果
2. 求解过程中，调整学习率

这样虽然找不到全局最优点，但是局部最优点有时候效果也不错。

实现

from sklearn.linear_model import LogisticRegression

参数：

• penalty：正则化形式，如l2
• C：正则化力度

方法：

• Logistic
• coef_

我们以《充电桩故障分类与检测》为例。

这也是百度曾经举办的一个比赛，但是比赛的数据已经不提供下载了。不过我的GitHub中还有数据。

赛题介绍：https://dianshi.bce.baidu.com/competition/19/question
数据下载：https://github.com/KakaWanYifan/BaiduPower

示例代码：

from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
import pandas as pd

# 读取数据
data = pd.read_csv('../data/data_train.csv',names = ['id','k1k2','lock','stop','gate','thdv','thdi','label'])
# 取出目标值和特征值
y = data['label']
x = data.drop(['label','id'],axis=1)
# 分割为训练集和测试集
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.25)

# 标准化数据，保证每个维度的特征数据方差为1，均值为0。使得预测结果不会被某些维度过大的特征值而主导
ss = StandardScaler()
x_train = ss.fit_transform(x_train)
x_test = ss.transform(x_test)

# 初始化 LogisticRegression
lr = LogisticRegression(C=1.0, penalty='l2', tol=0.01)

# 跳用LogisticRegression中的fit函数／模块来训练模型参数
lr.fit(x_train,y_train)
print(lr.predict(x_test))
# 均方误差
print(lr.score(x_test,y_test))
print(classification_report(y_test,lr.predict(x_test)))

运行结果：

[0 1 1 ... 0 0 1]
0.8746198830409356
              precision    recall  f1-score   support

           0       0.93      0.81      0.87     10684
           1       0.83      0.94      0.88     10691

    accuracy                           0.87     21375
   macro avg       0.88      0.87      0.87     21375
weighted avg       0.88      0.87      0.87     21375

完整的代码已经PUSH到了我的GitHub上
https://github.com/KakaWanYifan/BaiduPower

优缺点

1. 优点
   1. 对于二分类问题，简单快速
2. 缺点
   1. 只适合二分类问题

当然，实际上如果进行一些改进。逻辑回归也可以解决多分类问题。
比如

1. One VS REST
2. softmax方法-逻辑回归

如图：softmax方法-逻辑回归。

逻辑回归和朴素贝叶斯

	逻辑回归	朴素贝叶斯
解决问题	二分类	多分类
应用场景	二分类都可以用逻辑回归	一般用于文本分类
超参数	正则化力度	没有超参数
先验概率	无	有
判别或生成	判别模型	生成模型

• 朴素贝叶斯的先验概率是$P(F_1,F_2,F_3···|C)P(C)$中的$P(C)$，即需要从历史数据中总结出概率信息。
• 依据有无先验概率，又可分为判别模型和生成模型
  • 逻辑回归没有先验概率，属于判别模型
  • 朴素贝叶斯有先验概率，属于生成模型

常见的判别模型还有kNN、决策树、随机森林。
常见的生成模型还有朴素贝叶斯、隐马尔可夫模型。