14.k-means

从这一章开始，我们讨论无监督学习，即数据中不含有目标值，只有特征值。也正因为没有目标值，无监督学习做的也不是预测这件事情，而是聚类和降维等。

关于降维，我们在第三章讨论的PCA，实际上就属于无监督学习的降维。
这里，我们主要讨论聚类。

在聚类算法中根据样本之间的相似性，将样本划分到不同的类别中，对于不同的相似度计算方法，会得到不同的聚类结果。

我们从最典型的聚类算法，k-means开始。

简介

k-means，由两部分组成，k和means。

• k：把数据划分成k个类别
  • 也是初始质心（中心点）个数，也是计划聚类数
• means：质心到其他数据点距离的平均值
  • means就是mean的复数，就是平均值的复数。一共有k个平均值

k是一个超参数，但一般在真实的业务场景下，k值是已知的。

过程

上面过程的解释：
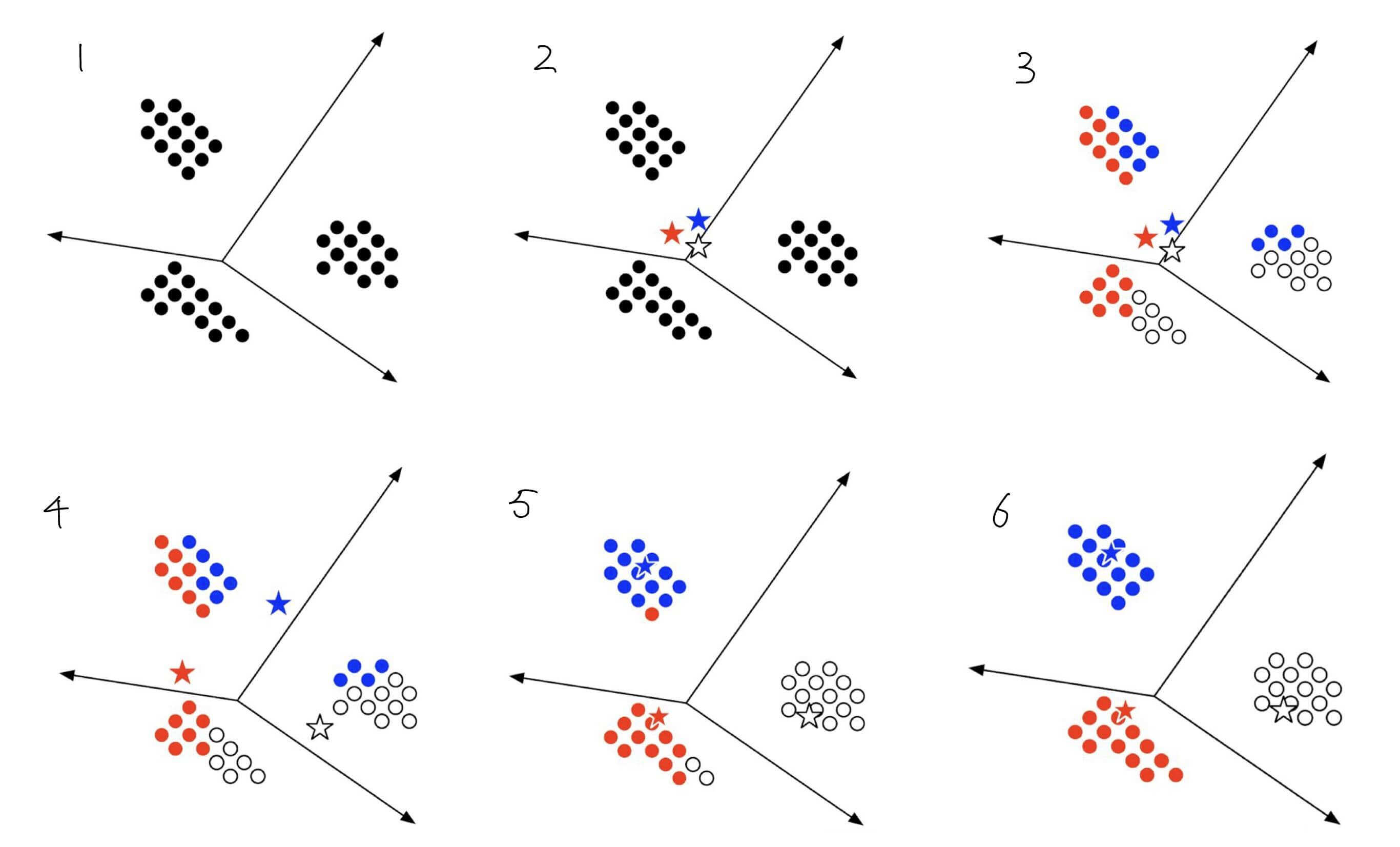
假设k等于3

1. 存在若干个点
2. 现在随机选取三个质心
3. 计算其余点到三个质心的距离，以最近的值作为分类
4. 计算新的质心，移动质心
5. 计算其余点到三个质心的距离，以最近的值作为分类。以此更新分类
6. 重复操作，直到所有质心的位置不再改动。
   (有时候我们也设置最大的迭代次数。)

我们再以具体的数字为例。
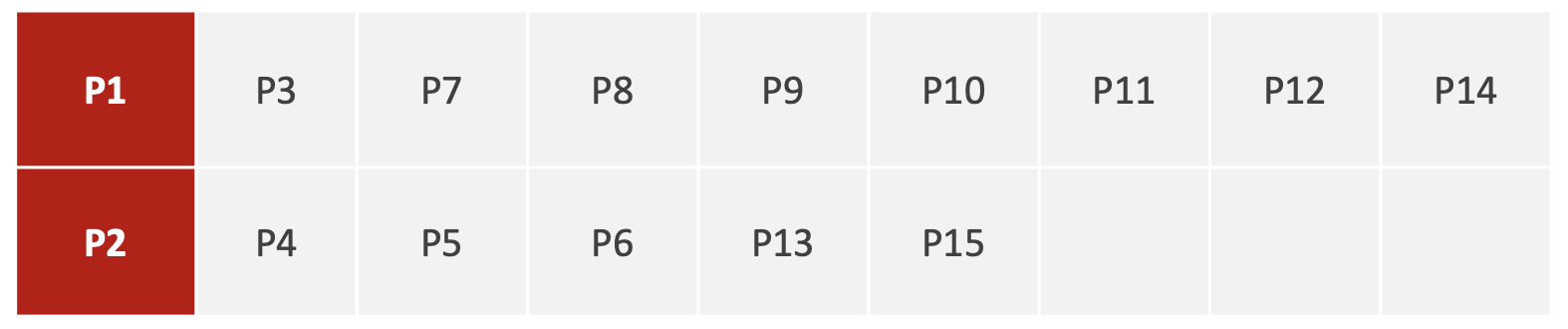
假设存在数据如下

	P1	P2	P3	P4	P5	P6	P7	P8	P9	P10	P11	P12	P13	P14	P15
X	7	2	6	1	1	3	8	9	10	5	7	9	2	5	5
Y	7	3	8	4	2	1	2	10	7	5	6	3	8	11	2

我们选择P1和P2作为初始的质心。则有

然后将所有P1大类的x都求平均，y求平均。P2大类操作相同。由此得到新的P'1和P'2，这就是新的质心。

再进行一轮迭代更新。

如此循环，直到质心不再变化，或到达最大迭代次数。

我们联系一下遗传算法的过程

graph LR; 开始 --> 初始化种群 --> 种群第一代G=0 --> 计算适应度 --> 选择操作 --> 交叉操作 --> 变异操作 --> 产生下第一代G=G+1 --> gen{G > GEN} gen -- 是 --> 123 gen -- 否 --> 计算适应度

其实思路比较相近。都是迭代计算，上一步的结算结果，作为这一步的输入。

评估

k-means的评估方法有

1. SSE
2. 轮廓系数
3. CH系数

SSE

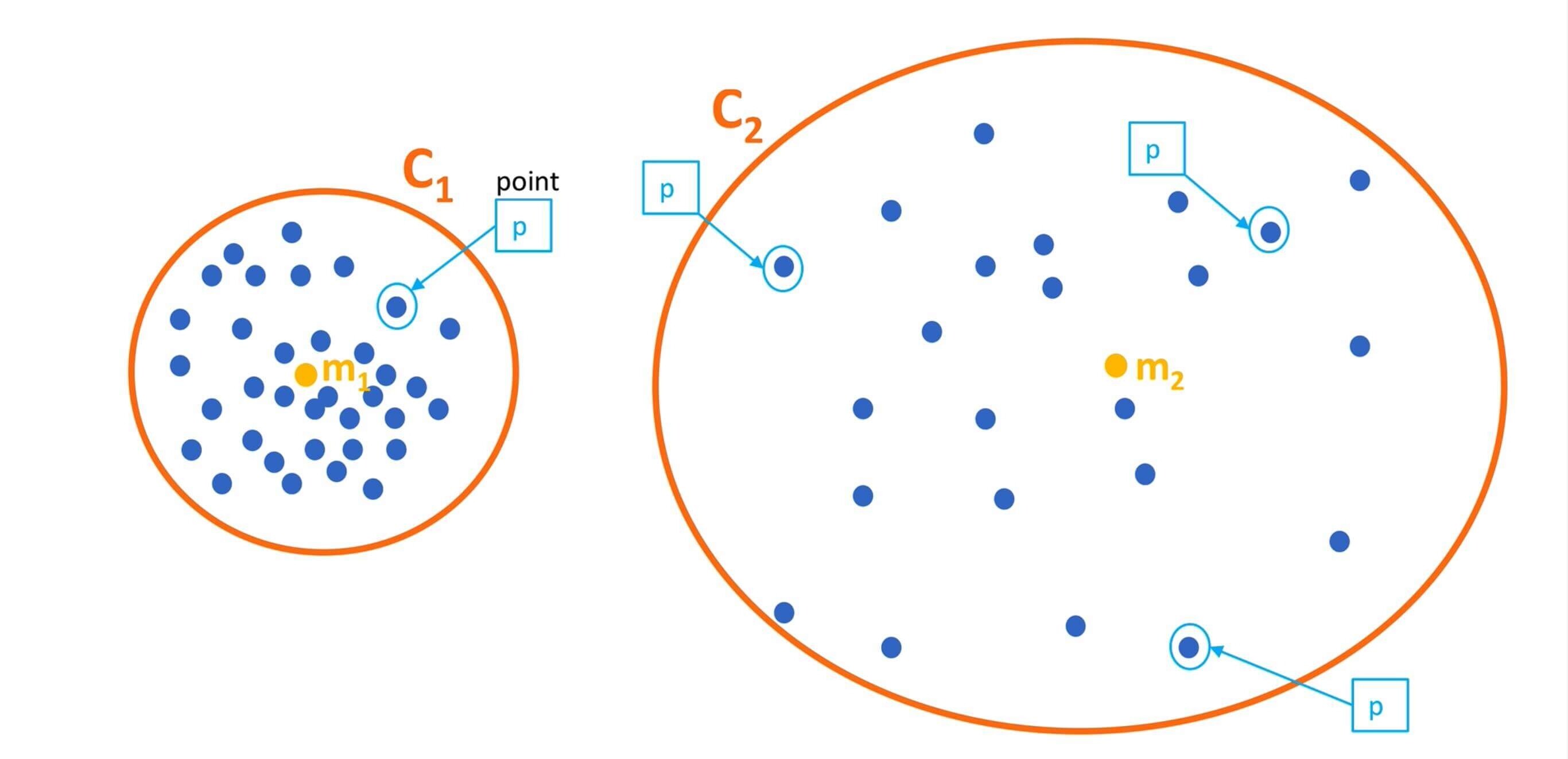
SSE：Sum of Squear due to Error 误差平方和

$$SSE = \sum_{i=1}^k\sum_{p\in C_i}|p-m_i|^2$$

如图

其中

• $k$为分类数，在图中是$C_1$，$C_2$。分类数是2
• 每一个蓝色点代表p
• m为每一个类的质心

轮廓系数

轮廓系数结合了凝聚度(Cohesion)和分离度(Separation)。

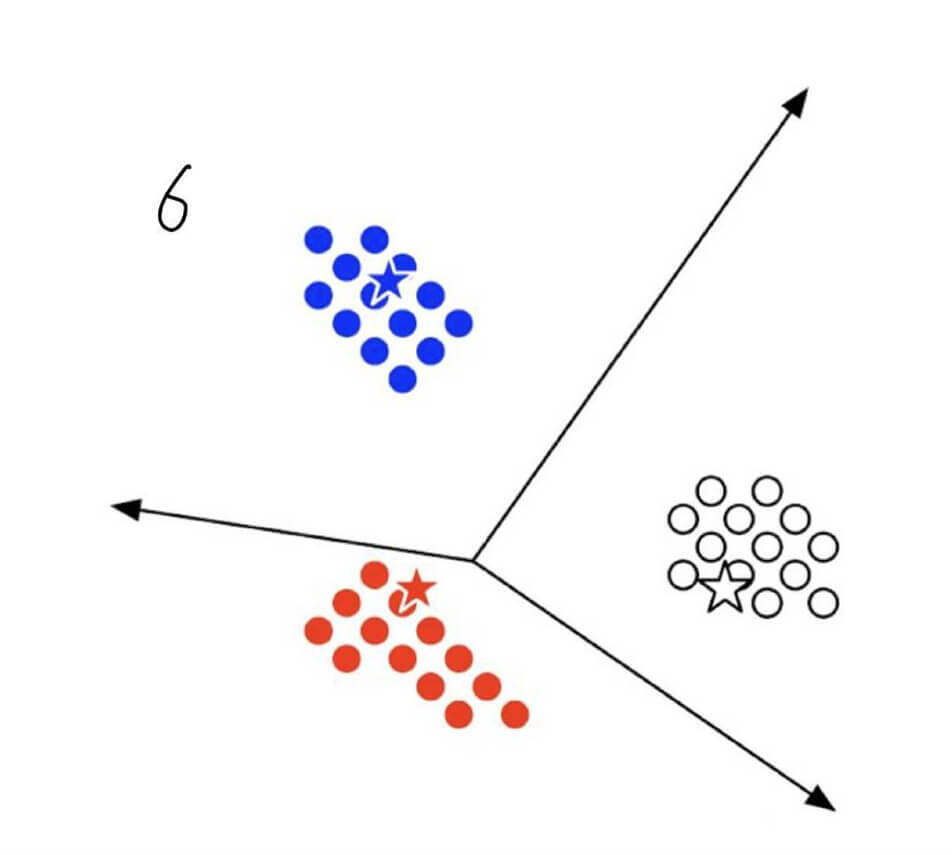
$$SC_i = \frac{b_i - a_i}{max(b_i,a_i)}$$

其中

• $a$ 代表凝聚度
• $b$ 代表分离度

我们以图6中，蓝点最下方的一个为例。

1. 计算该蓝点到其他蓝点的距离的平均值，记作$a_i$，这就是凝聚度。
2. 计算该蓝点分别到红色点和白色点的距离的平均值，此时我们会有两个平均值，取其中最小的值，记做$b_i$，这就是分离度。
3. 套入公式，计算的轮廓系数。

根据公式，我们也很容易知道

1. 当$b_i >> a_i$，轮廓系数趋于1，聚类效果好
2. 当$a_i = b_i$，轮廓系数等于0。
3. 当$a_i >> b_i$，轮廓系数趋于-1，聚类效果差
4. 轮廓系数的值$\in (-1,1)$

$>>$的含义是远远大于

实际情况中，一般轮廓系数很难超过0.7。

CH系数

CH：Calinski-Harabasz Index
类别内部数据的距离平方和越小越好，类别之间的距离平方和越大越好，这样的CH值越大，聚类效果越好。

高类聚低耦合

$$CH(k) = \frac{SSB}{SSW} \frac{m-k}{k-1}$$

其中

• $m$为样本数
• $k$为聚类数
• 乘以$\frac{m-k}{k-1}$的原因是，想用尽量少的类别聚类尽量多的样本。

SSB，不同类别之间的距离

$$SSB = \sum_{j=1}^k n_j ||C_j - \bar{X}||^2$$

其中

• 其中$C_j$是每一个类别的质心
• $\bar{X}$是所有类别质心的质心
• $n_j$是每一个类别样本的数量

SSW，同一类别不同点之间的距离

$$SSW = \sum_{i=1}^m ||x_i - C_{pi}||^2$$

其中

• m是点的个数
• $x_i$是每一个点
• $C_{pi}$是每一个类别的质心

实现

我们以对A股进行聚类为例

算法的实现

from sklearn.cluster import KMeans

• clusters：开始的聚类中心数量
• max_iter：最大迭代次数
• init，初始化方法，默认是k-means++

评估方法的实现

# 轮廓系数
from sklearn.metrics import silhouette_score
# CH值
from sklearn.metrics import calinski_harabasz_score

示例代码：

# 轮廓系数
from sklearn.metrics import silhouette_score
# CH值
from sklearn.metrics import calinski_harabasz_score
from sklearn.cluster import KMeans
import tushare as ts
ts.set_token('tushare的token')
pro = ts.pro_api()
df = pro.daily(trade_date='20200508')
df_drop = df.drop(['ts_code','trade_date'], axis=1)

print('数据的行数和列数')
print(df_drop.shape)

km = KMeans(n_clusters=9)
km.fit(df_drop)
predict = km.predict(df_drop)
df['label'] = predict

print('聚类结果')
print(df)

print('轮廓系数')
print(silhouette_score(df_drop,predict))

print('CH系数')
print(calinski_harabasz_score(df_drop,predict))

运行结果：

数据的行数和列数
(3806, 9)
聚类结果
        ts_code trade_date   open   high    low  close  pre_close  change  \
0     600712.SH   20200508   4.79   4.87   4.79   4.80       4.81   -0.01   
1     600713.SH   20200508   4.37   4.40   4.36   4.39       4.37    0.02   
2     600714.SH   20200508   5.04   5.34   5.01   5.22       5.06    0.16   
3     600715.SH   20200508   2.53   2.58   2.51   2.57       2.53    0.04   
4     600716.SH   20200508   3.63   3.69   3.63   3.68       3.62    0.06   
...         ...        ...    ...    ...    ...    ...        ...     ...   
3801  603353.SH   20200508  29.39  29.89  29.09  29.62      29.58    0.04   
3802  601869.SH   20200508  32.44  32.78  32.01  32.38      32.03    0.35   
3803  300759.SZ   20200508  64.61  65.61  64.36  64.40      64.65   -0.25   
3804  601066.SH   20200508  35.34  35.98  34.71  35.22      34.74    0.48   
3805  002937.SZ   20200508  13.11  13.32  13.10  13.18      13.01    0.17   

      pct_chg        vol       amount  label  
0     -0.2079  236024.18   113840.568      7  
1      0.4577   54652.99    23940.423      0  
2      3.1621   26940.45    13929.568      0  
3      1.5810   53728.73    13719.542      0  
4      1.6575   24988.95     9162.344      0  
...       ...        ...          ...    ...  
3801   0.1352   48950.72   143788.235      0  
3802   1.0927   34800.35   112915.499      0  
3803  -0.3867   46867.82   303829.857      7  
3804   1.3817  565749.86  2001463.707      2  
3805   1.3067   25585.60    33817.221      0  

[3806 rows x 12 columns]
轮廓系数
0.5540414778154246
CH系数
3881.61102352686

优缺点

1. 优点：迭代算法，直观简单，且实用
2. 缺点：
   1. 容易受异常点的影响。
   2. 在大规模数据集上，收敛太慢。
   3. 容易收敛到局部最优解。

进阶

Canopy

在一般的业务场景下，k值是已知的。但是也有k值不确定的情况，这时候我们需要自己来判断k值。
这就需要Canopy算法。
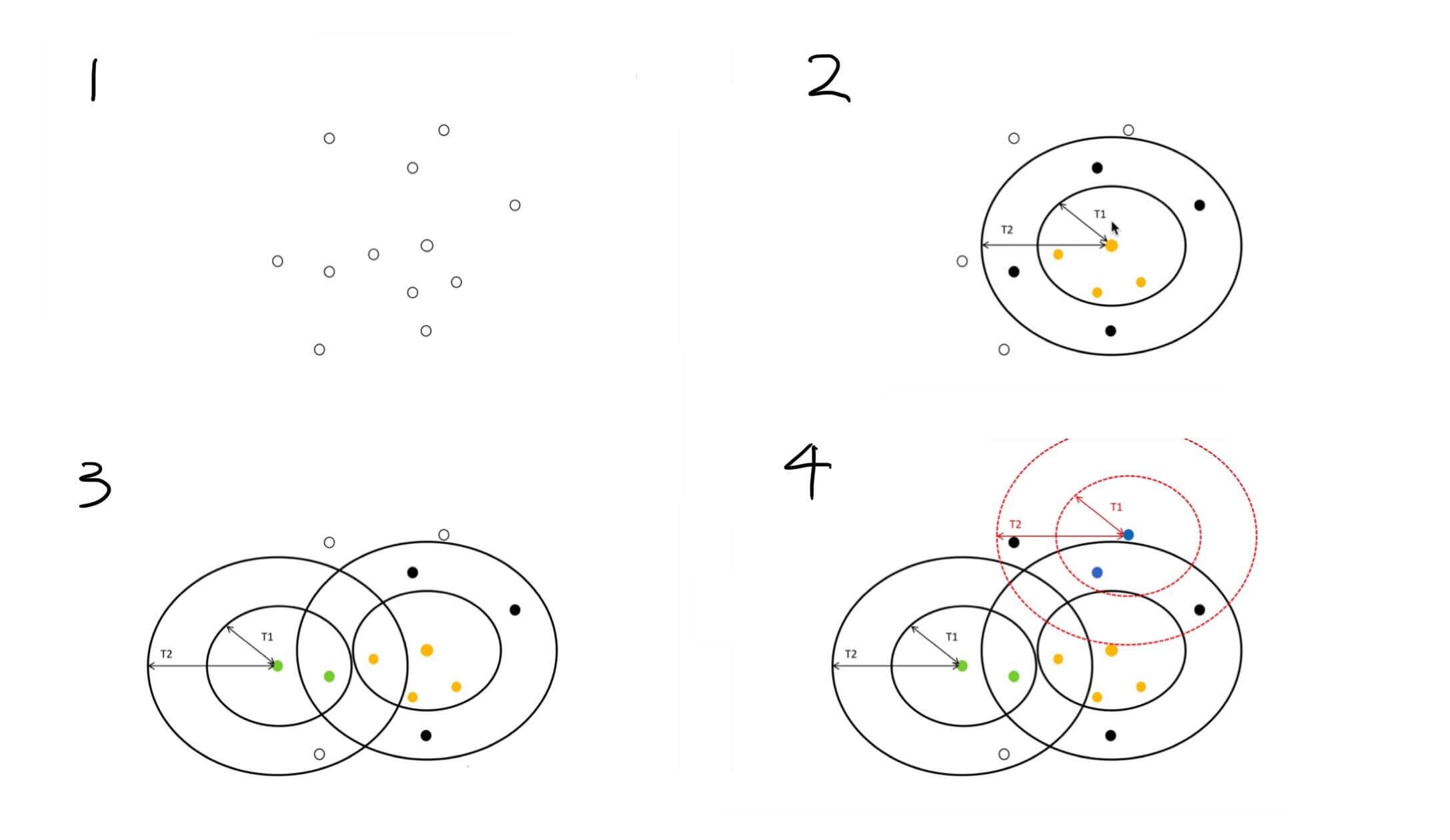
Canopy的过程

上面过程的解释

1. 存在若干个点
2. 随机选取一个点，标为黄色。
   1. 以T1为半径作圆，圆内的点就认为同属于一个类别，标为黄色。
   2. 以T2为半径作圆，认为T1和T2之间的点是疑似，标为黑色。
3. 在T2圆外，随机选取一个点，标为绿色
   1. 以T1为半径作圆，圆内的点就认为同属于一个类别，标为绿色。这时候上一步被标为黑色的点，这一步被标为了绿色，即不再是疑似。
   2. 以T2为半径作圆，认为T1和T2之间的点是疑似，标为黑色。
4. 再从两个T2圆外选择一个点，如此迭代操作

最后会的到一个类别的数量，认为这个就是k值

Canopy的优缺点

1. 优点
   1. Canopy还可以用来去除一些噪声
2. 缺点
   1. T1、T2的选择问题
      1. 实际上也是绝大部分的问题，不能作为Canopy的比较缺点

k-means++

k-means++的思想：离当前已有聚类中心较远的点有更大的概率被选为下一个聚类中心。通过这种方法尽量分散选质心。
每个样本被选为下一个聚类中心的概率

$$P = \frac{D(x)^2}{\sum_{x\in X} D(x)^2}$$

其中

• $D(x)$是欧式距离的函数
  举例如下：
  

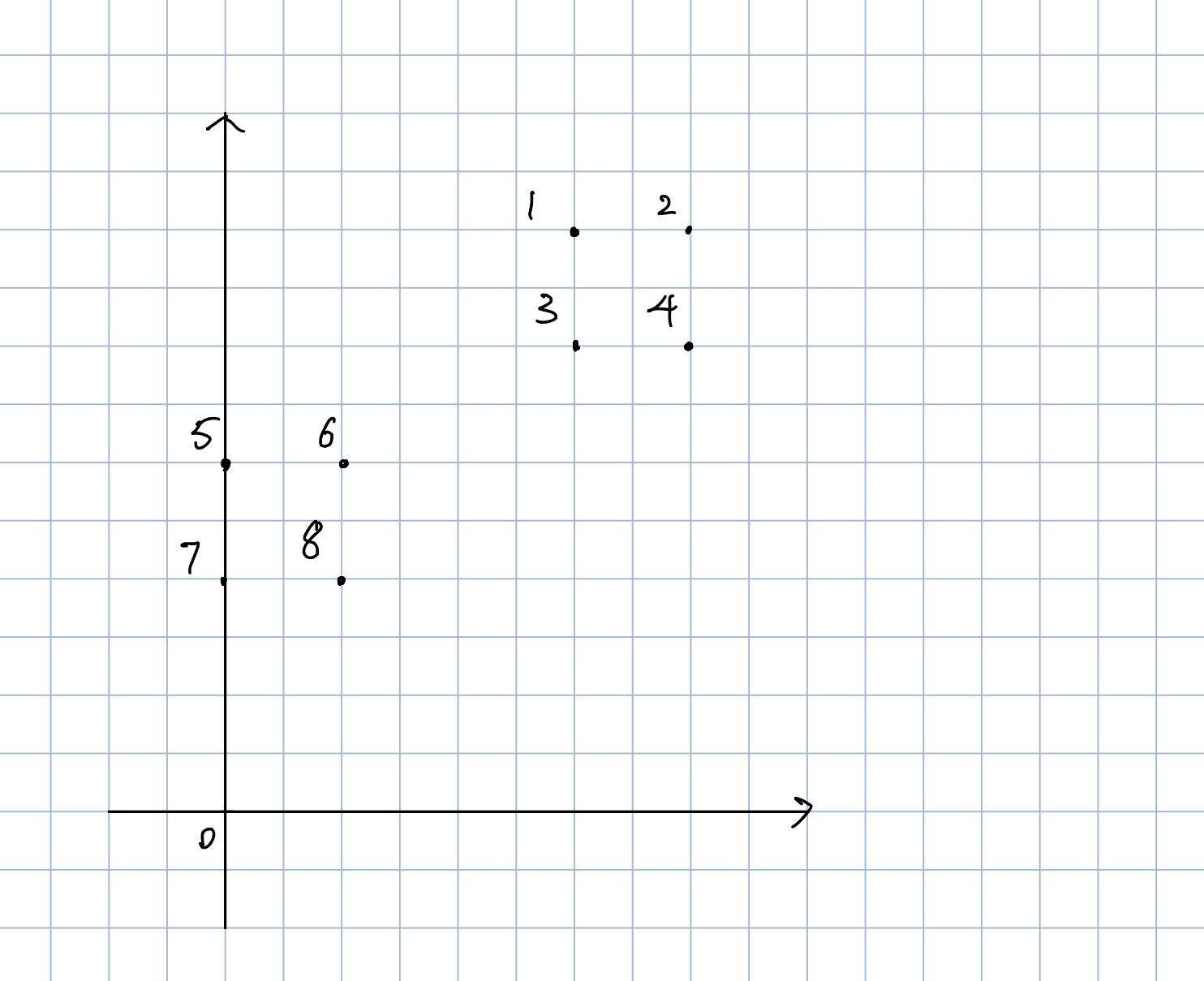
存在八个点，如上面的图所示。
现在我们选取6这个点作为第一个初始聚类中心。
则有

	1	2	3	4	5	6	7	8
$D(x)$	$2\sqrt{2}$	$\sqrt{13}$	$\sqrt{5}$	$\sqrt{10}$	1	0	$\sqrt{2}$	1
$D(x)^2$	8	13	5	19	1	0	2	1

则，1这个点，作为下一个聚类中心的概率是

$$\frac{8}{8 + 13 + 5 + 10 + 1 + 0 + 2 + 1} = 0.2$$

其他的点计算类似。

k-medoids

K-medoids和k-means的主要区别在于质心的选取。

1. 质心的资质
   • k-means中的质心，可以不是样本中的点。
   • k-medoids中的质心，必须是样本中的点。
2. 质心的生成规则
   • k-means中，将质心取为当前类别中所有数据点的平均值，这也导致其对异常点很敏感。
   • k-medoids中，将从当前类别中选取到当前类别的其他点的距离之和最小的点作为质心。

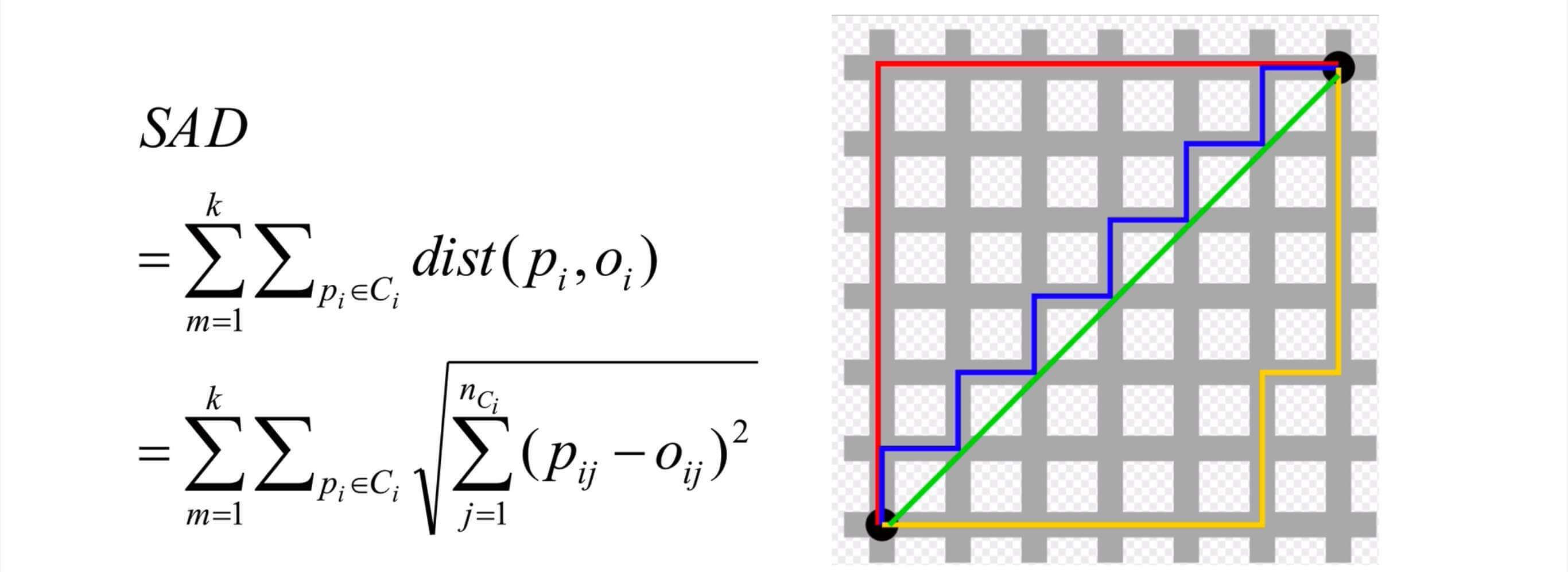
特别注意：K-medoids使用SAD来计算两点间的距离。
SAD：Sum of Absolute Differences，绝对差值和。其实也就是曼哈顿距离。
在n维空间中，计算SAD的公式如下所示:

除了上述不同，整体过程和k-means非常相似，这里不在赘述。

k-medoids的优缺点

1. 优点
   1. 抗噪声能力强
   2. 小规模数据性能更好。
2. 缺点
   1. 速度太慢（尤其是生成下一个质心的规则）
   2. 其实少数噪声对k-means影响有限，这也是为什么k-means比k-medoids更普遍的原因。

但是k-medoids和k-means都会陷入局部最优解的困境。