15.其他聚类算法

密度聚类：DBSCAN

DBSCAN是密度聚类的一种，最直观的感受就像这样。

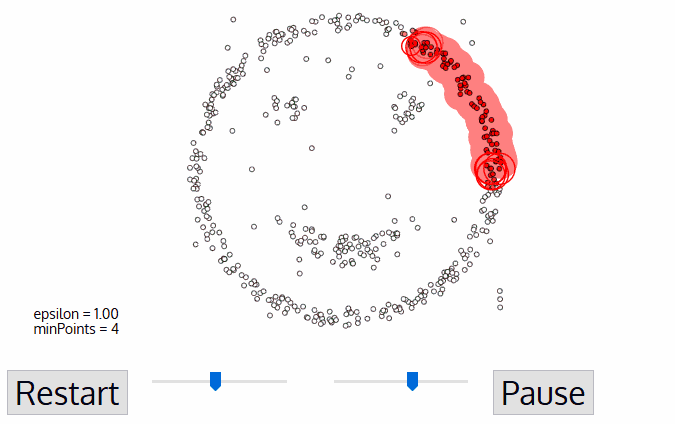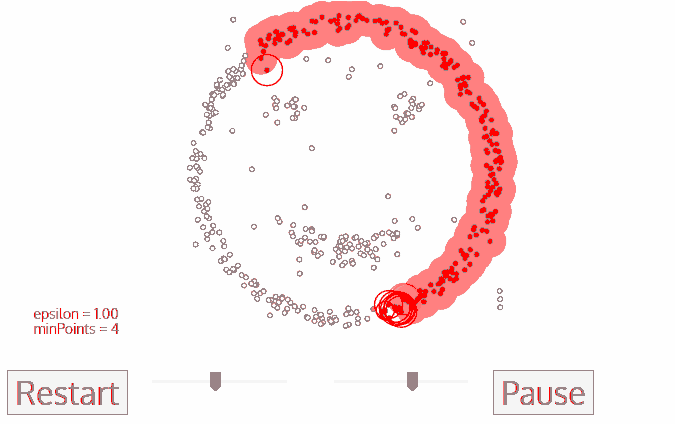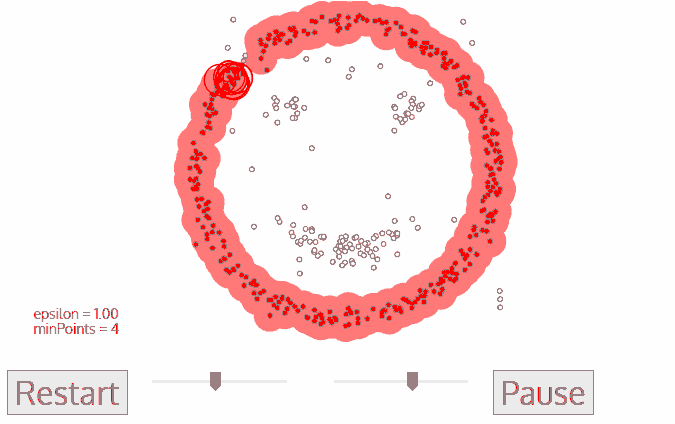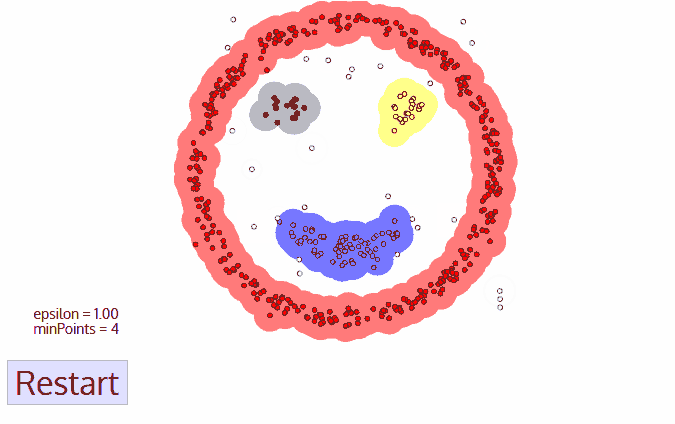
而这种聚类效果，是上一章的距离聚类所无法实现的。

密度的定义
密度和两个值有关。

• Eps：半径，表示给定一个点，以Eps为半径的邻域。
• MinPts：最少点的数量，表示领域内最少的点的数量。

这两个值均是超参数，所以在DBSCAN中，密度也是超参数。

而根据密度，点又可以分为三类。

• Core Point：核心点，该点的Eps邻域内至少有MinPts个其他点。
• Edge Point：边界点，该点落在某个核心点的邻域内。
• Outlier Point：噪音点，既不是核心点，也不在某个核心点的邻域内。

DBSCAN的优缺点

1. 优点
   1. 聚类速度快，且能够有效处理噪声点和在任意形状的空间聚类
   2. 与k-means相比，不需要确定类别个数
   3. 可以过滤噪声
2. 缺点
   1. Eps和MinPts的选取困难，DBSCAN对Eps和MinPts敏感。
   2. 在高维数据下，存在’维数灾难’。

OPTICS算法能够克服DBSCAN对Eps和MinPts敏感这个缺点。

层次聚类

层次聚类举例

层次最直观的感受，就像这样。

现在，我们以一维数据的为例，讨论什么是层次聚类。

A	B	C	D	E	F	G
16	38	40	80	82	35	110

我们求两两之间的距离。

	A	B	C	D	E	F	G
A	0	22	24	62	64	19	94
B	22	0	2	42	44	3	72
C	24	2	0	40	42	5	70
D	62	42	40	0	2	45	30
E	64	44	42	2	0	47	28
F	19	3	5	45	47	0	75
G	94	72	70	30	28	75	0

我们会看到，B和C的距离是2，D和E的距离也是2。所以，我们把B和C的归为一类，D和E归为一类。
则有

	A	(B,C)	(D,E)	F	G
A
(B,C)
(D,E)
F
G

那么
A到(B,C)的距离是多少呢？
(B,C)到(D,E)的距离是多少呢？

距离的度量

层次聚类中有多种多样的距离度量方法，一般对于距离度量方法无限制。我们甚至可以自定义距离度量方法。

这里介绍四种常见的方法。

1. MIN度量
2. MAX度量
3. Group Average平均距离度量
4. Distance Between Centroids质心度量

MIN度量

一个类别的$m$个元素分别与另一个类别的$n$个元素比较，共有$m*n$个距离。
【最小】的距离作为两个类之间的距离。
缺点是容易受极端值的影响。

MAX度量

一个类别的$m$个元素分别与另一个类别的$n$个元素比较，共有$m*n$个距离。
【最大】的距离作为两个类之间的距离。
缺点是容易受极端值的影响。

平均距离度量

一个类别的$m$个元素分别与另一个类别的$n$个元素比较，共有$m*n$个距离。
然后对$m*n$个距离求平均，作为两个类别之间的距离。

质心度量

两个类别分别求质心，然后质心的距离作为两个类别之间的距离。

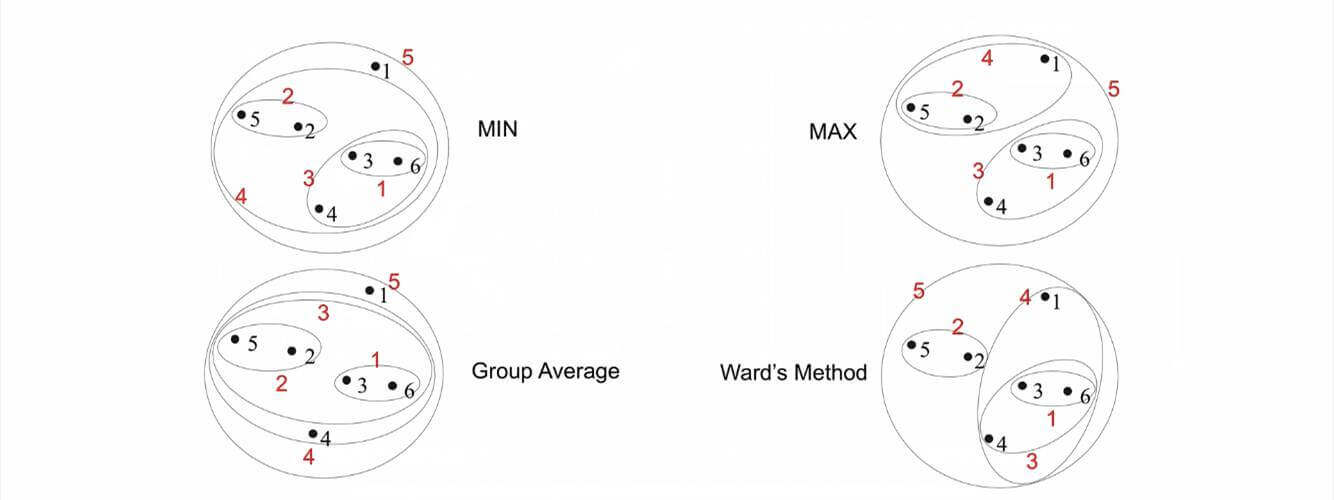
特别注意：不同的距离度量方法，会有产生不同的层次聚类。如图。

层次聚类的步骤

总结一下层次聚类的步骤

1. 将每个对象看作一个类，计算两两之间距离。
2. 将距离最小的两个类合并成一个新的类。
3. 重新计算所有类两两之间的距离。
4. 重复上述2和3的操作，知道所有的类都合成了一个大类。

就像这样

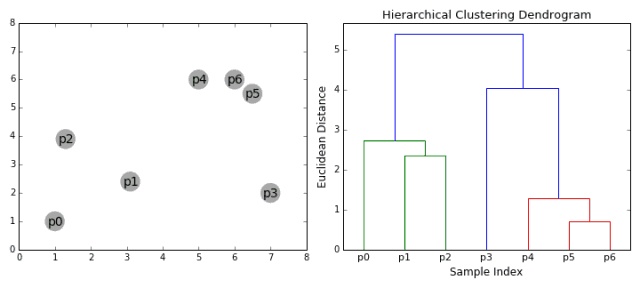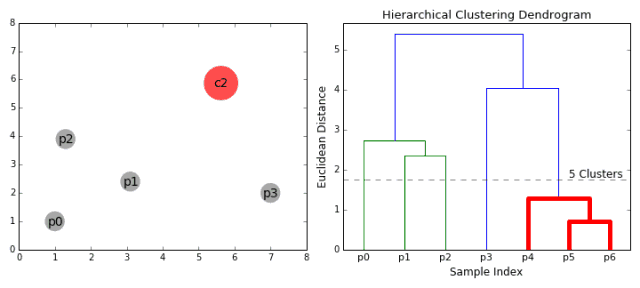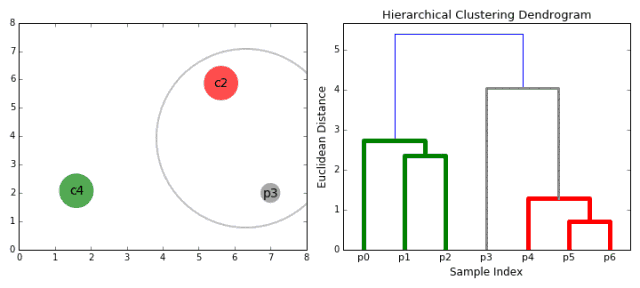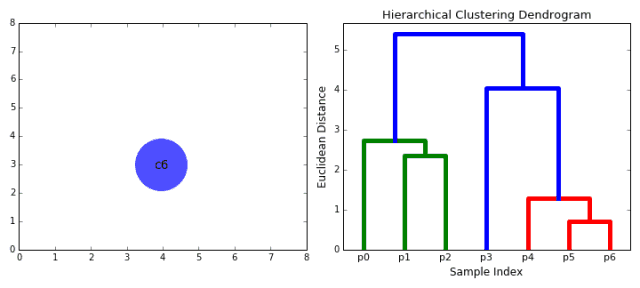
层次聚类的优缺点

1. 优点

   1. 距离度量方法无限制，还可以自定义距离。
   2. 不需要指定类别数。
   3. 可以发现不同类别之间的层次关系。

2. 缺点

   1. 每一个类别的划分，都和上一个类别有关，所以当前类别的合并决策会影响后续的类别划分。整个过程是不可逆的。
   2. 计算复杂度高。
   3. 容易受异常值的影响。

编辑距离

上面，我们提到了，层次聚类可以自定义距离，现在我们举一个例子。
编辑距离
比如，现在有这么一个问题。

熊猫到底是属于熊，还是猫？

在生物学上，首先我们要有熊的DNA，猫的DNA和熊猫的DNA。然后比较他们的编辑距离。如果熊猫的DNA和熊的DNA编辑距离近，熊猫就是熊；如果熊猫的DNA和猫的DNA编辑距离近，熊猫就是猫。

那么，什么是编辑距离呢？

我们以贝加尔湖畔和包贝尔湖畔为例。
比如，我们现在要把贝加尔湖畔改成包贝尔湖畔，并且我们约定只能有三种操作。新增、修改、删除，每次只能操作一个字符。

1. 把贝加尔湖畔的加删除，得到贝尔湖畔。
2. 插入一个包，这时候得到包贝尔湖畔。

上述，我们只用了两步，把贝加尔湖畔改成包贝尔湖畔，即编辑距离是二。