11.线性回归

之前我们讨论的都是分类问题。这一章，我们讨论的回归问题。
分类问题和回归问题的主要区别在于目标值。

• 分类：目标值是离散的
• 回归：目标值是连续的

矩阵

首先，我们复习一下"矩阵的定义及其基本运算"。

矩阵的定义：

由$m * n$个数，排成$m$行$n$列的矩形表格

$$\left[ \begin{matrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{matrix} \right]$$

称为一个$m * n$的矩阵。记作$\bold{A}$，或$(a_{ij})_{m * n}$。
特别的

• 当$m = n$时，称为$n$阶方阵。
• 对于两个矩阵，$\bold{A}=(a_{ij})_{m * n}$和$\bold{B}=(b_{ij})_{s * k}$，若$m=s$，$n=k$，则称$\bold{A}$和$\bold{B}$为同型矩阵。

矩阵的基本运算

相等

当$\bold{A}$，$\bold{B}$是同型矩阵，且各元素处处相等。则$\bold{A} = \bold{B}$

加法

只有$\bold{A}$，$\bold{B}$是同型矩阵时，才可以相加。
$\bold{C} = \bold{A} + \bold{B}$
$c_{ij} = a_{ij} + b_{ij}$，即对应元素相加。

数乘矩阵

$k$是一个数，$\bold{A}$是一个矩阵。

$$k\bold{A} = k \left[ \begin{matrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{matrix} \right] = \left[ \begin{matrix} k*a_{11} & k*a_{12} & \cdots & k*a_{1n} \\ k*a_{21} & k*a_{22} & \cdots & k*a_{2n} \\ \vdots & \vdots & & \vdots \\ k*a_{m1} & k*a_{m2} & \cdots & k*a_{mn} \\ \end{matrix} \right]$$

矩阵加法和数乘的运算律

1. 交换律 $\bold{A} + \bold{B} = \bold{B + \bold{A}}$
2. 结合率 $(\bold{A} + \bold{B}) + \bold{C} = \bold{A} + (\bold{B} + \bold{C})$
3. 分配律 $k(\bold{A} + \bold{B}) = k\bold{A} + k\bold{B}$

矩阵的乘法

当$\bold{A}$是$m * s$的矩阵，$\bold{B}$是$s * n$的矩阵，且只有$\bold{A}$的列数等于$\bold{B}$的行数时，$\bold{A}$，$\bold{B}$可乘。
记$\bold{C} = \bold{A}\bold{B}$，其中$\bold{C}$的第$i$行第$j$列的元素$c_{ij}$是$\bold{A}$的第$i$行的$s$个元素与$\bold{B}$的第$j$列的$s$个元素的两两乘积的和。
例如：

$$\bold{A} = \left[ \begin{matrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \end{matrix} \right] \bold{B} = \left[ \begin{matrix} b_{11} \\ b_{21} \\ b_{31} \end{matrix} \right]$$

$$c_{11} = a_{11} * b_{11} + a_{12} * b_{21} = a_{13} * b_{31}$$

$$c_{21} = a_{21} * b_{11} + a_{22} * b_{21} = a_{23} * b_{31}$$

$$\bold{C} = \left[ \begin{matrix} c_{11} \\ c_{21} \end{matrix} \right]$$

矩阵的转置

$m$行$n$列 变成 $n$行$m$列

$${\bold{A}_{m * n}}^T = \left[ \begin{matrix} a_{11} & a_{21} & \cdots & a_{m1} \\ a_{12} & a_{22} & \cdots & a_{m2} \\ \vdots & \vdots & & \vdots \\ a_{1n} & a_{2n} & \cdots & a_{mn} \\ \end{matrix} \right]$$

矩阵的逆

$\bold{A}$，$\bold{B}$是$n$阶的方阵，$\bold{E}$是$n$阶的单位矩阵。若$\bold{AB} = \bold{BA} = \bold{E}$，则称$\bold{B}$是$\bold{A}$的逆矩阵，记作$\bold{A}^{-1}$。

模型

线性回归模型：通过特征的线性组合来进行预测的函数。

$$h_w(x) = w_0 + w_1x_1 + w_2x_2 + ··· + w_dx_d$$

$$h_w(x) = \bold{w}^T \bold{x}$$

其中$\bold{w}$，$\bold{x}$为矩阵。

$$\bold{w} = \left[ \begin{matrix} w_0 \\ w_1 \\ \vdots \\ w_{m} \end{matrix} \right] \ \bold{x} = \left[ \begin{matrix} 1 \\ x_1 \\ \vdots \\ x_{m} \end{matrix} \right]$$

在上文，我们把矩阵的定义和运算都复习了一下，现在，问，我们这个模型的输出是什么？
$1$行$M$列乘以$M$行$1$列，得到的$1$行$1$列，即只得到$1$个数。

损失函数

我们还需要一个函数来对模型的拟合效果进行评估，这个函数叫做损失函数，计作$J(\bold{w})$

$$J(\bold{w}) = \sum_{i=1}^m(h_w(x_i) - y_i)^2$$

其中

• $y_i$为第$i$个训练样本的真实值
• $h_w(x_i)$为第$i$个训练样本$x_i$，在模型$h_w$下的预测值

所以，我们现在的目标是要使损失函数的值最小。

优化

优化，就是寻找一个$\bold{w}$，使得损失函数的值最小。

正规方程

正规方程的公式

$$\bold{W} = (\bold{X}^T\bold{X})^{-1}\bold{X}^T\bold{y}$$

其中

• $\bold{X}$是特征值矩阵
• $\bold{y}$是目标值矩阵

该方法的缺点有

• 求解速度太慢
• 如果$\bold{X}^T\bold{X}$不可逆，无法求出$\bold{W}$
• 无法解决拟合问题

梯度下降

我们以只有一个变量的为例。
即，只有$w_0$和$w_1$两个参数。
则有

$$w_0 = -w_0 - \alpha\frac{\partial J(w_0,w_1)}{\partial w_0}$$

$$w_1 = -w_1 - \alpha\frac{\partial J(w_0,w_1)}{\partial w_1}$$

其中

• $J(w_0,w_1)$是损失函数
• $\alpha$是学习率

梯度下降的动态过程如图：

正规方程与梯度下降的对比

梯度下降	正规方程
需要选择学习率$\alpha$	不需要
需要多次迭代计算	不需要
在特征数量n较大时也能较好适用	通常特征数量小于10000适用
适用于各种模型	只适用线性模型，不适合包括逻辑模型在内的其它模型

关于什么是梯度，我们在《深度学习初步及其Python实现：3.梯度下降》中有更好的论述。

评估

线性回归作为回归模型，评估方法当然按照我们第四章提到的回归模型评估方法。

1. 平均绝对误差
2. 平均方差
3. R平方

这么我们再发散一下。
平均绝对误差可以作为我们的损失函数吗？
不可以，平均绝对误差是误差的绝对值的平均，有了绝对值，那么这个不可导。
R平方可以作为我们的损失函数吗？

$$\begin{aligned} R^2 & = 1 - \frac{RSS}{TSS} \\ & = 1 - \frac{\sum_{i=1}^n(y_i - \hat{y_i})^2}{\sum_{i=1}^n(y_i - \bar{y_i})^2} \end{aligned}$$

• 分子部分是我们的模型预测产生的错误
• 分母部分是样本真实值的方差，是常数

在这里，我们的R平方越大越好，所以严格意义上，我们是不能把R平方作为我们的损失函数的，因为损失函数要尽量小。但是，不能作为严格意义上的损失函数，绝对可以作为目标函数，我们可以用梯度上升方法求。
但，为什么我们通常讨论回归问题的时候，不把R平方作为我们的目标函数呢？再来看看R平方的式子，分子部分其实就是一个非标的均方误差(没有除以样本数)。所以再除以方差，然后再拿$1$减，这么折腾，没有任何意义。

实现

注意：
在scikit-learn 0.19及以上的版本中，要求传入转换器、估计器的数据必须是二维的形式。
所以，对于一维数据，我们需要用reshape转换成二维的形式。

y_train.reshape(-1,1)

正规方程：

from sklearn.linear_model import LinearRegression

梯度下降：

from sklearn.linear_model import SGDRegressor

示例代码：

from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import SGDRegressor

# 获取数据
lb = load_boston()

# 分割数据集到训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)

# 特征值和目标值是都必须进行标准化处理, 实例化两个标准化API
std_x = StandardScaler()
x_train = std_x.fit_transform(x_train)
x_test = std_x.transform(x_test)

# 目标值
std_y = StandardScaler()
y_train = std_y.fit_transform(y_train.reshape(-1,1))
y_test = std_y.transform(y_test.reshape(-1,1))

print('正规方程')
lr = LinearRegression()
lr.fit(x_train,y_train)
print(lr.coef_)
print(lr.score(x_test,y_test))

print('梯度下降')
sr = SGDRegressor()
sr.fit(x_train,y_train)
print(sr.coef_)
print(sr.score(x_test,y_test))

运行结果：

正规方程
[[-0.0999584   0.15770857  0.02429477  0.0665903  -0.23935036  0.26475608
   0.02780978 -0.36994635  0.3173723  -0.23827149 -0.23136748  0.11666166
  -0.42261817]]
0.7440813832822074
梯度下降
[-0.07546204  0.11049403 -0.0201109   0.06968199 -0.15184666  0.30057596
  0.00334009 -0.29757264  0.14135882 -0.07130111 -0.2087188   0.11581215
 -0.39141166]
0.7476643999577666

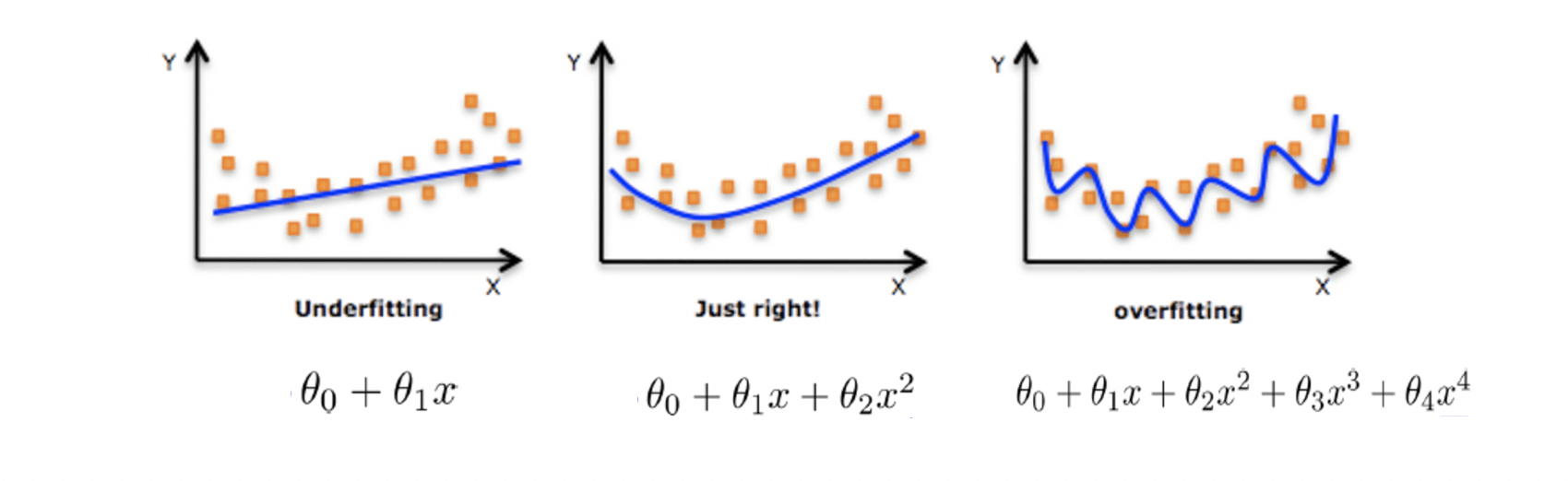
拟合问题

过拟合和欠拟合的定义

1. 过拟合：
   一个假设在训练数据上能获得比较好的拟合， 但是在训练数据外的数据集上却不能很好地拟合数据，此时认为这个假设出现了过拟合的现象。
   模型过于复杂

2. 欠拟合：
   一个假设在训练数据上不能获得更好的拟合， 但是在训练数据外的数据集上也不能很好地拟合数据，此时认为这个假设出现了欠拟合的现象。
   模型过于简单

过拟合和欠拟合的原因和办法

1. 欠拟合原因以及解决办法
   1. 原因：学习到数据的特征过少
   2. 办法：增加数据的特征数量
2. 过拟合原因以及解决办法
   1. 原因：原始特征过多，存在一些嘈杂特征。模型试图兼顾各个测试数据点，以至于模型过于复杂。
   2. 办法：
      1. 进行特征选择，消除关联性大的特征
      2. 交叉验证
         1. 交叉验证用以检查是过拟合或欠拟合
         2. 如果测试集效果不好，交叉验证效果好，那么可能过拟合
         3. 如果测试集效果不好，交叉验证效果也不好，那么就是欠拟合
      3. 正则化(尽量减小高次项特征的权重)
      4. 学习率衰减