卷积神经网络相比我们之前讨论的神经网络主要多了两个东西。一个是卷积,一个是池化。现在我们分别讨论。
卷积
卷积工作原理
现在,让我们回到影片开头这一段。张牧之和马邦德等人组成的队伍进城,黄四郎带着望远镜扫描这支队伍。
这里有两个主体:
张牧之和马邦德等人组成的队伍
带着望远镜的黄四郎
而这一段,又有两个特点:
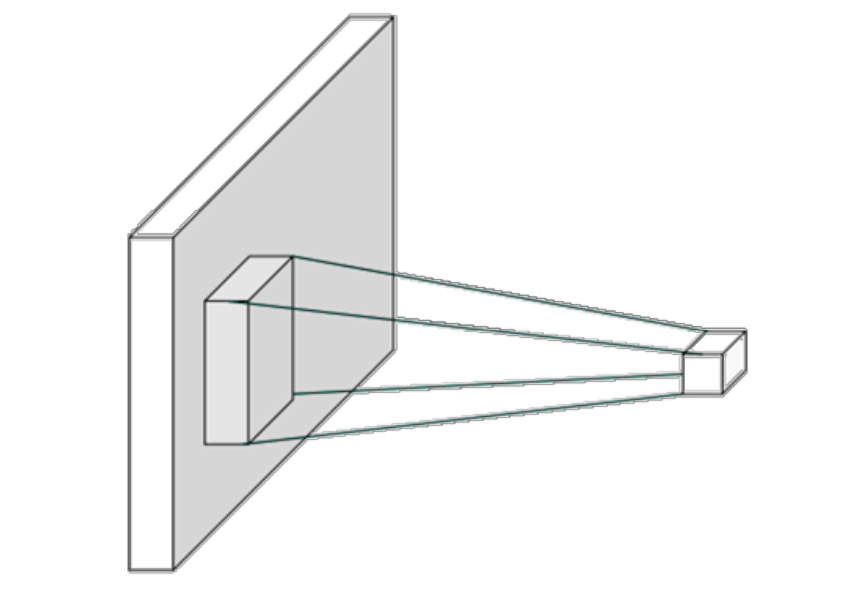
每次望远镜只能观察到这支队伍的局部。
全程都在用同一个望远镜进行观察。
现在,让我们把以这一段抽象出来。
卷积核每次只能观察到图像的局部,我们称之为局部连接 。
全程都在用同一个卷积核扫描图像,我们称之为权值共享 。
即卷积核的两个特点:
局部连接
权值共享
那么卷积核怎么对图像进行观察呢?卷积 。
卷积的运算法则
卷积和加减乘除一样,是一种运算。那么,既然是运算呢,就有运算法则。
一维
假设我们养金鱼,我们每隔一小时投放一次饲料,而且每次投放的饲料数是一个关于时刻的函数,在t t t x t x_t x t k k k w k w_k w k w 1 = 1 w_1 = 1 w 1 = 1 w 2 = 1 2 w_2 = \frac{1}{2} w 2 = 2 1 w 3 = 1 4 w_3 = \frac{1}{4} w 3 = 4 1 t t t y t y_t y t t t t
y t = 1 ⋅ x t + 1 2 ⋅ x t − 1 + 1 4 ⋅ x t − 2 = w 1 ⋅ x t + w 2 ⋅ x t − 1 + w 3 ⋅ x t − 2 = ∑ k = 1 3 w k ⋅ x t − k + 1 \begin{aligned}
y_t &= 1 \cdot x_t + \frac{1}{2} \cdot x_{t-1} + \frac{1}{4} \cdot x_{t-2} \\
&= w_1 \cdot x_t + w_2 \cdot x_{t-1} + w_3 \cdot x_{t-2} \\
&= \sum_{k=1}^{3} w_k \cdot x_{t-k+1}
\end{aligned}
y t = 1 ⋅ x t + 2 1 ⋅ x t − 1 + 4 1 ⋅ x t − 2 = w 1 ⋅ x t + w 2 ⋅ x t − 1 + w 3 ⋅ x t − 2 = k = 1 ∑ 3 w k ⋅ x t − k + 1
上述运算可总结为:
y t = ∑ k = 1 m w k ⋅ x t − k + 1 y_t = \sum_{k=1}^{m}w_k \cdot x_{t-k+1}
y t = k = 1 ∑ m w k ⋅ x t − k + 1
记作y = w ⊗ x y = w \otimes x y = w ⊗ x ⊗ \otimes ⊗
二维
我们发现卷积的运算法则是"倒着乘的乘积的和",根据一维的运算法则,我们很容易类比写出二维的运算法则。X ∈ R M ⋅ N \bold{X} \in \boldsymbol{R}^{M \cdot N} X ∈ R M ⋅ N W ∈ R m ⋅ n \bold{W} \in \boldsymbol{R}^{m \cdot n} W ∈ R m ⋅ n m < < M m << M m < < M n < < N n << N n < < N
y = ∑ u = 1 m ∑ v = 1 n = w u , v ⋅ x m − u + 1 , n − v + 1 y = \sum_{u=1}^{m} \sum_{v=1}^{n} = w_{u,v} \cdot x_{m-u+1,n-v+1}
y = u = 1 ∑ m v = 1 ∑ n = w u , v ⋅ x m − u + 1 , n − v + 1
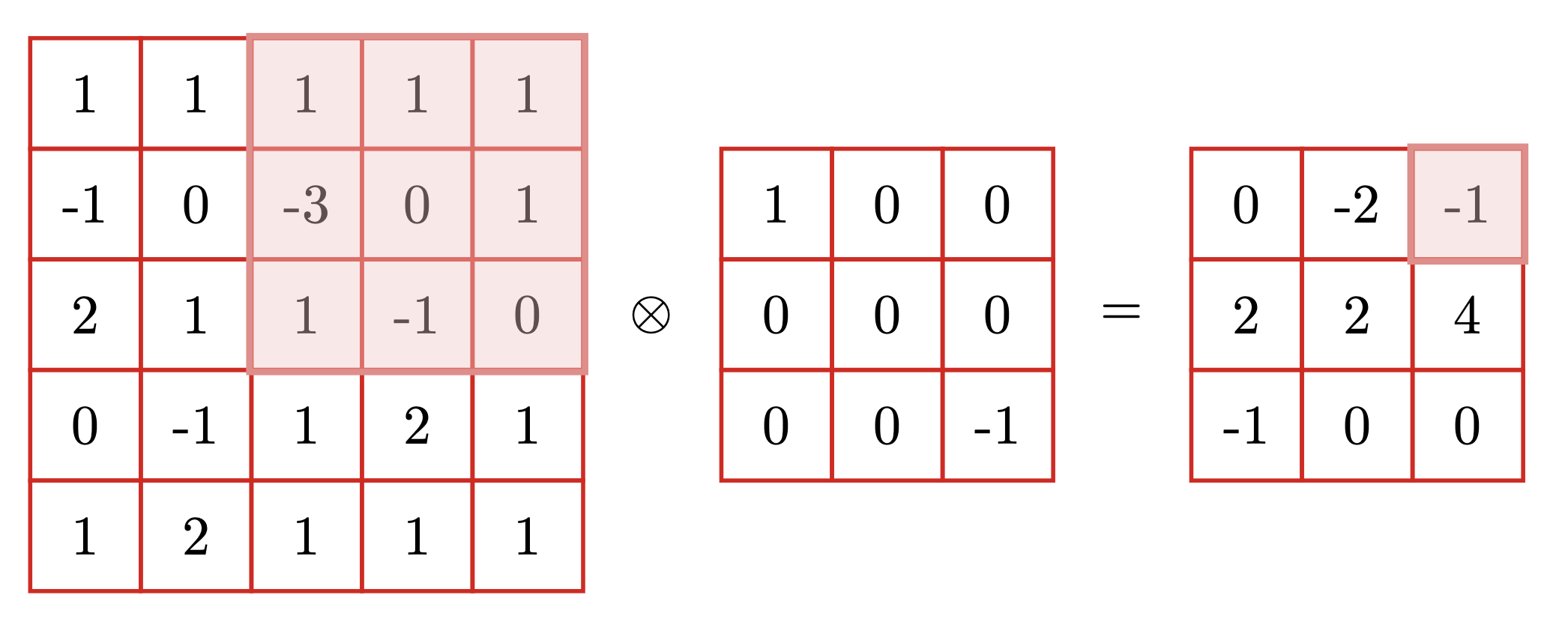
y = ∑ u = 1 m ∑ v = 1 n = w u , v ⋅ x m − u + 1 , n − v + 1 = ∑ u = 1 3 ∑ v = 1 3 = w u , v ⋅ x 3 − u + 1 , 3 − v + 1 = w 1 , 1 ⋅ x 3 − 1 + 1 , 3 − 1 + 1 + w 1 , 2 ⋅ x 3 − 1 + 1 , 3 − 2 + 1 + w 1 , 3 ⋅ x 3 − 1 + 1 , 3 − 3 + 1 + w 2 , 1 ⋅ x 3 − 2 + 1 , 3 − 1 + 1 + w 2 , 2 ⋅ x 3 − 2 + 1 , 3 − 2 + 1 + w 2 , 3 ⋅ x 3 − 2 + 1 , 3 − 3 + 1 + w 3 , 1 ⋅ x 3 − 3 + 1 , 3 − 1 + 1 + w 3 , 2 ⋅ x 3 − 3 + 1 , 3 − 2 + 1 + w 3 , 3 ⋅ x 3 − 3 + 1 , 3 − 3 + 1 = 1 ⋅ 0 + 0 ⋅ − 1 + 0 ⋅ 1 + 0 ⋅ 1 + 0 ⋅ 0 + 0 ⋅ − 3 + 0 ⋅ 1 + 0 ⋅ 1 + − 1 ⋅ 1 + = − 1 \begin{aligned}
y &= \sum_{u=1}^{m} \sum_{v=1}^{n} = w_{u,v} \cdot x_{m-u+1,n-v+1} \\
&= \sum_{u=1}^{3} \sum_{v=1}^{3} = w_{u,v} \cdot x_{3-u+1,3-v+1} \\
&=w_{1,1} \cdot x_{3-1+1,3-1+1} + w_{1,2} \cdot x_{3-1+1,3-2+1} + w_{1,3} \cdot x_{3-1+1,3-3+1} + \\
&\quad \ w_{2,1} \cdot x_{3-2+1,3-1+1} + w_{2,2} \cdot x_{3-2+1,3-2+1} + w_{2,3} \cdot x_{3-2+1,3-3+1} + \\
&\quad \ w_{3,1} \cdot x_{3-3+1,3-1+1} + w_{3,2} \cdot x_{3-3+1,3-2+1} + w_{3,3} \cdot x_{3-3+1,3-3+1} \\
&= 1 \cdot 0 + 0 \cdot -1 + 0 \cdot 1 + \\
&\quad \ 0 \cdot 1 + 0 \cdot 0 + 0 \cdot -3 + \\
&\quad \ 0 \cdot 1 + 0 \cdot 1 + -1 \cdot 1 + \\
&= -1
\end{aligned}
y = u = 1 ∑ m v = 1 ∑ n = w u , v ⋅ x m − u + 1 , n − v + 1 = u = 1 ∑ 3 v = 1 ∑ 3 = w u , v ⋅ x 3 − u + 1 , 3 − v + 1 = w 1 , 1 ⋅ x 3 − 1 + 1 , 3 − 1 + 1 + w 1 , 2 ⋅ x 3 − 1 + 1 , 3 − 2 + 1 + w 1 , 3 ⋅ x 3 − 1 + 1 , 3 − 3 + 1 + w 2 , 1 ⋅ x 3 − 2 + 1 , 3 − 1 + 1 + w 2 , 2 ⋅ x 3 − 2 + 1 , 3 − 2 + 1 + w 2 , 3 ⋅ x 3 − 2 + 1 , 3 − 3 + 1 + w 3 , 1 ⋅ x 3 − 3 + 1 , 3 − 1 + 1 + w 3 , 2 ⋅ x 3 − 3 + 1 , 3 − 2 + 1 + w 3 , 3 ⋅ x 3 − 3 + 1 , 3 − 3 + 1 = 1 ⋅ 0 + 0 ⋅ − 1 + 0 ⋅ 1 + 0 ⋅ 1 + 0 ⋅ 0 + 0 ⋅ − 3 + 0 ⋅ 1 + 0 ⋅ 1 + − 1 ⋅ 1 + = − 1
不翻转卷积
如上,在二维的时候,我们将卷积核进行了翻转,但是在机器学习、深度学习或者图像处理中,通常我们不这么做,我们不进行翻转。
y = ∑ u = 1 m ∑ v = 1 n = w u , v ⋅ x u , v y = \sum_{u=1}^{m} \sum_{v=1}^{n} = w_{u,v} \cdot x_{u,v}
y = u = 1 ∑ m v = 1 ∑ n = w u , v ⋅ x u , v
这种称为不翻转卷积,记做y = W ⊗ X y = \bold{W} \otimes \bold{X} y = W ⊗ X
特别注意: 通常,我们所指的的卷积,都是不翻转卷积。
步长和填充
再让我们回到《让子弹飞》电影的开头。现在我们知道了什么是"张牧之和马邦德的队伍",知道了什么是"带着望远镜的黄四郎",而且连"如何观察"我们也知道了。但是正如影片的描述,黄四郎并不是盯着一个地方一直看,我们注意到望远镜一直在动,黄四郎是在扫描。
步长
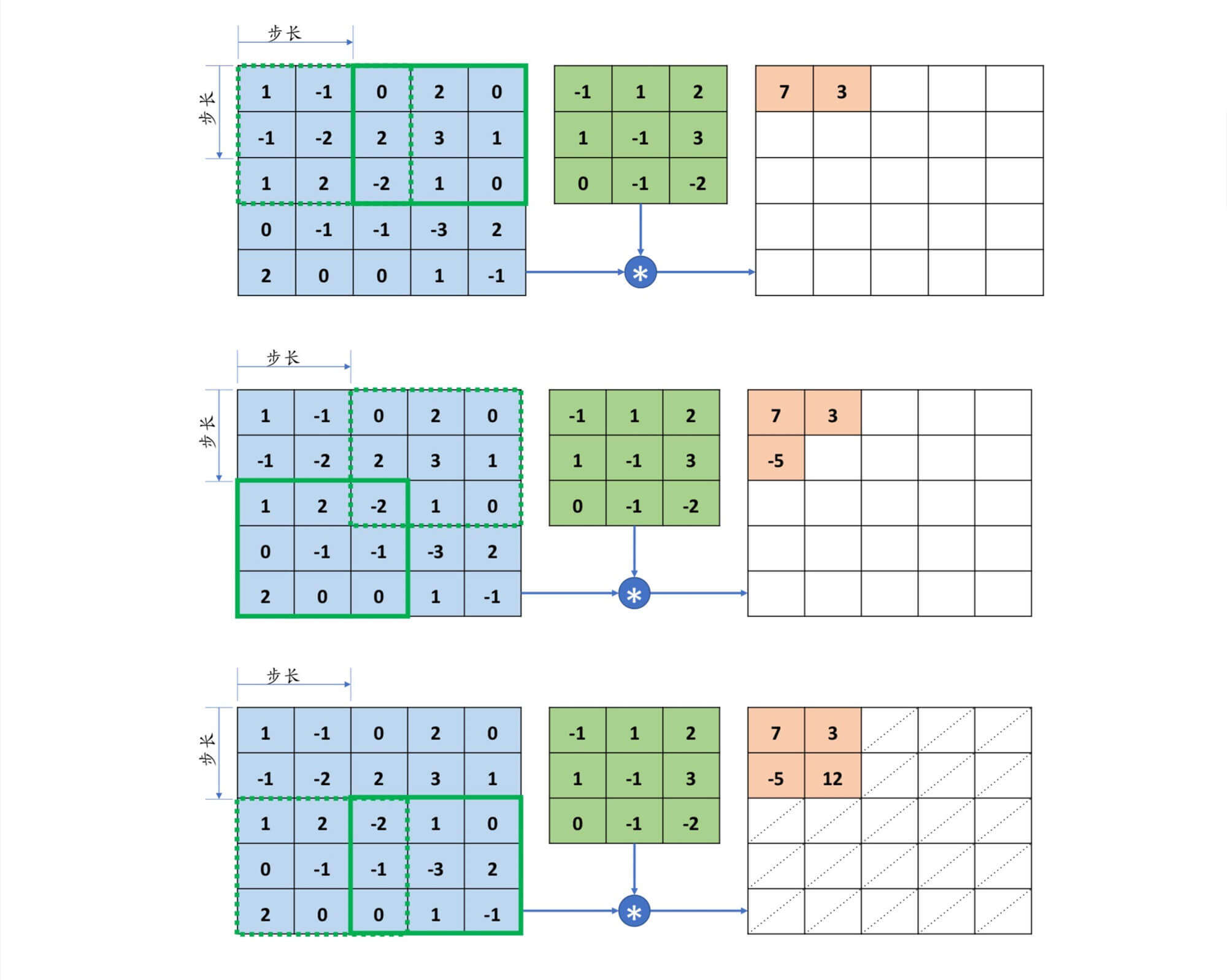
扫描其实很简单,我们按照从左到右,从上到下的顺序进行扫描。但是我们得定,我们每次移动多少,这就是步长。
填充
在上面的例子中,被观察对象是5*5的,卷积核是3*3的,步长是2。这时候恰好能扫描到被观察对象的每一个像素点。4*4的,这时候就无法恰好扫描到被观察对象的每一个像素点。那么这时候这么办呢?
放弃部分像素点。
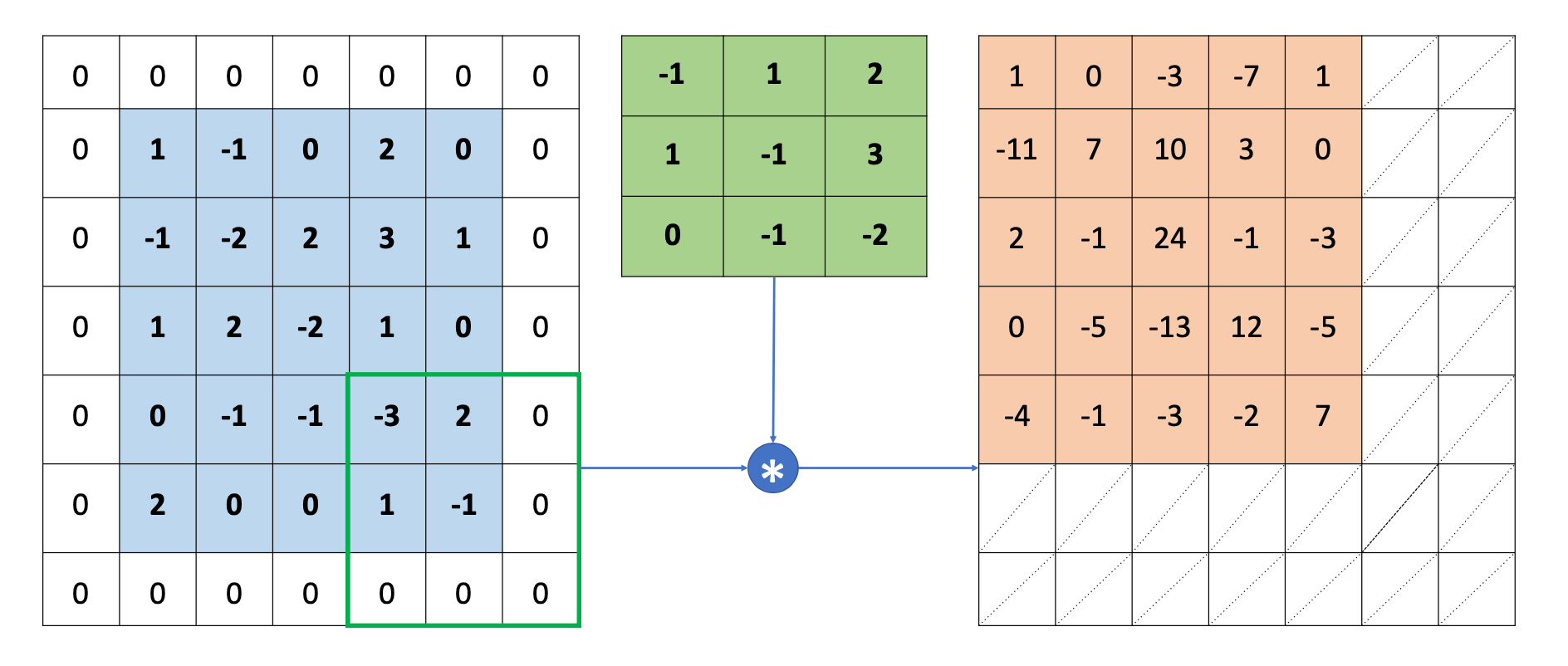
填充0。
此外,有些时候,即使我们能扫描到每一个像素点的时候,仍然会填充0。因为有时候我们会希望输出O \bold{O} O X \bold{X} X
输出和步长填充的关系
卷积层的输出尺寸[ h ′ , w ′ ] [h',w'] [ h ′ , w ′ ] k k k s s s p h p_h p h p w p_w p w X \bold{X} X [ h , w ] [h,w] [ h , w ]
h ′ = h + 2 ⋅ p h − k s + 1 h' = \frac{h + 2 \cdot p_h - k}{s} + 1
h ′ = s h + 2 ⋅ p h − k + 1
w ′ = w + 2 ⋅ p w − k s + 1 w' = \frac{w + 2 \cdot p_w - k}{s} + 1
w ′ = s w + 2 ⋅ p w − k + 1
特别注意:这里只考虑上下填充数量p h p_h p h p w p_w p w
在上面的例子中。h = 3 , w = 5 , k = 3 , p h = p w = 1 , s = 1 h=3,w=5,k=3,p_h=p_w=1,s=1 h = 3 , w = 5 , k = 3 , p h = p w = 1 , s = 1
h ′ = 5 + 2 ⋅ 1 − 3 1 + 1 = 4 + 1 = 5 h' = \frac{5 + 2 \cdot 1 - 3}{1} + 1 = 4 + 1 = 5
h ′ = 1 5 + 2 ⋅ 1 − 3 + 1 = 4 + 1 = 5
w ′ = 5 + 2 ⋅ 1 − 3 1 + 1 = 4 + 1 = 5 w' = \frac{5 + 2 \cdot 1 - 3}{1} + 1 = 4 + 1 = 5
w ′ = 1 5 + 2 ⋅ 1 − 3 + 1 = 4 + 1 = 5
在TensorFlow中,如果希望输出O \bold{O} O X \bold{X} X padding='SAME'、strides=1即可。
多通道输入
多通道输入、单卷积核
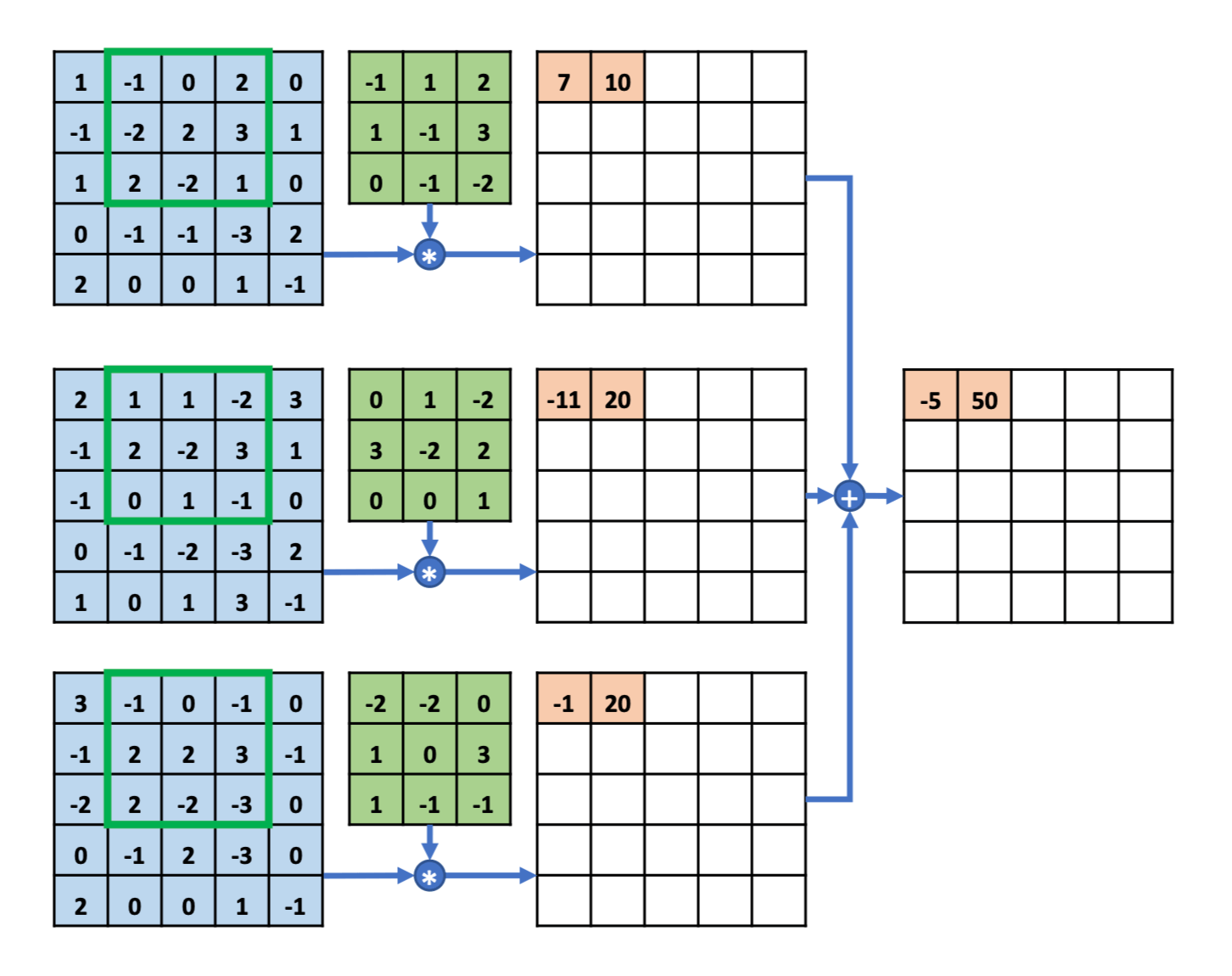
截至目前,我们讨论的被观察对象,都只有张牧之和马邦德等人所组成的一支队伍,这个在计算机中被称为单通道。单通道在计算机中只能表示黑白图像。那么对于彩色图像怎么办呢?我想这个问题,我们的周润发同学,能给出答案。25 6 3 256^3 2 5 6 3 一句话:各个击破,直接相加。
多通道输入、多卷积核
在影片结尾,黄四郎对张牧之说:“进城那天,如果我亲自去接你。不是叫胡万过去给你捣乱,结果会不会不一样?”
不同的卷积核相当于不同的特征提取器。我们之前讨论都是只有一个卷积核,观察结果是一维结构。既然卷积神经网络主要应用在图像处理上,而彩色图像为三维结构。为了更充分地利用图像的局部信息,通常将卷积核组织为三维结构,其大小为高度H H H W W W D D D D D D H × W H \times W H × W
特征映射(Feature Map)为一幅图像(或其它特征映射)在经过卷积提取到的特征,每个特征映射可以作为一类抽取的图像特征。为了提高卷积网络的表示能力,可以在每一层使用多个不同的特征映射,以更好地表示图像的特征。
那么,多通道的输入、多卷积核怎么处理呢?有几个卷积核,结果就有几个通道。
梯度传播
梯度
现在我们的思路已经很清楚了。
我们有一个单通道或多通道的图像,例如是[28,28,3]。
我们用多个卷积核去观察图像,或者我们说是用多个卷积核对图像进行特征提取。例如是5个[3,3,3]的卷积,步长为1,不进行填充。28 − 3 1 = 25 \frac{28-3}{1} = 25 1 2 8 − 3 = 2 5 [25,25,5]。
然后我们再对数据进行卷积、或者全连接层等等。
但,似乎还少了一样。5个[3,3,3]的卷积核。那权重是多少?偏置又是多少?
现在,我们讨论梯度。
我们以最简单的一种为例。
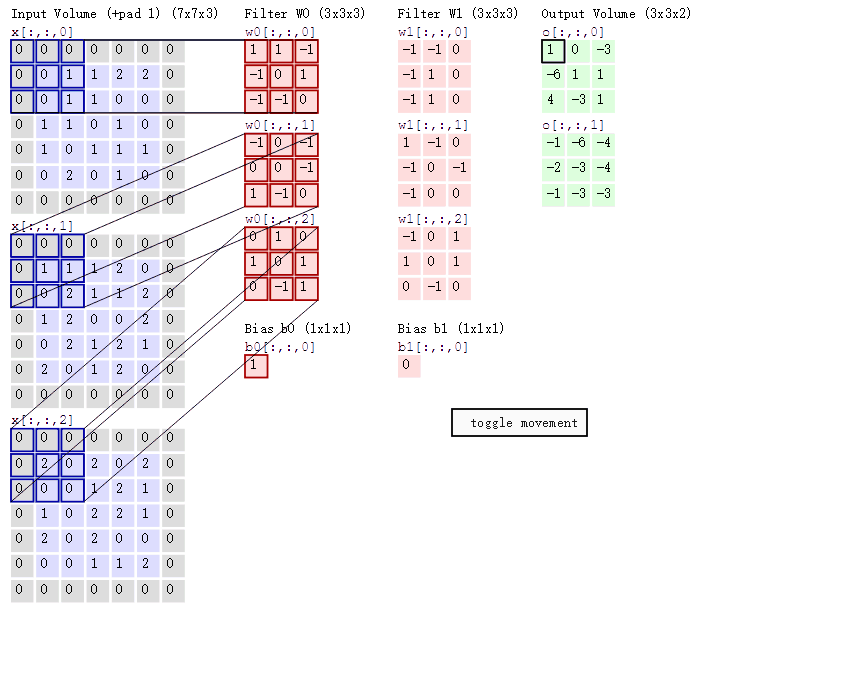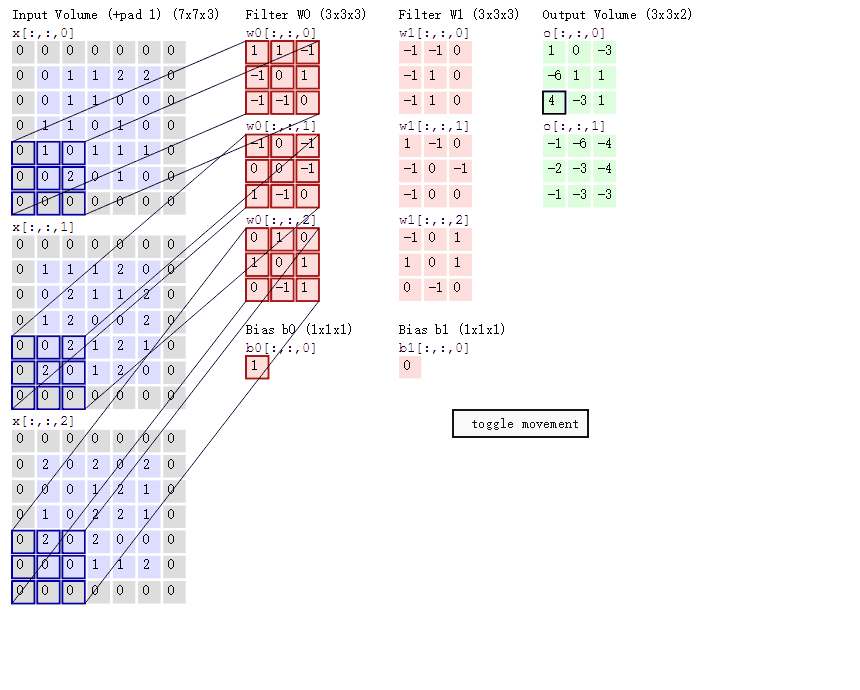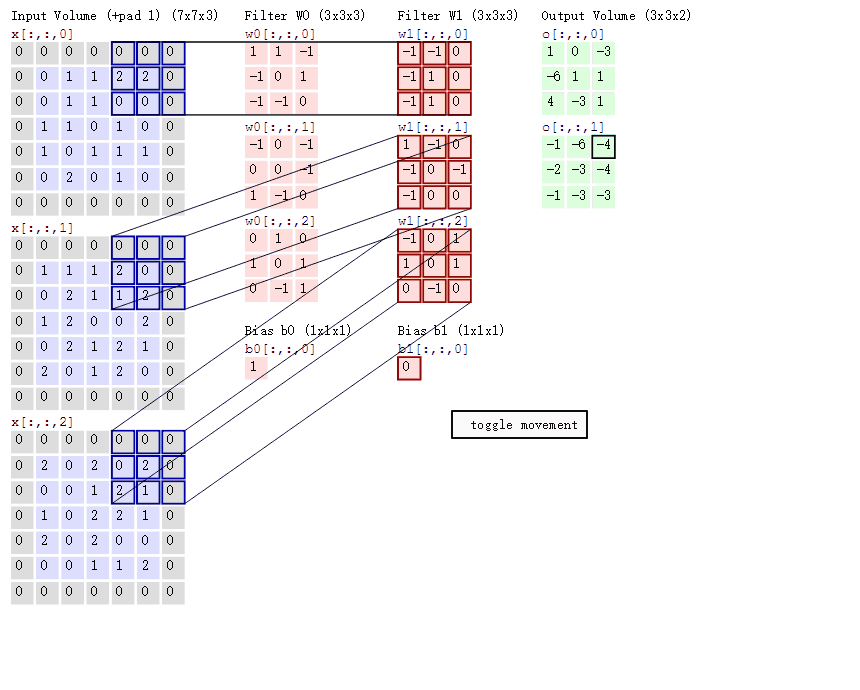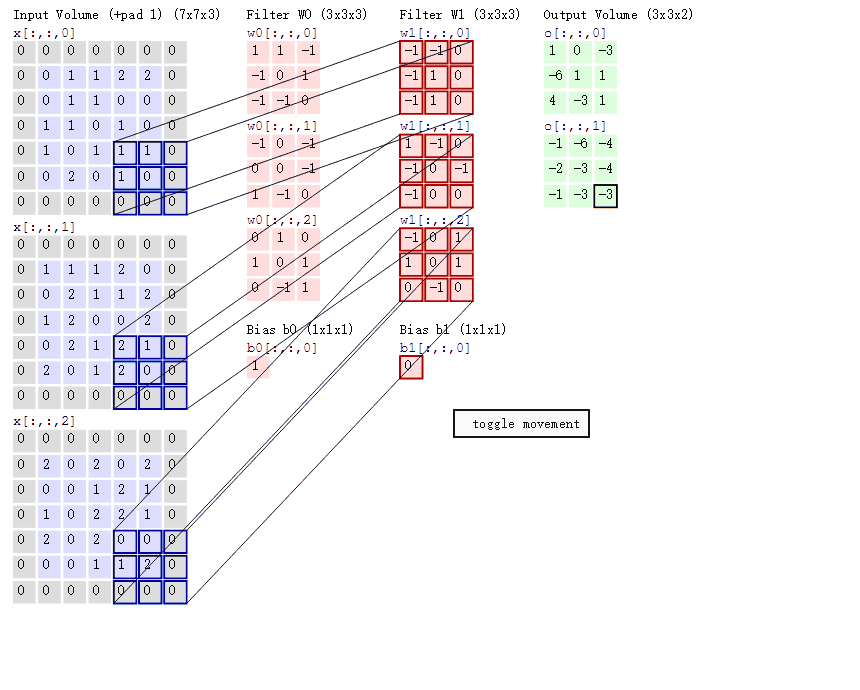
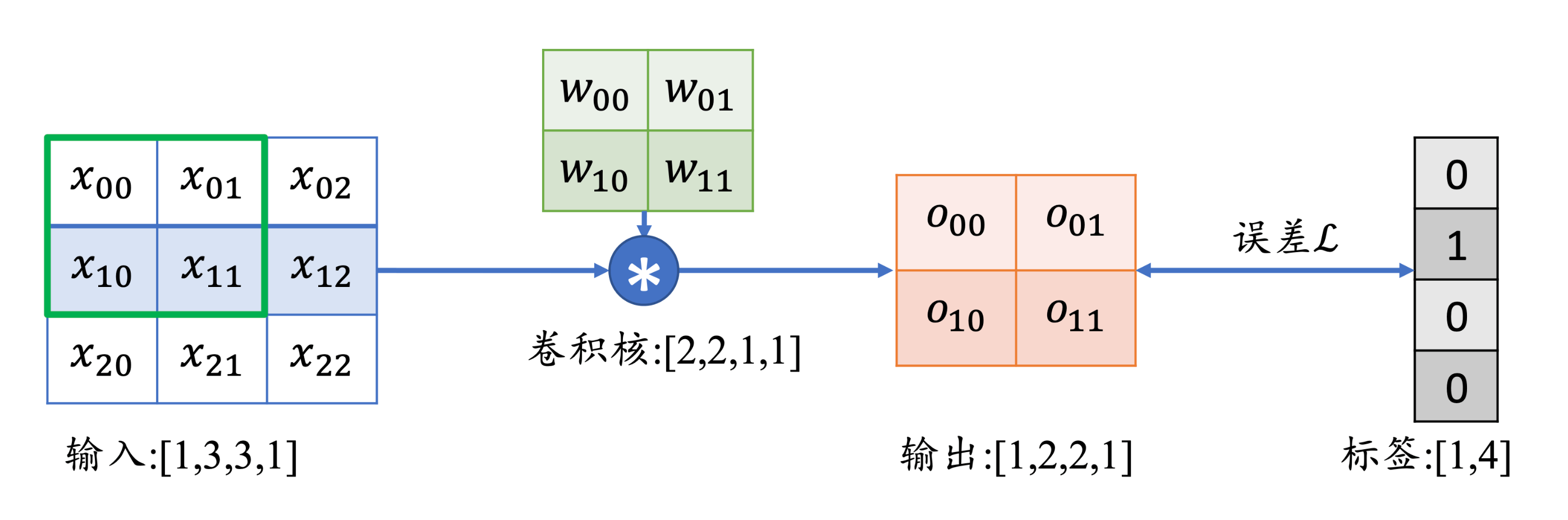
x[b,3,3,1]:代表b个样本,3*3的高宽,1个通道w[2,2,c,N]:代表2*2的滤波器,c个通道,N个卷积核o[b,2,2,c]:代表b个样本,2*2的高宽,c个通道,这里的通道数等于卷积核的个数
对于输出,我们有:
o 00 = x 00 w 00 + x 01 w 01 + x 10 w 10 + x 11 w 11 + b o_{00} = x_{00}w_{00} + x_{01}w_{01} + x_{10}w_{10} + x_{11}w_{11} + b o 0 0 = x 0 0 w 0 0 + x 0 1 w 0 1 + x 1 0 w 1 0 + x 1 1 w 1 1 + b o 01 = x 01 w 00 + x 02 w 01 + x 11 w 10 + x 12 w 11 + b o_{01} = x_{01}w_{00} + x_{02}w_{01} + x_{11}w_{10} + x_{12}w_{11} + b o 0 1 = x 0 1 w 0 0 + x 0 2 w 0 1 + x 1 1 w 1 0 + x 1 2 w 1 1 + b o 10 = x 10 w 00 + x 11 w 01 + x 20 w 10 + x 21 w 11 + b o_{10} = x_{10}w_{00} + x_{11}w_{01} + x_{20}w_{10} + x_{21}w_{11} + b o 1 0 = x 1 0 w 0 0 + x 1 1 w 0 1 + x 2 0 w 1 0 + x 2 1 w 1 1 + b o 11 = x 11 w 00 + x 12 w 01 + x 21 w 10 + x 22 w 11 + b o_{11} = x_{11}w_{00} + x_{12}w_{01} + x_{21}w_{10} + x_{22}w_{11} + b o 1 1 = x 1 1 w 0 0 + x 1 2 w 0 1 + x 2 1 w 1 0 + x 2 2 w 1 1 + b
我们以∂ L ∂ w 00 \frac{\partial L}{\partial w_{00}} ∂ w 0 0 ∂ L
∂ L ∂ w 00 = ∑ i ∈ { 00 , 01 , 10 , 11 } ∂ L ∂ o i ∂ o i ∂ w 00 \frac{\partial L}{\partial w_{00}} = \sum_{i \in \{00,01,10,11\}} \frac{\partial L}{\partial o_i} \frac{\partial o_i}{\partial w_{00}}
∂ w 0 0 ∂ L = i ∈ { 0 0 , 0 1 , 1 0 , 1 1 } ∑ ∂ o i ∂ L ∂ w 0 0 ∂ o i
而∂ o i ∂ w 00 \frac{\partial o_i}{\partial w_{00}} ∂ w 0 0 ∂ o i
∂ o 00 ∂ w 00 = x 00 ∂ o 01 ∂ w 00 = x 01 ∂ o 10 ∂ w 00 = x 10 ∂ o 11 ∂ w 00 = x 11 \frac{\partial o_{00}}{\partial w_{00}} = x_{00} \quad \frac{\partial o_{01}}{\partial w_{00}} = x_{01} \quad \frac{\partial o_{10}}{\partial w_{00}} = x_{10} \quad \frac{\partial o_{11}}{\partial w_{00}} = x_{11}
∂ w 0 0 ∂ o 0 0 = x 0 0 ∂ w 0 0 ∂ o 0 1 = x 0 1 ∂ w 0 0 ∂ o 1 0 = x 1 0 ∂ w 0 0 ∂ o 1 1 = x 1 1
关于sum的讨论
在∂ L ∂ w 00 \frac{\partial L}{\partial w_{00}} ∂ w 0 0 ∂ L ∑ \sum ∑
我们这里讨论一下,以加深我们对损失函数的理解。
我们知道,常见的损失函数一般有两种。
均方误差
交叉熵损失,这种通常和Softmax配合使用
均方误差
L o s s = 1 2 ∑ ( y i − o i ) 2 Loss = \frac{1}{2} \sum (y_i - o_i)^2
L o s s = 2 1 ∑ ( y i − o i ) 2
∂ L o s s ∂ w 00 = ∑ ( y i − o i ) ∂ o i ∂ w 00 \frac{\partial Loss}{\partial w_{00}} = \sum (y_i - o_i) \frac{\partial o_i}{\partial w_{00}}
∂ w 0 0 ∂ L o s s = ∑ ( y i − o i ) ∂ w 0 0 ∂ o i
所以,均方误差作为损失函数,其梯度要对o i w 00 \frac{o_i}{w_{00}} w 0 0 o i ∑ \sum ∑
交叉熵损失
L o s s = − log q 2 Loss = - \log q_2
L o s s = − log q 2
而,交叉熵损失,通常和Softmax配合使用。所以:
q 2 = e o 2 ∑ e o i q_2 = \frac{e^{o_2}}{\sum e^{o_i}}
q 2 = ∑ e o i e o 2
我们对q 2 q_2 q 2
q 2 ′ = ( e o 2 ) ′ ( ∑ e o i ) − ( e o 2 ) ( ∑ e o i ) ′ ( ∑ e o i ) 2 q_{2}' = \frac{(e^{o_2})'(\sum e^{o_i}) - (e^{o_2})(\sum e^{o_i})'}{(\sum e^{o_i})^2}
q 2 ′ = ( ∑ e o i ) 2 ( e o 2 ) ′ ( ∑ e o i ) − ( e o 2 ) ( ∑ e o i ) ′
所以,交叉熵损失,也是需要对o i w 00 \frac{o_i}{w_{00}} w 0 0 o i ∑ \sum ∑
卷积层的实现
至此,整个卷积层的主要内容,我们几乎都讨论过了。现在我们试图实现一个卷积层。
TensorFlow
Keras
基于TensorFlow
在TensorFLow中,实现一个卷积层的方法是
1 tf.nn.conv2d(input=x,filters=w,strides=1,padding=[[0,0],[0,0],[0,0],[0,0]])
其中需要特别说明的是,padding参数的设置格式:padding=[[0,0],[上,下],[左,右],[0,0]]。padding=[[0,0],[1,1],[1,1],[0,0]]。
1 2 3 4 5 6 7 8 9 10 import tensorflow as tfx = tf.random.normal([2 ,5 ,5 ,3 ]) w = tf.random.normal([3 ,3 ,3 ,4 ]) out = tf.nn.conv2d(input=x,filters=w,strides=1 ,padding=[[0 ,0 ],[0 ,0 ],[0 ,0 ],[0 ,0 ]]) print(out.shape)
运行结果:
解释:
第一个数字2,代表样本数:2。
第二个数字3,代表高:3。5 − 3 1 + 1 = 3 \frac{5-3}{1} + 1 = 3 1 5 − 3 + 1 = 3
第三个数字3,代表宽:3。5 − 3 1 + 1 = 3 \frac{5-3}{1} + 1 = 3 1 5 − 3 + 1 = 3
第四个数字4,代表通道数:4。也就是卷积核的个数。
特别的:通过设置参数padding='SAME',strides设置为大于1的值,可以直接得到输入、输出同大小的卷积层。
1 2 3 4 5 6 7 8 9 10 import tensorflow as tfx = tf.random.normal([2 ,5 ,5 ,3 ]) w = tf.random.normal([3 ,3 ,3 ,4 ]) out = tf.nn.conv2d(x,w,strides=1 ,padding='SAME' ) print(out.shape)
运行结果:
通过设置参数padding='SAME'、strides>1可以直接得到输出是输入1 s \frac{1}{s} s 1
1 2 3 4 5 6 7 import tensorflow as tfx = tf.random.normal([2 ,5 ,5 ,3 ]) w = tf.random.normal([3 ,3 ,3 ,4 ]) out = tf.nn.conv2d(x,w,strides=2 ,padding='SAME' ) print(out.shape)
运行结果:
如果我们还需要偏置,怎么办?
1 tf.nn.bias_add(value, bias, data_format=None, name=None)
基于Keras
在之前,我们都手动定义卷积核的W \bold{W} W b \bold{b} b
在TensorFlow中,API的命名有一定的规律,首字母大写的对象一般表示类,全部小写的一般表示函数。如layers.Conv2D表示卷积层类,nn.conv2d表示卷积运算函数。
调用示例的__call__方法即可完成前向运算。还可以通过layer.trainable_variable查看卷积核的W \bold{W} W b \bold{b} b
示例代码:
1 2 3 4 5 6 7 8 9 10 import tensorflow as tffrom tensorflow.keras import layersx = tf.random.normal([2 ,5 ,5 ,3 ]) layer = layers.Conv2D(filters=4 ,kernel_size=3 ,strides=1 ,padding='SAME' ) out = layer(x) print(out.shape) print(layer.trainable_variables)
运行结果:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 (2, 5, 5, 4) [<tf.Variable 'conv2d_1/kernel:0' shape=(3, 3, 3, 4) dtype=float32, numpy= array([[[[-0.10979834, 0.05611697, 0.07756695, -0.19519049], [-0.25532633, 0.20102468, -0.01257691, -0.19999951], [ 0.05867973, 0.21140966, 0.18826845, -0.11313015]], [[ 0.0214611 , -0.08925012, -0.09455462, 0.1089299 ], [ 0.09674495, -0.11473732, 0.16129279, -0.11318652], [-0.08330335, -0.12321712, 0.15122685, -0.08722048]], [[ 0.01963314, 0.24888834, -0.14285056, 0.2565213 ], [ 0.17318556, -0.22936352, 0.14522609, 0.16536382], [ 0.15357831, -0.2821764 , -0.2947683 , 0.29289815]]], [[[-0.17826964, 0.28726915, -0.24313128, 0.09069496], [ 0.15975893, 0.17163727, -0.24049374, -0.28351462], [-0.00981075, 0.29518244, -0.03597486, -0.07030587]], [[ 0.23602709, -0.13521343, 0.21714154, 0.06650102], [ 0.09308881, 0.01543975, 0.06182054, -0.22127749], [-0.1318672 , 0.20529953, 0.26045617, 0.06962284]], [[ 0.13752908, 0.24204233, -0.1383889 , 0.22505233], [ 0.20928249, -0.05574575, 0.04975668, 0.11022466], [-0.22181004, 0.21804205, -0.21576726, -0.10982512]]], [[[-0.18072543, -0.3039346 , 0.17995346, -0.1626617 ], [-0.0756432 , -0.15350364, 0.03744105, -0.02793446], [-0.03010941, -0.06961726, -0.07880872, 0.0398711 ]], [[-0.19787115, -0.19895059, 0.12084219, -0.25610667], [ 0.13629442, -0.18237923, -0.15923041, -0.00456873], [ 0.19431832, 0.21129027, 0.06643423, 0.07392919]], [[-0.24683592, -0.20284012, 0.18018603, 0.2478585 ], [ 0.08107573, -0.17767616, 0.11991593, -0.19584629], [ 0.22088405, -0.03678539, 0.0819014 , 0.03509244]]]], dtype=float32)>, <tf.Variable 'conv2d_1/bias:0' shape=(4,) dtype=float32, numpy=array([0., 0., 0., 0.], dtype=float32)>]
除了这种我们常见的卷积,还有三种卷积:
空洞卷积 转置卷积 分离卷积
池化
池化运算
除了用望远镜(卷积 )进行观察,还有一种方法:池化 。
之前我们讨论的卷积,有两个特点:
局部连接
权值共享
池化层同样是局部连接,通过从局部连接的一组元素中进行采样或信息聚合,从而得到新的元素值。常见的池化有两种:
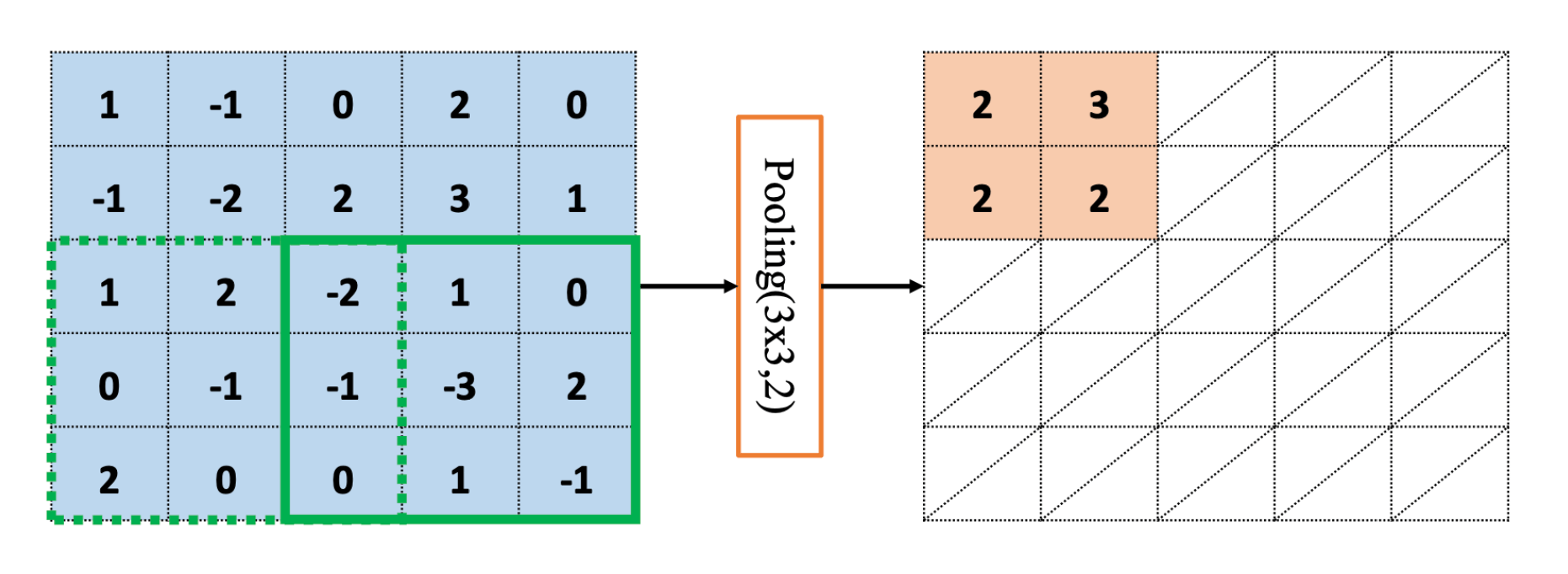
最大池化层(Max Pooling)从局部相关元素集中选取最大的一个元素值。
平均池化层(Average Pooling)从局部相关元素集中计算平均值并返回。
既然是最大和平均,权值共享的特点肯定是没有了,毕竟连权值都没了。
池化的运算也很简单,例如:最大池化层运算。
池化实现
和卷积层的实现一样,池化层的实现有两种方法。
示例代码:
1 2 3 4 5 6 7 8 import tensorflow as tffrom tensorflow.keras import layersx = tf.random.normal([2 ,5 ,5 ,3 ]) print(tf.nn.max_pool2d(input=x,ksize=3 ,strides=1 ,padding='SAME' ).shape) layer = layers.MaxPooling2D(pool_size=3 ,strides=1 ,padding='same' ) print(layer(x).shape)
运行结果
1 2 (2, 5, 5, 3) (2, 5, 5, 3)
卷积神经网络
通过之前的讨论,我们已经知道了什么是卷积。那么把卷积应用在神经网络中,就是卷积神经网络。现在,我们来实现一个卷积神经网络。
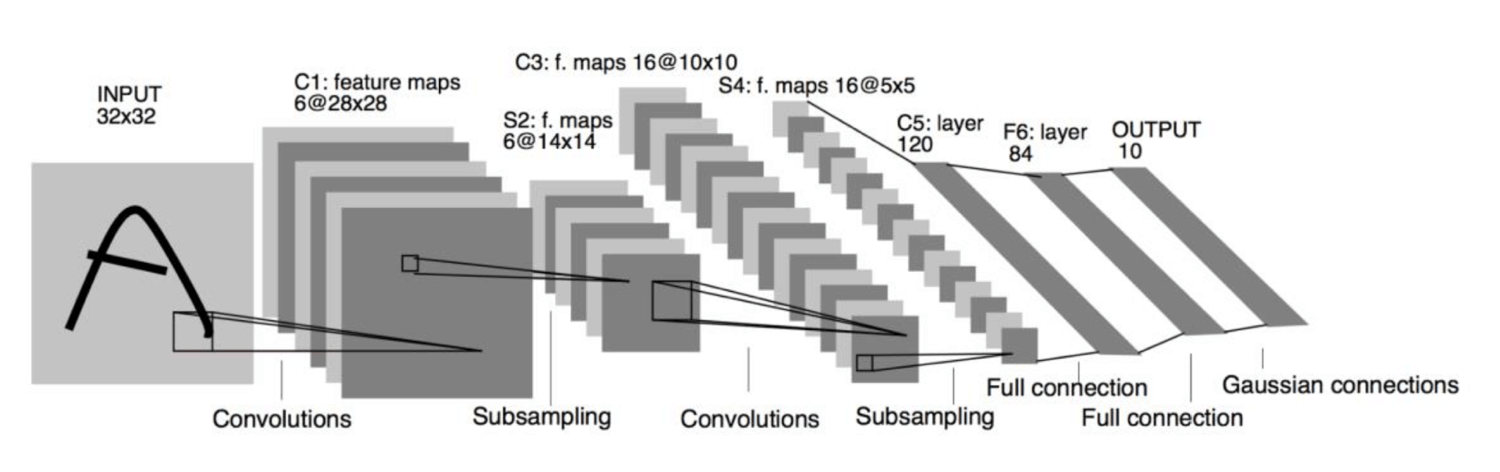
我们以LeNet-5,这是一个非常经典的卷积神经网络。出现30年前,当时Yann LeCun等人用于手写数字识别。其结构如下:
我们这里对其进行简单的修改,使其符合现代深度学习开发框架。
构建网络
首先,我们根据网络结构来构建网络。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 from tensorflow.keras import Sequential,layersnetwork = Sequential([ layers.Conv2D(filters=6 ,kernel_size=(5 ,5 ),activation="relu" ,input_shape=(28 ,28 ,1 ),padding="same" ), layers.MaxPool2D(pool_size=(2 ,2 ),strides=2 ), layers.Conv2D(filters=16 ,kernel_size=(5 ,5 ),activation="relu" ,padding="same" ), layers.MaxPool2D(pool_size=2 ,strides=2 ), layers.Conv2D(filters=32 ,kernel_size=(5 ,5 ),activation="relu" ,padding="same" ), layers.Flatten(), layers.Dense(200 ,activation="relu" ), layers.Dense(10 ,activation="softmax" ) ]) network.summary()
运行结果:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 Model: "sequential" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= conv2d (Conv2D) (None, 28, 28, 6) 156 _________________________________________________________________ max_pooling2d (MaxPooling2D) (None, 14, 14, 6) 0 _________________________________________________________________ conv2d_1 (Conv2D) (None, 14, 14, 16) 2416 _________________________________________________________________ max_pooling2d_1 (MaxPooling2 (None, 7, 7, 16) 0 _________________________________________________________________ conv2d_2 (Conv2D) (None, 7, 7, 32) 12832 _________________________________________________________________ flatten (Flatten) (None, 1568) 0 _________________________________________________________________ dense (Dense) (None, 200) 313800 _________________________________________________________________ dense_1 (Dense) (None, 10) 2010 ================================================================= Total params: 331,214 Trainable params: 331,214 Non-trainable params: 0 _________________________________________________________________
加载数据集
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 import tensorflow as tffrom tensorflow.keras.datasets import mnist(x_train, y_train), (x_test, y_test) = mnist.load_data() print(x_train.shape) print(y_train.shape) print(x_test.shape) print(y_test.shape) x_train = tf.expand_dims(x_train, axis=3 ) x_test = tf.expand_dims(x_test, axis=3 ) print(x_train.shape) print(x_test.shape) db_train = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(200 ) db_test = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(200 )
运行结果:
1 2 3 4 5 6 (60000, 28, 28) (60000,) (10000, 28, 28) (10000,) (60000, 28, 28, 1) (10000, 28, 28, 1)
训练模型
示例代码:
1 2 3 4 5 6 7 from tensorflow.keras import optimizers,lossesadam = optimizers.Adam() sparse_categorical_crossentropy = losses.SparseCategoricalCrossentropy() network.compile(optimizer=adam,loss=sparse_categorical_crossentropy,metrics=['accuracy' ]) network.fit(db_train,epochs=10 )
运行结果:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 Epoch 1/10 300/300 [==============================] - 15s 51ms/step - loss: 0.4975 - accuracy: 0.9157 Epoch 2/10 300/300 [==============================] - 15s 51ms/step - loss: 0.0659 - accuracy: 0.9785 Epoch 3/10 300/300 [==============================] - 16s 52ms/step - loss: 0.0385 - accuracy: 0.9877 Epoch 4/10 300/300 [==============================] - 16s 54ms/step - loss: 0.0259 - accuracy: 0.9914 Epoch 5/10 300/300 [==============================] - 16s 54ms/step - loss: 0.0217 - accuracy: 0.9929 Epoch 6/10 300/300 [==============================] - 16s 54ms/step - loss: 0.0185 - accuracy: 0.9936 Epoch 7/10 300/300 [==============================] - 16s 53ms/step - loss: 0.0181 - accuracy: 0.9938 Epoch 8/10 300/300 [==============================] - 16s 54ms/step - loss: 0.0140 - accuracy: 0.9950 Epoch 9/10 300/300 [==============================] - 16s 53ms/step - loss: 0.0140 - accuracy: 0.9954 Epoch 10/10 300/300 [==============================] - 16s 54ms/step - loss: 0.0152 - accuracy: 0.9947
测试模型
示例代码:
1 2 3 4 loss,accuracy=network.evaluate(db_test) print(loss) print(accuracy)
运行结果:
1 2 3 50/50 [==============================] - 1s 15ms/step - loss: 0.0780 - accuracy: 0.9835 0.07802382856607437 0.9835000038146973
画图
我们还可以画个图,这样更直观。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 import matplotlib.pyplot as pltfor i in range(25 ): plt.subplot(5 ,5 ,i+1 ) plt.imshow(x_test[i], cmap='gray' ) plt.show() result = network.predict(x_test)[0 :25 ] pred = tf.argmax(result, axis=1 ) pred_list=[] for item in pred: pred_list.append(item.numpy()) print(pred_list)
运行结果:
1 [7, 2, 1, 0, 4, 1, 4, 9, 5, 9, 0, 6, 9, 0, 1, 5, 9, 7, 3, 4, 9, 6, 6, 5, 4]
BatchNorm
BN层
2015年,Google研究人员Sergey Ioffe等人提出了一种参数标准化(Normalize)的手段,并基于参数标准化设计了Batch Nomalization(简写为BatchNorm,或 BN)。BatchNorm的提出,使得网络的超参数的设定更加自由,比如更大的学习率、更随意的网络初始化等,同时网络的收敛速度更快,性能也更好。BatchNorm广泛地应用在各种深度网络模型上,Conv-BN-ReLU-Pooling甚至一度成为标配。
那么,什么是BatchNorm呢?
BN的公式
在训练阶段和在测试阶段,还略有不同。我们分情况讨论。
训练阶段
x ~ t r a i n = x t r a i n − μ B σ B 2 + ϵ ⋅ γ + β \tilde{x}_{train} = \frac{x_{train} - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}} \cdot \gamma + \beta
x ~ t r a i n = σ B 2 + ϵ x t r a i n − μ B ⋅ γ + β
μ B \mu_B μ B σ B 2 \sigma_B^2 σ B 2 ϵ \epsilon ϵ 0错误而设置的较小数字,如1 0 − 9 10^{-9} 1 0 − 9 γ \gamma γ β \beta β
所以,Batch_Size也是一个超参数了,在Batch_Norm中。当然,如果数据集很大的话,可能影响有限。
同时按照
μ r ← m o m e n t u m ⋅ μ r + ( 1 − m o m e n t u m ) ⋅ μ B \mu_r \leftarrow momentum \cdot \mu_r + (1 - momentum) \cdot \mu_B
μ r ← m o m e n t u m ⋅ μ r + ( 1 − m o m e n t u m ) ⋅ μ B
σ r 2 ← m o m e n t u m ⋅ σ r 2 + ( 1 − m o m e n t u m ) ⋅ σ B 2 \sigma_r^2 \leftarrow momentum \cdot \sigma_r^2 + (1 - momentum) \cdot \sigma_B^2
σ r 2 ← m o m e n t u m ⋅ σ r 2 + ( 1 − m o m e n t u m ) ⋅ σ B 2
迭代更新全局训练数据的统计值μ r \mu_r μ r σ r 2 \sigma_r^2 σ r 2 m o m e n t u m momentum m o m e n t u m m o m e n t u m momentum m o m e n t u m 0.99 0.99 0 . 9 9
测试阶段
x ~ t e s t = x t e s t − μ r σ r 2 + ϵ ⋅ γ + β \tilde{x}_{test} = \frac{x_{test} - \mu_r}{\sqrt{\sigma_r^2 + \epsilon}} \cdot \gamma + \beta
x ~ t e s t = σ r 2 + ϵ x t e s t − μ r ⋅ γ + β
测试阶段的μ r \mu_r μ r σ r 2 \sigma_r^2 σ r 2 μ r \mu_r μ r σ r 2 \sigma_r^2 σ r 2
BN的实现和应用
创建BN层:
1 layer = layers.BatchNormalization()
应用: Sequential网络容器中即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 from tensorflow.keras import Sequential, layersnetwork = Sequential([ layers.Conv2D(filters=6 , kernel_size=(5 , 5 ), activation="relu" , input_shape=(28 , 28 , 1 ), padding="same" ), layers.MaxPool2D(pool_size=(2 , 2 ), strides=2 ), layers.BatchNormalization(), layers.Conv2D(filters=16 , kernel_size=(5 , 5 ), activation="relu" , padding="same" ), layers.MaxPool2D(pool_size=2 , strides=2 ), layers.BatchNormalization(), layers.Conv2D(filters=32 , kernel_size=(5 , 5 ), activation="relu" , padding="same" ), layers.Flatten(), layers.Dense(200 , activation="relu" ), layers.Dense(10 , activation="softmax" ) ]) network.summary()
运行结果:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 Model: "sequential" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= conv2d (Conv2D) (None, 28, 28, 6) 156 _________________________________________________________________ max_pooling2d (MaxPooling2D) (None, 14, 14, 6) 0 _________________________________________________________________ batch_normalization (BatchNo (None, 14, 14, 6) 24 _________________________________________________________________ conv2d_1 (Conv2D) (None, 14, 14, 16) 2416 _________________________________________________________________ max_pooling2d_1 (MaxPooling2 (None, 7, 7, 16) 0 _________________________________________________________________ batch_normalization_1 (Batch (None, 7, 7, 16) 64 _________________________________________________________________ conv2d_2 (Conv2D) (None, 7, 7, 32) 12832 _________________________________________________________________ flatten (Flatten) (None, 1568) 0 _________________________________________________________________ dense (Dense) (None, 200) 313800 _________________________________________________________________ dense_1 (Dense) (None, 10) 2010 ================================================================= Total params: 331,302 Trainable params: 331,258 Non-trainable params: 44 _________________________________________________________________
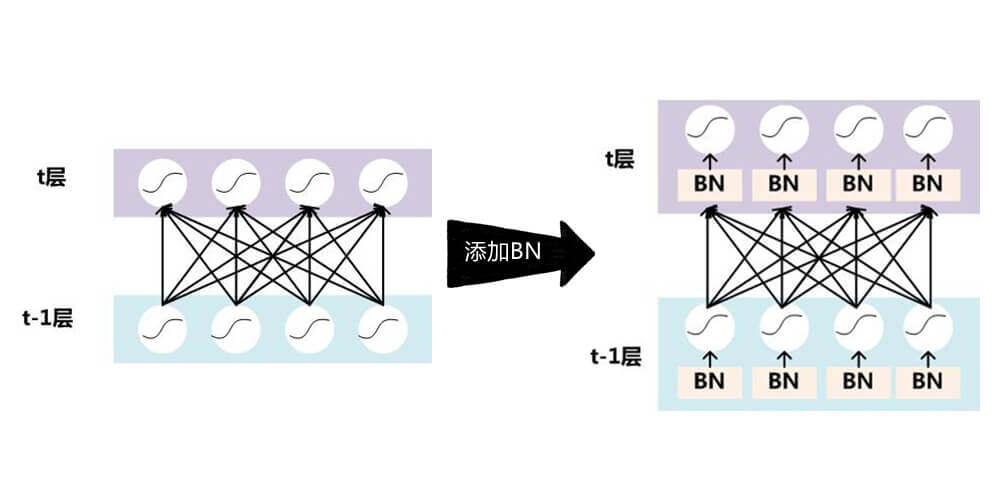
特别注意layers.BatchNormalization()的位置。第一层不用,后面两层都在输入的时候做。
BN的优点
BatchNorm已经广泛被证明其有效性和重要性,尽管有些细节处理还解释不清其理论原因。机器学习领域有个很重要的假设:独立同分布假设,即假设训练数据和测试数据是独立同分布的。那BatchNorm的作用是什么呢?BatchNorm就是在深度神经网络训练过程中使得每一层神经网络的输入保持相同分布的。
不仅仅极大提升了训练速度,收敛过程大大加快。
还能增加分类效果,一种解释是这是类似于Dropout的一种防止过拟合的正则化表达方式,所以不用Dropout也能达到相当的效果。
另外调参过程也简单多了,对于初始化要求没那么高,而且可以使用大的学习率等。