7.经典卷积神经网络

在上一章，我们差不多讨论了卷积神经网络所有的主要内容，和卷积神经网络有关的重点和难点，也都差不多集中在上一章。这一章，我们讨论几个经典的卷积神经网络，它们都是学界和业界的成功实践。它们是：

1. AlexNet
2. VGG
3. GoogLeNet
4. ResNet
5. DenseNet

接下来，我们分别讨论。

AlexNet

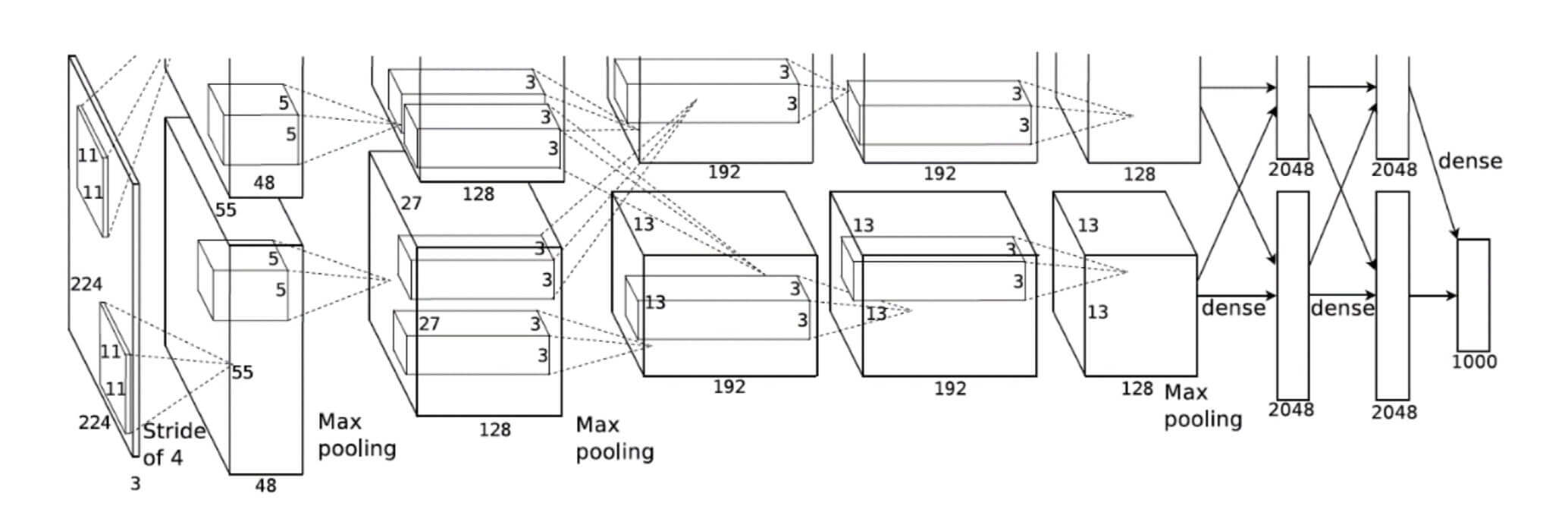
2012年，Alex Krizhevsky获得了ILSVRC12挑战赛的冠军，而他所采用的方案就是由他本人提出的AlexNet神经网络。

AlexNet所接收的输入是224*224*3的彩色图片，经过5个卷积层和3个全连接层后，输出当前图片分别属于1000个类别的概率分布。为了降低特征图的维度，AlexNet在第1、2、5个卷积层后添加了Max Pooling层。
其整体结构如图：

AlexNet的创新之处在于：

1. 层数达到了较深的8层，而在之前的ILSVRC10、ILSVRC11中只有4层的深度。
2. 采用了ReLU激活函数，过去的神经网络大多采用Sigmoid激活函数。
   相比之下，Sigmoid的计算相对复杂，容易出现梯度弥散现象。
3. 引入Dropout层。
4. Dropout提高模型的泛化能力，避免过拟合。

VGG

VGG介绍

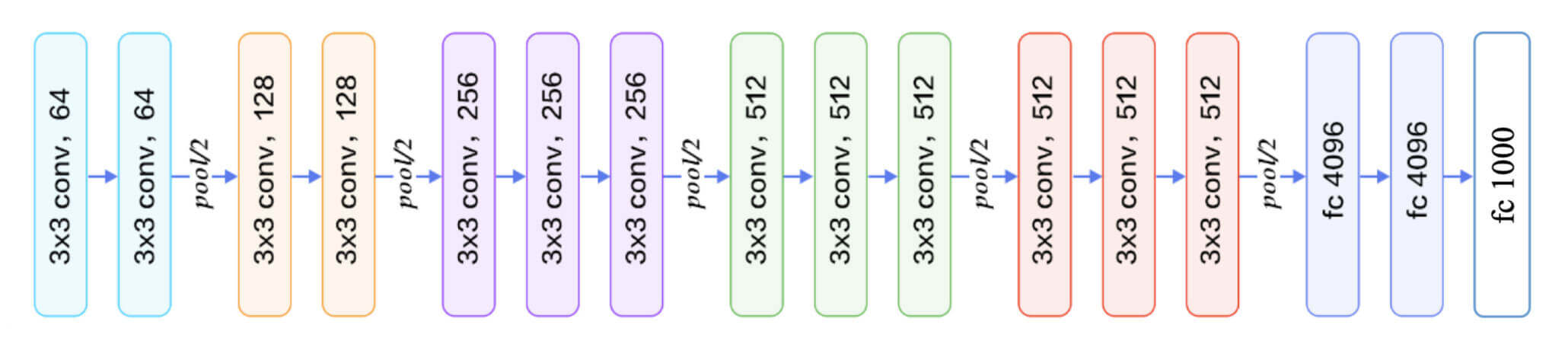
2014年，牛津大学VGG实验室获得了ILSVRC14挑战赛的亚军，而他们所采用的就是VGG11、VGG13、VGG16、VGG19等VGG系列的深度神经网络模型。

我们以VGG16为例。所接收的输入是224*224*3的彩色图片，经过2个Conv-Conv-Pooling单元和3个Conv-Conv-Conv-Pooling单元的堆叠，最后通过3层全连接层输出当前图片分别属于1000类别的概率分布。
其整体结构如图：

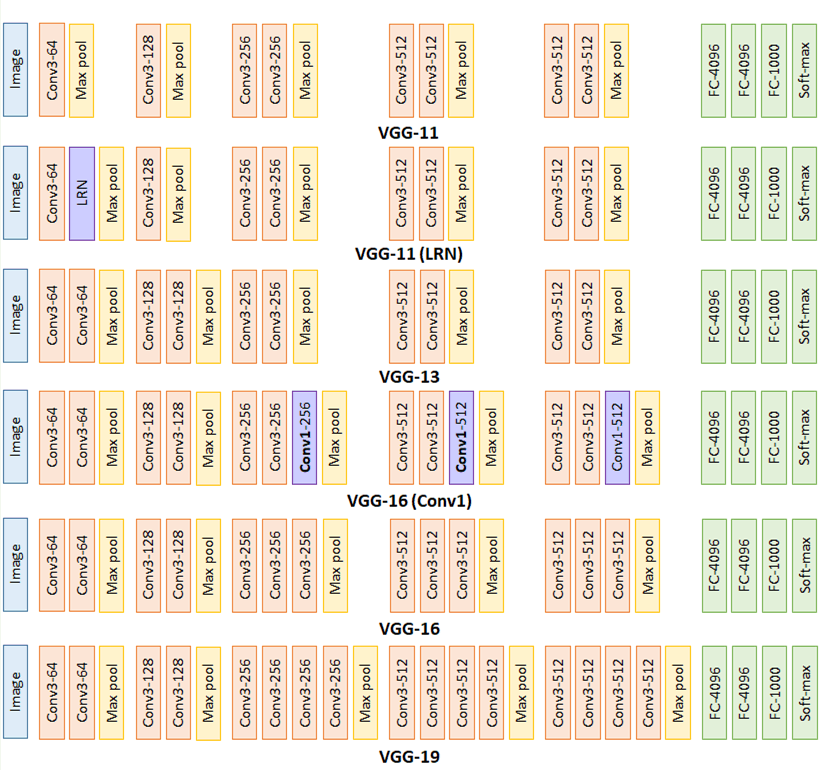
下图是整个VGG系列的网络结构比较：

VGG系列网络的创新之处在于:

1. 层数最深提升至19层。
2. 全部采用更小的3*3卷积核，拥有更少的参数量。
3. 采用更小的池化层2*2窗口和步长$s=2$。

总之一句话，“层数更深，每一层更小”。

VGG实现

完整可运行代码见：
https://github.com/KakaWanYifan/deep-learning-for-blog/blob/master/Ch07/Ch07-1.py

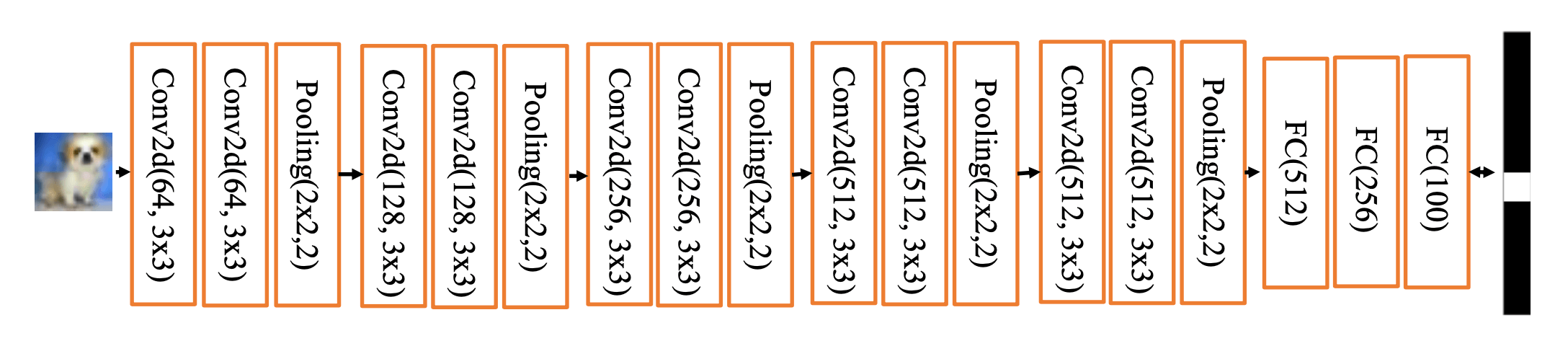
我们以CIFAR100数据集为例，即把图片分为100个类别。因此我们需要对标准的VGG13进行简单的修改。

• 把输入[224*224*3]改为[32*32*3]。
• 把三个全连接层从[4096,4096,1000]改成[512,256,100]。

并且，我们试图把这个网络拆开成两个网络，分别是：

1. 卷积池化网络
2. 全连接网络

卷积池化网络：

我们根据网络结构图，构建卷积层和池化层。并试图随机输入一个[32*32*3]的数据，观察输出。
示例代码：

import tensorflow as tf
from tensorflow.keras import layers,Sequential

conv_pool_layers = [

    # 第一个单元
    layers.Conv2D(filters=64,kernel_size=[3,3],padding='same',activation=tf.nn.relu),
    layers.Conv2D(filters=64,kernel_size=[3,3],padding='same',activation=tf.nn.relu),
    layers.MaxPooling2D(pool_size=[2,2],strides=2,padding='same'),

    # 第二个单元
    layers.Conv2D(filters=128,kernel_size=[3,3],padding='same',activation=tf.nn.relu),
    layers.Conv2D(filters=128,kernel_size=[3,3],padding='same',activation=tf.nn.relu),
    layers.MaxPooling2D(pool_size=[2,2],strides=2,padding='same'),

    # 第三个单元
    layers.Conv2D(filters=256,kernel_size=[3,3],padding='same',activation=tf.nn.relu),
    layers.Conv2D(filters=256,kernel_size=[3,3],padding='same',activation=tf.nn.relu),
    layers.MaxPooling2D(pool_size=[2,2],strides=2,padding='same'),

    # 第四个单元
    layers.Conv2D(filters=512,kernel_size=[3,3],padding='same',activation=tf.nn.relu),
    layers.Conv2D(filters=512,kernel_size=[3,3],padding='same',activation=tf.nn.relu),
    layers.MaxPooling2D(pool_size=[2,2],strides=2,padding='same'),

    # 第五个单元
    layers.Conv2D(filters=512,kernel_size=[3,3],padding='same',activation=tf.nn.relu),
    layers.Conv2D(filters=512,kernel_size=[3,3],padding='same',activation=tf.nn.relu),
    layers.MaxPooling2D(pool_size=[2,2],strides=2,padding='same'),
]

conv_pool_net = Sequential(conv_pool_layers)
conv_pool_net.build(input_shape=[None,32,32,3])
# 观察输出结构
x = tf.random.normal(shape=[1,32,32,3])
print(conv_pool_net(x).shape)

运行结果：

(1, 1, 1, 512)

即，一个[32*32*3]的图片数据，经过卷积层和池化层的层层操作后，转变为了[1*1*512]的数据。

全连接网络

正如之前讨论，我们把三个全连接层从[4096,4096,1000]改成[512,256,100]。
示例代码：

fc_layers = [
    layers.Dense(units=512,activation=tf.nn.relu),
    layers.Dense(units=256,activation=tf.nn.relu),
    layers.Dense(units=100)
]
fc_net = Sequential(fc_layers)
fc_net.build(input_shape=[None,512])

处理数据

接下来，我们加载数据，并对数据进行简单的处理。
示例代码：

from tensorflow.keras import datasets

def preprocess(x,y):
    """

    :param x:
    :param y:
    :return:
    """
    x = tf.cast(x,dtype=tf.float32) / 255.0
    y = tf.cast(y,dtype=tf.int32)

    return x,y

(x_train, y_train), (x_test, y_test) = datasets.cifar100.load_data()

# 把一个维度挤压掉
y_train = tf.squeeze(y_train,axis=1)
y_test = tf.squeeze(y_test,axis=1)

print(x_train.shape,y_train.shape,x_test.shape,y_test.shape)

db_train = tf.data.Dataset.from_tensor_slices((x_train, y_train))
db_train = db_train.shuffle(buffer_size=1000).map(preprocess).batch(200)
db_test = tf.data.Dataset.from_tensor_slices((x_test, y_test))
db_test = db_test.map(preprocess).batch(200)

sample = next(iter(db_train))
print(sample[0].shape)
print(sample[1].shape)

运行结果：

(50000, 32, 32, 3) (50000,) (10000, 32, 32, 3) (10000,)
(200, 32, 32, 3)
(200,)

训练网络

这里的训练网络和我们之前的有所不一样，我们把VGG拆分成了两个网络，所以这里我们同时需要训练两个网络。
其思路是：

1. 两个网络共用一个损失函数。
2. 损失函数对两个网络的参数求解梯度。
3. 同时优化两个网络的参数。

示例代码：

from tensorflow.keras import optimizers

optimizer = optimizers.Adam(learning_rate=0.0001)
variables = conv_pool_net.trainable_variables + fc_net.trainable_variables

# 时间有限，epochs设置为1
epochs = 1
for epoch in range(epochs):
    for step,(x,y) in enumerate(db_train):
        with tf.GradientTape() as tape:
            # [b,32,32,3] => [b,1,1,512]
            out = conv_pool_net(x)
            # [b,1,1,512] => [b,512]
            out = tf.reshape(out,[-1,512])
            # [b,512] => [b,100]
            logits = fc_net(out)

            # one hot
            y_onehot = tf.one_hot(y,depth=100)

            loss = tf.losses.categorical_crossentropy(y_onehot,logits,from_logits=True)
            loss = tf.reduce_mean(loss)

        grads = tape.gradient(loss,variables)
        optimizer.apply_gradients(zip(grads,variables))

        if step%10 == 0:
            print(epoch,step,'loss: ',loss.numpy())

运行结果：

0 0 loss:  4.605081
0 10 loss:  4.6054974
0 20 loss:  4.6071663

【部分运行结果略】

0 220 loss:  4.1778083
0 230 loss:  4.0723414
0 240 loss:  4.2223144

测试网络

我们再用测试集，测试我们的神经网络。
示例代码：

otal_num = 0
total_correct = 0
for x,y in db_test:
    out = conv_pool_net(x)
    out = tf.reshape(out,[-1,512])
    logits = fc_net(out)
    prob = tf.nn.softmax(logits,axis=1)
    pred = tf.argmax(prob,axis=1)
    pred = tf.cast(pred,tf.int32)
    correct = tf.cast(tf.equal(pred,y),dtype=tf.int32)
    correct = tf.reduce_sum(correct)

    total_num = total_num + x.shape[0]
    total_correct = total_correct + correct.numpy()

acc = total_correct / total_num
print(acc)

运行结果：

10000
537
0.0537

因为我们只训练了一个epoch，所以效果有限。但是我们看到准确率是0.0537，是高于0.01的。说明是有一定的效果的。

GoogLeNet

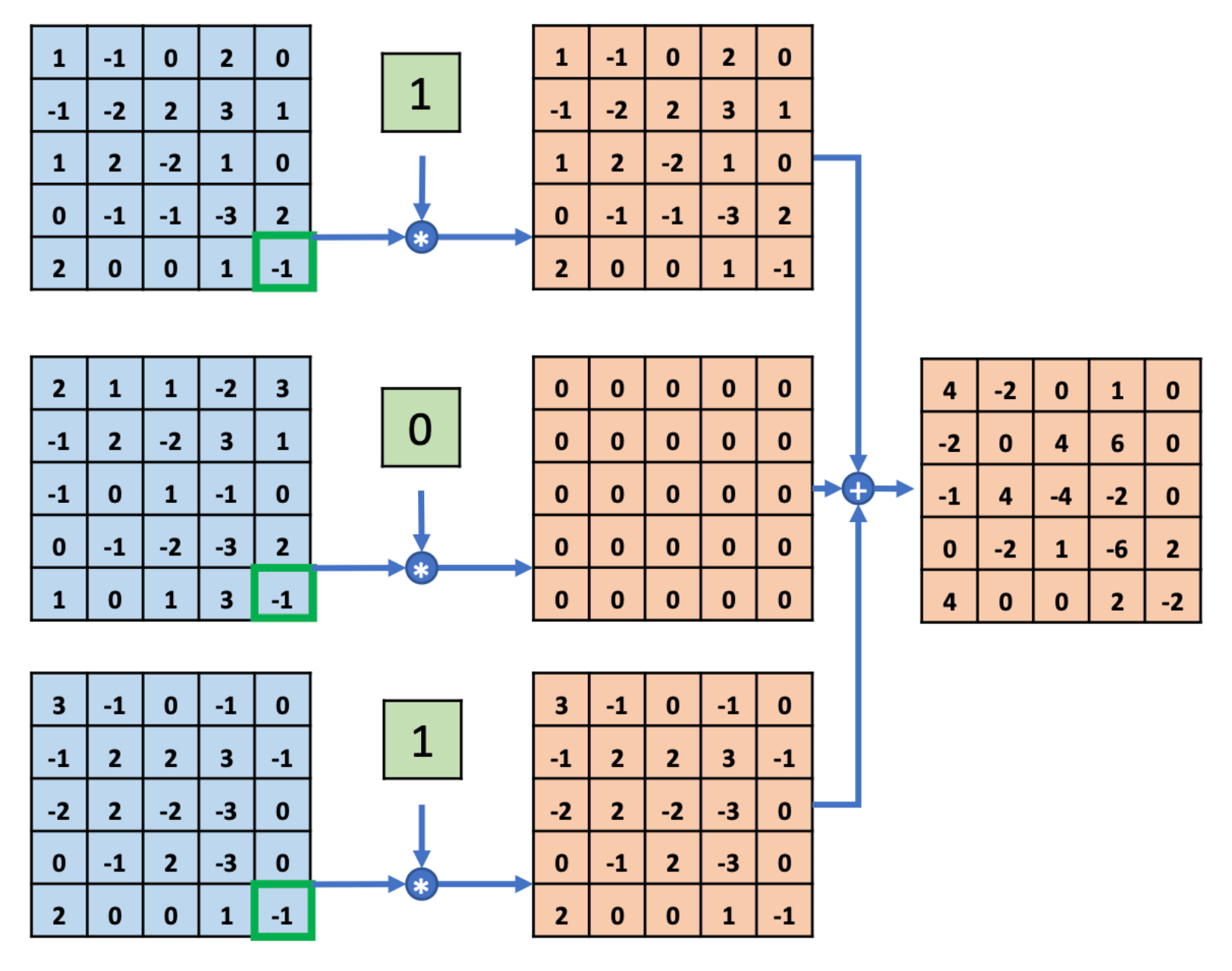
刚刚我们提到了，2014年，ILSVRC14挑战赛的亚军是VGG，那么冠军是谁呢？GoogLeNet。
正如VGG，特点是"层数更深，每一层更小"，GoogLeNet把这个发挥得更好。
其卷积核是1*1，这种卷积核的特别之处在于，不改变特征图的宽高，只对通道数进行变换。

如图，是1*1卷积核的计算过程，我们这里不赘述。

而且GoogLeNet比VGG深，GoogLeNet一共22层。

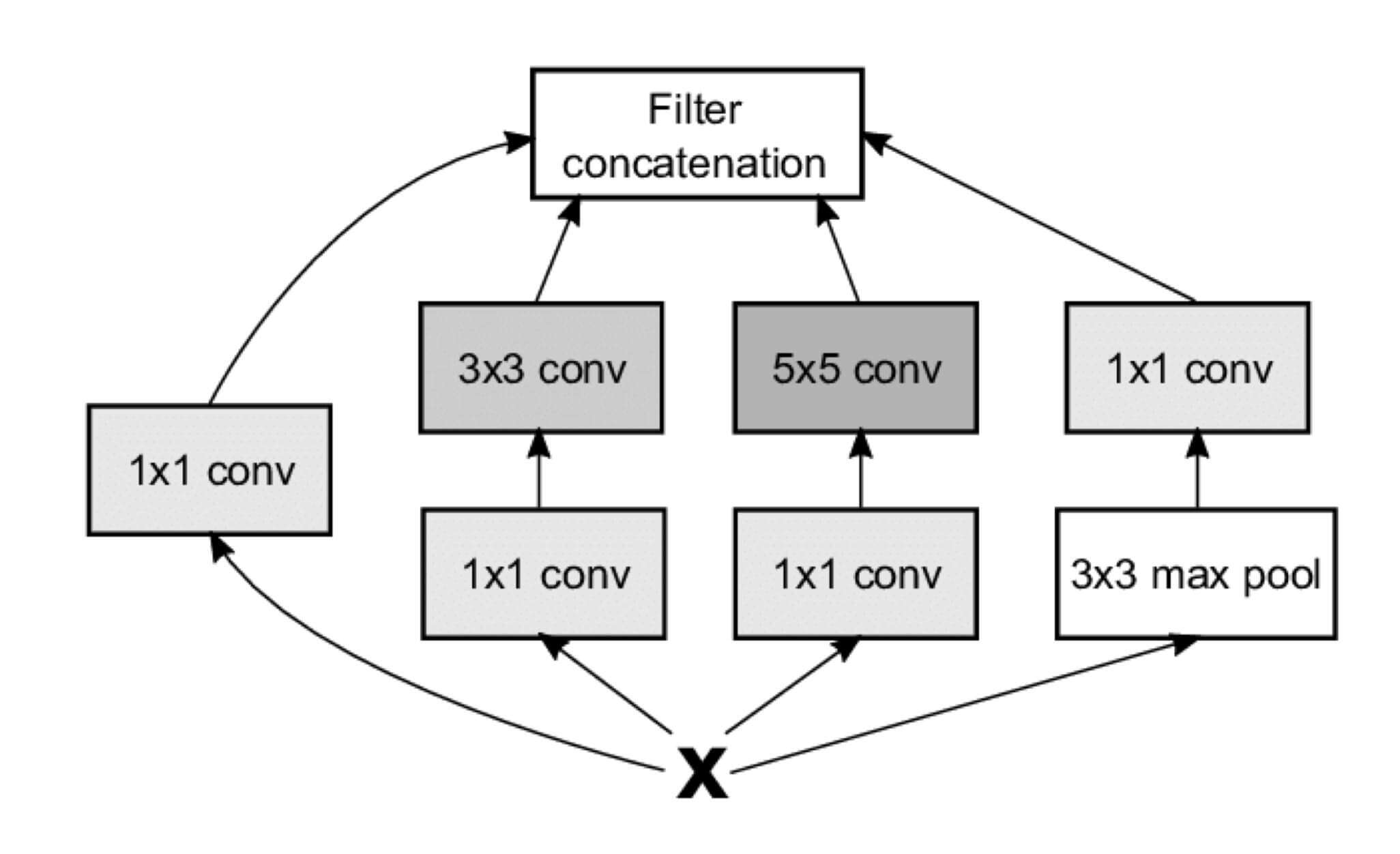
VGG是两个卷积加一个池化组成了一个模块，GoogLeNet同样有模块设计，而且其模型被命名为Inception。

Inception的结构如图所示：

由4个子网络组成，从左到右依次是：

1. 1*1卷积层
2. 1*1卷积层 + 3*3卷积层
3. 1*1卷积层 + 5*5卷积层
4. 3*3最大池化层 + 1*1卷积层

最后四个子网络的输出，会通过Filter concatenation进行合并。

那么Filter concatenation是如何合并的呢？
这里每一个卷积层和池化层的步长都是1，padding都是'same'。所以最后的四个子网络的输出和一开始的输入，h相同，w也相同。
而合并的代码是：

concatenated_tensor = tf.concat(3, [branch1, branch2, branch3, branch4])

即，如果存在4个[10*10*3]的数据，会按照深度拼接成[10*10*12]的数据。

Inception这个单词，还有一个意思：盗梦空间。

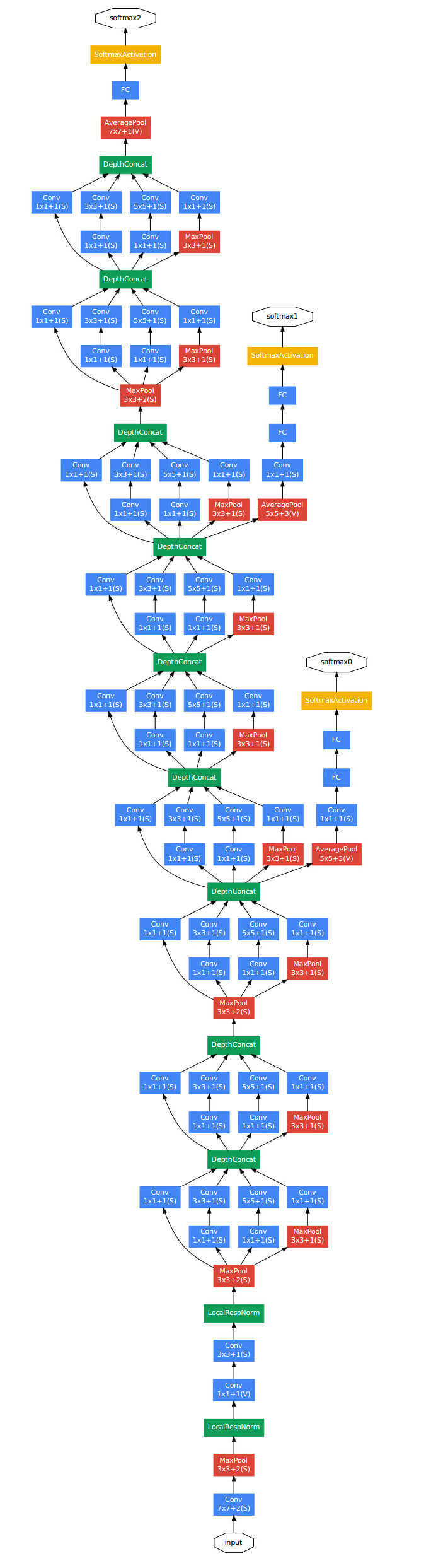
刚刚我们讨论了Inception的结构，而GoogLeNet的网络结构如下：

我们注意到，这个网络还有一个有意思的地方，中途露出了两个小尾巴，那是两个辅助分类器。这就是GoogLeNet的精妙之处了，除了最终的分类结果外，中间节点的分类效果还是不错的，所以GoogLeNet干脆从中间拉了两条分类器出来，然他们按一个较小的权重（如0.3）加到最终的分类结果中。这样做好处有：

1. 相当于做了模型整合
2. 给网络增加了反向传播的梯度信号，一定程度解决了深网络带来的梯度消失的问题

关于更高清的GoogLeNet网络结构，大家可以参考这篇论文的第七页。
https://arxiv.org/pdf/1409.4842.pdf

一般写作GoogLeNet，而不是GoogleNet，GoogLeNet的作者说是为了向LeNet致敬。

ResNet

刚刚提到Inception还有一个意思：盗梦空间。而这部电影，有一句很著名的台词，现在常被用来调侃深度学习。

的确，深度学习的一个发展趋势是越来越深。毕竟，网络的层数越深，越有可能获得更好的泛化能力。但是当模型越深，网络变得越来越难训练。越容易出现梯度弥散和梯度爆炸的现象。

那么？怎么解决这个问题呢？

那就让网络别那么深，可是网络不深呢，泛化能力又不好。想泛化能力好，网络就得深。

我们给深层神经网络添加一种回退到浅层神经网络的机制。

2015年，微软亚洲研究院何凯明等人发表了基于Skip Connection的深度残差网络(Residual Neural Network,简称ResNet)。

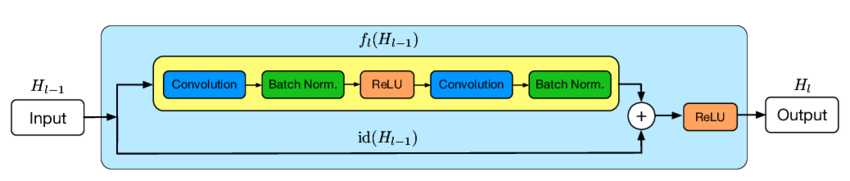
BasicBlock

在讨论ResNet之前，我们先讨论一下BasicBlock。如图，就是一个BasicBlock。为我们在卷积层的输入和输出之间添加Skip Connection实现层数回退机制。

$\bold{H}(x) = x + \bold{F}(x)$，所以需要保证$x$和$\bold{F}(x)$的Shape相同。如果不相同，通常在Skip Connection中添加额外的卷积运算，比如$identity(x)$。其中$identity(x)$以1*1的卷积运算居多，主要用于调整输入的通道数。

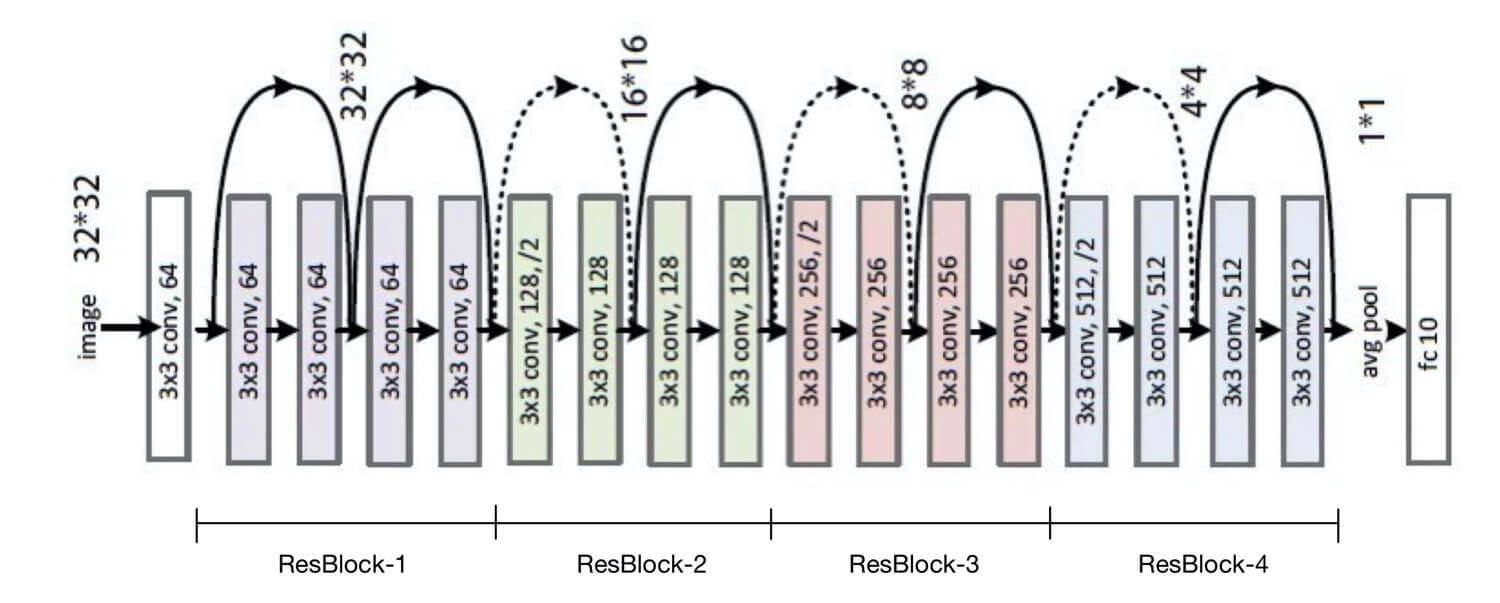
ResNet

讨论了BasicBlock，我们再来讨论一下ResBlock。

如图所示，ResBlock由一个或多个BasicBlock堆叠而成，一个或多个ResBlock堆叠成ResNet。

ResNet的实现

完整可运行代码见：
https://github.com/KakaWanYifan/deep-learning-for-blog/blob/master/Ch07/Ch07-2.py

现在，我们试图实现一个ResNet，通过我们以CIFAR100数据集为例。

BasicBlock

我们从BasicBlock开始。先实现BasicBlock图片的上半部分：$\bold{F}(x)$。

BasicBlock继承layers.Layer。
示例代码：

# BasicBlock
class BasicBlock(layers.Layer):
    def __init__(self, filter_num, strides=1):
        """

        :param filter_num: 卷积核的数量
        :param strides: 步长，默认为1
        """
        # 初始化函数，调用父类的初始化方法
        super(BasicBlock, self).__init__()

        # f(x)包含了2个普通卷积层
        # 创建卷积层 1
        self.conv1 = layers.Conv2D(filters=filter_num, kernel_size=(3, 3), strides=strides, padding='same')
        self.bn1 = layers.BatchNormalization()
        self.relu = layers.Activation('relu')

        # 创建卷积层 2
        self.conv2 = layers.Conv2D(filters=filter_num, kernel_size=(3, 3), strides=1, padding='same')
        self.bn2 = layers.BatchNormalization()

正如之前讨论，$x$的形状要和$\bold{F}(x)$相同，现在实现$identity(x)$。
示例代码：

if strides != 1:
    # 插入 identity 层
    self.identity = Sequential()
    self.identity.add(layers.Conv2D(filters=filter_num, kernel_size=(1, 1), strides=strides))
else:
    # 否则,直接连接
    self.identity = lambda x: x

最后，我们实现前向运算部分。
示例代码：

def call(self, inputs, training=None):
    """

    :param inputs:
    :param training:
    :return:
    """
    # 前向传播函数
    # 通过第一个卷积层
    out = self.conv1(inputs)
    out = self.bn1(out, training=training)
    out = self.relu(out)

    # 通过第二个卷积层
    out = self.conv2(out)
    out = self.bn2(out, training=training)

    # 输入通过 identity()转换
    idVal = self.identity(inputs)

    # f(x) + x 运算
    output = layers.add([out, idVal])

    # 再通过激活函数并返回
    # 特别注意：relu用了两次
    output = tf.nn.relu(output)
    return output

ResBlock

ResBlock由一个或多个BasicBlock组成。
示例代码：

def build_resblock(self,filter_num,blocks,strides=1):
    """

    :param filter_num:
    :param blocks:
    :param strides:
    :return:
    """
    res_blocks = Sequential()
    res_blocks.add(BasicBlock(filter_num=filter_num,strides=strides))

    for _ in range(blocks):
        res_blocks.add(BasicBlock(filter_num=filter_num,strides=1))
    return res_blocks

ResNet

ResNet由一个或多个ResBlock组成。
示例代码：

def __init__(self,layer_dims,num_class=100):
    """
    
    :param layer_dims:
    """
    super(ResNet,self).__init__()
    self.stem = Sequential([layers.Conv2D(filters=64,kernel_size=(3,3),strides=(1,1)),
                            layers.BatchNormalization(),
                            layers.Activation('relu'),
                            layers.MaxPool2D(pool_size=(2,2),strides=(1,1),padding='same')])

    self.layer1 = self.build_resblock(filter_num=64,blocks=layer_dims[0])
    self.layer2 = self.build_resblock(filter_num=128,blocks=layer_dims[0],strides=2)
    self.layer3 = self.build_resblock(filter_num=256,blocks=layer_dims[0],strides=2)
    self.layer4 = self.build_resblock(filter_num=512,blocks=layer_dims[0],strides=2)

    self.avgpool = layers.GlobalAveragePooling2D()

    self.fc = layers.Dense(units=num_class)

ResNet的前向运算

示例代码：

def call(self, inputs, training=None):
    """

    :param inputs:
    :param training:
    :param mask:
    :return:
    """
    x = self.stem(inputs,training=training)

    x = self.layer1(x,training=training)
    x = self.layer2(x,training=training)
    x = self.layer3(x,training=training)
    x = self.layer4(x,training=training)

    x = self.avgpool(x)

    x = self.fc(x)

    return x

实例化一个ResNet13

示例代码：

model = ResNet(layer_dims=[2,2,2,2])
model.build(input_shape=(None, 32, 32, 3))
model.summary()

运行结果：

Model: "res_net"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
sequential (Sequential)      (None, 30, 30, 64)        2048      
_________________________________________________________________
sequential_1 (Sequential)    (None, 30, 30, 64)        223104    
_________________________________________________________________
sequential_2 (Sequential)    (None, 15, 15, 128)       823168    
_________________________________________________________________
sequential_4 (Sequential)    (None, 8, 8, 256)         3284736   
_________________________________________________________________
sequential_6 (Sequential)    (None, 4, 4, 512)         13123072  
_________________________________________________________________
global_average_pooling2d (Gl multiple                  0         
_________________________________________________________________
dense (Dense)                multiple                  51300     
=================================================================
Total params: 17,507,428
Trainable params: 17,495,780
Non-trainable params: 11,648
_________________________________________________________________

处理数据

和VGG几乎一致。需要特别注意的是，添加了这段代码。

# 减少数据量，这要耗费时间少。毕竟只是demo
x_train = x_train[:10000]
y_train = y_train[:10000]
x_test = x_test[:2000]
y_test = y_test[:2000]

训练网络

示例代码：

epochs = 1
for epoch in range(epochs):
    for step, (x, y) in enumerate(db_train):
        with tf.GradientTape() as tape:
            # [b,32,32,3] => [b,100]
            logits = model(x)

            # one hot
            y_onehot = tf.one_hot(y, depth=100)

            loss = tf.losses.categorical_crossentropy(y_onehot, logits, from_logits=True)
            loss = tf.reduce_mean(loss)

        grads = tape.gradient(loss, model.trainable_variables)
        optimizer.apply_gradients(zip(grads, model.trainable_variables))

        if step % 10 == 0:
            print(epoch, step, 'loss: ', loss.numpy())

运行结果：

0 0 loss:  4.6136904
0 10 loss:  4.5993
0 20 loss:  4.559182
0 30 loss:  4.436839
0 40 loss:  4.4675236

测试网络

示例代码：

total_num = 0
total_correct = 0
for x, y in db_test:
    logits = model(x)
    prob = tf.nn.softmax(logits, axis=1)
    pred = tf.argmax(prob, axis=1)
    pred = tf.cast(pred, tf.int32)
    correct = tf.cast(tf.equal(pred, y), dtype=tf.int32)
    correct = tf.reduce_sum(correct)
    total_num = total_num + x.shape[0]
    total_correct = total_correct + correct.numpy()

print(total_num)
print(total_correct)
acc = total_correct / total_num
print(acc)

运行结果：

2000
47
0.0235

因为我们减少了训练数据的数量，而且epochs设定为1，所以效果有限。但是我们看到准确率是0.0235，大于0.01。说明是具有一定效果的。

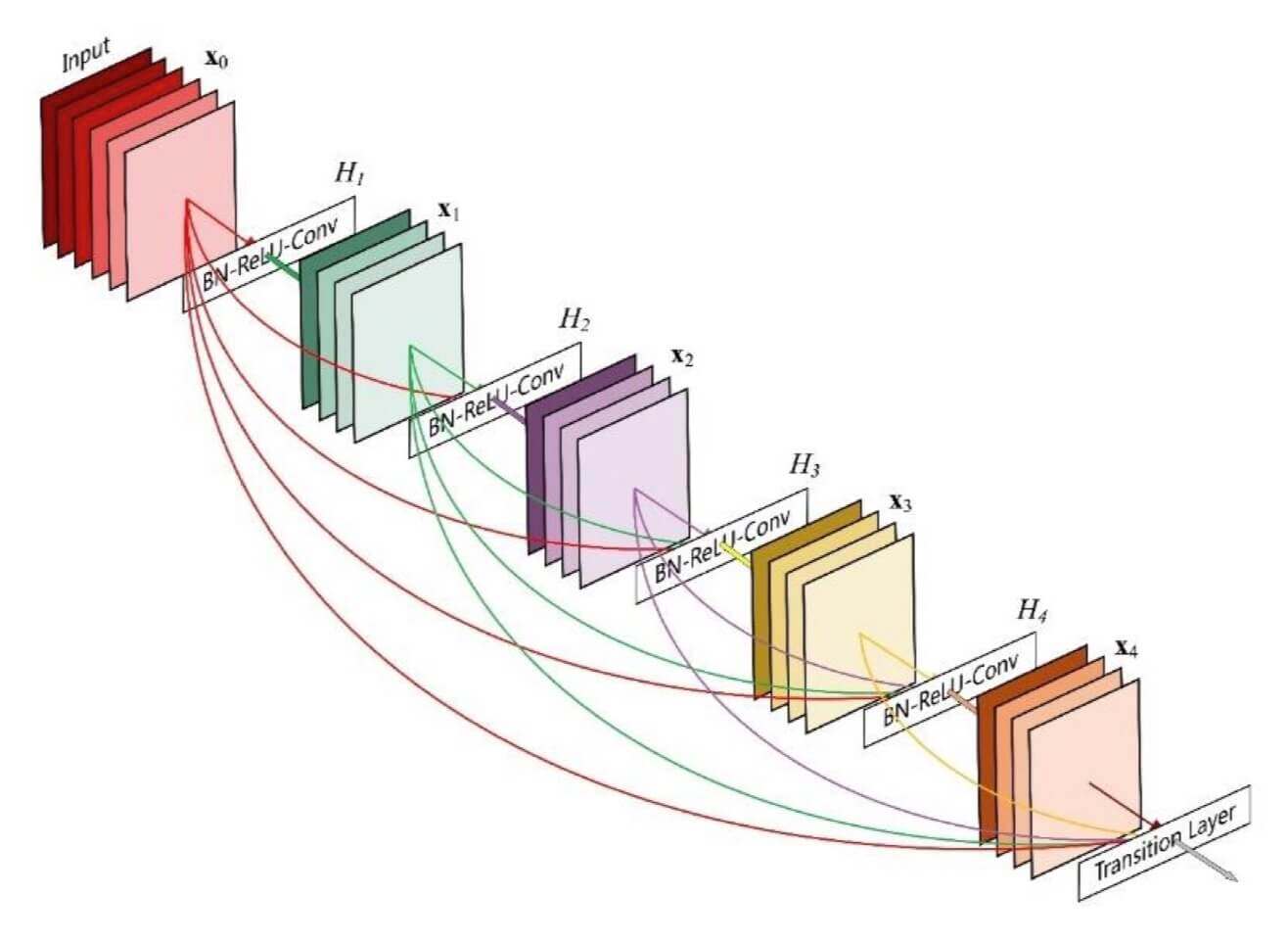
DenseNet

dense的意思是稠密的，浓厚的。
正如我们之前讨论的全连接层，每一个输出节点都和所有的输入节点相连。
ResBlock是由多个BasicBlock堆叠而成，如果这些BasicBlock不但进行堆叠，还进行了稠密连接，那么这个就是DenseBlock，如图：

而由多个DenseBlock堆叠而成的就是DenseNet，如图：