这一章，我们开始讨论一个新的神经网络，循环神经网络。循环神经网络主要是用来分析识别序列的，那么什么是序列呢？

序列

什么是序列

序列(Sequence)是具有先后顺序的数据。

比如：股市行情
比如：此时此刻，你正在看的这句话。

以股市行情为例的话，比如平安银行(000001)在上周五天的每天收盘价，我们可以表示为 $[x_1,x_2,x_3,x_4,x_5]$ 的张量，形状是(5)。
那么，如果我们要表示多只股票的上周五天的每天收盘价呢？

$[[x_1^{(1)},x_2^{(1)},x_3^{(1)},x_4^{(1)},x_5^{(1)}],[x_1^{(2)},x_2^{(2)},x_3^{(2)},x_4^{(2)},x_5^{(2)}],···,[x_1^{(b)},x_2^{(b)},x_3^{(b)},x_4^{(b)},x_5^{(b)}]]$

张量的形状是(b,5)，其中b是股票的数量。
那么，如果我们除了收盘价，还需要开盘价、成交量、换手率这些呢？这时候张量的形状就是(b,5,n)。

Embedding

刚刚我们提到的第二个例子此时此刻，你正在看的这句话，就是常见的第二种序列，句子。
那么，对于句子，我们怎么进行编码呢？

One-Hot的缺点

之前我们讨论过One-Hot编码，例如：

词语	One-Hot
上海	`[1,0,0,0]`
南昌	`[0,1,0,0]`
晴天	`[0,0,1,0]`
雨天	`[0,0,0,1]`

如果，我们只考虑常用的8000个中文词语的话，我们的每一个词语都可以编码成一个长度为8000，有且仅有一位是1的向量。如果这句话是有b个词语组成的话，这句话的形状就是(b,8000)。
这么看起来，我们解决了句子的编码？但这么做却存在问题，对于一个(b,8000)的句子，有且仅有b个1，其他都是0。这样的话，非常浪费存储性能。当然，这个问题可以通过计算机技术克服。
比如，我们保存为这种形式就OK了。

(0, 0)	1.0
(1, 1)	1.0
(2, 2)	1.0
(3, 3)	1.0

但是，还有一个问题。
例如：对于上海，我们编码为第1个位置是1，其他位置是0的一个向量；对于南昌，我们编码为第2个位置是1，其他位置是0的一个向量；那么现在还有一个词语，晴天，对于晴天我们编码为第3个位置是1，其他位置是0的一个向量。根据我们之前学过的线性代数， $\overrightarrow{\text{上海}}$ 和 $\overrightarrow{\text{南昌}}$ 是没有相似性的， $\overrightarrow{\text{上海}}$ 和 $\overrightarrow{\text{晴天}}$ 也是没有相似性的。但是，在现实生活中，上海和南昌都属于地名，或多或少有点相似性；上海和晴天，一个是地名，一个是天气，可能没有相似性。
这就是One-Hot编码的主要缺点，无法表达词语之间的相似性。

Embedding层

那么？怎么才能表达相似性呢？
举个例子，比方说，我们把上海表示为(1,2)，把南昌表示为(1,3)；把晴天表示为(2,-1)，并且用两个向量之间的余弦距离来量化相关性的话。 $\overrightarrow{\text{上海}}$ 和 $\overrightarrow{\text{南昌}}$ 之间的相似性是大于 $\overrightarrow{\text{上海}}$ 和 $\overrightarrow{\text{晴天}}$ 之间的相似性，这样就克服了One-Hot编码无法表达词语之间相似性的问题。
而这个过程，我们称之为Word Embedding或者Embedding，这个向量我们称之为表示向量。

那么，我们怎么把One-Hot转成Word Embedding呢？

$\begin{pmatrix}1 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 \end{pmatrix}\begin{pmatrix}w_{11} & w_{12} & w_{13}\\ w_{21} & w_{22} & w_{23}\\ w_{31} & w_{32} & w_{33}\\ w_{41} & w_{42} & w_{43}\\ w_{51} & w_{52} & w_{53}\\ w_{61} & w_{62} & w_{63}\end{pmatrix}=\begin{pmatrix}w_{11} & w_{12} & w_{13}\\ w_{21} & w_{22} & w_{23}\end{pmatrix}$

用一个全连接层。该全连接层的输入是One-Hot，权重参数就是"字向量表"。

这个运算其实也很简单。第一列为1，就是字向量表的第一行；第二列为1，就是字向量表的第二行，这个操作被称为查表。

但是问题又来了。"字向量表"怎么确定呢？通过神经网络进行训练得到。

在自然语言处理领域，还有专门的一个研究方向就是探索如何学习到单词的表示向量(Word Vector)。

此外，我们还知道，不管是上海和南昌相关性大，还是上海和北京相关性大，还是一样大。总之，都会大于上海和晴天的相似性。所以总有那种差不多可以直接用的Embedding层，而常见的两个就是Word2Vec和GloVe。

循环神经网络

现在，我们假设存在一个句子如下：

对于这个句子，我们可以将其表示为[1,4,n]的一个张量，其中1代表句子数量，4代表句子长度，也就是句子中汉字的个数，n代表词向量长度，也就是每个汉字表示向量的维度。
现在，我们来做一个很简单的二分类问题，看看这句话到底是积极的，还是消极的。

全连接层的缺点

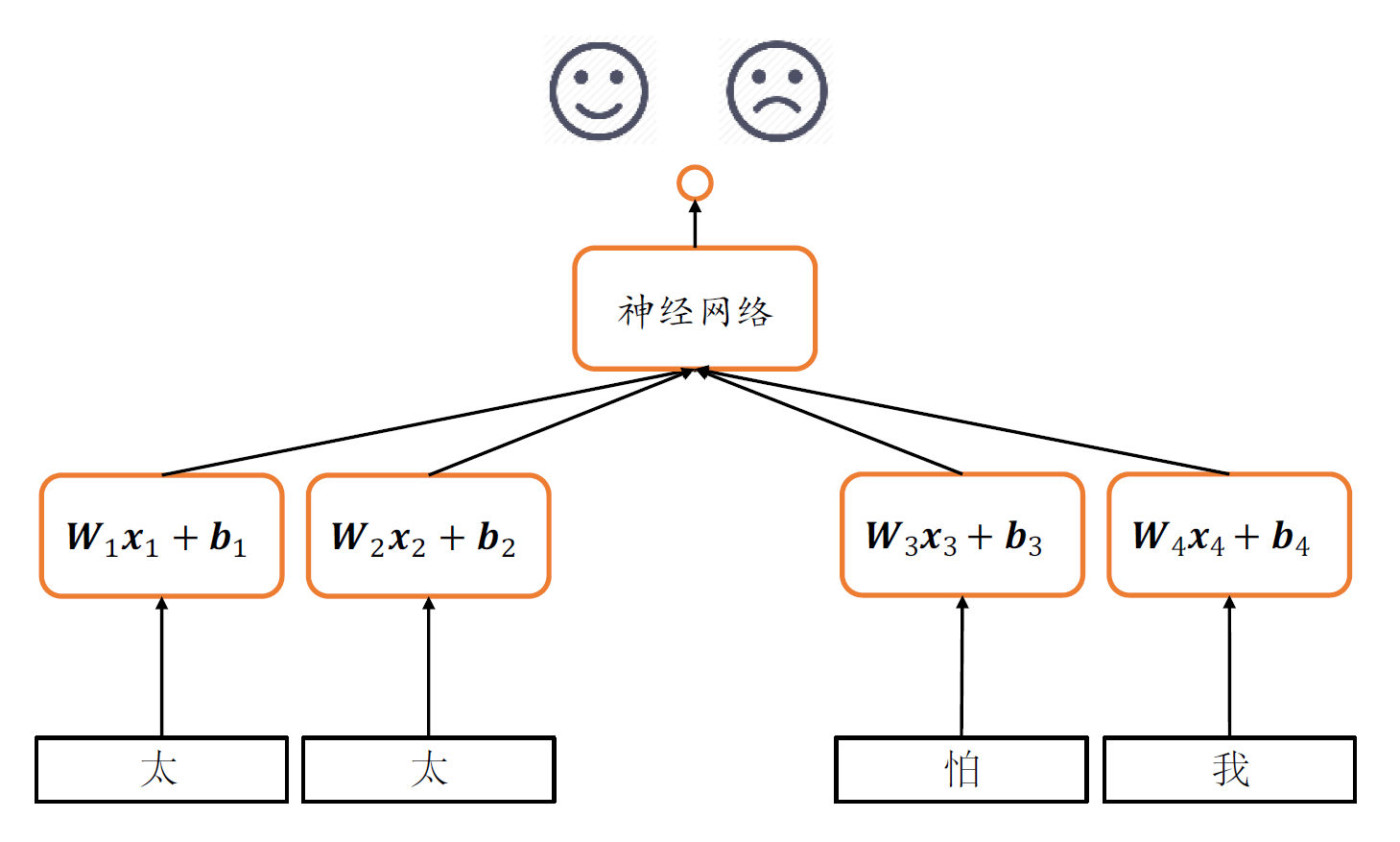
首先，我们用全连接层，网络结构如下：

我们看到四个字的话，我们需要维护4组参数。而通常我们有几十个甚至上百个字，这样参数了是非常大的。
为了解决这个问题，我们仿照卷积神经网络，做权值共享。

如图，我们做权值共享。当然为了准确率，我们可以用一个或几个不一样的 $\bold{W_x +b}$ ，就像卷积神经网络，一个卷积层用好几个卷积核。

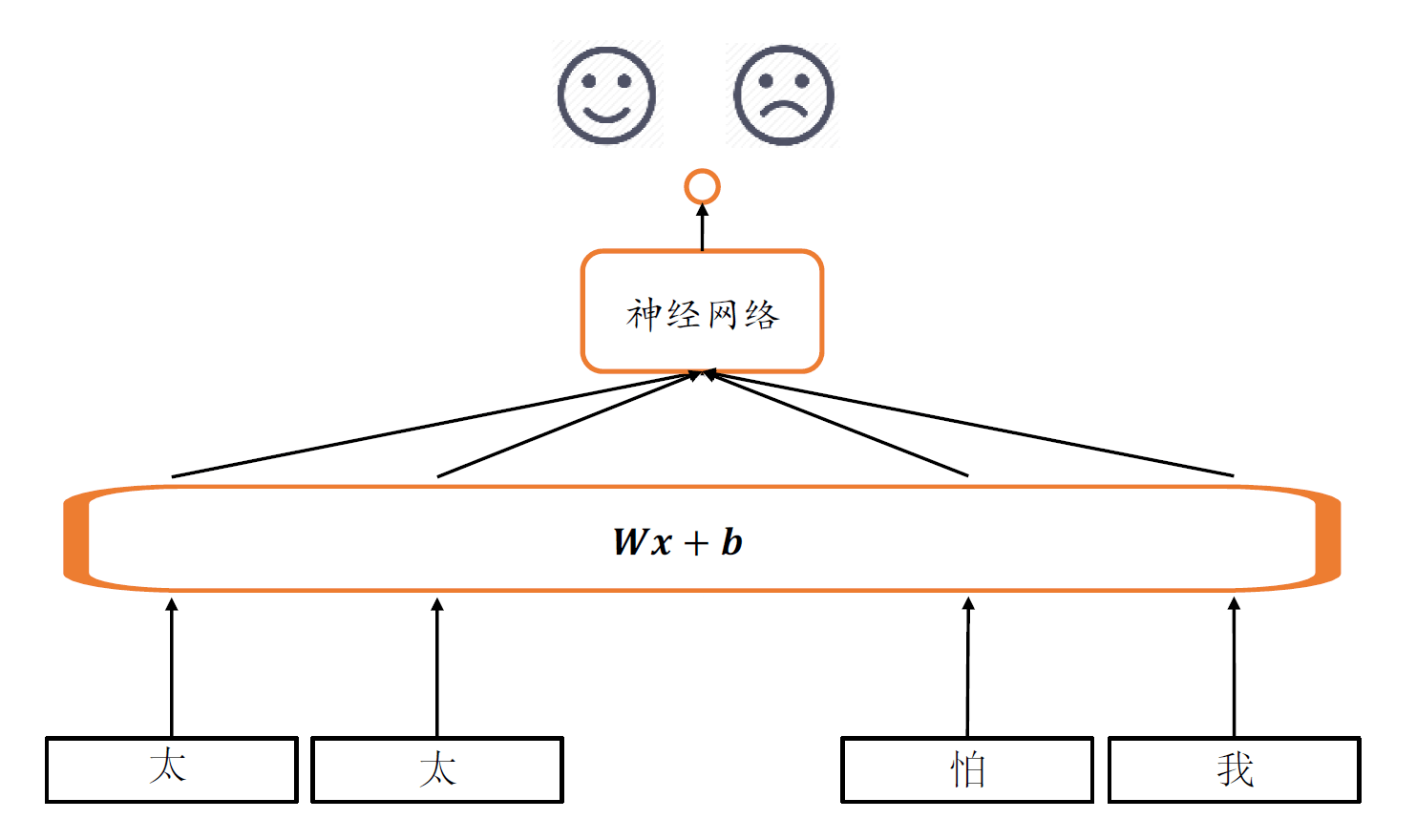
但总体，参数量太大的问题还是可以得到解决。

不过还有一个问题。
对于这个神经网络，太太怕我和我怕太太是一样的。
这怎么能一样呢？太太怕我，呐，这句话是积极的。我怕太太，呐，这句话是消极的！

所以：对于序列问题，全连接层的主要缺点是不能感知序列顺序，导致句子整体语义的缺失。

循环神经网络

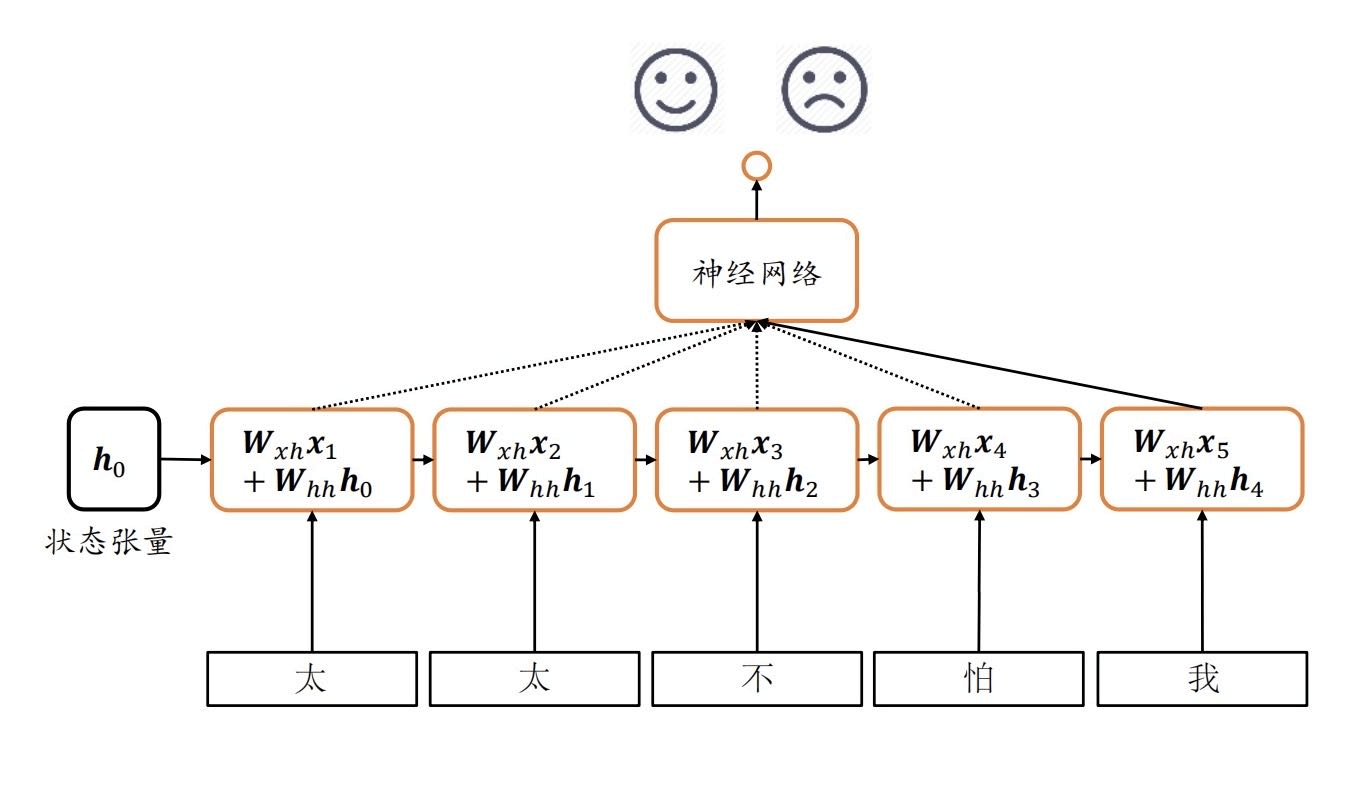
正如我们刚刚举的例子，词语的顺序会影响整个句子的含义，这时候我们就需要找个人来记下语义信息，我们称之为状态张量。

我们看到共用了一个 $\bold{W}_{xh}$ ，一个 $\bold{W}_{hh}$ ；如果还有偏置的话，还会共用一个偏置 $\bold{b}$ 。
也就是说依旧是权值共享的。

同时，我们看到 $\bold{h}_t$ 在这里进行了传递。其传递公式如下：

$\bold{h}_t = \tanh(\bold{W}_{xh}\bold{x}_t + \bold{W}_{hh}\bold{h}_{t-1} + b)$

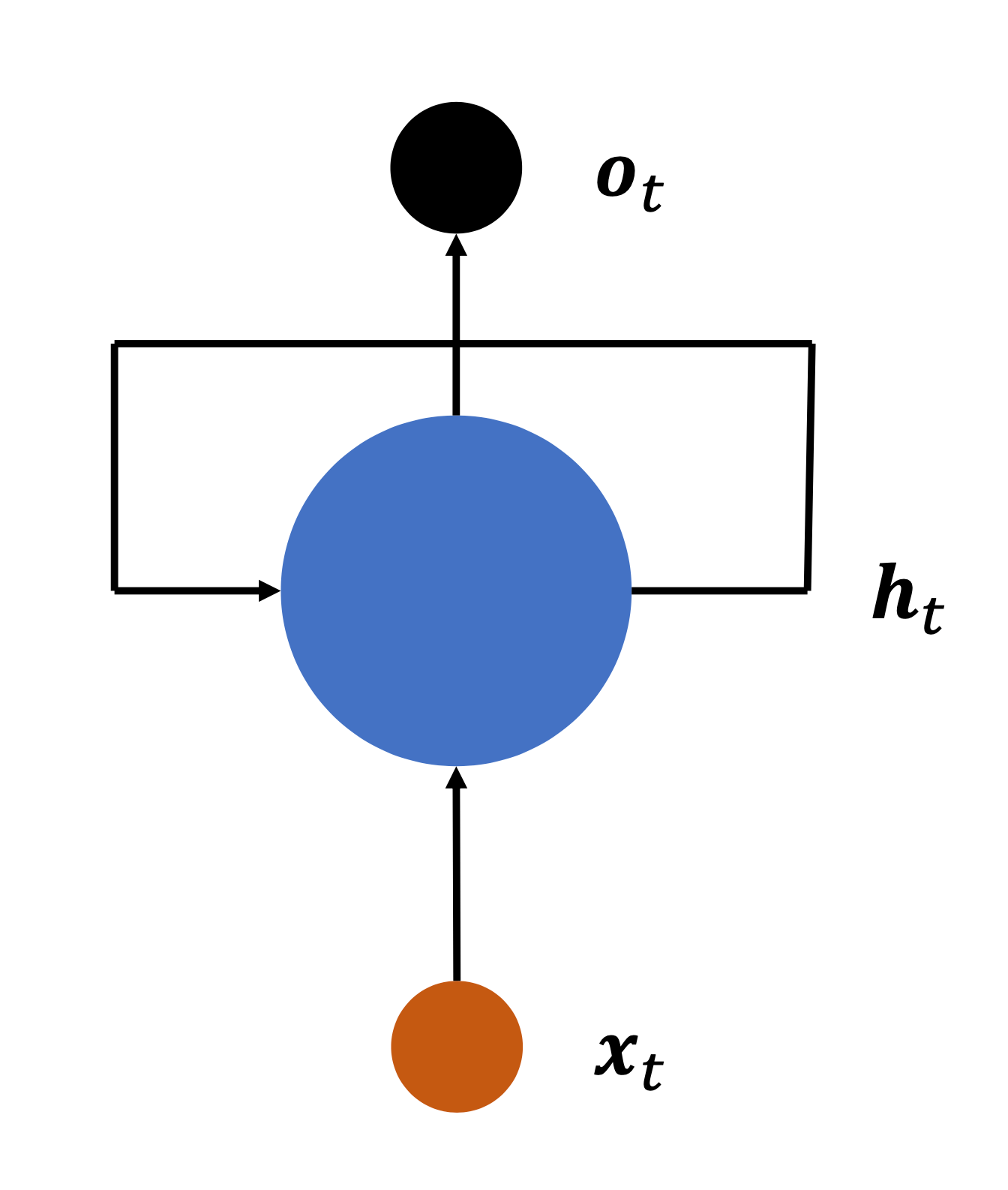
而且，我们发现每一个节点在进行传递的同时，还或有的进行输出。(前面的节点或许不进行输出，所以是虚线；但是最后一个节点一定进行了输出，所以是实线。)
那么节点的输出是什么呢？
可以是 $\bold{h}_t$ ，即 $\bold{o}_t = \bold{h}_t$ ；也可以在 $\bold{h}_t$ 的基础上再乘一个东西，即 $\bold{o}_t = \bold{W}_{ho}\bold{h}_t$ ，都可以。

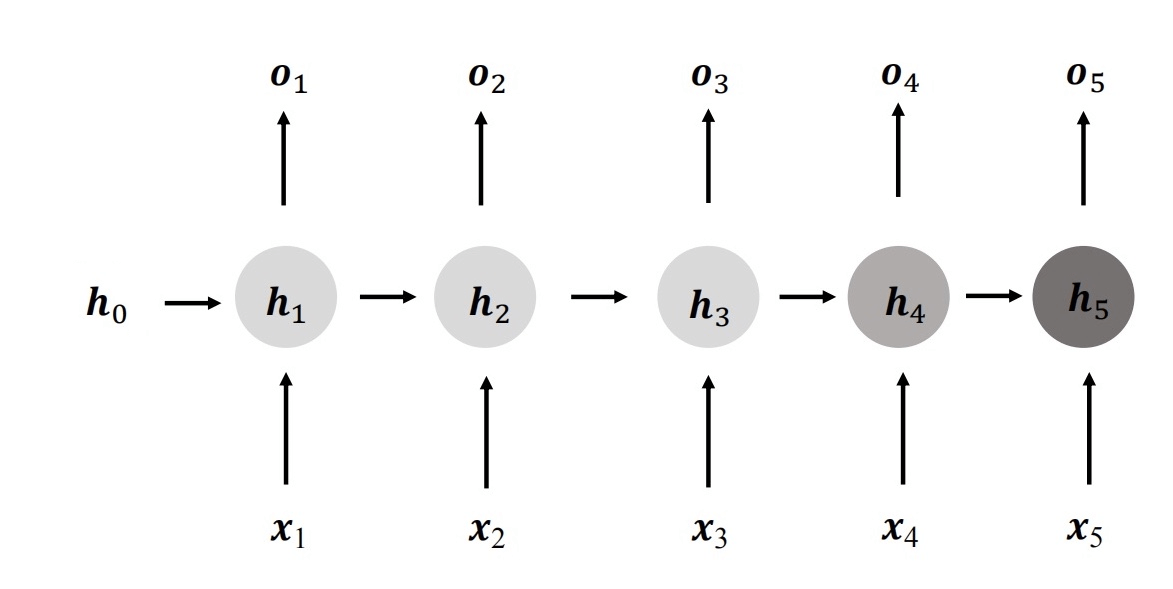
对于上面的神经网络结构，我们可以简化为：

也可以再进行折叠。

折叠之后，循环的模样就出来了，这就是循环神经网络(Recurrent Neural Network，简称 RNN)。

即：网络循环接受序列的每个特征向量 $\bold{x}_t$ ，并刷新内部状态向量 $\bold{h}_t$ ，同时形成输出 $\bold{o}_t$ 。

梯度

所以，我们已经知道了整个网络结构。接下来的操作，就是梯度下降去更新参数。

我们再以上面的"太太怕我"这个神经网络为例，并假设只在最后一个节点进行输出。在这种请求下，我们去求 $\bold{W}_{hh}$ 的梯度。则有：

$\frac{\partial loss}{\partial \bold{W}_{hh}} = \frac{\partial loss}{\partial \bold{o}} \frac{\partial \bold{o}}{\partial \bold{W}_{hh}}$

而 $\bold{o} = \bold{W}_{xh}x_{5} + \bold{W}_{hh}\bold{h}_{4}$ 。
则

$\begin{aligned} \frac{\partial \bold{o}}{\partial \bold{W}_{hh}} &= (\bold{W}_{xh}x_{5})' + {\bold{W}_{hh}}'{\bold{h}_{4}} + {\bold{W}_{hh}}{\bold{h}_{4}}' \\ &= 0 + {\bold{h}_{4}} + {\bold{W}_{hh}} \frac{\partial \bold{h}_{4}}{\partial \bold{W}_{hh}} \\ &= {\bold{h}_{4}} + {\bold{W}_{hh}} \frac{\partial \bold{h}_{4}}{\partial \bold{W}_{hh}} \end{aligned}$

而 $\bold{h}_{4} = \bold{W}_{xh}x_{4} + \bold{W}_{hh}\bold{h}_{3}$ 。
则

$\frac{\partial \bold{h}_{4}}{\partial \bold{W}_{hh}} = {\bold{h}_{3}} + {\bold{W}_{hh}} \frac{\partial \bold{h}_{3}}{\partial \bold{W}_{hh}}$

同理

$\begin{aligned} \frac{\partial \bold{h}_{3}}{\partial \bold{W}_{hh}} &= {\bold{h}_{2}} + {\bold{W}_{hh}} \frac{\partial \bold{h}_{2}}{\partial \bold{W}_{hh}} \\ \frac{\partial \bold{h}_{2}}{\partial \bold{W}_{hh}} &= {\bold{h}_{1}} + {\bold{W}_{hh}} \frac{\partial \bold{h}_{1}}{\partial \bold{W}_{hh}} \\ \frac{\partial \bold{h}_{1}}{\partial \bold{W}_{hh}} &= {\bold{h}_{0}} + {\bold{W}_{hh}} \frac{\partial \bold{h}_{0}}{\partial \bold{W}_{hh}} = {\bold{h}_{0}} \end{aligned}$

最后，我们将上述式子进行整理，则有

$\frac{\partial loss}{\partial \bold{W}_{hh}} = \frac{\partial loss}{\partial \bold{o}} \Bigg( {\bold{h}_{4}} + {\bold{W}_{hh}} \bigg( {\bold{h}_{3}} + {\bold{W}_{hh}} \bigg( {\bold{h}_{2}} + {\bold{W}_{hh}} \bigg( {\bold{h}_{1}} + {\bold{W}_{hh}} \bold{h}_{0} \bigg) \bigg) \bigg) \Bigg)$

对于其他参数的梯度或者其他循环神经网络的下不同参数的梯度，步骤类似，都是链式求导法则。

梯度爆炸与梯度弥散

在刚刚推导的梯度中，我们发现了一个特点：这里有 $\bold{W}_{hh}$ 的连乘。
那么连乘会导致什么呢？

这个式子告诉我们：积跬步以至千里，积懈怠以至深渊。

也告诉我们：如果 $\bold{W}_{hh}$ 略微大于1，连乘之后就是梯度爆炸；如果 $\bold{W}_{hh}$ 略微小于1，连乘之后就是梯度弥散。

那，怎么办呢？

梯度爆炸的解决方法

梯度爆炸，就是梯度的值太大。那么就对症下药，让梯度值小一点。这个叫做梯度裁剪。
我们有三种方法来做梯度裁剪。

1、直接对张量进行限幅

方法：

1	tf.clip_by_value(a,0.4,0.6)

示例代码：

1
2
3

a = tf.random.uniform([2,2])
print(a)
print(tf.clip_by_value(a,0.4,0.6))

运行结果：

tf.Tensor(
[[0.23047662 0.4244045 ]
 [0.06364775 0.75429416]], shape=(2, 2), dtype=float32)
tf.Tensor(
[[0.4       0.4244045]
 [0.4       0.6      ]], shape=(2, 2), dtype=float32)

2、通过限制张量W的范数进行梯度裁剪

对于 $\bold{W}$ 的二范数 $||\bold{W}||_2$ 约束在 $[0,max]$ 之间，如果 $||\bold{W}||_2$ 大于 $max$ 值，则：

$\bold{W} = \frac{\bold{W}}{||\bold{W}||_2} \cdot max$

方法：

1	tf.clip_by_norm(a,0.5)

示例代码：

1
2
3

a = tf.random.uniform([2,2])
print(a)
print(tf.clip_by_norm(a,0.5))

运行结果：

tf.Tensor(
[[0.9029136  0.643152  ]
 [0.38656533 0.38846624]], shape=(2, 2), dtype=float32)
tf.Tensor(
[[0.36507234 0.2600437 ]
 [0.1562988  0.15706739]], shape=(2, 2), dtype=float32)

3、全局范数裁剪

神经网络的更新方向是由所有参数的梯度张量 $\bold{W}$ 共同决定的，前两种方式只考虑单个梯度张量的限幅，会出现网络更新方向发生变动的情况。如果能够考虑所有参数的梯度 $\bold{W}$ 的范数，实现等比例的缩放，那么就能既很好地限制网络的梯度值，同时不改变网络的更新方向。
这就是第三种梯度裁剪的方式：全局范数裁剪。

$\text{globalNorm} = \sqrt{\sum_{i}{||\bold{W}^{(i)}||}_2^2}$

$\bold{W}^{(i)} = \frac{\bold{W}^{(i)} \cdot \text{maxNorm}}{\max(\text{globalNorm},\text{maxNorm})}$

方法：

1	tf.clip_by_global_norm([w1,w2],2)

示例代码：

# 创建梯度张量 1
w1=tf.random.normal([3,3])
# 创建梯度张量 2
w2=tf.random.normal([3,3])
# 计算 global_norm
global_norm=tf.math.sqrt(tf.norm(w1)**2+tf.norm(w2)**2)
# 根据 global_norm 和 max_norm=2 裁剪
(ww1,ww2),global_norm=tf.clip_by_global_norm([w1,w2],2)
print(w1)
print(ww1)
print('\n')
print(w2)
print(ww2)

运行结果：

tf.Tensor(
[[-0.8629622   0.40890458 -0.9399877 ]
 [ 0.15929171 -1.0480874   0.7361457 ]
 [-0.7518713  -0.34796828  0.8277537 ]], shape=(3, 3), dtype=float32)
tf.Tensor(
[[-0.36708537  0.17393912 -0.39985034]
 [ 0.06775923 -0.4458336   0.31314036]
 [-0.3198297  -0.14801814  0.35210845]], shape=(3, 3), dtype=float32)


tf.Tensor(
[[-0.34849733  0.33741903 -0.7820168 ]
 [-0.64187014 -0.27226803  0.33027136]
 [ 2.658648    2.8807082   0.681314  ]], shape=(3, 3), dtype=float32)
tf.Tensor(
[[-0.14824319  0.14353073 -0.33265296]
 [-0.2730376  -0.1158169   0.14049026]
 [ 1.130931    1.2253907   0.28981617]], shape=(3, 3), dtype=float32)

梯度弥散的解决方法

梯度弥散，就是梯度的值太小。

增大学习率。
我们知道每次参数更新是梯度值再乘以学习率，梯度的值小了，那我们就让学习率大一点。
减少网络深度。
skip connection
这个我们在经典卷积神经网络这一章已经讨论过了。

RNN层的实现

现在，我们来实现一个RNN层。

RNNCell的实现

正如之前的讨论，一个RNN层由很多个节点串联而成，我们把这些节点称作RNNCell。

对于RNNCell，我们发现有这些特点：

每一个RNNCell的有两个输入： $\bold{x}_t$ 和 $[\bold{h}_{t-1}]$ 。(这里我们把 $[\bold{h}_{t-1}]$ 用一个List包裹起来，是为了和LSTM、GRU等RNN变种格式统一。)
每一个RNNCell的有两个输出： $\bold{o}_t$ 和 $[\bold{h}_{t}]$ 。

而至于 $\bold{h}_t$ 的传递，以及输出 $\bold{o}_t$ 。都在之前讨论过了，这里不赘述。

我们也知道RNNCell内部有三个参数：

$\bold{W}_{xh}$
$\bold{W}_{hh}$
$\bold{b}$

为了发挥现代CPU和GPU的优势，我们决定来个并行计算，好几个句子同步进行，比如：4句。

示例代码：

# 5 的意思是经过神经元后，维度转化为5维
# [b, 10] -> [b, 5]，b是句子数量
cell = layers.SimpleRNNCell(5)
# 10 的意思是每个汉字的表示向量的维度是10
cell.build(input_shape=(None,10))

for var in cell.trainable_variables:
    print(var)

运行结果：

<tf.Variable 'kernel:0' shape=(10, 5) dtype=float32, numpy=
array([[-0.4235797 ,  0.5078381 ,  0.1656707 , -0.08279335, -0.26317865],
       [ 0.18025243,  0.60182637, -0.08209336,  0.20251465,  0.13268387],
       [ 0.1728267 ,  0.14476752,  0.49247402,  0.1616072 ,  0.04044557],
       [-0.5995954 , -0.0747878 , -0.3128495 ,  0.48853797,  0.48989183],
       [ 0.36338574, -0.5571276 , -0.5425282 , -0.24233836, -0.31473178],
       [ 0.51667887, -0.03607571, -0.32585987,  0.16823816,  0.10882169],
       [ 0.5186288 ,  0.08872557, -0.00450993,  0.11879426,  0.05240917],
       [-0.07220465, -0.2624936 ,  0.29591918,  0.530888  ,  0.21316099],
       [-0.35911384, -0.39650685, -0.11742538, -0.6202339 , -0.04354006],
       [-0.25780618,  0.31638277,  0.02769768,  0.17346424,  0.08121651]],
      dtype=float32)>
<tf.Variable 'recurrent_kernel:0' shape=(5, 5) dtype=float32, numpy=
array([[ 0.24548101, -0.3611387 , -0.29083446,  0.783044  , -0.33402914],
       [-0.29797602, -0.35216388, -0.81063664, -0.3598355 ,  0.02402965],
       [-0.33578852, -0.7312673 ,  0.4097485 ,  0.09858549,  0.41818818],
       [ 0.75288004, -0.10158028, -0.17691544, -0.08407468,  0.62006897],
       [-0.41396528,  0.44776008, -0.24308549,  0.4904822 ,  0.573132  ]],
      dtype=float32)>
<tf.Variable 'bias:0' shape=(5,) dtype=float32, numpy=array([0., 0., 0., 0., 0.], dtype=float32)>

如运行结果所示，有三个需要进行训练的变量：

'kernel:0'： $\bold{W}_{xh}$
'recurrent_kernel:0'： $\bold{W}_{hh}$
'bias:0'： $\bold{b}$

我们还可以试图进行一次前向运算

示例代码：

# 4个句子，且根据之前的设定，输出的维度是5维
# 4个句子并行进行前向计算
h0 = [tf.zeros([4, 5])]
# 4个句子，每个句子7个字，每个字的表示向量维度是10维
x = tf.random.normal([4, 7, 10])
# 取每个句子的第一个字
xt = x[:,0,:]
# 前向计算
out, h1 = cell(xt, h0)
print(out.shape, h1[0].shape)
print(id(out),id(h1[0]))

运行结果：

1 2	(4, 5) (4, 5) 140582470026160 140582470026160

我们发现两者的id还是一致，即状态向量直接作为了输出向量。

RNNCell的串联

只有一个RNNCell是不够的，我们还需要把他们串联起来。我们以两个RNNCell的串联为例。

示例代码：

import tensorflow as tf
from tensorflow.keras import layers

# 4个句子，每个句子7个字，每个字的表示向量维度是10维
x = tf.random.normal([4, 7, 10])

# cell1
cell1 = layers.SimpleRNNCell(5)
x0 = x[:,0,:]
h0 = [tf.zeros([4,5])]
out1, h1 = cell1(x0, h0)
print(out1)
print('\n')
print(h1)
print('\n')

# cell2
cell2 = layers.SimpleRNNCell(5)
x1 = x[:,1,:]
out2, h2 = cell1(x1, h1)
print(out2)
print('\n')
print(h2)

运行结果：

tf.Tensor(
[[ 0.506582    0.9822412  -0.6232924  -0.6819859   0.8855748 ]
 [-0.9204044   0.17930911 -0.03693175 -0.7058679   0.12057892]
 [ 0.28195506  0.9317265  -0.3874463   0.44433016  0.98963153]
 [ 0.8865424   0.83297026  0.6258346  -0.3060928  -0.758227  ]], shape=(4, 5), dtype=float32)


[<tf.Tensor: shape=(4, 5), dtype=float32, numpy=
array([[ 0.506582  ,  0.9822412 , -0.6232924 , -0.6819859 ,  0.8855748 ],
       [-0.9204044 ,  0.17930911, -0.03693175, -0.7058679 ,  0.12057892],
       [ 0.28195506,  0.9317265 , -0.3874463 ,  0.44433016,  0.98963153],
       [ 0.8865424 ,  0.83297026,  0.6258346 , -0.3060928 , -0.758227  ]],
      dtype=float32)>]


tf.Tensor(
[[-0.73549193  0.05291848  0.9711196   0.6167512   0.09884901]
 [ 0.83678526 -0.70965004 -0.84355277  0.5708952   0.18770611]
 [-0.76097465  0.11823282  0.01845365  0.73124224 -0.62737477]
 [-0.35610834 -0.8759841   0.14827573  0.26711637  0.89218175]], shape=(4, 5), dtype=float32)


[<tf.Tensor: shape=(4, 5), dtype=float32, numpy=
array([[-0.73549193,  0.05291848,  0.9711196 ,  0.6167512 ,  0.09884901],
       [ 0.83678526, -0.70965004, -0.84355277,  0.5708952 ,  0.18770611],
       [-0.76097465,  0.11823282,  0.01845365,  0.73124224, -0.62737477],
       [-0.35610834, -0.8759841 ,  0.14827573,  0.26711637,  0.89218175]],
      dtype=float32)>]

如此，我们便完成了RNNCell的串联。

在这里我们并没有做到权值共享，权值共享的方法我们会在接下来的内容中讨论。

RNN层的实现

除了通过串联多个RNNCell实现一个RNN层，我们还有更简洁的方法。

1	layers.SimpleRNN()

示例代码：

import tensorflow as tf
from tensorflow.keras import layers

# 状态向量是5维
layer = layers.SimpleRNN(5)
# 4句话，每句话7个字，每个字的表示向量是10维的
x = tf.random.normal([4, 7, 10])
out = layer(x)
print(out)
print('\n')

for var in layer.trainable_variables:
    print(var)

运行结果：

tf.Tensor(
[[ 0.08204459  0.04317476  0.30593142 -0.76046866  0.15787737]
 [-0.98848146  0.6531717  -0.58533347  0.8788158   0.54704   ]
 [ 0.93262446  0.96815926 -0.8240068   0.6790444   0.8851987 ]
 [ 0.46612775  0.9839063  -0.9326357   0.27518022  0.6429617 ]], shape=(4, 5), dtype=float32)


<tf.Variable 'simple_rnn/simple_rnn_cell/kernel:0' shape=(10, 5) dtype=float32, numpy=
array([[ 0.01278448, -0.07142729, -0.1156975 ,  0.62295896,  0.23864311],
       [-0.19498649, -0.08086956,  0.12783319, -0.05486643,  0.3196404 ],
       [-0.39465576,  0.06167322,  0.06187344,  0.06264728, -0.27841362],
       [-0.49463528,  0.16559124,  0.47284657,  0.04080987,  0.07728499],
       [-0.26065487,  0.5419939 , -0.493649  ,  0.5863394 ,  0.23518825],
       [-0.27638745,  0.3727594 , -0.5084812 ,  0.6022205 ,  0.42163724],
       [ 0.4565335 ,  0.20948565, -0.43491662,  0.56013614,  0.38524455],
       [ 0.6087578 ,  0.611378  , -0.5785291 , -0.09343225,  0.07728881],
       [-0.1473059 , -0.38367093, -0.00576425, -0.16634032, -0.349772  ],
       [ 0.18387246, -0.36261082,  0.38738722, -0.56461763, -0.1931817 ]],
      dtype=float32)>
<tf.Variable 'simple_rnn/simple_rnn_cell/recurrent_kernel:0' shape=(5, 5) dtype=float32, numpy=
array([[-0.25234544, -0.3871871 ,  0.30532643, -0.7751111 , -0.30395156],
       [ 0.54901195, -0.7856816 ,  0.12644674,  0.20233177,  0.15608758],
       [ 0.6325666 ,  0.47423178,  0.49091238, -0.31948704,  0.17859659],
       [-0.46171454, -0.04940245,  0.75003725,  0.3445074 ,  0.32115087],
       [-0.1469246 , -0.07385194, -0.29535756, -0.37082   ,  0.8649945 ]],
      dtype=float32)>
<tf.Variable 'simple_rnn/simple_rnn_cell/bias:0' shape=(5,) dtype=float32, numpy=array([0., 0., 0., 0., 0.], dtype=float32)>

在上面的代码中，我们还专门看了一下layer的trainable_variables，和RNNCell的trainable_variables是一样的，即做了权值共享。

如果需要每一个RNNCell都输出，可以通过设置return_sequences=True来实现。
示例代码：

# 状态向量是5维
layer = layers.SimpleRNN(5,return_sequences=True)
# 4句话，每句话7个字，每个字的表示向量是10维的
x = tf.random.normal([4, 7, 10])
out = layer(x)
print(out.shape)

运行结果：

(4, 7, 5)

在卷积神经网络中，我们可以堆叠多个卷积层，在循环神经网络中，我们同样可以堆叠多个RNN层。
示例代码：

import tensorflow as tf
from tensorflow.keras import layers,Sequential

net = Sequential([ # 构建 2 层 RNN 网络
# 除最末层外，都需要返回所有时间戳的输出，用作下一层的输入
layers.SimpleRNN(5, return_sequences=True),
layers.SimpleRNN(5),
])
# 4句话，每句话7个字，每个字的表示向量是10维的
x = tf.random.normal([4, 7, 10])
out = net(x)
print(out)

运行结果：

tf.Tensor(
[[ 0.04848028 -0.2728534   0.39700478 -0.2060745   0.19178297]
 [-0.6412452   0.10903205 -0.30632198 -0.5441217  -0.07050032]
 [-0.9426221  -0.7780494   0.6787768   0.17882977  0.05926314]
 [-0.7274192  -0.413902    0.8925262  -0.33624098  0.3179967 ]], shape=(4, 5), dtype=float32)

基于RNNCell的循环神经网络的实现

完整可运行代码见：
https://github.com/KakaWanYifan/deep-learning-for-blog/blob/master/Ch08/Ch08-1.py

刚刚我们已经实现了RNN层，而且还实现了多个RNN层的堆叠。现在我们实现一个完整的循环神经网络。
我们以IMDB电影评论的积极消极分类为例，网络结构如下：

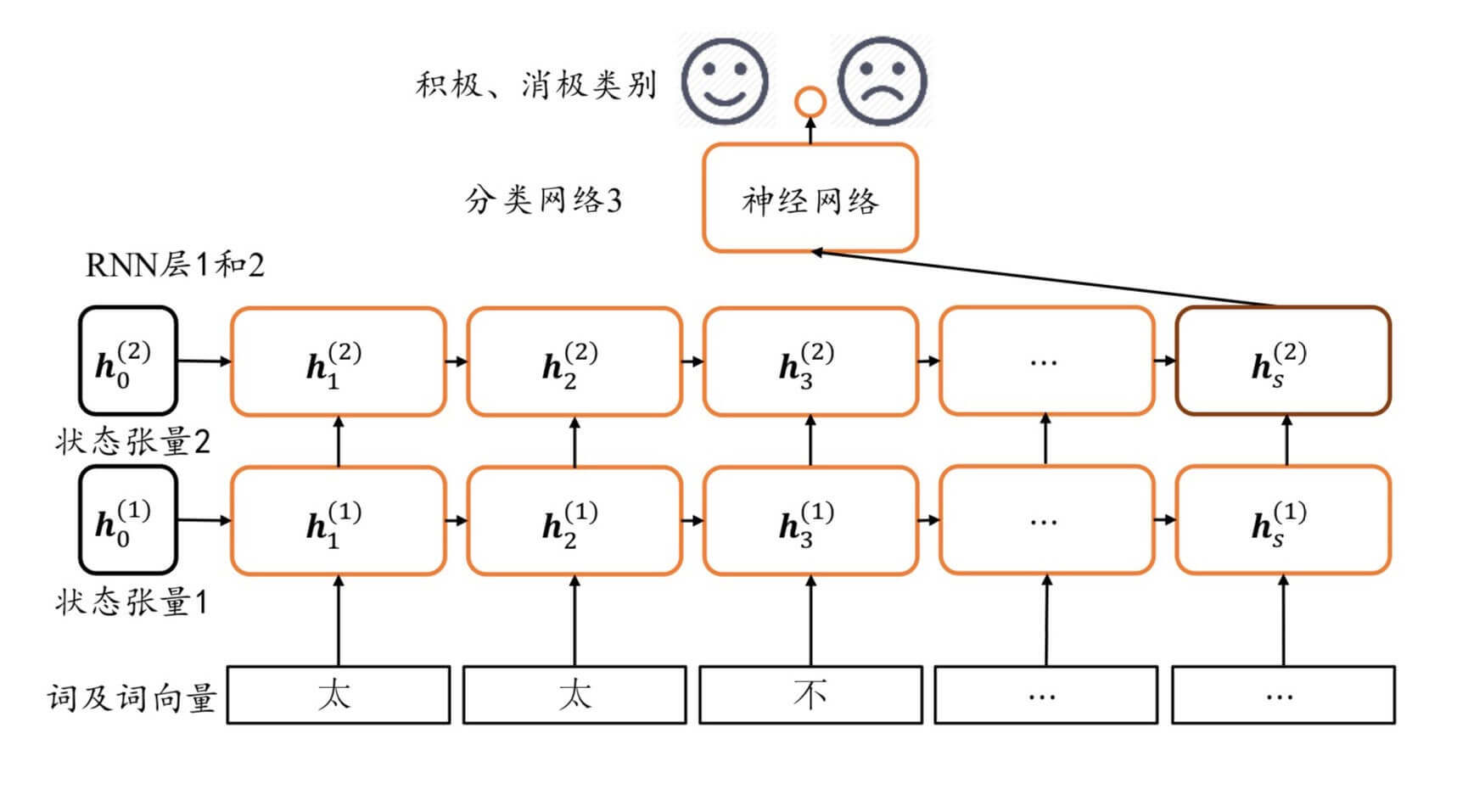
构建网络

我们根据上图来构建神经网络。
首先，创建一个RNN类，继承自Model，并且重写两个方法，初始化和前向计算。
示例代码：

class RNN(keras.Model):
    def __init__(self, units):
        super(RNN, self).__init__()
    def call(self, inputs, training=None):

接下来我们分别讨论这两个方法。

初始化

1、两个初始状态
我们需要两个初始状态，通常初始化为全为0的张量。
示例代码：

1 2	self.state0 = [tf.zeros([batchsz, units])] self.state1 = [tf.zeros([batchsz, units])]

2、Word Embedding
然后需要把词向量进行编码。
示例代码：

1	self.embedding = layers.Embedding(input_dim=total_words, output_dim=embedding_len, input_length=max_review_len)

total_words：词汇表大小
embedding_len：每个词的表示向量的维度数
max_review_len：每个句子的最大长度

3、RNNCell
现在让我们来分析一下，我们需要多少个RNNCell。
假设每条电影评论最大长度是100的话，每一层我们都需要100个RNNCell，现在我们一共有2层，那么我们需要2*100，一共200个RNNCell。
那来吧：

self.rnn_cell0 = keras.layers.SimpleRNNCell(units, dropout=0.5)
self.rnn_cell1 = keras.layers.SimpleRNNCell(units, dropout=0.5)
self.rnn_cell2 = keras.layers.SimpleRNNCell(units, dropout=0.5)
self.rnn_cell3 = keras.layers.SimpleRNNCell(units, dropout=0.5)
······

其实大可不必这么做。我们知道RNN是有权值共享的，要这么搞，这么多神经元，还要做权值共享，多麻烦？

既然权值共享呢，每一层的RNNCell都是一样的。我们不如这样？
示例代码：

1
2
3

# 构建 2 个 Cell，使用 dropout 技术防止过拟合 
self.rnn_cell0 = layers.SimpleRNNCell(units, dropout=0.5) 
self.rnn_cell1 = layers.SimpleRNNCell(units, dropout=0.5)

在做前向计算的时候，每一个RNNCell重复使用100次，两个RNNCell搞定。示例代码：

1
2
3

for word in tf.unstack(x, axis=1):
    out0, state0 = self.rnn_cell0(word, state0, training)  
    out1, state1 = self.rnn_cell1(out0, state1, training)

这也是循环神经网络的循环所在。

循环接受序列的每个特征向量 $\bold{x}_t$ ，并刷新内部状态向量 $\bold{h}_t$ ，同时形成输出 $\bold{o}_t$ 。

4、全连接层
最后，我们需要一个全连接层输出分类。
示例代码：

1	self.out = layers.Dense(1)

5、整个初始化方法
示例代码：

def __init__(self, units):
    super(RNN, self).__init__()

    # [b, 64]
    self.state0 = [tf.zeros([batch_size, units])]
    self.state1 = [tf.zeros([batch_size, units])]

    # transform text to embedding representation
    # [b, 100] => [b, 100, 150]
    self.embedding = layers.Embedding(input_dim=total_words, output_dim=embedding_len, input_length=max_review_len)
    
    # SimpleRNNCell
    # units=64
    self.rnn_cell0 = layers.SimpleRNNCell(units, dropout=0.5)
    self.rnn_cell1 = layers.SimpleRNNCell(units, dropout=0.5)
    
    # 全连接层
    # [b, 100, 150] => [b, 64] => [b, 1]
    self.out = layers.Dense(1)

前向计算

我想前向计算的代码应该是很简单的。不需要和初始化一样，掰开来讨论。
唯一的难点是两个RNNCell，却对包含100个词的句子做了前向计算，这个我们在之前已经讨论过了。

循环接受序列的每个特征向量 $\bold{x}_t$ ，并刷新内部状态向量 $\bold{h}_t$ ，同时形成输出 $\bold{o}_t$ 。

示例代码：

def call(self, inputs, training=None): 
    x = inputs # [b, 80] 
    # 获取词向量: [b, 80] => [b, 80, 100] 
    x = self.embedding(x) 
    # 通过 2 个 RNN CELL,[b, 80, 100] => [b, 64] 
    state0 = self.state0 
    state1 = self.state1 
    for word in tf.unstack(x, axis=1): # word: [b, 100]  
        out0, state0 = self.rnn_cell0(word, state0, training)  
        out1, state1 = self.rnn_cell1(out0, state1, training) 
    # 末层最后一个输出作为分类网络的输入: [b, 64] => [b, 1] 
    x = self.out(out1, training) 
    # 通过激活函数，p(y is pos|x) 
    prob = tf.sigmoid(x) 
 
    return prob

加载数据集

1、加载数据
数据集可以从keras加载。
示例代码：

from tensorflow import keras

# 加载 IMDB 数据集，此处的数据采用数字编码，一个数字代表一个单词
(x_train, y_train), (x_test, y_test) = keras.datasets.imdb.load_data()
# 打印输入的形状，标签的形状
print(x_train.shape, y_train.shape)
print(x_test.shape, y_test.shape)

运行结果：

1 2	(25000,) (25000,) (25000,) (25000,)

如运行结果所示，25000条影评用于训练，25000条用于测试。

2、查看其中一条影评的内容
我们还可以打印其中一条影评看看内容。
示例代码：

1	print(x_train[0])

运行结果：

1
2
3

[1, 14, 22, 16, 43, 530, 973, 1622, 1385, 65, 458, 4468, 66, 3941, 4, 173, 36, 256, 5, 25, 100, 43, 838, 112, 50, 670, 22665, 9, 35, 480, 284, 5, 150, 4, 172, 112, 167, 

【部分运行结果略】

如运行结果所示，这里的每个单词都是一个数字，那么这些数字都有什么含义呢？

3、word_index
每一个数字都是一个单词所对应的index，我们可以打印word_index看看内容
示例代码：

word_index = keras.datasets.imdb.get_word_index()

for k,v in word_index.items():
    print(k,v)

运行结果：


【部分运行结果略】

loren 8059
pyle's 52274
shootout 6704
mike's 18517
driscoll's 52275
cogsworth 40935
britian's 52276
childs 34744

【部分运行结果略】

4、还原第一条影评
现在我们来把第一条影评还原。
示例代码：

# 翻转编码表
reverse_word_index = dict([(value, key) for (key, value) in word_index.items()])

print(' '.join([reverse_word_index.get(i, '?') for i in x_train[0]]))

运行结果：

1
2
3

the as you with out themselves powerful lets loves their becomes reaching had journalist of lot from anyone to have after out atmosphere never more room titillate it so heart 

【部分运行结果略】

还原是还原了，但是好像不太对啊？这都不通顺啊？这是因为有四个约定的特殊位，我们把特殊位补充上，再来一次。

示例代码：

# 前面 4 个 ID 是特殊位
word_index = {k:(v+3) for k,v in word_index.items()}
word_index["<PAD>"] = 0  # 填充标志
word_index["<START>"] = 1 # 起始标志
word_index["<UNK>"] = 2  # 未知单词的标志
word_index["<UNUSED>"] = 3

# 翻转编码表
reverse_word_index = dict([(value, key) for (key, value) in word_index.items()])

print(' '.join([reverse_word_index.get(i, '?') for i in x_train[0]]))

运行结果：

1
2
3

<START> this film was just brilliant casting location scenery story direction everyone's really suited the part they played and you could just imagine being there robert 

【部分运行结果略】

这样我们就把句子还原了。

5、统一每句话的长度
我们再来看个东西。
示例代码：

print(len(x_train[0]))
print(len(x_train[1]))
print(len(x_train[2]))
print(len(x_test[0]))
print(len(x_test[1]))
print(len(x_test[2]))

运行结果：

每句话的长度还不一样。这个当然是意料之中的事情，影评嘛，怎么可能每条影评的字数都一模一样多呢？

但，根据之前我们画的循环神经网络的图，我们知道RNN层中的RNNCell的数量可是固定的，不是动态的。如果RNNCell的数量不能动，那么就只能动影评句子了。
对于长度参差不齐的句子，人为设置一个阈值，对大于此长度的句子，选择截断部分单词，可以选择截去句首单词，也可以截去句末单词；对于小于此长度的句子，可以选择在句首或句尾填充。

0号特殊位就是"<PAD>"填充。

在TensorFlow中，我们有很好的方法进行填充。

1	keras.preprocessing.sequence.pad_sequences()

示例代码：

# 截断和填充句子，使得等长，此处长句子保留句子后面的部分，短句子在前面填充
x_train = keras.preprocessing.sequence.pad_sequences(x_train,maxlen=100)
x_test = keras.preprocessing.sequence.pad_sequences(x_test,maxlen=100)

print(x_train.shape)
print(x_test.shape)

运行结果：

1 2	(25000, 100) (25000, 100)

6、Dataset数据集
截断或填充为相同长度后，通过Dataset类包裹成数据集对象，并添加常用的数据集处理流程。
示例代码：

db_train = tf.data.Dataset.from_tensor_slices((x_train, y_train))
db_train = db_train.shuffle(1000).batch(batch_size=128, drop_remainder=True)

db_test = tf.data.Dataset.from_tensor_slices((x_test, y_test))
db_test = db_test.batch(batch_size=128, drop_remainder=True)

# 统计数据集属性
print('x_train shape:', x_train.shape, tf.reduce_max(y_train),tf.reduce_min(y_train))
print('x_test shape:', x_test.shape)

运行结果：

1 2	x_train shape: (25000, 100) tf.Tensor(1, shape=(), dtype=int64) tf.Tensor(0, shape=(), dtype=int64) x_test shape: (25000, 100)

训练和测试

示例代码：

model = RNN(units)
model.compile(optimizer=keras.optimizers.Adam(0.001), 
              loss=tf.losses.BinaryCrossentropy(), 
              metrics=['accuracy'],
              experimental_run_tf_function=False)
model.fit(db_train, epochs=epochs, validation_data=db_test)

for var in model.trainable_variables:
    print(var.name, var.shape)

model.evaluate(db_test)

运行结果：

Epoch 1/4
195/195 [==============================] - 10s 50ms/step - loss: 0.6045 - accuracy: 0.6415 - val_loss: 0.4212 - val_accuracy: 0.8148
Epoch 2/4
195/195 [==============================] - 8s 40ms/step - loss: 0.3799 - accuracy: 0.8387 - val_loss: 0.4689 - val_accuracy: 0.8089
Epoch 3/4
195/195 [==============================] - 8s 42ms/step - loss: 0.3144 - accuracy: 0.8735 - val_loss: 0.3945 - val_accuracy: 0.8365
Epoch 4/4
195/195 [==============================] - 8s 40ms/step - loss: 0.2247 - accuracy: 0.9145 - val_loss: 0.4507 - val_accuracy: 0.8284
rnn/embedding/embeddings:0 (10000, 150)
rnn/simple_rnn_cell/kernel:0 (150, 64)
rnn/simple_rnn_cell/recurrent_kernel:0 (64, 64)
rnn/simple_rnn_cell/bias:0 (64,)
rnn/simple_rnn_cell_1/kernel:0 (64, 64)
rnn/simple_rnn_cell_1/recurrent_kernel:0 (64, 64)
rnn/simple_rnn_cell_1/bias:0 (64,)
rnn/dense/kernel:0 (64, 1)
rnn/dense/bias:0 (1,)
evaluate:
195/195 [==============================] - 2s 11ms/step - loss: 0.4507 - accuracy: 0.8284

我们还把模型的训练参数打印出来了：

embedding层：rnn/embedding/embeddings
第一层RNNCell：
1. rnn/simple_rnn_cell/kernel
2. rnn/simple_rnn_cell/recurrent_kernel
3. rnn/simple_rnn_cell/bias
第二层RNNCell：
1. rnn/simple_rnn_cell_1/kernel
2. rnn/simple_rnn_cell_1/recurrent_kernel
3. rnn/simple_rnn_cell_1/bias
最后全连接层：
1. rnn/dense/kernel
2. rnn/dense/bias

基于RNN层的循环神经网络的实现

完整可运行代码见：
https://github.com/KakaWanYifan/deep-learning-for-blog/blob/master/Ch08/Ch08-2.py

在之前讨论RNN层的时候，我们讨论了基于SimpleRNNCell的RNN层的实现，也讨论了直接基于SimpleRNN的RNN层的实现。现在我们试图基于SimpleRNN来实现一个循环神经网络。
我们只需要修改RNN这个类的初始化方法和前向计算方法就可以了。

初始化方法

示例代码：

def __init__(self, units):
    super(RNN, self).__init__()

    # transform text to embedding representation
    # [b, 100] => [b, 100, 150]
    self.embedding = layers.Embedding(total_words, embedding_len, input_length=max_review_len)

    # [b, 100, 150]
    self.rnnlayer = keras.Sequential([
        layers.SimpleRNN(units, dropout=0.5, return_sequences=True, unroll=True),
        layers.SimpleRNN(units, dropout=0.5, unroll=True)
    ])

    # fc, [b, 100, 150] => [b, 64] => [b, 1]
    self.outlayer = layers.Dense(1)

前向计算方法

示例代码：

def call(self, inputs, training=None):
    """
    net(x) net(x, training=True) :train mode
    net(x, training=False): test
    :param inputs: [b, 80]
    :param training:
    :return:
    """
    # [b, 100]
    x = inputs
    # embedding: [b, 100] => [b, 100, 150]
    x = self.embedding(x)
    # rnn cell compute
    # x: [b, 100, 150] => [b, 64]
    x = self.rnnlayer(x, training=training)

    # out: [b, 64] => [b, 1]
    x = self.outlayer(x)
    # p(y is pos|x)
    prob = tf.sigmoid(x)

    return prob

其他方法略

循环神经网络的缺点

循环神经网络虽然被设计成可以处理整个时间序列信息，但是作用最大的还是最后输入的一些信号。而更早之前的信号的强度则越来越低，最后只能起到一点辅助的作用。

对于某些简单的问题，可能只需要最后输入少量时序信息即可解决。但对某些复杂问题，可能需要更早的一些信息，甚至是时间序列开头的信息。长程依赖(Long-term Dependencies)是传统循环神经网络的的硬伤。

下一章，我们讨论循环神经网络的衍生：LSTM和GRU。

文章作者: Kaka Wan Yifan

文章链接: https://kakawanyifan.com/10408

留言板