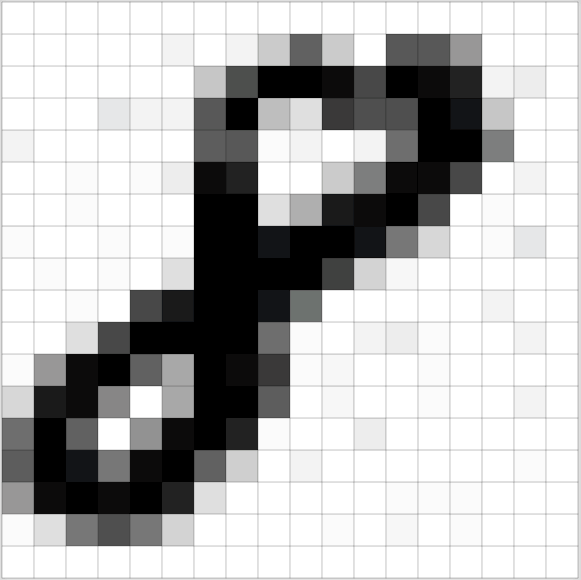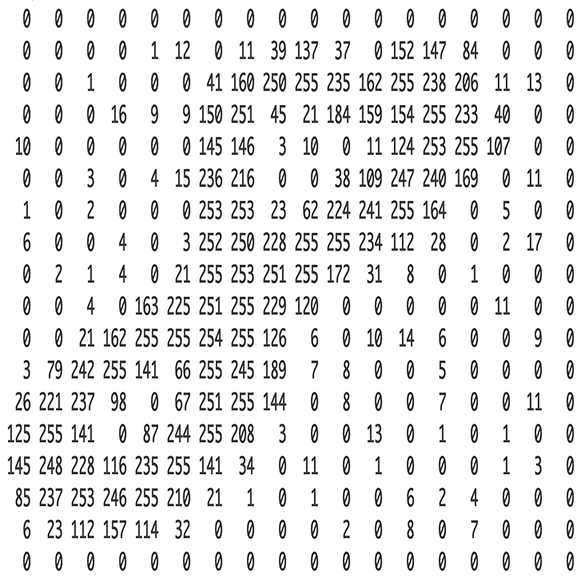回归和分类是监督学习中,最常见的两类问题。
我们依次讨论回归和分类这两个问题,并试图借此引出一个深度学习的简单雏形。
回归
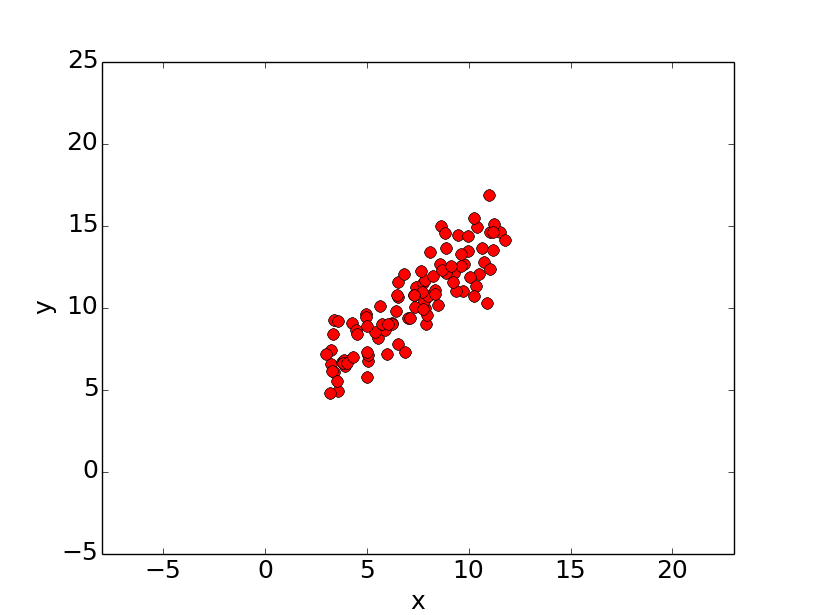
在回归问题中,线性回归是一种最常见的一种。
损失函数
首先,我们讨论一下,为什么需要损失函数?什么是损失函数?
我们假设存在一个线性方程如下:
y = w x + b y = wx +b
y = w x + b
现在,存在两个点:(1,2),(2,3)。w和b。
但,这是在非常理想的情况下。w和b。
这时候,想通过消元法来求线性方程的w和b,是不可能的。
那么,我们换一个思路。我们不求精确解,我们求近似解。我们构造一个模型去拟合。损失函数 。
l o s s = ∑ i n ( w ∗ x i + b − y i ) 2 n loss = \frac{\sum_i^n{(w * x_i + b - y_i)}^2}{n}
l o s s = n ∑ i n ( w ∗ x i + b − y i ) 2
这里,我们把均方误差作为损失函数。
梯度下降
但是,我们还有一个问题没解决,w和b的近似解,还是不知道。梯度下降 。
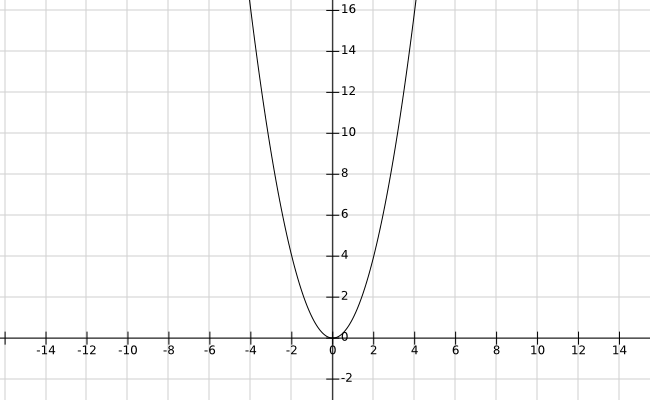
例如f ( x ) = x 2 f(x) = x^2 f ( x ) = x 2
我们随机选取一点,比如选取了(4,16)。
求该点处的导数,导数为8。
所以我们往后退8个单位,选取新的点。
如果,我们的单位是1,则新的点是(-4,16)。
如果,我们的单位是0.1,则新的点是(3.2,9.4)。
所以每次后退几个单位,这个要调到一个合适的值。
如此循环往复,直到取到了极小值,或达到了一定的迭代次数。
这就是梯度下降的方法,而在这里的单位就是学习率。
梯度下降的过程,用数学公式表达如下:
w ′ = w − l r ∗ ∂ l o s s ∂ w w' = w - lr * \frac{\partial loss}{\partial w}
w ′ = w − l r ∗ ∂ w ∂ l o s s
b ′ = b − l r ∗ ∂ l o s s ∂ b b' = b - lr * \frac{\partial loss}{\partial b}
b ′ = b − l r ∗ ∂ b ∂ l o s s
线性回归的实现
通过刚刚的讨论,我们知道了需要损失函数、知道了用梯度下降求解w和b的。现在我们试图通过Python代码实现。
计算损失
梯度下降
用梯度下降得到的新的w和b,再计算损失。如此迭代更新。
计算损失
l o s s = ∑ i n ( w ∗ x i + b − y i ) 2 n loss = \frac{\sum_i^n{(w * x_i + b - y_i)}^2}{n}
l o s s = n ∑ i n ( w ∗ x i + b − y i ) 2
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 def loss (b,w,xArr,yArr) : ''' 损失函数 :param b: 偏置 :param w: 权重 :param xArr: xArr :param yArr: yArr :return: 损失函数的值 ''' total_loss = 0 for i in range(0 ,len(xArr)): x = xArr[i] y = yArr[i] total_loss = total_loss + (y - (w * x + b)) ** 2 return total_loss/(float(len(xArr)))
梯度下降
w ′ = w − l r ∗ ∂ l o s s ∂ w w' = w - lr * \frac{\partial loss}{\partial w}
w ′ = w − l r ∗ ∂ w ∂ l o s s
b ′ = b − l r ∗ ∂ l o s s ∂ b b' = b - lr * \frac{\partial loss}{\partial b}
b ′ = b − l r ∗ ∂ b ∂ l o s s
其中
∂ l o s s ∂ w = ∑ i n 2 ( w x i + b − y i ) x i n \frac{\partial loss}{\partial w} = \frac{\sum_i^n 2(w x_i + b - y_i) x_i}{n}
∂ w ∂ l o s s = n ∑ i n 2 ( w x i + b − y i ) x i
∂ l o s s ∂ b = ∑ i n 2 ( w x i + b − y i ) n \frac{\partial loss}{\partial b} = \frac{\sum_i^n 2(w x_i +b - y_i)}{n}
∂ b ∂ l o s s = n ∑ i n 2 ( w x i + b − y i )
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 def step_gradient (b_cur,w_cur,xArr,yArr,lr) : ''' 一步,梯度 :param b_cur: 当前的偏置 :param w_cur: 当前的权重 :param xArr: xArr :param yArr: yArr :param lr: 学习率 :return: ''' b_gradient = 0 w_gradient = 0 n = float(len(xArr)) for i in range(0 ,len(xArr)): x = xArr[i] y = yArr[i] w_gradient = w_gradient + (2 /n) * ((w_cur * x + b_cur) - y) * x b_gradient = b_gradient + (2 /n) * ((w_cur * x + b_cur) - y) b_new = b_cur - (lr * b_gradient) w_new = w_cur - (lr * w_gradient) return b_new,w_new
迭代更新
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 import numpy as npdef gradient_descent (b_start,w_start,xArr,yArr,lr,iterations) : ''' 迭代更新 :param points: 数据点 :param b_start: 偏置的初始值 :param w_start: 权重的初始值 :param lr: 学习率 :param iterations: 最大迭代次数 :return: ''' b = b_start w = w_start for i in range(iterations): b,w = step_gradient(b_cur=b,w_cur=w,xArr=xArr,yArr=yArr,lr=lr) return b,w
Main方法
我们还需要一个Main方法把这些方法组装在一起。
1 2 3 4 xData = np.linspace(-10 ,10 ,100 ) yData = 2.0 * xData + 1.0 + np.random.randn(xData.shape[0 ]) * 0.2
我们对训练前的损失和训练后的损失进行比较。
1 2 3 4 5 6 7 8 9 10 11 b = 0 w = 0 print('初值的损失:' ,loss(b=b,w=w,xArr=xArr,yArr=yArr)) b,w = gradient_descent(b_start=b,w_start=w,xArr=xArr,yArr=yArr,lr=0.001 ,iterations=100000 ) print('b:' ,b,' w:' ,w) print('训练后的损失:' ,loss(b=b,w=w,xArr=xArr,yArr=yArr))
运行结果:
1 2 3 初值的损失: 136.91315134241083 b: 1.0170737051230807 w: 1.9987051102211508 训练后的损失: 0.027859262495676634
分类问题
在讨论回归问题之后,我们再讨论分类问题。
我们来个有点挑战,也更有意思的:手写数字识别。
手写数字识别分析
我们首先分析一下整个应用场景。
输入
[28,28,1],代表这是一张28*28个像素的单通道黑白图片。我们把这张图片转换形状为[784]的向量,即把每一行拼接在上一行的后面。而且,我们会有很多张样本图片,所以我们的输入数据为[N,784],其中N代表输入的样本图片数量。
输出
我们用One-Hot编码作为输出,关于One-Hot编码,在《经典机器学习及其Python实现:1.特征抽取》 中有讨论。
例如,数字零的One-Hot编码是[1,0,0···0]。当然,我们得到的输出大概不会那么恰到好处的非0即1,更有可能是[0.8,0.02,0.05,···0.01]这种。
线性模型
在上一章中,我们的模型是
y = w x + b y = wx +b
y = w x + b
现在,我们换成矩阵模式,则有:
o u t = X ∗ W + b \bold{out} = \bold{X} * \bold{W} + \bold{b}
o u t = X ∗ W + b
X : [ N , 784 ] \bold{X}: [N,784] X : [ N , 7 8 4 ] W : [ 784 , 10 ] \bold{W}: [784,10] W : [ 7 8 4 , 1 0 ] b : [ 10 ] \bold{b}: [10] b : [ 1 0 ]
例如,当N = 1 N=1 N = 1
[ 1 , 784 ] ∗ [ 784 , 10 ] + [ 10 ] [1,784] * [784,10] + [10]
[ 1 , 7 8 4 ] ∗ [ 7 8 4 , 1 0 ] + [ 1 0 ]
最后我们得到的结果为[ 1 , 10 ] [1,10] [ 1 , 1 0 ]
但是,这么做,是有问题的。激活函数 。
激活函数
我们对之前的线性模型进行修改。
o u t = f ( X ∗ W + b ) \bold{out} = f(\bold{X}*\bold{W} + \bold{b})
o u t = f ( X ∗ W + b )
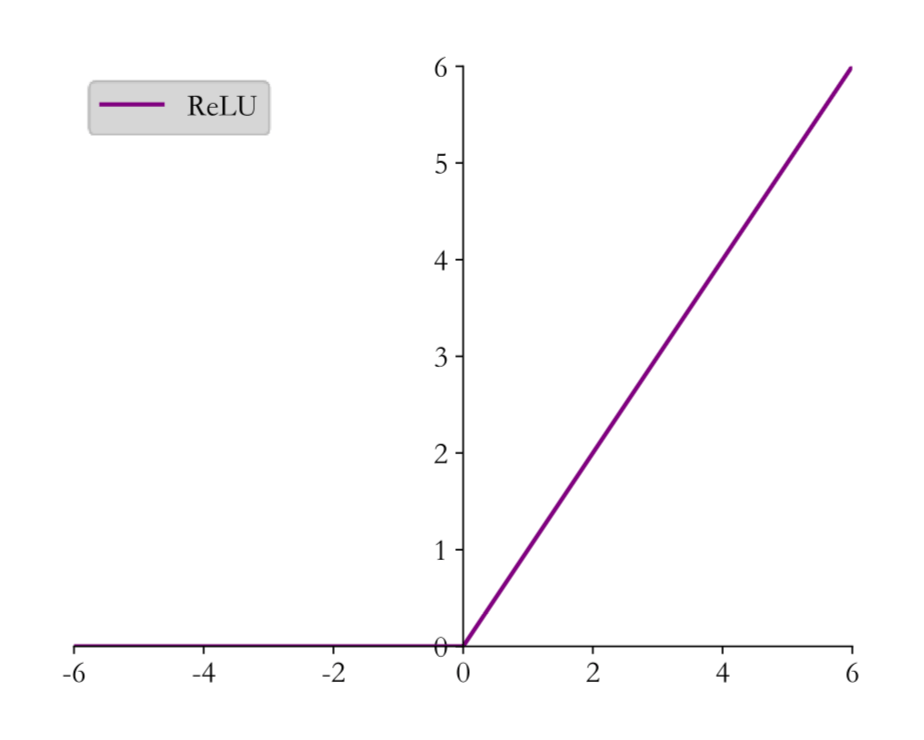
激活函数有很多种,最简单的最常见的一种是ReLU。
f ( x ) = { x for x ≥ 0 0 for x < 0 f(x) = \begin{cases}
x & \text{for } x \ge 0 \\
0 & \text{for } x < 0
\end{cases}
f ( x ) = { x 0 for x ≥ 0 for x < 0
我们可以看到,ReLU函数是一个非线性函数,这个函数的引入使得我们的模型不再是线性模型。
但是这个模型的效果其实仍不好,因为只有一层,无法学习到复杂的函数映射。
多个模型串行
h 1 = r e l u ( x ∗ w 1 + b 1 ) \bold{h_1} = relu(\bold{x} * \bold{w_1} + \bold{b_1})
h 1 = r e l u ( x ∗ w 1 + b 1 )
h 2 = r e l u ( h 1 ∗ w 2 + b 2 ) \bold{h_2} = relu(\bold{h_1} * \bold{w_2} + \bold{b_2})
h 2 = r e l u ( h 1 ∗ w 2 + b 2 )
o u t = r e l u ( h 2 ∗ w 3 + b 3 ) \bold{out} = relu(\bold{h_2} * \bold{w_3} + \bold{b_3})
o u t = r e l u ( h 2 ∗ w 3 + b 3 )
我们继续以一张图片为例。
x : [ 1 , 784 ] \bold{x}:[1,784] x : [ 1 , 7 8 4 ]
假设第一层的参数为:
w 1 : [ 784 , 512 ] \bold{w_1}:[784,512] w 1 : [ 7 8 4 , 5 1 2 ] b 1 : [ 1 , 512 ] \bold{b_1}:[1, 512] b 1 : [ 1 , 5 1 2 ]
则,经过第一道工序后:
h 1 : [ 1 , 512 ] \bold{h_1}:[1,512] h 1 : [ 1 , 5 1 2 ]
假设第二层的参数为:
w 2 : [ 512 , 256 ] \bold{w_2}:[512,256] w 2 : [ 5 1 2 , 2 5 6 ] b 2 : [ 1 , 256 ] \bold{b_2}:[1,256] b 2 : [ 1 , 2 5 6 ]
则,经过第二道工序后:
h 2 : [ 1 , 256 ] \bold{h_2}:[1,256] h 2 : [ 1 , 2 5 6 ]
假设第三层的参数为:
w 3 : [ 256 , 10 ] \bold{w_3}:[256,10] w 3 : [ 2 5 6 , 1 0 ] b 3 : [ 1 , 10 ] \bold{b_3}:[1,10] b 3 : [ 1 , 1 0 ]
则,经过第三道工序后:
o u t : [ 1 , 10 ] \bold{out}:[1,10] o u t : [ 1 , 1 0 ]
损失函数
现在,我们还剩下最后一项。损失函数。我们采用均方误差。
l o s s = ∑ i n ( w ∗ x i + b − y i ) 2 n loss = \frac{\sum_i^n{(w * x_i + b - y_i)}^2}{n}
l o s s = n ∑ i n ( w ∗ x i + b − y i ) 2
小结
现在,我们做个小结。
初始化w 1 \bold{w_1} w 1 b 1 \bold{b_1} b 1 w 2 \bold{w_2} w 2 b 2 \bold{b_2} b 2 w 3 \bold{w_3} w 3 b 3 \bold{b_3} b 3 h 1 \bold{h_1} h 1 h 2 \bold{h_2} h 2 o u t \bold{out} o u t
计算损失
计算梯度,迭代更新w 1 \bold{w_1} w 1 b 1 \bold{b_1} b 1 w 2 \bold{w_2} w 2 b 2 \bold{b_2} b 2 w 3 \bold{w_3} w 3 b 3 \bold{b_3} b 3
基于keras的实现
准备数据
在TensorFlow中自带MNIST数据,我们直接用TensorFlow中的数据。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 import tensorflow as tffrom tensorflow.keras import datasets(x_train, y_train), (x_test, y_test) = datasets.mnist.load_data() xs = tf.convert_to_tensor(x_train, dtype=tf.float32) / 255.0 db = tf.data.Dataset.from_tensor_slices((x_train, y_train)) for step, (x, y) in enumerate(db): print(step) print(x.shape) print(y) print(y.shape) print('\n' )
运行结果:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 (28, 28) tf.Tensor(5, shape=(), dtype=uint8) () 1 (28, 28) tf.Tensor(0, shape=(), dtype=uint8) () 2 (28, 28) tf.Tensor(4, shape=(), dtype=uint8) () 【部分运行结果略】
from_tensor_slices from_tensor_slices。from_tensor_slices的作用是把给定的元组、列表和张量等数据进行特征切片,从第一个维度进行切片。from_tensor_slices。
正如我们刚刚的代码,把60000张28*28的图片,从最外层,剥开。
再比如,这个例子。
1 2 3 4 5 6 7 8 9 10 11 import tensorflow as tfimport numpy as npfeatures, labels = (np.random.sample((6 , 3 )), np.random.sample((6 , 1 ))) print((features, labels)) data = tf.data.Dataset.from_tensor_slices((features, labels)) for var in enumerate(data): print(var)
运行结果:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 (array([[0.45108748, 0.23347295, 0.38551173], [0.19734783, 0.43067265, 0.25006582], [0.7943179 , 0.25185879, 0.95525868], [0.51064133, 0.02124388, 0.25417909], [0.90138399, 0.94569396, 0.00832238], [0.55127232, 0.15551541, 0.18047405]]), array([[0.10617923], [0.51067773], [0.58266726], [0.24896404], [0.64681774], [0.59264838]])) (0, (<tf.Tensor: shape=(3,), dtype=float64, numpy=array([0.45108748, 0.23347295, 0.38551173])>, <tf.Tensor: shape=(1,), dtype=float64, numpy=array([0.10617923])>)) (1, (<tf.Tensor: shape=(3,), dtype=float64, numpy=array([0.19734783, 0.43067265, 0.25006582])>, <tf.Tensor: shape=(1,), dtype=float64, numpy=array([0.51067773])>)) (2, (<tf.Tensor: shape=(3,), dtype=float64, numpy=array([0.7943179 , 0.25185879, 0.95525868])>, <tf.Tensor: shape=(1,), dtype=float64, numpy=array([0.58266726])>)) (3, (<tf.Tensor: shape=(3,), dtype=float64, numpy=array([0.51064133, 0.02124388, 0.25417909])>, <tf.Tensor: shape=(1,), dtype=float64, numpy=array([0.24896404])>)) (4, (<tf.Tensor: shape=(3,), dtype=float64, numpy=array([0.90138399, 0.94569396, 0.00832238])>, <tf.Tensor: shape=(1,), dtype=float64, numpy=array([0.64681774])>)) (5, (<tf.Tensor: shape=(3,), dtype=float64, numpy=array([0.55127232, 0.15551541, 0.18047405])>, <tf.Tensor: shape=(1,), dtype=float64, numpy=array([0.59264838])>))
准备模型
根据之前的讨论,我们的模型如下:
h 1 = r e l u ( x ∗ w 1 + b 1 ) \bold{h_1} = relu(\bold{x} * \bold{w_1} + \bold{b_1})
h 1 = r e l u ( x ∗ w 1 + b 1 )
h 2 = r e l u ( h 1 ∗ w 2 + b 2 ) \bold{h_2} = relu(\bold{h_1} * \bold{w_2} + \bold{b_2})
h 2 = r e l u ( h 1 ∗ w 2 + b 2 )
o u t = r e l u ( h 2 ∗ w 3 + b 3 ) \bold{out} = relu(\bold{h_2} * \bold{w_3} + \bold{b_3})
o u t = r e l u ( h 2 ∗ w 3 + b 3 )
现在我们实现这个模型。
1 2 3 4 5 6 7 8 9 10 from tensorflow import kerasfrom tensorflow.keras import layers,optimizersmodel = keras.Sequential([ layers.Dense(512 ,activation='relu' ), layers.Dense(256 ,activation='relu' ), layers.Dense(10 , activation='relu' ) ]) optimizer = optimizers.SGD(learning_rate=0.001 )
损失函数
示例代码:
1 2 3 4 5 6 7 8 with tf.GradientTape() as tape: x = tf.reshape(x,(-1 ,28 *28 )) out = model(x) loss = tf.reduce_mean(tf.square(out - y))
迭代更新
示例代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 def train_epoch (epoch) : for step,(x,y) in enumerate(train_dataset): with tf.GradientTape() as tape: x = tf.reshape(x,(-1 ,28 *28 )) out = model(x) loss = tf.reduce_mean(tf.square(out - y)) grads = tape.gradient(loss,model.trainable_variables) optimizer.apply_gradients(zip(grads,model.trainable_variables)) print(epoch,step,loss.numpy())
epoch、batch、step
Main方法
示例代码:
1 2 for epoch in range(10 ): train_epoch(epoch)
运行结果:
1 2 3 4 5 6 7 8 9 0 0 1.11935 0 1 1.1162438 0 2 1.1197898 【部分运行结果略】 9 297 0.18006939 9 298 0.24696392 9 299 0.19443126
基于TensorFlow的实现
在上述基于keras的实现中,有很多技术都被封装了。现在我们试图基于TensorFlow,用比较底层的方法重新实现一遍。
准备数据
准备数据的方法和之前基于keras的类似,这里不再赘述。
准备模型
这里,我们用比较底层的方法来实现一个模型。
w 1 : [ 784 , 512 ] , b 1 : [ 1 , 512 ] \bold{w_1}:[784,512],\bold{b_1}:[1,512] w 1 : [ 7 8 4 , 5 1 2 ] , b 1 : [ 1 , 5 1 2 ] w 2 : [ 512 , 256 ] , b 2 : [ 1 , 256 ] \bold{w_2}:[512,256],\bold{b_2}:[1,256] w 2 : [ 5 1 2 , 2 5 6 ] , b 2 : [ 1 , 2 5 6 ] w 3 : [ 256 , 10 ] , b 3 : [ 1 , 10 ] \bold{w_3}:[256,10],\bold{b_3}:[1,10] w 3 : [ 2 5 6 , 1 0 ] , b 3 : [ 1 , 1 0 ]
而且,这些参数在训练过程都是变量,不是常量。所以要用tf.Variable。
1 2 3 4 5 6 7 8 import tensorflow as tfw1 = tf.Variable(tf.random.truncated_normal([784 , 512 ], stddev=0.1 )) b1 = tf.Variable(tf.zeros([512 ])) w2 = tf.Variable(tf.random.truncated_normal([512 , 256 ], stddev=0.1 )) b2 = tf.Variable(tf.zeros([256 ])) w3 = tf.Variable(tf.random.truncated_normal([256 , 10 ], stddev=0.1 )) b3 = tf.Variable(tf.zeros([10 ]))
计算损失
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 x = tf.reshape(x, [-1 ,28 *28 ]) with tf.GradientTape() as tape: h1 = x@w1 + b1 h1 = tf.nn.relu(h1) h2 = h1@w2 + b2 h2 = tf.nn.relu(h2) out = h2@w3 + b3 out = tf.nn.relu(out) loss = tf.square(y - out) loss = tf.reduce_mean(loss)
为了便于后面的梯度下降,我们这里把这一段代码用tf.GradientTape()包裹起来。
其中@是矩阵相乘。
梯度下降
示例代码:
1 2 3 4 5 6 7 8 9 10 11 grads = tape.gradient(loss, [w1, b1, w2, b2, w3, b3]) w1.assign_sub(lr * grads[0 ]) b1.assign_sub(lr * grads[1 ]) w2.assign_sub(lr * grads[2 ]) b2.assign_sub(lr * grads[3 ]) w3.assign_sub(lr * grads[4 ]) b3.assign_sub(lr * grads[5 ])
必须用assign_sub,原地更新,这样可以维持这些参数更新后还是变量。
迭代更新
与基于keras的实现方式类似,计算损失和梯度下降的方法需要进行迭代更新。这里不再赘述。
Main方法
与基于keras的实现方式类似,这里不再赘述。