之前的所有章节,都有一个特点,我们的动作空间是离散的。
对于这种问题,一种解决方案是连续的动作空间离散化。
在我读高中时期,我就已经把连续的动作空间进行离散化了,并且进行了很好的实践。那时候,对于我来说,骑电动车只有两个动作,急刹车和全速前进。但是呢,如果想让车技更上一层楼,我们不能只有急刹车和全速前进两个动作,我们还需要有二分之一速度、四分之一速度、四分之三速度等等,我们需要离散(抽样)出更多的动作。但是之前的方法,当动作太多的时候,训练会更困难,效果也不好。这时候就不能再强行把连续的动作空间离散化了,要真正的连续控制,这就涉及到我们这一章讨论的内容了。
确定策略梯度方法,Deterministic Policy Gradient,简写作DPG。除了DPG,我们还听过一个名词,DDPG,Deep Deterministic Policy Gradient,深度策略梯度方法。但本质上,只是把策略函数和价值函数用深度学习的神经网络来替代,所以这时候的策略函数,我们称其为策略网络,这时候的价值函数,我们称其为价值网络。
我们直接讨论DDPG,所以接下来的名词都是策略网络,目标网络。而不是策略函数,目标函数。
Actor-Critic
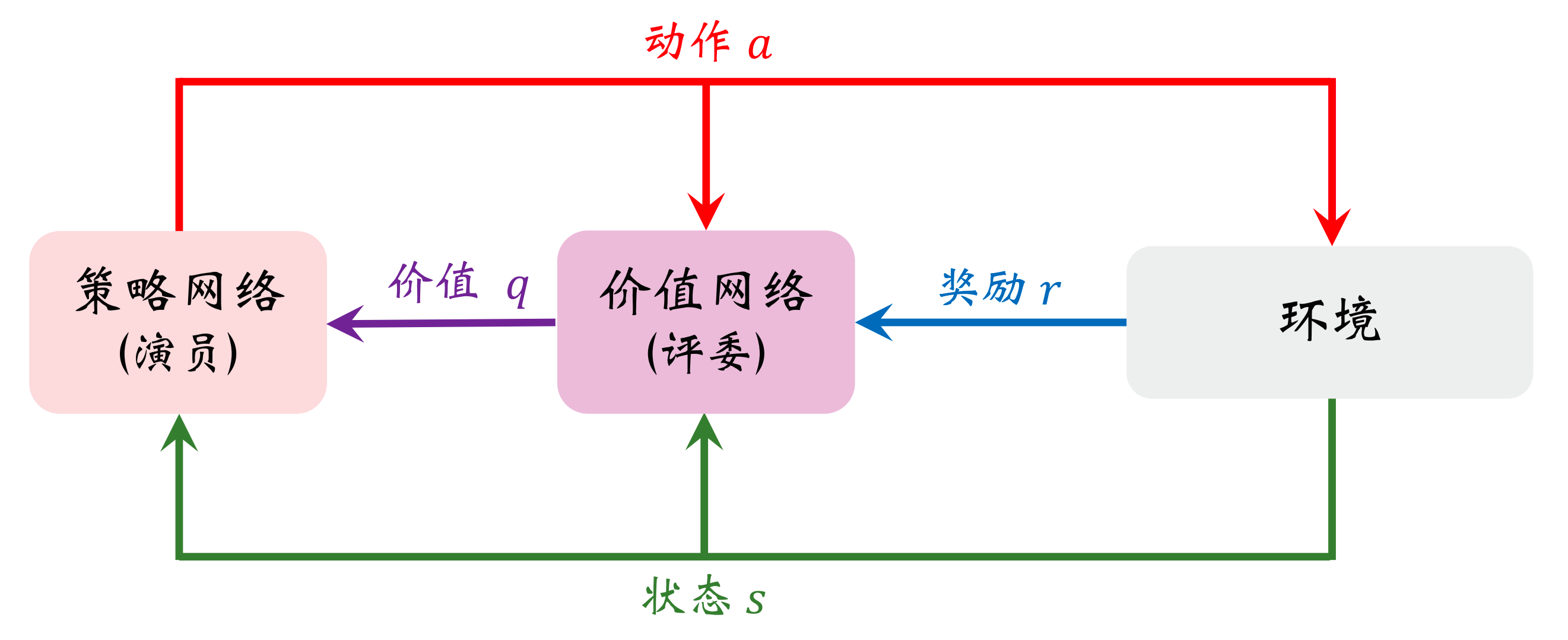
在上一章,我们讨论了一个话题,“Actor-Critic”。s s s a a a r r r s s s a a a r r r
现在呢,我们策略网络的输出可以是一个具体的数字,也可以是多个具体的数字(向量)。总之,不再是概率了。比如说,对于开电动车,输出可以是[ 0 , 40 ] [0,40] [ 0 , 4 0 ]
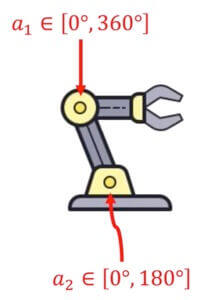
有两个地方可以转动,输出的就是一个向量。
输出不同,这个,我们在《深度学习初步及其Python实现:2.神经网络基础》 有过讨论。如果输出的都是各个动作的概率,输出层用Softmax。那么,这一章呢,我们的输出层可以用Sigmoid,再乘以一个数,比如对于电动车,车速是[ 0 , 40 ] [0,40] [ 0 , 4 0 ] 40 40 4 0
对于价值网络,输出依旧是一个数字,价值,没有具体的区别。
所以呢,确定策略梯度和上一章的随机策略梯度,区别只是在于策略网络的输出层?
用行为策略收集经验
在之前的章节中,我们讨论过离线策略(Off Policy)方法。即我们有目标策略(Target Policy)和行为策略(Behavior Policy)。μ ( s ; θ 新 ) \mu(s;\theta_{\text{新}}) μ ( s ; θ 新 ) θ 新 \theta_{\text{新}} θ 新 θ 旧 \theta_{\text{旧}} θ 旧 a = μ ( s ; θ 旧 ) + ε a = \mu(s;\theta_{\text{旧}}) + \varepsilon a = μ ( s ; θ 旧 ) + ε ε \varepsilon ε
我们用行为策略控制智能体和环境交互,把智能体的轨迹整理成( s t , a t , r t , s t + 1 ) (s_t,a_t,r_t,s_{t+1}) ( s t , a t , r t , s t + 1 ) D \mathcal{D} D s t , a t , r t , s t + 1 , a t + 1 , r t + 1 , s t + 2 s_t,a_t,r_t,s_{t+1},a_{t+1},r_{t+1},s_{t+2} s t , a t , r t , s t + 1 , a t + 1 , r t + 1 , s t + 2 ( s t , a t , r t , s t + 1 ) (s_t,a_t,r_t,s_{t+1}) ( s t , a t , r t , s t + 1 )
然后在训练的时候,我们从经历库中再进行抽样。( s j , a j , r j , s j + 1 ) (s_j, a_j, r_j, s_{j+1}) ( s j , a j , r j , s j + 1 ) μ ( s ; θ ) \mu(s;\theta) μ ( s ; θ ) s j s_j s j q ( s , a ; ω ) q(s,a;\omega) q ( s , a ; ω ) ( s j , a j , r j , s j + 1 ) (s_j, a_j, r_j, s_{j+1}) ( s j , a j , r j , s j + 1 )
训练策略网络
我们给定状态s s s a = μ ( s ; θ ) a = \mu(s;\theta) a = μ ( s ; θ ) a a a q ^ = Q ( s , a ; ω ) \hat{q} = Q(s,a;\omega) q ^ = Q ( s , a ; ω ) θ \theta θ a a a q ^ \hat{q} q ^
q ^ = Q ( s , μ ( s ; θ ) ; ω ) \hat{q} = Q(s,\mu(s;\theta);\omega)
q ^ = Q ( s , μ ( s ; θ ) ; ω )
这个分数q ^ \hat{q} q ^ θ \theta θ θ \theta θ q ^ \hat{q} q ^ θ \theta θ q ^ \hat{q} q ^ 均值 更高。
需要注意的是,这里还有一个东西,s s s s s s s s s s s s
复习一下,在第一章《1.基础概念》 的开头,我们举了一个例子,g ( X , Y ) = X Y g(X,Y) = XY g ( X , Y ) = X Y X X X Y Y Y g ( X , Y ) g(X,Y) g ( X , Y ) X X X X X X
那么,现在一样的,我们求关于S S S
J ( θ ) = E S [ q ( S , μ ( S ; θ ) ; ω ) ] J(\theta) = \mathbb{E}_{S}\bigg[q(S,\mu(S;\theta);\omega)\bigg]
J ( θ ) = E S [ q ( S , μ ( S ; θ ) ; ω ) ]
现在提一个问题,我们是要最大化还是最小化?
θ ⋆ = arg max θ J ( θ ) \theta_{\star} = \argmax_{\theta} J(\theta)
θ ⋆ = θ a r g m a x J ( θ )
在训练策略网络的时候,价值网络的参数ω \omega ω
那么,接下来的内容,就很简单了,根据梯度上升和链式法则:
θ ← θ + β ∂ Q ( s j , a ^ j ; ω ) ∂ a ∂ μ ( s j ; θ ) ∂ θ \theta \leftarrow \theta + \beta \frac{\partial Q(s_j,\hat{a}_j;\omega)}{\partial a} \frac{\partial \mu(s_j;\theta)}{\partial \theta}
θ ← θ + β ∂ a ∂ Q ( s j , a ^ j ; ω ) ∂ θ ∂ μ ( s j ; θ )
训练价值网络
训练价值网络的目标是让价值网络Q ( s , a ; ω ) Q(s,a;\omega) Q ( s , a ; ω ) Q π ( s , a ) Q_{\pi}(s,a) Q π ( s , a ) r r r r r r
我们每次从经验回放数组中取出一个四元组s j , a j , r j , s j + 1 s_j,a_j,r_j,s_{j+1} s j , a j , r j , s j + 1 ω \omega ω q ^ j \hat{q}_j q ^ j q ^ j + 1 \hat{q}_{j+1} q ^ j + 1
q ^ j = Q ( s j , a j ; ω ) q ^ j + 1 = Q ( s j + 1 , μ ( s j + 1 ; θ ) ; ω ) \begin{aligned}
\hat{q}_j & = Q(s_j,a_j;\omega) \\
\hat{q}_{j+1} & = Q(s_{j+1},\mu(s_{j+1};\theta);\omega)
\end{aligned}
q ^ j q ^ j + 1 = Q ( s j , a j ; ω ) = Q ( s j + 1 , μ ( s j + 1 ; θ ) ; ω )
然后,我们来计算一个略微带点"真理"的TD目标
y ^ j = r j + γ q ^ j + 1 \hat{y}_j = r_j + \gamma \hat{q}_{j+1}
y ^ j = r j + γ q ^ j + 1
所以,有目标函数
L ( ω ) = 1 2 [ Q ( s j , a j ; ω ) − y ^ j ] 2 L(\omega) = \frac{1}{2}\bigg[Q(s_j,a_j;\omega) - \hat{y}_j\bigg]^2
L ( ω ) = 2 1 [ Q ( s j , a j ; ω ) − y ^ j ] 2
计算梯度
∂ L ( ω ) ∂ ω = ( q ^ j − y ^ j ) ∂ Q ( s j , a j ; ω ) ∂ ω \frac{\partial L(\omega)}{\partial \omega}= (\hat{q }_j - \hat{y}_j) \frac{\partial Q(s_j,a_j;\omega)}{\partial \omega}
∂ ω ∂ L ( ω ) = ( q ^ j − y ^ j ) ∂ ω ∂ Q ( s j , a j ; ω )
提一个问题,接下来是梯度上升,还是梯度下降?
ω ← ω − α ∂ L ( ω ) ∂ ω \omega \leftarrow \omega - \alpha \frac{\partial L(\omega)}{\partial \omega}
ω ← ω − α ∂ ω ∂ L ( ω )
确定策略梯度方法的训练
在训练开始之前,我们需要收集足够多的经历,这个过程就是用相对旧的策略去和环境做交互,然后把轨迹以元祖的形式,存在经历库D \mathcal{D} D ( s j , a j , r j , s j + 1 ) (s_j,a_j,r_j,s_{j+1}) ( s j , a j , r j , s j + 1 )
1、让策略网络做预测:
a ^ j = μ ( s j ; θ 新 ) a ^ j + 1 = μ ( s j + 1 ; θ 新 ) \begin{aligned}
\hat{a}_j & = \mu(s_j;\theta_{\text{新}}) \\
\hat{a}_{j+1} & = \mu(s_{j+1};\theta_{\text{新}})
\end{aligned}
a ^ j a ^ j + 1 = μ ( s j ; θ 新 ) = μ ( s j + 1 ; θ 新 )
注意:a ^ j \hat{a}_j a ^ j a j a_j a j a ^ j \hat{a}_j a ^ j μ ( s j ; θ 新 ) \mu(s_j;\theta_{\text{新}}) μ ( s j ; θ 新 ) a j a_j a j μ ( s j ; θ 旧 ) \mu(s_j;\theta_\text{旧}) μ ( s j ; θ 旧 ) a j a_j a j ω \omega ω a ^ j \hat{a}_j a ^ j a j a_j a j
2、让价值网络做预测:
q ^ j = Q ( s j , a j ; ω ) q ^ j + 1 = Q ( s j + 1 , a ^ j + 1 ; ω ) \begin{aligned}
\hat{q}_j & = Q(s_j,a_j;\omega) \\
\hat{q}_{j+1} & = Q(s_{j+1},\hat{a}_{j+1};\omega)
\end{aligned}
q ^ j q ^ j + 1 = Q ( s j , a j ; ω ) = Q ( s j + 1 , a ^ j + 1 ; ω )
3、计算TD目标和TD误差
y ^ j = r j + γ q ^ j + 1 δ j = q ^ j − y ^ j \begin{aligned}
\hat{y}_j & = r_j + \gamma \hat{q}_{j+1} \\
\delta_j & = \hat{q}_j - \hat{y}_j
\end{aligned}
y ^ j δ j = r j + γ q ^ j + 1 = q ^ j − y ^ j
4、更新价值网络:
ω ← ω − α δ j ∂ Q ( s j , a j ; ω ) ∂ ω \omega \leftarrow \omega - \alpha \delta_j \frac{\partial Q(s_j,a_j;\omega)}{\partial \omega}
ω ← ω − α δ j ∂ ω ∂ Q ( s j , a j ; ω )
5、更新策略网络:
θ 新 ← θ 新 + β ∂ Q ( s j , a ^ j ; ω ) ∂ a ∂ μ ( s j ; θ 新 ) ∂ θ 新 \theta_{\text{新}} \leftarrow \theta_{\text{新}} + \beta \frac{\partial Q(s_j,\hat{a}_j;\omega)}{\partial a} \frac{\partial \mu(s_j;\theta_{\text{新}})}{\partial \theta_{\text{新}}}
θ 新 ← θ 新 + β ∂ a ∂ Q ( s j , a ^ j ; ω ) ∂ θ 新 ∂ μ ( s j ; θ 新 )
关于价值网络的讨论
价值网络是在动作价值函数做近似,还是对最优动作价值函数做近似
确定策略梯度中有一个确定策略网络μ ( s ; θ ) \mu(s;\theta) μ ( s ; θ ) Q ( s , a ; ω ) Q(s,a;\omega) Q ( s , a ; ω ) Q ( s , a ; ω ) Q(s,a;\omega) Q ( s , a ; ω ) Q π ( s , a ) Q_{\pi}(s,a) Q π ( s , a ) Q ⋆ ( s , a ) Q_{\star}(s,a) Q ⋆ ( s , a )
是对动作价值函数Q π ( s , a ) Q_{\pi}(s,a) Q π ( s , a )
在确定策略梯度的训练流程中,更新价值网络用到TD目标:
y ^ j = r j + γ Q ( s j + 1 , μ ( s j + 1 ; θ ) ; ω ) \hat{y}_j = r_j + \gamma Q(s_{j+1},\mu(s_{j+1};\theta);\omega) y ^ j = r j + γ Q ( s j + 1 , μ ( s j + 1 ; θ ) ; ω )
策略μ ( s , θ ) \mu(s,\theta) μ ( s , θ ) Q Q Q Q Q Q
不过,虽然价值网络Q ( s , a ; ω ) Q(s,a;\omega) Q ( s , a ; ω ) Q π ( s , a ) Q_{\pi}(s,a) Q π ( s , a ) Q ( s , a ; ω ) Q(s,a;\omega) Q ( s , a ; ω ) Q ⋆ ( s , a ) Q_{\star}(s,a) Q ⋆ ( s , a ) μ ( s ; θ ) \mu(s;\theta) μ ( s ; θ ) π ⋆ \pi_{\star} π ⋆ Q ( s , a ; ω ) Q(s,a;\omega) Q ( s , a ; ω ) Q π ( s , a ) Q_{\pi}(s,a) Q π ( s , a )
价值网络是在行为策略做评估,还是在对目标策略做评估
确定策略梯度的训练中有行为策略μ ( s ; θ 旧 ) \mu(s;\theta_{\text{旧}}) μ ( s ; θ 旧 ) μ ( s ; θ 新 ) \mu(s;\theta_{\text{新}}) μ ( s ; θ 新 ) Q ( s , a ; ω ) Q(s,a;\omega) Q ( s , a ; ω ) Q π ( s , a ) Q_{\pi}(s,a) Q π ( s , a ) π \pi π
是目标策略μ ( s ; θ 新 ) \mu(s;\theta_{\text{新}}) μ ( s ; θ 新 )
行为策略对价值网络几乎没有影响。
Q ( s j , a j ; ω ) = r j + γ Q ( s j + 1 , μ ( s j + 1 ; θ 新 ) ; ω ) Q(s_j,a_j;\omega) = r_j + \gamma Q(s_{j+1},\mu(s_{j+1};\theta_{\text{新}});\omega) Q ( s j , a j ; ω ) = r j + γ Q ( s j + 1 , μ ( s j + 1 ; θ 新 ) ; ω )
在收集经验的过程中,行为策略决定了如何基于s j s_j s j a j a_j a j a j a_j a j
高估的问题及办法
上述过程有没有问题?θ \theta θ a ^ \hat{a} a ^ Q ( s , μ ( s ; θ ) ; ω ) Q(s,\mu(s;\theta);\omega) Q ( s , μ ( s ; θ ) ; ω )
对于所有的 s ∈ S μ ( s ; θ ⋆ ) = arg max a ∈ A Q ( s , a ; ω ) \text{对于所有的}s\in\mathcal{S} \qquad \mu(s;\theta_{\star}) = \argmax_{a \in \mathcal{A}} Q(s,a;\omega)
对于所有的 s ∈ S μ ( s ; θ ⋆ ) = a ∈ A a r g m a x Q ( s , a ; ω )
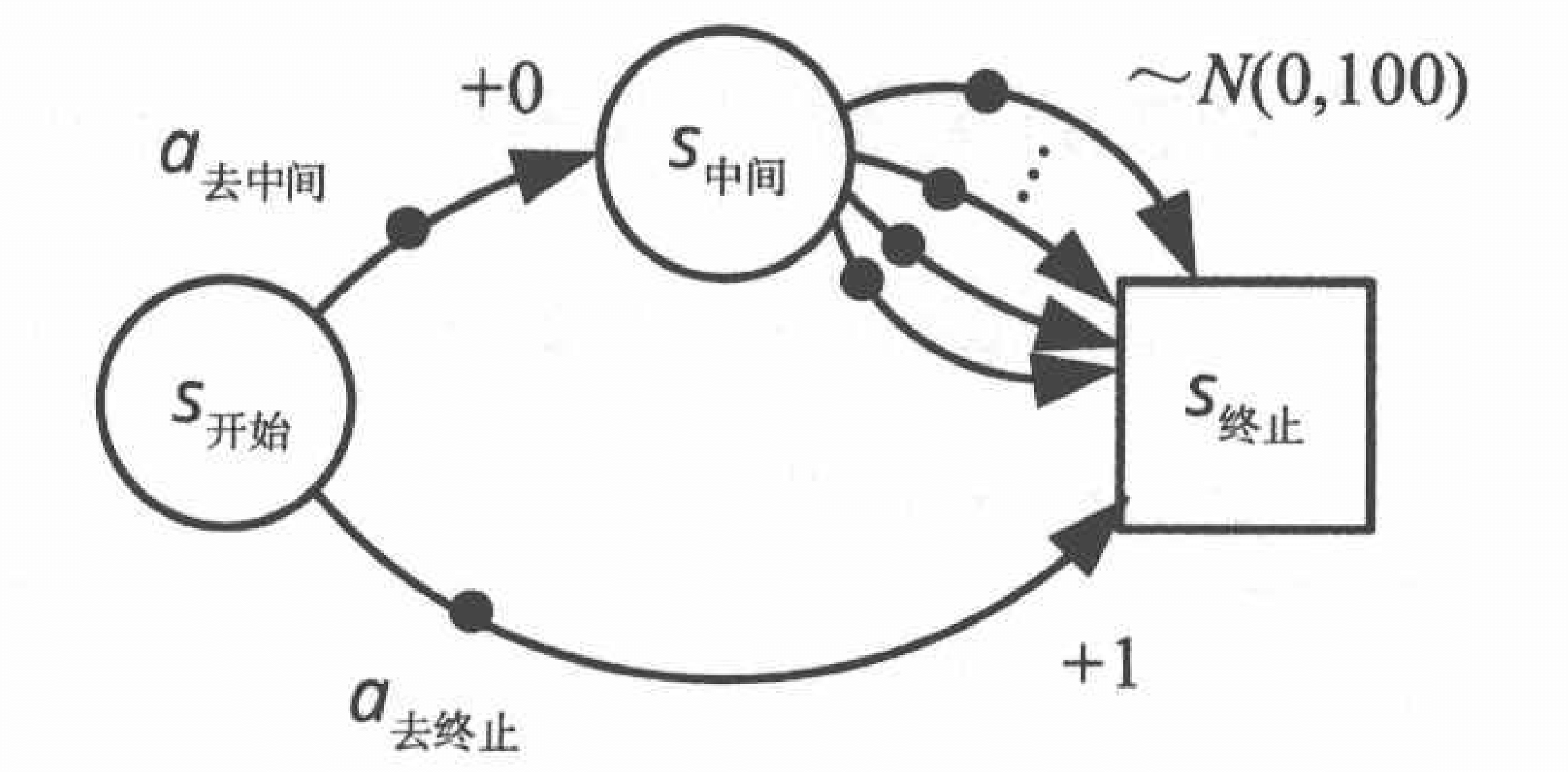
这是我们的目标。《5.函数近似》 这一章,DQN的决策方式是a j = arg max a Q ( s j , a ; ω ) a_j = \argmax_a Q(s_j,a;\omega) a j = a r g m a x a Q ( s j , a ; ω ) s 中间 s_{\text{中间}} s 中间 s 终止 s_{\text{终止}} s 终止 s 终止 s_{\text{终止}} s 终止 0 0 0 1 1 1 s 中间 s_{\text{中间}} s 中间 max a ∈ A ( s 中间 ) Q ( s 中间 , a ) \max_{a \in \mathcal{A}(s_{\text{中间}})} Q(s_{\text{中间}},a) max a ∈ A ( s 中间 ) Q ( s 中间 , a ) y ^ j \hat{y}_j y ^ j Q ⋆ ( s j , a j ) Q_{\star}(s_j,a_j) Q ⋆ ( s j , a j )
y ^ j = r j + γ Q ( s j + 1 , μ ( s j + 1 ; θ ) ; ω ) ≈ r j + γ max a j + 1 Q ( s j + 1 , a j + 1 ; ω ) \begin{aligned}
\hat{y}_j & = r_j + \gamma Q(s_{j+1},\mu(s_{j+1};\theta);\omega) \\
& \approx r_j + \gamma \max_{a_{j+1}} Q(s_{j+1},a_{j+1};\omega)
\end{aligned}
y ^ j = r j + γ Q ( s j + 1 , μ ( s j + 1 ; θ ) ; ω ) ≈ r j + γ a j + 1 max Q ( s j + 1 , a j + 1 ; ω )
也是高估真实动作价值。然后我们又鼓励价值网络Q ( s j , a j ; ω ) Q(s_j,a_j;\omega) Q ( s j , a j ; ω ) y ^ j \hat{y}_j y ^ j Q ( s j , a j ; ω ) Q(s_j,a_j;\omega) Q ( s j , a j ; ω )
当时,我们提出了一个方案,DoubleDQN。现在,我们的思路也类似。
首先,我们用价值网络来计算t t t q t q_t q t
q t = Q ( s t , a t ; ω ) q_t = Q(s_t,a_t;\omega)
q t = Q ( s t , a t ; ω )
但是,计算TD目标的方式有所不同,与上文不一样了。对于t + 1 t+1 t + 1 q t + 1 q_{t+1} q t + 1 ω − \omega^- ω −
q t + 1 = Q ( s t + 1 , a t + 1 ′ ; ω − ) q_{t+1} = Q(s_{t+1},a'_{t+1};\omega^-)
q t + 1 = Q ( s t + 1 , a t + 1 ′ ; ω − )
其中,a t + 1 ′ a'_{t+1} a t + 1 ′ θ − \theta^- θ −
a t + 1 ′ = π ( s t + 1 ; θ − ) a'_{t+1} = \pi(s_{t+1};\theta^-)
a t + 1 ′ = π ( s t + 1 ; θ − )
ω − \omega^- ω − θ − \theta^- θ −
ω − ← k ω + ( 1 − k ) ω − θ − ← k ω + ( 1 − k ) θ − \begin{aligned}
\omega^- & \leftarrow k \omega + (1 - k) \omega^- \\
\theta^- & \leftarrow k \omega + (1 - k) \theta^-
\end{aligned}
ω − θ − ← k ω + ( 1 − k ) ω − ← k ω + ( 1 − k ) θ −
然后,我们通过这种方式得到的q t + 1 q_{t+1} q t + 1 δ t \delta_t δ t
δ t = q t − ( r t + γ q t + 1 ) \delta_t = q_t - (r_t + \gamma q_{t+1})
δ t = q t − ( r t + γ q t + 1 )
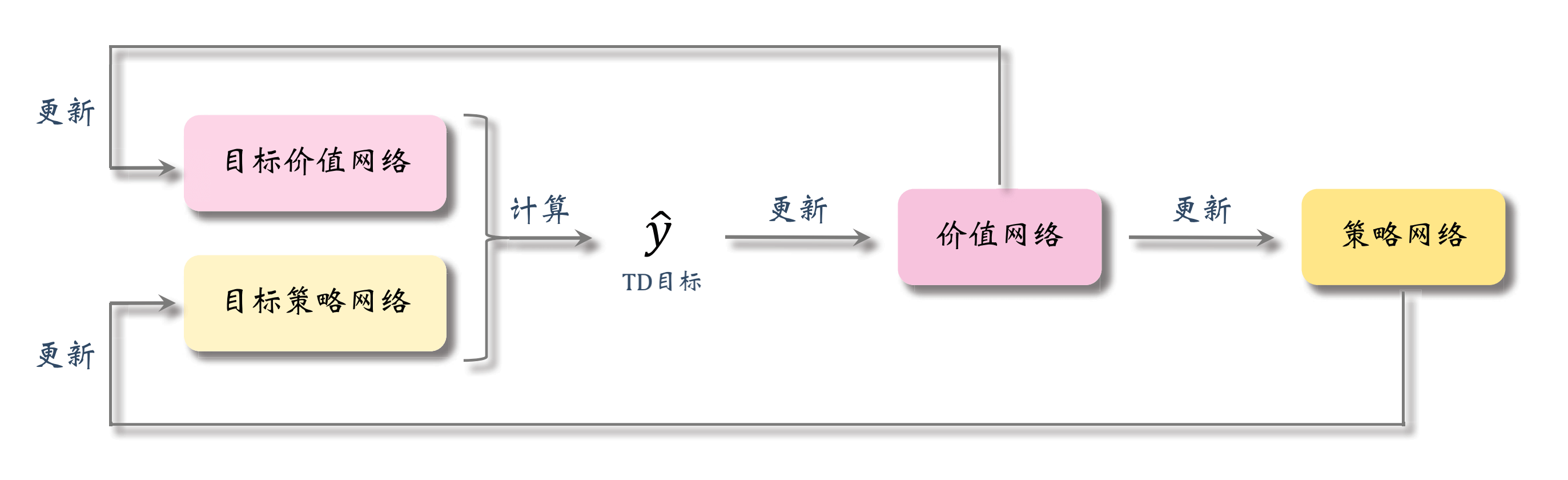
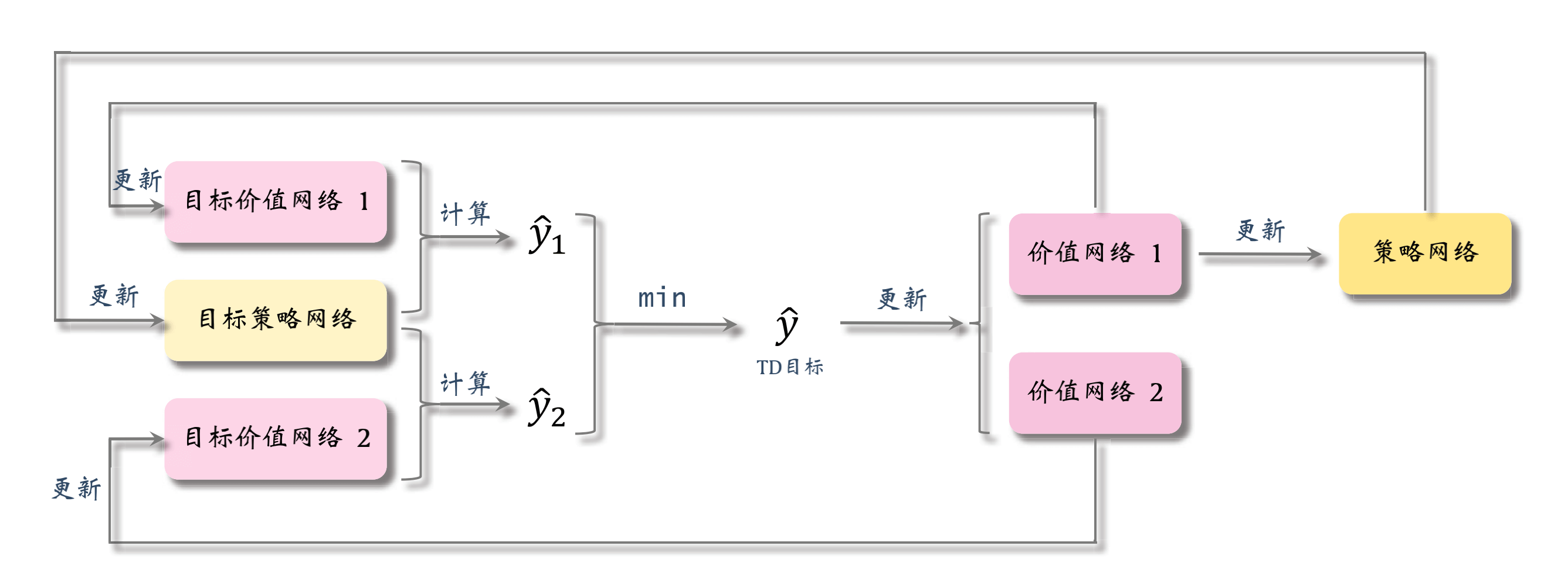
DDPG的组织关系
我们把上文讨论的解决方案绘制成组织关系图,这其实也就是DDPG的组织关系图。
DDPG的过程
我们来讨论一下DDPG的过程。
DDPG算法 输入 :输出 :θ \theta θ 参数 :θ \theta θ η \eta η ω \omega ω β \beta β γ \gamma γ k k k 初始化 :θ \theta θ θ − ← θ \theta^{-}\leftarrow\theta θ − ← θ ω \omega ω ω − ← ω \omega^{-}\leftarrow\omega ω − ← ω 循环执行以下操作 :累积经验 :从起始状态s s s π ( s ; θ ) \pi(s;\theta) π ( s ; θ ) a a a a a a r r r s ′ s' s ′ ( s , a , r , s ′ ) (s,a,r,s') ( s , a , r , s ′ ) D \mathcal{D} D 更新 :D \mathcal{D} D ( s j , a j , r j , s j + 1 ) (s_j,a_j,r_j,s_{j+1}) ( s j , a j , r j , s j + 1 ) a ^ j + 1 − = μ ( s j + 1 ; θ − ) \hat{a}^{-}_{j+1}=\mu(s_{j+1};\theta^-) a ^ j + 1 − = μ ( s j + 1 ; θ − ) q ^ j + 1 − = q ( s j + 1 , a ^ j + 1 − ; ω − ) \hat{q}^{-}_{j+1}=q(s_{j+1},\hat{a}^{-}_{j+1};\omega^{-}) q ^ j + 1 − = q ( s j + 1 , a ^ j + 1 − ; ω − ) q j = q ( s j , a j , ω ) q_j=q(s_j,a_j,\omega) q j = q ( s j , a j , ω ) y ^ j = r j + γ q ^ j + 1 − \hat{y}_j=r_j+\gamma\hat{q}^{-}_{j+1} y ^ j = r j + γ q ^ j + 1 − δ j = q ^ j − y ^ j \delta_j=\hat{q}_j-\hat{y}_j δ j = q ^ j − y ^ j ω ← ω − α δ j ∂ q ( s j , a j ; ω ) ∂ ω \omega\leftarrow\omega-\alpha\delta_{j} \frac{\partial q(s_j,a_j;\omega)}{\partial \omega} ω ← ω − α δ j ∂ ω ∂ q ( s j , a j ; ω ) k k k a ^ j = μ ( s j ; θ ) \hat{a}_j = \mu(s_j;\theta) a ^ j = μ ( s j ; θ ) θ ← θ + β ∂ Q ( s j , a ^ j ; ω ) ∂ ω ∂ μ ( s j ; θ ) ∂ θ \theta\leftarrow\theta+\beta\frac{\partial Q(s_j,\hat{a}_j;\omega)}{\partial \omega}\frac{\partial \mu(s_j;\theta)}{\partial \theta} θ ← θ + β ∂ ω ∂ Q ( s j , a ^ j ; ω ) ∂ θ ∂ μ ( s j ; θ ) θ − ← k θ + ( 1 − k ) θ − \theta^-\leftarrow k\theta+(1-k)\theta^- θ − ← k θ + ( 1 − k ) θ − ω − ← k ω + ( 1 − k ) ω − \omega^-\leftarrow k\omega+(1-k)\omega^- ω − ← k ω + ( 1 − k ) ω − D \mathcal{D} D
DDPG的实现
接下来,我们来实现一个DDPG。
该例子来自《强化学习:原理与Python实现(肖智清著)》这本书的第九章。
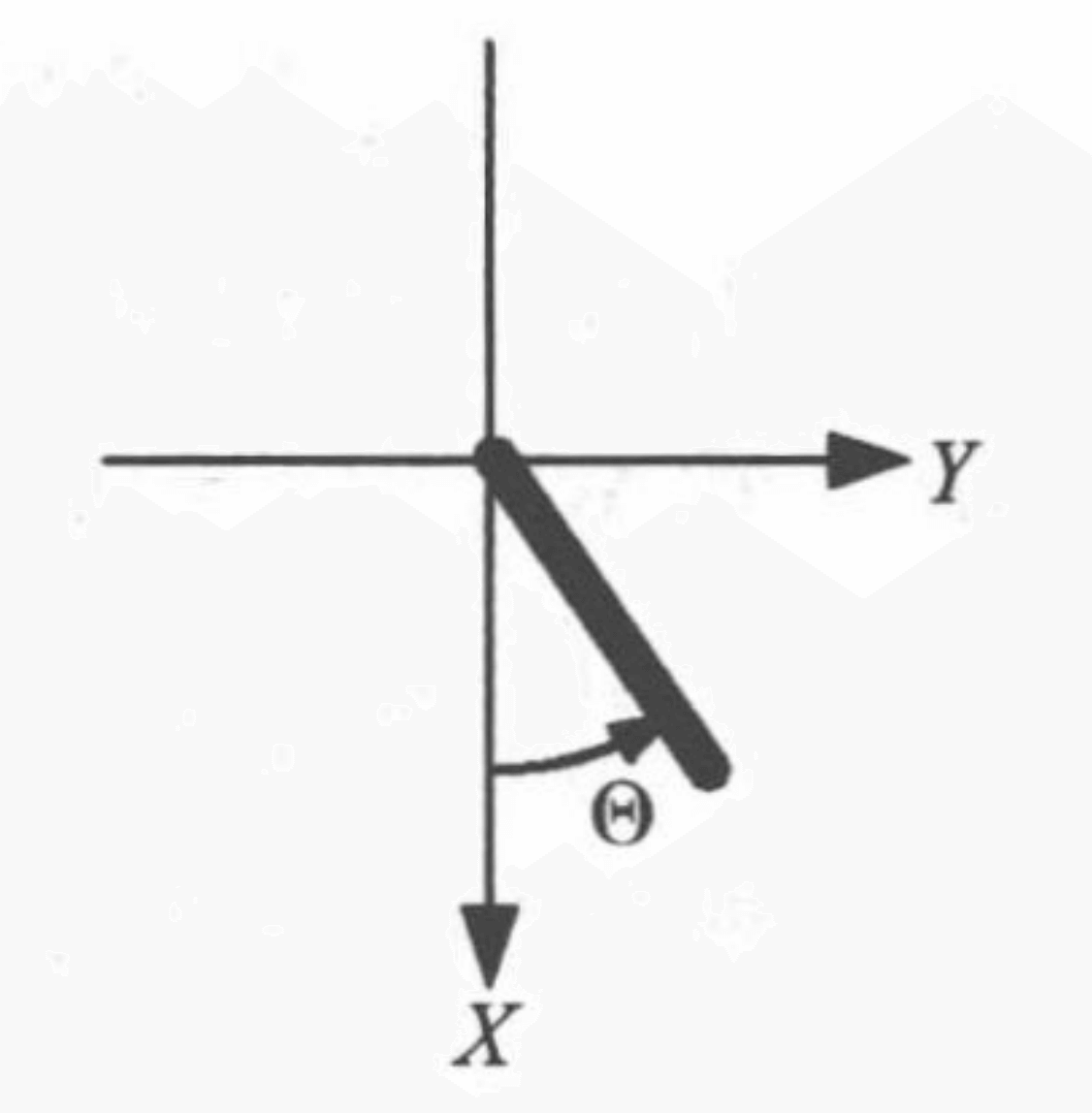
倒立摆控制问题描述
我们以倒立摆控制问题为例。1 1 1 ( 0 , 0 ) (0,0) ( 0 , 0 ) X X X Y Y Y t ( t = 0 , 1 , 2 , ⋯ ) t(t=0,1,2,\cdots) t ( t = 0 , 1 , 2 , ⋯ ) ( X t , Y t ) = ( cos Θ t , sin Θ t ) ( Θ t ∈ [ − π , + π ) ) (X_t,Y_t)=(\cos\Theta_t,\sin\Theta_t)(\Theta_t\in[-\pi,+\pi)) ( X t , Y t ) = ( cos Θ t , sin Θ t ) ( Θ t ∈ [ − π , + π ) ) Θ t ^ ( Θ ^ t ∈ [ − 8 , + 8 ] ) \hat{\Theta_t}(\hat{\Theta}_t\in[-8,+8]) Θ t ^ ( Θ ^ t ∈ [ − 8 , + 8 ] ) A t ( A t ∈ [ − 2 , + 2 ] ) A_t(A_t\in[-2,+2]) A t ( A t ∈ [ − 2 , + 2 ] ) r t + 1 r_{t+1} r t + 1 ( cos Θ t + 1 , sin Θ t + 1 , Θ ^ ) (\cos\Theta_{t+1},\sin\Theta_{t+1},\hat{\Theta}) ( cos Θ t + 1 , sin Θ t + 1 , Θ ^ )
特别注意,动作空间A t ( A t ∈ [ − 2 , + 2 ] ) A_t(A_t\in[-2,+2]) A t ( A t ∈ [ − 2 , + 2 ] )
环境描述
示例代码:
1 2 3 4 5 6 import gymenv = gym.make('Pendulum-v0' ) env.seed(0 ) print('状态空间 = {}' .format(env.observation_space)) print('动作空间 = {}' .format(env.action_space))
运行结果:
1 2 状态空间 = Box(-8.0, 8.0, (3,), float32) 动作空间 = Box(-2.0, 2.0, (1,), float32)
经历回放
复用《5.函数近似》 的经历回放代码。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 import pandas as pdimport numpy as npnp.random.seed(0 ) class DQNReplayer : def __init__ (self, capacity) : self.memory = pd.DataFrame(index=range(capacity),columns=['observation' , 'action' , 'reward' ,'next_observation' , 'done' ]) self.i = 0 self.count = 0 self.capacity = capacity def store (self, *args) : self.memory.loc[self.i] = args self.i = (self.i + 1 ) % self.capacity self.count = min(self.count + 1 , self.capacity) def sample (self, size) : indices = np.random.choice(self.count, size=size) return (np.stack(self.memory.loc[indices, field]) for field in self.memory.columns)
随机扰动
随机扰动用奥恩斯坦-乌伦贝克过程(Ornstein-Uhlenbeck Process, OU)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class OrnsteinUhlenbeckProcess : def __init__ (self, size, mu=0. , sigma=1. , theta=.15 , dt=.01 ) : self.size = size self.mu = mu self.sigma = sigma self.theta = theta self.dt = dt def __call__ (self) : n = np.random.normal(size=self.size) self.x += (self.theta * (self.mu - self.x) * self.dt +self.sigma * np.sqrt(self.dt) * n) return self.x def reset (self, x=0. ) : self.x = x * np.ones(self.size)
DDPG
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 import tensorflow as tftf.random.set_seed(0 ) from tensorflow import kerasclass DDPGAgent : def __init__ (self, env, actor_kwargs, critic_kwargs,replayer_capacity=20000 , replayer_initial_transitions=2000 ,gamma=0.99 , batches=1 , batch_size=64 ,net_learning_rate=0.005 , noise_scale=0.1 , explore=True) : observation_dim = env.observation_space.shape[0 ] action_dim = env.action_space.shape[0 ] observation_action_dim = observation_dim + action_dim self.action_low = env.action_space.low self.action_high = env.action_space.high self.gamma = gamma self.net_learning_rate = net_learning_rate self.explore = explore self.batches = batches self.batch_size = batch_size self.replayer = DQNReplayer(replayer_capacity) self.replayer_initial_transitions = replayer_initial_transitions self.noise = OrnsteinUhlenbeckProcess(size=(action_dim,),sigma=noise_scale) self.noise.reset() self.actor_evaluate_net = self.build_network(input_size=observation_dim, **actor_kwargs) self.actor_target_net = self.build_network(input_size=observation_dim, **actor_kwargs) self.critic_evaluate_net = self.build_network(input_size=observation_action_dim, **critic_kwargs) self.critic_target_net = self.build_network(input_size=observation_action_dim, **critic_kwargs) self.update_target_net(self.actor_target_net, self.actor_evaluate_net) self.update_target_net(self.critic_target_net, self.critic_evaluate_net) def update_target_net (self, target_net, evaluate_net,learning_rate=1. ) : target_weights = target_net.get_weights() evaluate_weights = evaluate_net.get_weights() average_weights = [(1. - learning_rate) * t + learning_rate * e for t, e in zip(target_weights, evaluate_weights)] target_net.set_weights(average_weights) def build_network (self, input_size, hidden_sizes, output_size=1 ,activation=tf.nn.relu, output_activation=None,loss=tf.losses.mse, learning_rate=0.001 ) : model = keras.Sequential() for layer, hidden_size in enumerate(hidden_sizes): kwargs = {'input_shape' : (input_size,)} if layer == 0 else {} model.add(keras.layers.Dense(units=hidden_size,activation=activation, **kwargs)) model.add(keras.layers.Dense(units=output_size,activation=output_activation)) optimizer = tf.optimizers.Adam(learning_rate) model.compile(optimizer=optimizer, loss=loss) return model def decide (self, observation) : if self.explore and self.replayer.count < self.replayer_initial_transitions: return np.random.uniform(self.action_low, self.action_high) action = self.actor_evaluate_net.predict(observation[np.newaxis])[0 ] if self.explore: noise = self.noise() action = np.clip(action + noise, self.action_low, self.action_high) return action def learn (self, observation, action, reward, next_observation, done) : self.replayer.store(observation, action, reward, next_observation,done) if self.replayer.count >= self.replayer_initial_transitions: if done: self.noise.reset() for batch in range(self.batches): observations, actions, rewards, next_observations,dones = self.replayer.sample(self.batch_size) observation_tensor = tf.convert_to_tensor(observations,dtype=tf.float32) with tf.GradientTape() as tape: action_tensor = self.actor_evaluate_net(observation_tensor) input_tensor = tf.concat([observation_tensor,action_tensor], axis=1 ) q_tensor = self.critic_evaluate_net(input_tensor) loss_tensor = -tf.reduce_mean(q_tensor) grad_tensors = tape.gradient(loss_tensor,self.actor_evaluate_net.variables) self.actor_evaluate_net.optimizer.apply_gradients(zip(grad_tensors, self.actor_evaluate_net.variables)) next_actions = self.actor_target_net.predict(next_observations) observation_actions = np.hstack([observations, actions]) next_observation_actions = np.hstack([next_observations, next_actions]) next_qs = self.critic_target_net.predict(next_observation_actions)[:, 0 ] targets = rewards + self.gamma * next_qs * (1. - dones) self.critic_evaluate_net.fit(observation_actions, targets,verbose=0 ) self.update_target_net(self.actor_target_net,self.actor_evaluate_net, self.net_learning_rate) self.update_target_net(self.critic_target_net,self.critic_evaluate_net, self.net_learning_rate)
play_qlearning
复用play_qlearning的代码。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 def play_qlearning (env, agent, train=False, render=False) : episode_reward = 0 observation = env.reset() while True : if render: env.render() action = agent.decide(observation) next_observation, reward, done, _ = env.step(action) episode_reward += reward if train: agent.learn(observation, action, reward, next_observation, done) if done: break observation = next_observation return episode_reward
训练
示例代码:
1 2 3 4 5 6 7 8 9 10 11 actor_kwargs = {'hidden_sizes' : [32 , 64 ], 'learning_rate' : 0.0001 } critic_kwargs = {'hidden_sizes' : [64 , 128 ], 'learning_rate' : 0.001 } agent = DDPGAgent(env, actor_kwargs=actor_kwargs,critic_kwargs=critic_kwargs) episodes = 50 episode_rewards = [] for episode in range(episodes): episode_reward = play_qlearning(env, agent, train=True ) episode_rewards.append(episode_reward) print('{} {}' .format(episode,episode_reward))
运行结果:
1 2 3 4 5 6 7 8 9 10 11 12 13 0 -1771.6710473932135 1 -855.8647011844732 2 -1547.6336582197753 3 -879.8661867384465 4 -1684.3831016441832 【部分运行结果略】 45 -126.7990780607278 46 -118.68338360149839 47 -532.1535582045923 48 -11.971887950776678 49 -145.32406988179974
测试
示例代码:
1 2 3 4 agent.explore = False episode_rewards = [play_qlearning(env, agent) for _ in range(100 )] print('平均回合奖励 = {} / {} = {}' .format(sum(episode_rewards),len(episode_rewards), np.mean(episode_rewards)))
运行结果:
1 平均回合奖励 = -129641.6907660435 / 100 = -1296.4169076604344
双延时确定策略梯度
有一种和DDPG差不多,但是结构更复杂的方法,双延时确定策略梯度(Twin Delayed Deep Deterministic,TD3),也被称为截断双Q学习(Clipped Double Q-Learning)。需要注意的是,这种方法只改进神经网络之间的组织关系,并不改变神经网络自身的结构。即只改进了训练用的算法。
这种方法使用两个价值网络和一个策略网络:
Q ( s , a ; ω 1 ) Q ( s , a ; ω 2 ) μ ( s , ; θ ) \begin{aligned}
& Q(s,a;\omega_1) \\
& Q(s,a;\omega_2) \\
& \mu(s,;\theta)
\end{aligned}
Q ( s , a ; ω 1 ) Q ( s , a ; ω 2 ) μ ( s , ; θ )
三个神经网络对应各自的目标网络:
Q ( s , a ; ω 1 − ) Q ( s , a ; ω 2 − ) μ ( s , ; θ − ) \begin{aligned}
& Q(s,a;\omega_1^-) \\
& Q(s,a;\omega_2^-) \\
& \mu(s,;\theta^-)
\end{aligned}
Q ( s , a ; ω 1 − ) Q ( s , a ; ω 2 − ) μ ( s , ; θ − )
用目标策略网络计算动作:
a ^ j + 1 − = μ ( s j + 1 ; θ − ) \hat{a}_{j+1}^- = \mu(s_{j+1};\theta^-)
a ^ j + 1 − = μ ( s j + 1 ; θ − )
然后用两个目标价值网络计算:
y ^ j , 1 = r j + γ Q ( s j + 1 , a ^ j + 1 − ; ω 1 − ) y ^ j , 2 = r j + γ Q ( s j + 1 , a ^ j + 1 − ; ω 2 − ) \begin{aligned}
\hat{y}_{j,1} & = r_j + \gamma Q(s_{j+1},\hat{a}_{j+1}^-;\omega_1^-) \\
\hat{y}_{j,2} & = r_j + \gamma Q(s_{j+1},\hat{a}_{j+1}^-;\omega_2^-)
\end{aligned}
y ^ j , 1 y ^ j , 2 = r j + γ Q ( s j + 1 , a ^ j + 1 − ; ω 1 − ) = r j + γ Q ( s j + 1 , a ^ j + 1 − ; ω 2 − )
取两者较小者为TD目标:
y ^ j = min { y ^ j , 1 , y ^ j , 2 } \hat{y}_j = \min\{\hat{y}_{j,1},\hat{y}_{j,2}\}
y ^ j = min { y ^ j , 1 , y ^ j , 2 }
这种算法相比DDPG,效果更好。
随机策略和确定策略的比较
最后一个话题,随机策略方法和确定策略方法的比较。
随机策略
确定策略
函数
π ( a ∣ s ; θ ) \pi(a\mid s;\theta) π ( a ∣ s ; θ ) π ( s ; θ ) \pi(s;\theta) π ( s ; θ )
输出
不同动作的概率分布
动作
控制
根据概率分布随机抽样
输出的就是动作
应用
大多数时候用于离散问题
连续控制