5.函数近似

函数近似简介

在前面三章，我们讨论了"动态规划"、“蒙特卡洛"和"时序差分”，这三种方法，其实做的都是同样的事情，更新表格和查表。毕竟，状态和动作都是有限的。
我们把状态价值函数看成表格，其索引是状态；把动作价值函数，其索引是状态动作对。价值函数的迭代更新，其实也就是对表进行迭代更新。因此，这一类的也被称为表格型强化学习。
但是呢，如果状态特别多，比如围棋，状态有$10^{170}$种；再比如，跑步的时候，其手脚的状态还是连续的不可数的。那么，就没法用表格法了。

这时候，换一个思路，利用函数近似的方法对价值函数进行表示。
比如：
对于状态价值函数

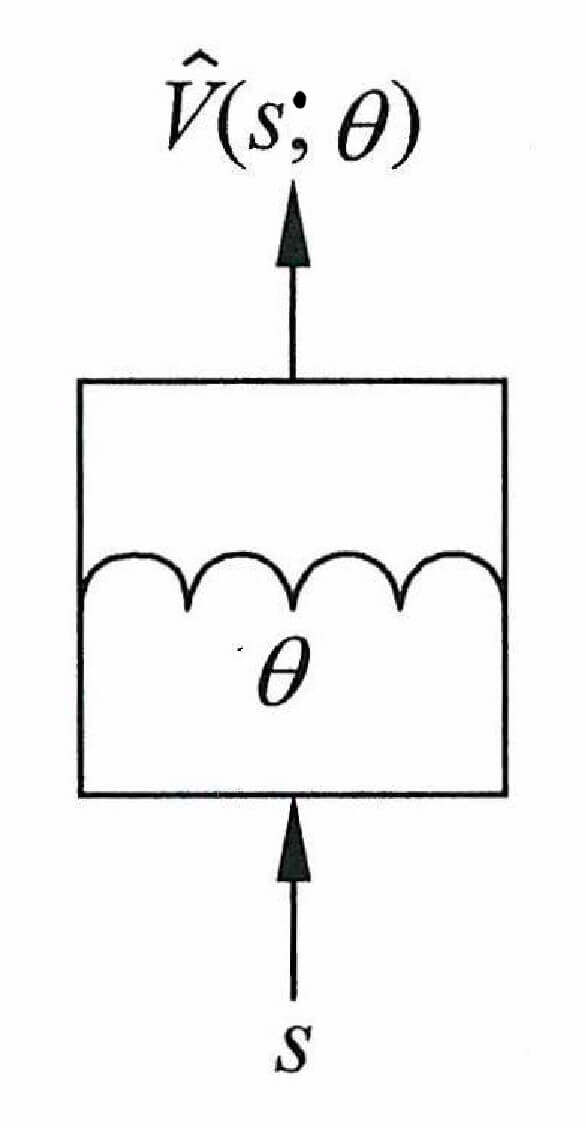
$$V(s) = \hat{V}(s;\theta)$$

• 其中，$\hat{V}(s;\theta)$是近似函数，$\theta$是参数。

对于动作价值函数

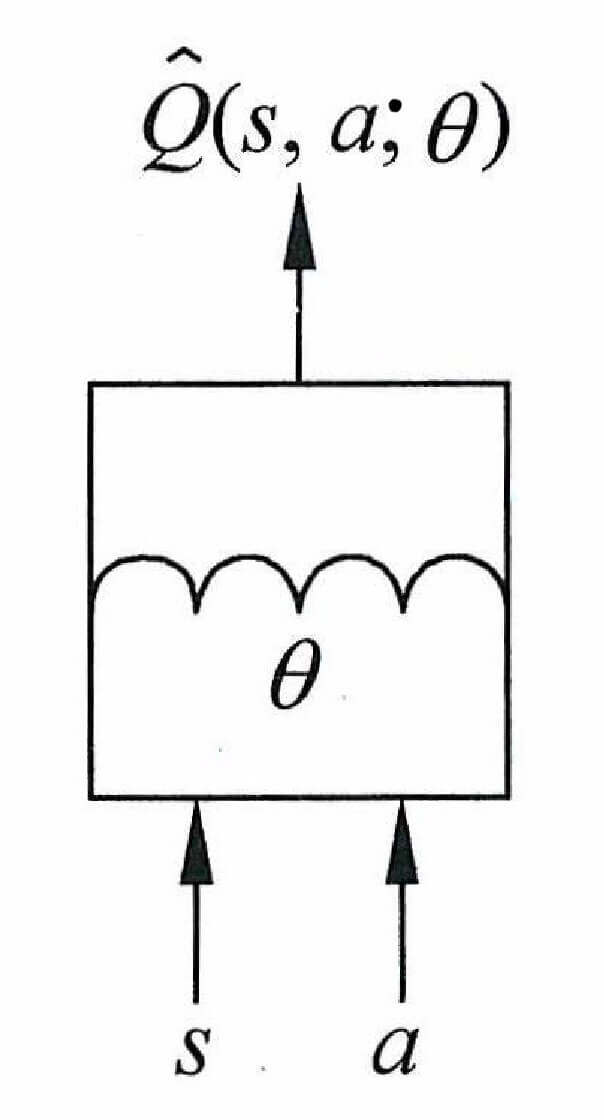
$$Q(s,a) = \hat{Q}(s,a;\theta)$$

• 其中$\hat{Q}(s,a;\theta)$是近似函数，$\theta$是参数。

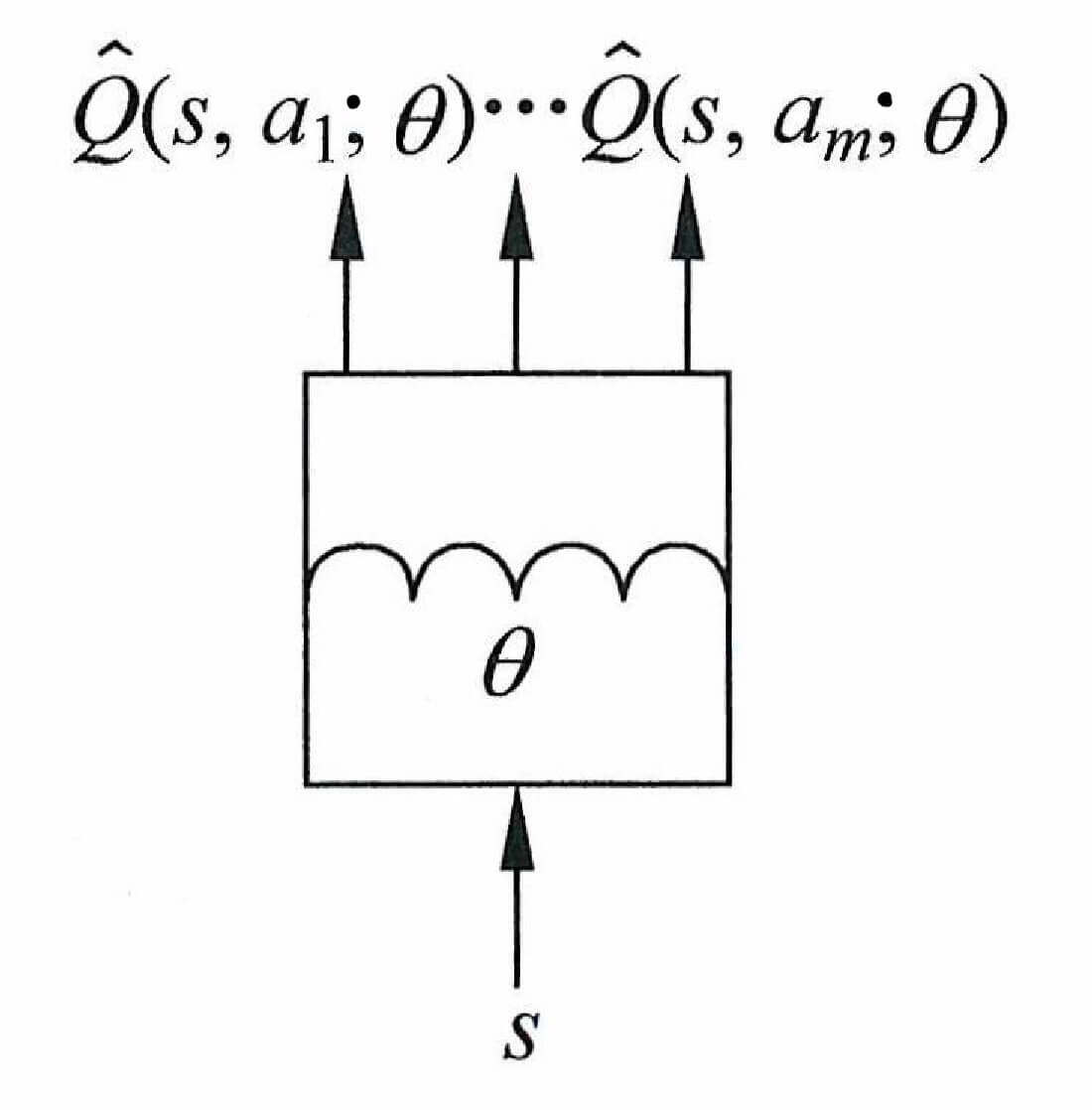
除了上述两种近似函数，还有一种，输入是状态$s$，输出是该状态下，可能采取的动作的价值$\hat{Q}(s,a_1,\theta),\hat{Q}(s,a_2,\theta),\cdots,\hat{Q}(s,a_m,\theta)$。我们在下文会见到这种近似函数。

函数近似方法可以分为两种：

1. 线性近似
2. 非线性近似

线性近似是指，用多个基函数的线性组合来表示近似函数，即：

$$\hat{V}(\bold{s},{\theta}) = \sum_{i}^d {\theta}_i x_i(\bold{s})$$

常见的基函数有多项式函数、傅立叶函数和径向函数。

• 傅立叶函数是将周期表现为不同频率的正弦函数和余弦函数的加权和
• 径向函数是一个取值仅仅依赖于距离远点距离的函数

线性近似的方法有可以分为两类，一类是"增量法"，针对每一步(轨迹中的每一个状态转换序列)，一旦有增量发生，则立即优化近似函数；另一类是"批量法"，针对一批历史数据(如一段轨迹)集中进行近似。

近似的过程就是先确定基函数的个数和形式，然后调参。但是呢，因为基函数的个数和形式有限，又需要在近似之前确定，在近似过程中又无法改变，因此这种方法的近似能力非常有限。

线性近似有点类似与集成学习中的Boosting方法，基函数就像基学习器，但是又不完全一样，在集成学习中，我们的基学习器主要是决策树，而决策树的个数和决策树的深度、叶子节点的个数等，不需要在训练之前就确定。
关于集成学习，可以参考《集成学习概览及其Python实现》。

线性近似的近似能力非常有限，但是一个东西，近似能力极强。
来看一篇重要的论文。

这篇论文，从理论上证明了，多层的神经网络可以逼近任何的数据分布，也就是说神经网络是"万能"的。
而且，我们也的确看到神经网络在许多方面，有非常好的实践。

关于神经网络，可以参考《深度学习初步及其Python实现》。

接下来，我们着重讨论一个非线性近似的代表，DQN(Deep Q-Network)，深度Q学习

DQN的要点

DQN建立在Q-Learing的基础上，在上一章，我们讨论过Q-Learning。

Q-Learning是一种离线策略时序差分方法，使用$\varepsilon$探索策略$\mu$产生数据，利用该数据对目标策略$\pi$进行评估改进；利用查表法对动作价值进行预测，迭代更新目标是时序差分目标$r + \gamma \max_{a_{t+1}}Q(s_{t+1},a_{t+1})$。

DQN在Q-Learning上的改进有：

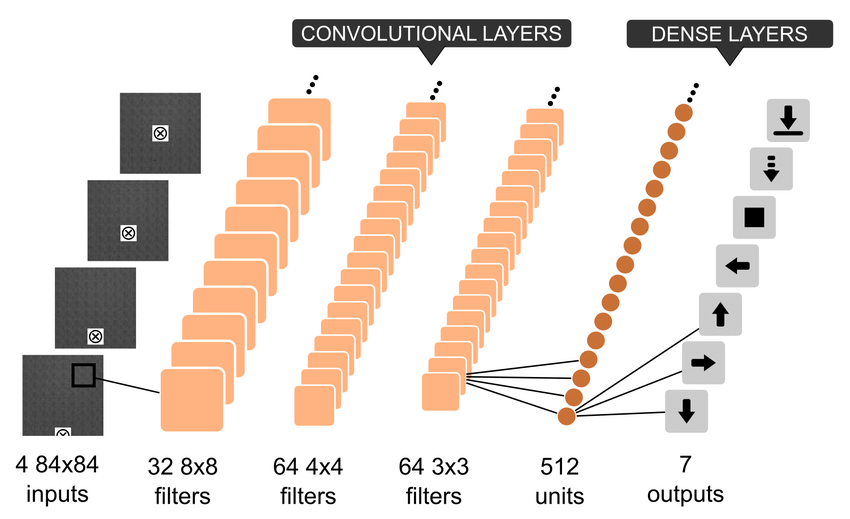
1. DQN使用神经网络来替换"表格"。
2. DQN利用经历回放对神经网络进行训练。
3. DQN设置了单独的目标网络来处理TD偏差。

接下来，我们来解释一下，为什么要做这些改进。

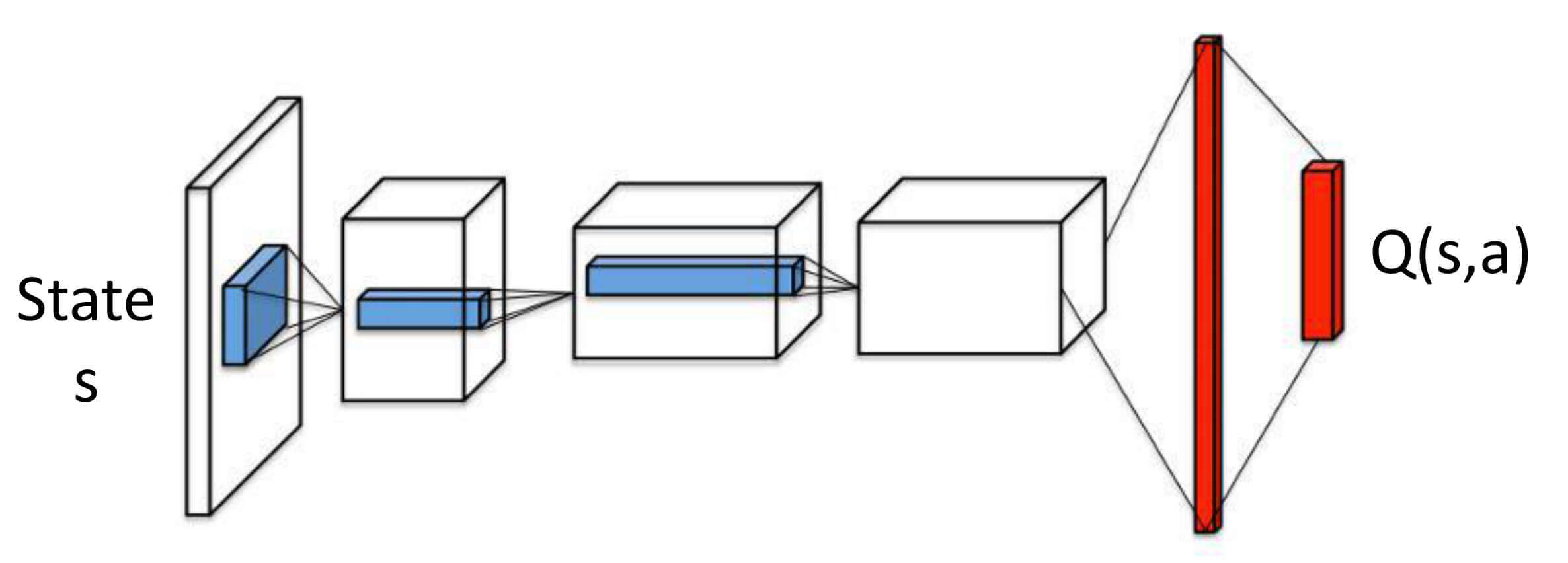
DQN使用神经网络来替换"表格"

这个很容易理解，我们在上文也有过讨论，因为状态空间很大或者连续，无法用查表法来求解每个状态的价值，因此考虑使用神经网络来表示价值函数，在这里，神经网络就是动作价值函数。参数为每层网络的权重及偏置，用${\theta}$表示。对动作价值函数进行更新也就是于对参数${\theta}$的更新。参数确定了，则动作价值函数也就知道了。
例如，下图是一个DQN的神经网络结构，输入是状态$s$，经过三个卷积层和一个全连接层侯，输出在$s$下，7个动作的动作价值。
这就是我们在上文讨论的第三种近似函数，输入是一个状态$s$，输出是该状态下，可能采取的动作的价值$\hat{Q}(s,a_1,\theta),\hat{Q}(s,a_2,\theta),\cdots,\hat{Q}(s,a_m,\theta)$。

• 输出的是所有可能动作的$Q$值

DQN利用经历回放对神经网络进行训练

接下来，我们讨论第二个改进，DQN利用经历回放对神经网络进行训练，也有资料把"经历回放"称为"经验回放"。

在上一章，以出租车调度为例的Q-Learing的代码中，我们在play_qlearning这个函数中，专门写了这么两行：

i = i+1
if i > 10000:
    return 'drop'

因为我们可能会得到一个很不好的策略，这个策略可能一直在地图上转圈，一直不接乘客或者一直不放乘客下车。当时，我们处理这个问题的方法非常简单粗暴，直接把这个不好的轨迹drop，在100个轨迹中，出现了两次这样的轨迹，都被我们drop了。那么，这一章呢，我们并不打算改进，继续看看这个问题。出租车每移动一次，就会得到$-1$的奖励，那么出租车一直转圈，不接乘客又不让乘客下车的话，回报的绝对值会非常的大。回报的绝对值非常的大，会有什么问题呢？这样在反向传播的时候，会出现梯度爆炸。
但是这个没关系，在《深度学习初步及其Python实现：8.循环神经网络》中，我们专门讨论过梯度爆炸的解决方法：

1. 直接对张量进行限幅
2. 通过限制张量$\bold{W}$的范数进行梯度裁剪
3. 全局范数裁剪

有些资料认为利用"经历回放"的原因是为了解决"梯度爆炸"，我对这个略有疑虑，至少我感觉"经历回放"是充分但不是必要的方法。
我认为"经历回放"的主要作用是下面这个。

在《深度学习初步及其Python实现：5.过拟合》中，我们有讨论过：“在训练集上表现很好的模型，在测试集中也会表现很好。这是基于一个假设，训练集和测试集是独立同分布的。”
但是，在强化学习过程中，数据是智能体通过与环境交互产生的数据，所以，相邻的数据之间高度相关。

类似的问题，我们在之前也遇到过。在《深度学习初步及其Python实现》中，我们拿到的训练数据可能把有同一个标签的数据放在一块了，所以，当时，我们用多次用到这么一段代码：

db_train = db_train.shuffle()

利用这个方法，把训练数据打乱。

现在，同样的，我们的思路也是把训练数据打乱，使得数据更像是独立同分布。

接下来，我们讨论经历回放的具体操作。
智能体跟环境不断交互，将在环境中学习积累的数据存储到记忆库中。存储的时候，是按照时间步为单元进行存储的，如$<s_1,a_1,s_2,a_2>$(也可以多步)。每一次对神经网络的参数进行更新时，利用均匀随机采样的方法从数据库中抽数据，然后通过抽取的数据对神经网络进行训练。

利用"经历回放"还有一个好处，可以重复使用经历，对于数据获取困难的情况尤其适用。

小结一下，经历回放的作用：

1. 使得数据更像是独立同分布
2. 可以重复使用经历

DQN设置了单独的目标网络来处理TD偏差

TD偏差，这个并不是新的概念，只是在上一章我们讨论时序差分的时候没有提而已。
TD：$r_t + \gamma \max_{a_{t+1}}Q(s_{t+1},a_{t+1})$
TD偏差：$r_t + \gamma \max_{a_{t+1}}Q(s_{t+1},a_{t+1}) - Q(s_t,a_t)$
仅此而已。

最后一个改进点是DQN设置了单独的目标网络来处理TD偏差。
在Q-Learning中，我们是怎么更新$Q(s,a)$的？

$$Q(s_t,a_t) \leftarrow Q(s_t,a_t) + \alpha(r_t + \gamma \max_{a_{t+1}}Q(s_{t+1},a_{t+1}) - Q(s_t,a_t))$$

那么，现在呢？我们应该怎么更新神经网络中的参数${\theta}$？
似乎很简单，我们把函数$Q(s',a')$换成神经网络$Q(s',a';\theta)$，即

$${\theta} = {\theta} + \alpha\bigg(r + \gamma \max_{a_{t+1}} Q(s_{t+1},a_{t+1};{\theta}) - Q(s,a;{\theta})\bigg) \frac{\partial Q(s,a;{\theta})}{\partial {\theta}}$$

但是，这样做的话，我们在更新$\theta$的时候，除了我们的TD值$r + \gamma \max_{a_{t+1}} Q(s_{t+1},a_{t+1};{\theta})$进行了更新，$Q(s,a;{\theta})$也进行了更新，毕竟是同一个网络，同一组参数。在学习的过程中，$Q(s,a;{\theta})$试图追逐一个变化的$r + \gamma \max_{a_{t+1}} Q(s_{t+1},a_{t+1};{\theta})$，容易出现不稳定的情况。
那么，我们怎么办？
那么，我们就用不同的网络，不同的参数，即设置单独的目标网络来处理TD偏差。
V.Mnih等在2015年发表了论文《Human-level control through deep reinforcement learning》，提出了目标网络(target network)这一概念。
目标网络是在原有的神经网络之外再搭建一份结构完全相同的网络。原先就有的神经网络，我们称之为评估网络(evaluation network)。在学习的过程中，使用目标网络来进行自益得到回报的评估值，作为学习的目标。在权重更新的过程中，更新评估网络的权重，暂时不更新目标网络的权重。注意，暂时。

这样，更新权重时针对的目标不会在每次迭代都变化，是一个固定的目标。在完成一定次数的更新后，再将评估网络的权重值赋给目标网络，进而进行下一批更新。这样，目标网络也能得到更新。

这就像在户外徒步的时候，我们有对路线熟悉的同学走在前面，我们称之为向导或前锋(雇佣的当地人称之为向导，和我们一起来玩的称之为前锋)。向导前锋要负责把大家带到营地。但是如果大家走的太慢，向导前锋又一直在往前走的话，岂不是分分钟，这个队伍就丢了？所以，这时候，请向导前锋停下来，等一等。

由于在目标网络没有变化的一段时间内回报的估计是相对固定的，目标网络的引入增加了学习的稳定性。
目前，目标网络已经成为DQN的主流做法。

除了DQN有两个神经网络，我们在《深度学习初步及其Python实现：11.生成对抗网络》也讨论过拥有两个神经网络的模型，生成对抗网络。而且，在生成对抗网络中，我们有一个比较像的小技巧，在一个step中多次训练鉴别器。有点类似。

综上所述，我们把参数更新的方法修改为：

$${\theta} = {\theta} + \alpha\bigg(r_1 + \gamma \max_{a_{t+1}} Q(s_{t+1},a_{t+1};\bold{\theta_{\text{目标}}}) - Q(s_t,a_t;{\theta})\bigg) \frac{\partial Q(s_t,a_t;{\theta})}{\partial {\theta}}$$

DQN的流程

DQN算法
输入：
  环境
输出：
  最优网络参数$\theta$
初始化：
  经历库$\mathcal{D}$
  初始化网络参数$\theta$为任意值(随机初始化)，并利用该参数初始化动作价值函数$Q_{\theta}$
  初始化目标网络参数$\theta_{\text{目标}} \leftarrow \theta$，利用$\theta_{\text{目标}}$初始化动作价值函数$Q_{\theta_{\text{目标}}}$
对每一条轨迹执行以下操作：
  初始化状态$s_t$，此时$t=1$
  $t = 1,2,\cdots,T$，轨迹内的每一个时间步执行以下操作：
    根据$\varepsilon$探索策略$\mu$选择行为$a_t$。(以$\varepsilon$的概率选择任一随机动作，以$1-\varepsilon$的概率选择使动作价值函数的值最大的动作。)
    环境给出奖励$r_{t+1}$，状态转移至$s_{t+1}$
    将序列{$s_t,a_t,r_{t+1},s_{t+1}$}存入经历库$\mathcal{D}$
 
    当经历库$\mathcal{D}$中有一定的经历时，随机采样$k$个经历。
      例如，其中一个经历是$s_j,a_j,r_{j+1},s_{j+1}$
      TD值$y_j$：如果$s_{j+1}$不是终止状态，$y_j = r_j + \gamma \max_{a'} Q(s',a';{\theta}_{\text{目标}})$；如果$s_{j+1}$是终止状态，$y_j = r_j$
    $k$个经历的损失函数为：$Loss(\theta) = \frac{1}{k} \sum^k_{i=1}(y_i - Q(s_i,a_j;\theta))^2$
    对$Loss(\theta)$执行梯度下降：$\nabla \theta = \frac{\partial Loss(\theta)}{\partial \theta}$
    更新网络参数：$\theta \leftarrow \theta + \alpha \nabla \theta$
 
    每隔一定的步数，更新$\theta_{\text{目标}} \leftarrow \theta$

DQN的实现

我们以小车上山问题为例。

该例子来自《强化学习：原理与Python实现(肖智清著)》这本书的第六章。

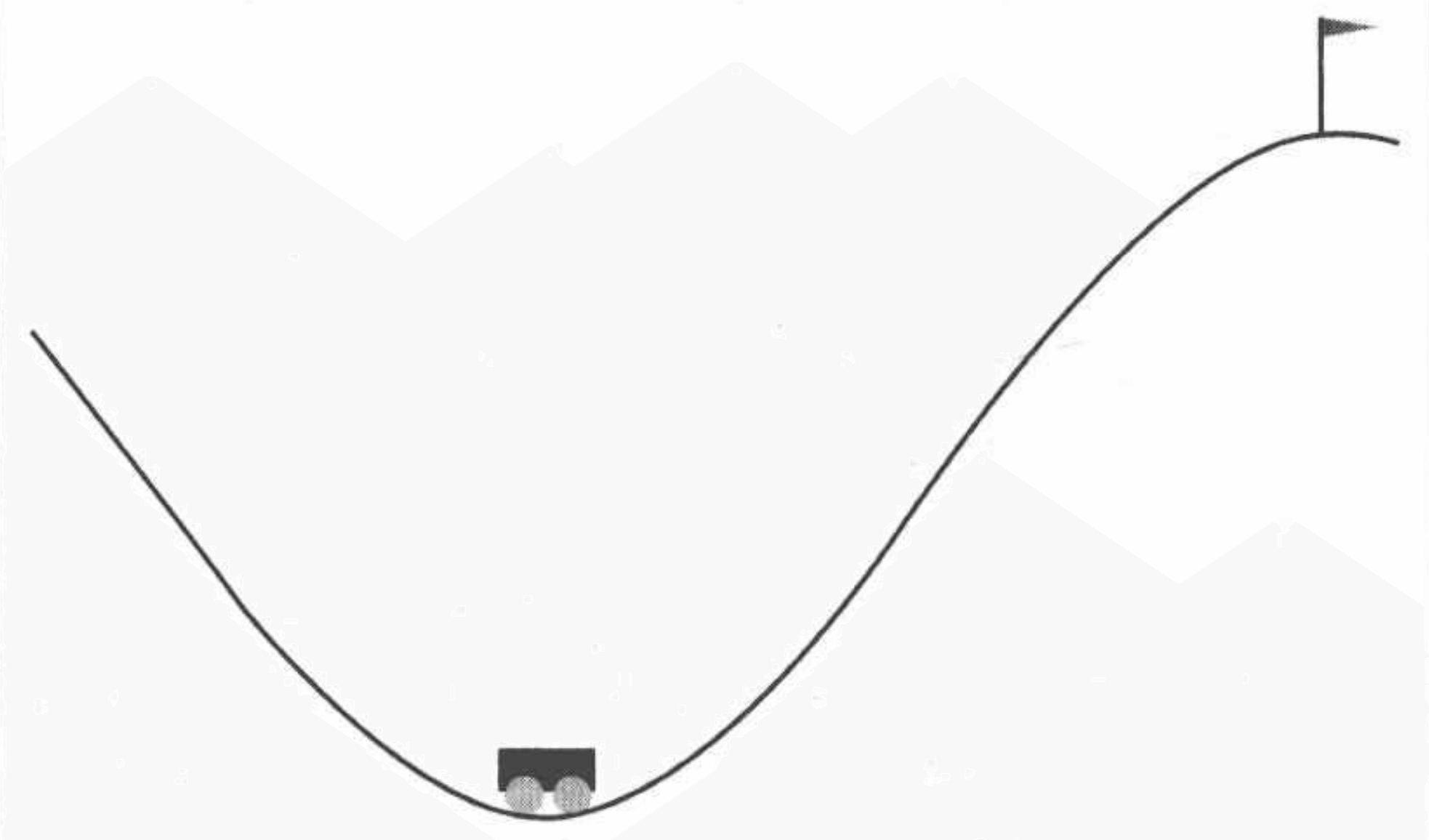
小车上山问题描述

如图所示，一辆小车在一段范围内行驶。在任一时刻，在水平方向看，小车位置的范围是$[-1.2,0.6]$，速度的范围是$[-0.07,0.07]$，在每个时刻，智能体可以对小车施加3种动作中的一种：向左施力、不施力、向右施力。智能体施力和小车的水平位置会共同决定小车下一时刻的速度。当某时刻小车的水平位置大于$0.5$时，控制目标成功达成，回合结束。控制的目标是让小车以尽可能少的步骤达到目标。在绝大多数情况下，智能体简单向右施力并足以让小车成功越过目标。

小车的位置和速度是有数学表达式的，记$t$时刻$(t=0,1,2,\cdots)$，小车的位置为$X_t$，速度为$V_t$，智能体施力为$A_t \in \{0,1,2\}$分别代表向左施力、不施力和向右施力，初始状态$X_0 \in [-0.6,-0.4)$，$V_0 = 0$。
从$t$时刻到$t+1$时刻的表达式为

$$\begin{aligned} X_{t+1} &= X_t + V_t \\ V_{t+1} &= V_t + 0.001(A_t - 1) - 0.0025 \cos (3 X_t) \end{aligned}$$

• 注意！小车位置的范围是$[-1.2,0.6]$，速度的范围是$[-0.07,0.07]$，所以如果$X_{t+1}$和$V_{t+1}$的值也都存在上下界。
• 我们通过这个表达式也可以看到，总是向右施加力量的话，并不能使小车到达目的地。

而且！当然！这个表达式，只是为了描述问题用。

我们构造的智能体不知道环境确定小车位置速度的表达式。

环境及其使用

示例代码：

import gym
env = gym.make('MountainCar-v0')
# 限制最多200步，unwrapped这一行注释掉
# env = env.unwrapped
env.seed(0)
print('状态空间 = {}'.format(env.observation_space))
print('动作空间 = {}'.format(env.action_space))
print('位置范围 = {}'.format((env.unwrapped.min_position, env.unwrapped.max_position)))
print('速度范围 = {}'.format((-env.unwrapped.max_speed,env.unwrapped.max_speed)))
print('目标位置 = {}'.format(env.unwrapped.goal_position))

运行结果：

状态空间 = Box(-1.2000000476837158, 0.6000000238418579, (2,), float32)
动作空间 = Discrete(3)
位置范围 = (-1.2, 0.6)
速度范围 = (-0.07, 0.07)
目标位置 = 0.5

• 注意这里打印的状态空间，不再是离散的了。

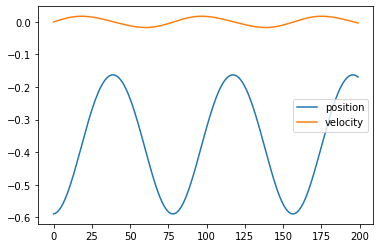
在上文，我们通过数学表达式发现，总是向右施加力量，并不能使小车成功抵达目的地。现在，我们来试一下，看看是不是这样。

示例代码：

import matplotlib.pyplot as plt
positions, velocities = [], []
observation = env.reset()
while True:
    positions.append(observation[0])
    velocities.append(observation[1])
    next_observation, reward, done, _ = env.step(2)
    if done:
        break
    observation = next_observation

if next_observation[0] > 0.5:
    print('成功到达')
else:
    print('失败退出')

# 绘制位置和速度图像
fig, ax = plt.subplots()
ax.plot(positions, label='position')
ax.plot(velocities, label='velocity')
ax.legend()

运行结果：

失败退出

DQN的代码

接下来，我们来实现一个DQN。

经历库

示例代码：

import pandas as pd

# 经历库
class DQNReplayer:
    def __init__(self, capacity):
        '''

        :param capacity: 经历库的大小
        '''
        self.memory = pd.DataFrame(index=range(capacity),columns=['observation', 'action', 'reward','next_observation', 'done'])
        self.i = 0
        self.count = 0
        self.capacity = capacity

    def store(self, *args):
        self.memory.loc[self.i] = args
        self.i = (self.i + 1) % self.capacity
        self.count = min(self.count + 1, self.capacity)

    def sample(self, size):
        indices = np.random.choice(self.count, size=size)
        return (np.stack(self.memory.loc[indices, field]) for field in self.memory.columns)

DQN智能体

示例代码：

import tensorflow as tf
tf.random.set_seed(0)
from tensorflow import keras

class DQNAgent:
    def __init__(self, env, net_kwargs={}, gamma=0.99, epsilon=0.001,replayer_capacity=10000, batch_size=64):
        '''

        :param env: 环境
        :param net_kwargs:
        :param gamma: 折扣因子
        :param epsilon: epsilon探索策略
        :param replayer_capacity: 经历库的大小
        :param batch_size: batch
        '''
        observation_dim = env.observation_space.shape[0]
        self.action_n = env.action_space.n
        self.gamma = gamma
        self.epsilon = epsilon

        self.batch_size = batch_size
        # 经历回放
        self.replayer = DQNReplayer(replayer_capacity)
        # 评估网络
        self.evaluate_net = self.build_network(input_size=observation_dim,output_size=self.action_n, **net_kwargs)
        # 目标网络
        self.target_net = self.build_network(input_size=observation_dim,output_size=self.action_n, **net_kwargs)

        self.target_net.set_weights(self.evaluate_net.get_weights())

    # 构建网络
    def build_network(self, input_size, hidden_sizes, output_size,activation=tf.nn.relu, output_activation=None,learning_rate=0.01):
        model = keras.Sequential()
        for layer, hidden_size in enumerate(hidden_sizes):
            kwargs = dict(input_shape=(input_size,)) if not layer else {}
            model.add(keras.layers.Dense(units=hidden_size,activation=activation, **kwargs))
        model.add(keras.layers.Dense(units=output_size,activation=output_activation)) # 输出层
        optimizer = tf.optimizers.Adam(lr=learning_rate)
        model.compile(loss='mse', optimizer=optimizer)
        return model

    def learn(self, observation, action, reward, next_observation, done):
        # 存储经验
        self.replayer.store(observation, action, reward, next_observation,done)
        # 经验回放
        observations, actions, rewards, next_observations, dones = self.replayer.sample(self.batch_size)
        next_qs = self.target_net.predict(next_observations)
        next_max_qs = next_qs.max(axis=-1)
        us = rewards + self.gamma * (1. - dones) * next_max_qs
        targets = self.evaluate_net.predict(observations)
        targets[np.arange(us.shape[0]), actions] = us
        self.evaluate_net.fit(observations, targets, verbose=0)

        if done: # 更新目标网络
            self.target_net.set_weights(self.evaluate_net.get_weights())

    # epsilon探索策略
    def decide(self, observation):
        if np.random.rand() < self.epsilon:
            return np.random.randint(self.action_n)
        qs = self.evaluate_net.predict(observation[np.newaxis])
        return np.argmax(qs)

play_qlearning

正如我们上文讨论的，DQN的训练过程和Q-Learning的训练过程并无主要区别，在这里，我们复用上一章的play_qlearning方法。
示例代码：

def play_qlearning(env, agent, train=False, render=False):
    episode_reward = 0
    observation = env.reset()
    while True:
        if render:
            env.render()
        action = agent.decide(observation)
        next_observation, reward, done, _ = env.step(action)
        episode_reward += reward
        if train:
            agent.learn(observation, action, reward, next_observation,
                    done)
        if done:
            break
        observation = next_observation
    return episode_reward

训练

示例代码：

net_kwargs = {'hidden_sizes' : [64, 64], 'learning_rate' : 0.001}
agent = DQNAgent(env, net_kwargs=net_kwargs)

# 训练
episodes = 500
episode_rewards = []
for episode in range(episodes):
    episode_reward = play_qlearning(env, agent, train=True)
    episode_rewards.append(episode_reward)
    print('{}  {}'.format(episode,episode_reward))

运行结果：

0  -200.0
1  -200.0
2  -200.0
3  -200.0
4  -200.0

【部分运行结果略】

495  -172.0
496  -89.0
497  -113.0
498  -147.0
499  -149.0

测试

再来看看效果。
示例代码：

# 测试
agent.epsilon = 0. # 取消探索
episode_rewards = [play_qlearning(env, agent) for _ in range(100)]
print('平均回合奖励 = {} / {} = {}'.format(sum(episode_rewards),len(episode_rewards), np.mean(episode_rewards)))

运行结果：

平均回合奖励 = -13435.0 / 100 = -134.35

DoubleDQN

最大化偏差的缺点

在来看看我们的TD偏差

$$r_t + \gamma \max_{a_{t+1}}Q(s_{t+1},a_{t+1}) - Q(s_t,a_t)$$

我们要$\max_{a_{t+1}}Q(s_{t+1},a_{t+1})$，即最大化偏差，这当然没问题，肯定要去拟合去逼近最佳的策略。

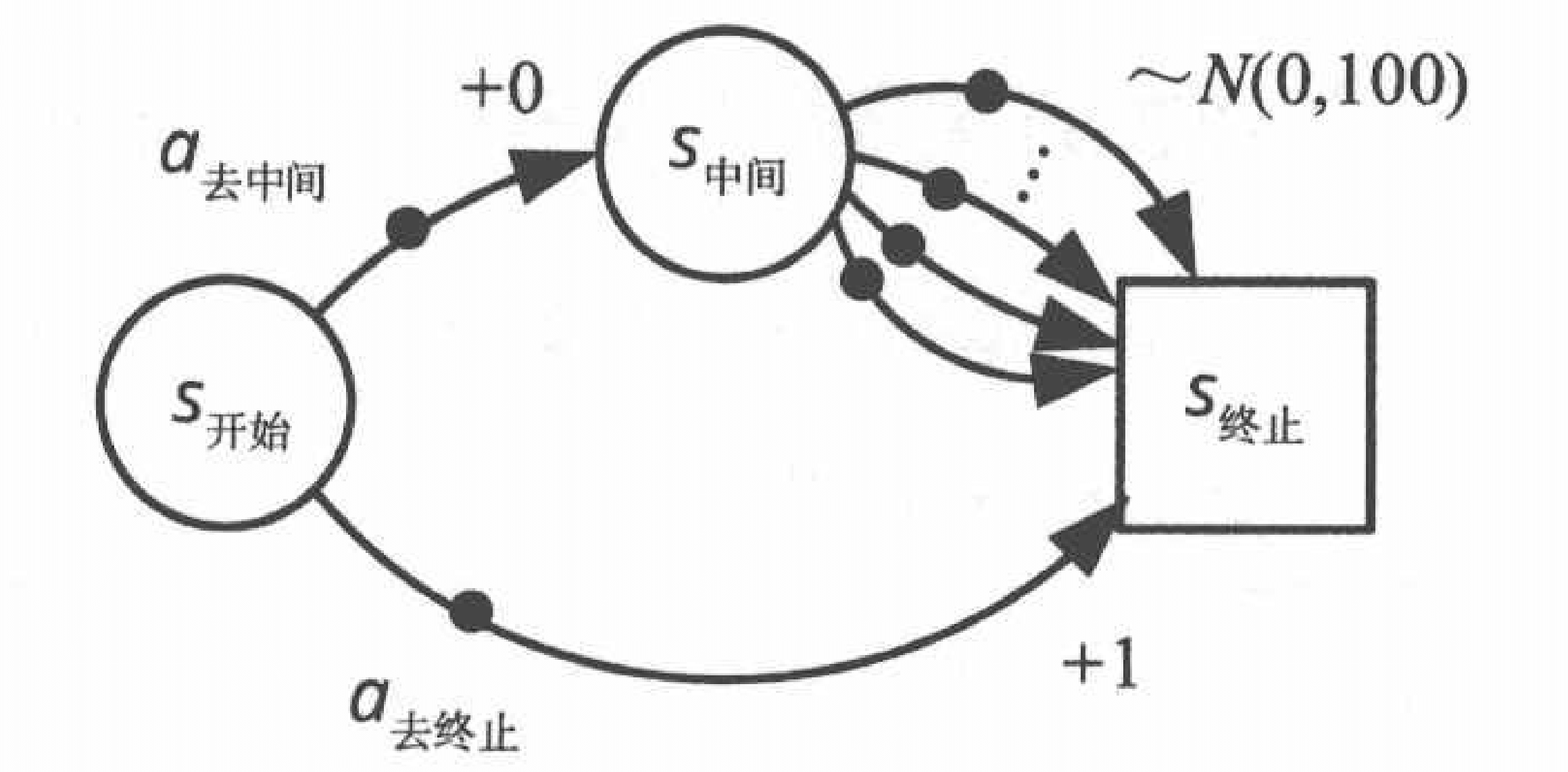
但！假设存在这么一个环境：

我们解释以下从$S_{\text{中间}}$到$S_{\text{终止}}$这一部分的含义。
从$S_{\text{中间}}$到$S_{\text{终止}}$有很多动作可以做，所有的动作都会让状态转移到$S_{\text{终止}}$，并且所有的奖励服从均值为$0$，方差为$1$的正态分布。
那么，毫无疑问。最优状态函数$V_{\star}(S_{\text{中间}}) = 0$，$V_{\star}(S_{\text{开始}}) = 1$。最优策略是$\pi_{\star}(S_{\text{开始}})=a_{\text{去终止}}$。
但如果我们采用Q-Learning，无论是传统的Q-Learning或DQN，从$S_{\text{中间}}$出发采取的某些动作会采样到比较大的奖励值，从而导致$\max_{a \in \mathcal{A}(S_{\text{中间}})} Q(S_{\text{中间}},a)$的值较大。如果运气又很不好，真有可能就迭代出一个策略$\pi(S_{\text{开始}}) = a_{\text{去中间}}$。
这就是最大化偏差的缺点，使得估计的动作价值偏大。

为了在一定程度上克服这个问题，我们引进一个新的方法DoubleDQN。特别注意，其实DoubleDQN并没有完全解决估计的动作价值偏大的问题，只是在一定的程序上克服了。

DoubleDQN，顾名思义，两个DQN。在上文我们讨论过，一个DQN有两个神经网络，一个目标网络，一个评估网络。那么DoubleDQN有几个网络呢？还是两个。

我们用评估网络选择动作，网络参数为$\theta$。

$$a_{\star} = \argmax_{a_{t+1}} Q(s_{t+1},{a_{t+1}};\theta)$$

然后，使用目标网络找到这个动作对应的$Q$值，以构成TD目标，网络参数为$\theta_{\text{目标}}$

$$Y^{DDQN} = r + \gamma Q(s_{t+1},a_{\star};\theta_{\text{目标}})$$

即

$$Y^{DDQN} = r + \gamma Q(s_{t+1},\argmax_{a_{t+1}} Q(s_{t+1},{a_{t+1}};\theta);\theta_{\text{目标}})$$

和DQN对比一下，在DQN中，最佳动作来自于目标网络。即最佳动作$a_{\star} = \argmax_a(s,a;\theta_{\text{目标}})$。但是在DuobleDQN中，最佳动作来自于评估网络。那么，这个Q值在目标网络中还真不一定是最大的，因此可以避免选到被高估的次优行为。
除此之外，其他与DQN一致。

DoubleDQN的过程

DoubleDQN算法
输入：
  环境
输出：
  最优网络参数$\theta$
初始化：
  经历库$\mathcal{D}$
  初始化评估网络参数$\theta$为任意值(随机初始化)，并利用该参数初始化动作价值函数$Q_{\theta}$
  初始化目标网络参数$\theta_{\text{目标}} \leftarrow \theta$，利用$\theta_{\text{目标}}$初始化动作价值函数$Q_{\theta_{\text{目标}}}$
对每一条轨迹执行以下操作：
  初始化状态$s_t$，此时$t=1$
  $t = 1,2,\cdots,T$，轨迹内的每一个时间步执行以下操作：
    根据$\varepsilon$探索策略$\mu$选择行为$a_t$，并执行。(以$\varepsilon$的概率选择任一随机动作，以$1-\varepsilon$的概率选择使动作价值函数的值最大的动作。)
    环境给出奖励$r_{t+1}$，状态转移至$s_{t+1}$
    将经历{$s_t,a_t,r_{t+1},s_{t+1}$}存入经历库$\mathcal{D}$
 
    当经历库$D$中有一定的经历，随机采样$k$个经历。
      例如，其中一个经历是$s_j,a_j,r_{j+1},s_{j+1}$
      TD值$y_j$：如果$s_{j+1}$不是终止状态，$y_j = r_j + \gamma Q(s_{t+1},\argmax_{a'}(s_{t+1},a';{\theta});{\theta}_{\text{目标}})$；如果$s_{j+1}$是终止状态，$y_j = r_j$
    $k$个经历的损失函数为：$Loss(\theta) = \frac{1}{k} \sum^k_{i=1}(y_i - Q(s_i,a_j;\theta))^2$
    对$Loss(\theta)$执行梯度下降：$\nabla \theta = \frac{\partial Loss(\theta)}{\partial \theta}$
    更新网络参数：$\theta \leftarrow \theta + \alpha \nabla \theta$
 
    每隔一定的步数步，更行$\theta_{\text{目标}} \leftarrow \theta$

DoubleDQN的实现

DoubleDQN

接下来，我们来实现一个DoubleDQN。
示例代码：

class DoubleDQNAgent(DQNAgent):
    def learn(self, observation, action, reward, next_observation, done):
        self.replayer.store(observation, action, reward, next_observation,done) # 存储经验
        observations, actions, rewards, next_observations, dones = self.replayer.sample(self.batch_size) # 经验回放
        next_eval_qs = self.evaluate_net.predict(next_observations)
        next_actions = next_eval_qs.argmax(axis=-1)
        next_qs = self.target_net.predict(next_observations)
        next_max_qs = next_qs[np.arange(next_qs.shape[0]), next_actions] 
        us = rewards + self.gamma * next_max_qs * (1. - dones)
        targets = self.evaluate_net.predict(observations)
        targets[np.arange(us.shape[0]), actions] = us
        self.evaluate_net.fit(observations, targets, verbose=0)

        if done:
            self.target_net.set_weights(self.evaluate_net.get_weights())

训练

示例代码：

net_kwargs = {'hidden_sizes' : [64, 64], 'learning_rate' : 0.001}
agent = DoubleDQNAgent(env, net_kwargs=net_kwargs)

# 训练
episodes = 500
episode_rewards = []
for episode in range(episodes):
    episode_reward = play_qlearning(env, agent, train=True)
    episode_rewards.append(episode_reward)
    print('{}  {}'.format(episode,episode_reward))

运行结果：

0  -200.0
1  -200.0
2  -200.0
3  -200.0
4  -200.0

【部分运行结果略】

495  -144.0
496  -196.0
497  -151.0
498  -119.0
499  -94.0

测试

再来看看效果。

示例代码：

# 测试
agent.epsilon = 0. # 取消探索
episode_rewards = [play_qlearning(env, agent) for _ in range(100)]
print('平均回合奖励 = {} / {} = {}'.format(sum(episode_rewards),len(episode_rewards), np.mean(episode_rewards)))

运行结果：

平均回合奖励 = -12786.0 / 100 = -127.86

Deuling DQN

我们讨论的最后一种是Deuling DQN，这种算法对神经网络的结构进行了修改。
在DQN和Doubel DQN中，我们的神经网络的结构是

而Deuling DQNd的神经网络结构是

$V(s)$被称为价值(Value)，代表当前状态的价值。$A(s,a)$被称为优势(Advantage)，代表当前状态下的所有动作的优势。而最后的动作价值函数是

$$Q(s,a) = V(s) + A(s,a)$$

在实际中，我们还会对$A(s,a)$优势函数做限制，我们限制所有的$A(s,a)$之和为$0$。这样的话，$V(s)$代表的是$Q(s,a)$的平均值。
相较于DQN，Dueling DQN的训练更容易，收敛速度更快。