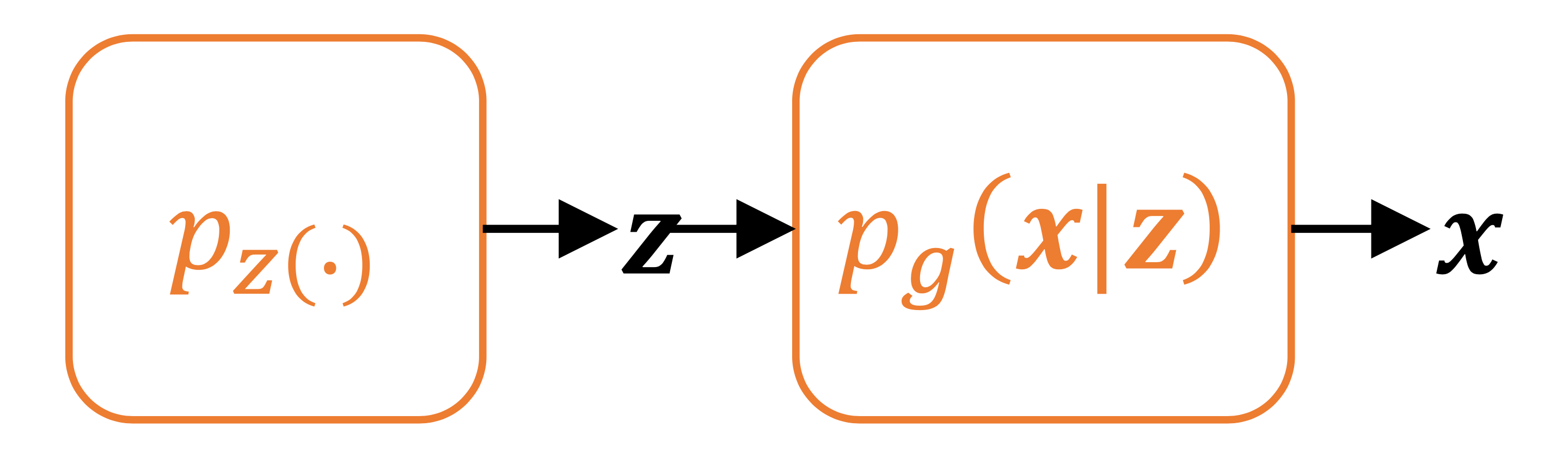在金庸的武侠小说中有这么一个情节，黄蓉伪造了一本《九阴真经》。欧阳锋错练这本伪造的《九阴真经》，导致心神大乱。
那么？怎么伪造九阴真经呢？我想最简单的方法是，有一位精通《九阴真经》的高手，黄蓉先伪造一本给高手看看，高手打回，黄蓉再伪造，高手再打回。在这期间，黄蓉的造假水平一直再提升，如此多次，直到这位高手觉得满意，然后黄蓉再故意泄漏给欧阳锋。但是，整部小说，并没有谁精通《九阴真经》。唯一精通《九阴真经》的是写这本武功秘籍的人，北宋时期的黄裳，而整部小说的背景却是南宋。
如此情况下，怎么伪造九阴真经呢？

这就涉及到我们这一章的主题：生成对抗网络。

生成对抗网络的原理

网络模型介绍

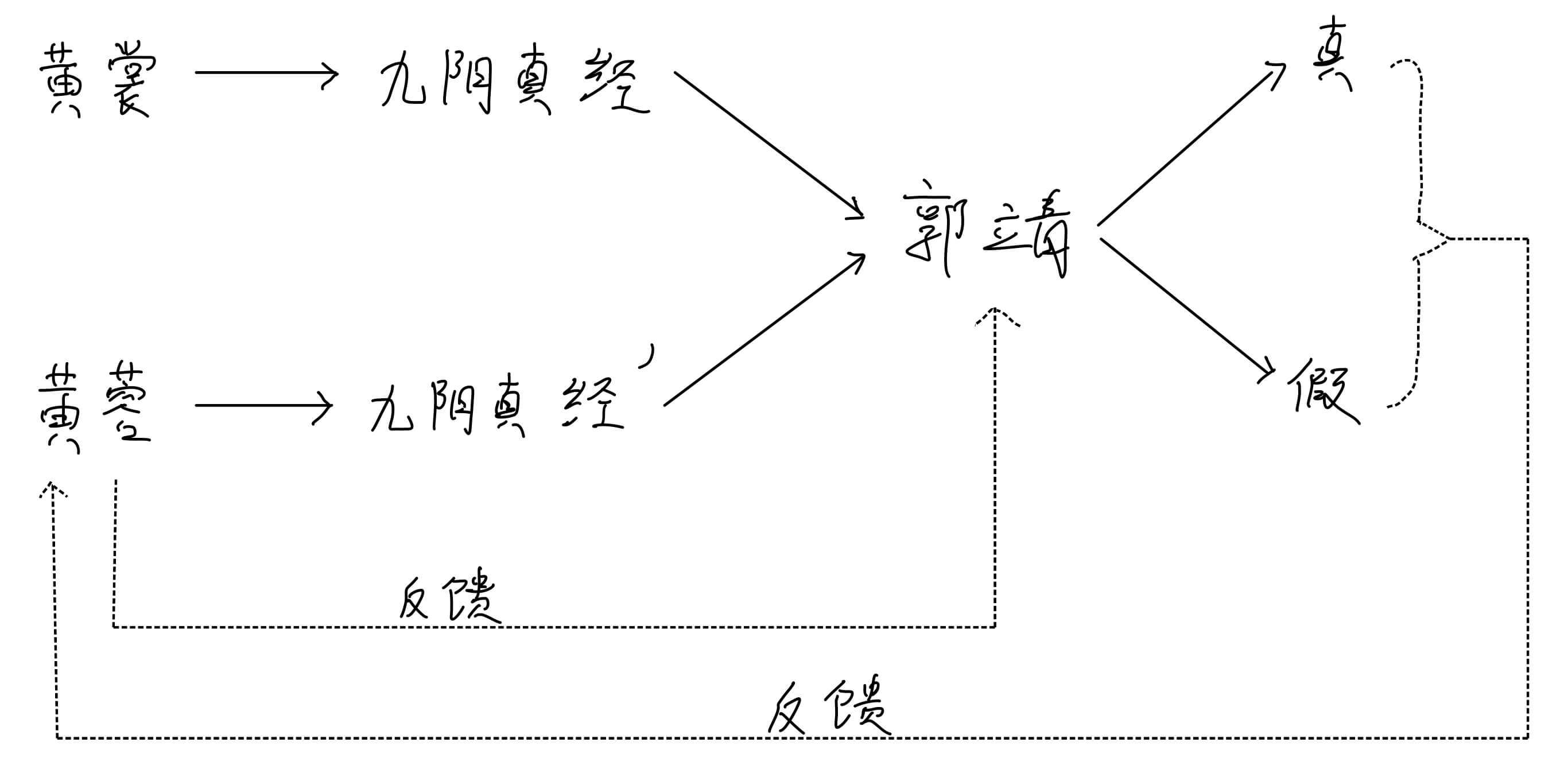
下图就是我们伪造《九阴真经》的方案。

这里解释一下。

九阴真经是北宋时期黄裳所著，小说的背景是南宋。所以在这个过程中，九阴真经是静态的，就像我们的样本数据。
九阴真经 $\bold{'}$ 是黄蓉所编撰的，是动态的。
郭靖也是动态的，郭靖的鉴别水平是在不断提升的。
当然，我们的目标不是培养鉴别水平高超的郭靖，而是培养伪造水平高超的黄蓉。
图中还有两条虚线。真和假到黄蓉的这条虚线，含义是鉴别结果会反馈给黄蓉。
当然郭靖也要提高自己的水平，所以，黄蓉也会反馈信息给郭靖。

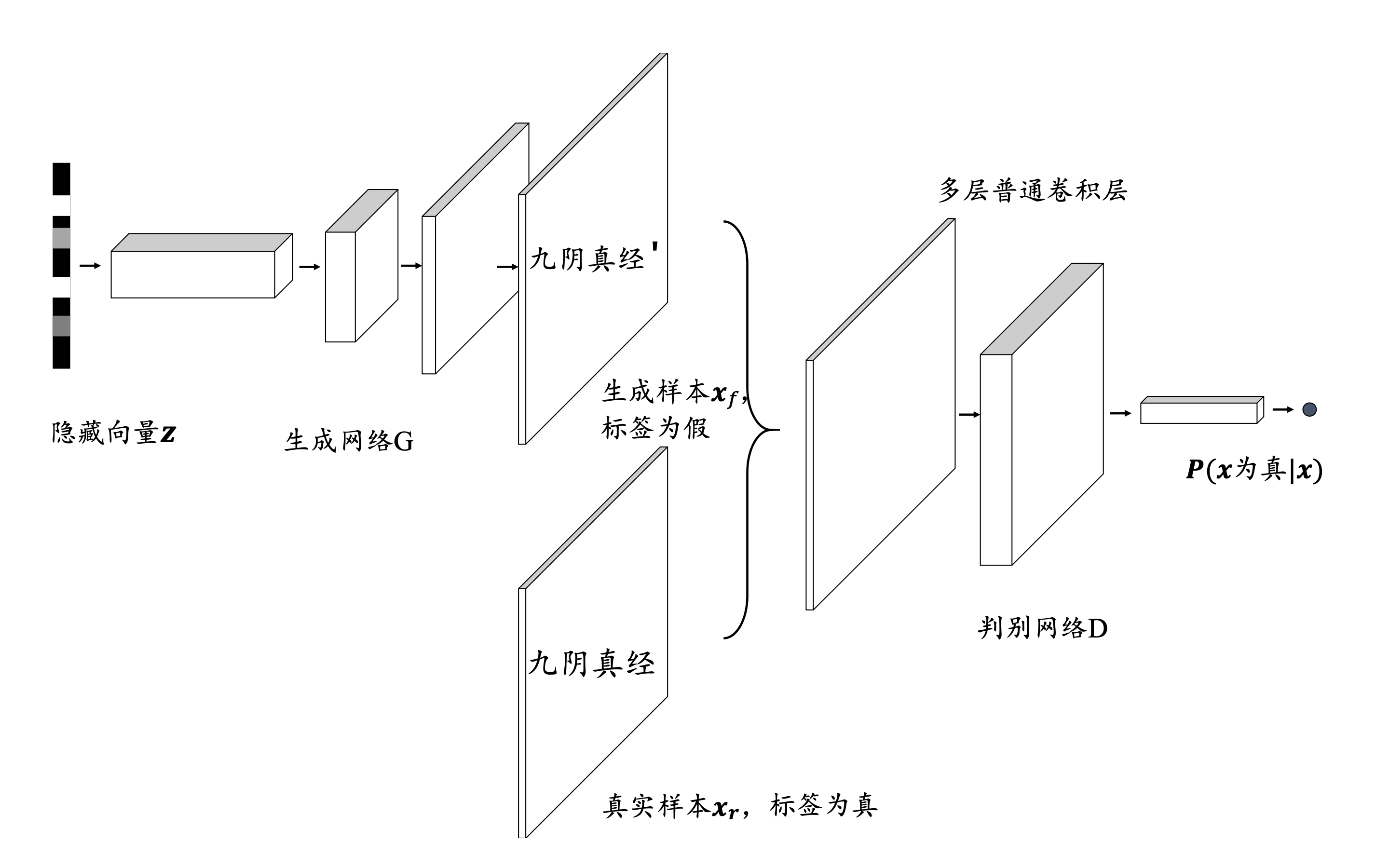
现在，我们把这个过程抽象出来。

1、样本数据

黄裳写的九阴真经是我们的样本数据，我们表示成 $\{\bold{x_i}\}_{i=1}^{n}$ ，服从一个分布 $p_{data}$ 。

2、生成网络

黄蓉写的九阴真经 $\bold{'}$ 也会服从一个分布，我们记做 $p_g(\bold{x}|\bold{z})$ ；再假设存在 $\bold{z} \sim p_z$ 。则有：

3、郭靖的鉴别

郭靖会对来自黄裳的九阴真经和来自黄蓉的九阴真经 $\bold{'}$ 进行鉴别，即输入 $\bold{x}$ 包含来自真实数据分布 $p_r$ 的样本 $\bold{x_r} \sim p_r$ ，和来自生成器的假样本 $\bold{x}_f \sim p_g(\bold{x}|\bold{z})$ 。

最后，我们把上面的那个方案，抽象成如下。

在《基于Hexo的博客搭建：10.Hexo中的信息安全实践》有一个非常相近的操作，自己想破解的方法，自己来反破解，然后再自己想破解的方法，自己反破解…
循环往复，破解的能力和反破解的能力，都得到了提升。
当然，我们的目标是反破解能力很高。

目标函数

首先，我们的目标是培养伪造水平高超的黄蓉。那么，为了实现这个目标，我们需要：

鉴别水平高超的郭靖
伪造水平高超的黄蓉

鉴别水平高超的郭靖

那么郭靖的鉴别水平高，体现在什么地方？
首先，如果鉴别的是九阴真经，那么应该鉴别为真；如果鉴别的是九阴真经 $\bold{'}$ ，那么应该鉴别为假。

即

如果 $\bold{x} \sim p_{data}$ ，那么， $D(\bold{x})$ 应该较大。
如果 $\bold{x} \sim p_g(x)$ ，那么， $1 - D(\bold{\bold{x}})$ 应该较大。
换句话说，如果 $\bold{z} \sim p_z$ ，那么， $1 - D(G(\bold{z}))$ 应该较大。

需要注意的是，为了计算方便，我们通常用 $\log(D(\bold{x}))$ 和 $\log(1 - D(G(\bold{z})))$

那么，我们的目标就是：

$\max_D \ \mathbf{E}_{(x \sim p_data)}[\log(D(\bold{x}))] + \mathbf{E}_{\bold{z} \sim p_z}[\log(1 - D(G(\bold{z})))]$

伪造水平高超的黄蓉

那么？怎么体现黄蓉的伪造水平高超呢？如果编撰出来的九阴真经 $\bold{'}$ ，鉴别水平高超的郭靖认为是真的；就说明黄蓉的伪造水平高超。
即，目标是：

$\min_G \ \mathbf{E}_{\bold{z} \sim p_z}[\log(1 - D(G(\bold{z})))]$

总目标

先成就郭靖，再实现黄蓉。毕竟要先郭靖鉴别水平高超，然后看不出黄蓉的九阴真经 $\bold{'}$ 是伪造的，这样才有意义。
所以我们的总目标是，先 $\max$ ，再 $\min$ 。

$\min_G \max_D \ \mathbf{E}_{(x \sim p_data)}[\log(D(\bold{x}))] + \mathbf{E}_{\bold{z} \sim p_z}[\log(1 - D(G(\bold{z})))]$

其实，还有一个问题。我们在构造目标函数的时候，完全是类比推理了一个我们认为有道理的目标函数。
那么，这个目标函数到底有没有最优解？如果存在的话， $p_g$ 到底等不等于 $p_{data}$ ？
结论是：存在最优解， $p_g = p_{data}$ 。

算法流程

生成对抗网络的算法流程

随机初始化参数 $\theta$ 和 $\phi$
repeat
for step = 1,2,…,N do
随机采样 $\bold{z} \sim p_z$
随机采样真实样本 $\bold{x_r} \sim p_r$
根据梯度上升算法更新鉴别器D网络：

$\nabla_{\theta}\ \mathbf{E}_{\bold{x_r} \sim p_r} \log D_{\theta}(\bold{x_r}) + \mathbf{E}_{\bold{x_f} \sim p_g} \log(1 - D_{\theta}(\bold{x}_f))$

随机采样隐向量 $\bold{z} \sim p_z$
根据梯度下降算法更新生成器G网络：

$\nabla_{\phi}\ \mathbf{E}_{\bold{z} \sim p_z} \log (1 - D_{\theta}(G_{\phi}(\bold{z})))$

end
until 训练达到最大回合数 Epoch 或者达到要求
输出：训练之后的生成器 $G_{\phi}$

说明：

$\theta$ 是鉴别器D的参数。
$\phi$ 是生成器G的参数。
对于鉴别器要梯度上升，因为目标是 $\max$ 。
对于生成器要梯度下降，因为目标是 $\min$ 。

DCGAN的实现

完整可运行代码见：
https://github.com/KakaWanYifan/deep-learning-for-blog/blob/master/Ch11/Ch11-1.py

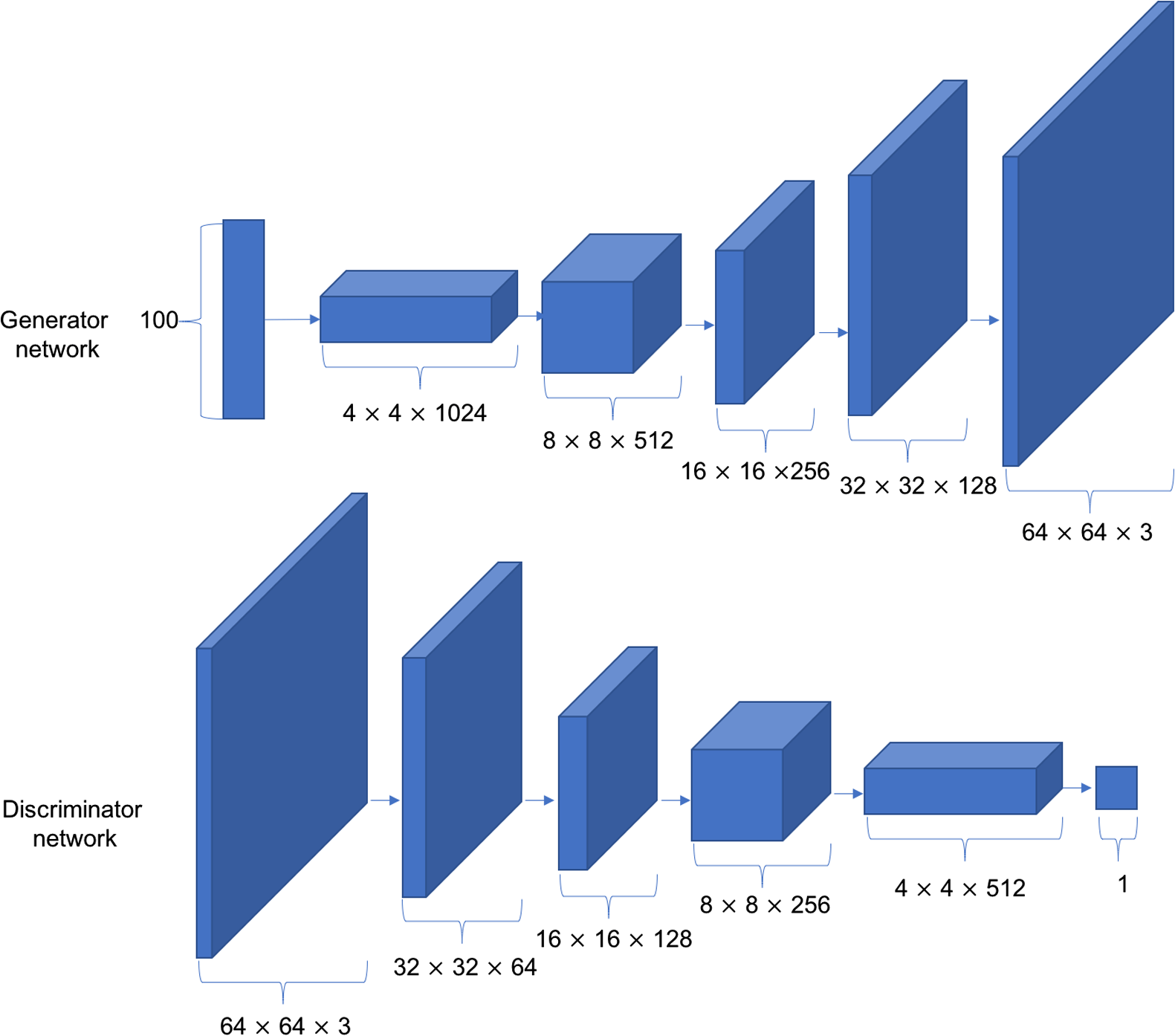
刚刚我们讨论生成对抗网络的时候，一直没有讨论生成器内部结构是什么，鉴别器内部结构是什么。其实这个可以多种多样，完全可以自定义的。其中，最经典的是深度卷积生成对抗网络(Deep Convolution Generative Adversarial Networks，简称DCGAN)。

其网络结构如图：
生成器：

接下来，我们来实现一个DCGAN，我们以动漫头像的生成为例。

生成器

生成生成器G由5个转置卷积层单元堆叠而成，实现特征图高宽的层层放大，特征图通道数的层层减少。每个卷积层中间插入BN层来提高训练稳定性。

示例代码：

# 生成器
class Generator(Model):

    def __init__(self):
        super(Generator, self).__init__()

        # z: [b, 100] => [b, 3*3*512] => [b, 3, 3, 512] => [b, 64, 64, 3]
        self.fc = layers.Dense(3 * 3 * 512)

        self.conv1 = layers.Conv2DTranspose(256, 3, 3, 'valid')
        self.bn1 = layers.BatchNormalization()

        self.conv2 = layers.Conv2DTranspose(128, 5, 2, 'valid')
        self.bn2 = layers.BatchNormalization()

        self.conv3 = layers.Conv2DTranspose(3, 4, 3, 'valid')

    def call(self, inputs, training=None):
        # [z, 100] => [z, 3*3*512]
        x = self.fc(inputs)
        x = tf.reshape(x, [-1, 3, 3, 512])
        x = tf.nn.leaky_relu(x)

        x = tf.nn.leaky_relu(self.bn1(self.conv1(x), training=training))
        x = tf.nn.leaky_relu(self.bn2(self.conv2(x), training=training))
        x = self.conv3(x)
        x = tf.tanh(x)

        return x

x = tf.tanh(x)，所以之后我们的图片数据都要从[0,255]缩小到[-1,1]。

我们还可以传一个 $\bold{z}$ 进来，试一下。
示例代码：

1
2
3

g = Generator()
z = tf.random.normal([2,100])
print(g(z).shape)

运行结果：

1	(2, 64, 64, 3)

鉴别器

鉴别器D与普通的分类网络相同，最后通过一个全连接层获得二分类任务的概率。

示例代码：

# 鉴别器
class Discriminator(Model):
    def __init__(self):
        super(Discriminator, self).__init__()

        # [b, 64, 64, 3] -> [b, 1]

        self.conv1 = layers.Conv2D(64, 5, 3, 'valid')

        self.conv2 = layers.Conv2D(128, 5, 3, 'valid')
        self.bn2 = layers.BatchNormalization()

        self.conv3 = layers.Conv2D(256, 5, 3, 'valid')
        self.bn3 = layers.BatchNormalization()

        # [b, h, w ,c] => [b, -1]
        self.flatten = layers.Flatten()
        self.fc = layers.Dense(1)

    def call(self, inputs, training=None):
        x = tf.nn.leaky_relu(self.conv1(inputs))
        x = tf.nn.leaky_relu(self.bn2(self.conv2(x), training=training))
        x = tf.nn.leaky_relu(self.bn3(self.conv3(x), training=training))

        # [b, h, w, c] => [b, -1]
        x = self.flatten(x)

        # [b, -1] => [b, 1]
        logits = self.fc(x)

        return logits

我们还可以传一张图片 $\bold{x}$ 进来，试一下。
示例代码：

1
2
3

d = Discriminator()
x = tf.random.normal([2,64,64,3])
print(d(x))

运行结果：

1
2
3

tf.Tensor(
[[-0.11715111]
 [-0.02971719]], shape=(2, 1), dtype=float32)

损失函数

$\min_G \max_D \ \mathbf{E}_{(x \sim p_data)}[\log(D(\bold{x}))] + \mathbf{E}_{\bold{z} \sim p_z}[\log(1 - D(G(\bold{z})))]$

鉴别器的损失函数

对于鉴别器，我们的目标是最大化上面那个式子。
即，使得真实样本预测为真的概率接近于1，生成样本预测为真的概率接近于0。
示例代码：

# 鉴别器的损失函数
def d_loss_fn(generator, discriminator, batch_z, batch_x, is_training):
    # 采样生成图片
    fake_image = generator(batch_z, is_training)
    # 判定生成图片
    d_fake_logits = discriminator(fake_image, is_training)

    # 判定真实图片
    d_real_logits = discriminator(batch_x, is_training)
    # 真实图片与 1 之间的误差
    d_loss_real = celoss_ones(d_real_logits)
    # 生成图片与 0 之间的误差
    d_loss_fake = celoss_zeros(d_fake_logits)

    # 合并误差
    loss = d_loss_fake + d_loss_real

    return loss

celoss_ones计算当前预测概率与标签1之间的交叉熵损失。
示例代码：

def celoss_ones(logits):
    y = tf.ones_like(logits)
    loss = losses.binary_crossentropy(y, logits, from_logits=True)
    return tf.reduce_mean(loss)

celoss_zeros计算当前预测概率与标签0之间的交叉熵损失。
示例代码：

def celoss_zeros(logits):
    y = tf.zeros_like(logits)
    loss = losses.binary_crossentropy(y, logits, from_logits=True)
    return tf.reduce_mean(loss)

生成器的损失函数

对于生成器来说，真实样本与生成器没有关系。所以只需要最小化 $\mathbf{E}_{\bold{z} \sim p_z}[\log(1 - D(G(\bold{z})))]$ 。
示例代码：

# 生成器的损失函数
def g_loss_fn(generator, discriminator, batch_z, is_training):
    # 采样生成图片
    fake_image = generator(batch_z, is_training)
    # 在训练生成网络时,需要迫使生成图片判定为真
    d_fake_logits = discriminator(fake_image, is_training)
    # 计算生成图片与1 之间的误差
    loss = celoss_ones(d_fake_logits)

    return loss

加载数据集

与之前的章节不一样的是，不是来自keras.datasets，需要我们额外进行下载。

数据可以从这里下载：
链接：https://pan.baidu.com/s/1Kyk3_iCxL5Lt78m7tUocfA
提取码：kaka
解压密码：kaka

我们先把数据下载解压之后，然后加载数据。

示例代码：

img_paths = glob.glob('./Ch11-Data/*.jpg')
print(len(img_paths))

dataset, img_shape, len_dataset = Ch11Util.make_anime_dataset(img_paths=img_paths, batch_size=128, resize=64)
print(dataset, img_shape, len_dataset)
sample = next(iter(dataset))
print(sample.shape)

运行结果：

1
2
3

51223
<PrefetchDataset shapes: (128, 64, 64, 3), types: tf.float32> (64, 64, 3) 400
(128, 64, 64, 3)

这里有一个resize的操作
Ch11Util参考：https://github.com/KakaWanYifan/deep-learning-for-blog/blob/master/Ch11/Ch11Util.py

然后我们还可以把数据还原回图片。
示例代码：

for i in range(25):
    plt.subplot(5, 5, i + 1)
    x = (images[i] + 1.0) * 127.5
    x = tf.cast(x=x, dtype=tf.int32)
    plt.imshow(x)
plt.show()

运行结果：

另外，我还需要设置一个dataset.repeat()，让dataset的迭代无限。
示例代码：

1 2	dataset = dataset.repeat() db_iter = iter(dataset)

模型训练

实例化生成器和鉴别器

示例代码：

generator = Generator()
generator.build(input_shape=(None, 100))
discriminator = Discriminator()
discriminator.build(input_shape=(None, 64, 64, 3))

print(generator.summary())
print('\n' * 2)
print(discriminator.summary())

运行结果：

Model: "generator_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_2 (Dense)              multiple                  465408    
_________________________________________________________________
conv2d_transpose_3 (Conv2DTr multiple                  1179904   
_________________________________________________________________
batch_normalization_4 (Batch multiple                  1024      
_________________________________________________________________
conv2d_transpose_4 (Conv2DTr multiple                  819328    
_________________________________________________________________
batch_normalization_5 (Batch multiple                  512       
_________________________________________________________________
conv2d_transpose_5 (Conv2DTr multiple                  6147      
=================================================================
Total params: 2,472,323
Trainable params: 2,471,555
Non-trainable params: 768
_________________________________________________________________
None



Model: "discriminator_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv2d_3 (Conv2D)            multiple                  4864      
_________________________________________________________________
conv2d_4 (Conv2D)            multiple                  204928    
_________________________________________________________________
batch_normalization_6 (Batch multiple                  512       
_________________________________________________________________
conv2d_5 (Conv2D)            multiple                  819456    
_________________________________________________________________
batch_normalization_7 (Batch multiple                  1024      
_________________________________________________________________
flatten_1 (Flatten)          multiple                  0         
_________________________________________________________________
dense_3 (Dense)              multiple                  257       
=================================================================
Total params: 1,031,041
Trainable params: 1,030,273
Non-trainable params: 768
_________________________________________________________________
None

创建两个优化器

示例代码：

1 2	g_optimizer = tf.optimizers.Adam(learning_rate=0.002, beta_1=0.5) d_optimizer = tf.optimizers.Adam(learning_rate=0.002, beta_1=0.5)

一个模型一个优化器，所以需要两个优化器

迭代更新，查看效果

示例代码：

for epoch in range(1000000):

    batch_z = tf.random.uniform([128, 100], minval=-1.0, maxval=1.0)
    batch_x = next(db_iter)

    # 训练 D
    with tf.GradientTape() as tape:
        d_loss = d_loss_fn(generator, discriminator, batch_z, batch_x, True)
    grads = tape.gradient(d_loss, discriminator.trainable_variables)
    d_optimizer.apply_gradients(zip(grads, discriminator.trainable_variables))

    # 训练 G
    with tf.GradientTape() as tape:
        g_loss = g_loss_fn(generator, discriminator, batch_z, True)
    grads = tape.gradient(g_loss, generator.trainable_variables)
    g_optimizer.apply_gradients(zip(grads, generator.trainable_variables))

    if epoch % 100 == 0:
        print(epoch, 'd-loss:', float(d_loss), 'g-loss:', float(g_loss))

        z = tf.random.uniform([25, 100])
        fake_image = generator(z, training=False)
        paintImg(fake_image)

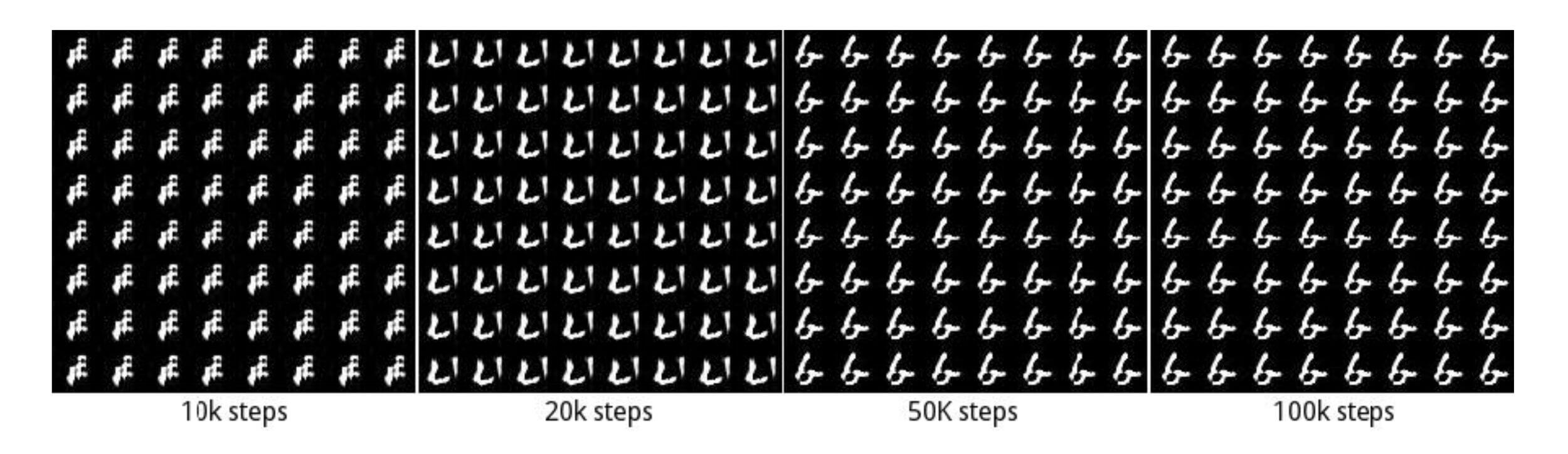
运行结果：

(2, 64, 64, 3)
51223
<PrefetchDataset shapes: (128, 64, 64, 3), types: tf.float32> (64, 64, 3) 400
(128, 64, 64, 3)
0 d-loss: 1.5906527042388916 g-loss: 1.8171882629394531
100 d-loss: 1.2427457571029663 g-loss: 0.8827457427978516
200 d-loss: 1.4038290977478027 g-loss: 0.8095071911811829

【部分运行结果略】

29800 d-loss: 0.15395832061767578 g-loss: 5.291758060455322
29900 d-loss: 0.18237310647964478 g-loss: 4.279458999633789
30000 d-loss: 0.1850486397743225 g-loss: 4.413983345031738

我找了一台废弃的电脑，那台电脑只有一张集成显卡Intel HD Graphics 520，这玩意不支持TensorFlow的GPU运算，所以只能用CPU运算。且CPU的性能也有限，在运行了近36个小时之后，迭代了30000个epoch，效果如上图。如果有GPU的话，速度会更快。

GAN的不稳定

GAN的不稳定主要体现在超参数敏感和模式崩塌。

超参数敏感

网络结构、学习率、初始化状态等这些都是超参数。这些超参数的一个微小的调整可能导致网络的训练结果截然不同。

为此，DCGAN论文作者提出了不使用Pooling层、多使用Batch Normalization层、不使用全连接层、生成网络中激活函数应使用ReLU、最后一层使用tanh、判别网络激活函数应使用LeakyLeLU等一系列经验性的训练技巧。

模式崩塌

模式崩塌(Mode Collapse)是指模型生成的样本单一，多样性很差的现象。由于鉴别器只能鉴别单个样本是否采样自真实分布，并没有对样本多样性进行约束，导致生成模型倾向于生成真实分布的部分区间中的少量高质量样本，以此来在鉴别器中获得较高的概率值，而不会学习到全部的真实分布。

如图所示，我们可以看到生成的图片种类非常单一，生成器总是倾向于生成某种单一风格的样本图片，以此骗过判别器。

原因

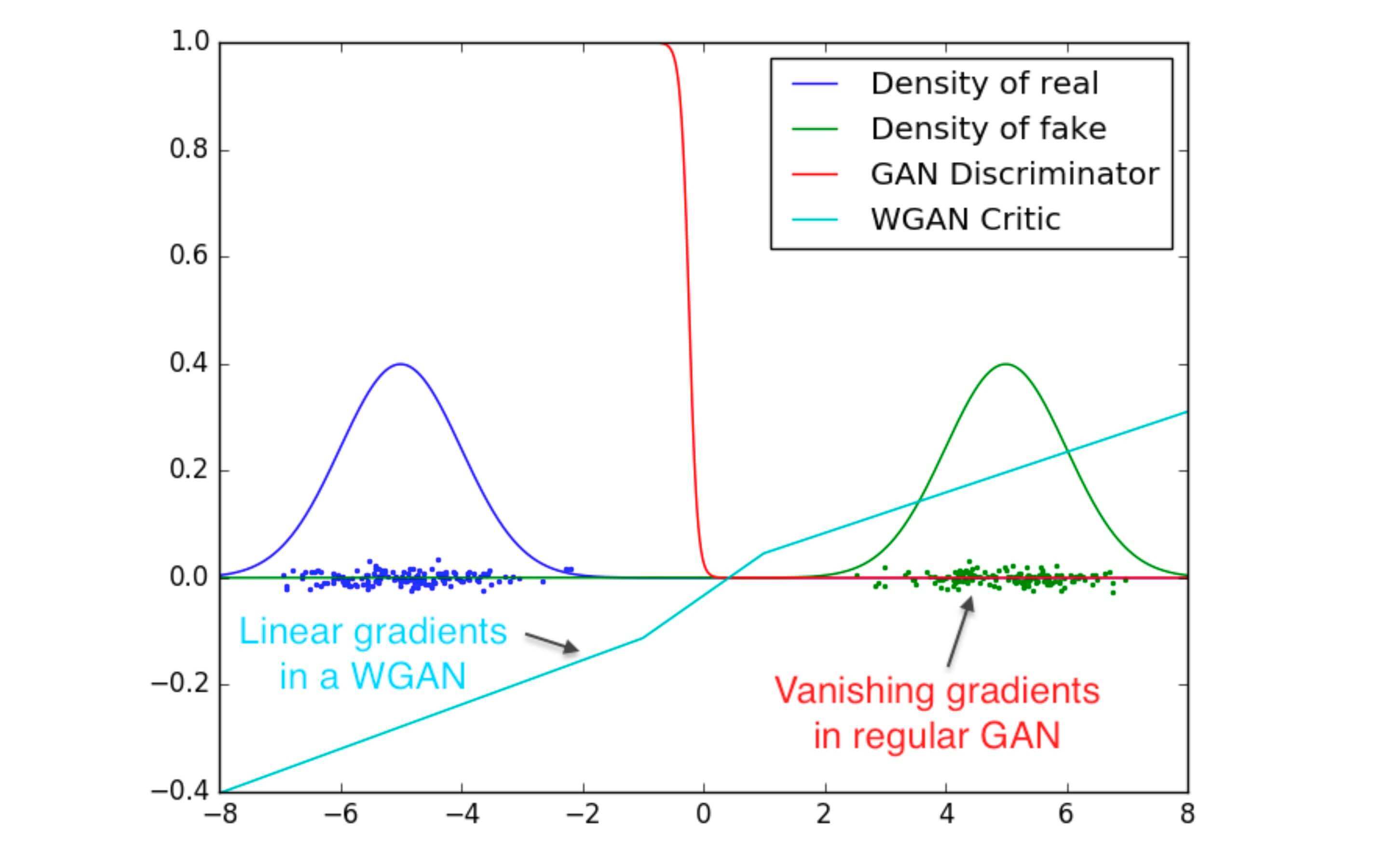
GAN的不稳定性是因为JS散度在不重叠的分布 $p$ 和 $q$ 上的梯度曲面是恒为0的。

如图所示，当分布 $p$ 和 $q$ 不重叠时，JS散度的梯度值始终为0，从而导致此时GAN的训练出现梯度弥散现象，参数长时间得不到更新，网络无法收敛。解决办法是WGAN。

更通俗的解释是：
当鉴别器非常准确时，鉴别器的损失很快收敛到0，从而无法提供可靠的路径使生成器的梯度继续更新，造成生成器梯度消失。GAN的训练因为一开始随机噪声分布，与真实数据分布相差距离太远，两个分布之间几乎没有任何重叠的部分，这时候鉴别器能够很快的学习把真实数据和生成的假数据区分开来达到鉴别的最优，造成生成器的梯度无法继续更新甚至梯度消失。

WGAN-GP及其实现

完整可运行代码见：
https://github.com/KakaWanYifan/deep-learning-for-blog/blob/master/Ch11/Ch11-2.py

WGAN-GP是一种常见的WGAN模型。和GAN的区别主要在三个地方：

梯度惩罚项
鉴别器的损失函数
生成器的损失函数

其他和GAN基本相同。

梯度惩罚项

示例代码：

# 梯度惩罚项
def gradient_penalty(discriminator, batch_x, fake_image):
    batchsz = batch_x.shape[0]

    # 每个样本均随机采样 t,用于插值
    t = tf.random.uniform([batchsz, 1, 1, 1])
    # 自动扩展为 x 的形状,[b, 1, 1, 1] => [b, h, w, c]
    t = tf.broadcast_to(t, batch_x.shape)

    # 在真假图片之间做线性插值
    interplate = t * batch_x + (1 - t) * fake_image

    # 在梯度环境中计算 D 对插值样本的梯度
    with tf.GradientTape() as tape:
        # 加入梯度观察列表
        tape.watch([interplate])
        d_interplote_logits = discriminator(interplate)
    # 计算每个样本的梯度的范数:[b, h, w, c] => [b, -1]
    grads = tape.gradient(d_interplote_logits, interplate)
    grads = tf.reshape(grads, [grads.shape[0], -1])
    # [b]
    gp = tf.norm(grads, axis=1)
    # 计算梯度惩罚项
    gp = tf.reduce_mean( (gp-1.)**2 )

    return gp

鉴别器的损失函数

WGAN-GP鉴别器D的损失函数和GAN的不一样。WGAN-GP直接最大化真实样本的输出值，最小化生成样本的输出值，没有交叉熵计算的过程。
示例代码：

# 鉴别器的损失函数
def d_loss_fn(generator, discriminator, batch_z, batch_x, is_training):
    # 假样本
    fake_image = generator(batch_z, is_training)
    # 假样本的输出
    d_fake_logits = discriminator(fake_image, is_training)
    # 真样本的输出
    d_real_logits = discriminator(batch_x, is_training)
    # 计算梯度惩罚项
    gp = gradient_penalty(discriminator, batch_x, fake_image)
    # 最小化假样本的输出和梯度惩罚项
    loss = tf.reduce_mean(d_fake_logits) - tf.reduce_mean(d_real_logits) + 10. * gp
    return loss, gp

生成器的损失函数

WGAN-GP生成器G的损失函数只需要最大化生成样本在判别器D的输出值即可，同样没有交叉熵的计算过程。
示例代码：

# 生成器的损失函数
def g_loss_fn(generator, discriminator, batch_z, is_training):
    # 生成器的损失函数
    fake_image = generator(batch_z, is_training)
    d_fake_logits = discriminator(fake_image, is_training)
    # WGAN-GP G 损失函数,最大化假样本的输出值
    loss = - tf.reduce_mean(d_fake_logits)
    return loss

最后一个小技巧，我们可以在一个step中多次训练鉴别器。因为鉴别器越准确，对生成器越有利。
因为：严师出高徒。

文章作者: Kaka Wan Yifan

文章链接: https://kakawanyifan.com/10411

留言板