12.强化学习初探

在电影《逃学威龙》中，有一个情节。周星星因为在课堂上不认真，经常被用黑板擦丢。在数次之后，周星星同学虽然没有学会认真，但学会了用手接住黑板擦。这却也是为了趋利避害，实施了对自己有利的策略。

我们这一章的主题：强化学习，就和这个类似。

关于强化学习，在《强化学习浅谈及其Python实现》中有更系统的讨论。

强化学习

什么是强化学习

现在让我们来分析这一情节。
两个主体：

1. 周星星，我们称之为智能体(agent)
2. 课堂，我们称之为环境(environment)

三个要素：

1. 正在丢来的黑板擦，我们称之为状态(state)
2. 没有去接住黑板擦/用手接住黑板擦，我们称之为动作(action)
3. 身上都是灰/身上是干净的。我们称之为反馈(reward)

所以，周星星从被黑板擦丢的身上都是灰，到用手接住黑板擦。
这个过程其实是：智能体(agent)在和环境(environment)的交互中学习，根据环境的状态(state)，执行动作(action)，并根据环境的反馈(reward)来指导更好的动作。
这就是强化学习(Reinforcement Learning，简称RL)。

从环境中获取的状态，有时候叫state，有时候叫observation，这两个其实一个代表全局状态，一个代表局部观测值，在多智能体环境里会有差别，在这里我们暂时把这两个概念划上等号。

和监督学习，无监督学习的区别

强化学习和我们之前讨论的模型都不一样。之前我们讨论的所有模型，或者属于监督学习，或者属于无监督学习。卷积神经网络(CNN)、循环神经网络(RNN)、长短期记忆神经网络(LSTM)、门控循环网络(GRU)等是监督学习，自编码器(AE)、变分自编码器(VAE)、对抗生成网络(GAN)等是无监督学习。而强化学习不属于监督学习、也不属于无监督学习。

我们来讨论一下，什么是监督学习？监督学习是寻找输入到输出之间的映射，比如分类和回归问题。那么什么是无监督学习呢？无监督学习主要寻找数据之间的隐藏关系，比如聚类和生成。那么什么是强化学习呢？强化学习是在与环境的交互中学习和寻找最佳决策。

强化学习、监督学习、无监督学习、机器学习、深度学习之间的关系可以用下面的图表示。

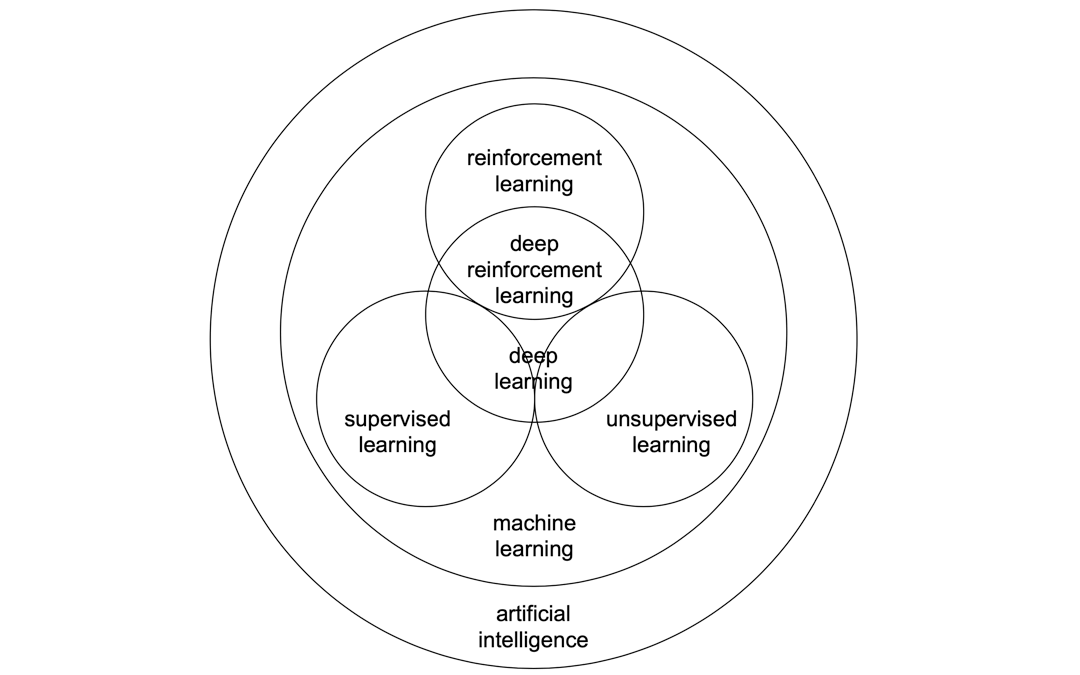
由于近些年来的技术突破，强化学习和深度学习的整合，使得强化学习有了进一步的发展运用，就是图中的deep reinforcement learning(深度强化学习)。

强化学习的分类

首先，按照环境是否已知，强化学习可以分为两类：

1. Model-Based，环境已知，代表算法是动态规划。
2. Model-Free，环境未知，在这种情况下，只有一种办法，探索与利用。

我们这一章的讨论重点是Model-Free。

• 有一些资料认为，只有Model-Free，环境未知的，才属于强化学习。
• 关于Model-Based，环境已知，在《强化学习浅谈及其Python实现：2.动态规划》中有更多的讨论。

而Model-Free又可以分为两类：

1. Value-Based：基于价值
2. Policy-Based：基于策略

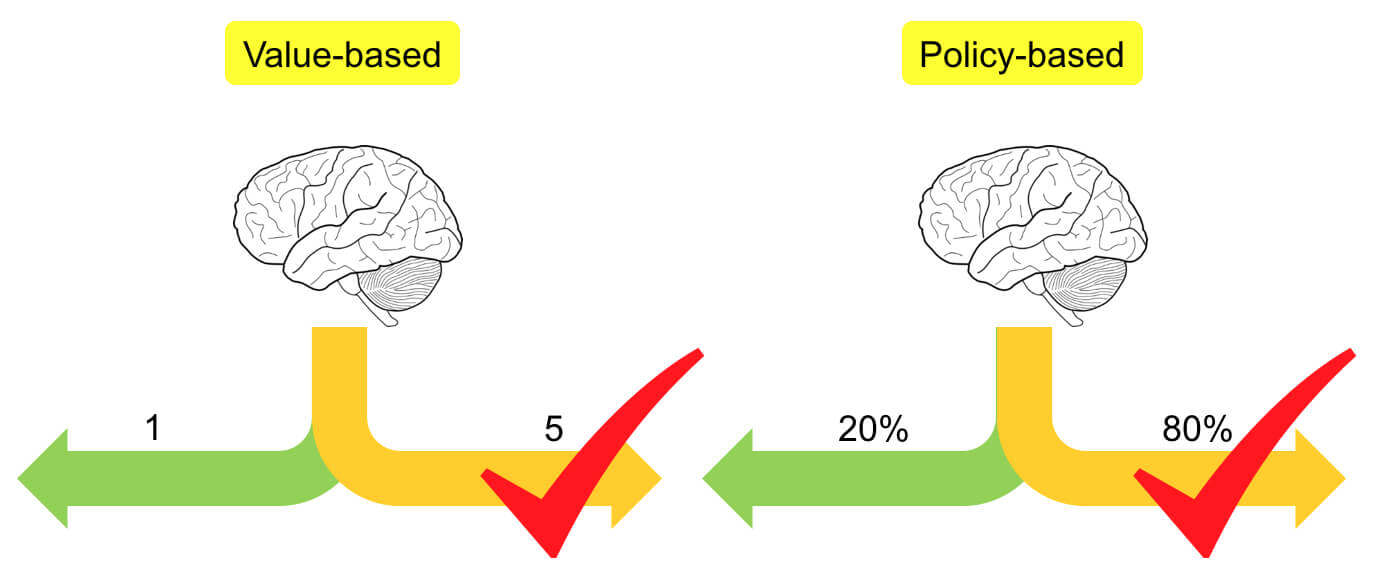
Value-Based基于价值的方法是分析所有动作的价值，选择最高价值的动作，不考虑其他动作，即确定性策略。
我们主要会讨论三个：

1. Sarsa
2. Q-Learning
3. DQN

• 关于Sarsa和Q-Learning，在《强化学习浅谈及其Python实现：4.时序差分》有更详细的讨论。
• 关于DQN，在《强化学习浅谈及其Python实现：5.函数近似》有更详细的讨论。

Policy-Based基于策略的方法会分析下一步要采取各种动作的概率，然后根据概率采取行动。既然是概率了，那么概率高不一定就能被选中，概率低也不一定就选不中，即随机性策略。
我们会讨论Policy gradient。

基于表格型方法求解RL

首先，我们来讨论Sarsa和Q-Learning。

马尔可夫决策过程

通过刚刚讨论的周星星同学的例子，我们知道强化学习有三个要素：

1. S：state，状态
2. A：action，动作
3. R：reward，反馈

我们也知道在强化学习中，智能体和环境的交互，是一步一步交互的。

如图所示，是一个和时间相关的序列决策问题。

如果举一个更形象的例子话，问在野外遇到熊怎么办？

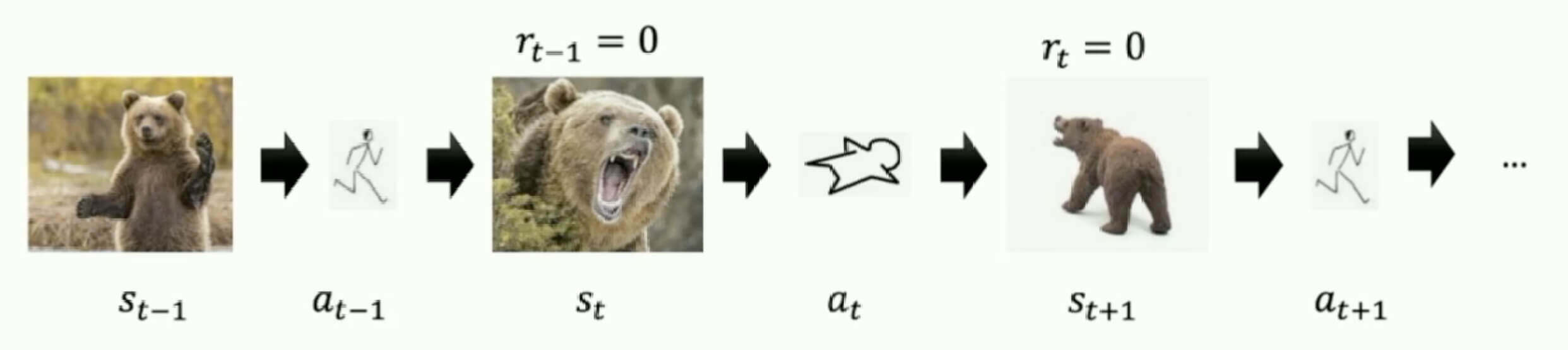
• 在$t-1$时刻，我们看到熊在朝我们招手$(s_{t-1})$，输出动作跑$(a_{t-1})$。
• 在$t$时刻，熊的状态是咆哮$(s_{t})$，我们很机智的输出新动作装死$(a_{t})$。
• 在$t+1$时刻，熊的状态是选择离开$(s_{t+1})$，我们再输出动作跑$(a_{t+1})$。

这样的话，我们能够逃生。但是我们在每一个时刻，都有不同的选择。比如在$t$时刻，我们继续选择跑，这样当然有一定的概率逃跑成功$r_t = 0$，但也有一定的概率是Game Over$r_t = -100$。

对于这个概率，我们称之为状态转移概率$p(s_{t+1},r_t|s_t,a_t)$，表示在$s_t$时刻选择动作$a_t$，转移到状态$s_{t+1}$，并拿到反馈$r_t$的概率。
而且我们发现，$s_{t+1}$只取决于$t$时刻，和更早的时刻无关。这个是什么？马尔可夫。

马尔可夫性质: 当前时刻的状态仅与前一时刻的状态和动作有关，与其他时刻的状态和动作条件独立。

而这样的一个过程，我们称之为马尔可夫决策过程(Markov Decision Process，简称MDP)。

Q表格

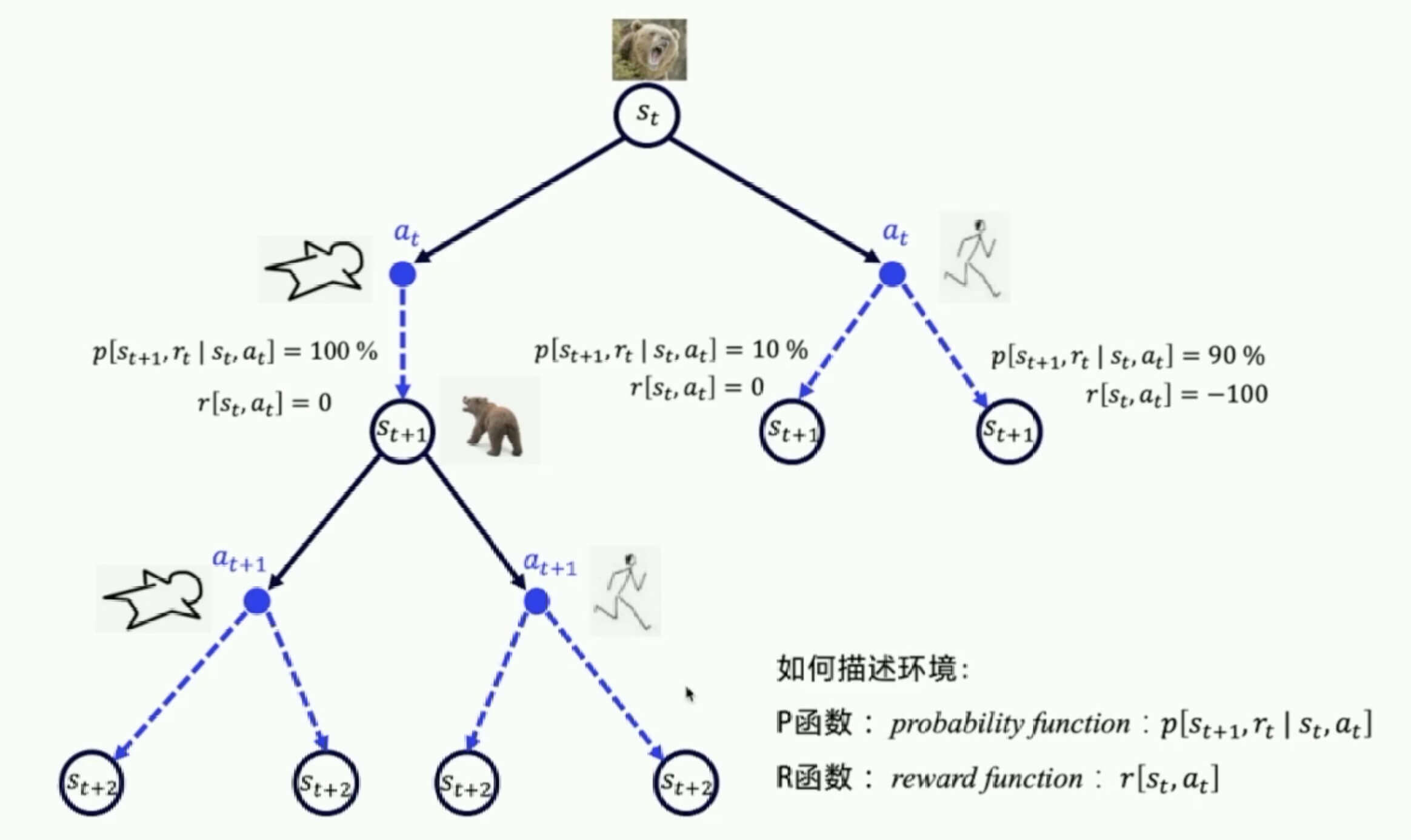
我们可以把所有可能的动作和可能的状态转移的关系画成一个树状图。
在这里，我们用P函数和R函数来描述环境，如果P函数和R函数已知的话，我们就说环境是已知的Model-Based那么？如果都已知了？就不需要强化学习了，我想我们用纸和笔，就能规划出最佳决策。
可是现在问题就是，不是已知的。那么，我们只能试错和探索了。在试错和探索足够多次之后，我们会迭代更新出一本《野外求生指南》，这就是我们的Q表格。

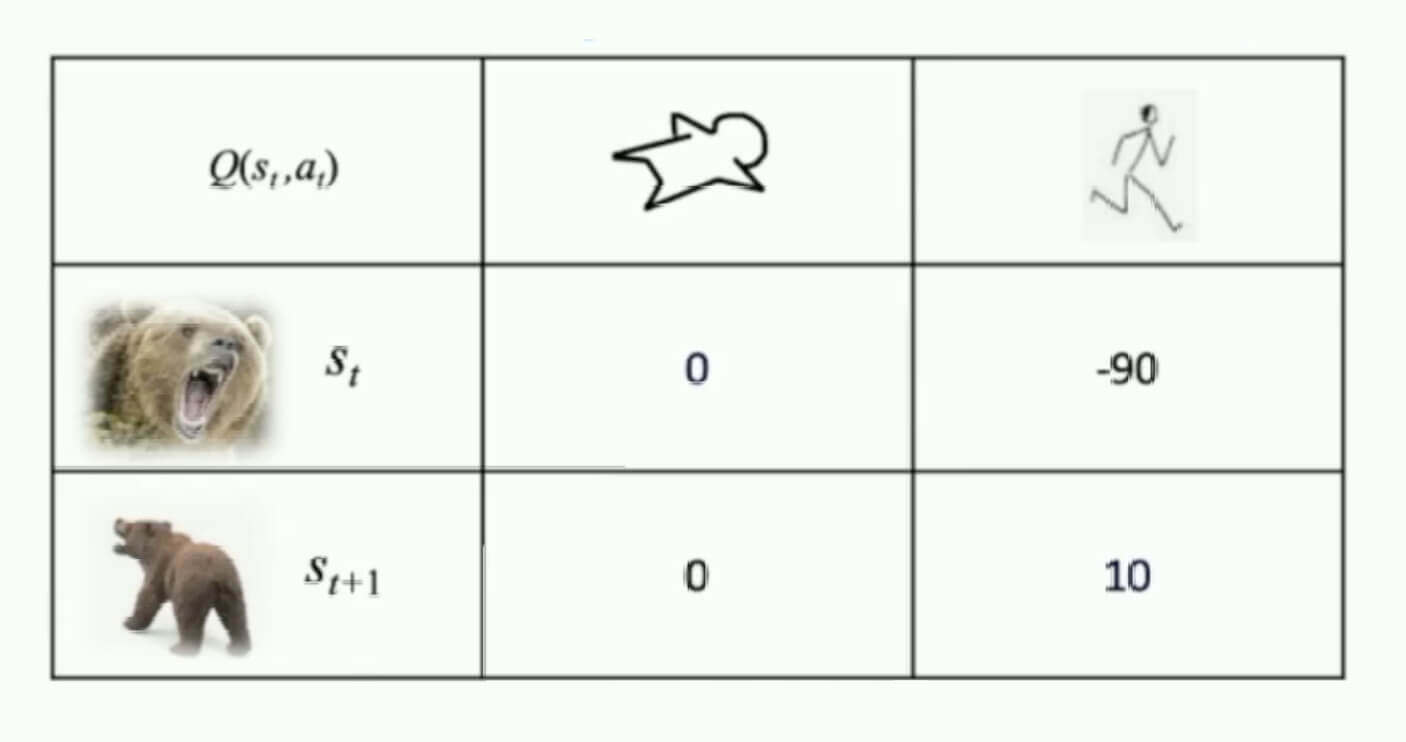
那么，这本《野外求生指南》怎么用呢？我们为每个状态下的每一个动作都赋予了一个价值，我们的目标就是根据Q表格实现未来总收益的最大。

如图所示，小汽车不应该闯红灯，但是救护车应该闯红灯。

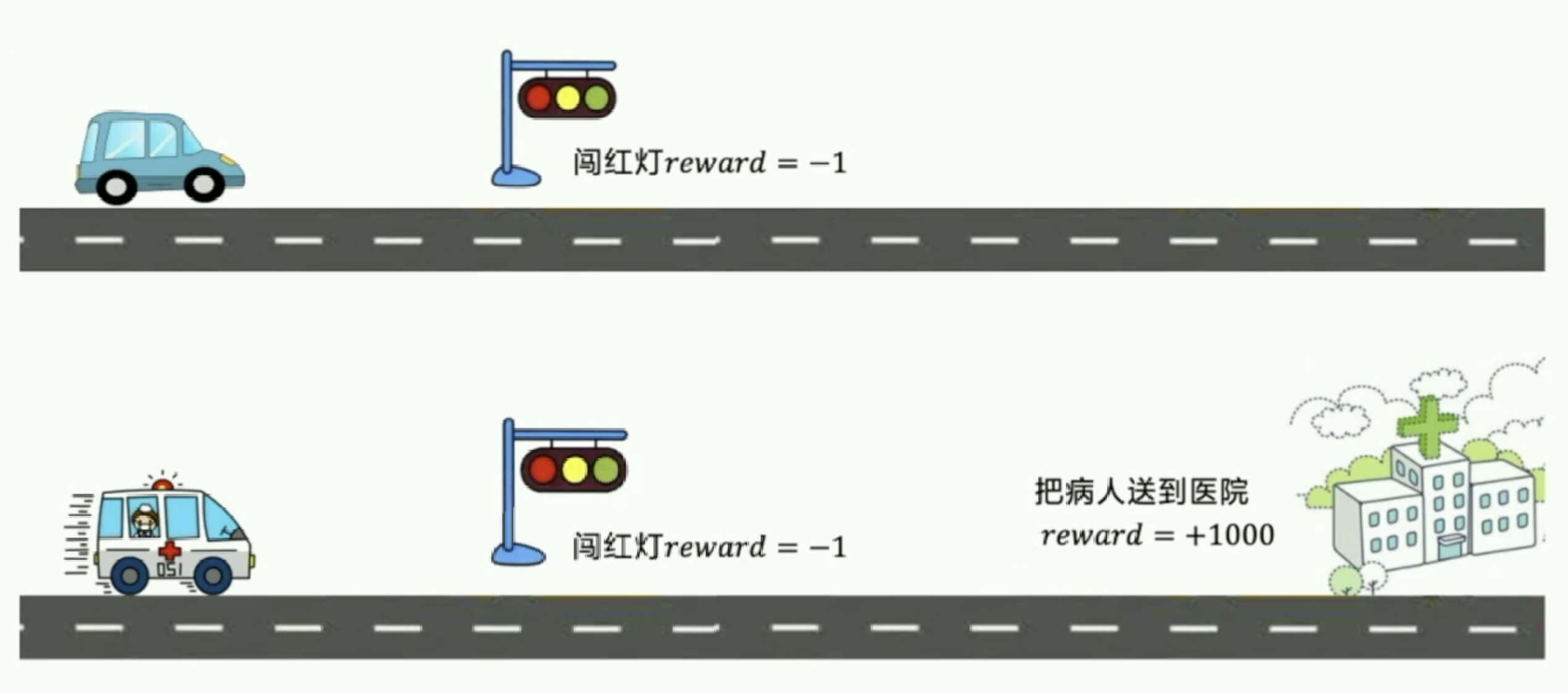
因为$\text{总收益：} G_t = R_{t+1} + R_{t+2} + R_{t+3} + \cdot\cdot\cdot$

但是，就像在金融里面，我们会把未来的收益按照一定的方法，折现到现在，以此来做出现在的决策。Q表格中一样，我们通常还会乘上一个衰减因子。所以，总收益的公式是

$$G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdot\cdot\cdot$$

• $\gamma$被称为衰减率，甚至有些资料直接说$\gamma$是折现率。这是一个超参数，需要我们来调，通常$\gamma \in [0,1]$。

Q表格的更新

刚刚我们讨论了。在试错和探索足够多次之后，我们会迭代更新出一本《野外求生指南》，这就是我们的Q表格，告诉我们在不同的$S$下采取不同的$A$，分别有多少价值。
我们根据Q表格实现未来总收益最大就ok了。
现在，我们来讨论，怎么迭代更新Q表格。
我们先来讲一个故事，巴普洛夫的狗。

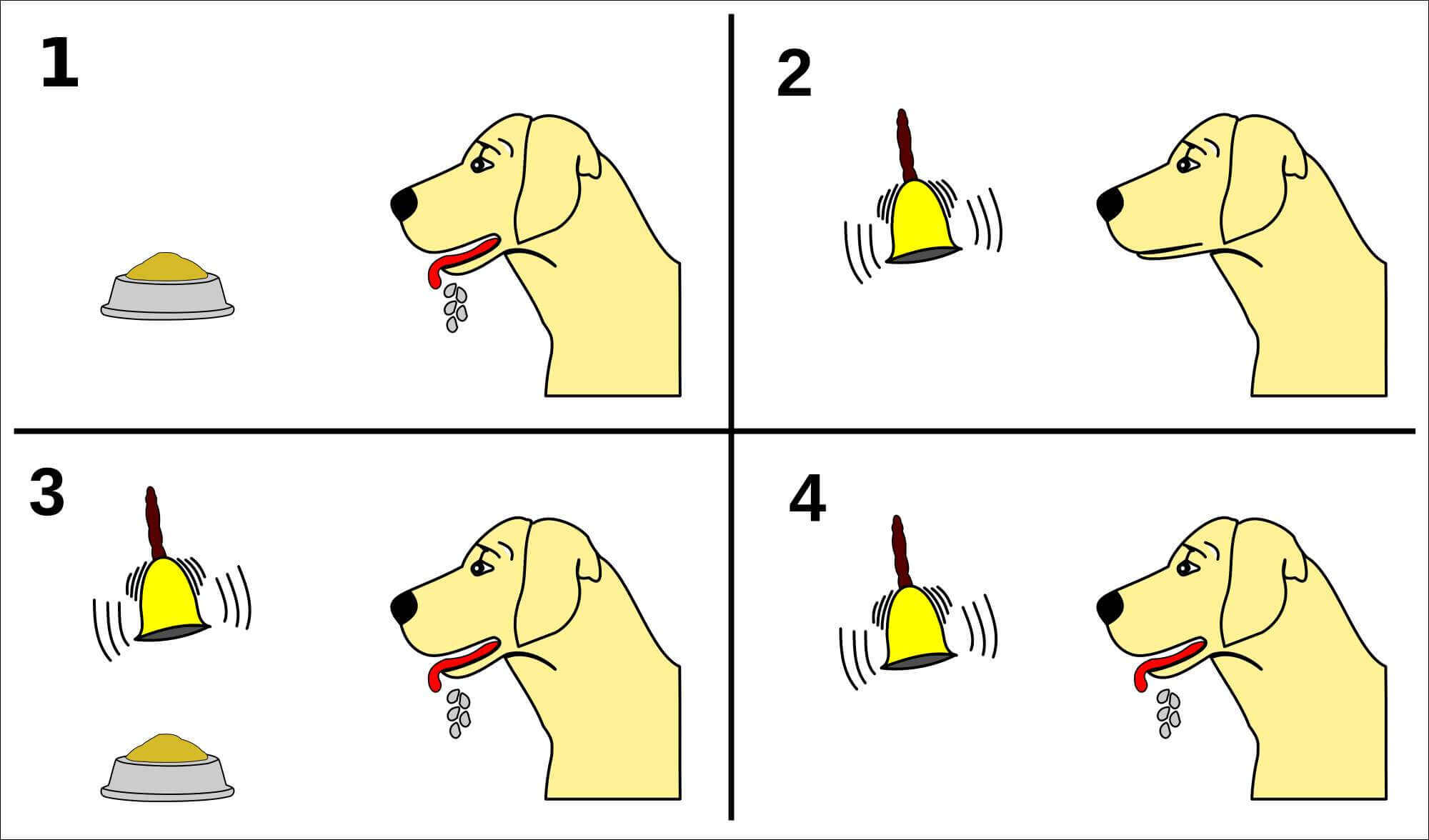
一开始摇铃铛狗没有反应，然后摇铃铛之后，再给食物，狗会流口水。最后只摇铃铛，狗也会留口水。
我们把摇铃铛记做$S_t$，放食物记做$S_{t+1}$，这个故事告诉我们什么？
下一个状态的价值，会强化去影响当前状态的价值。

"巴普洛夫的狗"这个过程，我们用下面的式子表达。

$$Q(S_t,A_t) \leftarrow Q(S_t,A_t) + \alpha[R_{t+1} + \gamma Q(S_{t+1},A_{t+1}) - Q(S_t,A_t)]$$

我们用$R_{t+1} + \gamma Q(S_{t+1},A_{t+1})$表示放食物这一个状态的价值，用$Q(S_t,A_t)$表示摇铃铛这一个状态的价值。两者之间的差，再乘以学习率$\alpha$，最后更新到$Q(S_t,A_t)$。如此足够多次之后，摇铃铛的价值就会逼近放食物的价值，这样狗就流口水了。

SARSA

我们再看看这个更新公式。一共有五个参数：$S_t$、$A_t$、$R_{t+1}$、$S_{t+1}$、$A_{t+1}$，我们把这5个参数连起来，就是我们的这个算法：SARSA。

SARSA算法过程
输入：迭代轮数$T$，状态集$S$, 动作集$A$, 学习率$\alpha$，衰减率$\gamma$, 探索率$\varepsilon$
输出：所有的状态和动作对应的价值$Q$
1、随机初始化所有的状态和动作对应的价值$Q$，对于终止状态其$Q$值初始化为$0$
2、For $i$ From $1$ To $T$，进行迭代
 a、初始化$S$为当前状态序列的第一个状态。设置$A$为$\varepsilon -\text{greddy}$在当前状态$S$选择的动作
 b、在状态$S$执行当前动作$A$，得到新状态$S'$和奖励$R$
 c、用$\varepsilon$−贪婪法在状态$S'$选择新的动作$A'$
 d、更新价值函数$Q(S,A)$：

$$Q(S_t,A_t) \leftarrow Q(S_t,A_t) + \alpha[R_{t+1} + \gamma Q(S_{t+1},A_{t+1}) - Q(S_t,A_t)]$$

 e、$S=S'$，$A=A'$
 f、如果$S'$是终止状态，当前轮迭代完毕，否则回到步骤b。

• 一般为了收敛，我们的学习率$\alpha$会进行衰减。
• $\varepsilon -\text{greddy}$是一个探索与利用算法。

$$\begin{cases} \argmax_a Q(a) \quad \text{概率}(1 - \varepsilon) \ (\text{利用}) \\ \text{随机选择一个动作} \quad \text{概率}\varepsilon \ (\text{探索}) \end{cases}$$

SARSA算法的流程图表示如下：

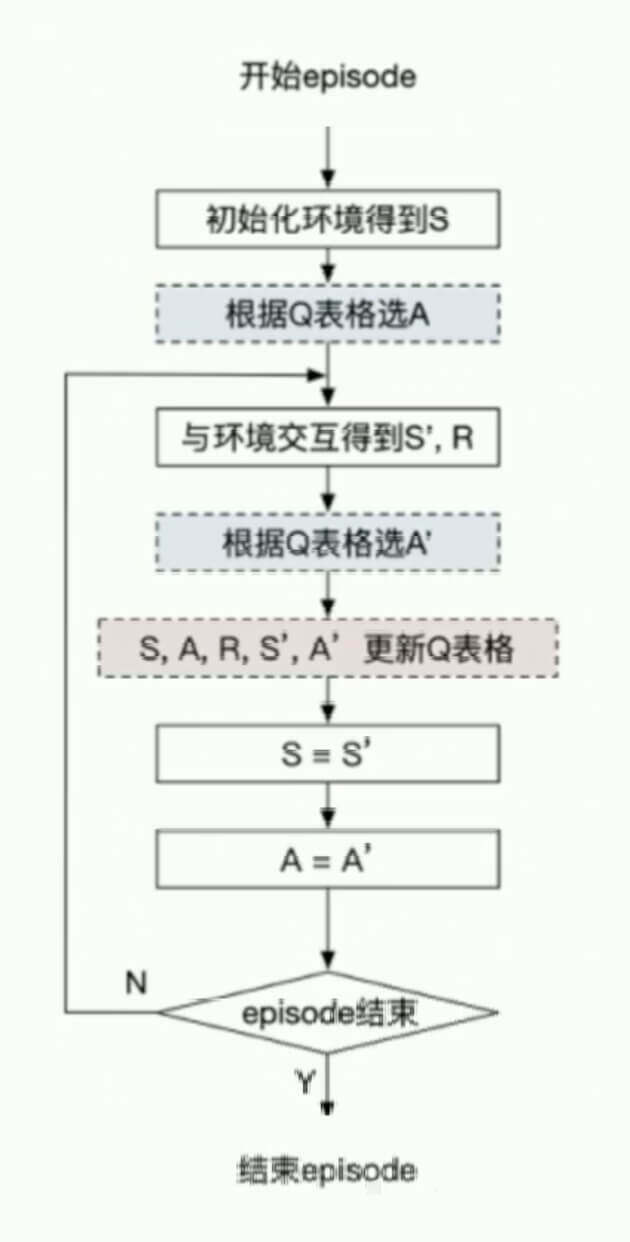
Q-Learing

在上一小节，我们看到，SARSA更新Q表的策略是

$$Q(S_t,A_t) \leftarrow Q(S_t,A_t) + \alpha[R_{t+1} + \gamma Q(S_{t+1},A_{t+1}) - Q(S_t,A_t)]$$

那么，这里的$A_{t+1}$是怎么得到的？根据$\varepsilon -\text{greddy}$算法，可能是根据Q表得到的，也可能是探索得到的。现在，改一下，我们不去探索了，我们的$A_{t+1}$就是Q表中的最佳策略。即

$$Q(S_t,A_t) \leftarrow Q(S_t,A_t) + \alpha[R_{t+1} + \gamma \max_a Q(S_{t+1},a) - Q(S_t,A_t)]$$

另外，我们还看到。在更新Q表之后，SARSA还做了两件事情。把$S'$赋值给$S$，把$A'$赋值给$A$。现在，我们只把$S'$赋值给$S$。

这就是我们的Q-Learning算法。

Q-Learning算法过程
输入：迭代轮数$T$，状态集$S$, 动作集$A$, 学习率$\alpha$，衰减率$\gamma$, 探索率$\varepsilon$
输出：所有的状态和动作对应的价值$Q$
1、随机初始化所有的状态和动作对应的价值$Q$. 对于终止状态其$Q$值初始化为$0$
2、For $i$ From $1$ To $T$，进行迭代
 a、初始化$S$为当前状态序列的第一个状态
 b、用$\varepsilon -\text{greddy}$在当前状态$S$选择出动作$A$
 c、在状态$S$执行当前动作$A$，得到新状态$S'$和奖励$R$
 d、更新价值函数$Q(S,A)$

$$Q(S_t,A_t) \leftarrow Q(S_t,A_t) + \alpha[R_{t+1} + \gamma \max_a Q(S_{t+1},a) - Q(S_t,A_t)]$$

 e、$S=S'$
 f、如果$S'$是终止状态，当前轮迭代完毕，否则转到步骤b

Q-Learning算法的流程图表示如下：

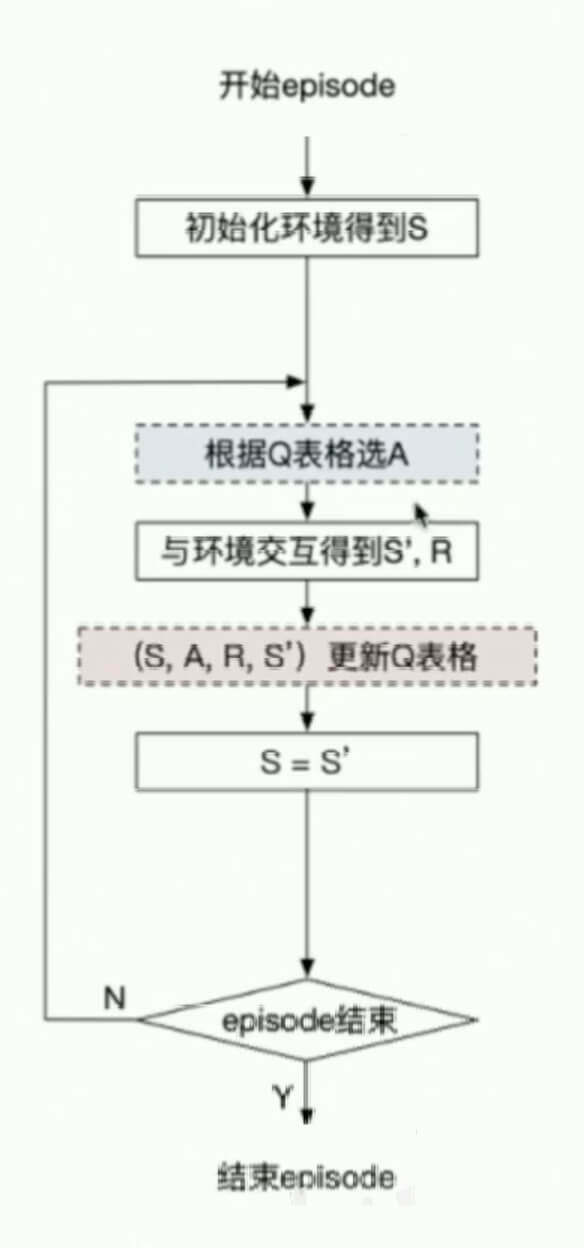
最后，我们再把SARSA和Q-Learning展开，做一个对比

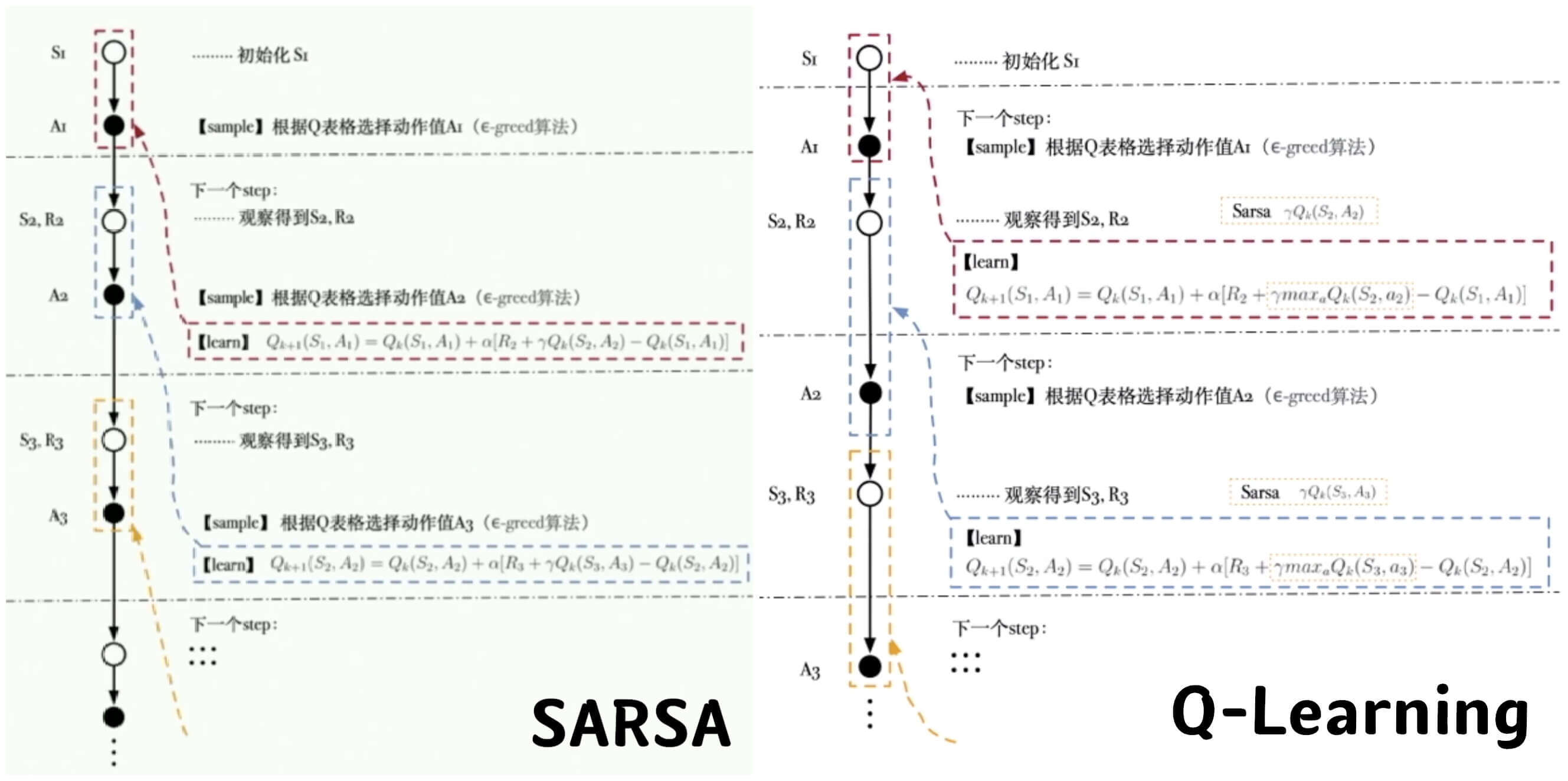
小结

最后，我们做一个小结。

1. MDP四元组：S、A、P、R。(也有些资料认为是五元祖，多了一个$\gamma$。)
2. Q表格与状态价值：
   1. Q表格指定每一个Step的动作选择
   2. 目标导向：加入衰减率的总收益最大
   3. 状态价值迭代：“巴普洛夫的狗”
3. 两个算法：
   1. SARSA：$Q(S_t,A_t) \leftarrow Q(S_t,A_t) + \alpha[R_{t+1} + \gamma Q(S_{t+1},A_{t+1}) - Q(S_t,A_t)]$
   2. Q-Learning：$Q(S_t,A_t) \leftarrow Q(S_t,A_t) + \alpha[R_{t+1} + \gamma \max_a Q(S_{t+1},a) - Q(S_t,A_t)]$

基于神经网络方法求解RL

刚刚我们讨论的一个在野外遇到熊的例子，在这个例子中，熊的状态有三个：招手、咆哮、离开，又或者再加一个状态"eat"。但总之，状态数是非常有限的。现在，我们换一下，下围棋，这个有$10^{170}$种状态，这就非常多了。如果是一个人在奔跑的话，其手脚的状态还是连续的不可数的。

那么？这个时候，显然无法用Q表格的方法。
那我们用值函数近似的方法。去构造一个值函数$\hat{q}(s,a,\bold{w}) \approx Q(s,a)$
那么，怎么构造值函数呢？神经网络。

DQN

首先，我们复习一下之前讨论的监督学习。

现在，我们把输入改成一批状态$S_1,S_2,S_3···$，输出对应的$Q_1,Q_2,Q_3···$，特别的这里的$Q$值是一个向量，表示不同的动作不同的值。然后我们要让我们输出的$Q$值，逼近我们的目标值。

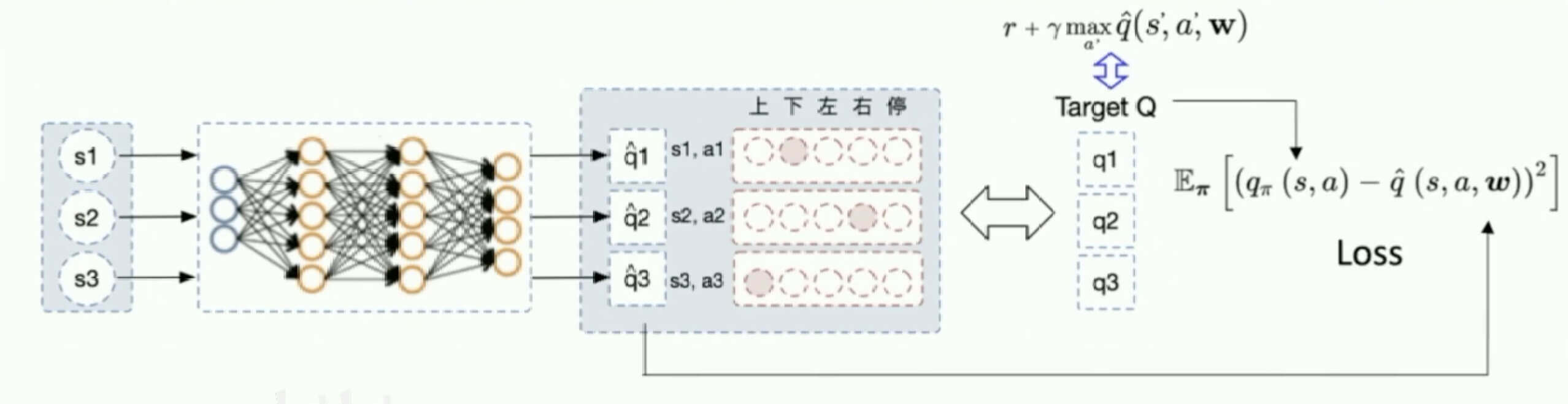
DQN算法过程
输入：迭代轮数$T$，状态特征维度$n$, 动作集$A$, 学习率$\alpha$，衰减因子$\gamma$，探索率$\varepsilon$，$Q$网络结构，批量梯度下降的样本数$m$。
输出：$Q$网络参数
1、随机初始化$Q$网络的所有参数$w$，基于$w$初始化所有的状态和动作对应的价值$Q$。清空经验回放的集合$D$。
2、For $i$ From $1$ To $T$，进行迭代
 a、初始化$S$为当前状态序列的第一个状态，拿到其特征向量$\Phi(S)$
 b、在$Q$网络中使用$\Phi(S)$作为输入，得到$Q$网络的所有动作对应的$Q$值输出。用$\varepsilon -\text{greddy}$在当前$Q$值输出中选择对应的动作$A$
 c、在状态$S$执行当前动作$A$，得到新状态$S'$对应的特征向量$\Phi(S')$和奖励$R$，是否终止状态$\text{is-end}$
 d、将$\{\Phi(S),A,R,\Phi(S'),\text{is-end}\}$这个五元组存入经验回放集合$D$
 e、$S=S'$
 f、从经验回放集合$D$中采样$m$个样本$\{\Phi(S_j),A_j,R_j,\Phi(R_j),\text{is-end}\},j=1,2,3...m$，计算当前目标$Q$值$y_j$

$$y_j = \begin{cases}R_j \quad \text{is-end}_j = \text{true} \\R_j + \gamma \max_{a'} Q(\Phi(S'_j,A'_j,w)) \quad \text{is-end}_j = \text{false}\end{cases}$$

 g、使用均方差损失函数$\frac{1}{m}\sum\limits_{j=1}^m(y_j-Q(\Phi(S_j),A_j,w))^2$，通过神经网络的梯度反向传播来更新Q网络的所有参数𝑤
 h、如果$S'$是终止状态，当前轮迭代完毕，否则转到步骤b

• f步和g步的$Q$值计算也需要通过$Q$网络计算得到
• 为了收敛，通常探索率$\varepsilon$需要随着迭代的进行而变小

DQN的结构如图所示：

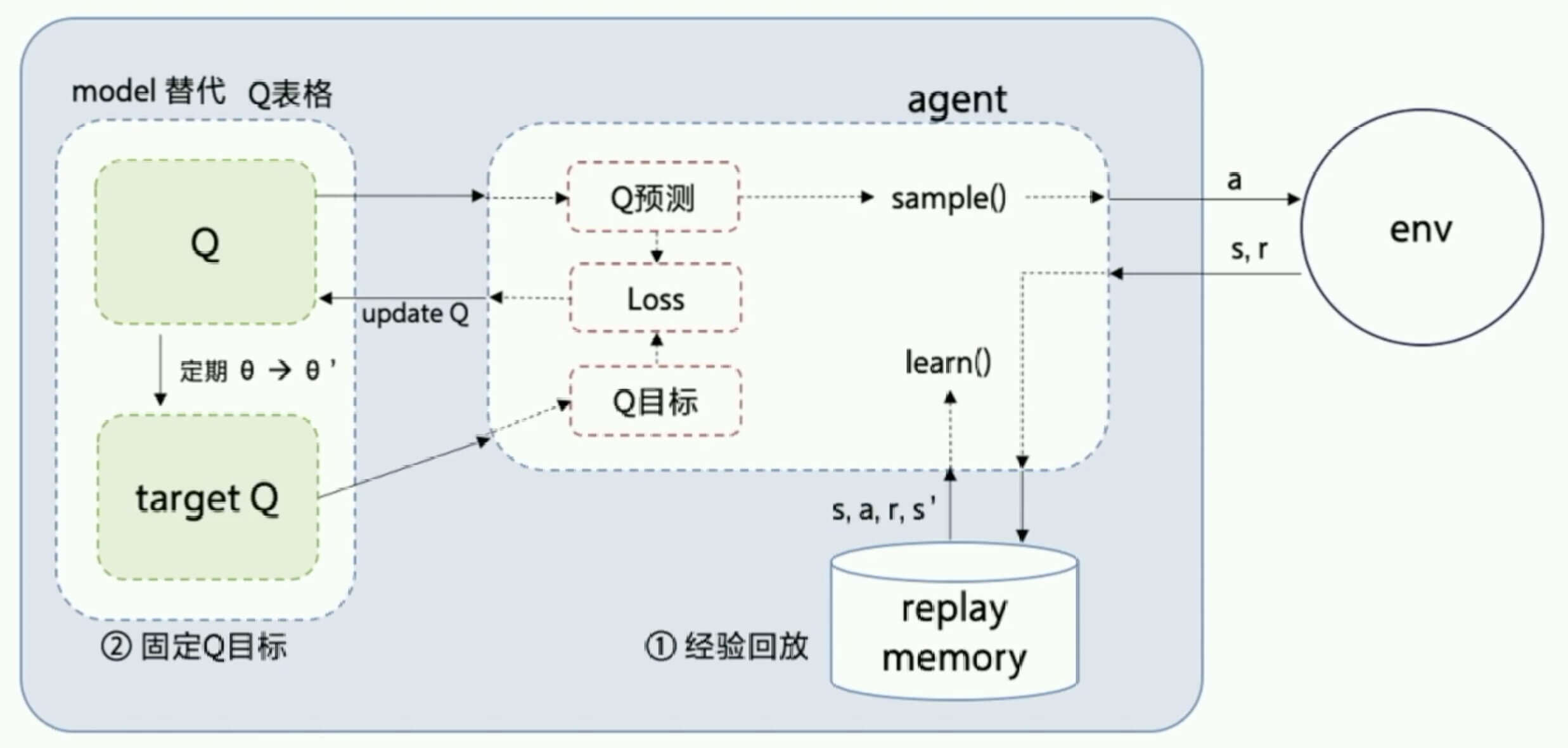
基于策略梯度求解RL

之前我们讨论了，Model-Free可以分为Value-Based和Policy-Based。在基于表格型方法求解RL这一节，我们讨论的就是Value-Based，而在基于神经网络方法求解RL这一节，我们只不过是用神经网络替代了Q表格，本质还是Value-Based。
这一小节，我们讨论一个新的话题，Policy-Based。

在上一节的Value-Based中，我们通过神经网络去拟合价值，然后再根据价值做出动作。那么在Policy-Based中，我们直接用神经网络输出每种动作的概率。既然是每种动作的概率呢，那么这里就需要激活函数。

需要哪个激活函数？
复习一下：

激活函数	值域	备注
阶跃函数	$0$或$1$	不可以用梯度下降
sigmoid	$[0,1]$
tanh	$[-1,1]$
ReLU	$[0,+\infty)$
SoftMax	$[0,1]$	多个输出值，所有输出值之和为1

显然，我们决定用SoftMax作为激活函数。

如图所示，我们在每一步都能有多种选择，而环境的反馈也是随机的。当然，这是链式的，所以一次只能走一条路。

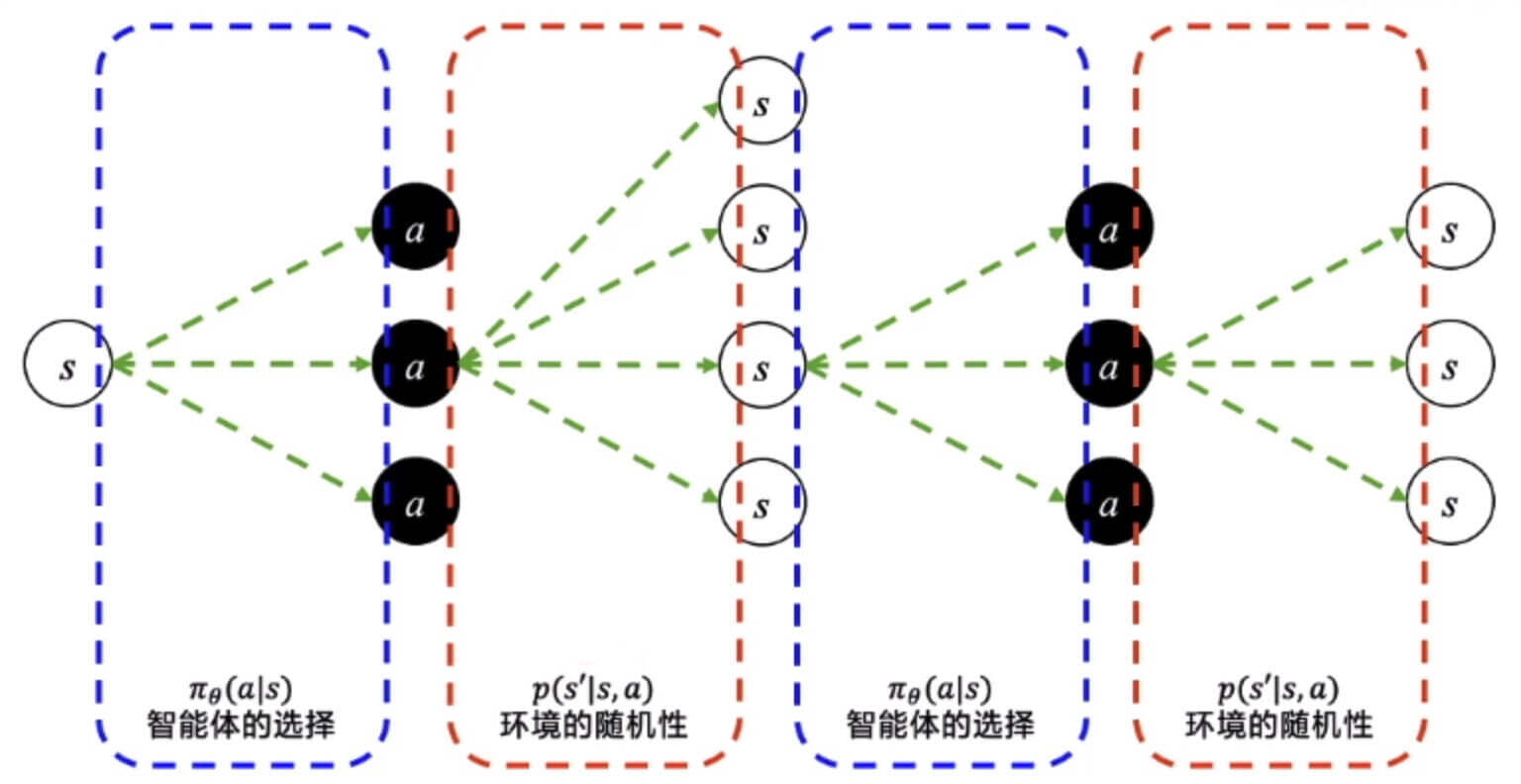
比如，走了这么一条路。

我们把这个称为episode，这个episode的所有轨迹我们记作$\tau$，即

$$\tau = \{S_1,a_1,S_2,a_2,...,S_T,a_T\}$$

第一问，这个episode发生的概率是多少？

$$p_{\theta}(\tau) = p(S_1)\pi_{\theta}(a_1|s_1)p(s_2|s_1,a_1)\pi_{\theta}(a_2|s_2) + ···$$

第二问，这个episode的总回报是多少呢？

$$R(\tau) = \sum_{t=1}^T r_t$$

第三问，这个episode的期望回报是多少？

$$R(\tau)p_{\theta}(\tau)$$

第四问，一个$\pi_{\theta}(a|s)$后面可能连着多个episode，那么$\pi_{\theta}(a|s)$的期望回报是多少？

$$\overline{R}_{\theta} = \sum_{\tau}R(\tau)p_{\theta}(\tau)$$

最后一个问题，$\overline{R}_{\theta}$到底是多少？

$$\text{穷举}$$

其实不用这么麻烦，我们换一个思路，去抽样调查。和环境交互$N$个episode，就会有$N$个$R(\tau)p_{\theta}(\tau)$，然后求平均。即

$$\overline{R}_{\theta} \approx \frac{1}{N} \sum_{n=1}^{N} R(\tau)$$

只要$N$足够大，就可以近似的得到期望回报。
这个方法被称为蒙特卡洛法

求$\overline{R}_{\theta}$有什么用呢？因为我们的目标是

$$\max \ \overline{R}_{\theta}$$

这种目标函数越大越好的更新策略，在生成对抗网络中，我们也用过。梯度上升。
梯度是

$$\nabla_{\theta} \overline{R}_{\theta} \approx \frac{1}{N}\sum_{n=1}^{N}\sum_{t=1}^{T_n}R(\tau^n)\nabla\log\pi_{\theta}(a_t^n|s_t^n)$$

蒙特卡罗策略梯度算法过程
输入：$N$个蒙特卡罗完整序列，学习率$\alpha$
输出：策略函数的参数$\theta$
1、 For 每个蒙特卡罗序列:
 a、用蒙特卡罗法计算序列每个时间位置$t$的状态价值$v_t$
 b、对序列每个时间位置$t$，使用梯度上升法，更新策略函数的参数$\theta$

$$\theta = \theta + \alpha \ \frac{1}{N}\sum_{n=1}^{N}\sum_{t=1}^{T_n}R(\tau^n)\nabla\log\pi_{\theta}(a_t^n|s_t^n)$$

返回策略函数的参数$\theta$

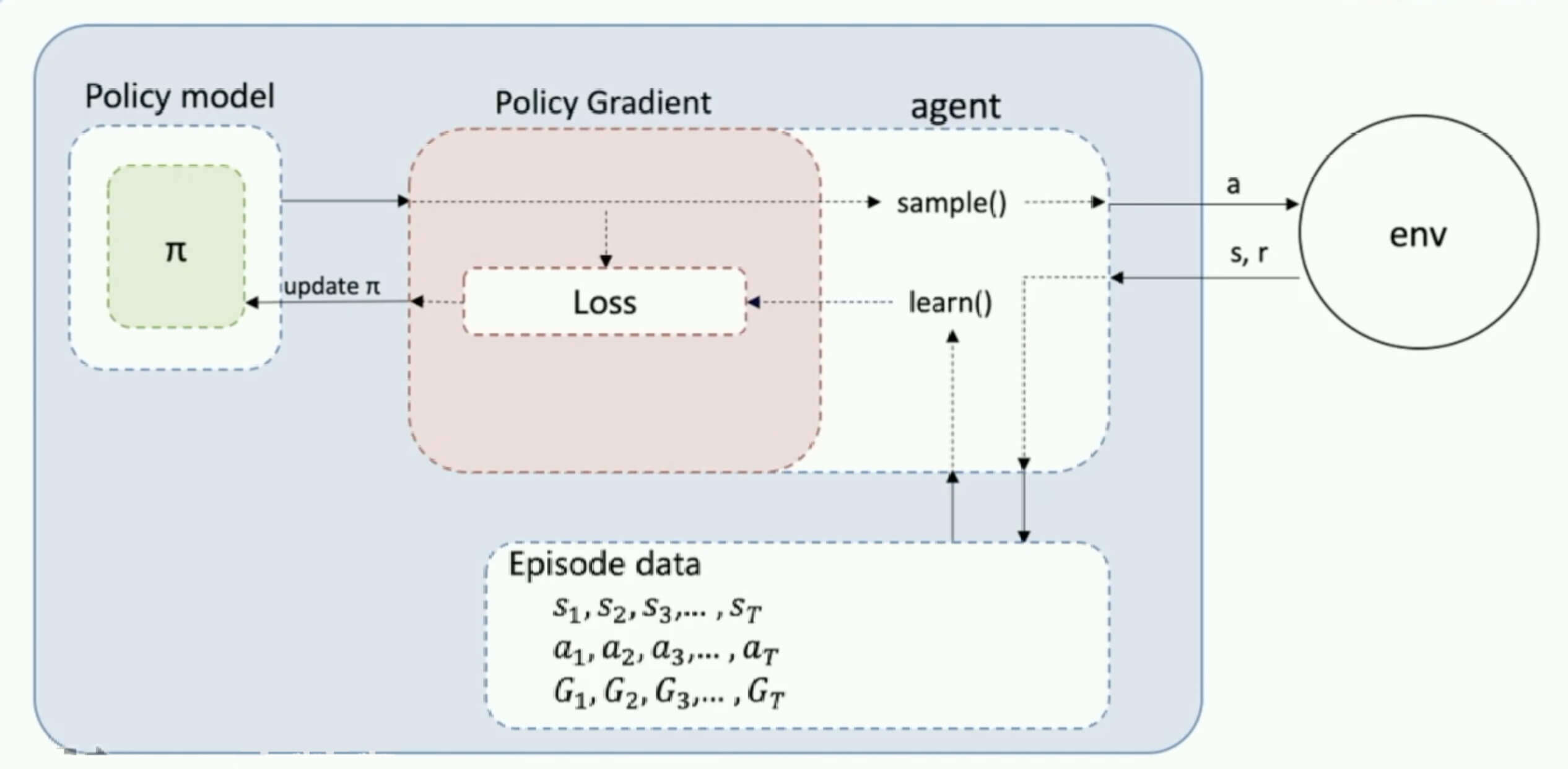
蒙特卡罗策略梯度算法的结构：