2.动态规划

在上一章，我们通过Bellman最优方程求解了最优策略。但我们也看到我们只有两个状态，两个动作。而且，其实我们考虑的只是$s_1,a_1,r_1,s_2$这么一个非常简单的过程。可是我们的方程组就已经略复杂，那么状态和动作更多呢？如果我们考虑的时间更长呢？那么就需要非常多的计算资源。
现在，我们讨论如何从算法模型的思路出发，解决这个问题。
动态规划
这不是我们第一次讨论动态规划，在《算法入门经典(Java与Python描述)：11.动态规划》中，我们也讨论过动态规划，当时主要是讨论了一种把代码从递归改成动态规划的技巧。这次我们讨论利用动态规划的方法求解强化学习。

动态规划的前提是环境已知，在强化学习中，被称为"模型已知"或"有模型"。是强化学习中的Planning问题。
(也有资料认为，模型已知的不属于强化学习，只有模型未知，依靠数据驱动的属于强化学习。)

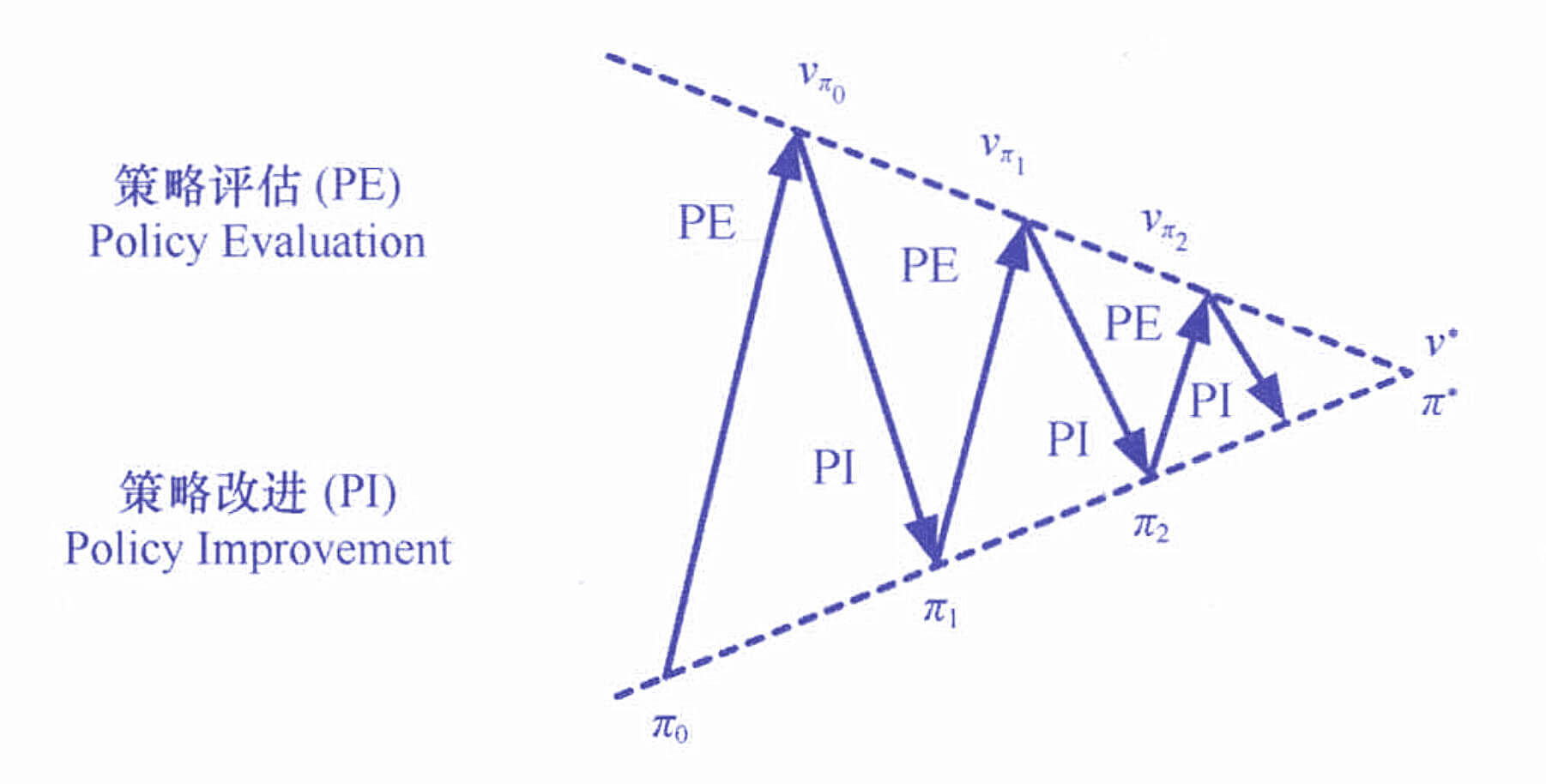
我们的思路是"迭代出一个最优策略"，我们从任意一个策略出发，一步一步逼近最优策略。
所以我们需要知道的是：

1. 当前策略到底怎么样？
   策略评估
2. 如果当前策略不行，怎么改进？
   策略改进
3. 上述两步，循环往复，迭代。
   策略迭代

策略评估

策略评估的方法

怎么评估一个策略的好坏？

在上一章，我们讨论了两个东西，状态价值和动作价值。而且我们当时还举了这么一个例子：在相同的状态$s$下，两位将军做出了相同的动作决策$a=\text{撤退}$，但是第一位将军是因为水平不行，第二位将军是想以退为进，诱敌深入。策略$\pi$不同，虽然在当前状态$s$下，都做出了相同的动作$a=\text{撤退}$，但是后续的$A$却可能差距很大，最后结果也不同。那么这个动作的价值自然也不同，当前状态的价值也不同。
我们就用状态价值来评估一个策略。

在上一章，我们讨论了可以用$t+1$时刻的状态价值表示$t$时刻的状态价值。

$$V_{\pi}(s_t) = \sum_{a_t}\pi(a_t|s_t)\bigg[ r(s_t,a_t) + \gamma \sum_{s_{t+1}} p(s_{t+1}|s_t,a_t) V_{\pi}(s_{t+1}) \bigg]$$

• $r(s_t,a_t)$是奖励。
• $p(s_{t+1}|s_t,a_t)$是状态转移函数，表示在$s_t$状态下，做出动作$a_t$，然后状态转移到$s_{t+1}$的概率。
• $\pi(a_t|s_t)$是策略函数，表示在状态$s_t$下，做出动作$a_t$的概率。

知道了用状态价值评估策略，也知道了状态价值函数之间的关系，接下来，就可以评估策略了。
基本思路是：
首先初始化所有状态的价值都是$0$，即对于每一个$s\in\mathcal{S}$，$s_t = s_1,s_2,s_3,\cdots,s_T$，都有$V(s_t)=0$。
然后，在第$k$轮迭代求解$V_{k}(s_t)$时，使用上一轮第$k-1$轮计算出来的价值函数$V_{k-1}(s_{t+1})$来更新$V_{k}(s_t)$，更新方法就是刚刚我们讨论的式子，“用$t+1$时刻的状态价值表示$t$时刻的状态价值”。

整个算法的过程描述如下：

策略评估算法
输入：
  已知的模型(环境)$p$
  待评估的策略$\pi$
  初始化的状态值(对于每一个$s\in\mathcal{S}$，$V(s)=0$)
输出：
  $V_{\pi}$的估计值
参数：
  $\theta$：最小更新值
  $K_{\max}$：最大迭代次数
迭代，对于$k=1,2,3,\cdots,K_{\max}$，执行以下操作：
  $\Delta\leftarrow0$
  遍历$s\in\mathcal{S}$，$s_t = s_1,s_2,s_3,\cdots,s_T$：
    把上一轮迭代的价值赋给$V$，$V\leftarrow V_{k-1}(s_t)$
    计算本轮的迭代价值，赋值给$V_k(s_t)$，$V_k(s_t) \leftarrow \sum_{a_t}\pi(a_t|s_t)\bigg[ r(s_t,a_t) + \gamma \sum_{s_{t+1}} p(s_{t+1}|s_t,a_t) V_{k-1}(s_{t+1}) \bigg]$
    更新最大$\Delta$，$\Delta\leftarrow\max(\Delta,|V-V_{k}(s_t)|)$

  如果$\Delta$几乎不更新($\Delta<\theta$)，或者已经到了最大迭代次数($k=k_{\max}$)，结束迭代。
  (这么做的含义其实是，在某一轮，第$k$轮的$s_t = s_1,s_2,s_3,\cdots,s_T$，但凡有一个状态的价值和上一轮相比变化大于$\theta$，那就继续下一轮$k+1$的迭代。注意，但凡有一个。)

策略评估的实现

接下来，我们就实现一个策略评估，我们以"冰面滑行"为例。

该例子来自《强化学习：原理与Python实现(肖智清著)》这本书的第三章。

冰面滑行背景

冰面滑行问题(FrozenLake-v0)是Gym里内置的一个文本环境任务。该问题的背景是这样的：在一个大小为$4*4$的湖面上，有些地方结冰了，有些地方没有结冰。我们可以用一个的字符矩阵来表示湖面的情况，例如：

$$\begin{matrix} S & F & F & F \\ F & H & F & H \\ F & H & F & H \\ H & F & F & G \end{matrix}$$

其中字母"F"(Frozen)表示结冰的区域，字母"H"(Hole)表示未结冰的冰窟窿，字母"S"(Start)和字母"G"(Goal)分别表示移动任务的起点和目标。在这个湖面上要执行以下移动任务：要从"S"处移动到"G"处。每一次移动，可以选择"左"、“下”、“右”、"上"4个方向之一进行移动，每次移动一格。如果移动到"G"处，回合结束，获得1个单位的奖励；如果移动到"H"处，回合结束，没有获得奖励；如果移动到其他字母，不获得奖励，可以继续。由于冰面滑，所以实际移动的方向和想要移动的方向并不一定完全一致。例如，如果在某个地方想要左移，但是由于冰面滑，实际也可能下移、右移和上移。任务的目标是尽可能达到"G"处，以获得奖励。

环境及其使用

示例代码：

import gym
env = gym.make('FrozenLake-v0')
env = env.unwrapped
env.seed(0)
print('观察空间 = {}'.format(env.observation_space))
print('动作空间 = {}'.format(env.action_space))
print('状态空间大小 = {}'.format(env.unwrapped.nS))
print('动作空间大小 = {}'.format(env.unwrapped.nA))
env.render()

• 关于env = env.unwrapped这段代码的作用，网上有三种解释：
  1、如果你想访问一个特定环境的场景动态后面的东西，需要使用unwrapped属性。
  2、还原env的原始设置，env外包了一层防作弊层
  这两种解释，似乎都没有把问题说清楚。
  比较清楚的解释是：
  gym的多数环境都用TimeLimit包装了，以限制Epoch。用env.unwrapped可以得到原始的类，不会有限制。

运行结果：

观察空间 = Discrete(16)
动作空间 = Discrete(4)
状态空间大小 = 16
动作空间大小 = 4

FHFH
FFFH
HFFG

• Discrete的含义是离散的

这个环境的状态空间有16个不同的状态$\{s_0,s_1,\cdots,s_{15}\}$，表示当前处在哪一个位置；动作空间有4个不同的动作$\{a_0,a_1,a_2,a_3\}$，分别表示"左"、“下”、“右”、"上"四个方向。在Gym中，直接用int型数值来表示这些状态和动作。

特别的，我们可以看看环境的状态转移方程。
示例代码：

print(env.P[0][1])

运行结果：

[(0.3333333333333333, 0, 0.0, False), (0.3333333333333333, 4, 0.0, False), (0.3333333333333333, 1, 0.0, False)]

这是一个元组列表，每个元组包括概率、下一状态、奖励值、回合结束指示这4个部分。
其含义是，在状态$s_0$，执行动作$a_1$，即向下滑：

$$\begin{aligned} P(s_0,0 | s_0,a_1) &= \frac{1}{3} \\ P(s_4,0 | s_0,a_1) &= \frac{1}{3} \\ P(s_1,0 | s_0,a_1) &= \frac{1}{3} \end{aligned}$$

然后，我们还可以用一个随机策略，试一试。

示例代码：

import numpy as np

def play_policy(env, policy, render=False):
    # 回报
    total_reward = 0.
    # 状态
    observation = env.reset()
    while True:
        if render:
            env.render() # 此行可显示
        action = np.random.choice(env.action_space.n,p=policy[observation])
        # 状态、奖励、是否完成
        observation, reward, done, _ = env.step(action)
        # 累积奖励
        total_reward += reward
        # 游戏结束
        if done:
            break
    return total_reward

# 随机策略
random_policy = np.ones((env.nS, env.nA)) / env.nA

episode_rewards = [play_policy(env, random_policy)  for _ in range(100)]
print("随机策略 平均奖励：{}".format(np.mean(episode_rewards)))

运行结果：

随机策略 平均奖励：0.02

策略评估的代码

接下来，就是代码实现策略评估算法，在具体的代码实现方面有两个技巧：

1. 可以用矩阵相乘代替循环累加
2. 如果知道了状态价值，就可以知道动作价值

就以我们上文的随机策略为例。
示例代码：

def v2q(env, v, s=None, gamma=1.):
    """
    根据状态价值函数计算动作价值函数
    :param env: 环境
    :param v: 状态价值
    :param s: 状态
    :param gamma: 衰减率
    :return: 动作价值
    """
    # 针对单个状态求解
    if s is not None:
        q = np.zeros(env.unwrapped.nA)
        for a in range(env.unwrapped.nA):
            for prob, next_state, reward, done in env.unwrapped.P[s][a]:
                q[a] += prob * (reward + gamma * v[next_state] * (1. - done))
    # 针对所有状态求解
    else:
        q = np.zeros((env.unwrapped.nS, env.unwrapped.nA))
        for s in range(env.unwrapped.nS):
            q[s] = v2q(env, v, s, gamma)
    return q

def evaluate_policy(env, policy, gamma=1., theta=1e-6,kmax=1000000):
    """
    评估策略的状态价值
    :param env: 环境
    :param policy: 策略
    :param gamma: 衰减率
    :param theta: 最小更新值
    :param kmax: 最大迭代次数
    :return:
    """
    # 初始化状态价值函数
    v = np.zeros(env.unwrapped.nS)
    for k in range(kmax):
        delta = 0
        for s in range(env.unwrapped.nS):
            # 更新状态价值函数
            vs = sum(policy[s] * v2q(env, v, s, gamma))
            # 更新最大误差
            delta = max(delta, abs(v[s]-vs))
            # 更新状态价值函数
            v[s] = vs
        if delta < theta: # 查看是否满足迭代条件
            break
    return v


print('状态价值函数：')
v_random = evaluate_policy(env, random_policy)
print(v_random.reshape(4, 4))

print('动作价值函数：')
q_random = v2q(env, v_random)
print(q_random)

运行结果：

状态价值函数：
[[0.0139372  0.01162942 0.02095187 0.01047569]
 [0.01624741 0.         0.04075119 0.        ]
 [0.03480561 0.08816967 0.14205297 0.        ]
 [0.         0.17582021 0.43929104 0.        ]]
动作价值函数：
[[0.01470727 0.01393801 0.01393801 0.01316794]
 [0.00852221 0.01162969 0.01086043 0.01550616]
 [0.02444416 0.0209521  0.02405958 0.01435233]
 [0.01047585 0.01047585 0.00698379 0.01396775]
 [0.02166341 0.01701767 0.0162476  0.01006154]
 [0.         0.         0.         0.        ]
 [0.05433495 0.04735099 0.05433495 0.00698396]
 [0.         0.         0.         0.        ]
 [0.01701767 0.04099176 0.03480569 0.04640756]
 [0.0702086  0.11755959 0.10595772 0.05895286]
 [0.18940397 0.17582024 0.16001408 0.04297362]
 [0.         0.         0.         0.        ]
 [0.         0.         0.         0.        ]
 [0.08799662 0.20503708 0.23442697 0.17582024]
 [0.25238807 0.53837042 0.52711467 0.43929106]
 [0.         0.         0.         0.        ]]

策略改进

策略改进的方法

现在，我们已经知道了，我们的这个随机策略不怎么样。接下来，我们就要想办法对策略进行改进。
怎么改进策略？
之前我们的随机策略，在每一个状态下，做出的动作都是随机的。
现在不要随机了，我们在每一个状态下，都做出当前状态下的最优动作。
这是什么？
在《算法入门经典(Java与Python描述)：10.图》这一章，我们讨论了最小生成树的算法：“Kruskal"和"Prim”，"Kruskal"是每次选择所有的边中权重最小的边，"Prim"是每次选择当前能选择的边中权重最小的边。这两种算法都属于贪心算法。
那么现在呢？我们每次选择当前状态下的最优动作，也属于贪心算法。

贪心不一定有效，但是在这里，我们的贪心算法是有效的。
因为我们这里贪心策略公式中的价值函数已经考虑了未来的回报。

策略改进算法
输入：
  已知的模型(环境)$p$
  待改进的策略$\pi$
  状态价值函数$V$
输出：
  改进之后的策略$\pi$
  是否已经达到最优的标志$o$

初始化$o$为$\text{True}$
遍历$s\in\mathcal{S}$，$s_t = s_1,s_2,s_3,\cdots,s_T$：
  对于每个$a_t\in\mathcal{A}$，求其动作价值函数$Q(s_t,a_t) \leftarrow r(s_t,a_t) + \gamma\sum_{s_{t+1}}p(s_{t+1}|s_t,a_t)V(s_{t+1})$
  找到使$Q(s_t,a_t)$最大的动作$a_{\star}$，也就是说令$a_{\star}=\argmax_{a_t} Q(s_t,a_t)$
  如果当前状态的下的动作$\pi(s)\neq a_{\star}$，更新$\pi(s) \leftarrow a_{\star}$。$o\leftarrow\text{False}$，还有优化空间，反之$o\leftarrow\text{True}$。

策略改进的实现

示例代码：

def improve_policy(env, v, policy, gamma=1.):
    optimal = True
    # 遍历所有的状态
    for s in range(env.nS):
        # 求当前状态的所有动作的价值
        q = v2q(env, v, s, gamma)
        # 选取价值对好的动作
        a = np.argmax(q)
        # 如果当前策略的当前动作的概率不是1
        if policy[s][a] != 1.:
            # 优化没有完成
            optimal = False
            policy[s] = 0.
            policy[s][a] = 1.
    return optimal

policy = random_policy.copy()
optimal = improve_policy(env, v_random, policy)
if optimal:
    print('无更新，最优策略为：')
else:
    print('有更新，更新后的策略为：')

print(np.argmax(policy, axis=1).reshape(4, 4))

运行结果：

有更新，更新后的策略为：
[[0 3 0 3]
 [0 0 0 0]
 [3 1 0 0]
 [0 2 1 0]]

策略迭代

策略迭代的方法

有了策略评估的方法，又有了策略改进的方法，把这几个串起来，就是策略迭代了。
在策略评估中，根据当前策略计算价值。在策略改进中，通过贪心算法选择最大价值所对应的动作。策略评估和策略改进交替进行，不断迭代。

策略迭代的实现

示例代码：

def iterate_policy(env, gamma=1., tolerant=1e-6):
    # 初始化为任意一个策略
    policy = np.ones((env.unwrapped.nS, env.unwrapped.nA)) / env.unwrapped.nA
    while True:
        v = evaluate_policy(env, policy, gamma, tolerant) # 策略评估
        if improve_policy(env, v, policy): # 策略改进
            break
    return policy, v

policy_pi, v_pi = iterate_policy(env)
print('状态价值函数 =')
print(v_pi.reshape(4, 4))
print('最优策略 =')
print(np.argmax(policy_pi, axis=1).reshape(4, 4))

运行结果：

状态价值函数 =
[[0.82351246 0.82350689 0.82350303 0.82350106]
 [0.82351416 0.         0.5294002  0.        ]
 [0.82351683 0.82352026 0.76469786 0.        ]
 [0.         0.88234658 0.94117323 0.        ]]
最优策略 =
[[0 3 3 3]
 [0 0 0 0]
 [3 1 0 0]
 [0 2 1 0]]

看看效果

示例代码：

# 看看效果
episode_rewards = [play_policy(env, policy_pi) for _ in range(100)]
print("平均奖励：{}".format(np.mean(episode_rewards)))

运行结果：

平均奖励：0.86

价值迭代

价值迭代的方法

在讨论价值迭代之前，再来看看我们的策略迭代方法。首先，我们初始化一个策略，然后先进行策略评估(计算策略的价值函数)，看看这个策略到底怎么样，再进行策略改进，然后再评估(计算策略的价值函数)，再改进。如此循环往复，最后迭代出一个策略。
但在这个过程中，却存在两个问题：

1. 多轮迭代导致效率下降
2. 策略初始化的随机性
   如果最初的策略$\pi_0$就是一个不合理或者错误的策略，可能会导致算法无法收敛，得不到最优的策略$\pi_{\star}$

那我们换一个思路，不去迭代策略，直接迭代最优价值函数。如果能迭代出最优价值函数，最优策略就知道了。
这时候，我们借助的是最优价值函数的Bellman期望方程。

$$V_{\star}(s_t) = \max_{a\in\mathcal{A}} \bigg[ r(s_t,a_t) + \gamma \sum_{s_{t+1}} p(s_{t+1}|s_{t},a_{t}) V_{\star}(s_{t+1}) \bigg]$$

基本思路是，在第$k$轮迭代中，在某个状态$s$下，我们价值函数$V(s)$，和能选择的很多动作$a$。我们每做一个动作$a$，就会得到一个奖励$r(s,a)$，同时状态转移至$s_{t+1}$，状态$s_{t+1}$的价值的期望就是$\sum_{s_{t+1}}p(s_{t+1}|s,a)V(s_{t+1})$，其中$V(s_{t+1})$来自上一轮的结果。
我们就用在$s$下，最佳动作带来的回报来更新我们的的状态价值函数$V(s)$。

具体算法如下：

价值迭代算法
输入：
  已知的模型(环境)$p$
  初始化的状态值(对于每一个$s\in\mathcal{S}$，$V(s)=0$)
输出：
  最优策略$\pi$
参数：
  策略评估需要的参数，即最小更新值$\theta$和最大迭代次数$K_{\max}$
迭代，对于$k=1,2,3,\cdots,K_{\max}$，执行以下操作：
  $\Delta\leftarrow0$
  遍历$s\in\mathcal{S}$，$s_t=s_1,s_2,s_3,\cdots,s_T$：
    把上一轮迭代的价值赋给$V$，$V\leftarrow V_k(s_t)$
    计算新状态的价值$V_k(s_t)\leftarrow\max_{a_t}\{r(s_t,a_t)+\gamma\sum_{s_{t+1}}p(s_{t+1}|s_t,a_t)V_{k-1}(s_{t+1})\}$
    $\Delta\leftarrow\max(\Delta,|V_{k}(s_t)|)$

  如果$\Delta$几乎不更新($\Delta<\theta$)，或者已经到了最大迭代次数($k=k_{\max}$)，结束迭代。
策略：
  根据最优价值函数，输出确定性的策略：

$$\pi(s_t)=\argmax_{a_t}\{r(s_t,a_t)+\gamma\sum_{s_{t+1}}p(s_{t+1}|s_t,a_t)V(s_{t+1})\}$$

价值迭代的实现

示例代码：

def iterate_value(env, gamma=1, tolerant=1e-6,kmax=1000000):
    v = np.zeros(env.unwrapped.nS) # 初始化
    for i in range(kmax):
        delta = 0
        for s in range(env.unwrapped.nS):
            vmax = max(v2q(env, v, s, gamma)) # 更新价值函数
            delta = max(delta, abs(v[s]-vmax))
            v[s] = vmax
        if delta < tolerant: # 满足迭代需求
            break

    policy = np.zeros((env.unwrapped.nS, env.unwrapped.nA)) # 计算最优策略
    for s in range(env.unwrapped.nS):
        a = np.argmax(v2q(env, v, s, gamma))
        policy[s][a] = 1.
    return policy, v

policy_vi, v_vi = iterate_value(env)
print('状态价值函数 =')
print(v_vi.reshape(4, 4))
print('最优策略 =')
print(np.argmax(policy_vi, axis=1).reshape(4, 4))

episode_rewards = [play_policy(env, policy_vi) for _ in range(100)]
print("价值迭代 平均奖励：{}".format(np.mean(episode_rewards)))

运行结果：

状态价值函数 =
[[0.82351232 0.82350671 0.82350281 0.82350083]
 [0.82351404 0.         0.52940011 0.        ]
 [0.82351673 0.82352018 0.76469779 0.        ]
 [0.         0.88234653 0.94117321 0.        ]]
最优策略 =
[[0 3 3 3]
 [0 0 0 0]
 [3 1 0 0]
 [0 2 1 0]]
价值迭代 平均奖励：0.86

• 同样，我们得到了最优策略。