1.基础概念

这一系列的笔记我们讨论强化学习，在《深度学习初步及其Python实现：12.强化学习初探》中，我们有简单的讨论过强化学习，但当时的讨论太浅显。这次，我们用七章的篇幅，试图较为深刻的讨论强化学习。

注意！

• 我在深度学习的系列笔记中讨论强化学习，容易让大家误会，认为强化学习属于深度学习的一种。实际上，这是两个独立的概念，但是深度学习的一些方法会被用来解决强化学习的问题，这个也被称为深度强化学习。
• 另外，强化学习其实是一个非常博大精深的话题，除了我们这系列会讨论的内容外，还有多智能体的强化学习、逆强化学习以及考虑方差的强化学习等内容。所以我们的标题是"强化学习浅谈及其Python实现"。

强化学习中最重要，最基础的数学模型是马尔可夫决策过程(Markov Decision Process)。
为了更好的讨论马尔可夫决策过程，我们先快速的回顾一下概率论的一些知识。

概率论

随机变量和观测值

随机变量是一个不确定的量，它的值取决于一次随机事件的结果。
比如，我们抛硬币，可能正面朝上，也可能反面朝上。抛硬币这件事情就是随机事件。抛硬币的结果就是随机变量，记做$X$。随机变量$X$有两个可能的取值：正面朝上、反面朝上。抛硬币之后，我们会观测到具体是哪一面朝上，这时候随机变量$X$就有了观测值$x$。比如正面朝上，那么

$$x=\text{正面}$$

概率分布

强化学习中会反复用到概率分布函数(Probability Distribution Function)。
概率分布函数分为概率质量函数(Probability Mass Function, PMF)和概率密度函数(Probability Density Function, PDF)两种。

概率质量函数

概率质量函数，其实这并不是什么新东西，我们在高中数学就学过，只是那个时候我们称之为分布律，或者分布列。
比如，在刚刚抛硬币的例子中：

	正面	反面
概率	$0.5$	$0.5$

概率质量函数描述离散随机变量在各特定取值上的概率。
其性质有：

$$\sum_{x \in X\text{的所有可能取值}} p(x) = 1$$

概率密度函数

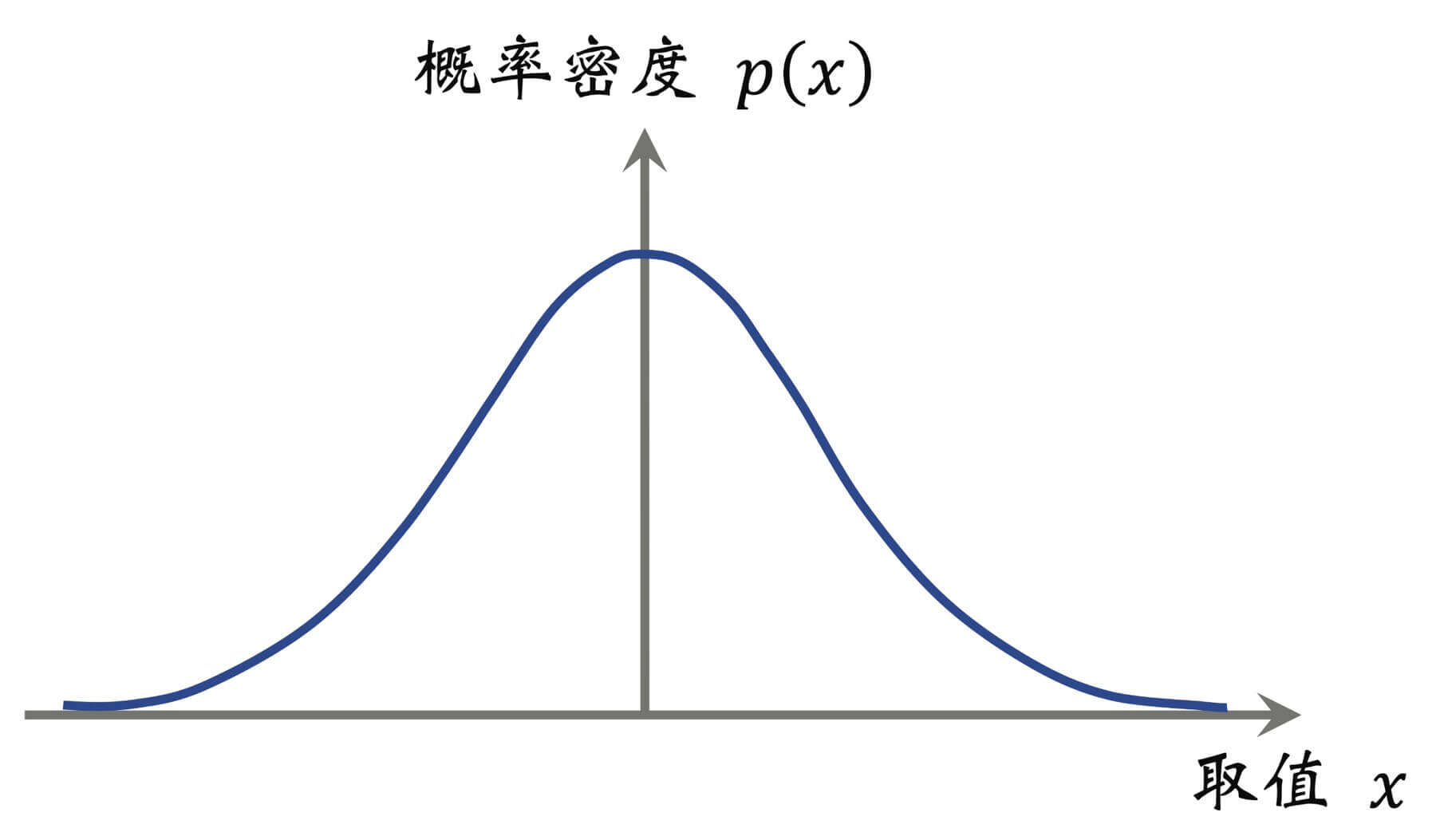
但是对于连续随机变量，其一切可能取值充满一个区间，在这个区间内有无穷多个实数。所以我们描述连续随机变量的概率分布就不能再用概率质量函数了，要用概率密度函数。

比如，正态分布，就是一种常见的连续概率分布，其概率密度函数如下：

$$p(x) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp\bigg(-\frac{(x-\mu)^2}{2\sigma^2}\bigg)$$

如图所示，$X$在均值附近取值的可能性大，在远离均值的地方取值的可能性小。
概率密度函数描述连续随机变量在某个确定的取值点附近的概率。
其性质有：

$$\int_{X\text{的值域}} p(x) dx = 1$$

期望

离散随机变量

$$\mathbb{E}[f(X)] = \sum_{x\in X\text{的所有可能取值}} p(x) f(x)$$

连续随机变量

$$\mathbb{E}[f(X)] = \int_{X\text{的值域}} p(x) f(x) dx$$

例子

我们再来举一个相关的例子，因为在讨论"价值函数"的时候，我们会大量用到与这个例子相近的思路。
假设$g(X,Y) = XY$是一个关于随机变量$X$和随机变量$Y$的二元函数，且已知随机变量$X$的取值范围是$[0,10]$，概率密度函数$p(x) = \frac{1}{10}$。求$g(X,Y)$关于随机变量$X$的期望。

$$\begin{aligned} \mathbb{E}_{X \sim p(\cdot)}[g(X,Y)] &= \int_{X\text{的值域}} g(x,Y) * p(x) dx \\ &= \int_{0}^{10} xY \frac{1}{10} dx \\ &= 5Y \end{aligned}$$

即：$g(X,Y)$关于随机变量$X$求期望，消除了随机变量$X$的影响。

随机抽样

随机抽样，这个其实很好理解。
我们这里用Python实现一个随机抽样，带来一个更直观的感受。
继续以抛硬币为例。

示例代码：

from numpy.random import choice
samples = choice(a=['正', '反'], size=100, p=[0.5, 0.5])
print(samples)

运行结果：

['反' '正' '正' '正' '反' '反' '正' '正' '正' '正' '反' '反' '反' '正' '正' '反' '反' '反'
 '反' '正' '反' '正' '正' '正' '正' '反' '正' '反' '正' '反' '反' '正' '反' '正' '反' '正'
 '反' '正' '正' '正' '反' '反' '反' '正' '正' '正' '反' '反' '正' '反' '反' '反' '反' '反'
 '正' '正' '反' '正' '反' '反' '正' '反' '反' '正' '反' '正' '正' '反' '正' '反' '正' '正'
 '反' '正' '反' '反' '正' '正' '反' '反' '正' '反' '正' '反' '反' '反' '正' '正' '正' '正'
 '正' '正' '反' '反' '正' '正' '反' '反' '反' '正']

马尔可夫决策过程的基本概念

关于马尔可夫决策过程的基本概念，我们在《深度学习初步及其Python实现：12.强化学习初探》有过简单的讨论，当时我们举了两个例子，电影《逃学威龙》和"在野外遇到熊"。这次，我们换一个例子，游戏《超级玛丽》。

现在，让我们来好好的拆解一下这款游戏。

环境

《超级玛丽》这款游戏就是环境(Environment)。

状态

在这张图中，玛丽的上面有金币，右边有蘑菇，左边有乌龟，等等等等，总之就是这么个情况。这些共同构成了状态(State)，用字母$s$表示，状态是我们做决策的唯一依据。

所有可能的状态的集合被称为状态空间(State Space)，用花体字母$\mathcal{S}$表示。状态空间可以是有限集合(离散的)，也可以是无限集合(连续的)。

特别注意！在《超级玛丽》这款游戏中，我们可以说当前的画面就是状态，但是换一个游戏，就不一定。比如《王者荣耀》，因为在《王者荣耀》中，我们看到的画面并不是对当前情况的完整概括，毕竟总有时候，我们忽然就被偷塔了，这时候的我们看到的画面只是部分观测(Partial Observation)。

所以更为严格的说法是观察环境的状态$s(s \in \mathcal{S})$，得到观测$o(o \in \mathcal{O})$。只是，有时候我们简单的认为当前环境是完全可观测的，所以我们人为把状态$s$和观测$o$等同起来了。

动作

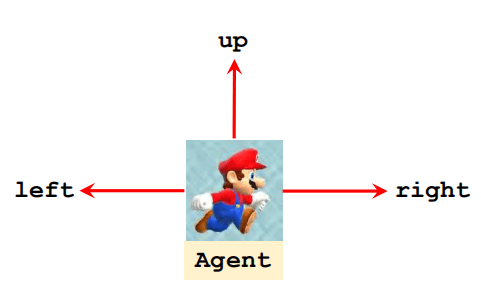
我们回到游戏《超级玛丽》，在当前状态$s$下，玛丽可以向上、向左或者向右。

这就是动作(Action)，用字母$a$表示，指可以做出的动作。
所有可能的动作的集合被称为动作空间(Action Space)，用花体字$\mathcal{A}$表示。和状态空间一样，动作空间也有两种，有限集合(离散的)和无限集合(连续的)。

智能体

做动作的主体就是智能体(Agent)。在这里，玛丽就是智能体。

策略

正如我们上文的讨论，状态是我们做决策的唯一依据。那么，我们怎么根据状态做出决策呢？
策略函数。
我们用$\pi$表示策略函数，其数学表达如下：

$$\pi(a|s) = \mathbb{P}(A=a|S=s)$$

比如，我们刚刚的例子中，当前的状态$s$，有：

$$\begin{aligned} & \pi(left|s) = 0.2 \\ & \pi(right|s) = 0.1 \\ & \pi(up|s) = 0.7 \\ \end{aligned}$$

那么，玛丽究竟会做什么动作呢？
不知道。
三种动作都有可能，随机抽样。

这就是强化学习两个随机性来源中的一个，动作的随机性。

实际上，动作不一定是随机的。在我们这系列的笔记中，我们会见到大量的确定性策略，即在给定的状态下，智能体做出的动作也是固定的。
但，因为也确实有随机性策略，所以，通常，我们仍认为动作的随机性是强化学习随机性的来源之一。

奖励

智能体执行一个动作之后，环境返回给智能体一个奖励(Reward)。

在《生活大爆炸》中，我们可以看到一个非常形象的过程。

 
奖励是环境给的，但是奖励的值，或者说奖励函数，是由我们定义的。
比如：

• 收集金币：奖励 = +1
• 解救公主：奖励 = +10000
• 触碰蘑菇：奖励 = -10000
• 没有事情：奖励 = 0

特别的，我们还可以把收集金币设置大一些，解救公主设置小一些。(我只想捡金币，救公主只是顺带的。)

状态转移

状态转移(State Transition)，顾名思义，由当前状态$s$转移到新状态$s'$。
在当前状态$s$下，智能体执行动作$a$，环境给出新的状态$s'$。
那么，环境怎么根据状态$s$和动作$a$，给出新的状态$s'$呢？
状态转移函数。

比如在电影《大话西游》中，当前的状态$s$是紫霞仙子的剑距离至尊宝的喉咙只有零点零一公分。这时候至尊宝做出动作$a$说一个谎话。

然后，状态就从$s$转移到$s'$，而且根据至尊宝的描述，我们知道只要至尊宝做出动作$a$说谎，紫霞仙子一定会爱上至尊宝，就是说这个状态转移函数是确定的。

但更多情况下，状态转移函数不是确定的，而是服从某一个概率分布，毕竟不是每一次表白都会成功。
再比如说，在游戏《超级玛丽》中。

当玛丽在当前状态$s$，做出动作$a$向上跳之后，蘑菇可能会向左也可能会向右，服从某一个概率分布，这个是随机的。
函数表达式如下：

$$p(s'|s,a) = \mathbb{P}(S' = s'|S = s,A = a)$$

这就是强化学习随机性的第二个来源，状态转移的随机性。

小结一下，在强化学习中，随机性有两个来源：

1. 动作的随机性
2. 状态转移的随机性

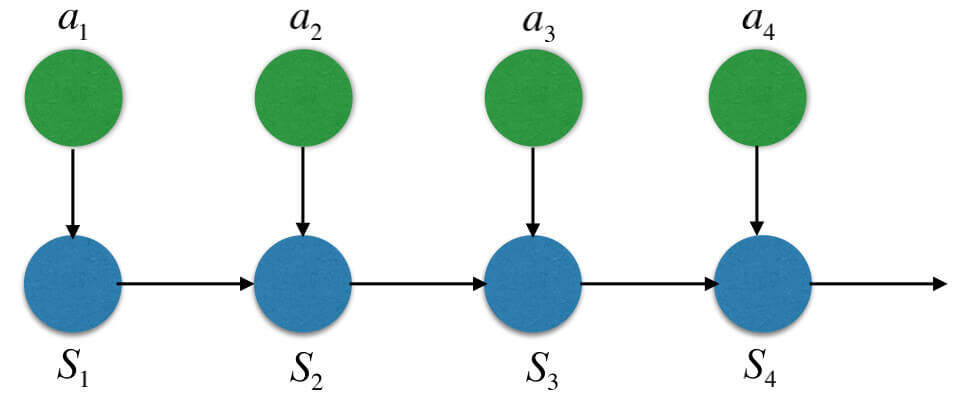
马尔可夫模型

最后，我们讨论一下，什么是马尔可夫模型(Markov Model)，和马尔可夫决策过程(Markov Decision Process, MDP)有什么关系。

马尔可夫模型的特点是，当前的状态仅依赖于上一个状态。
所以，其状态转移函数是：

$$p(s_t|s_{t-1})$$

而，现在我们假设，当前状态依赖于上一个状态和我们在上一个状态做的动作，这就是马尔可夫决策过程了。

其状态转移函数是：

$$p(s_t|s_{t-1},a_{t-1})$$

回报

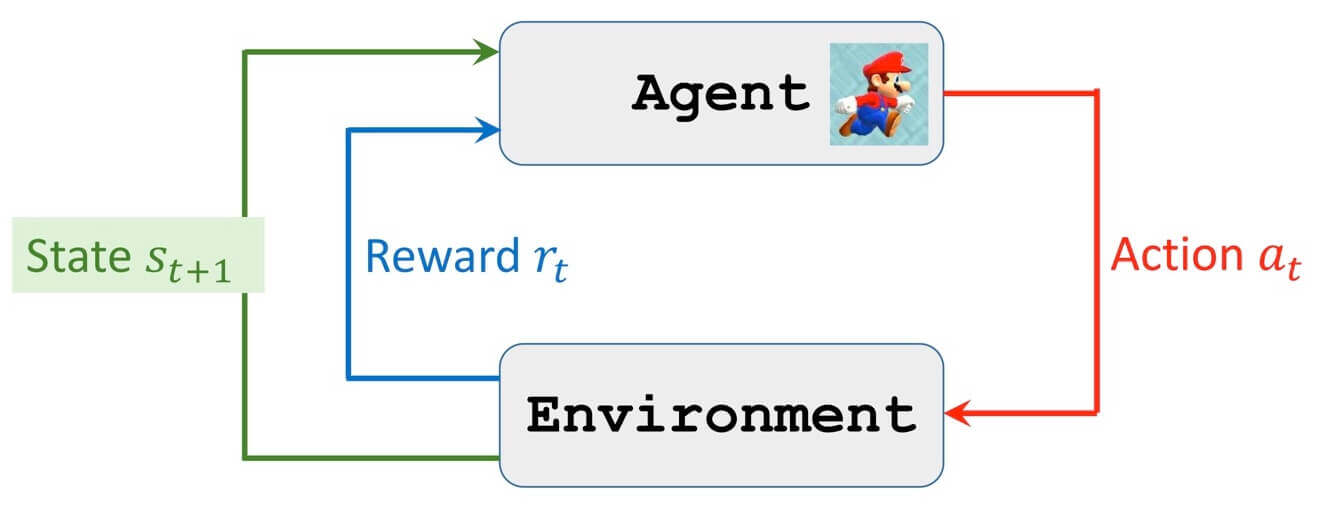
接下来，我们讨论回报(Return)。但在这之前，我们先看看智能体和环境的交互。

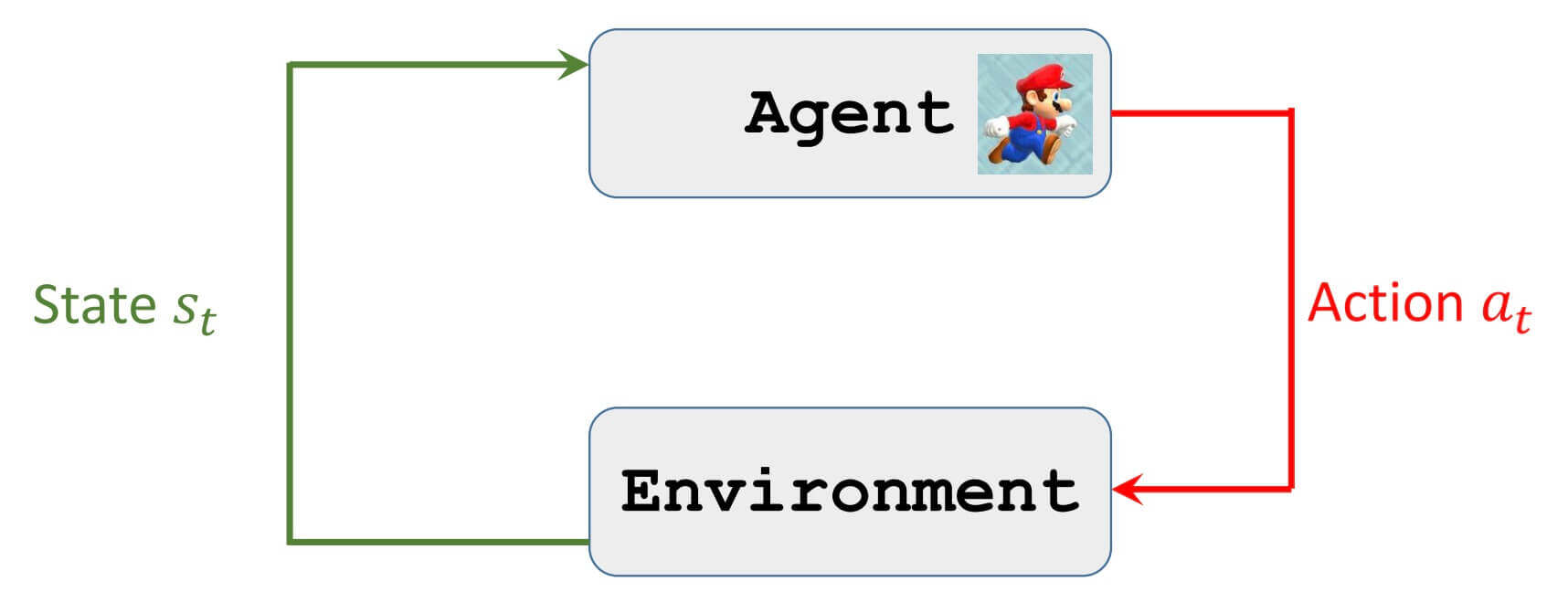
智能体和环境的交互

首先，智能体观测到环境给的状态$s_t$，并根据$s_t$，做出相应的动作$a_t$。

然后，环境会根据$s_t$和$a_t$，更新状态$s_{t+1}$，并给智能体一个奖励$r_{t}$。

上述过程循环往复，最后我们会得到：

$$s_1,a_1,r_1,s_2,a_2,r_2,s_3,\cdots$$

这就是轨迹(Trajectory)，指一个回合(Episode)游戏中，智能体观测到的所有状态、做出的所有动作、收到的所有奖励。

提一个问题，在上文，我们还特别讨论了完全可观测的环境和部分可观测的环境，那么在一个部分可观测的环境中，轨迹应该是怎样的呢？

$$s_1,o_1,a_1,r_1,s_2,o_2,a_2,r_2,s_3,\cdots$$

也有一些资料把动作$a_t$之后的奖励记作$r_{t+1}$，因为在$t$时刻的状态$s_t$，做出$t$时刻的动作$a_t$，共同确定了$t+1$时刻的状态$s_{t+1}$和$t+1$时刻的奖励$r_{t+1}$。我本人非常认同这个观点，这种记法的确更有道理，而且强化学习领域的一本非常重要的书，Sutton的《Reinforcement Learning:An Introduction》就是采用这种记法。

但我们还是把动作$a_t$之后的奖励记作$r_{t}$，因为绝大部分资料采用的这种记法。为了便捷，我们还是选择遵守大多数的惯例。

回报

把未来的奖励累积起来，就是回报。
在这里我们用大写字母$R$表示随机变量奖励，用小写字母$r$表示已经观察到的奖励值。而对于回报，我们用大写字母$G$表示随机变量回报。
那么，$t$时刻的回报如下

$$G_t = R_{t} + R_{t+1} + R_{t+2} + R_{t+3} + \cdots$$

但，就像在金融中，货币都有时间价值，今天的一块钱和明天的一块钱是不一样的，在这里奖励也有"时间价值"。
所以，通常情况下，我们会乘以$\gamma$折扣因子，也有资料称之为折现率，衰减率，通常$\gamma \in [0,1]$。

$$G_t = R_{t} + \gamma R_{t+1} + \gamma^2 R_{t+2} + \gamma^3 R_{t+3} + \cdots$$

而强化学习的目标是最大化回报，而不是最大化当前的奖励。毕竟，我们应该着眼于解救公主，而不是眼前的这一两枚金币。

回报的随机性

我们再来看看回报来源于什么？来源于未来的累积奖励。
那么奖励来源于什么呢？智能体在当前状态下，每做一个动作，都有会收到一个奖励。
在有些情况下，只有在回合结束的时候，奖励的值才可能不为$0$，其他时候都是$0$，比如，我们下一章《2.动态规划》的例子，冰面滑行。但是，每做一个动作，都有会收到一个奖励，只是有时候奖励的值为$0$。

奖励是关于状态和动作的函数。
状态是随机的，动作是随机的。所以奖励是随机的，所以回报是随机的，其随机性来自于状态和动作。
即，$G_t$的随机性来自于

$$A_t,S_{t+1},A_{t+1},S_{t+2},A_{t+2},\cdots,S_{n},A_{n}$$

• 当然没有$S_t$，因为在$t$时刻，我们已经观测到了$s_t$。
• 如果动作还没做的话，$A_t$是$G_t$的随机性来源。如果动作已经做了的话，$A_t$将不是$G_t$的随机性来源(比如本章要讨论的动作价值函数)。

价值函数

动作价值函数

假设我们已经观测到了状态$s_t$，并且也做出了动作$a_t$。那么，问$G_t$是多少？
不知道。
$G_t$依旧是一个随机变量，其随机性来源于

$$S_{t+1},A_{t+1},S_{t+2},A_{t+2},\cdots,S_{n},A_{n},\cdots$$

没关系，我们对这个随机变量求期望。
在这一章开始，讨论期望的时候，我们举了这么一个例子：$g(X,Y) = XY$是一个关于随机变量$X$和随机变量$Y$的二元函数，求$g(X,Y)$关于随机变量$X$的期望，然后我们成功的把随机变量$X$消掉了。
那么，现在一样的。
我们求$G_t$关于$S_{t+1},A_{t+1},S_{t+2},A_{t+2},\cdots,S_{n},A_{n}$的期望。

$$\mathbb{E}_{S_{t+1},A_{t+1},S_{t+2},A_{t+2},\cdots,S_{n},A_{n}}[G_t|S_t=s_t,A_t=a_t]$$

更多的时候，写作：

$$\mathbb{E}[G_t|S_t=s_t,A_t=a_t]$$

这就是我们的动作价值函数(Action-Value Function)，记做$Q_{\pi}(s_t,a_t)$，其含义是在$s_t$状态下，做动作$a_t$的价值。

$Q_{\pi}(s_t,a_t)$依赖于$s_t$和$a_t$，而不依赖于$t+1$时刻及之后的动作和状态，因为随机变量$S_{t+1},A_{t+1},S_{t+2},A_{t+2},\cdots,S_{n},A_{n}$，都被求期望消除了。

状态价值函数

在讨论了什么是动作价值函数之后，状态价值函数(State-Value Function)就非常的简单。
当前状态$s_t$的价值。
在当前状态$s_t$下，我们可以选择的动作很多，但是我们都没有做。
即$G_t$依赖于随机变量

$$A_t,S_{t+1},A_{t+1},S_{t+2},A_{t+2},\cdots,S_{n},A_{n}$$

同样，我们对其求期望

$$\mathbb{E}_{A_t,S_{t+1},A_{t+1},S_{t+2},A_{t+2},\cdots,S_{n},A_{n}}[G|S_t=s_t]$$

更多的时候，写作：

$$\mathbb{E}[G_t|S_t=s_t]$$

这就是我们的状态价值函数，记做$V_{\pi}(s_t)$。

价值函数的性质

价值函数的性质，也就是Bellman期望方程(Bellman Expectation Equations)，刻画的是状态价值函数和动作价值函数之间的关系。
其基本性质有：

1. 可以用$t$时刻的动作价值函数来表示$t$时刻的状态价值函数。
2. 可以用$t+1$时刻的状态价值函数来表示$t$时刻的动作价值函数。

接下来，我们分别讨论。

可以用$t$时刻的动作价值函数来表示$t$时刻的状态价值函数。

状态价值函数是在当前状态$s_t$下，可以选择的动作很多，但是我们都没有做。
动作价值函数是在状态$s_t$，已经做了动作$a_t$。
那么，我们关于所有的$a_t$求动作价值的期望，就是在$t$时刻的状态价值函数。

$$V_{\pi}(s_t) = \sum_{a_t} \pi(a_t|s_t)Q_{\pi}(s_t,a_t)$$

• $\pi(a_t|s_t)$是策略函数，同时还属于概率质量函数，$\sum$之和等于$1$。

可以用$t+1$时刻的状态价值函数来表示$t$时刻的动作价值函数。

这个也很好理解，在$t$时刻的状态$s_t$做出动作$a_t$后，得到奖励$r_{t}$，同时状态从$s_t$转移到$s_{t+1}$

$$Q_{\pi}(s_t,a_t) = r(s_t,a_t) + \gamma \sum_{s_{t+1}} p(s_{t+1}|s_t,a_t) V_{\pi}(s_{t+1})$$

• $r(s_t,a_t)$是奖励。
• $p(s_{t+1}|s_t,a_t)$是状态转移函数，表示在$s_t$状态下，做出动作$a_t$，然后状态转移到$s_{t+1}$的概率。

通过上述两个基本性质，又可以衍生出两个性质：

1. 可以用$t+1$时刻的状态价值函数表示$t$时刻的状态价值函数。
2. 可以用$t+1$时刻的动作价值函数表示$t$时刻的动作价值函数。

可以用$t+1$时刻的状态价值函数表示$t$时刻的状态价值函数。

正如我们上文的讨论，可以用$t+1$时刻的状态价值函数来表示$t$时刻的动作价值函数，可以用$t$时刻的动作价值函数来表示$t$时刻的状态价值函数。
所以，可以用$t+1$时刻的状态价值函数表示$t$时刻的状态价值函数。

$$V_{\pi}(s_t) = \sum_{a_t}\pi(a_t|s_t)\bigg[ r(s_t,a_t) + \gamma \sum_{s_{t+1}} p(s_{t+1}|s_t,a_t) V_{\pi}(s_{t+1}) \bigg]$$

可以用$t+1$时刻的动作价值函数表示$t$时刻的动作价值函数。

这个也很好理解，我们可以用$t+1$时刻的动作价值函数来表示$t+1$时刻的状态价值函数，可以用$t+1$时刻的状态价值函数来表示$t$时刻的动作价值函数。
所以，可以用$t+1$时刻的动作价值函数表示$t$时刻的动作价值函数。

$$Q_{\pi}(s_t,a_t) = \sum_{s_{t+1},r} p(s_{t+1},r|s_t,a_t) \bigg[ r+ \gamma \sum_{a_{t+1}} \pi(a_{t+1}|s_{t+1})Q_{\pi}(s_{t+1},a_{t+1}) \bigg]$$

这也就是Bellman期望方程

也有资料认为：用动作价值表示状态价值、用状态价值表示动作价值不能称为Bellman方程，只有用动作价值表示动作价值、用状态价值表示状态价值才能称为Bellman方程。

求解价值函数

那么，上述的四个性质，都有什么用呢？

举个例子。

该例子来自《强化学习：原理与Python实现(肖智清著)》这本书的第二章。

假设，我们已知环境的状态转移如下：

$s_t$	$a_t$	$r_{t}$	$s_{t+1}$	$p(s_{t+1},r_{t} \mid s_t,a_t)$
饿	不吃	$-2$	饿	$1$
饿	吃	$2$	饱	$\alpha$
饿	吃	$1$	饿	$1-\alpha$
饱	不吃	$2$	饱	$\beta$
饱	不吃	$1$	饿	$1-\beta$
饱	吃	$0$	饱	$1$

而我们的策略函数如下：

$s$	$a$	$\pi(a\mid s)$
饿	不吃	$1-x$
饿	吃	$x$
饱	不吃	$y$
饱	吃	$1-y$

根据状态价值函数的定义，我们有

$$\begin{aligned} & V_{\pi}(\text{饿}) = \mathbb{E}_{\pi}[G|S=\text{饿}] \\ & V_{\pi}(\text{饱}) = \mathbb{E}_{\pi}[G|S=\text{饱}] \\ & Q_{\pi}(\text{饿},\text{吃}) = \mathbb{E}_{\pi}[G|S=\text{饿},A=\text{吃}] \\ & Q_{\pi}(\text{饿},\text{不吃}) = \mathbb{E}_{\pi}[G|S=\text{饿},A=\text{不吃}] \\ & Q_{\pi}(\text{饱},\text{吃}) = \mathbb{E}_{\pi}[G|S=\text{饱},A=\text{吃}] \\ & Q_{\pi}(\text{饱},\text{不吃}) = \mathbb{E}_{\pi}[G|S=\text{饱},A=\text{不吃}] \end{aligned}$$

根据Bellman期望方程，用动作价值表示状态价值

$$V_{\pi}(s_t) = \sum_{a_t} \pi(a_t|s_t)Q_{\pi}(s_t,a_t)$$

我们有

$$\begin{aligned} & V_{\pi}(\text{饿}) = (1-x)Q_{\pi}(\text{饿},\text{不吃}) + xQ_{\pi}(\text{饿},\text{吃}) \\ & V_{\pi}(\text{饱}) = yQ_{\pi}(\text{饱},\text{不吃}) + (1-y)Q_{\pi}(\text{饱},\text{吃}) \\ \end{aligned}$$

根据Bellman期望函数，用状态价值表示动作价值

$$Q_{\pi}(s_t,a_t) = r(s_t,a_t) + \gamma \sum_{s_{t+1}} p(s_{t+1}|s_t,a_t) V_{\pi}(s_{t+1})$$

比如：
当$s_t=\text{饿}$，动作$a=\text{不吃}$，那么$s_{t+1}$只有一种可能，$\text{饿}$，所以有

$$Q_{\pi}(\text{饿},\text{不吃}) = -2 + \gamma V_{\pi}(\text{饿}) + 0$$

• 最后一个$0$的含义是说另一种可能的情况不存在

当$s_t = \text{饿}$，动作$a=\text{吃}$，有$\alpha$的概率，$s_{t+1} = \text{饱}$，同时存在$1-\alpha$的概率，$s_{t+1} = \text{饿}$。即：

$$Q_{\pi}(\text{饿},\text{吃}) = \alpha (2 + \gamma V_{\pi}(\text{饱})) + (1-\alpha)(1 + \gamma V_{\pi}(\text{饿}))$$

同理，我们有如下的式子

$$\begin{aligned} & Q_{\pi}(\text{饱},\text{不吃}) = \beta (2 + \gamma V_{\pi}(\text{饱})) + (1 - \beta)(1 + \gamma V_{\pi}(\text{饿})) \\ & Q_{\pi}(\text{饱},\text{吃}) = 0 + \gamma V_{\pi}(\text{饱}) + 0 \end{aligned}$$

通过这个，我们就构建了一个方程组，然后其中未知数就是状态价值和动作价值，六个方程，六个未知数(暂时把$\alpha,\beta,\gamma,x,y$看成不知道是多少的常数)，解方程组。

在这里介绍一个Python的包：sympy。
我实际测试发现，这个包在解微分方程的时候存在缺解的情况，具体大家可以试试下面的例子。应该只会求得一个$C=0$情况下的特解。

但是我想解方程组还是没问题的。

示例代码：

import sympy
from sympy import symbols
from sympy import solve
from sympy import Eq
from sympy import latex

v_hungry = symbols('v_hungry')
v_full = symbols('v_full')
q_hungry_eat = symbols('q_hungry_eat')
q_hungry_dont_eat = symbols('q_hungry_dont_eat')
q_full_eat = symbols('q_full_eat')
q_full_dont_eat = symbols('q_full_dont_eat')
alpha = symbols('alpha')
beta = symbols('beta')
gamma = symbols('gamma')
x = symbols('x')
y = symbols('y')

ans = solve([Eq((1 - x) * q_hungry_dont_eat + x * q_hungry_eat, v_hungry),
             Eq(y * q_full_dont_eat + (1 - y) * q_full_eat, v_full),
             Eq(-2 + gamma * v_hungry, q_hungry_dont_eat),
             Eq(alpha * (2 + gamma * v_full) + (1 - alpha) * (1 + gamma * v_hungry), q_hungry_eat),
             Eq(beta * (2 + gamma * v_full) + (1 - beta) * (1 + gamma * v_hungry), q_full_dont_eat),
             Eq(gamma * v_full, q_full_eat)],
            [v_hungry, v_full, q_hungry_eat, q_hungry_dont_eat, q_full_eat, q_full_dont_eat])

for k,v in ans.items():
    print(k)
    print(v)
    print(latex(v))

运行结果：

v_hungry
(-2*alpha*gamma*x*y + alpha*gamma*x - alpha*x + 3*beta*gamma*x*y - 2*beta*gamma*y - 3*gamma*x*y + 3*gamma*x + 2*gamma*y - 2*gamma - 3*x + 2)/(alpha*gamma**2*x - alpha*gamma*x - beta*gamma**2*y + beta*gamma*y + gamma**2*y - gamma**2 - gamma*y + 2*gamma - 1)

$$\frac{- 2 \alpha \gamma x y + \alpha \gamma x - \alpha x + 3 \beta \gamma x y - 2 \beta \gamma y - 3 \gamma x y + 3 \gamma x + 2 \gamma y - 2 \gamma - 3 x + 2}{\alpha \gamma^{2} x - \alpha \gamma x - \beta \gamma^{2} y + \beta \gamma y + \gamma^{2} y - \gamma^{2} - \gamma y + 2 \gamma - 1}$$

v_full
(-2*alpha*gamma*x*y + 3*beta*gamma*x*y - beta*gamma*y - beta*y - 3*gamma*x*y + 3*gamma*y - y)/(alpha*gamma**2*x - alpha*gamma*x - beta*gamma**2*y + beta*gamma*y + gamma**2*y - gamma**2 - gamma*y + 2*gamma - 1)

$$\frac{- 2 \alpha \gamma x y + 3 \beta \gamma x y - \beta \gamma y - \beta y - 3 \gamma x y + 3 \gamma y - y}{\alpha \gamma^{2} x - \alpha \gamma x - \beta \gamma^{2} y + \beta \gamma y + \gamma^{2} y - \gamma^{2} - \gamma y + 2 \gamma - 1}$$

q_hungry_eat
(-2*alpha*gamma**2*x*y - alpha*gamma**2*x + 2*alpha*gamma**2*y + alpha*gamma**2 + alpha*gamma*x - 2*alpha*gamma*y - alpha + 3*beta*gamma**2*x*y - 3*beta*gamma**2*y + beta*gamma*y - 3*gamma**2*x*y + 3*gamma**2*x + 3*gamma**2*y - 3*gamma**2 - 3*gamma*x - gamma*y + 4*gamma - 1)/(alpha*gamma**2*x - alpha*gamma*x - beta*gamma**2*y + beta*gamma*y + gamma**2*y - gamma**2 - gamma*y + 2*gamma - 1)

$$\frac{- 2 \alpha \gamma^{2} x y - \alpha \gamma^{2} x + 2 \alpha \gamma^{2} y + \alpha \gamma^{2} + \alpha \gamma x - 2 \alpha \gamma y - \alpha + 3 \beta \gamma^{2} x y - 3 \beta \gamma^{2} y + \beta \gamma y - 3 \gamma^{2} x y + 3 \gamma^{2} x + 3 \gamma^{2} y - 3 \gamma^{2} - 3 \gamma x - \gamma y + 4 \gamma - 1}{\alpha \gamma^{2} x - \alpha \gamma x - \beta \gamma^{2} y + \beta \gamma y + \gamma^{2} y - \gamma^{2} - \gamma y + 2 \gamma - 1}$$

q_hungry_dont_eat
(-2*alpha*gamma**2*x*y - alpha*gamma**2*x + alpha*gamma*x + 3*beta*gamma**2*x*y - 2*beta*gamma*y - 3*gamma**2*x*y + 3*gamma**2*x - 3*gamma*x + 2*gamma*y - 2*gamma + 2)/(alpha*gamma**2*x - alpha*gamma*x - beta*gamma**2*y + beta*gamma*y + gamma**2*y - gamma**2 - gamma*y + 2*gamma - 1)

$$\frac{- 2 \alpha \gamma^{2} x y - \alpha \gamma^{2} x + \alpha \gamma x + 3 \beta \gamma^{2} x y - 2 \beta \gamma y - 3 \gamma^{2} x y + 3 \gamma^{2} x - 3 \gamma x + 2 \gamma y - 2 \gamma + 2}{\alpha \gamma^{2} x - \alpha \gamma x - \beta \gamma^{2} y + \beta \gamma y + \gamma^{2} y - \gamma^{2} - \gamma y + 2 \gamma - 1}$$

q_full_eat
(-2*alpha*gamma**2*x*y + 3*beta*gamma**2*x*y - beta*gamma**2*y - beta*gamma*y - 3*gamma**2*x*y + 3*gamma**2*y - gamma*y)/(alpha*gamma**2*x - alpha*gamma*x - beta*gamma**2*y + beta*gamma*y + gamma**2*y - gamma**2 - gamma*y + 2*gamma - 1)

$$\frac{- 2 \alpha \gamma^{2} x y + 3 \beta \gamma^{2} x y - \beta \gamma^{2} y - \beta \gamma y - 3 \gamma^{2} x y + 3 \gamma^{2} y - \gamma y}{\alpha \gamma^{2} x - \alpha \gamma x - \beta \gamma^{2} y + \beta \gamma y + \gamma^{2} y - \gamma^{2} - \gamma y + 2 \gamma - 1}$$

q_full_dont_eat
(-2*alpha*gamma**2*x*y + 2*alpha*gamma**2*x - 2*alpha*gamma*x + 3*beta*gamma**2*x*y - 3*beta*gamma**2*x - beta*gamma**2*y + beta*gamma**2 + 3*beta*gamma*x - beta*gamma*y - beta - 3*gamma**2*x*y + 3*gamma**2*x + 3*gamma**2*y - 3*gamma**2 - 3*gamma*x - gamma*y + 4*gamma - 1)/(alpha*gamma**2*x - alpha*gamma*x - beta*gamma**2*y + beta*gamma*y + gamma**2*y - gamma**2 - gamma*y + 2*gamma - 1)

$$\frac{- 2 \alpha \gamma^{2} x y + 2 \alpha \gamma^{2} x - 2 \alpha \gamma x + 3 \beta \gamma^{2} x y - 3 \beta \gamma^{2} x - \beta \gamma^{2} y + \beta \gamma^{2} + 3 \beta \gamma x - \beta \gamma y - \beta - 3 \gamma^{2} x y + 3 \gamma^{2} x + 3 \gamma^{2} y - 3 \gamma^{2} - 3 \gamma x - \gamma y + 4 \gamma - 1}{\alpha \gamma^{2} x - \alpha \gamma x - \beta \gamma^{2} y + \beta \gamma y + \gamma^{2} y - \gamma^{2} - \gamma y + 2 \gamma - 1}$$

这样的话，我们可以知道每一个状态的价值，每一个动作的价值。

最优价值函数

为什么需要最优价值函数

通过上文的讨论，我们可以知道每一个状态的价值，每一个动作的价值。那么，我们就在每次做决策的时候，选择价值最大的一个动作。
现在问$Q_{\pi}(\text{饿},\text{吃})$和$Q_{\pi}(\text{饿},\text{不吃})$，哪个价值更大？
这个还真不好说，我们刚刚是暂时把$\alpha,\beta,\gamma,x,y$看成不知道是多少的常数。你真要问我谁大谁小，那我必须知道$\alpha,\beta,\gamma,x,y$到底是多少。
我们举个例子，战场上作战，当然应该寸土必争，但是现在有两位将军都做了撤退的决定，第一位将军是因为水平不行，怂；第二位将军是想以退为进，诱敌深入。策略$\pi$不同，虽然在当前状态$s$下，都做出了相同的动作$a=\text{撤退}$，但是后续的$A$却可能差距很大，最后结果也不同。那么这个动作价值函数的值自然也不同。
所以说，价值函数的值无法确定，类似的问题在上文我们也遇到了，当时我们做的是求关于未来的$S$和未来的$A$的期望，因为未来的$s$和$a$都是在未来某一时刻随机抽样出来的，那么现在呢？求关于策略$\pi$的期望？
当然不是，在随机策略$\pi$中，具体执行的动作$a$是随机抽样的。但是随机策略$\pi$本身，不是随机抽样的，你干嘛不直接选择最猛的那个策略？
所以呢，就有最优状态价值函数(optimal state value function)：

$$V_{\star}(s) = \max_{\pi}V_{\pi}(s),\ s\in\mathcal{S}$$

最优动作价值函数(optimal action value function)：

$$Q_{\star}(s,a) = \max_{\pi}Q_{\pi}(s,a),\ s\in\mathcal{S},a\in\mathcal{A}$$

所以，我们每次依据最优价值函数，来选择动作，这样实际上也就得到了一个最优的策略。

最优价值函数的性质

与价值函数一样，最优价值函数的性质也就是Bellman方程。

1. 可以用$t$时刻的最优动作价值函数表示$t$时刻的最优状态价值函数。
2. 可以用$t+1$时刻的最优状态价值函数表示$t$时刻的最优动作价值函数。

可以用$t$时刻的最优动作价值函数表示$t$时刻的最优状态价值函数

在上一小节，我们是求期望，因为动作是抽样出来的，但是现在我们直接选择最佳动作，就不抽样了。

$$V_{s_t} = \max_{a\in\mathcal{A}}Q_{*}(s_t,a_t)$$

可以用$t+1$时刻的最优状态价值函数表示$t$时刻的最优动作价值函数

在上一小节中，我们是求期望，因为状态转移方程其实是一个概率质量函数(或概率密度函数)，这次我们直接选择最佳的状态，就不抽样了。

$$\bold{\text{错了！}}$$

状态转移是由环境所控制的，我们并不能直接控制状态转移。
所以是：

$$Q_{\star}(s_t,a_t) = r(s_t,a_t) + \gamma \sum_{s_{t+1}}p(s_{t+1|s_t,a_t})V_{\star}(s_{t+1})$$

与上文一样，我们可以用$t+1$时刻的最优状态价值函数表示$t$时刻的最优动作价值函数，可以用$t$时刻的最优动作价值函数表示$t$时刻的最优状态价值函数。所以：

可以用$t+1$时刻的最优状态价值函数表示$t$时刻的最优状态价值函数

$$V_{\star}(s_t) = \max_{a\in\mathcal{A}} \bigg[ r(s_t,a_t) + \gamma \sum_{s_{t+1}} p(s_{t+1}|s_{t},a_{t}) V_{\star}(s_{t+1}) \bigg]$$

同理

可以用$t+1$时刻的最优动作价值函数表示$t$时刻的最优动作价值函数

$$Q_{\star}(s_t,a_t) = r(s_t,a_t) + \gamma \sum_{s_{t+1}} p(s_{t+1}|s_t,a_t) \max_{a_{t+1}}Q_{\star}(s_{t+1},a_{t+1})$$

求解最优价值函数

我们同样可以列出方程组：

$$\begin{aligned} V_{\star}(\text{饿}) &= \max\{Q_{\star}(\text{饿},\text{不吃}),Q_{\star}(\text{饿},\text{吃})\} \\ V_{\star}(\text{饱}) &= \max\{Q_{\star}(\text{饱},\text{不吃}),Q_{\star}(\text{饱},\text{吃})\} \\ Q_{\star}(\text{饿},\text{不吃}) &= -2 + \gamma V_{\star}(\text{饿}) + 0 \\ Q_{\star}(\text{饿},\text{吃}) &= \alpha (2 + \gamma V_{\star}(\text{饱})) + (1-\alpha)(1 + \gamma V_{\star}(\text{饿})) \\ Q_{\star}(\text{饱},\text{不吃}) &= \beta (2 + \gamma V_{\star}(\text{饱})) + (1 - \beta)(1 + \gamma V_{\star}(\text{饿})) \\ Q_{\star}(\text{饱},\text{吃}) &= 0 + \gamma V_{\star}(\text{饱}) + 0 \end{aligned}$$

对于这个方程组，同样可以用sympy求解，求解方法与上文的基本相同，但是需要注意的是。
我们要分情况讨论：

1. $Q_{\star}(\text{饿},\text{不吃}) \geq Q_{\star}(\text{饿},\text{吃})$ 且 $Q_{\star}(\text{饱},\text{不吃}) \geq Q_{\star}(\text{饱},\text{吃})$
2. $Q_{\star}(\text{饿},\text{不吃}) \geq Q_{\star}(\text{饿},\text{吃})$ 且 $Q_{\star}(\text{饱},\text{不吃}) < Q_{\star}(\text{饱},\text{吃})$
3. $Q_{\star}(\text{饿},\text{不吃}) < Q_{\star}(\text{饿},\text{吃})$ 且 $Q_{\star}(\text{饱},\text{不吃}) \geq Q_{\star}(\text{饱},\text{吃})$
4. $Q_{\star}(\text{饿},\text{不吃}) < Q_{\star}(\text{饿},\text{吃})$ 且 $Q_{\star}(\text{饱},\text{不吃}) < Q_{\star}(\text{饱},\text{吃})$

比如，对于第一种情况，我们的求解代码如下：

示例代码：

from sympy import symbols
from sympy import solve
from sympy import Eq
from sympy import latex

v_hungry = symbols('v_hungry')
v_full = symbols('v_full')
q_hungry_eat = symbols('q_hungry_eat')
q_hungry_dont_eat = symbols('q_hungry_dont_eat')
q_full_eat = symbols('q_full_eat')
q_full_dont_eat = symbols('q_full_dont_eat')
alpha = symbols('alpha')
beta = symbols('beta')
gamma = symbols('gamma')

ans = solve([Eq(q_hungry_dont_eat, v_hungry),
             Eq(q_full_dont_eat, v_full),
             Eq(-2 + gamma * v_hungry, q_hungry_dont_eat),
             Eq(alpha * (2 + gamma * v_full) + (1 - alpha) * (1 + gamma * v_hungry), q_hungry_eat),
             Eq(beta * (2 + gamma * v_full) + (1 - beta) * (1 + gamma * v_hungry), q_full_dont_eat),
             Eq(gamma * v_full, q_full_eat)],
            [v_hungry, v_full, q_hungry_eat, q_hungry_dont_eat, q_full_eat, q_full_dont_eat])

for k, v in ans.items():
    print(k)
    print(v)
    print(latex(v))

运行结果：

v_hungry
2/(gamma - 1)

$$\frac{2}{\gamma - 1}$$

v_full
(beta*gamma + beta - 3*gamma + 1)/(beta*gamma**2 - beta*gamma - gamma + 1)

$$\frac{\beta \gamma + \beta - 3 \gamma + 1}{\beta \gamma^{2} - \beta \gamma - \gamma + 1}$$

q_hungry_eat
(-3*alpha*gamma**2 + 2*alpha*gamma + alpha + 3*beta*gamma**2 - beta*gamma - 3*gamma + 1)/(beta*gamma**2 - beta*gamma - gamma + 1)

$$\frac{- 3 \alpha \gamma^{2} + 2 \alpha \gamma + \alpha + 3 \beta \gamma^{2} - \beta \gamma - 3 \gamma + 1}{\beta \gamma^{2} - \beta \gamma - \gamma + 1}$$

q_hungry_dont_eat
2/(gamma - 1)

$$\frac{2}{\gamma - 1}$$

q_full_eat
(beta*gamma**2 + beta*gamma - 3*gamma**2 + gamma)/(beta*gamma**2 - beta*gamma - gamma + 1)

$$\frac{\beta \gamma^{2} + \beta \gamma - 3 \gamma^{2} + \gamma}{\beta \gamma^{2} - \beta \gamma - \gamma + 1}$$

q_full_dont_eat
(beta*gamma + beta - 3*gamma + 1)/(beta*gamma**2 - beta*gamma - gamma + 1)

$$\frac{\beta \gamma + \beta - 3 \gamma + 1}{\beta \gamma^{2} - \beta \gamma - \gamma + 1}$$

对于其他情况，代码类似，主要区别在与

$$\begin{aligned} V_{\star}(\text{饿}) &= \max\{Q_{\star}(\text{饿},\text{不吃}),Q_{\star}(\text{饿},\text{吃})\} \\ V_{\star}(\text{饱}) &= \max\{Q_{\star}(\text{饱},\text{不吃}),Q_{\star}(\text{饱},\text{吃})\} \end{aligned}$$

即，主要区别在于这两行：

q_hungry_dont_eat - v_hungry,
q_full_dont_eat - v_full,

如果直接给出了$\alpha$、$\beta$和$\gamma$的值的话，那么也就没必要分四种情况了。我们可以直接推算最优动作价值，这样也就知道了最优策略。
比如：

$$\alpha=\frac{2}{3} \quad \beta=\frac{3}{4} \quad \gamma=\frac{4}{5}$$

示例代码：

from sympy import symbols
from sympy import solve
from sympy import Eq
from sympy import maximum

v_hungry = symbols('v_hungry')
v_full = symbols('v_full')
q_hungry_eat = symbols('q_hungry_eat')
q_hungry_dont_eat = symbols('q_hungry_dont_eat')
q_full_eat = symbols('q_full_eat')
q_full_dont_eat = symbols('q_full_dont_eat')
alpha = 2.0/3.0
beta = 3.0/4.0
gamma = 4.0/5.0

ans = solve([Eq(maximum(q_hungry_eat, q_hungry_dont_eat), v_hungry),
             Eq(maximum(q_full_eat, q_full_dont_eat), v_full),
             Eq(-2 + gamma * v_hungry, q_hungry_dont_eat),
             Eq(alpha * (2 + gamma * v_full) + (1 - alpha) * (1 + gamma * v_hungry), q_hungry_eat),
             Eq(beta * (2 + gamma * v_full) + (1 - beta) * (1 + gamma * v_hungry), q_full_dont_eat),
             Eq(gamma * v_full, q_full_eat)],
            [v_hungry, v_full, q_hungry_eat, q_hungry_dont_eat, q_full_eat, q_full_dont_eat])

for k, v in ans.items():
    print(k)
    print(v)

运行结果：

v_hungry
2.27272727272727
v_full
0.0
q_hungry_eat
2.27272727272727
q_hungry_dont_eat
-0.181818181818182
q_full_eat
0.0
q_full_dont_eat
2.20454545454545

即：

$$\begin{aligned} Q_{\star}(\text{饿},\text{吃}) &\approx 2.2 \\ Q_{\star}(\text{饿},\text{不吃}) &\approx -0.2 \\ Q_{\star}(\text{饱},\text{吃}) &\approx 0.0 \\ Q_{\star}(\text{饿},\text{不吃}) &\approx 2.2 \\ \end{aligned}$$

即：
最优策略是

$$\begin{aligned} \pi(\text{吃}\mid\text{饿}) &= 1 \\ \pi(\text{不吃}\mid\text{饿}) &= 0 \\ \pi(\text{吃}\mid\text{饱}) &= 0 \\ \pi(\text{不吃}\mid\text{饱}) &= 1 \\ \end{aligned}$$

关于风险的讨论

再回过头看看我们讨论的价值函数和最优价值函数，其实我们都在做一件事情：对回报求期望。
到这一步，或许有疑虑了，只看期望吗？
比如说，我们构建一个投资组合，只考虑这个投资组合的期望收益率吗？风险呢？风险要不要考虑。
当然要考虑，我们甚至会用投资组合收益分布的方差来衡量风险。
而在强化学习中，同样，也有考虑风险的，这被称为风险敏感的强化学习。

我们这一系列的笔记，讨论的都是"风险中性的强化学习"。