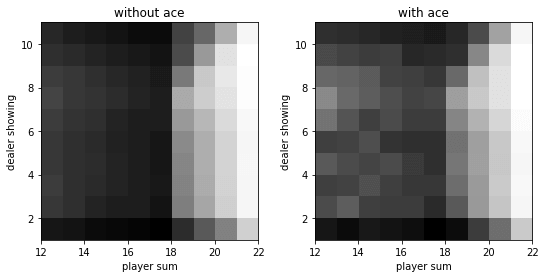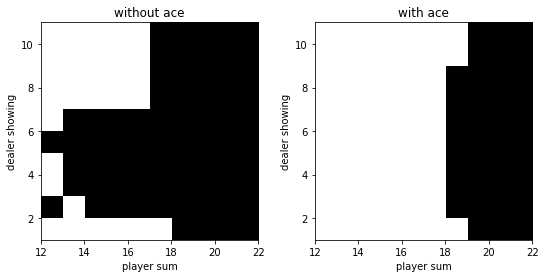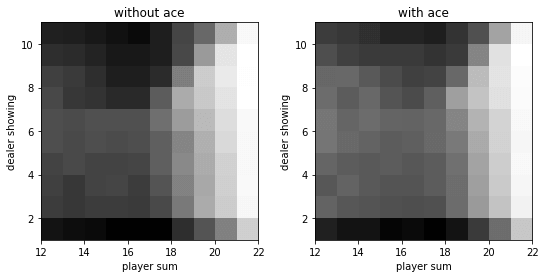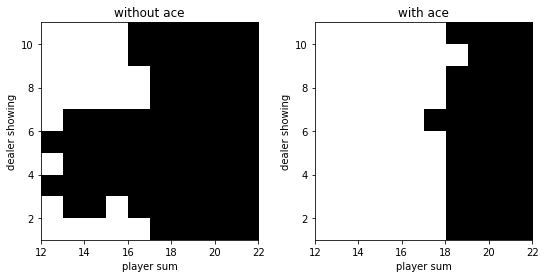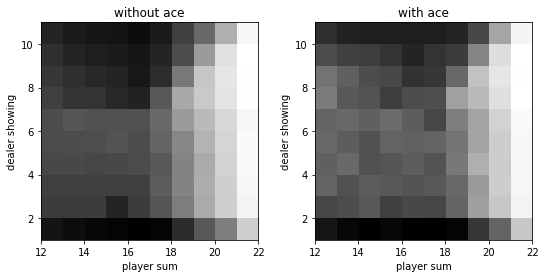3.蒙特卡洛

上一章，我们讨论了动态规划。有策略迭代和价值迭代两种。
在策略迭代中，我们每一轮更新当前策略的状态价值是这样的

$$V_k(s_t) \leftarrow \sum_{a_t}\pi(a_t|s_t)\bigg[ r(s_t,a_t) + \gamma \sum_{s_{t+1}} p(s_{t+1}|s_t,a_t) V_{k-1}(s_{t+1}) \bigg]$$

在价值迭代中，我们每一轮更新更新状态价值是这样的

$$V_k(s_t)\leftarrow\max_{a_t}\{r(s_t,a_t)+\gamma\sum_{s_{t+1}}p(s_{t+1}|s_t,a_t)V_{k-1}(s_{t+1})\}$$

无论是哪一种方法，其实都用到了$p(s_{t+1}|s_t,a_t)$，那么，如果$p(s_{t+1}|s_t,a_t)$不知道呢？

无模型和有模型的主要区别

让我们再回到第一章《1.基础概念》，我们可以用动作价值表示状态价值，用状态价值表示动作价值。

可以用$t$时刻的动作价值函数来表示$t$时刻的状态价值函数。

$$V_{\pi}(s_t) = \sum_{a_t} \pi(a_t|s_t)Q_{\pi}(s_t,a_t)$$

可以用$t+1$时刻的状态价值函数来表示$t$时刻的动作价值函数。

$$Q_{\pi}(s_t,a_t) = r(s_t,a_t) + \gamma \sum_{s_{t+1}} p(s_{t+1}|s_t,a_t) V_{\pi}(s_{t+1})$$

• $r(s_t,a_t)$是奖励。
• $p(s_{t+1}|s_t,a_t)$是状态转移函数，表示在$s_t$状态下，做出动作$a_t$，然后状态转移到$s_{t+1}$的概率。

有了这两个，又可以衍生出：

1. 可以用$t+1$时刻的状态价值函数表示$t$时刻的状态价值函数。
2. 可以用$t+1$时刻的动作价值函数表示$t$时刻的动作价值函数。

但其实，上述过程，基于了一个假设。我们假设状态转移函数$p(s_{t+1}|s_t,a_t)$是已知的，即假设环境是已知的，即有模型。

但更多的时候，我们的环境是未知的，即无模型。
这时候，$p(s_{t+1}|s_t,a_t)$是未知的。
那么，我们上面的链路就断了，
我们只能用动作价值表示状态价值。
这就是有模型和无模型的主要区别，无模型的时候，环境的状态转移方程不知道，只能用动作价值表示状态价值。

那怎么办？
我们还有其他办法，比如蒙特卡洛(Monte Carlo)(也有资料写作：蒙特卡罗)。

蒙特卡洛方法

我们先讨论什么是蒙特卡洛方法。
假设现在箱子里有100个球，其中写着数字0的球有50个，写着数字100的球有50个。问，箱子里球的平均数是多少？很简单，答案是50。
这就像环境是已知的，我们直接求解。
那么，现在，另一个箱子，这个箱子里有多少个球是不知道的，都有那些球也不知道的，每种球的个数也不知道。这时候环境就是未知的。现在，问，所有球的平均数是多少？
这就像环境是未知的，那怎么办呢？
我们随机的从箱子里摸球，然后我们可以计算摸出来的球的平均数。当摸出来的球的数量足够多，那么摸出来的球的平均数就接近真实的平均数。
抽样调查，这就是蒙特卡洛。
这种方法，其实我们无论是在工作学习还是生活中，都已经用了很多很多次了。最近的一次，在上一章，我们得到最优策略后，用最优策略实验100次，然后求平均看看效果，这也是蒙特卡洛。
接下来，直接举几个例子，以加深我们对蒙特卡洛的理解。

求不规则图形的面积

比如，求校徽的面积。

我们随机的抽足够多的点，比如100000个点，然后我们统计一下有多少点恰好落在校徽中。落在校徽中的点的个数除以样本总数100000，再乘以图片的大小，就是校徽的面积。

示例代码：

import random
from PIL import Image

img = Image.open('TongjiLogo.jpg')
total = 100000
inCount = 0
for i in range(total):
    x = random.randint(0, img.width - 1)
    y = random.randint(0, img.height - 1)
    color = img.getpixel((x, y))
    # 白色的RGB是 (255,255,255)
    if color != (255, 255, 255):
        inCount = inCount + 1

print('蒙特卡洛求校徽面积：')
print(img.width * img.height * inCount / total)

运行结果：

蒙特卡洛求校徽面积：
308806.208

近似定积分

在《高等数学(同济7版)》这本书的《第五章 定积分》，用多个矩形的面积去拟合曲边梯形的面积，通过这么一个例子引入定积分。

而用蒙特卡洛去近似定积分与这个有异曲同工之妙，只是我们是用一个矩形去拟合曲边梯形的面积。所以，我们要找到这一个矩形的恰到好处的高。

一元函数的定积分

例如，求函数在$a$到$b$区间上的定积分。

$$I = \int_a^b f(x) dx$$

方法如下：

1. 我们在$[a,b]$上均匀随机抽样足够多的样本：$x_1$,$x_2$,$x_3\ \cdots \ x_n$
2. 对函数值$f(x_1)$,$f(x_2)$,$f(x_3) \ \cdots \ f(x_n)$求平均，再乘以区间长度$b-a$。

   $$q_n = (b-a) * \frac{1}{n} \sum_{i=1}^{n}f(x_i)$$

3. $q_n$就是定积分$I$的估计值。

多元函数的定积分

在高中时候，我们就学过多元函数。多元函数是指自变量的个数是两个或两个以上的函数。
但，这次，我们这么理解。
多元函数的自变量$x$是一个$n$维的向量。

$$I = \int_{\Omega} f(x)dx$$

方法如下：

1. 在集合$\Omega$上均匀随机抽样足够多的样本：$\vec{x_1}$,$\vec{x_2}$,$\vec{x_3}\ \cdots \ \vec{x_n}$
2. 计算集合$\Omega$的体积

   $$v = \int_{\Omega}dx$$

3. 对函数值$f(\vec{x_1})$,$f(\vec{x_2})$,$f(\vec{x_3}) \ \cdots \ f(\vec{x_n})$求平均，再乘以体积$v$。

   $$q_n = v * \frac{1}{n} \sum_{i=1}^n f(\vec{x_i})$$

4. $q_n$就是定积分$I$的估计值。

提个问题，第二步，计算集合$\Omega$的体积。如果$\Omega$是规则形状，当然好办。如果$\Omega$不规则呢？
参考：蒙特卡洛的应用之求不规则图形(校徽)的面积。

近似期望

随机变量的期望，这个我们知道。比如对于连续随机变量，我们有：

$$\mathbb{E}[f(X)] = \int_{X\text{的值域}} p(x) f(x) dx$$

此外，我们还讨论了蒙特卡洛去近似定积分。
那么，我们是不是可以用蒙特卡洛去近似期望了？
当然可以。
但，我们需要注意的是：
之前我们都是均匀抽样，这次要根据概率分布函数$p(x)$做非均匀抽样了。
方法如下：

1. 根据概率分布函数$p(x)$，在集合$\Omega$上非均匀随机抽样足够多的样本：$x_1$,$x_2$,$x_3\ \cdots \ x_n \sim p(\cdot)$。
2. 对函数值$f(x_1)$,$f(x_2)$,$f(x_3) \ \cdots \ f(x_n)$求平均。

   $$q_n = \frac{1}{n} \sum_{i=1}^n f(x_i)$$

3. $q_n$就是随机变量的期望的估计值。

提个问题，在讨论多元函数的定积分的时候，我们乘以了集合$\Omega$的体积$v$，为什么这次不乘？
因为，我们求的是期望，不是定积分。

再提一个问题，如果让我们来编程实现，我们会怎么做？

• 方案一：定义一个list，在for循环求$f(x)$的时候，把结果一个一个添加进list。循环结束后，对list进行sum。
• 方案二：定义一个变量sum=0，在for循环的每一个循环中，更新sum的值，sum = sum + $f(x)$。

问，那种方案更省内存？
这个问题我们在《算法入门经典(Java与Python描述)：4.递归》讨论空间复杂度的时候讨论过。
方案一属于线性空间，其空间复杂度是$O(n)$；方案二属于常量空间，其空间复杂度是$O(1)$，方案二更节省内存。
(其实，就算我们不懂空间复杂度，凭直觉，也知道方案二更节省内存。)

而Robbins-Monro算法的思路，就和我们的方案二非常的相似。
我们初始化$q_0 = 0$，$t$从$1$到$n$依次计算

$$q_t = (1 - \frac{1}{t}) q_{t-1} + \frac{1}{t}f(x_t)$$

即：

$$\begin{aligned} q_1 &= q_0 + f(x_1) \\ &= f(x_1) \\ q_2 &= \frac{1}{2} q_1 + \frac{1}{2}f(x_2) \\ &= \frac{1}{2} f(x_1) + \frac{1}{2}f(x_2) \\ q_3 &= \frac{2}{3} q_2 + \frac{1}{3}f(x_3) \\ &= \frac{1}{3}f(x_1) + \frac{1}{3}f(x_2) + \frac{1}{3}f(x_3) \\ \cdots \end{aligned}$$

如果我们把$\frac{1}{t}$替换成$a_t$，则有：

$$q_t = (1 - a_t) q_{t-1} + a_t f(x_t)$$

同时$a_t$需要满足如下两个性质

1. $\lim_{n \rightarrow \infty} \sum_{t=1}^n a_t = \infty$
2. $\lim_{n \rightarrow \infty} \sum_{t=1}^n a_t^2 = \infty$

这里就是Robbins-Monro算法，$a_t$就是学习率。

随机梯度

刚刚，我们讨论了用蒙特卡洛去近似期望。现在，回忆一下，在机器学习中，我们什么时候需要去求期望？
梯度下降。
我们根据训练数据集，去求损失函数的梯度，并用该梯度对模型参数进行更新。
如果我们利用所有的训练数据集，尤其是训练数据还特别多的时候，就会很慢。
为了克服这个问题，我们提出了一个算法：随机梯度下降。
这就是蒙特卡洛近似期望在梯度下降中的应用。
方法如下：

1. 根据概率分布函数$p(x)$，做非均匀随机抽样，得到b个样本，记作$\tilde{x}_1$,$\tilde{x}_2$,$\tilde{x}_3 \ \cdots \ \tilde{x}_b$。
2. 求随机梯度$\tilde{g}$

   $$\tilde{g} = \frac{1}{b} \sum_{j=1}^b \nabla_\omega L(\tilde{x}_j;\omega)$$

3. 用随机梯度$\tilde{g}$更新$\omega$。

   $$\omega \leftarrow \omega - \alpha \tilde{g}$$

策略评估

通过上文的讨论，我们知道了在环境未知的情况下，我们的Bellman期望方程和我们的动态规划方法不再有效，因为我们再也不能用$t+1$时刻的状态价值来表示$t$时刻的状态价值。然后我们又讨论了蒙特卡洛方法，似乎给了我们一些启示，我们似乎可以用抽样调查的方法来更新价值。

策略评估的方法

那么既然是抽样调查呢，首先回答第一个问题，“样本"是什么？
那么，在这里"样本"就是我们的"轨迹”。
什么是轨迹？
智能体与环境交互，智能体观测到环境给的状态$s_t$，并根据$s_t$，做出相应的动作$a_t$。然后，环境会根据$s_t$和$a_t$，更新状态$s_{t+1}$，并给智能体一个奖励$r_{t}$。
上述过程循环往复，最后我们会得到：

$$s_1,a_1,r_1,s_2,a_2,r_2,s_3,\cdots$$

这就是轨迹(Trajectory)。

假设现在给定一个策略，然后我们根据这个策略，智能体和环境交互足够多的次数，就会得到足够多的轨迹，也就是足够多的样本，那么就可以基于蒙特卡洛评估我们的策略了。

比如说现在给定了一个策略，然后我们根据这个策略，让智能体和环境交互，得到了一个轨迹(样本)：$s_0,a_0,r_0,s_1,\cdots,s_{T-1},a_{T-1},r_{T-1},s_T$，我们计算每一个时刻$t$的累积回报，$t=T-1,T-2,T-3,\cdots,2,1,0$，比如，$t=T-1$时，回报$G_{T-1} = r_{T-1}$；$t=T-2$时，回报$G_{T-2} = r_{T-2} + \gamma r_{T-1}$，然后，我们再去更新状态价值。
比如，对于第一个样本：

$$Q(s_t,a_t) \leftarrow 0 + G_t$$

对于第二个样本：

$$Q(s_t,a_t) \leftarrow Q(s_t,a_t) + \frac{1}{2} [G_t - Q(s_t,a_t)]$$

道理是这么一个道理，一般情况下也就这样的，但有特例。

每次访问和首次访问

现在，我们来看一个特例。在电影《大话西游》中，有这么一段。

$$\text{同一个状态在一个轨迹中多次出现}$$

那么，对于这种情况，怎么办？

两种方法：

1. 每次访问蒙特卡洛更新(Every Visit Mente Carlo Update)
   采用轨迹样本内全部的回报样本更新价值函数
2. 首次访问蒙特卡洛更新(First Visit Mente Carlo Update)
   每个轨迹样本只采用第一次访问的回报样本更新价值函数

我们以动作价值为例，来看具体的做法。

每次访问蒙特卡洛更新
输入：
  未知的模型
  待评估的策略$\pi$
输出：
  动作价值函数，$Q(s,a)\leftarrow\text{任意值},s\in\mathcal{S},a\in\mathcal{A}$
初始化：初始化计数器，$C(s,a)\leftarrow 0,s\in\mathcal{S},a\in\mathcal{A}$
蒙特卡洛：(对于每个轨迹样本执行以下操作)
  采样，根据待评估的策略$\pi$，和环境进行交互。得到轨迹$s_0,a_0,r_0,s_1,a_1,r_1,s_2\cdots,s_{T-1},a_{T-1},r_{T-1},s_T$
  初始化回报，$G\leftarrow 0$
  逐步更新，对$t=T-1,T-2,\cdots,0$，执行以下步骤：
    更新回报，$G\leftarrow\gamma G+r_{t}$
    更新动作价值函数：
      $C(s,a)\leftarrow C(s,a)+1$
      $Q(s,a)\leftarrow Q(s,a)+\frac{1}{C(s,a)}[G-Q(s,a)]$

首次访问蒙特卡洛更新
输入：
  未知的模型
  待评估的策略$\pi$
输出：
  动作价值函数，$Q(s,a)\leftarrow\text{任意值},s\in\mathcal{S},a\in\mathcal{A}$
初始化：初始化计数器，$C(s,a)\leftarrow 0,s\in\mathcal{S},a\in\mathcal{A}$
蒙特卡洛：(对于每个轨迹样本执行以下操作)
  采样，根据待评估的策略$\pi$，和环境进行交互。得到轨迹$s_0,a_0,r_0,s_1,a_1,r_1,s_2,\cdots,s_{T-1},a_{T-1},r_{T-1},s_T$
  初始化回报，$G\leftarrow 0$
  初始化首次出现的步骤数，$f(s,a)\leftarrow -1,s\in\mathcal{S},a\in\mathcal{A}$
  统计首次出现的步骤数，对于$t=0,1,2,\cdots,T-1$，执行以下步骤：
    如果$f(s,a)<0$，则$f(s,a)\leftarrow t$
  逐步更新，对$t=T-1,T-2,\cdots,0$，执行以下步骤：
    更新回报，$G\leftarrow\gamma G+r_{t}$
    首次出现则更新，如果$f(s,a)=t$：
      $C(s,a)\leftarrow C(s,a)+1$
      $Q(s,a)\leftarrow Q(s,a)+\frac{1}{C(s,a)}[G-Q(s,a)]$

那么，对于状态价值呢？
虽然无模型了，但是只是不知道状态转移函数而已，只是不能用状态价值来表示动作价值了。但是，策略还是知道的，策略还是牢牢的掌握在我们自己的手中。
所以，状态价值依然可以用动作价值表示。

策略评估的实现

接下来，我们就来看实现。

21点游戏介绍

我们以一个知名的纸牌游戏"21点"为例。

该例子来自《强化学习：原理与Python实现(肖智清著)》这本书的第四章。

游戏规则是这样的：游戏里有一个玩家(player)和一个庄家(dealer)，每个回合的结果可能是玩家获胜、庄家获胜或打成平手。回合开始时，玩家和庄家各有两张牌，玩家可以看到玩家的两张牌和庄家的其中一张牌。接着，玩家可以选择是不是要更多的牌。如果选择要更多的牌，玩家可以再得到一张牌，并统计玩家手上所有牌的点数之和。
牌面和点数的对应关系见下表：

牌面	点数
A	1或11
2	2
3	3
···	···
9	9
10,J,Q,K	10

如果点数和大于21则称玩家输掉这一回合，庄家获胜；如果点数和小等于21，那么玩家可以再次决定是否要更多的牌，直到玩家不再要更多的牌。如果玩家在总点数小等于21的情况下不要更多的牌，那么这时候玩家手上的总点数就是最终玩家的点数。接下来，庄家展示其没有显示的那张牌，并且在其点数小于17的情况下抽取更多的牌。如果庄家在抽取的过程中总点数超过21，则庄家输掉这一回合，玩家获胜；如果最终庄家的总点数小于等于21，则比较玩家的总点数和庄家的总点数。如果玩家的总点数大于庄家的总点数，则玩家获胜；如果玩家和庄家的总点数相同，则为平局；如果玩家的总点数小于庄家的总点数，则庄家获胜。

提起这个纸牌游戏，大家可能还都会想到一部电影。《决胜21点》。

影片讲述了一个由MIT的教授和学生组成的团队，靠数学在拉斯维加斯的赌场上，通过21点纸牌游戏赚钱的故事。这个过程和量化投资极为相似(当然，金融市场不是赌场，但同样充满了不确定性)，因此这部电影也被看作是一部和量化投资有关的电影。

总之，这一章，我们要做的是一件很酷的事情。设计并开发一个人工智能，来玩"21点"这个纸牌游戏。

环境及其使用

首先，我们介绍环境，并用一个策略来试一下。
示例代码：

import gym
import numpy as np

# 环境使用
env = gym.make("Blackjack-v0")
env = env.unwrapped
env.seed(0)
print('观察空间 = {}'.format(env.observation_space))
print('动作空间 = {}'.format(env.action_space))
print('动作数量 = {}'.format(env.action_space.n))

运行结果：

观察空间 = Tuple(Discrete(32), Discrete(11), Discrete(2))
动作空间 = Discrete(2)
动作数量 = 2

我们的策略很简单，只要点数之和小于18，就继续摸牌。否则，不摸。
示例代码：

def ob2state(observation):
    # 分别是：玩家的点数，庄家的亮牌, 是否把A作为11
    return observation[0], observation[1], int(observation[2])

def play_once(env,policy):
    total_reward = 0
    observation = env.reset()
    print('观测 = {}'.format(observation))
    while True:
        print('玩家 = {}, 庄家 = {}'.format(env.player, env.dealer))
        # 状态
        state = ob2state(observation)
        action = np.random.choice(env.action_space.n, p=policy[state])
        print('动作 = {}'.format(action))
        observation, reward, done, _ = env.step(action)
        print('观测 = {}, 奖励 = {}, 结束指示 = {}'.format(
                observation, reward, done))
        total_reward += reward
        if done:
            return total_reward # 回合结束

policy = np.zeros((22, 11, 2, 2))
# >= 18 时收手
policy[18:, :, :, 0] = 1
# < 18 时继续
policy[:18, :, :, 1] = 1

print("奖励：{}".format(play_once(env,policy)))

运行结果：

观测 = (18, 1, False)
玩家 = [10, 8], 庄家 = [1, 7]
动作 = 0
观测 = (18, 1, False), 奖励 = 0.0, 结束指示 = True
奖励：0.0

策略评估的代码

在上文，我们讨论了"每次访问和首次访问"。
即：同一个状态在一个轨迹中多次出现。
但是，在21点这个游戏中，这个现象不存在，我们不需要区分首次访问和每次访问。每个状态，肯定只有一次访问。

示例代码：

import matplotlib.pyplot as plt

def evaluate_action_monte_carlo(env, policy, episode_num=500000):
    q = np.zeros_like(policy)
    c = np.zeros_like(policy)
    for _ in range(episode_num):
        # 玩一回合
        state_actions = []
        observation = env.reset()
        while True:
            state = ob2state(observation)
            action = np.random.choice(env.action_space.n, p=policy[state])
            state_actions.append((state, action))
            observation, reward, done, _ = env.step(action)
            if done:
                break # 回合结束
        g = reward # 回报
        for state, action in state_actions:
            c[state][action] += 1.
            q[state][action] += (g - q[state][action]) / c[state][action]
    return q

q = evaluate_action_monte_carlo(env, policy) # 动作价值
v = (q * policy).sum(axis=-1) # 状态价值

def plot(data):
    fig, axes = plt.subplots(1, 2, figsize=(9, 4))
    titles = ['without ace', 'with ace']
    have_aces = [0, 1]
    extent = [12, 22, 1, 11]
    for title, have_ace, axis in zip(titles, have_aces, axes):
        dat = data[extent[0]:extent[1], extent[2]:extent[3], have_ace].T
        axis.imshow(dat, cmap='gray',extent=extent, origin='lower')
        axis.set_xlabel('player sum')
        axis.set_ylabel('dealer showing')
        axis.set_title(title)


plot(v)

• extent = [12, 22, 1, 11]
• 因为动作价值是一个四维的数组，而状态价值是一个三维的数组。所以，我们绘制的是状态价值。

运行结果：

• 颜色越浅价值越大。

策略迭代

起始探索法

在上文，我们先估计了动作价值，然后为了画图方便，我们还计算了状态价值。
既然已经估计出来了动作价值呢，那么剩下的内容就和上一章一样了，每次选择动作价值最大的动作做迭代。然后再评估策略，再迭代。如此循环。
道理是这么个道理，但是在上一章我们讨论策略迭代的时候，提了一句，如果一开始的策略不太好，可能不会收敛到最佳策略。
我们来看一个特例。

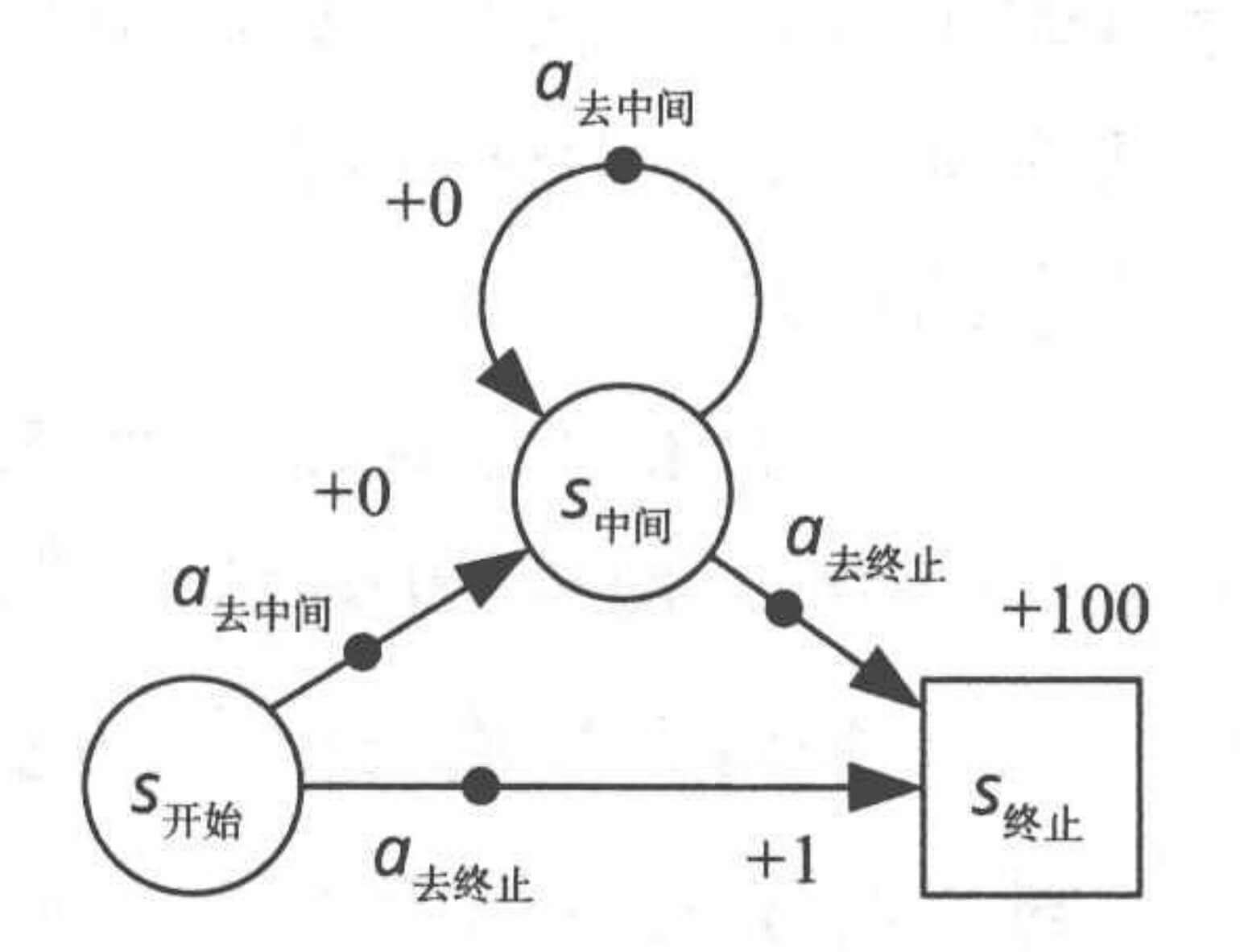
很明显，我们的最优策略是

$$\begin{aligned} \pi(s_{\text{开始}}) &= a_{\text{去中间}} \\ \pi(s_{\text{中间}}) &= a_{\text{去终止}} \end{aligned}$$

现在，我们把所有的动作价值和状态价值均初始化为0，并且随机从一个策略出发。
很不幸，我们从这么一个策略出发。

$$\begin{aligned} \pi(s_{\text{开始}}) &= a_{\text{去终止}} \\ \pi(s_{\text{中间}}) &= a_{\text{去终止}} \end{aligned}$$

根据我们随机出来的这个倒霉的策略，如果我们从$s_{\text{开始}}$出发，那么轨迹就是

$$s_0 = s_{\text{开始}},a_0 = a_{\text{去终止}},r_{0}=+1,s_1=s_{\text{终止}}$$

然后我们更新我们的动作价值函数。

$$Q(s_{\text{开始}},a_{\text{去终止}}) = 1$$

之后，再迭代，再评估，永远得不到最优策略。

因为，我们一开始随机初始化的那个策略就不太好。
但是，没关系。

我们让所有可能的状态动作对都成为可能的回合起点，这样就不会遗漏任何状态动作对。这就是起始探索(exploring start)。

起始探索蒙特卡洛更新同样存在每次访问和首次访问的问题，我们这里暂且以每次访问为例。

带起始探索的每次访问蒙特卡洛更新
输入：
  未知的模型
  待更新的策略$\pi$
初始化：
  动作价值函数，$Q(s,a)\leftarrow\text{任意值},s\in\mathcal{S},a\in\mathcal{A}$
  初始化计数器，$C(s,a)\leftarrow 0,s\in\mathcal{S},a\in\mathcal{A}$
  确定性策略，$\pi(s)\leftarrow\text{任意动作}$，$s\in\mathcal{S}$
蒙特卡洛：(对于每个轨迹样本执行以下操作)
  起始探索，选择$s_0\in\mathcal{S}$，$a_0\in\mathcal{A}$。要让每一个状态动作对都可能被选为$(s_0,a_0)$。
  采样，根据待更新的策略$\pi$，和环境进行交互。得到轨迹$s_0,a_0,r_0,s_1,a_1,r_1,s_2,\cdots,s_{T-1},a_{T-1},r_{T-1},s_T$
  初始化回报，$G\leftarrow 0$
  逐步更新，对$t=T-1,T-2,\cdots,0$，执行以下步骤：
    更新回报，$G\leftarrow\gamma G+r_{t}$
    更新计数和动作价值：
      $C(s,a)\leftarrow C(s,a)+1$
      $Q(s,a)\leftarrow Q(s,a)+\frac{1}{C(s,a)}[G-Q(s,a)]$
    策略改进，$\pi(s_t)\leftarrow\argmax_aQ(s_t,a)$
 
 
需要特别注意的是这一行：起始探索，选择$s_0\in\mathcal{S}$，$a_0\in\mathcal{A}$。要让每一个状态动作对都可能被选为$(s_0,a_0)$。
这是我们起始探索算法的核心。

示例代码：

def monte_carlo_with_exploring_start(env, episode_num=500000):
    policy = np.zeros((22, 11, 2, 2))
    policy[:, :, :, 1] = 1.
    q = np.zeros_like(policy)
    c = np.zeros_like(policy)
    for _ in range(episode_num):
        # 这么做的原因是，希望所有的都能遍历到
        # 随机选择起始状态和起始动作
        state = (np.random.randint(12, 22),
                 np.random.randint(1, 11),
                 np.random.randint(2))
        action = np.random.randint(2)
        # 确定手上的牌
        env.reset()
        if state[2]: # 有A
            env.player = [1, state[0] - 11]
        else: # 没有A
            if state[0] == 21:
                env.player = [10, 9, 2]
            else:
                env.player = [10, state[0] - 10]
        env.dealer[0] = state[1]
        state_actions = []
        while True:
            state_actions.append((state, action))
            observation, reward, done, _ = env.step(action)
            if done:
                break # 回合结束
            state = ob2state(observation)
            action = np.random.choice(env.action_space.n, p=policy[state])
        g = reward # 回报
        for state, action in state_actions:
            c[state][action] += 1.
            q[state][action] += (g - q[state][action]) / c[state][action]
            a = q[state].argmax()
            policy[state] = 0.
            policy[state][a] = 1.
    return policy, q

policy, q = monte_carlo_with_exploring_start(env)
v = q.max(axis=-1)

plot(policy.argmax(-1))
plot(v)

运行结果：

• 白色表示继续要牌，黑色表示不要牌

• 颜色越浅价值越大。

epsilon探索法

起始探索法在实际中存在一个很严重的限制，要求能指定任意一个状态作为回合的起始状态。但是实际中，很难做到，比如我们开发玩游戏的强化学习程序。
那么，有没有别的办法呢？
回到我们举的例子。
如果一开始在状态$S_{\text{开始}}$的时候，如果能选择$a_{\text{去中间}}$就好了。

可是，问题就在，初始策略到底哪个，谁也不知道。我们运气不太好，在一开始初始化得到了一个不好的策略，$\pi(s_{\text{开始}}) = a_{\text{去终止}}$。
但是！

为什么要严格遵守策略呢？
我们把原本的

$$\pi(a|s) = \begin{cases} 1, & a=a_{\star} \\ 0, & a\neq a_{\star} \end{cases}$$

修改为

$$\pi(a|s) = \begin{cases} 1 - \varepsilon + \frac{\varepsilon}{|\mathcal{A}(s)|}, & a=a_{\star} \\ \frac{\varepsilon}{|\mathcal{A}(s)|}, & a\neq a_{\star} \end{cases}\quad(\varepsilon > 0)$$

• $\mathcal{A}(s)$是指当前状态$s$下的动作空间，$|\mathcal{A}(s)|$是动作的数量。

这就是$\varepsilon$探索法，也称$\varepsilon$柔性策略，$\varepsilon$贪心策略、$\varepsilon$贪婪策略。
注意！很多时候，我们说的探索，都是指$\varepsilon$探索。

$\varepsilon$探索蒙特卡洛更新
输入：
  未知的模型
  待更新的策略$\pi$
初始化：
  动作价值函数，$Q(s,a)\leftarrow\text{任意值},s\in\mathcal{S},a\in\mathcal{A}$
  初始化计数器，$C(s,a)\leftarrow 0,s\in\mathcal{S},a\in\mathcal{A}$
  初始化策略，$\pi(\cdot|\cdot)$为$\varepsilon$探索策略。
蒙特卡洛：(对于每个轨迹样本执行以下操作)
  采样，根据待更新的策略$\pi$，和环境进行交互。得到轨迹$s_0,a_0,r_0,s_1,a_1,r_1,\cdots,s_{T-1},a_{T-1},r_{T-1},s_T$
  初始化回报，$G\leftarrow 0$
  逐步更新，对$t=T-1,T-2,\cdots,0$，执行以下步骤：
    更新回报，$G\leftarrow\gamma G+r_{t}$
    更新计数和动作价值：
      $C(s,a)\leftarrow C(s,a)+1$
      $Q(s,a)\leftarrow Q(s,a)+\frac{1}{C(s,a)}[G-Q(s,a)]$
    策略改进：
      $a_{\star}\leftarrow\argmax_aQ(s_t,a)$
      更新策略$\pi(\cdot|s_t)$，注意是$\varepsilon$柔性策略。

示例代码：

def monte_carlo_with_soft(env, episode_num=500000, epsilon=0.1):
    policy = np.ones((22, 11, 2, 2)) * 0.5 # 柔性策略
    q = np.zeros_like(policy)
    c = np.zeros_like(policy)
    for _ in range(episode_num):
        # 玩一回合
        state_actions = []
        observation = env.reset()
        while True:
            state = ob2state(observation)
            action = np.random.choice(env.action_space.n, p=policy[state])
            state_actions.append((state, action))
            observation, reward, done, _ = env.step(action)
            if done:
                break # 回合结束
        g = reward # 回报
        for state, action in state_actions:
            c[state][action] += 1.
            q[state][action] += (g - q[state][action]) / c[state][action]
            # 更新策略为柔性策略
            a = q[state].argmax()
            policy[state] = epsilon / 2.
            policy[state][a] += (1. - epsilon)
    return policy, q

policy, q = monte_carlo_with_soft(env)
v = q.max(axis=-1)

plot(policy.argmax(-1))
plot(v)

运行结果：

• 白色表示继续要牌，黑色表示不要牌。

• 颜色越浅价值越大。

离线策略蒙特卡洛

在上文，我们讨论的都是在线策略蒙特卡洛的情况，其特点是当前遵循的策略就是智能体学习改进的策略。即"在线策略蒙特卡洛"，也有资料称其为"固定策略回合更新"、“同策回合更新”等。
还有一种离线策略蒙特卡洛，则是在遵循一个策略的同时评估另一个策略，即计算另一个策略的状态价值函数或状态行为价值函数，也有资料称其为"非固定策略回合更新"、“异策回合更新”。

不过，需要注意的是，离线策略蒙特卡洛仅有理论上的研究价值，在实际任务中的效果并不明显，难以获得最优策略或者最优动作值函数，所以，我们不做太多的讨论。

但，离线策略方法在接下来的四个章节中，都会有重要的应用！