4.时序差分

时序差分简介

时序差分(Temporal Difference,TD)，也有资料称其为时间差分。
我们先通过一个通俗易懂的例子来讨论时序差分。

现在，我们开车从"上海"去"南昌"，然后我们打开导航软件，预估时间是$8$个小时，在这个过程中，存在一个神经网络模型$Q(s,d;\omega)$，其中$s$是状态，在这里就是"上海"，$d$是动作，在这里就是"去南昌"，$\omega$就是模型的参数。神经网络模型$Q(s,d;\omega)$的输出就是模型估计的值，在这里$q = Q(s,d;\omega) = 8$。然后我们真实的去开了一次，这时候就有了一个真实值，比如$y=7$。
所以，其损失函数是：

$$L(\omega) = \frac{1}{2}(q - y)^2$$

梯度是：

$$\frac{\partial L}{\partial \omega} = (q - y)\frac{\partial Q(s,d;\omega)}{\omega}$$

梯度下降是：

$$\omega \leftarrow \omega - \alpha \frac{\partial L}{\partial \omega}$$

• $\alpha$是学习率

我们的导航软件可以根据这种方法来更新预估时间，最后得到更准确的预估时间。

那么，假如我们现在到了"杭州"，耗费的时间是$3$。这时候我们准备换一个导航软件，所以上一个导航软件只收集到了我们从"上海"到"杭州"所耗费的时间$3$个小时，那么这个数据有价值吗？
也有价值。
模型再估计一下从"杭州"到"南昌"所需要的时间，比如模型估计从"杭州"到"南昌"需要$4.5$小时，那么从"上海"到"南昌"的估计时间就是$7.5$小时。
现在提一个问题：在上文中，模型一共做了两次估计，一次是直接估计"上海"到"南昌"所需要的时间，一次是基于"上海"到"杭州"的实际时间，在这个基础上估计"上海"到"南昌"所需要的时间，哪个估计更可靠？
当然是第二次的估计，因为第二次的估计含有真实成分在其中。
那么，我们也可以用第二次的估计近似看成"真实值"，来更新我们的模型。
第二次的估计，也被称为TD目标(TD Target)。

所以，我们有如下的式子

$$T_{\text{上海}\rightarrow\text{南昌}} \approx \bold{T_{\text{上海}\rightarrow\text{杭州}}} + T_{\text{杭州}\rightarrow\text{南昌}}$$

• $\bold{T_{\text{上海}\rightarrow\text{杭州}}}$是真实值

然后，我们再把我们刚刚的模型$Q(s,d;\omega)$代入上式，则有

$$Q(s_t,a_t;\omega) \approx r_t + Q(s_{t+1},a_{t+1};\omega)$$

• $r_t$是真实观测值

时序差分应用

继续看上面的例子，我们再来梳理一遍。
如果顺利的话，导航软件能成功的收集到我们从"上海"到"南昌"所耗费的时间，那么每收集到一条从"上海"到"南昌"所耗费的时间，导航软件就对预估时间更新一次。更新方法如下：

$$V \leftarrow V + \alpha(G - V)$$

• $V$是导航软件的预估时间
• $G$是导航软件收集到的时间
• $\alpha$是学习率

这个是不是和上一章的蒙特卡洛非常相似？
我们把耗费的时间换成状态价值，则有：

$$V(s_t) \leftarrow V(s_t) + \alpha(G_t - V(s_t))$$

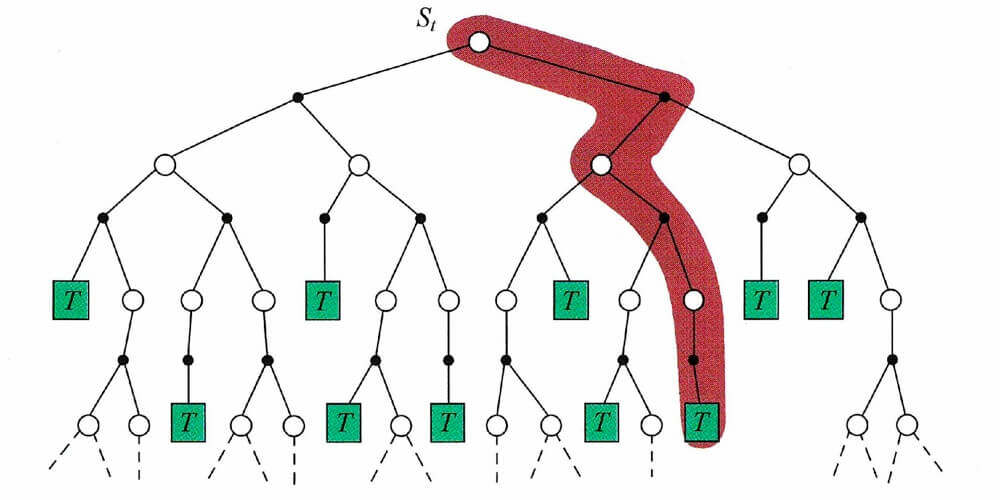
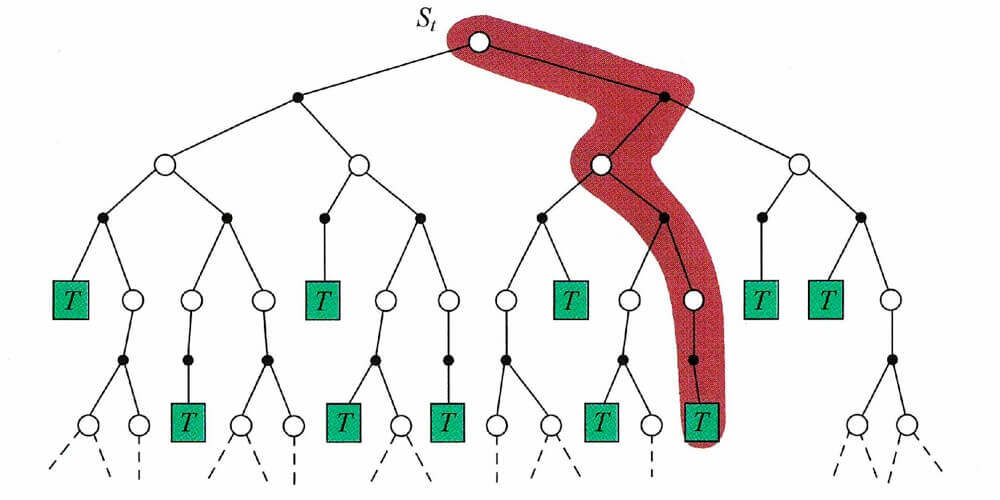
用图表示如下：

可是，如果不顺利呢？不顺利的话，导航软件只能收集到我们从"上海"到"杭州"所耗费的时间，那么这时候怎么更新预估时间呢？

$$V \leftarrow V + \alpha(H + V' - V)$$

• $V$是从"上海"到"南昌"的时间
• $H$是从"上海"到"杭州"的时间
• $V'$是从"杭州"到"南昌"的预估时间
• $\alpha$是学习率

同样，我们把耗费的时间换成状态价值，则有：

$$V(s_t) \leftarrow V(s_t) + \alpha(r_{t+1} + \gamma V(s_{t+1}) - V(s_t))$$

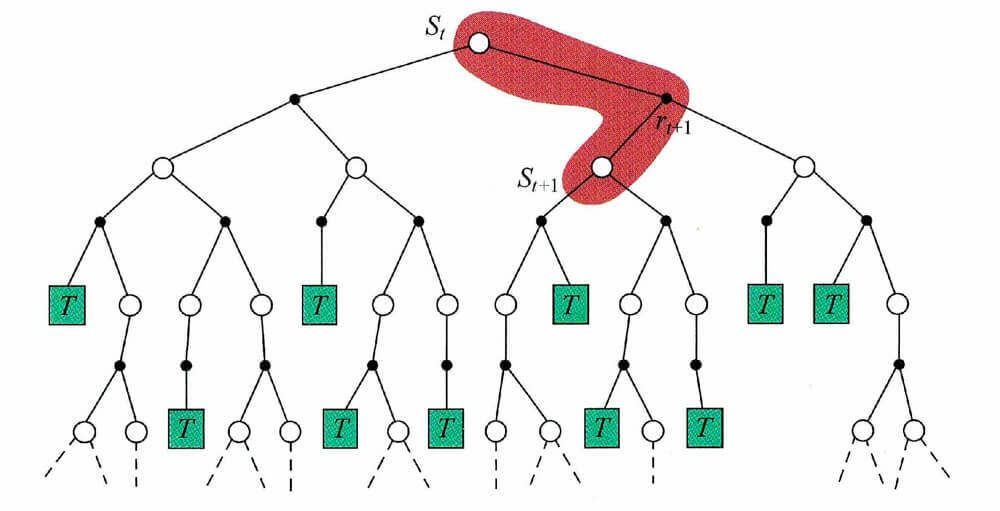
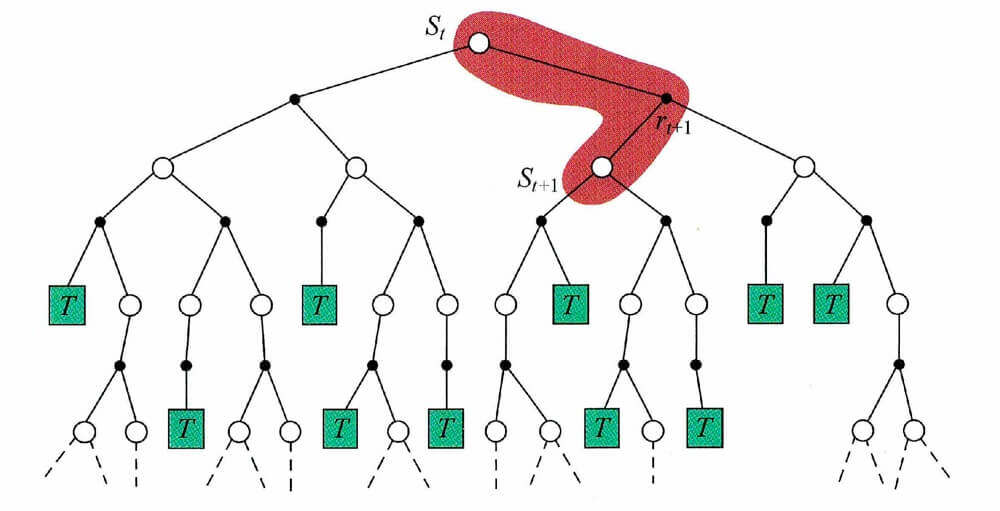
用图表示如下：

除了这两种方法，在第二章我们还讨论了"动态规划"，更新方法如下：

$$V(s_t) \leftarrow \mathbb{E}_{\pi}[r_{t+1} + \gamma V(s_{t+1})]$$

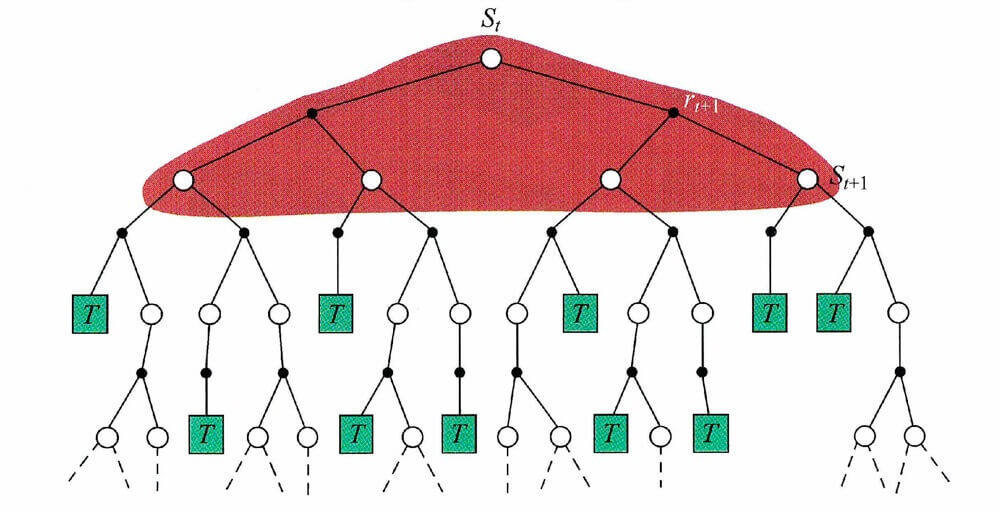
用图表示如下：

SARSA：在线策略时序差分方法

所以呢，我们现在又有了一种评估策略的方法，时序差分。现在，我们把时序差分应用到强化学习中。
同时，时序差分方法，只是一种评估策略的方法，我们依旧要依赖的策略迭代这个框架，策略评估和策略改进交替进行，直至得到最优解。

题外话，其实不仅是是动态规划、蒙特卡洛和这一章的时序差分，我们的整个强化学习，甚至包括我们之前深度学习，都蕴含着迭代的思想在其中，我们把迭代的过程称之为学习的过程。我在一本描写费马大定理的四百年的证明过程的书中，看到这么一段。

当时，我的第一感受是，欧拉没有把故事讲好啊，他那时候应该说这是"人工智能"。但，或许又是那时候，没人需要人工智能这个故事把。

SARSA的过程

回到主题。
SARSA是一种在线策略方法。
在线策略是指产生数据的策略与要评估改进的策略是同一个策略。其基本思想是遵循一个已有策略进行采样，根据样本数据中的回报更新值函数。或者遵循该策略采取动作，根据动作得到的回报更新值函数。最后根据更新的值函数来优化这个已有的策略，以得到更优的策略。由于要优化改进的策略就是当前遵循的策略，所以此方法被称为在线策略。

SARSA的名字，来自于我们之前讨论的轨迹，在当前状态$S$下，我们基于一个已有的策略，采取动作$A$，得到回报$R$，然后进入到下一个状态$S'$，我们再做出动作$A'$，连起来就是SARSA。(所以呢，我个人观点，有些资料把SARSA写成Sarsa，是不合适的。)

那么，现在我们可以利用时序差分方法了，我们用动作价值$Q(s_{t+1},a_{t+1})$来更新动作价值$Q(s_t,a_t)$：

$$Q(s_t,a_t) \leftarrow Q(s_t,a_t) + \alpha(r + \gamma Q(s_{t+1},a_{t+1}) - Q(s_t,a_t))$$

SARSA的更新方法就是这么一个更新方法，在具体实现方面，我们可以再利用我们上一章讨论的$\varepsilon$探索策略。

具体算法流程如

SARSA算法
输入：
  环境
输出：
  最优动作价值估计$Q(s,a),s \in \mathcal{S},a \in \mathcal{A}(s)$
参数：
  学习率$\alpha$
  折扣因子$\gamma$
初始化：
  动作价值估计$Q(s,a) \leftarrow \text{任意值},s \in \mathcal{S},a \in \mathcal{A}$。如果有终止状态，令$Q(s_{\text{终止}},a) \leftarrow 0,a \in \mathcal{A}$。
时序差分：(对每一条轨迹执行以下操作)
  初始化状态$s_0$
  根据动作价值估计$Q$得到$\varepsilon$探索策略，并以此采取动作$a_0$，得到第一个状态动作对$(s_0,a_0)$
  对于$t=0,1,2,\cdots,T$，依此执行以下操作，直到$t=T$，$s_t=s_{\text{终止}}$：
    采样，环境反馈执行动作$a_t$所得到的回报$r_t$和状态$s_{t+1}$
    基于$s_{t+1}$，同样通过$\varepsilon$探索策略采取动作$a_{t+1}$，得到状态动作对$s_{t+1},a_{t+1}$
    更新$Q(s_t,a_t)$：$Q(s_t,a_t) \leftarrow Q(s_t,a_t) + \alpha(r_t + \gamma Q(s_{t+1},a_{t+1}) - Q(s_t,a_t))$
     * 其中$r_t + \gamma Q(s_{t+1},a_{t+1}$)就是TD目标

SARSA的实现

接下来，我们实现SARSA算法，以调度系统为例。调度系统在我们生活中非常的常见，比如外卖配送调度，网约车调度等。这些系统都极其的庞大复杂，我们只能以一个非常简单的DEMO为例，Gym中的出租车调度。

该例子来自《强化学习：原理与Python实现(肖智清著)》这本书的第五章。

出租车调度问题描述

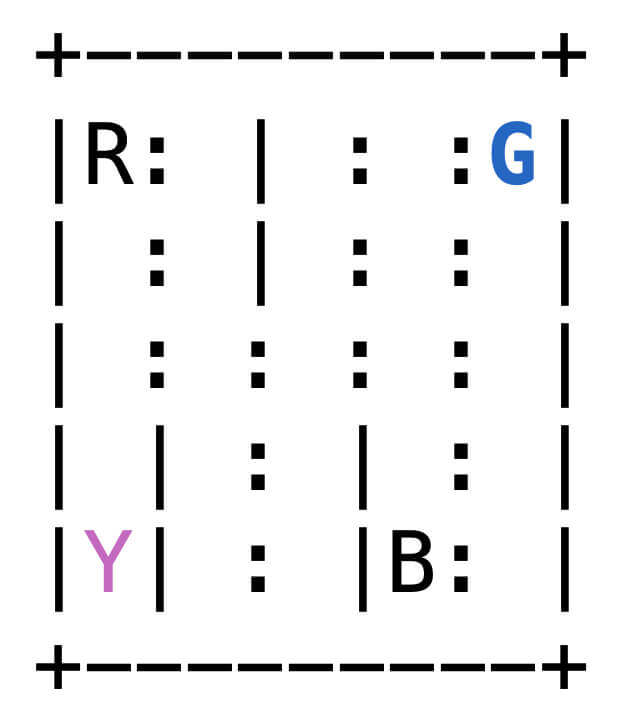
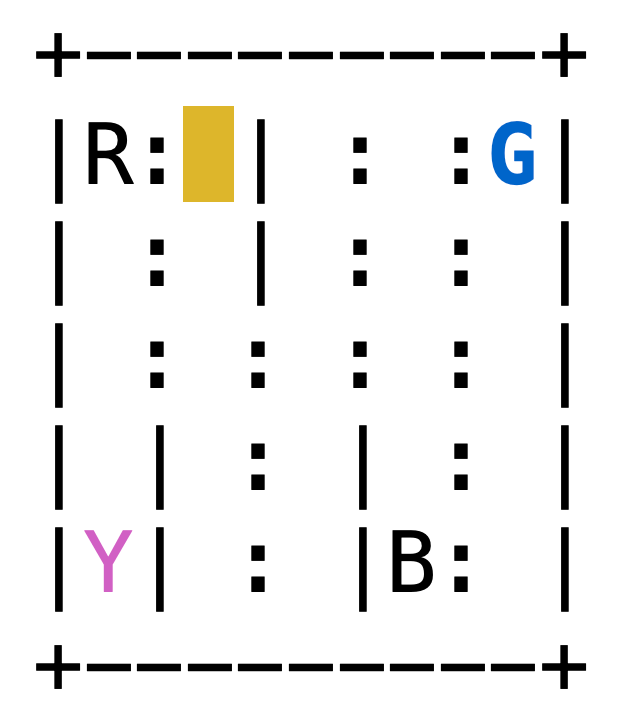
如图所示，是一个用5×5方格表示的地图，有4个出租车停靠点，分别是B、G、R、Y。在每个回合开始时，有一个乘客会随机出现在4个出租车停靠点中的一个，并想在任意一个出租车停靠点下车。出租车会随机出现在25个位置的任意一个位置。出租车需要通过移动自己的位置，到达乘客所在的位置，并将乘客接上车，然后移动到乘客想下车的位置，再让乘客下车。出租车只能在地图范围内上下左右移动一格，并且在有竖线阻拦地方不能横向移动。出租车完成一次任务可以得到20个奖励，每次试图移动得到-1个奖励，不合理地邀请乘客上车(例如目前车和乘客不在同一位置，或乘客已经上车)或让乘客下车(例如车不在目的地，或车上没有乘客)得到-10个奖励。希望调度出租车让总奖励的期望最大。

环境及其使用

示例代码：

import numpy as np
np.random.seed(0)
import gym

env = gym.make('Taxi-v3')
env = env.unwrapped
env.seed(0)
print('观察空间 = {}'.format(env.observation_space))
print('动作空间 = {}'.format(env.action_space))
print('状态数量 = {}'.format(env.observation_space.n))
print('动作数量 = {}'.format(env.action_space.n))

运行结果：

观察空间 = Discrete(500)
动作空间 = Discrete(6)
状态数量 = 500
动作数量 = 6

然后，我们试着来操作一下。

示例代码：

# 状态初始化
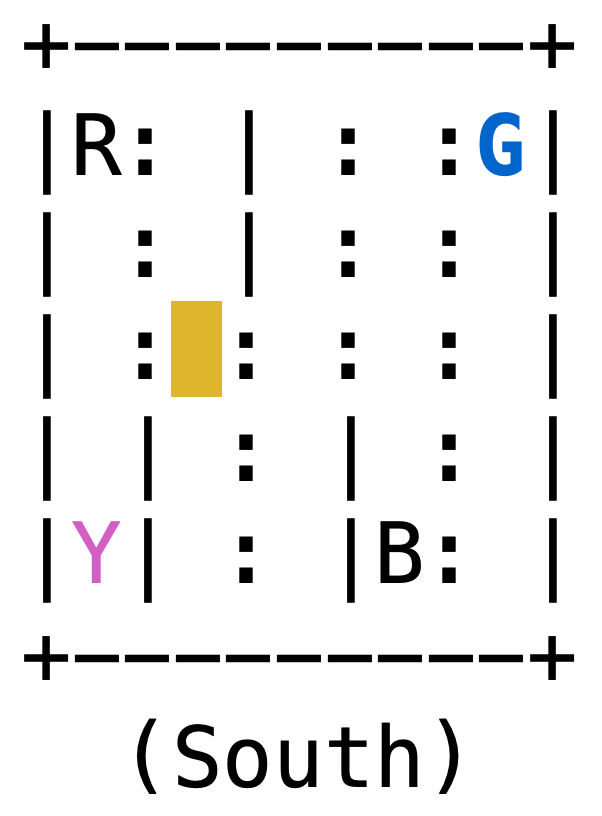
state = env.reset()
# state是[0,500)的数字，进行解码
taxirow, taxicol, passloc, destidx = env.unwrapped.decode(state)
print(taxirow, taxicol, passloc, destidx)
print('的士位置 = {}'.format((taxirow, taxicol)))
print('乘客位置 = {}'.format(env.unwrapped.locs[passloc]))
print('目标位置 = {}'.format(env.unwrapped.locs[destidx]))
env.render()

运行结果：

0 1 1 2
的士位置 = (0, 1)
乘客位置 = (0, 4)
目标位置 = (4, 0)

解释一下，这个环境中的观测是一个范围为$[0,500)$的int型数值，用env.decode()函数进行解码，得到长度为4的元组(tarrow,taxicab,passloc,destidx)，其各元素含义如下：

• taxirow和taxicol是取值为{0,1,2,3,4}的int型变量，表示当前出租车的位置。
• passloc是取值为{0,1,2,3,4}的int型数值，表示乘客的位置，其中{0,1,2,3}表示乘客在"出租车停靠点表"中对应的位置等待，4表示乘客在车上。
• destidx是取值为{0,1,2,3}的int型数值，表示目的地，目的地的位置同样由"出租车停靠点表"给出。
• 乘客的位置、目地会用彩色字母显示、出租车的位置会高亮显示。
  • 如果乘客不在车上，乘客等待地点(位置)的字母会显示为蓝色、目的地所在的字母会显示为洋红色、出租车所在的位置会用黄色高亮
  • 如果乘客在车上，出租车所在的位置会用绿色高亮。

出租车停靠点表

passloc或destidx	字母	坐标
0	R	(0,0)
1	G	(0,4)
2	Y	(4,0)
3	B	(4,3)

再移动一下出租车。
示例代码：

# 传入参数action
s = env.step(0)
print(s)
s = env.step(0)
print(s)
env.render()

运行结果：

(126, -1, False, {'prob': 1.0})
(226, -1, False, {'prob': 1.0})

解释一下，其中env.step()传入动作，用{0,1,2,3,4,5}表示，具体含义参考"出租车动作表"。

出租车动作表

动作数值	含义	env.render()的提示	执行后的奖励
0	向下	South	-1
1	向上	North	-1
2	向右	East	-1
3	向左	West	-1
4	上车	Pickup	-1或-10
5	下车	Dropoff	+20或-10

SARSA的代码

首先，我们创建一个SARSA智能体类。
示例代码：

class SARSAAgent:
    def __init__(self, env, gamma=0.9, learning_rate=0.2, epsilon=.01):
        '''
        初始化
        :param env: 环境
        :param gamma: 折扣因子
        :param learning_rate: 学习率
        :param epsilon: epsilon贪心策略
        '''
        self.gamma = gamma
        self.learning_rate = learning_rate
        self.epsilon = epsilon
        self.action_n = env.action_space.n
        self.q = np.zeros((env.observation_space.n, env.action_space.n))

    def decide(self, state):
        '''
        epsilon贪心策略
        :param state: 状态
        :return:
        '''
        if np.random.uniform() > self.epsilon:
            action = self.q[state].argmax()
        else:
            action = np.random.randint(self.action_n)
        return action

    def learn(self, state, action, reward, next_state, next_action ,done):
        '''
        学习，也就是价值函数更新方法
        :param state: 状态
        :param action: 动作
        :param reward: 奖励
        :param next_state: 下一个状态
        :param next_action: 下一个动作
        :param done: 是否结束
        :return:
        '''
        u = reward + self.gamma * self.q[next_state, next_action] * (1. - done)
        td_error = u - self.q[state, action]
        self.q[state, action] += self.learning_rate * td_error

• 智能体负责决策和学习，决策就是我们上文提到的$\varepsilon$贪心策略，学习就是我们上文提到的价值函数更新。

接下来是SARSA算法，就是我们上文所讨论的SARSA的过程。
示例代码：

def play_sarsa(env, agent, train=False, render=False):
    '''
    SARSA
    :param env: 环境
    :param agent: 智能体
    :param train: 是否训练
    :param render: 是否render
    :return:
    '''
    # 轨迹回报
    episode_reward = 0
    # 状态
    observation = env.reset()
    # 动作
    action = agent.decide(observation)
    while True:
        if render:
            env.render()
        next_observation, reward, done, _ = env.step(action)
        episode_reward += reward
        next_action = agent.decide(next_observation)
        if train:
            agent.learn(observation, action, reward, next_observation, next_action, done)
        if done:
            break
        observation, action = next_observation, next_action
    return episode_reward

然后，我们可以实例化智能体，并进行训练，再试一试效果。

实例化智能体，并训练。
示例代码：

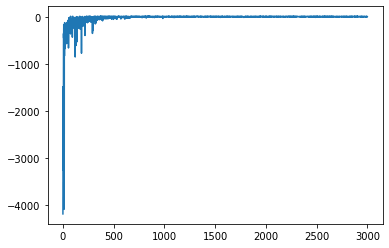
import matplotlib.pyplot as plt

agent = SARSAAgent(env)

# 训练
episodes = 3000
episode_rewards = []
for episode in range(episodes):
    episode_reward = play_sarsa(env, agent, train=True)
    episode_rewards.append(episode_reward)

# 训练过程画图
plt.plot(episode_rewards)

运行结果：

试一试效果。
示例代码：

# 测试
agent.epsilon = 0. # 取消探索

episode_rewards = [play_sarsa(env, agent) for _ in range(100)]
print('平均回合奖励 = {} / {} = {}'.format(sum(episode_rewards),len(episode_rewards), np.mean(episode_rewards)))

运行结果：

平均回合奖励 = 817 / 100 = 8.17

Q-Learning：离线策略时序差分方法

接下来，我们讨论离线策略方法。

Q-Learning的过程

离线策略是指产生数据的策略与评估改进的策略不是同一个策略。其基本思想是，虽然已有一个原始策略，但是并不针对这个原始策略进行采样，而是基于另一个策略进行采样。这另一个策略可以是先前学习到的策略，也可以是人类的策略等一些较为成熟的策略。观察这类策略的行为和回报，并根据这些回报评估和改进原始策略，以此达到学习的目的。

这么说或许略显晦涩难懂，我们来看具体的。

很多资料会在这时候讨论"重要性采样"，因为离线策略的理论基础就是重要性采样。我们在这里不讨论，在《6.策略梯度》这一章，再讨论"重要性采样"，因为我认为，我们反过来，先弄明白什么是离线策略，再去讨论重要性采样，或许更容易理解。

在Q-Learning方法中，实际在与环境交互的时候，我们遵循的依旧是一个$\varepsilon$探索策略，以保证经历足够丰富的新状态，我们把遵循的策略记作$\mu$。但是我们的目标策略是一个单纯的贪心策略，保证策略最终收敛到最佳，我们把目标策略记作$\pi$。

$$\pi(s) = \argmax_{a\in\mathcal{A}(s)} Q(s,a)$$

我们的更新方法是：

$$Q(s,a) \leftarrow Q(s,a) + \alpha(r + \gamma \max_{a_{t+1}}Q(s_{t+1},a_{t+1}) - Q(s,a))$$

具体算法流程如下：

Q-Learning算法
输入：
  环境
输出：
  最优动作价值估计$Q(s,a),s \in \mathcal{S},a \in \mathcal{A}(s)$。
参数：
  学习率$\alpha$
  折扣因子$\gamma$
初始化：
  动作价值估计$Q(s,a) \leftarrow \text{任意值},s \in \mathcal{S},a \in \mathcal{A}$。如果有终止状态，令$Q(s_{\text{终止}},a) \leftarrow 0,a \in \mathcal{A}$。
时序差分更新：(对每一条轨迹执行以下操作)
  初始化状态$s_0$
  对于$t=0,1,2,\cdots$，依此执行以下操作，直到$s_t=s_{\text{终止}}$：
    在状态$s_t$下，根据$\varepsilon$探索策略$\mu$，采取动作$a_t$
    环境反馈执行动作$a_t$所得到的回报$r_t$和状态$s_{t+1}$
    更新$Q(s,a)$：$Q(s,a) \leftarrow Q(s,a) + \alpha(r + \gamma \max_{a_{t+1}}Q(s_{t+1},a_{t+1}) - Q(s_t,a_t))$

注意和SARSA的区别。
在SARSA中，要基于$s_{t+1}$，同样通过$\varepsilon$探索策略采取动作$a_{t+1}$，得到状态动作对$s_{t+1},a_{t+1}$。然后更新更新$Q(s_t,a_t)$

$$Q(s_t,a_t) \leftarrow Q(s_t,a_t) + \alpha(r_t + \gamma Q(s_{t+1},a_{t+1}) - Q(s_t,a_t))$$

而在Q-Learning中，不需要再去采取动作$a_{t+1}$，以此得到状态动作对$s_{t+1},a_{t+1}$。直接选最大的。

$$Q(s,a) \leftarrow Q(s,a) + \alpha(r + \gamma \max_{a_{t+1}}Q(s_{t+1},a_{t+1}) - Q(s_t,a_t))$$

Q-Learning的实现

接下来，我们来实现一个Q-Learning算法，继续以出租车调度为例。

首先，我们创建一个Q-Learning智能体。
示例代码：

class QLearningAgent:
    def __init__(self, env, gamma=0.9, learning_rate=0.1, epsilon=.01):
        '''
        初始化
        :param env: 环境
        :param gamma: 折扣因子
        :param learning_rate: 学习率
        :param epsilon: epsilon贪心策略
        '''
        self.gamma = gamma
        self.learning_rate = learning_rate
        self.epsilon = epsilon
        self.action_n = env.action_space.n
        # 动作价值
        self.q = np.zeros((env.observation_space.n, env.action_space.n))

    def decide(self, state):
        '''
        epsilon贪心策略
        :param state: 状态
        :return: 
        '''
        if np.random.uniform() > self.epsilon:
            action = self.q[state].argmax()
        else:
            action = np.random.randint(self.action_n)
        return action

    def learn(self, state, action, reward, next_state, done):
        '''
        学习，也就是更新
        :param state: 状态 
        :param action: 动作 
        :param reward: 奖励
        :param next_state: 下一个状态 
        :param done: 是否完成
        :return: 
        '''
        # 注意！max
        u = reward + self.gamma * self.q[next_state].max() * (1. - done)
        td_error = u - self.q[state, action]
        self.q[state, action] += self.learning_rate * td_error

接下来是Q-Learning算法，就是我们上文所讨论的Q-Learning的过程。
示例代码：

def play_qlearning(env, agent, train=False, render=False):
    '''
    qlearning算法
    :param env: 环境
    :param agent: 智能体
    :param train: 是否训练
    :param render: 是否render
    :return:
    '''
    # 轨迹回报
    episode_reward = 0
    # 状态
    observation = env.reset()
    i = 0
    while True:
        # 确实有时候这个策略不太好，死循环
        i = i+1
        if i > 10000:
            return 'drop'
        if render:
            env.render()
        # 动作
        action = agent.decide(observation)
        next_observation, reward, done, _ = env.step(action)
        episode_reward += reward
        if train:
            agent.learn(observation, action, reward, next_observation,done)
        if done:
            break
        observation = next_observation
    return episode_reward

然后，我们可以实例化智能体，并进行训练，再试一试效果。

实例化智能体，并训练。
示例代码：

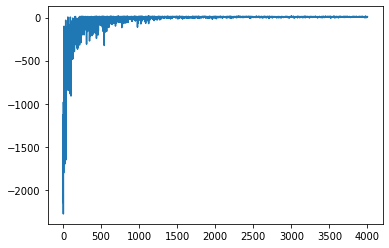
import matplotlib.pyplot as plt

agent = QLearningAgent(env)

# 训练
episodes = 4000
episode_rewards = []
for episode in range(episodes):
    episode_reward = play_qlearning(env, agent, train=True)
    episode_rewards.append(episode_reward)

plt.plot(episode_rewards)

试一试效果。
示例代码：

# 测试
agent.epsilon = 0. # 取消探索

episode_rewards = [play_qlearning(env, agent) for _ in range(100)]
# 死循环的都drop
episode_rewards = [e for e in episode_rewards if e != 'drop']
print('平均回合奖励 = {} / {} = {}'.format(sum(episode_rewards),len(episode_rewards), np.mean(episode_rewards)))

运行结果：

平均回合奖励 = 759 / 98 = 7.744897959183674

多步时序差分法

在上文，我们有这么两张图片。

第一张是蒙特卡洛的，第二张是时序差分的。这两张图片很好的反映了两种方法的关键不同点。
更新当前状态的值函数的时候，基于当前状态往未来看的距离不同。
在蒙特卡洛中，这个距离是整个轨迹的长度$N$。更新方法如下

$$V(s_t) \leftarrow V(s_t) + \alpha(G_t - V(s_t))$$

$G_t$为累积回报

$$G_t = r_{t} + \gamma r_{t+1} + \gamma^2 r_{t+2} + \cdots + \gamma^{T-t} r_T$$

而在时序差分中，距离是$1$，即

$$G_t = G_t^1 = r_{t} + \gamma V(s_{t+1})$$

那么，如果在$(1,N)$之间呢，这个就是多步时序差分法(Multi-Step TD Targets)。

$$\begin{aligned} G_t^m & = r_{t} + \gamma r_{t+1} + \cdots + \gamma^{m-1} r_{t+m-1} + \gamma^m G_{t+m} \\ & = \bigg[\sum_{i=0}^{m-1} \gamma^i r_{t+i}\bigg] + G_{t+m} \end{aligned}$$

• 在SARSA和Q-Learning中，$\gamma^m Q(s_{t+m},a_{t+m})$不一样。
  • 在SARSA中，$\gamma^m Q(s_{t+m},a_{t+m}) = Q(s_{t+m},a_{t+m})$。
  • 在Q-Learning中，$\gamma^m Q(s_{t+m},a_{t+m}) = \max_{a_{t+m}}Q(s_{t+m},a_{t+m})$。

多步时序差分比单步时序差分更准一些，毕竟"从上海到杭州的实际时间加上杭州到南昌的预估时间"总是比"从上海到嘉兴的实际时间加上嘉兴到南昌的预估时间"要准一些。但是呢，时序差分可每一步在线学习，不必等到回合结束，可以从不完整的序列中学习，虽然收敛性差，但是耗费的时间少。蒙特卡洛必须等到回合结束，虽然收敛性较好，但是耗费的时间多。
所以有一个话题就是，有没有折衷的办法？这个涉及到资格迹，我们不作太多的讨论。