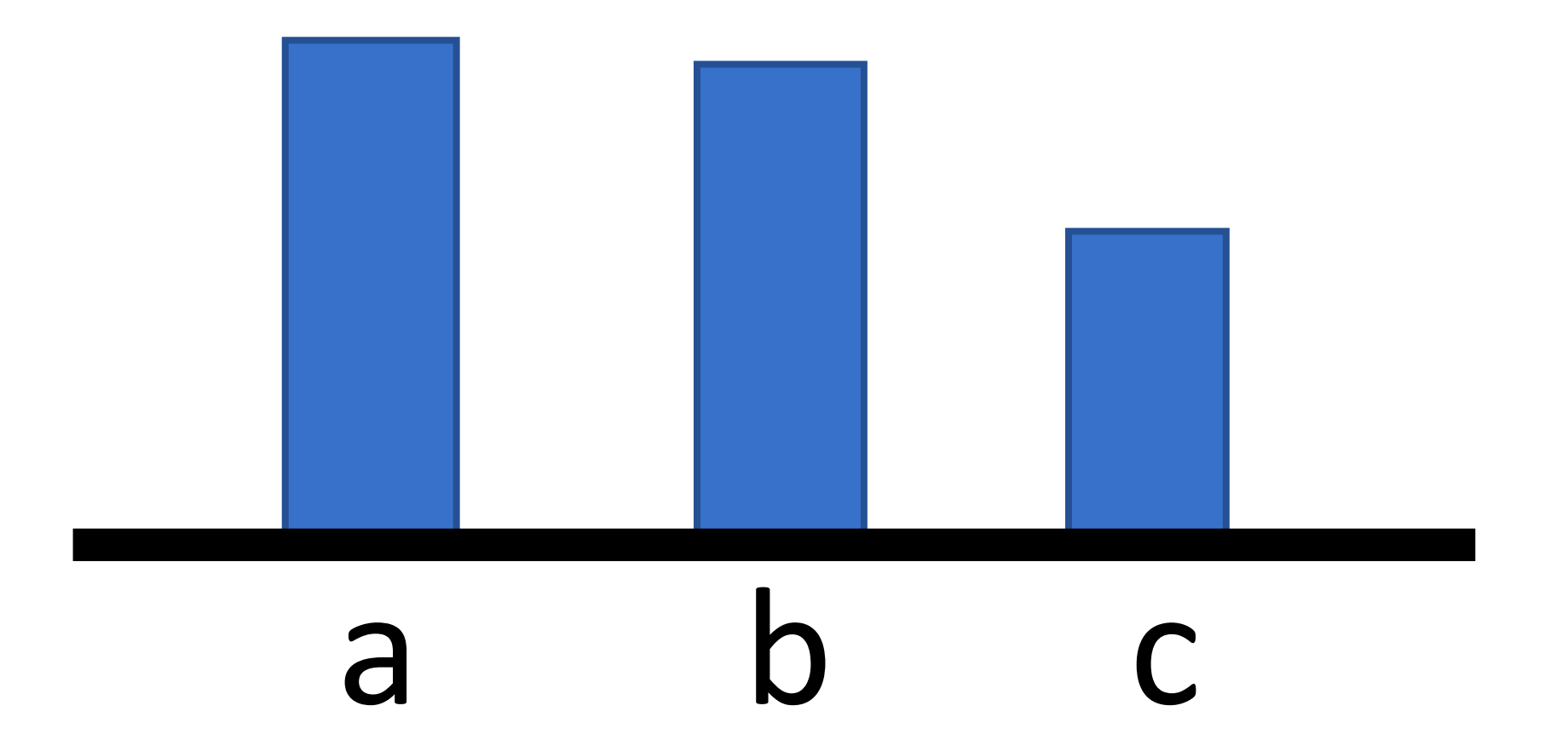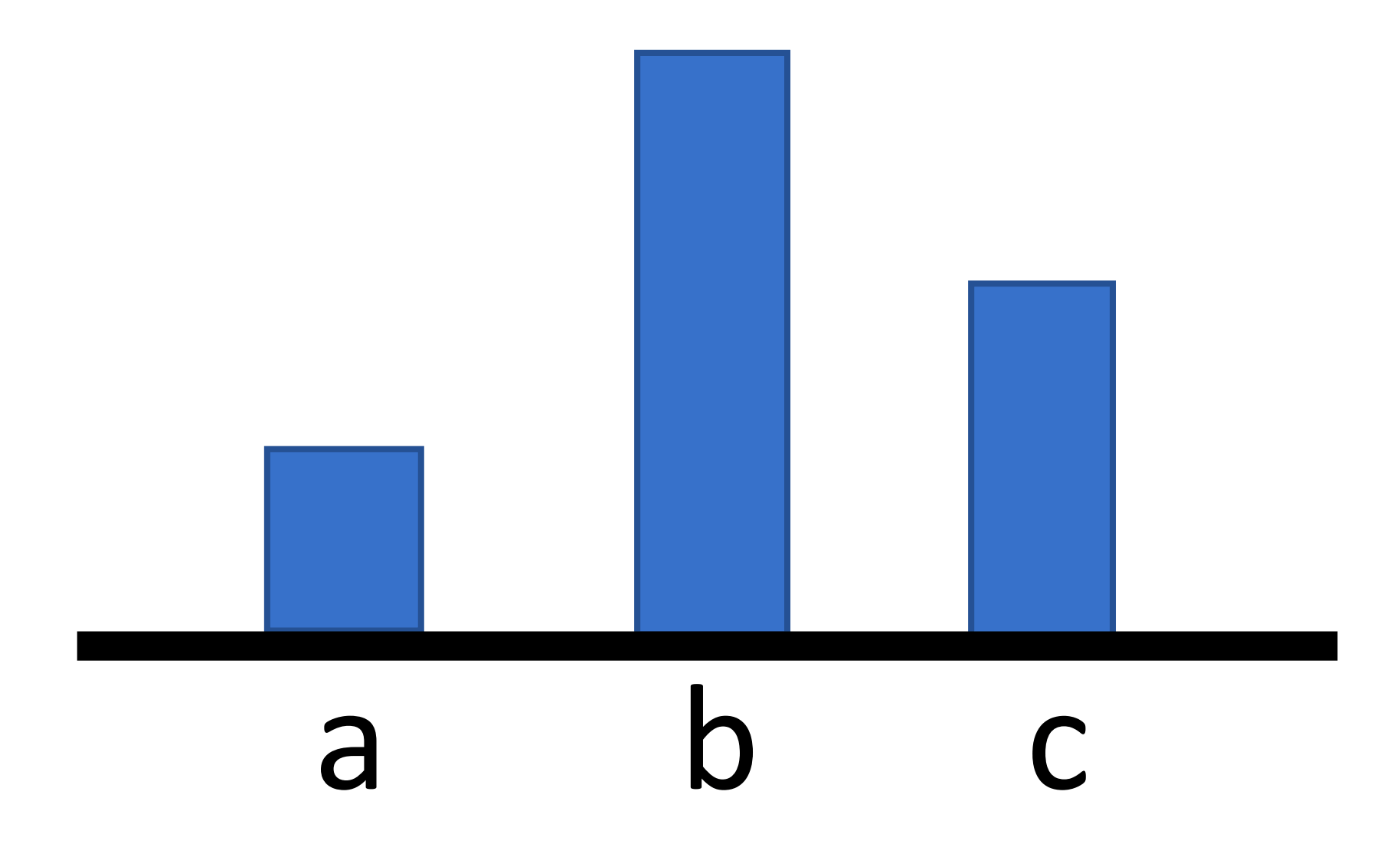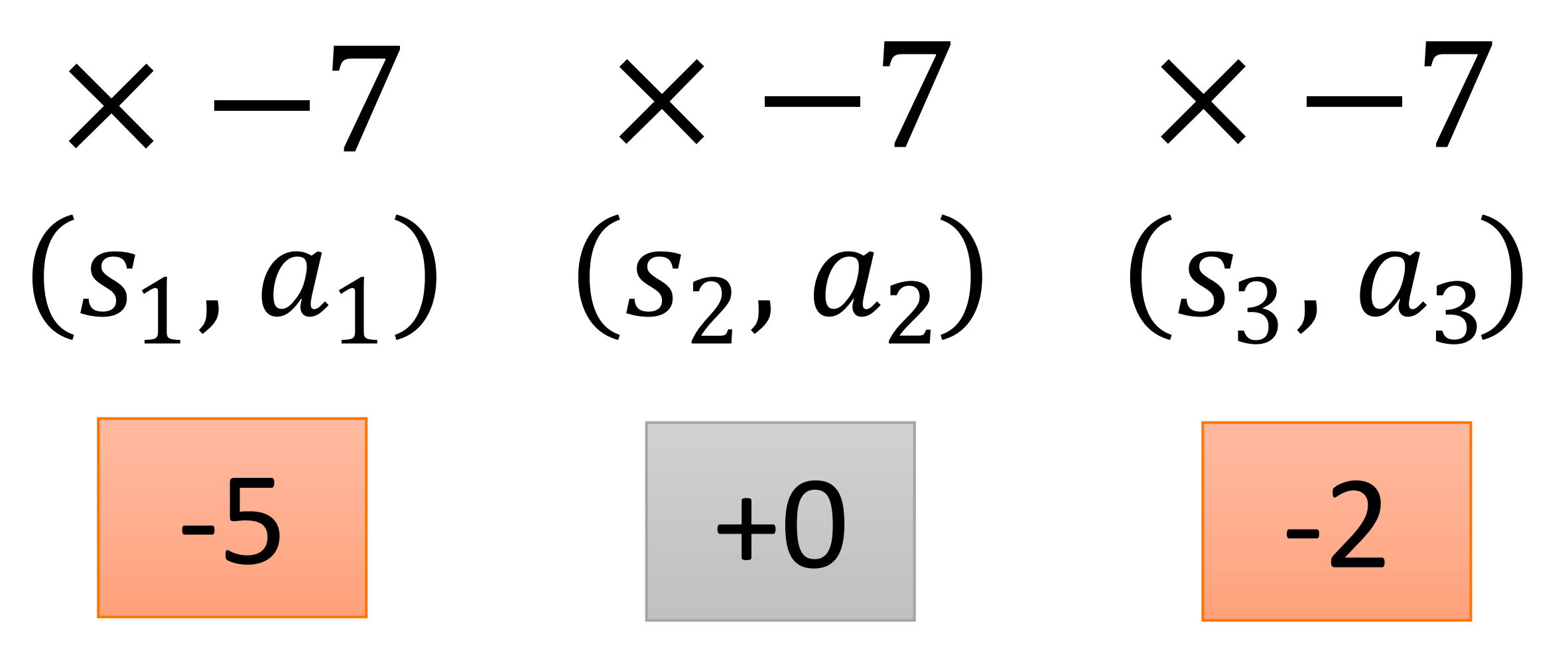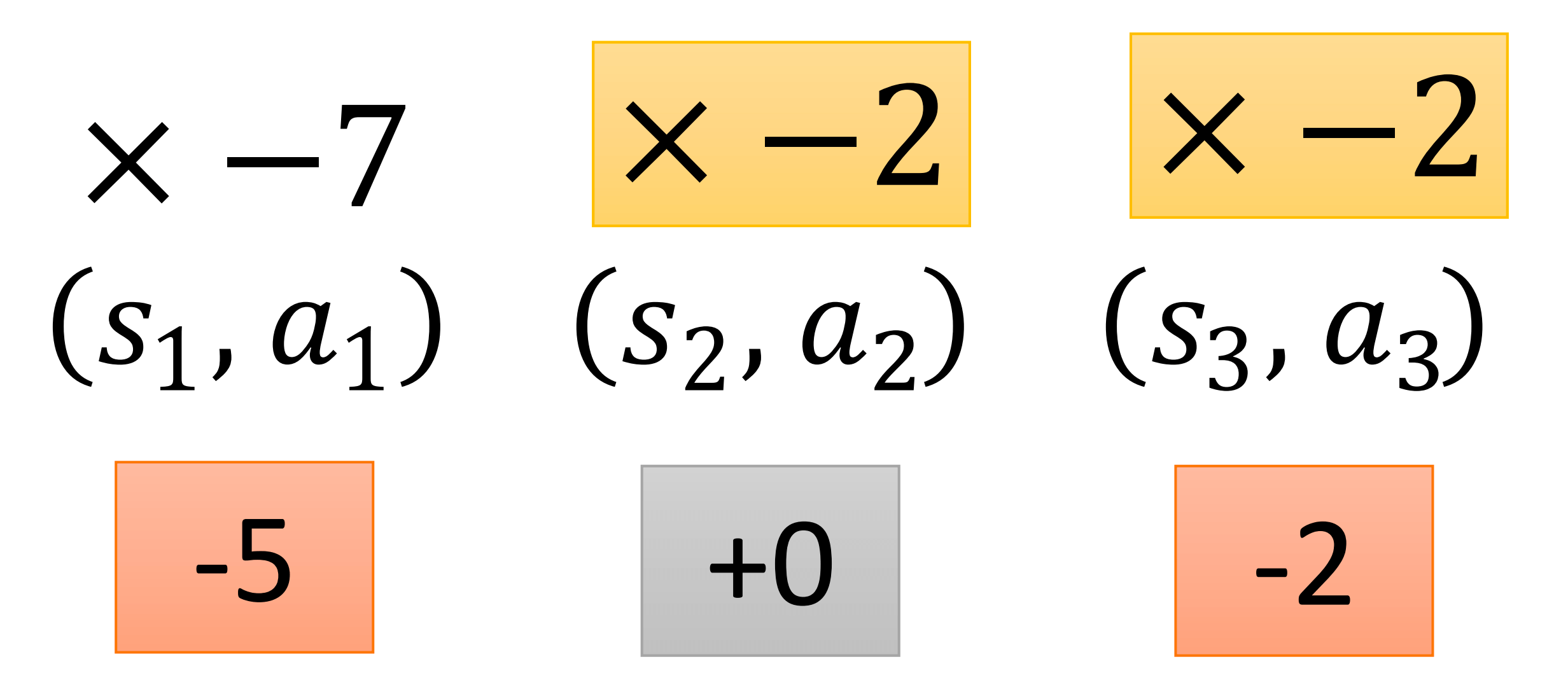6.策略梯度

随机策略简介

之前的章节，我们讨论的所有内容都是迭代最优的动作价值函数，然后我们在状态$s$下，选择动作价值最大的那个动作。
这一章，我们讨论一个新的方法，直接去迭代最优的策略，策略梯度方法。
直接迭代最优的策略，这个不是新方法，我们在我们这一系列笔记的第一个真正意义上的强化学习算法，《2.动态规划》中的第一种方法就是这么做的。但策略梯度是新的方法。

根据我们迭代的策略是随机策略还是确定性策略，又可以分为随机策略梯度(Stochastic Policy Gradient,SPG)和确定性策略梯度(Deterministic Policy Gradient,DPG)。

随机策略是在某个状态$s$下，做出某个动作$a$的概率。即

$$\pi_{\theta}(a|s) = P(a|s;\theta)$$

而之前的所有基于价值函数的方法，得到的都是确定性策略。
相比之下，随机策略在进行博弈的时候更有优势。
比如，下围棋，如果智能体采取的是确定性策略的话，可能在若干局之后，就被高手掌握了规律。但是如果采取的随机策略的话，就不那么容易被掌握了。
(有些观点认为，在环境不是完全可观测的情况下，随机策略相比确定性策略更有优势，说实话，这个我不是很理解，金融市场就是一个不可完全观测的环境，但是我不认为在金融市场，随机策略一定会优于确定性策略。)

这一章，除非有特别说明，否则，我们所指的策略都是随机策略。

随机策略梯度同样有在线和离线两种方法，我们从在线开始。

在线策略方法

回报

现在，让我们来看看如何迭代最优策略。
既然是迭代呢，那么我们就随便从一个策略出发。比如，现在有一个策略$\pi_{\theta}$，其中$\theta$是这个策略网络的参数。(我们仿照上一章的DQN，用一个神经网络来作为我们的策略函数。)
如图

然后，我们用这个策略和环境交互。在状态$s_1$，做出动作$a_1$，环境给出奖励$r_1$，状态转移至$s_2$，做出动作$a_2$，···，直到，在状态$s_T$，做出动作$a_T$，环境给出奖励$r_T$。这就是我们第一章讨论的轨迹。
在策略$\pi_\theta$下，这个轨迹$\tau$的回报是

$$G_{\theta} = \sum_{t=1}^T r_t$$

但是，$G_\theta(\tau)$是不足以评估我们的策略$\pi_\theta$的，因为$G_\theta(\tau)$是一个随机变量，这个我们在第一章也讨论过，因为动作是随机的，状态转移也是随机的。

只有$G_\theta(\tau)$这个随机变量的期望$\bar{G}_\theta$才可以评估我们的策略$\pi_\theta$。

那么，$\bar{G}_\theta$是多少呢？让我们看看。

轨迹$\tau$是$\{s_1,a_1,r_1,s_2,a_2,r_2,\cdots,s_T,a_T,r_T\}$，这个轨迹发生的概率是

$$\begin{aligned} P(\tau;\theta) &= P(s_1) P(a_1|s_1;\theta) P(r_1,s_2|s_1,a_1) P(a_2|s_2;\theta) P(r_2,s_3|s_2,a_2) \cdots P(a_T|s_T;\theta) P(r_T,s_{T+1}|s_T,a_T)\\ &= P(s_1) \Pi_{t=1}^T P(a_t|s_t;\theta) P(r_t,s_{t+1}|s_t,a_t) \end{aligned}$$

• $s_1$是初始化的时候，环境直接给定的。
• 严格意义上，当$t=T$时，没有状态$s_{T+1}$。但这个不影响我们后续的讨论，因为我们更关心的是奖励$r$。

知道了轨迹$\tau$的回报，知道了轨迹$\tau$发生的概率，那么期望$\bar{G}_{\theta}$就非常简单了。

$$\bar{G}_{\theta} = \sum_{\tau \in \text{所有的}\tau} G_{\theta}(\tau) P(\tau;\theta)$$

根据我们之前讨论的蒙特卡洛，我们知道还有这么一个式子成立。

$$\bar{G}_\theta \approx \frac{1}{N} \sum_{n=1}^N G_{\theta}(\tau_n)$$

这个式子暂且先放这里，我们很快就会用到。

梯度和梯度上升

所以，接下来我们的目标就很明确了，我们要寻找一个$\theta_{\star}$，使得$\bar{G}_{\theta}$的值最大。
即

$$\theta_{\star} = \argmax_{\theta} \bar{G}_{\theta}$$

在之前的《经典机器学习及其Python实现》和《深度学习初步及其Python实现》，我们也有过类似的操作，我们要寻找一组参数，使损失函数的值最小，当时，采用的是梯度下降法。而在《集成学习概览及其Python实现》中，我们有大量用到"梯度上升"。

这里我们的目标使回报的值最大，采用的方法是梯度上升。

$$\begin{aligned} & \text{初始化}\theta \\ & \theta \leftarrow \theta + \eta \frac{\bar{G}_{\theta}}{\theta} \\ & \theta \leftarrow \theta + \eta \frac{\bar{G}_{\theta}}{\theta} \\ & \cdots \end{aligned}$$

其中：

• $\theta$是一组参数

$$\theta = \{\omega_1,\omega_2,\cdots,b_1,\cdots\}$$

• $\frac{\bar{G}_{\theta}}{\theta}$是梯度

$$\frac{\bar{G}_{\theta}}{\theta} = \left[ \begin{matrix} \frac{\partial \bar{G}_\theta}{\partial \omega_1} \\ \frac{\partial \bar{G}_\theta}{\partial \omega_2} \\ \vdots \\ \frac{\partial \bar{G}_\theta}{\partial b_1} \\ \vdots \end{matrix} \right]$$

• $\eta$是学习率。(在强化学习中，绝大部分资料，梯度下降的学习率用$\alpha$表示，梯度上升的学习率用$\eta$或者$\beta$表示)

所以，接下来我们的目标就很明确了，我们需要求$\frac{\bar{G}_\theta}{\theta}$。
在上文我们讨论过，$\bar{G}_{\theta} = \sum_{\tau \in \text{所有的}\tau} G_{\theta} P(\tau;\theta)$，所以

$$\frac{\partial \bar{G}_\theta}{\partial \theta} = \sum_{\tau \in \text{所有的}\tau} G(\tau) \frac{P(\tau;\theta)}{\theta}$$

然后我们来做一个"迷"操作，乘以$\frac{P(\tau;\theta)}{P(\tau;\theta)}$，得到

$$\frac{\partial \bar{G}_\theta}{\partial \theta} = \sum_{\tau \in \text{所有的}\tau} G(\tau) P(\tau;\theta) \frac{1}{P(\tau;\theta)} \frac{\partial P(\tau;\theta)}{\partial \theta}$$

根据我们的导数公式和复合函数求导法则，我们知道下面这个等式是成立的。

$$\frac{d \log(f(x))}{d x} = \frac{1}{f(x)} \frac{d f(x)}{d x}$$

看看$\frac{1}{f(x)}\frac{d f(x)}{d x}$，再看看$\frac{1}{P(\tau;\theta)} \frac{\partial P(\tau;\theta)}{\partial \theta}$，立即推

$$\frac{\partial \bar{G}_\theta}{\partial \theta} = \sum_{\tau \in \text{所有的}\tau} G(\tau) P(\tau;\theta) \frac{\partial \log P(\tau;\theta)}{\partial \theta}$$

在上文，我们还留了一个式子。

$$\bar{G}_\theta \approx \frac{1}{N} \sum_{n=1}^N G_{\theta}(\tau_n)$$

我们说很快会用到，就在这里。
看看这个式子，再看看上式的$\sum_{\tau \in \text{所有的}\tau} G(\tau) P(\tau;\theta)$这一部分。
立即推

$$\frac{\partial \bar{G}_\theta}{\theta} \approx \frac{1}{N} \sum_{n=1}^N G(\tau_n) \frac{\partial \log P(\tau_n;\theta)}{\partial \theta}$$

所以，接下来我们的目标就很明确了，求$\frac{\partial \log P(\tau_n;\theta)}{\partial \theta}$。

在上文我们讨论过

$$\begin{aligned} P(\tau;\theta) &= P(s_1) P(a_1|s_1;\theta) P(r_1,s_2|s_1,a_1) P(a_2|s_2;\theta) P(r_2,s_3|s_2,a_2) \cdots P(a_T|s_T;\theta) P(r_T,s_{T+1}|s_T,a_T)\\ &= P(s_1) \Pi_{t=1}^T P(a_t|s_t;\theta) P(r_t,s_{t+1}|s_t,a_t) \end{aligned}$$

所以

$$\begin{aligned} \log P(\tau;\theta) = \log P(s_1) + \sum_{t=1}^T \log P(a_t|s_t;\theta) + \sum_{t=1}^T \log P(r_t,s_{t+1}|s_t,a_t) \end{aligned}$$

所以

$$\frac{\partial \log P(\tau;\theta)}{\partial \theta} = \sum_{t=1}^T \frac{\partial \log P(a_t|s_t;\theta)}{\partial \theta}$$

• 只要是不基于$\theta$的，即$\theta$不是自变量的，都看成常数。

综上所述

$$\begin{aligned} \frac{\bar{G}_\theta}{\partial \theta} & \approx \frac{1}{N} \sum_{n=1}^N G(\tau_n) \frac{\partial \log P(\tau_n;\theta)}{\partial \theta} \\ & \approx \frac{1}{N} \sum_{n=1}^N G(\tau_n) \sum_{t=1}^{T_n} \frac{\partial \log P(a_t^n|s_t^n;\theta)}{\partial \theta} \\ & \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n} G(\tau_n) \frac{\partial \log P(a_t^n|s_t^n;\theta)}{\partial \theta} \end{aligned}$$

最后一步，梯度上升

$$\theta \leftarrow \theta + \eta \frac{\partial \bar{G}_\theta}{\partial \theta}$$

梯度的业务含义

在上文，我们通过数学推导，得到了梯度。

$$\frac{\partial \bar{G}_\theta}{\partial \theta} \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n} G(\tau_n) \frac{\partial \log P(a_t^n|s_t^n;\theta)}{\partial \theta}$$

现在，让我们来看看，这个梯度，到底在做什么，到底有什么业务含义。

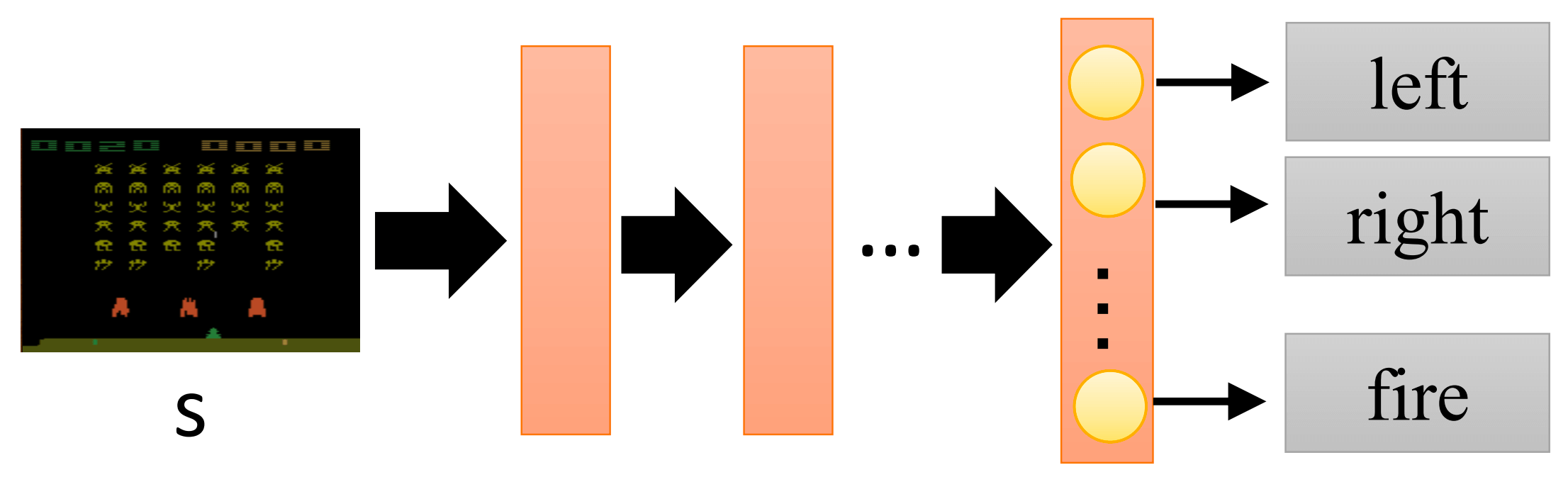
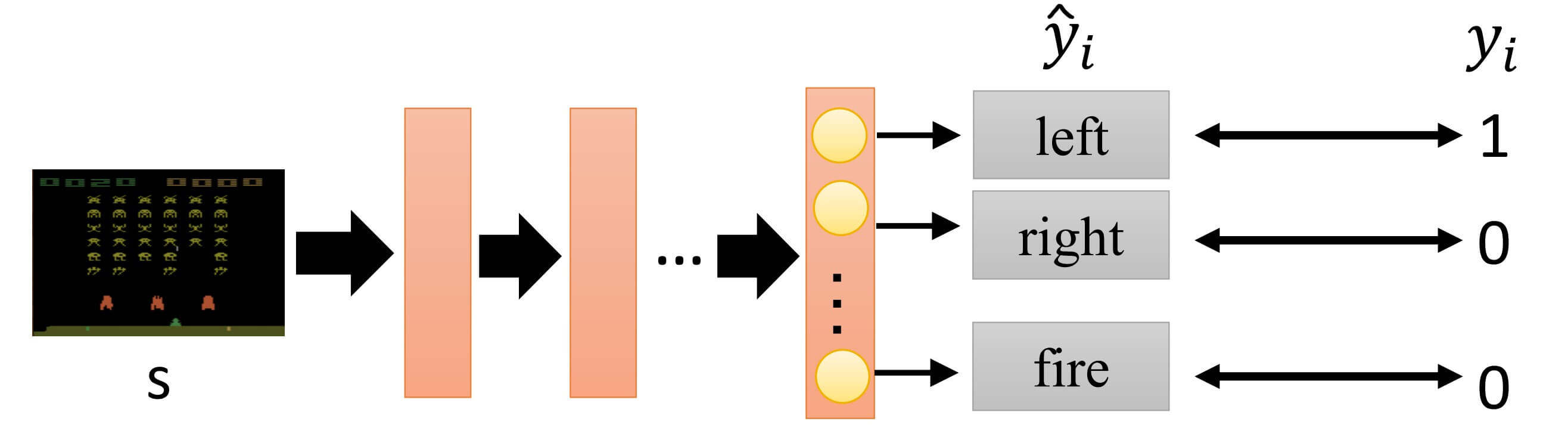
我们从一个很经典的分类问题开始，但是与以往不同的是，我们的类别是"应该向左"、“应该向右"和"应该开火”。

• $\hat{y_i}$是输出的三种类别的概率，是模型的估计预测
• $y_i$是真实值，也就是Label

在《深度学习初步及其Python实现：2.神经网络基础》我们讨论过，这种的分类问题，其损失函数是交叉熵损失。

$$H(\bold{p}||\bold{q}) = - \sum_i p_i \log_2 q_i$$

在这里，损失函数就是

$$-\sum_{i=1}^3 y_i \log \hat{y}_i$$

• 需要注意的是，损失函数是$-\sum_{i=1}^3 y_i \log \hat{y}_i$，而不是$-\sum_{i=1}^3 \hat{y}_i \log y_i$，因为交叉熵的不对称性，具体可以参考《深度学习初步及其Python实现：2.神经网络基础》。

当时，我们的目标是要最小化这个损失函数的值。
现在，我们把负号去掉，这时候我们的目标就是最大化$\sum_{i=1}^3 y_i \log \hat{y}_i$。

又因为，只有第一个$y_i$的值为$1$。
所以，其实我们的目标也就最大化$\log \hat{y}_1$，即最大化$\log P(\text{left}|\text{s})$，即

$$\text{Maxmize} \quad \log P(\text{left}|\text{s})$$

那么，怎么更新$\theta$的值呢？
既然负号去掉了，那就梯度上升。

$$\theta \leftarrow \theta + \eta \frac{\partial \log P(\text{left}|\text{s})}{\partial \theta}$$

这个式子，$\frac{\log P(\text{left}|\text{s})}{\partial \theta}$ 这一部分，和我们的上文中的$\frac{\partial \log P(a_t^n|s_t^n;\theta)}{\partial \theta}$太像了。

$$\text{但是，不一样！}$$

在$\frac{\partial \log P(\text{left}|\text{s})}{\partial \theta}$中，$\text{left}$是什么？是真实值。
在$\frac{\partial \log P(a_t^n|s_t^n;\theta)}{\partial \theta}$中呢，$a_t^n$不是真实值，是我们的那个不怎么样的策略，输出的动作。

那么，在分类问题中，我们梯度上升(或梯度下降，具体看目标函数的形式)是为了逼近真实值。现在呢？我们梯度上升，是为了去逼近我们之前那个不怎么样的策略输出的动作？

$$\text{到底怎么回事？}$$

注意看

$$\frac{\partial \bar{G}_\theta}{\partial \theta} \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n} G(\tau_n) \frac{\partial \log P(a_t^n|s_t^n;\theta)}{\partial \theta}$$

有一个$G(\tau_n)$，如果$G(\tau_n)$大于$0$，就加大执行动作$a_t^n$的概率。如果$G(\tau_n)$小于$0$，就减小执行动作$a_t^n$的概率。
也就是说，虽然我们得到的是一个不怎么样的策略，但是我们学习好的，同时规避不好。
要么说是强化学习呢，这就是强化啊！

添加基线

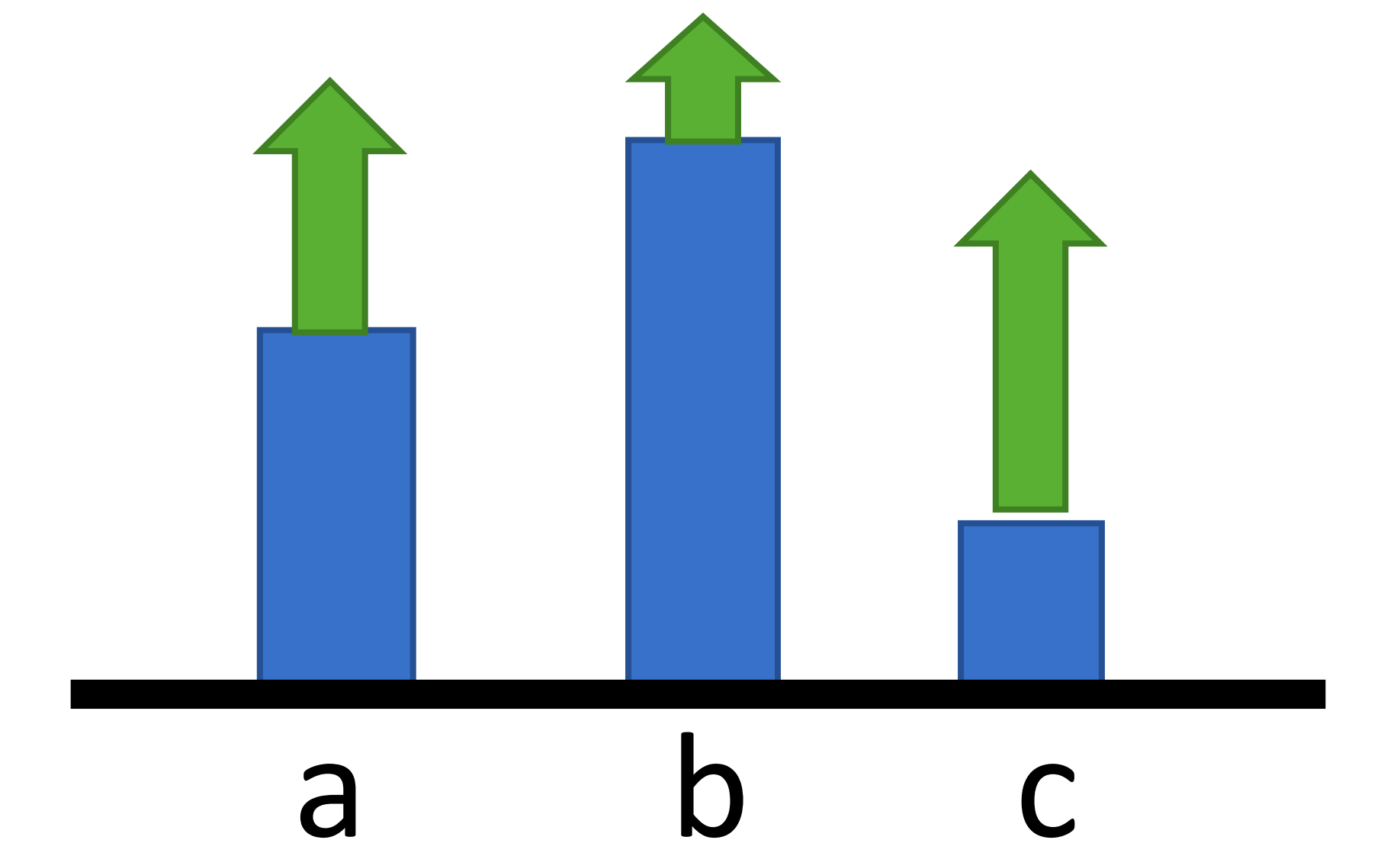
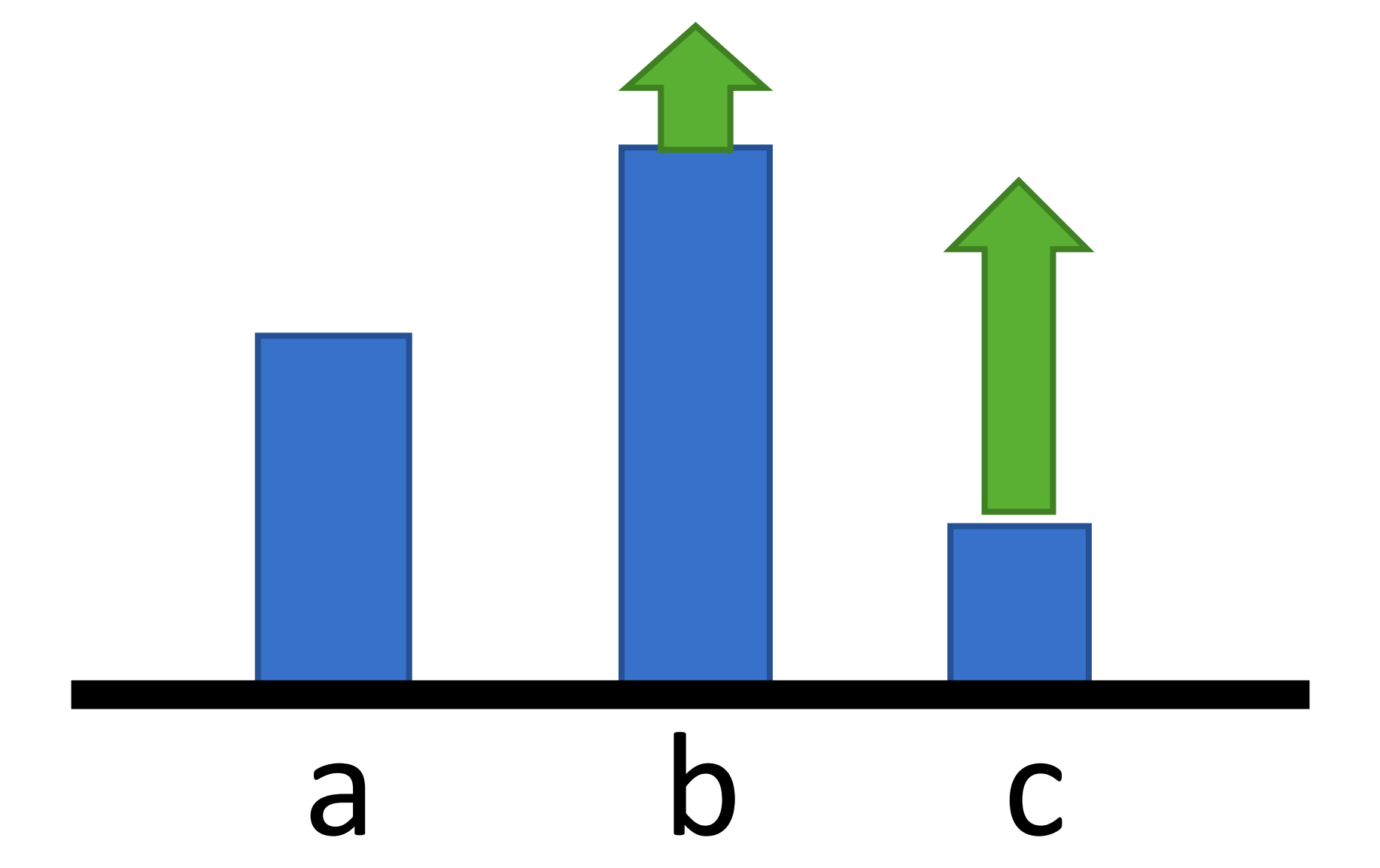
现在，我们来看一个问题，如果对于所有的$\tau_n$，$G(\tau_n)$都大于等于$0$，会怎么样？
比如，电玩城的投篮机，这个游戏只有得分或者不得分，没有丢分。$G(\tau_n)$会永远大于等于$0$。

那么，会有什么问题吗？
比如说

有a、b、c三个动作，方框表示概率大小，箭头的长度表示回报。虽然回报都是大于$0$的，但是a和c的回报明显大于b的回报。所以经过迭代后，a、b、c的新的概率如图。

没问题啊，即使$G(\tau_n)$永远大于等于$0$，看起来也没问题啊。

是没问题。
但是，别忘了一件事情，抽样。
举个例子，如果没有抽中a。

然后迭代之后，我们会得到

即，没有被抽中的动作，其概率会下降。

那么，怎么办？我们添加一个baseline(基线)，这样比基线小的回报，即使回报大于$0$，其动作的概率还是会下降。

$$\frac{\partial \bar{G}_\theta}{\partial \theta} \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n} \bigg(G(\tau_n) - b\bigg) \frac{\partial \log P(a_t^n|s_t^n;\theta)}{\partial \theta}$$

• 也有资料称$b$为bias(偏置)，这么解释的话，就忽略了其业务作用，但是或许在数学上更通顺。

特别注意，$b$不一定就是常数，可以是一个函数，可以是一个神经网络。但一定是只和状态有关而和动作无关的量。
我们很快就会见到$b$不是一个常数。

Assign Suitable Credit

再来看看上面的式子

$$\frac{\partial \bar{G}_\theta}{\partial \theta} \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n} \bigg(G(\tau_n) - b\bigg) \frac{\partial \log P(a_t^n|s_t^n;\theta)}{\partial \theta}$$

有这么一个部分

$$\bigg(G(\tau_n) - b\bigg) \frac{\partial \log P(a_t^n|s_t^n;\theta)}{\partial \theta}$$

上文，我们讨论了，虽然我们得到的是一个不怎么样的策略，但是我们学习好的，同时规避不好。我们的好坏是根据什么定义的？是$G(\tau_n)$，轨迹的回报。
不，我们还在轨迹回报的基础上加了基线。

$$G(\tau_n) - b$$

在回报大的轨迹中，不一定所有的动作都是最佳动作。如果这个轨迹的回报非常大，那么其中滥竽充数，鱼目混珠的一些不好的动作也可能会不断的被加强。同理，如果轨迹的回报是较小，甚至是负数。那么，其中一些较好的动作，可能会被规避。

那么，怎么办？

那，要么这样好了，我们不用回报了，用每个动作的奖励。

把每一步都做当前的最佳决策，这是贪心算法。
贪心本身是没有问题的，不是说贪心算法就一定无效。几个经典的图算法"Kruskal"、"Prim"和"Dijkstra"都是贪心算法。(关于这部分，可以参考《算法入门经典(Java与Python描述)：10.图》)

而且，我们之前的章节的模型，不都是贪心吗？我们每次选择价值最大的动作，即回报最大的那个动作。

之前贪心贪的是什么？是回报最大。现在呢？现在贪心奖励最大？
那不行，在《1.基础概念》我们就讨论过，强化学习的目标是最大化回报，而不是最大化当前的奖励。当时我们还举了一个例子，说我们应该着眼于解救公主，而不是眼前的这一两枚金币。
我们要追求整体回报最大，每个动作都是当前奖励最大的动作，不一定能保证整体回报最大。同理，可能在某个状态下，我们做了一个奖励不大，甚至奖励是负数的动作。但，为的是整体最优。

题外话
这就可以理解，为什么滴滴不把最近的车派给我们，因为滴滴的追求是整体最优。为了做到整体最优，可能会给我们派了一辆较远的车。
当然，滴滴的系统很复杂，其整体最优可能不是简单意义上的整体等车时间最短，还会考虑很多因素。

好了，题外话就聊到这里。

如果拳头收回去，是为了更好的出拳的话。那么我们似乎应该把下一步出拳的奖励也算给这一步把拳头收回去，最多打点折扣的算进去。

我们来看一个具体的例子。

在$s_1$，做出动作$a_1$，得到奖励$-5$；在$s_2$，做出动作$a_2$，得到奖励$+0$；在$s_3$，做出动作$a_3$，得到奖励$-2$。所以，回报是$-7$。然后我们对每一步都乘以$-7$。之前就是这样做的，但这样，是不是对$(s_2,a_2)$太不公平了？

$$\text{冤有头，债有主}$$

把$(s_3,a_3)$的$-2$算给$(s_2,a_2)$还可以接受，或许是在$s_2$没做好，导致在$s_3$遭受了$-2$。
但是把$(s_1,a_1)$的$-5$也算给$(s_2,a_2)$确实不应该。

所以，我们改成下图的形式。

综上所述，我们修改$\frac{\partial \bar{G}_\theta}{\partial \theta}$

$$\frac{\partial \bar{G}_\theta}{\partial \theta} \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n} \bigg(\sum_{t' = t}^{T_n} r_{t'}^n - b\bigg) \frac{\partial \log P(a_t^n|s_t^n;\theta)}{\partial \theta}$$

如果再乘上折扣因子$\gamma$，则是

$$\frac{\partial \bar{G}_\theta}{\partial \theta} \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n} \bigg(\sum_{t' = t}^{T_n} \gamma^{t'-t} r_{t'}^n - b\bigg) \frac{\partial \log P(a_t^n|s_t^n;\theta)}{\partial \theta}$$

离线策略方法

接下来，我们讨论离线策略方法，也就是近端策略优化(Proximal Policy Optimization)。

重要性采样

《4.时序差分》这一章，我们第一次真正意义上讨论离线策略。当时我们提到过，离线策略的理论基础就是重要性采样，很多资料先讨论"重要性采样"，当时我们不讨论，是因为我认为，我们反过来，先弄明白什么是离线策略，再去讨论重要性采样，或许更容易理解重要性采样。
现在，我想，是时候讨论重要性采样了(Importance Sampling)。

我们从一个问题出发，假如随机变量$x$服从分布$p(x)$，求$\mathbb{E}_{x\sim p}[f(x)]$。

$$\mathbb{E}_{x\sim p}[f(x)] = \int f(x)p(x)dx$$

一个"迷"操作，乘以$\frac{q(x)}{q(x)}$，得到

$$\begin{aligned} \mathbb{E}_{x\sim p}[f(x)] &= \int f(x)\frac{p(x)}{q(x)}q(x)dx \\ &= \mathbb{E}_{x\sim q}\bigg[f(x)\frac{p(x)}{q(x)}\bigg] \end{aligned}$$

通过上述，我们知道$\mathbb{E}_{x\sim p}[f(x)]=\mathbb{E}_{x\sim q}\bigg[f(x)\frac{p(x)}{q(x)}\bigg]$，那么现在提一个问题。
$x \sim p$的$f(x)$和$x \sim q$的$f(x)\frac{p(x)}{q(x)}$会是一样的吗？
这个还真不一样。
我们分别计算一下$Var_{x \sim p}[f(x)]$和$Var_{x \sim q}[f(x)\frac{p(x)}{q(x)}]$就可以知道。
方差计算公式为

$$Var(X) = E(X^2) - E(X)^2$$

计算过程和结果略，总之，就是不一样。

所以呢，$p(x)$和$q(x)$，不能相差太多，这个我们之前讨论过，有一个东西可以衡量之间的距离，KL散度。

近端策略优化

在上文我们讨论了$\frac{\partial \bar{G}_\theta}{\partial \theta}$。

$$\frac{\partial \bar{G}_\theta}{\partial \theta} \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n} \bigg(\sum_{t' = t}^{T_n} \gamma^{t'-t} r_{t'}^n - b\bigg) \frac{\partial \log P(a_t^n|s_t^n;\theta)}{\partial \theta}$$

为了表述简单，我们把$\sum_{t' = t}^{T_n} \gamma^{t'-t} r_{t'}^n - b$这部分写成$A_\theta(s_t,a_t)$。
即

$$\frac{\partial \bar{G}_\theta}{\partial \theta} = \mathbb{E}_{(s_t,a_t)\sim\pi_\theta}\bigg[A_\theta(s_t,a_t)\frac{\partial \log P(a_t|s_t;\theta)}{\partial \theta}\bigg]$$

然后，我们利用刚刚讨论的重要性采样，则有

$$\frac{\partial \bar{G}_\theta}{\partial \theta} = \mathbb{E}_{(s_t,a_t)\sim\pi_{\theta '}}\bigg[\frac{P_\theta(s_t,a_t)}{P_{\theta '}(s_t,a_t)}A_{\theta'}(s_t,a_t)\frac{\partial \log P(a_t|s_t;\theta)}{\partial \theta}\bigg]$$

$P_\theta(s_t,a_t)$可以写成什么呢？

$$P_\theta(s_t,a_t) = P_\theta(a_t|s_t)P_\theta(s_t)$$

所以，上式又可以写成

$$\frac{\partial \bar{G}_\theta}{\partial \theta} = \mathbb{E}_{(s_t,a_t)\sim\pi_{\theta '}}\bigg[\frac{P_\theta(a_t|s_t)P_\theta(s_t)}{P_{\theta '}(a_t|s_t)P_{\theta '}(s_t)}A_{\theta '}(s_t,a_t)\frac{\partial \log P(a_t|s_t;\theta)}{\partial \theta}\bigg]$$

接下来，我们认为$P_{\theta}(s_t)$和$P_{\theta '}(s_t)$可以约去，总之，就是这么认为。
则有

$$\frac{\partial \bar{G}_\theta}{\partial \theta} = \mathbb{E}_{(s_t,a_t)\sim\pi_\theta}\bigg[\frac{P_\theta(a_t|s_t)}{P_{\theta '}(a_t|s_t)}A_{\theta '}(s_t,a_t)\frac{\partial \log P(a_t|s_t;\theta)}{\partial \theta}\bigg]$$

但，注意了，刚刚我们弄的一直是梯度，目标函数是什么？目标函数$J_{\theta '}$是

$$J_{\theta '}(\theta) = \mathbb{E}_{(s_t,a_t)\sim\pi_{\theta '}}\bigg[\frac{P_\theta(a_t|s_t)}{P_{\theta '}(a_t|s_t)}A_{\theta '}(s_t,a_t)\bigg]$$

• $\theta$是需要去优化的参数
• $\theta'$是环境互动的参数

那么，什么是近端策略优化(Proximal Policy Optimization)呢？
再加上KL散度。(至于为什么加KL散度，我们在讨论重要性采样的时候讨论过了。)

$$J^{PPO}_{\theta '}(\theta) = J_{\theta '}(\theta) - \beta KL(\theta,\theta ')$$

以控制$\theta$和$\theta '$不能相差太远。

还有一种方法是信任域策略优化(Trust Region Policy Optimization,TRPO)，这种方法是在额外添加对$KL(\theta,\theta')$的限制。
即

$$J^{TRPO}_{\theta '}(\theta) = J_{\theta '}(\theta) \quad \text{同时要求：}KL(\theta,\theta') < \delta$$

这种方法实现起来极为不便，所以更多的还是用的近端策略优化。

剩下的内容，就和之前的在线策略方法一样了。我们用$J^{PPO}_{\theta '}$做梯度下降乘上学习率，去更新$\theta$。
这就是离线策略方法。

AC

在上文，我们讨论了随机策略梯度方法。
在线策略的梯度是

$$\frac{\partial \bar{G}_\theta}{\partial \theta} \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n} \bigg(\sum_{t' = t}^{T_n} \gamma^{t'-t} r_{t'}^n - b\bigg) \frac{\partial \log P(a_t^n|s_t^n;\theta)}{\partial \theta}$$

离线策略的目标函数是

$$\begin{aligned} J^{PPO}_{\theta '}(\theta) & = J_{\theta '}(\theta) - \beta KL(\theta,\theta ') \\ J_{\theta '}(\theta) & = \mathbb{E}_{(s_t,a_t)\sim\pi_{\theta '}}\bigg[\frac{P_\theta(a_t|s_t)}{P_{\theta '}(a_t|s_t)}A_{\theta '}(s_t,a_t)\bigg] \\ A_{\theta '}(s_t,a_t) & = \sum_{t' = t}^{T_n} \gamma^{t'-t} r_{t'}^n - b \end{aligned}$$

无论是在线策略还是离线策略，都有这么一个东西，$\sum_{t' = t}^{T_n} \gamma^{t'-t} r_{t'}^n$，这个东西有一个问题，非常不稳定。
当然不稳定，这个我们讨论过很多次了，动作是随机的，状态转移是随机的，自然这个东西也是随机的，是不稳定的。
所以呢，我们会抽样很多次。如果抽样足够多次的话，那没问题，但是那就太慢了。
那么，有没有办法快一点呢？

我们再来仔细看这个式子

$$\sum_{t' = t}^{T_n} \gamma^{t'-t} r_{t'}^n - b$$

$\sum_{t' = t}^{T_n} \gamma^{t'-t} r_{t'}^n$是什么？是回报，我们记作$G_t^n$。
$\mathbb{E}[G_t^n]$是什么？就是我们的动作价值！$Q_{\pi_\theta}(s_t^n,a_t^n)$。
那么，这时候再把$b$用状态价值$V_{\pi_\theta}(s_t^n)$表示是绝佳的。这就是我们上文讨论的$b$不一定是常数。
所以，我们把$\sum_{t' = t}^{T_n} \gamma^{t'-t} r_{t'}^n - b$替换成$Q_{\pi_\theta}(s_t^n,a_t^n) - V_{\pi_\theta}(s_t^n)$。
这就是大名鼎鼎的Actor-Critic。
我们不再用实际观测的回报近似$Q_{\pi}$，而用神经网络来近似$Q_{\pi}$，这是Actorl-Critic。

比如，对于在线方法

$$\frac{\partial \bar{G}_\theta}{\partial \theta} \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n} \bigg(Q_{\pi_\theta}(s_t^n,a_t^n) - V_{\pi_\theta}(s_t^n)\bigg) \frac{\partial \log P(a_t^n|s_t^n;\theta)}{\partial \theta}$$

那么，现在问，谁是Actor，谁是Critic？
$Q_{\pi_\theta}(s_t^n,a_t^n)$是Actor？$V_{\pi_\theta}(s_t^n)$是Critic？不，错了！
这是策略梯度的估计！

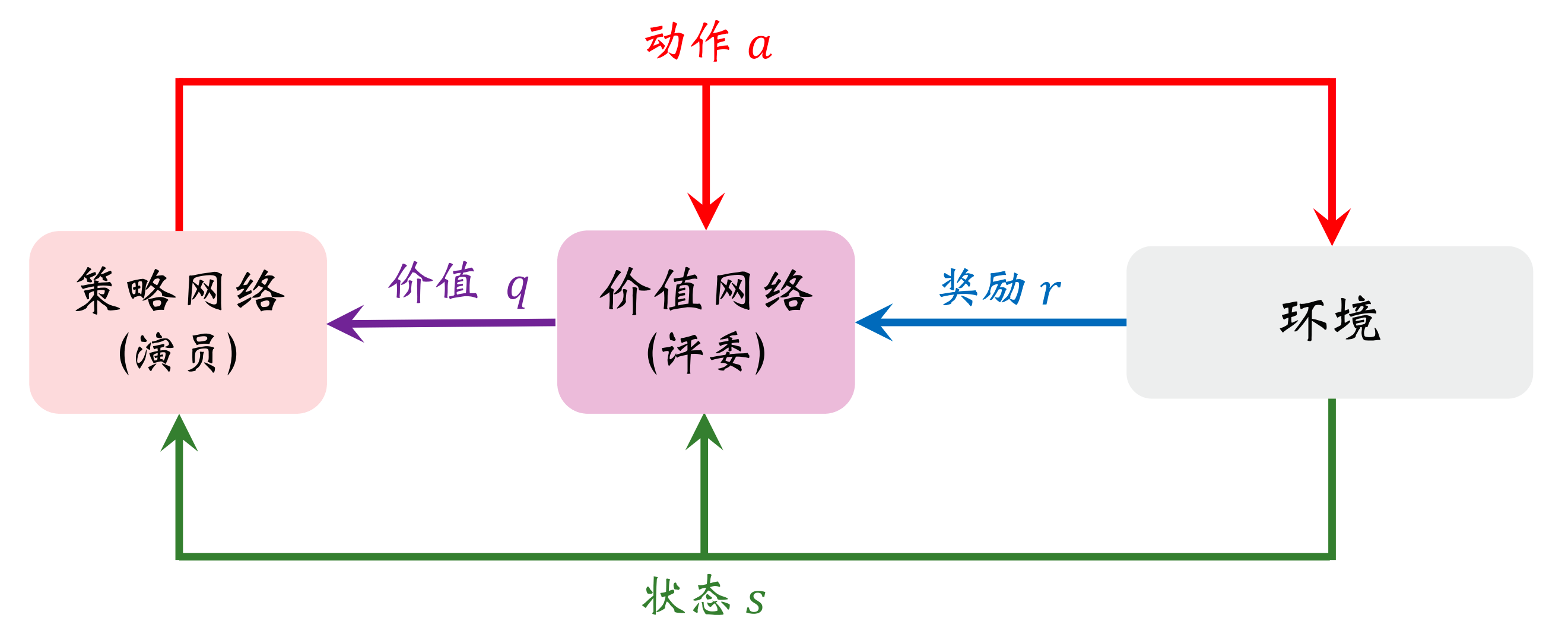
我们来看这张图。

解释一下，在上图中，我们策略网络的输入是状态$s$，输出是一个向量，向量中的每个元素表示一个动作的概率，然后会抽样出其中一个动作$a$并执行，并得到奖励$r$。价值网络的输入是状态$s$，和基于策略网络的输入而抽样得到的动作$a$。把$r$给价值网络呢，是因为价值网络也需要训练。

接下来，我们讨论具体训练过程。

训练价值网络

Actor-Critic方法中用一个神经网络近似动作价值函数$Q_{\pi}(s,a)$，这个神经网络被称为"价值网络"，我们记作$Q(s,a;\omega)$。
用神经网络来近似价值函数？这个我们似乎见过？对，就是上一章的DQN。
但是两者的意义不同，训练算法也不同。

1. 价值网络是对动作价值函数$Q_{\pi}(s,a)$的近似。而DQN则是对最优动作价值函数$Q_\star(s,a)$的近似。
2. 价值网络的训练使用的是SARSA算法，它属于在线策略，不能用经验回放。对DQN的训练使用的是Q-Learning算法，它属于离线策略，可以用经验回放。

SARSA算法，我们已经讨论过了。接下来，我们来看看SARSA在训练价值网络中的具体应用。
在$t$时刻，价值网络输出$\hat{q}_t=Q(s_t,a_t;\omega)$，是对动作价值函数$Q_{\pi}(s_t,a_t)$的估计。
在$t+1$时刻，实际观测到$r_t,s_{t+1},a_{t+1}$，于是可以计算TD目标$\hat{y}_t=r_t+\gamma Q(s_{t+1},a_{t+1};\omega)$，它也是对动作价值函数$Q_{\pi}(s_t,a_t)$的估计。由于$\hat{y}_t$部分基于实际观测到的奖励$r_t$，我们认为$\hat{y}_t$比$\hat{q}_t$更接近事实真相。所以把$\hat{y}_t$固定住，鼓励$Q(s_t,a_t;\omega)$去接近$\hat{y}_t$。
即，定义损失函数

$$L(\omega) = \frac{1}{2}\bigg[Q(s_t,a_t;\omega) - \hat{y}_t\bigg]^2$$

计算梯度

$$\frac{\partial L(\omega)}{\partial \omega} = (\hat{q}_t - \hat{y}_t) \frac{\partial Q(s_t,a_t;\omega)}{\partial \omega}$$

做一轮梯度下降

$$\omega \leftarrow \omega - \beta \frac{\partial L(\omega)}{\partial \omega}$$

训练策略网络

Actor利用当前状态$s$，自己的动作$a$，以及评委的打分$Q_{\pi_\theta}(s_t^n,a_t^n) - V_{\pi_\theta}(s_t^n)$，来计算近似策略梯度$\frac{\partial \bar{G}_\theta}{\partial \theta}$，然后更新自己的参数$\theta$。
即

$$\theta \leftarrow \theta + \eta \frac{\partial \bar{G}_\theta}{\partial \theta}$$

A2C

A2C的梯度

但是呢，这个还有一点小问题。我们有两个网络，一个$Q_{\pi_\theta}(s_t^n,a_t^n)$。一个$V_{\pi_\theta}(s_t^n)$。
两个网络，也就意味着两倍的风险，两个中有一个没训练好，都可能结束。
那么，有没有办法只训练一个网络呢？
比如，我们只训练状态价值的，然后我们用状态价值来表示动作价值。
来，找到这篇文章《3.蒙特卡洛》，开篇我们就讨论了无模型和有模型的主要区别，无模型，我们只能用动作价值表示状态价值。
但是，我们这次说的是这个意思。

$$Q_{\pi}(s_t^n,a_t^n) = \mathbb{E}[r_t^n + V_{\pi}(s_{t+1}^n)]$$

那没问题，要用蒙特卡洛抽样，求平均，那当然OK。

所以，我们把上文$\frac{\partial \bar{G}_\theta}{\partial \theta}$的表达式中的$Q_{\pi_\theta}(s_t^n,a_t^n) - V_{\pi_\theta}(s_t^n)$替换成$r_t^n + V_{\pi_\theta}(s_{t+1}^n) - V_{\pi_\theta}(s_t^n)$

比如，对于在线方法的策略梯度

$$\frac{\partial \bar{G}_\theta}{\partial \theta} \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n} \bigg(r_t^n + V_{\pi_\theta}(s_{t+1}^n) - V_{\pi_\theta}(s_t^n)\bigg) \frac{\partial \log P(a_t^n|s_t^n;\theta)}{\partial \theta}$$

其中$r_t^n + V_{\pi_\theta}(s_{t+1}^n) - V_{\pi_\theta}(s_t^n)$又被称为优势函数(Advantage Function)。
这就是A2C，2的含义是两个A，Advantage Actor-Critic。
除此之外，和AC方法并无本质区别。

A2C的过程

A2C算法
输入：
  环境
输出：
  最优策略参数$\theta$
参数：
  $\theta$的学习率$\eta$
  $\omega$的学习率$\beta$
初始化：
  初始化$\theta$为任意值(随机初始化)
  初始化$\omega$为任意值(随机初始化)
对每一条轨迹执行以下操作：
  初始化累积折扣因子，$I \leftarrow 1$
  初始化状态$s_0$
  $t = 1,2,\cdots,T$，轨迹内的每一个时间步执行以下操作：
    在状态$s_t$下，根据$\pi(\cdot|s;\theta)$，执行动作$a_t$
    环境给出奖励$r$，状态转移至$s_{t+1}$
    估计回报，$g\leftarrow r+\gamma V(s_{t+1};\omega)$
    策略改进，更新$\theta$，$\theta \leftarrow \theta + \eta I[g - V(s;\omega)]\frac{\partial \ln\pi(a|s;\theta)}{\partial \theta}$
    更新价值，更新$\omega$，$\omega \leftarrow \omega + \beta[g - V(s;\omega)]\frac{\partial V(s;\omega)}{\partial \omega}$
    更新累积折扣因子$I \leftarrow \gamma I$

A2C的实现

我们以双节倒立摆问题为例。

该例子来自《强化学习：原理与Python实现(肖智清著)》这本书的第八章。

双节倒立摆问题描述

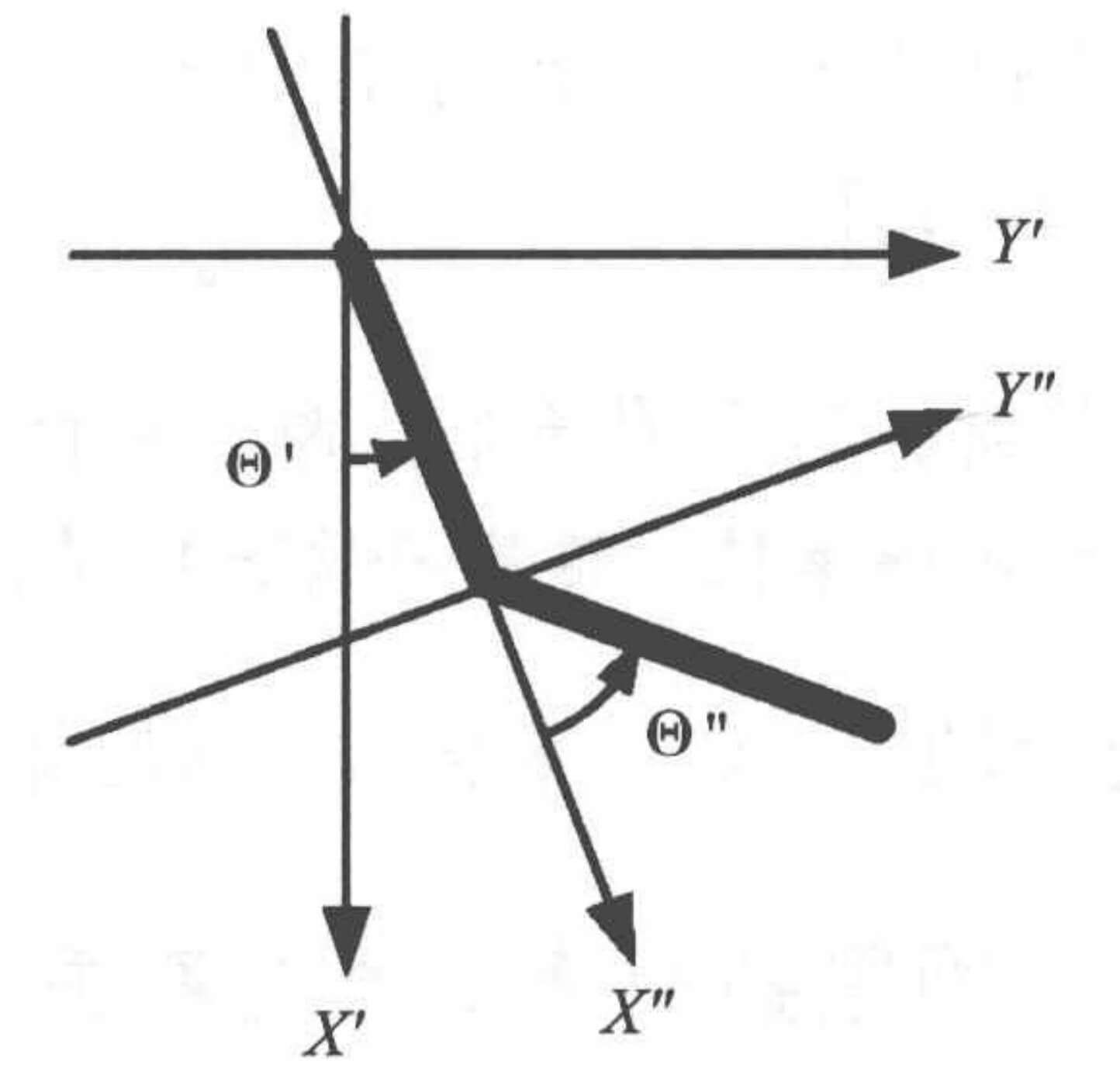
有两根在二维垂直面上活动的杆子首尾相接，一端固定在原点，另一端在二维垂直面上活动。基于原点可以在二维垂直面上建立一个绝对坐标系$X'Y'$，$X'$轴是垂直向下的，$Y'$轴是水平向右的；基于连接在原点的杆的位置可以建立另外一个相对的坐标系$X''Y''$，$X''$轴向外，$Y''$轴与$X''$轴垂直。在任一时刻$t(t=0,1,2,\cdots)$，可以观测到棍子连接处在绝对坐标系的坐标$(X'_t,Y'_t)=(\cos \Theta'_t,\sin \Theta'_t)$和活动端在相对坐标系上的坐标$(X''_t,Y''_t)=(\cos \Theta''_t,\sin \Theta''_t)$，还有当前的角速度$\hat{\Theta}'_t$和$\hat{\Theta}''_t$。可以在两个杆子的连接处施加动作，动作取自动作空间$A =\{0,1,2\}$。每过一步，惩罚奖励值$-1$。活动端在绝对坐标系中的$X'$坐标小于$-1$时，或回合达到500步，回合结束。我们希望回合步数尽量少。

与我们上一章的"小车上山问题"一样，这个环境其实也有其数学表示式的。但是我们不讨论，反之我们认为环境是未知的。

环境描述

示例代码：

import numpy as np
np.random.seed(0)
import gym
env = gym.make('Acrobot-v1')
env.seed(0)

print('状态空间 = {}'.format(env.observation_space))
print('动作空间 = {}'.format(env.action_space))

运行结果：

状态空间 = Box(-28.274333953857422, 28.274333953857422, (6,), float32)
动作空间 = Discrete(3)

• 状态空间是连续的，动作空间是离散的

A2C的代码

示例代码：

import tensorflow as tf
tf.random.set_seed(0)
from tensorflow import keras

class AdvantageActorCriticAgent():
    def __init__(self, env, actor_kwargs, critic_kwargs, gamma=0.99):
        self.action_n = env.action_space.n
        self.gamma = gamma
        self.discount = 1.

        self.actor_net = self.build_network(output_size=self.action_n,output_activation=tf.nn.softmax,loss=tf.losses.categorical_crossentropy,**actor_kwargs)
        self.critic_net = self.build_network(output_size=1,**critic_kwargs)

    def build_network(self, hidden_sizes, output_size, input_size=None,activation=tf.nn.relu, output_activation=None,loss=tf.losses.mse, learning_rate=0.01):
        model = keras.Sequential()
        for idx, hidden_size in enumerate(hidden_sizes):
            kwargs = {}
            if idx == 0 and input_size is not None:
                kwargs['input_shape'] = (input_size,)
            model.add(keras.layers.Dense(units=hidden_size,activation=activation, **kwargs))
        model.add(keras.layers.Dense(units=output_size,activation=output_activation))
        optimizer = tf.optimizers.Adam(learning_rate)
        model.compile(optimizer=optimizer, loss=loss)
        return model
        
    def decide(self, observation):
        probs = self.actor_net.predict(observation[np.newaxis])[0]
        action = np.random.choice(self.action_n, p=probs)
        return action

    def learn(self, observation, action, reward, next_observation, done):
        x = observation[np.newaxis]
        u = reward + (1. - done) * self.gamma * self.critic_net.predict(next_observation[np.newaxis])
        td_error = u - self.critic_net.predict(x)

        # 训练执行者网络
        x_tensor = tf.convert_to_tensor(observation[np.newaxis],dtype=tf.float32)
        with tf.GradientTape() as tape:
            pi_tensor = self.actor_net(x_tensor)[0, action]
            logpi_tensor = tf.math.log(tf.clip_by_value(pi_tensor,1e-6, 1.))
            loss_tensor = -self.discount * td_error * logpi_tensor
        grad_tensors = tape.gradient(loss_tensor, self.actor_net.variables)
        self.actor_net.optimizer.apply_gradients(zip(grad_tensors, self.actor_net.variables)) # 更新执行者网络

        # 训练评论者网络
        self.critic_net.fit(x, u, verbose=0) # 更新评论者网络

        if done:
            self.discount = 1. # 为下一回合初始化累积折扣
        else:
            self.discount *= self.gamma # 进一步累积折扣

play_qlearning

示例代码：

def play_qlearning(env, agent, train=False, render=False):
    episode_reward = 0
    observation = env.reset()
    step = 0
    while True:
        if render:
            env.render()
        action = agent.decide(observation)
        next_observation, reward, done, _ = env.step(action)
        episode_reward += reward
        if train:
            agent.learn(observation, action, reward, next_observation,done)
        if done:
            break
        step += 1
        observation = next_observation
    return episode_reward

训练

示例代码：

actor_kwargs = {'hidden_sizes' : [100,], 'learning_rate' : 0.0001}
critic_kwargs = {'hidden_sizes' : [100,], 'learning_rate' : 0.0002}
agent = AdvantageActorCriticAgent(env, actor_kwargs=actor_kwargs,critic_kwargs=critic_kwargs)

# 训练
episodes = 100
episode_rewards = []
for episode in range(episodes):
    episode_reward = play_qlearning(env, agent, train=True)
    episode_rewards.append(episode_reward)
    print('{}  {}'.format(episode,episode_reward))

运行结果：

0  -419.0
1  -500.0
2  -500.0
3  -500.0
4  -500.0

【部分运行结果略】

95  -73.0
96  -81.0
97  -76.0
98  -107.0
99  -63.0

测试

示例代码：

# 测试
episode_rewards = [play_qlearning(env, agent) for _ in range(100)]
print('平均回合奖励 = {} / {} = {}'.format(sum(episode_rewards),len(episode_rewards), np.mean(episode_rewards)))

运行结果：

平均回合奖励 = -9390.0 / 100 = -93.9

A3C

如果还想更快一点呢？
那就要开多线程了。
最后一种方法，Asynchronous Advantage Actor-Critic，A3C。Asynchronous的意思是异步。
如图所示

有一个Global Network和多个Worker。
首先，初始化Global Network的参数$\theta$，每个Worker都从Global Network拷贝一份$\theta$，然后开始训练，得到$\nabla \theta$，再把$\nabla \theta$传回给Global Netword，Global Network更新$\theta$，$\theta \leftarrow \theta + \eta \nabla \theta$。然后Worker再拷贝一份新的$\theta$，每个Worker都这么做。

就像我们平时编程中的多线程。比如，有一个线程，要做10件事情，原本要一件一件做。现在，我们把这个线程看作主线程，然后我们开10个子线程，让子线程去做，子线程完成之后，把结果返回给主线程。

或者，我们直接举生活中的例子，比如你在工作中，有10项任务，本来你要一件一件做；但是，现在你是领导了，你把这10项任务分给你手下的10个人去做，他们完成之后，把结果汇报给你。

这就是A3C。