这一章,我们讨论一个全新的数据结构,图。
图的特点
首先,什么是图,图都有什么特点?
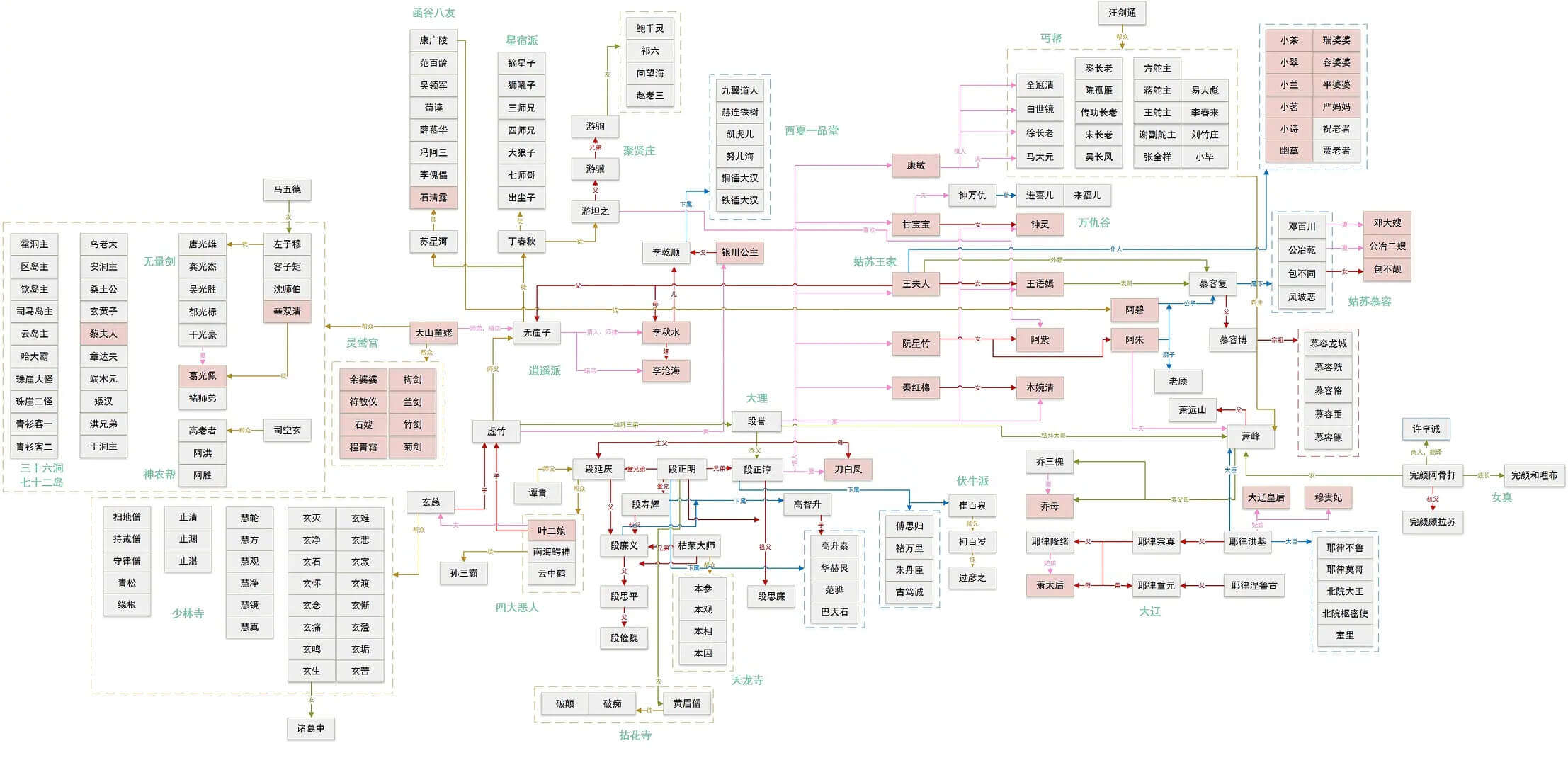
金庸先生有一部小说《天龙八部》,"天龙八部"这个名字出自佛经,意思是芸芸众生。所以,这部小说的一个特点就是人多,而且关系复杂。比如,这是《天龙八部》的人物关系图:
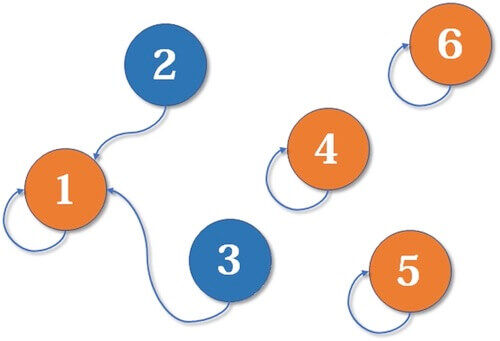
上面的图什么特点?
图由点的集合和边的集合组成
边上可能会带有权值
边会有方向
前两个特点,大家都是这么认为的。
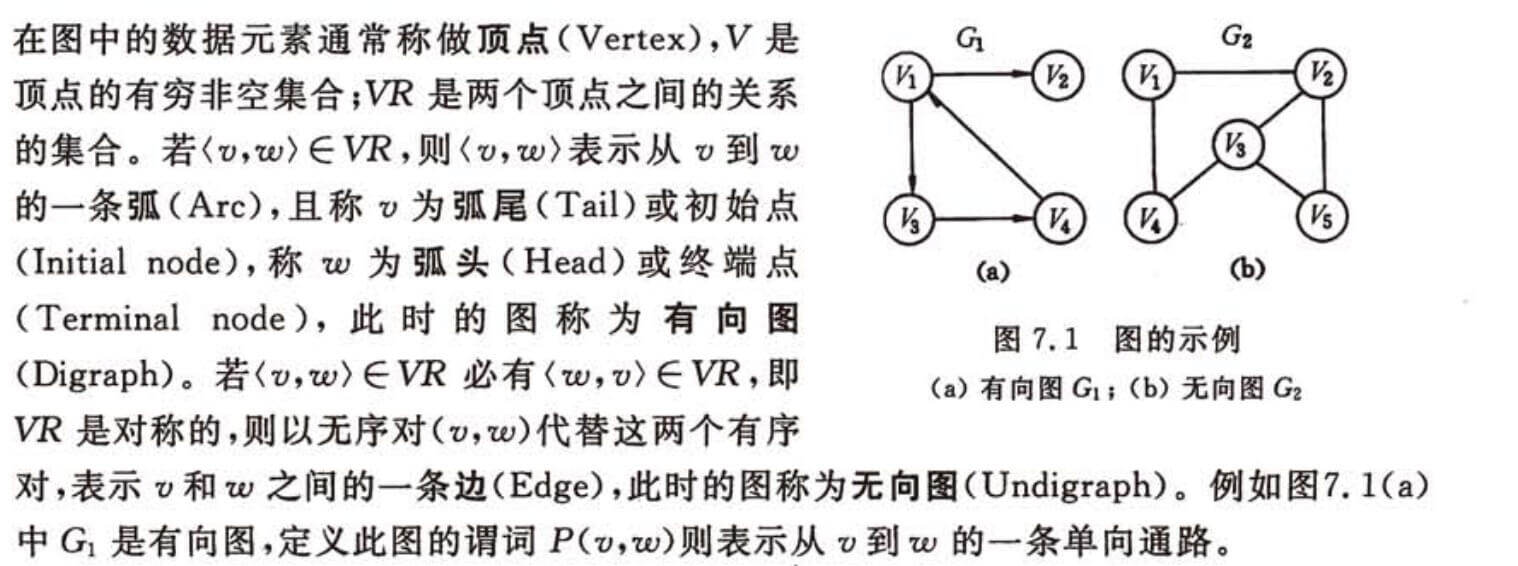
严蔚敏老师是这么说的:< v , w > ∈ V R <v,w> \in \bold{VR} < v , w > ∈ V R < w , v > ∈ V R <w,v> \in \bold{VR} < w , v > ∈ V R V R \bold{VR} V R ( v , w ) (v,w) ( v , w ) v v v w w w
你们看!用无序对代替两个有序对,那么我们也可以不代替咯,就用两个有序对表示一个无序对。 即:我们也可以用两个方向相反的有向边代替一个无向边。
图的表示
那么,图怎么表示呢?
邻接表法
我们讨论的第一个表示图的方法是邻接表法。
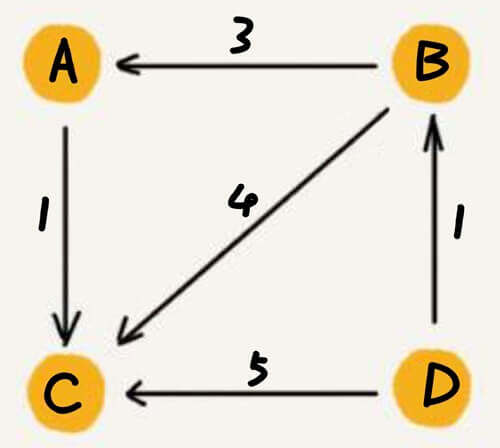
那么,对于权重怎么办呢?那我们这样。
邻接表
A
(C,1)
B
(A,3),(C,4)
C
D
(B,1),(C,5)
这就是邻接表法。
邻接矩阵法
我们讨论的第二种方法是邻接矩阵法。∞ \infty ∞
A
B
C
D
A 0 0 0 ∞ \infty ∞ 1 1 1 ∞ \infty ∞
B 3 3 3 0 0 0 4 4 4 ∞ \infty ∞
C ∞ \infty ∞ ∞ \infty ∞ 0 0 0 ∞ \infty ∞
D ∞ \infty ∞ 1 1 1 5 5 5 0 0 0
这就是邻接矩阵法
Node-Edge-Graph
那么?还有没有第三种方法呢?
[ 3 1 4 1 5 9 2 6 5 ] \left[
\begin{matrix}
3 & 1 & 4 \\
1 & 5 & 9 \\
2 & 6 & 5 \\
\end{matrix}
\right]
⎣ ⎢ ⎡ 3 1 2 1 5 6 4 9 5 ⎦ ⎥ ⎤
这里每一行的第一个数字表示权重,第二个数字表示from,第三个数字表示to。
我们只写一个标准的,剩下的用转接口。Node-Edge-Graph。
Node
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 package ch10;import java.util.ArrayList;public class Node public Integer id; public Integer in; public Integer out; public ArrayList<Node> nexts; public ArrayList<Edge> edges; public Node (Integer id) this .id = id; in = 0 ; out = 0 ; nexts = new ArrayList<>(); edges = new ArrayList<>(); } @Override public String toString () return "Node{" + "id=" + id + ", in=" + in + ", out=" + out + '}' ; } }
示例代码:
1 2 3 4 5 6 7 8 9 10 class Node : def __init__ (self, v) : self.id = v self.in_size = 0 self.out_size = 0 self.nexts = [] self.edges = [] def __str__ (self) : return "Node{" + "id=" + str(self.id) + ", in_size =" + str(self.in_size) + ", out_size =" + str(self.out_size) + "}"
Edge
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 package ch10;public class Edge public Integer weight; public Node from; public Node to; public Edge (Integer weight,Node from,Node to) this .weight = weight; this .from = from; this .to = to; } @Override public String toString () return "Edge{" + "weight=" + weight + ", from=" + from.id + ", to=" + to.id + '}' ; } }
示例代码:
1 2 3 4 5 6 7 8 class Edge : def __init__ (self, w, f, t) : self.weight = w self.from_node = f self.to_node = t def __str__ (self) : return "Edge{" + "weight=" + str(self.weight) + ", from_node=" + str(self.from_node.id) + ", to=" + str(self.to_node.id) + "}"
Graph
图是由点和集合和边的集合所组成的。
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 package ch10;import java.util.HashMap;import java.util.HashSet;public class Graph public HashMap<Integer,Node> nodes; public HashSet<Edge> edges; public Graph () nodes = new HashMap<>(); edges = new HashSet<>(); } }
示例代码:
1 2 3 4 class Graph : def __init__ (self) : self.nodes = dict() self.edges = set()
如此,我们图的结构就定义好了。之后,如果我们收到了各种奇奇怪怪的图表示方法,都可以转换成这种的。比如就以我们刚刚说的矩阵为例,每一行的第一个数字表示权重,第二个数字表示from,第三个数字表示to。
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 package ch10;public class Converter public static Graph FromMatrixToGraph (Integer[][] matrix) Graph graph = new Graph(); for (int i = 0 ; i < matrix.length; i++) { Integer weight = matrix[i][0 ]; Integer fromId = matrix[i][1 ]; Integer toId = matrix[i][2 ]; if (!graph.nodes.containsKey(fromId)){ Node node = new Node(fromId); graph.nodes.put(fromId,node); } if (!graph.nodes.containsKey(toId)){ Node node = new Node(toId); graph.nodes.put(toId,node); } Node fromNode = graph.nodes.get(fromId); Node toNode = graph.nodes.get(toId); Edge edge = new Edge(weight,fromNode,toNode); fromNode.out++; toNode.in++; fromNode.nexts.add(toNode); fromNode.edges.add(edge); graph.edges.add(edge); } return graph; } public static void main (String[] args) Integer[][] m = { {1 ,1 ,2 },{2 ,1 ,3 },{3 ,2 ,3 } }; Graph g = FromMatrixToGraph(m); System.out.println(g.nodes); System.out.println(g.edges); } }
运行结果:
1 2 {1=Node{id=1, in=0, out=2}, 2=Node{id=2, in=1, out=1}, 3=Node{id=3, in=2, out=0}} [Edge{weight=1, from=1, to=2}, Edge{weight=3, from=2, to=3}, Edge{weight=2, from=1, to=3}]
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 from Node_Edge_Graph import *def from_matrix_to_graph (matrix) : graph = Graph() for i in range(0 , len(matrix)): weight = matrix[i][0 ] from_id = matrix[i][1 ] to_id = matrix[i][2 ] if from_id not in graph.nodes.keys(): node = Node(from_id) graph.nodes[from_id] = node if to_id not in graph.nodes.keys(): node = Node(to_id) graph.nodes[to_id] = node from_node = graph.nodes.get(from_id) to_node = graph.nodes.get(to_id) edge = Edge(weight, from_node, to_node) from_node.out_size = from_node.out_size + 1 to_node.in_size = to_node.in_size + 1 from_node.nexts.append(to_node) from_node.edges.append(edge) graph.edges.add(edge) return graph if __name__ == '__main__' : m = [[1 , 1 , 2 ], [2 , 1 , 3 ], [3 , 2 , 3 ]] g = from_matrix_to_graph(m) for n in g.nodes: print(g.nodes.get(n)) for e in g.edges: print(e)
运行结果:
1 2 3 4 5 6 Node{id=1, in_size =0, out_size =2} Node{id=2, in_size =1, out_size =1} Node{id=3, in_size =2, out_size =0} Edge{weight=1, from_node=1, to=2} Edge{weight=2, from_node=1, to=3} Edge{weight=3, from_node=2, to=3}
在讨论了图之后,我们开始讨论图的各种算法。而图作为一个综合的数据结构,在接下来,我们会重新见到我们之前讨论的各种数据结构在图算法中的应用。
图的遍历
我们讨论的第一个算法是图的遍历。
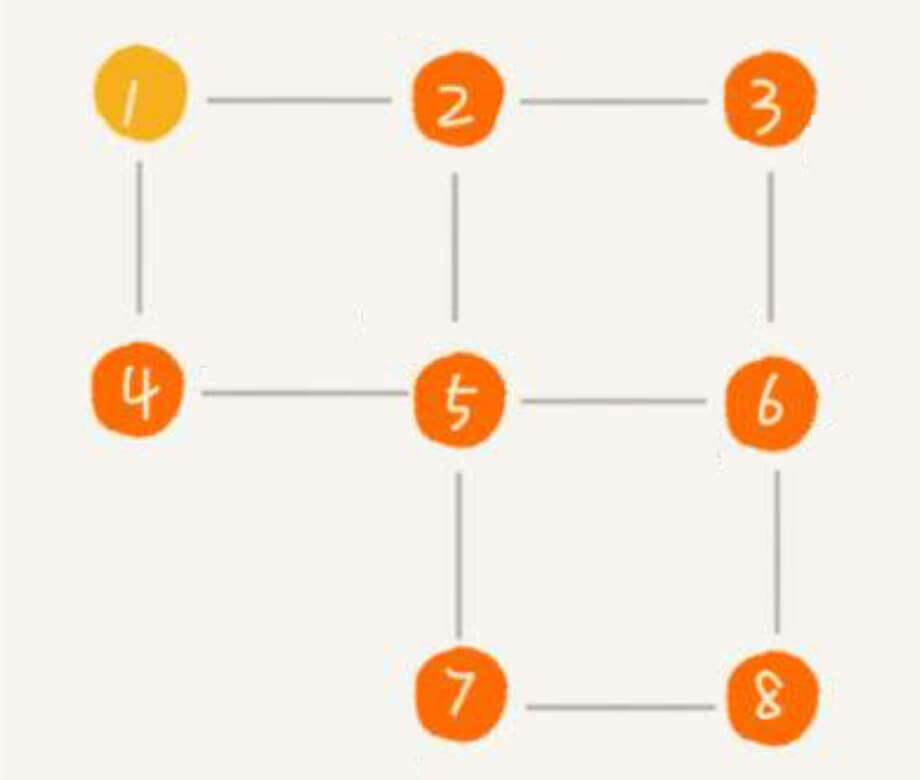
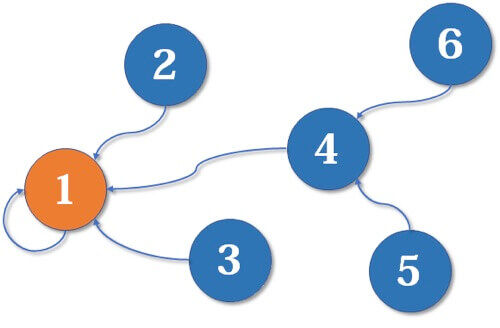
我们以这张无向图为例。
深度优先
对于深度优先:
从1出发,可以遍历2、4,比如2。
从2出发,可以遍历3、5,比如3。
从3出发,可以遍历6。
从6出发,可以遍历5、8,比如5。
从5出发,可以遍历4。
从4出发,回到5。
从5出发,遍历7。
从7出发,遍历8。
即:1、2、3、6、5、4、7、8
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 package ch10;import java.util.HashSet;import java.util.Stack;public class DFS public static HashSet<Node> dfs (Node node) if (null == node){ return null ; } Stack<Node> stack = new Stack<>(); HashSet<Node> set = new HashSet<>(); stack.add(node); set.add(node); System.out.println(node); while (!stack.empty()){ Node cur = stack.pop(); for (Node iter: cur.nexts){ if (!set.contains(iter)) { stack.add(cur); stack.add(iter); set.add(iter); System.out.println(iter); break ; } } } return set; } public static void main (String[] args) Integer[][] m = { {null ,1 ,2 },{null ,2 ,1 }, {null ,2 ,3 },{null ,3 ,2 }, {null ,1 ,4 },{null ,4 ,1 }, {null ,2 ,5 },{null ,5 ,2 }, {null ,3 ,6 },{null ,6 ,3 }, {null ,4 ,5 },{null ,5 ,4 }, {null ,5 ,6 },{null ,6 ,5 }, {null ,5 ,7 },{null ,7 ,5 }, {null ,6 ,8 },{null ,8 ,6 }, {null ,7 ,8 },{null ,8 ,7 } }; Graph g = Converter.FromMatrixToGraph(m); HashSet<Node> set = dfs(g.nodes.get(1 )); System.out.println(set); } }
运行结果:
1 2 3 4 5 6 7 8 9 Node{id=1, in=2, out=2} Node{id=2, in=3, out=3} Node{id=3, in=2, out=2} Node{id=6, in=3, out=3} Node{id=5, in=4, out=4} Node{id=4, in=2, out=2} Node{id=7, in=2, out=2} Node{id=8, in=2, out=2} [Node{id=3, in=2, out=2}, Node{id=7, in=2, out=2}, Node{id=8, in=2, out=2}, Node{id=5, in=4, out=4}, Node{id=6, in=3, out=3}, Node{id=4, in=2, out=2}, Node{id=2, in=3, out=3}, Node{id=1, in=2, out=2}]
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 from ch10 import Converterdef dfs (node) : if node is None : return None stack = [] s = set() stack.append(node) s.add(node) print(node) while len(stack) > 0 : cur = stack.pop() for iter in cur.nexts: if iter not in s: stack.append(cur) stack.append(iter) s.add(iter) print(iter) break return s if __name__ == '__main__' : m = [[None , 1 , 2 ], [None , 2 , 1 ], [None , 2 , 3 ], [None , 3 , 2 ], [None , 1 , 4 ], [None , 4 , 1 ], [None , 2 , 5 ], [None , 5 , 2 ], [None , 3 , 6 ], [None , 6 , 3 ], [None , 4 , 5 ], [None , 5 , 4 ], [None , 5 , 6 ], [None , 6 , 5 ], [None , 5 , 7 ], [None , 7 , 5 ], [None , 6 , 8 ], [None , 8 , 6 ], [None , 7 , 8 ], [None , 8 , 7 ]] g = Converter.from_matrix_to_graph(m) s = dfs(g.nodes.get(1 )) print('-' * 20 ) for iter in s: print(iter)
运行结果:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 Node{id=1, in_size =2, out_size =2} Node{id=2, in_size =3, out_size =3} Node{id=3, in_size =2, out_size =2} Node{id=6, in_size =3, out_size =3} Node{id=5, in_size =4, out_size =4} Node{id=4, in_size =2, out_size =2} Node{id=7, in_size =2, out_size =2} Node{id=8, in_size =2, out_size =2} -------------------- Node{id=5, in_size =4, out_size =4} Node{id=7, in_size =2, out_size =2} Node{id=3, in_size =2, out_size =2} Node{id=2, in_size =3, out_size =3} Node{id=4, in_size =2, out_size =2} Node{id=1, in_size =2, out_size =2} Node{id=6, in_size =3, out_size =3} Node{id=8, in_size =2, out_size =2}
广度优先
对于广度优先:
从1出发,依次遍历2、4。
从2出发,依次遍历3、5。
从4出发,没有遍历。
从3出发,遍历6。
从5出发,遍历7。
从7出发,遍历8。
即:1、2、4、3、5、6、7、8。
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 package ch10;import java.util.HashSet;import java.util.LinkedList;import java.util.Queue;public class BFS public static HashSet<Node> bfs (Node node) if (null == node){ return null ; } Queue<Node> queue = new LinkedList<>(); HashSet<Node> set = new HashSet<>(); queue.add(node); set.add(node); System.out.println(node); while (!queue.isEmpty()){ Node cur = queue.poll(); for (Node iter : cur.nexts){ if (!set.contains(iter)){ queue.add(iter); set.add(iter); System.out.println(iter); } } } return set; } public static void main (String[] args) Integer[][] m = { {null ,1 ,2 },{null ,2 ,1 }, {null ,2 ,3 },{null ,3 ,2 }, {null ,1 ,4 },{null ,4 ,1 }, {null ,2 ,5 },{null ,5 ,2 }, {null ,3 ,6 },{null ,6 ,3 }, {null ,4 ,5 },{null ,5 ,4 }, {null ,5 ,6 },{null ,6 ,5 }, {null ,5 ,7 },{null ,7 ,5 }, {null ,6 ,8 },{null ,8 ,6 }, {null ,7 ,8 },{null ,8 ,7 } }; Graph g = Converter.FromMatrixToGraph(m); HashSet<Node> set = bfs(g.nodes.get(1 )); System.out.println(set); } }
运行结果:
1 2 3 4 5 6 7 8 9 Node{id=1, in=2, out=2} Node{id=2, in=3, out=3} Node{id=4, in=2, out=2} Node{id=3, in=2, out=2} Node{id=5, in=4, out=4} Node{id=6, in=3, out=3} Node{id=7, in=2, out=2} Node{id=8, in=2, out=2} [Node{id=4, in=2, out=2}, Node{id=7, in=2, out=2}, Node{id=8, in=2, out=2}, Node{id=5, in=4, out=4}, Node{id=3, in=2, out=2}, Node{id=6, in=3, out=3}, Node{id=2, in=3, out=3}, Node{id=1, in=2, out=2}]
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 from queue import Queuefrom ch10 import Converterdef bfs (node) : if node is None : return None q = Queue() s = set() q.put(node) s.add(node) print(node) while not q.empty(): cur = q.get() for iter in cur.nexts: if iter not in s: q.put(iter) s.add(iter) print(iter) return s if __name__ == '__main__' : m = [[None , 1 , 2 ], [None , 2 , 1 ], [None , 2 , 3 ], [None , 3 , 2 ], [None , 1 , 4 ], [None , 4 , 1 ], [None , 2 , 5 ], [None , 5 , 2 ], [None , 3 , 6 ], [None , 6 , 3 ], [None , 4 , 5 ], [None , 5 , 4 ], [None , 5 , 6 ], [None , 6 , 5 ], [None , 5 , 7 ], [None , 7 , 5 ], [None , 6 , 8 ], [None , 8 , 6 ], [None , 7 , 8 ], [None , 8 , 7 ]] g = Converter.from_matrix_to_graph(m) s = bfs(g.nodes.get(1 )) print('-' * 20 ) for iter in s: print(iter)
运行结果:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 Node{id=1, in_size =2, out_size =2} Node{id=2, in_size =3, out_size =3} Node{id=4, in_size =2, out_size =2} Node{id=3, in_size =2, out_size =2} Node{id=5, in_size =4, out_size =4} Node{id=6, in_size =3, out_size =3} Node{id=7, in_size =2, out_size =2} Node{id=8, in_size =2, out_size =2} -------------------- Node{id=4, in_size =2, out_size =2} Node{id=8, in_size =2, out_size =2} Node{id=6, in_size =3, out_size =3} Node{id=7, in_size =2, out_size =2} Node{id=2, in_size =3, out_size =3} Node{id=3, in_size =2, out_size =2} Node{id=5, in_size =4, out_size =4} Node{id=1, in_size =2, out_size =2}
拓扑排序
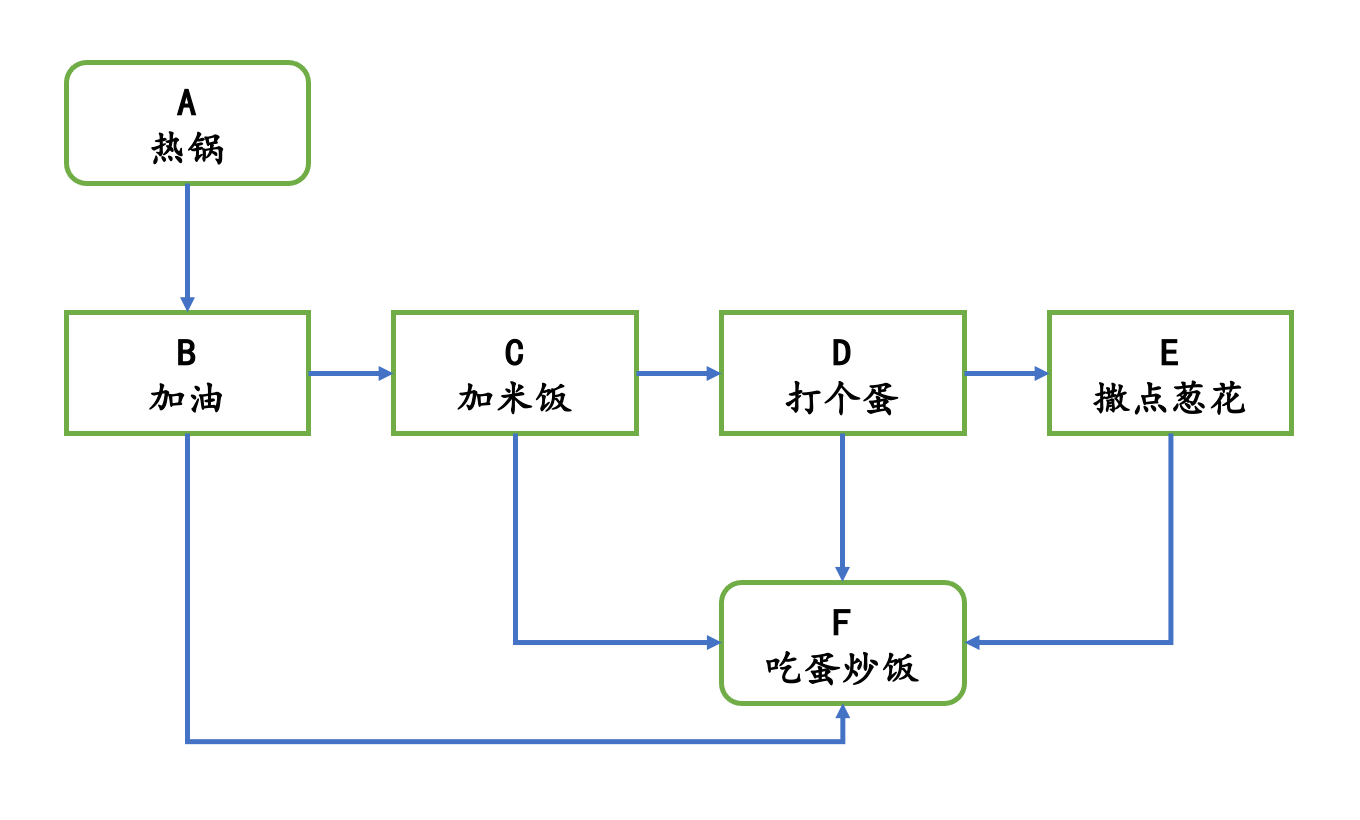
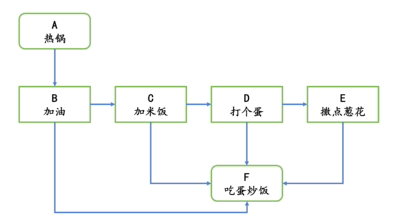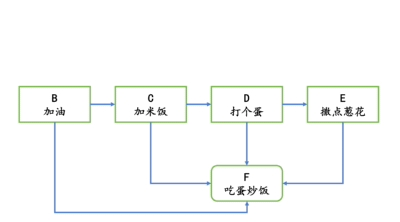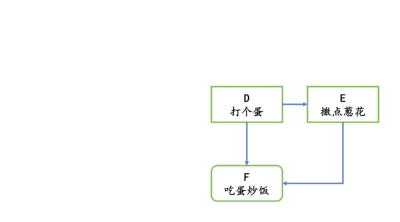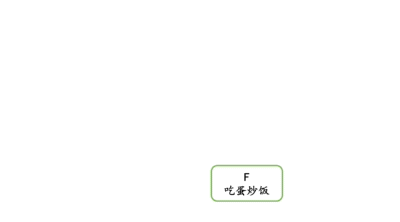
在第二章,我们讨论的第一个数据结构数组之前,还专门讨论了算法和数据结构的关系。当时我们以蛋炒饭为例。我们说热锅、倒油、打蛋等,这些就是算法;而米饭、鸡蛋、油、盐就是数据结构。
即,加油依赖于热锅,加米饭依赖于加油,打个蛋依赖于加米饭,撒点葱花依赖于打个蛋,最后吃蛋炒饭依赖于加油、加米饭、打个蛋和撒点葱花。
这就是拓扑排序。
我们用1、2、3、4、5、6,分别代表蛋炒饭的热锅、加油、加米饭、打个蛋、撒点葱花、吃蛋炒饭。以此为例,实现拓扑排序。
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 package ch10;import java.util.ArrayList;import java.util.HashMap;import java.util.LinkedList;import java.util.Queue;public class TopologySort public static ArrayList<Node> topologySort (Graph graph) ArrayList<Node> rnt = new ArrayList<>(); HashMap<Node,Integer> inMap = new HashMap<>(); Queue<Node> zeroInQueue = new LinkedList<>(); for (Node iter: graph.nodes.values()) { inMap.put(iter,iter.in); if (iter.in == 0 ){ zeroInQueue.add(iter); } } while (!zeroInQueue.isEmpty()){ Node cur = zeroInQueue.poll(); rnt.add(cur); for (Node iter: cur.nexts) { inMap.put(iter,inMap.get(iter) - 1 ); if (inMap.get(iter) == 0 ){ zeroInQueue.add(iter); } } } return rnt; } public static void main (String[] args) Integer[][] m = { {null ,1 ,2 }, {null ,2 ,3 }, {null ,3 ,4 }, {null ,4 ,5 }, {null ,2 ,6 }, {null ,3 ,6 }, {null ,4 ,6 }, {null ,5 ,6 } }; Graph g = Converter.FromMatrixToGraph(m); ArrayList<Node> list = topologySort(g); System.out.println(list); } }
运行结果:
1 [Node{id=1, in=0, out=1}, Node{id=2, in=1, out=2}, Node{id=3, in=1, out=2}, Node{id=4, in=1, out=2}, Node{id=5, in=1, out=1}, Node{id=6, in=4, out=0}]
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 from queue import Queuefrom ch10 import Converterdef topologySort (graph) : rnt = [] in_dict = dict() zero_in_queue = Queue() for iter_key in graph.nodes: iter = graph.nodes.get(iter_key) in_dict[iter] = iter.in_size if iter.in_size == 0 : zero_in_queue.put(iter) while not zero_in_queue.empty(): cur = zero_in_queue.get() rnt.append(cur) for iter in cur.nexts: in_dict[iter] = in_dict.get(iter) - 1 if in_dict.get(iter) == 0 : zero_in_queue.put(iter) return rnt if __name__ == '__main__' : m = [[None , 1 , 2 ], [None , 2 , 3 ], [None , 3 , 4 ], [None , 4 , 5 ], [None , 2 , 6 ], [None , 3 , 6 ], [None , 4 , 6 ], [None , 5 , 6 ]] g = Converter.from_matrix_to_graph(m) l = topologySort(g) for iter in l: print(iter)
运行结果:
1 2 3 4 5 6 Node{id=1, in_size =0, out_size =1} Node{id=2, in_size =1, out_size =2} Node{id=3, in_size =1, out_size =2} Node{id=4, in_size =1, out_size =2} Node{id=5, in_size =1, out_size =1} Node{id=6, in_size =4, out_size =0}
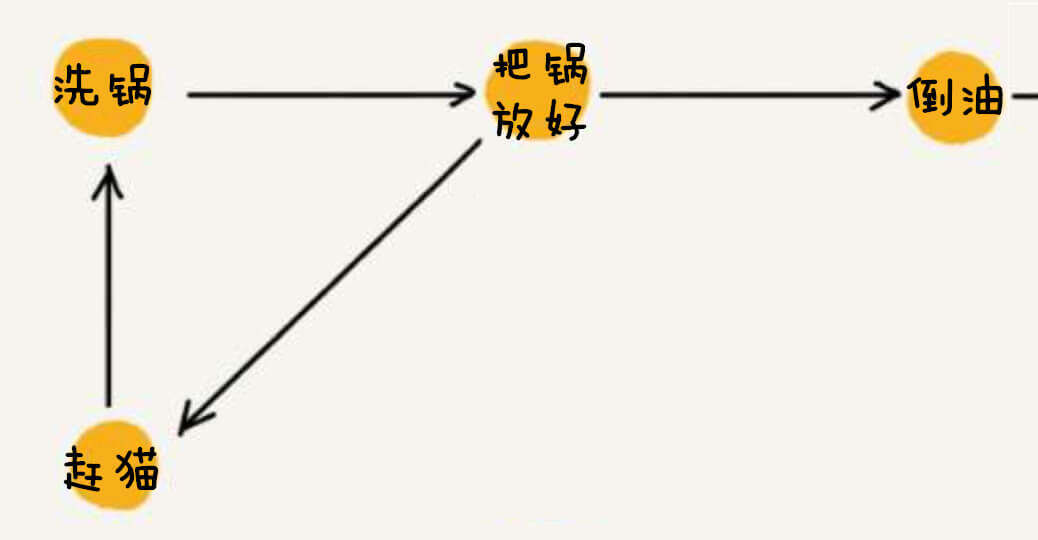
特别的,如果我们养了猫呢?而且这猫还特别喜欢在锅里。
那么蛋炒饭的工序就是:首先,把猫从锅里赶出去,洗锅,把锅放好,再把猫从锅里赶出去,再洗锅,再把把锅放好,第三次把猫从锅里赶出去,第三次洗锅······,点个外卖。
即,出现了环,无法进行拓扑排序。
拓扑排序在计算机方面最常见的一个应用就是编译过程,而出现了环就无法进行拓扑排序,任务无法进行。这也是我们写代码不要循环依赖的原因。
并查集
在电影《我不是潘金莲》中有一幕特别有意思,就是影片开头李雪莲第一次见王公道的时候。
王公道和陈阿大是亲戚陈阿大和陈阿大他老婆的妹妹是亲戚陈阿大他老婆的的妹妹和陈阿大他老婆的妹妹的婆家是亲戚陈阿大他老婆的妹妹的婆家和陈阿大他老婆的妹妹的婆家的叔伯侄子是亲戚······
总之,最后,李雪莲和王公道是亲戚。
过程
那么,在上述过程中,李雪莲主要做的事情有:
合并(Union):把两个不相交的集合合并为一个集合。
查询(Find):查询两个元素是否在同一个集合中。
合并,查找,这也就是并查集名字的由来,而这两个方法就是并查集的核心方法。
我们举个例子。1、2、3、4、5、6,他们每个人都是独立的个体,一个人就是一个家族,这个家族的代表就是他们自己。
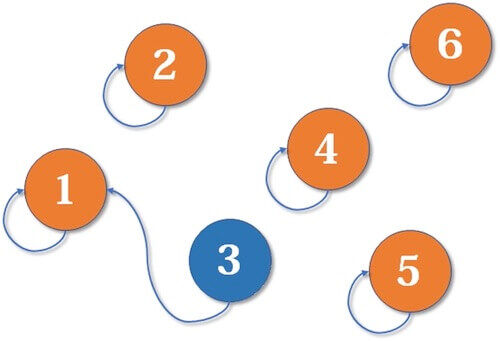
然后,我们发现,原来1和3是亲戚,那么1和3合并成一个新的家族之后,谁是代表呢?1是代表。
接下来,我们发现2和3也是亲戚,那么,又可以合并成一个新的家族了。这时候谁是代表呢?大家族的代表继续作为代表 。
直到最后,李雪莲和王公道就是亲戚了。
实现
过程就是这么一个过程,在具体实现中,我们还可以做一些简单的优化,大家特别注意我们的find_top()。find_top()的效率。
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 package ch10;import java.util.ArrayList;import java.util.HashMap;import java.util.List;import java.util.Stack;public class UnionFindExample public static class Node <V > V value; public Node (V v) value = v; } @Override public String toString () return "Node{" + "value=" + value + '}' ; } } public static class UnionFind <V > public HashMap<V, Node<V>> nodes; public HashMap<Node<V>, Node<V>> ups; public HashMap<Node<V>, Integer> sizeMap; public UnionFind (List<V> values) nodes = new HashMap<>(); ups = new HashMap<>(); sizeMap = new HashMap<>(); for (V cur : values) { Node<V> node = new Node<>(cur); nodes.put(cur, node); ups.put(node, node); sizeMap.put(node, 1 ); } } public Node<V> findTop (Node<V> cur) Stack<Node<V>> path = new Stack<>(); while (cur != ups.get(cur)) { path.push(cur); cur = ups.get(cur); } while (!path.isEmpty()) { ups.put(path.pop(), cur); } return cur; } public boolean isSameSet (V a, V b) return findTop(nodes.get(a)) == findTop(nodes.get(b)); } public void union (V a, V b) Node<V> aHead = findTop(nodes.get(a)); Node<V> bHead = findTop(nodes.get(b)); if (aHead != bHead) { int aSetSize = sizeMap.get(aHead); int bSetSize = sizeMap.get(bHead); if (aSetSize >= bSetSize){ ups.put(bHead,aHead); sizeMap.put(aHead,aSetSize + bSetSize); sizeMap.remove(bHead); }else { ups.put(aHead,bHead); sizeMap.put(bHead,aSetSize + bSetSize); sizeMap.remove(aHead); } } } } public static void main (String[] args) List<Integer> l = new ArrayList<>(); l.add(1 ); l.add(2 ); l.add(3 ); l.add(4 ); l.add(5 ); l.add(6 ); UnionFind<Integer> unionFind = new UnionFind<Integer>(l); System.out.println(unionFind.nodes); System.out.println(unionFind.ups); System.out.println(unionFind.sizeMap); System.out.println(unionFind.isSameSet(1 ,2 )); unionFind.union(1 ,2 ); System.out.println(unionFind.isSameSet(1 ,2 )); System.out.println(unionFind.nodes); System.out.println(unionFind.ups); System.out.println(unionFind.sizeMap); } }
运行结果:
1 2 3 4 5 6 7 8 {1=Node{value=1}, 2=Node{value=2}, 3=Node{value=3}, 4=Node{value=4}, 5=Node{value=5}, 6=Node{value=6}} {Node{value=1}=Node{value=1}, Node{value=4}=Node{value=4}, Node{value=5}=Node{value=5}, Node{value=3}=Node{value=3}, Node{value=2}=Node{value=2}, Node{value=6}=Node{value=6}} {Node{value=1}=1, Node{value=4}=1, Node{value=5}=1, Node{value=3}=1, Node{value=2}=1, Node{value=6}=1} false true {1=Node{value=1}, 2=Node{value=2}, 3=Node{value=3}, 4=Node{value=4}, 5=Node{value=5}, 6=Node{value=6}} {Node{value=1}=Node{value=1}, Node{value=4}=Node{value=4}, Node{value=5}=Node{value=5}, Node{value=3}=Node{value=3}, Node{value=2}=Node{value=1}, Node{value=6}=Node{value=6}} {Node{value=1}=2, Node{value=4}=1, Node{value=5}=1, Node{value=3}=1, Node{value=6}=1}
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 class Node : def __init__ (self, v) : self.value = v def __str__ (self) : return str(self.value) class UnionFind : def __init__ (self, values) : self.nodes = dict() self.ups = dict() self.size_map = dict() for iter in values: node = Node(iter) self.nodes[iter] = node self.ups[node] = node self.size_map[node] = 1 def find_top (self, cur) : path = [] while cur is not self.ups.get(cur): path.append(cur) cur = self.ups.get(cur) while len(path) > 0 : self.ups[path.pop()] = cur return cur def is_same_set (self, a, b) : """ 是否是同一个集合 查 :param a: :param b: :return: """ return self.find_top(self.nodes.get(a)) == self.find_top(self.nodes.get(b)) def union (self, a, b) : a_head = self.find_top(self.nodes.get(a)) b_head = self.find_top(self.nodes.get(b)) if a_head is not b_head: a_set_size = self.size_map.get(a_head) b_set_size = self.size_map.get(b_head) if a_set_size >= b_set_size: self.ups[b_head] = a_head self.size_map[a_head] = a_set_size + b_set_size self.size_map.pop(b_head) else : self.ups[a_head] = b_head self.size_map[b_head] = a_set_size + b_set_size self.size_map.pop(a_head) if __name__ == '__main__' : unionFind = UnionFind([1 , 2 , 3 , 4 , 5 , 6 ]) for iter in unionFind.nodes: print(iter, unionFind.nodes.get(iter)) print('-' * 10 ) for iter in unionFind.ups: print(iter, unionFind.ups.get(iter)) print('-' * 10 ) for iter in unionFind.size_map: print(iter, unionFind.size_map.get(iter)) print('-' * 10 ) print(unionFind.is_same_set(1 , 2 )) unionFind.union(1 , 2 ) print(unionFind.is_same_set(1 , 2 )) for iter in unionFind.nodes: print(iter, unionFind.nodes.get(iter)) print('-' * 10 ) for iter in unionFind.ups: print(iter, unionFind.ups.get(iter)) print('-' * 10 ) for iter in unionFind.size_map: print(iter, unionFind.size_map.get(iter))
运行结果:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 1 1 2 2 3 3 4 4 5 5 6 6 ---------- 1 1 2 2 3 3 4 4 5 5 6 6 ---------- 1 1 2 1 3 1 4 1 5 1 6 1 ---------- False True 1 1 2 2 3 3 4 4 5 5 6 6 ---------- 1 1 2 1 3 3 4 4 5 5 6 6 ---------- 1 2 3 1 4 1 5 1 6 1
通过代码,我们可以发现,我们每调用一次find_top()都会把该链路打平,那么find_top()调用的越频繁,复杂度越低。n n n find_top()的调用次数达到或者超过O ( n ) O(n) O ( n ) find_top()的时间复杂度是O ( 1 ) O(1) O ( 1 )
接下来我们就会见识到并查集的作用。
最小生成树
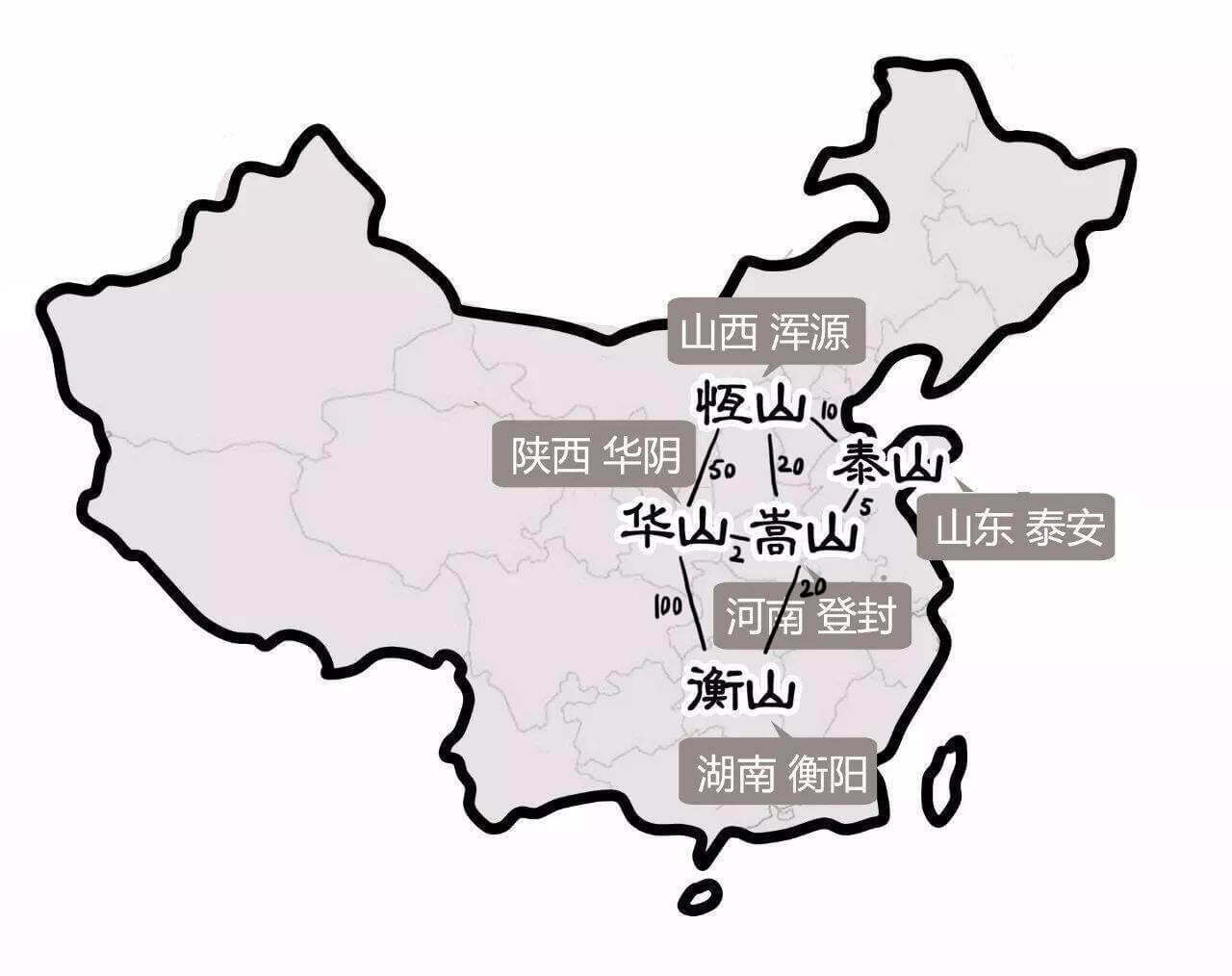
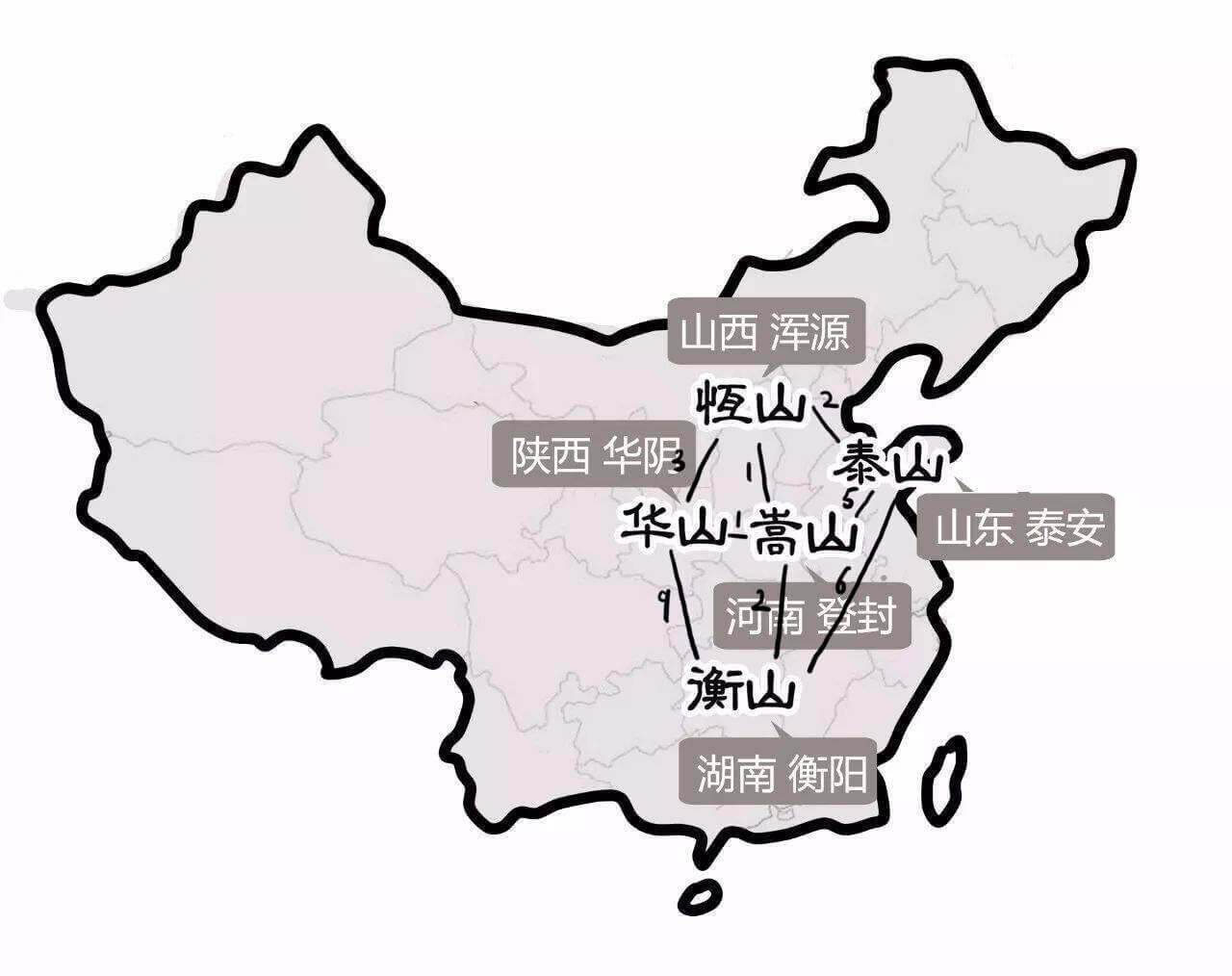
金庸先生还有一部小说《笑傲江湖》。在这部小说中,推动剧情发展的一个主要矛盾是五岳剑派的合并。
如图,是五岳剑派所处的位置,和之间的修路所需要花费的黄金(单位万两)。
这里,我们讨论两种方案:
Kruskal
Prim
Kruskal
过程
首先,我们把所有的路,根据成本从小到大排序。所以,我们有:
路名
From
To
成本
华嵩路
华山
嵩山
2
恒泰路
恒山
泰山
5
嵩泰路
嵩山
泰山
10
嵩恒路
嵩山
恒山
20
嵩衡路
衡山
衡山
20
华恒路
华山
恒山
50
华衡路
华山
衡山
100
我们从成本最小的路开始修,华嵩路,连通集合有:
{ 华山 , 嵩山 } \{\text{华山},\text{嵩山}\}
{ 华山 , 嵩山 }
然后再修恒泰路,恒山和泰山都不在连通集合中,所以这时候连通集合有两个有:
{ 华山 , 嵩山 } , { 恒山 , 泰山 } \{\text{华山},\text{嵩山}\},\{\text{恒山},\text{泰山}\}
{ 华山 , 嵩山 } , { 恒山 , 泰山 }
再修嵩泰路。嵩山和泰山都在连通集合中,但是各自在不同的集合中。所以这条路修。这时候得到的连通集合有
{ 华山 , 嵩山 , 恒山 , 泰山 } \{\text{华山},\text{嵩山},\text{恒山},\text{泰山}\}
{ 华山 , 嵩山 , 恒山 , 泰山 }
那么嵩恒路修不修,不修。因为嵩山和恒山在同一个连通集合中。
{ 华山 , 嵩山 , 恒山 , 泰山 , 衡山 } \{\text{华山},\text{嵩山},\text{恒山},\text{泰山},\text{衡山}\}
{ 华山 , 嵩山 , 恒山 , 泰山 , 衡山 }
需要修的路有
{ 华嵩路 , 恒泰路 , 嵩泰路 , 嵩衡路 } \{\text{华嵩路},\text{恒泰路},\text{嵩泰路},\text{嵩衡路}\}
{ 华嵩路 , 恒泰路 , 嵩泰路 , 嵩衡路 }
这个算法叫做Kruskal。
特点如下:
每次都从权值最小的边开始考虑
当前考虑的边要么进入最小生成树的集合,要么丢弃。
如果当前考虑的边进入最小生成树的集合中不会形成环,就要当前考虑的边。
如果当前考虑的边计入最小生成树的集合中会形成环,就不要当前考虑的边。
考察完所有边之后,最小生成树的集合也得到了。
实现
在具体实现中,我们就会见到之前讨论的并查集的作用了。把所有的边,按照权重从小到大排序,做并查集。
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 package ch10;import java.util.*;public class Kruskal public static class UnionFind private HashMap<Node, Node> upsMap; private HashMap<Node, Integer> sizeMap; public UnionFind (Collection<Node> nodes) upsMap = new HashMap<Node, Node>(); sizeMap = new HashMap<Node, Integer>(); for (Node node : nodes) { upsMap.put(node, node); sizeMap.put(node, 1 ); } } private Node findTop (Node n) Stack<Node> path = new Stack<>(); while (n != upsMap.get(n)) { path.add(n); n = upsMap.get(n); } while (!path.isEmpty()) { upsMap.put(path.pop(), n); } return n; } public boolean isSameSet (Node a, Node b) return findTop(a) == findTop(b); } public void union (Node a, Node b) if (a == null || b == null ) { return ; } Node aDai = findTop(a); Node bDai = findTop(b); if (aDai != bDai) { int aSetSize = sizeMap.get(aDai); int bSetSize = sizeMap.get(bDai); if (aSetSize <= bSetSize) { upsMap.put(aDai, bDai); sizeMap.put(bDai, aSetSize + bSetSize); sizeMap.remove(aDai); } else { upsMap.put(bDai, aDai); sizeMap.put(aDai, aSetSize + bSetSize); sizeMap.remove(bDai); } } } } public static class EdgeComparator implements Comparator <Edge > @Override public int compare (Edge o1, Edge o2) return o1.weight - o2.weight; } } public static Set<Edge> kruskal (Graph graph) UnionFind unionFind = new UnionFind(graph.nodes.values()); PriorityQueue<Edge> priorityQueue = new PriorityQueue<>(new EdgeComparator()); for (Edge edge : graph.edges) { priorityQueue.add(edge); } Set<Edge> result = new HashSet<>(); while (!priorityQueue.isEmpty()) { Edge edge = priorityQueue.poll(); if (!unionFind.isSameSet(edge.from, edge.to)) { result.add(edge); unionFind.union(edge.from, edge.to); } } return result; } public static void main (String[] args) Integer[][] m = { {50 , 1 , 2 }, {50 , 2 , 1 }, {20 , 1 , 3 }, {20 , 3 , 1 }, {10 , 1 , 4 }, {10 , 4 , 1 }, {2 , 2 , 3 }, {2 , 3 , 2 }, {5 , 3 , 4 }, {5 , 4 , 3 }, {100 , 2 , 5 }, {100 , 5 , 2 }, {20 , 4 , 5 }, {20 , 5 , 4 }}; Graph g = Converter.FromMatrixToGraph(m); System.out.println(Kruskal.kruskal(g)); } }
运行结果:
1 [Edge{weight=2, from=3, to=2}, Edge{weight=10, from=1, to=4}, Edge{weight=20, from=4, to=5}, Edge{weight=5, from=4, to=3}]
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 import heapqfrom ch10 import Converterclass UnionFind : def __init__ (self, nodes) : self.ups_map = dict() self.size_map = dict() for iter in nodes: node = nodes[iter] self.ups_map[node] = node self.size_map[node] = 1 def find_top (self, n) : path = [] while n is not self.ups_map[n]: path.append(n) n = self.ups_map[n] while len(path) > 0 : self.ups_map[path.pop()] = n return n def is_same_set (self, a, b) : return self.find_top(a) == self.find_top(b) def union (self, a, b) : if a is None and b is None : return a_dai = self.find_top(a) b_dai = self.find_top(b) if a_dai != b_dai: a_set_size = self.size_map[a_dai] b_set_size = self.size_map[b_dai] if a_set_size <= b_set_size: self.ups_map[a_dai] = b_dai self.size_map[b_dai] = a_set_size + b_set_size self.size_map.pop(a_dai) else : self.ups_map[b_dai] = a_dai self.size_map[a_dai] = a_set_size + b_set_size self.size_map.pop(b_dai) def kruskal (graph) : unionFind = UnionFind(graph.nodes) p = [] for edge in graph.edges: heapq.heappush(p, edge) result = set() while len(p) > 0 : edge = heapq.heappop(p) if not unionFind.is_same_set(edge.from_node, edge.to_node): result.add(edge) unionFind.union(edge.from_node, edge.to_node) return result if __name__ == '__main__' : m = [[50 , 1 , 2 ], [50 , 2 , 1 ], [20 , 1 , 3 ], [20 , 3 , 1 ], [10 , 1 , 4 ], [10 , 4 , 1 ], [2 , 2 , 3 ], [2 , 3 , 2 ], [5 , 3 , 4 ], [5 , 4 , 3 ], [100 , 2 , 5 ], [100 , 5 , 2 ], [20 , 4 , 5 ], [20 , 5 , 4 ]] g = Converter.from_matrix_to_graph(m) r = kruskal(g) for iter in r: print(iter)
运行结果:
1 2 3 4 Edge{weight=2, from_node=3, to=2} Edge{weight=10, from_node=4, to=1} Edge{weight=5, from_node=4, to=3} Edge{weight=20, from_node=5, to=4}
Prim
过程
刚刚我们的修路方案是先修成本最小的路,这样先联通的华山和嵩山,但是其他门派不答应了,为了掌握修路的控制权,纷纷表示要先修自己家门口的路。
{ 泰山 } \{\text{泰山}\}
{ 泰山 }
在泰山的可控范围内,可以修的路有:
{ 恒泰路 , 嵩泰路 } \{\text{恒泰路},\text{嵩泰路}\}
{ 恒泰路 , 嵩泰路 }
我们选择最便宜的一条路:嵩泰路。
{ 泰山 , 嵩山 } \{\text{泰山},\text{嵩山}\}
{ 泰山 , 嵩山 }
在泰山的可控范围内,可以修的路有:
{ 恒泰路 , 华嵩路 , 嵩恒路 , 嵩衡路 } \{\text{恒泰路},\text{华嵩路},\text{嵩恒路},\text{嵩衡路}\}
{ 恒泰路 , 华嵩路 , 嵩恒路 , 嵩衡路 }
再选择最便宜的一条路:华嵩路。
{ 泰山 , 嵩山 , 华山 } \{\text{泰山},\text{嵩山},\text{华山}\}
{ 泰山 , 嵩山 , 华山 }
在华山的可控范围内,可以修的路有:
{ 恒泰路 , 嵩恒路 , 嵩衡路 , 华恒路 , 嵩衡路 } \{\text{恒泰路},\text{嵩恒路},\text{嵩衡路},\text{华恒路},\text{嵩衡路}\}
{ 恒泰路 , 嵩恒路 , 嵩衡路 , 华恒路 , 嵩衡路 }
如此循环,得到最小生成树。
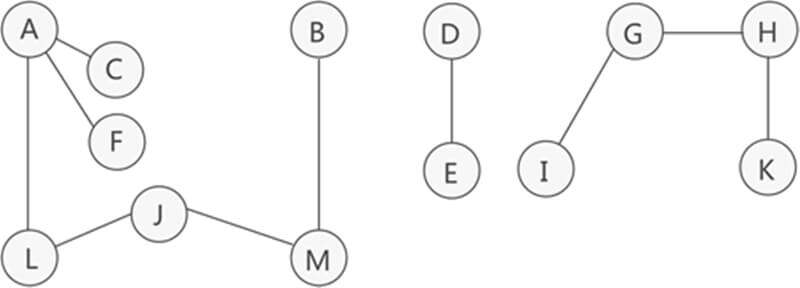
这个算法有没有问题?
假如在图中就存在本来就无法联通的点呢?A,那么D,E,G,H,I,K都无法处理。
实现
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 package ch10;import java.util.Comparator;import java.util.HashSet;import java.util.PriorityQueue;import java.util.Set;public class Prim public static class EdgeComparator implements Comparator <Edge > @Override public int compare (Edge o1, Edge o2) return o1.weight - o2.weight; } } public static Set<Edge> prim (Graph graph) Set<Edge> rnt = new HashSet<>(); PriorityQueue<Edge> priorityQueue = new PriorityQueue<>(new EdgeComparator()); HashSet<Node> nodeSet = new HashSet<>(); Set<Edge> edgeSet = new HashSet<>(); for (Node node : graph.nodes.values()) { if (!nodeSet.contains(node)) { nodeSet.add(node); for (Edge edge : node.edges) { if (!edgeSet.contains(edge)) { edgeSet.add(edge); priorityQueue.add(edge); } } while (!priorityQueue.isEmpty()) { Edge edge = priorityQueue.poll(); Node toNode = edge.to; if (!nodeSet.contains(toNode)) { nodeSet.add(toNode); rnt.add(edge); for (Edge nextEdge : toNode.edges) { if (!edgeSet.contains(nextEdge)) { edgeSet.add(nextEdge); priorityQueue.add(nextEdge); } } } } } } return rnt; } public static void main (String[] args) Integer[][] m = { {50 , 1 , 2 }, {50 , 2 , 1 }, {20 , 1 , 3 }, {20 , 3 , 1 }, {10 , 1 , 4 }, {10 , 4 , 1 }, {2 , 2 , 3 }, {2 , 3 , 2 }, {5 , 3 , 4 }, {5 , 4 , 3 }, {100 , 2 , 5 }, {100 , 5 , 2 }, {20 , 4 , 5 }, {20 , 5 , 4 }}; Graph g = Converter.FromMatrixToGraph(m); System.out.println(Prim.prim(g)); } }
运行结果:
1 [Edge{weight=2, from=3, to=2}, Edge{weight=10, from=1, to=4}, Edge{weight=20, from=4, to=5}, Edge{weight=5, from=4, to=3}]
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 import heapqfrom ch10 import Converterdef prim (graph) : rnt = set() p = [] node_set = set() edge_set = set() for iter in graph.nodes: node = graph.nodes[iter] if node not in node_set: node_set.add(node) for edge in node.edges: if edge not in edge_set: edge_set.add(edge) heapq.heappush(p, edge) while len(p) > 0 : edge = heapq.heappop(p) to_node = edge.to_node if to_node not in node_set: node_set.add(to_node) rnt.add(edge) for next_edge in to_node.edges: if next_edge not in edge_set: edge_set.add(next_edge) heapq.heappush(p, next_edge) return rnt if __name__ == '__main__' : m = [[50 , 1 , 2 ], [50 , 2 , 1 ], [20 , 1 , 3 ], [20 , 3 , 1 ], [10 , 1 , 4 ], [10 , 4 , 1 ], [2 , 2 , 3 ], [2 , 3 , 2 ], [5 , 3 , 4 ], [5 , 4 , 3 ], [100 , 2 , 5 ], [100 , 5 , 2 ], [20 , 4 , 5 ], [20 , 5 , 4 ]] g = Converter.from_matrix_to_graph(m) r = prim(g) for iter in r: print(iter)
运行结果:
1 2 3 4 Edge{weight=5, from_node=4, to=3} Edge{weight=2, from_node=3, to=2} Edge{weight=10, from_node=1, to=4} Edge{weight=20, from_node=4, to=5}
Dijkstra
过程
现在我们的路已经修好了,为了方便五岳剑派的各位弟子出行,我们修的还是路网。新的地图如下:
其中不同的数字,代表的是这条路需要多少天。当然天数肯定不会是负数,即边的权值必须大于0,这就是Dijkstra的前提。
首先,我们从华山派可以去恒山派、嵩山派和衡山派,其距离分别为3、1、9,无法直接达到泰山派。
华山
嵩山
泰山
恒山
衡山
0 ^ \widehat{\bold{0}} 0 1
∞ \infty ∞ 3
9
粗体字并戴帽子表示已经确定了的天数,不修改,下同。
那么,从华山去哪座山的距离最小呢?嵩山。我们从华山出发,经由嵩山,还可以去恒山派、泰山派和衡山派,距离分别是1+1、1+5、1+2。所以,我们更新上面的表格
华山
嵩山
泰山
恒山
衡山
0 ^ \widehat{\bold{0}} 0 1 ^ \widehat{\bold{1}} 1 6
2
3
那么在剩下的三座山中,最方便的恒山,我们从华山出发,经由恒山之后,可以去泰山,距离是2+2。所以,我们更新上面的表格
华山
嵩山
泰山
恒山
衡山
0 ^ \widehat{\bold{0}} 0 1 ^ \widehat{\bold{1}} 1 4
2 ^ \widehat{\bold{2}} 2 3
那么在剩下的两座山中,最方便的衡山,我们从华山出发,经由衡山之后,也可以去泰山,距离是3+6。所以,对于上面的表格,我们不更新。
华山
嵩山
泰山
恒山
衡山
0 ^ \widehat{\bold{0}} 0 1 ^ \widehat{\bold{1}} 1 4
2 ^ \widehat{\bold{2}} 2 3 ^ \widehat{\bold{3}} 3
最后
华山
嵩山
泰山
恒山
衡山
0 ^ \widehat{\bold{0}} 0 1 ^ \widehat{\bold{1}} 1 4 ^ \widehat{\bold{4}} 4 2 ^ \widehat{\bold{2}} 2 3 ^ \widehat{\bold{3}} 3
实现
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 package ch10;import java.util.HashMap;import java.util.HashSet;import java.util.Map.Entry;public class Dijkstra public static HashMap<Node, Integer> dijkstra (Node from) HashMap<Node, Integer> distanceMap = new HashMap<>(); distanceMap.put(from, 0 ); HashSet<Node> recordNodes = new HashSet<>(); Node minNode = getMinDistanceInUnrecordedNode(distanceMap, recordNodes); while (minNode != null ) { Integer distance = distanceMap.get(minNode); for (Edge edge : minNode.edges) { Node toNode = edge.to; if (!distanceMap.containsKey(toNode)) { distanceMap.put(toNode, distance + edge.weight); } else { distanceMap.put(edge.to, Math.min(distanceMap.get(toNode), distance + edge.weight)); } } recordNodes.add(minNode); minNode = getMinDistanceInUnrecordedNode(distanceMap, recordNodes); } return distanceMap; } public static Node getMinDistanceInUnrecordedNode (HashMap<Node, Integer> distanceMap, HashSet<Node> recordNodes) Node minNode = null ; Integer minDistance = Integer.MAX_VALUE; for (Entry<Node, Integer> iter : distanceMap.entrySet()) { Node node = iter.getKey(); Integer distance = iter.getValue(); if (!recordNodes.contains(node) && distance < minDistance) { minNode = node; minDistance = distance; } } return minNode; } public static void main (String[] args) Integer[][] m = { {3 , 1 , 2 }, {3 , 2 , 1 }, {1 , 1 , 3 }, {1 , 3 , 1 }, {2 , 1 , 4 }, {2 , 4 , 1 }, {1 , 2 , 3 }, {1 , 3 , 2 }, {5 , 3 , 4 }, {5 , 4 , 3 }, {9 , 2 , 5 }, {9 , 5 , 2 }, {2 , 3 , 5 }, {2 , 5 , 3 }, {6 , 4 , 5 }, {6 , 5 , 4 }}; Graph g = Converter.FromMatrixToGraph(m); System.out.println(dijkstra(g.nodes.get(2 ))); } }
运行结果:
1 {Node{id=2, in=3, out=3}=0, Node{id=1, in=3, out=3}=2, Node{id=3, in=4, out=4}=1, Node{id=5, in=3, out=3}=3, Node{id=4, in=3, out=3}=4}
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 import sysfrom ch10 import Converterdef dijkstra (from_node) : distance_dict = dict() distance_dict[from_node] = 0 record_nodes = set() min_node = get_min_distance_in_unrecorded_node(distance_dict, record_nodes) while min_node is not None : distance = distance_dict[min_node] for edge in min_node.edges: to_node = edge.to_node if to_node not in distance_dict: distance_dict[to_node] = distance + edge.weight else : distance_dict[edge.to_node] = min(distance_dict[to_node], distance + edge.weight) record_nodes.add(min_node) min_node = get_min_distance_in_unrecorded_node(distance_dict, record_nodes) return distance_dict def get_min_distance_in_unrecorded_node (distance_dict, record_nodes) : min_node = None min_distance = sys.maxsize for iter in distance_dict: distance = distance_dict[iter] if iter not in record_nodes and distance < min_distance: min_node = iter min_distance = distance return min_node if __name__ == '__main__' : m = [[3 , 1 , 2 ], [3 , 2 , 1 ], [1 , 1 , 3 ], [1 , 3 , 1 ], [2 , 1 , 4 ], [2 , 4 , 1 ], [1 , 2 , 3 ], [1 , 3 , 2 ], [5 , 3 , 4 ], [5 , 4 , 3 ], [9 , 2 , 5 ], [9 , 5 , 2 ], [2 , 3 , 5 ], [2 , 5 , 3 ], [6 , 4 , 5 ], [6 , 5 , 4 ]] g = Converter.from_matrix_to_graph(m) r = dijkstra(g.nodes.get(2 )) for i in r: print(i, r[i])
运行结果:
1 2 3 4 5 Node{id=2, in_size =3, out_size =3} 0 Node{id=1, in_size =3, out_size =3} 2 Node{id=3, in_size =4, out_size =4} 1 Node{id=5, in_size =3, out_size =3} 3 Node{id=4, in_size =3, out_size =3} 4