avatar
主页
计算机
金融
关于
本站文章数 :
161
本站总字数 :
1137.2K
已运行天数 :
Kaka Wan Yifan
主页
计算机
金融
关于
9.堆
计算机算法入门经典(Java与Python描述)
字数总计:4.9K

在上一章我们讨论了几种特别的二叉树。

  1. 满二叉树：
    最后一层的节点都是叶子节点，其它各层的所有节点都具有左右两个子节点。
  2. 完全二叉树：
    每层节点都完全填满，在最后一层如果不是满的，则只缺少右边的若干节点。
  3. 二叉查找树：
    对于树中的每一个节点，其左子树中的每个节点的值都要小于这个节点的值，而右子树的每个节点的值都大于这个节点的值。
  4. 平衡二叉树：
    任何节点的左右子树高度差的绝对值小于等于1。

这一章，我们的主题是"堆"，也是一种特别的二叉树。

堆的特点

大家如果去户外徒步的时候，经常会见到这种小石头堆。
玛尼堆

这个叫做玛尼堆，是当地人辟邪祈福之用。
玛尼堆有两个特点，最顶上有且仅有一颗石头，而且下面的石头通常比上面的石头大。而我们要讨论的堆，就和这个非常相似。

堆有两个特点：

  1. 堆必须是一个完全二叉树。
  2. 堆中每一个节点的值都必须大于等于(或小于等于)其子树中每个节点的值。

对于每个节点的值都大于等于子树中每个节点值的堆，我们叫做大顶堆。
对于每个节点的值都小于等于子树中每个节点值的堆，我们叫做小顶堆。

堆

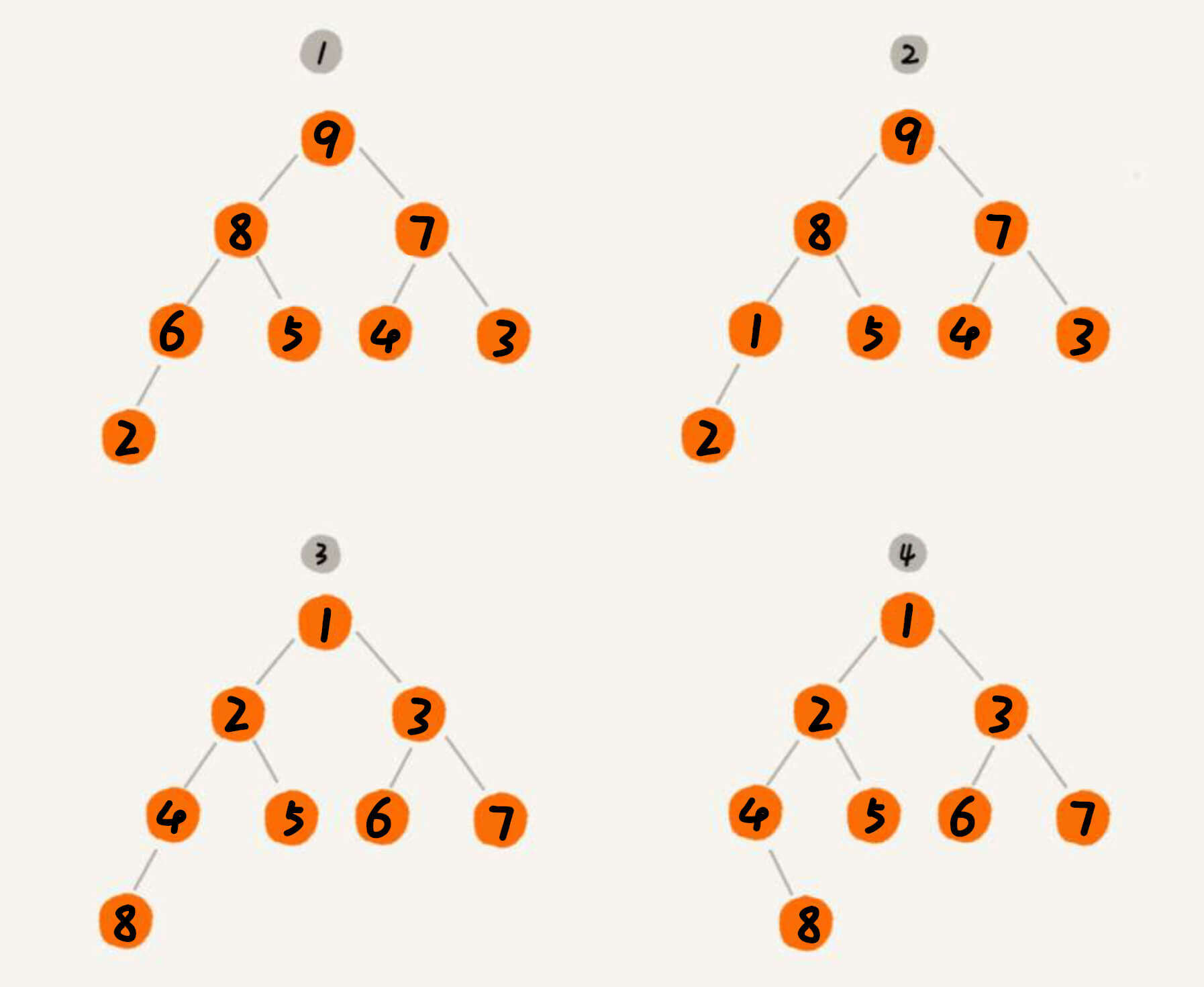
例如，在图中：

  • 1是大顶堆，因为其是 完全二叉树 ，而且每个节点的值都 大于等于 其子树中每个节点的值。
  • 2不是堆，虽然是 完全二叉树 ，但是1节点的子节点是2，不符合每个节点的都 大于等于(或小于等于) 其子树中每个节点的值。
  • 3是小顶堆，因为其是 完全二叉树 ，而且每个节点的值都 小于等于 其子树中每个节点的值。
  • 4不是堆，虽然每个节点的值都 小于等于 其子树中每个节点的值，但不是 完全二叉树 。

堆的实现

在了解什么是堆之后，我们来实现一个堆。

堆的表示

我们知道二叉树有两种存储方式：

  1. 链表存储法(也称，链式存储法)
  2. 数组存储法(也称，顺序存储法)

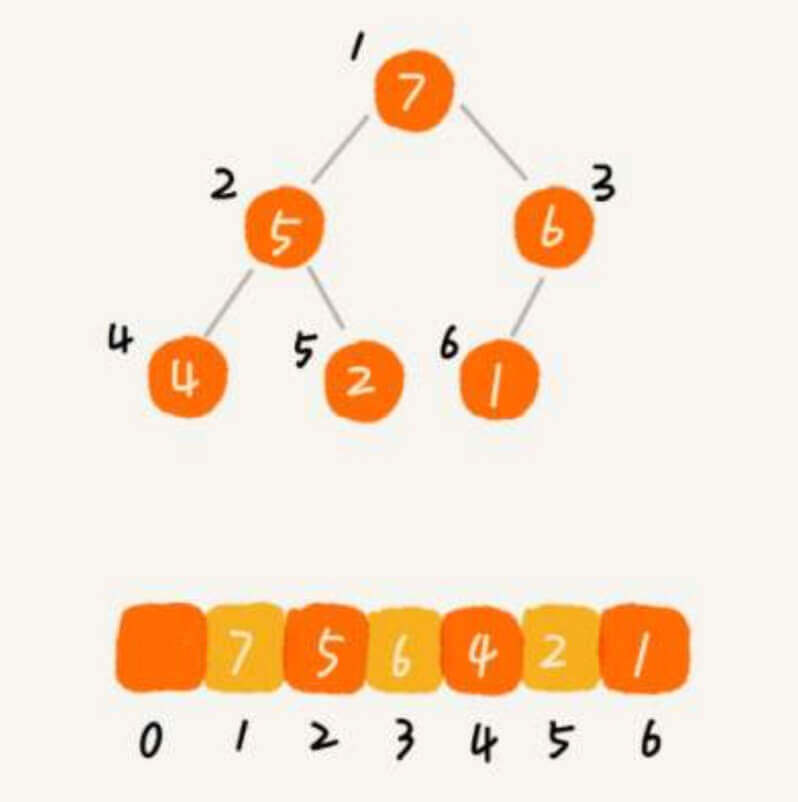
在之前讨论二叉查找树和平衡二叉树的时候，我们都毫不犹豫的选择了链表存储法。
但是对于堆呢？
我们知道，堆其实是一种完全二叉树，而完全二叉树之所以被称为"完全"，是因为用数组来存储完全二叉树的时候，不存在任何的浪费。
例如：
堆

查找

既然已经知道堆的结构就是数组了，那么查找这件事情就特别简单了，遍历数组。

新增

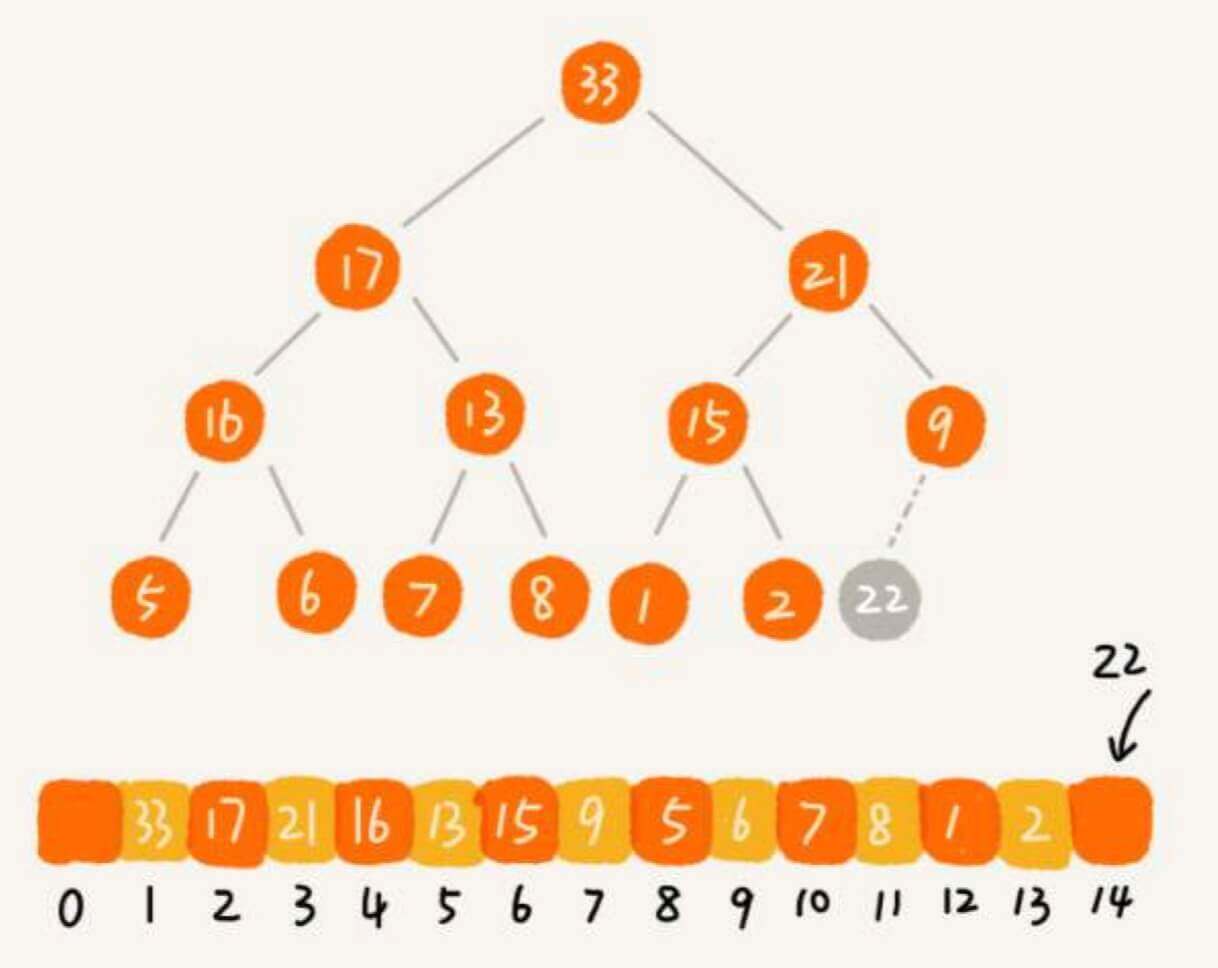
那么，如果我们要新增一个元素呢？
新增的元素不能破坏堆的两个特点。

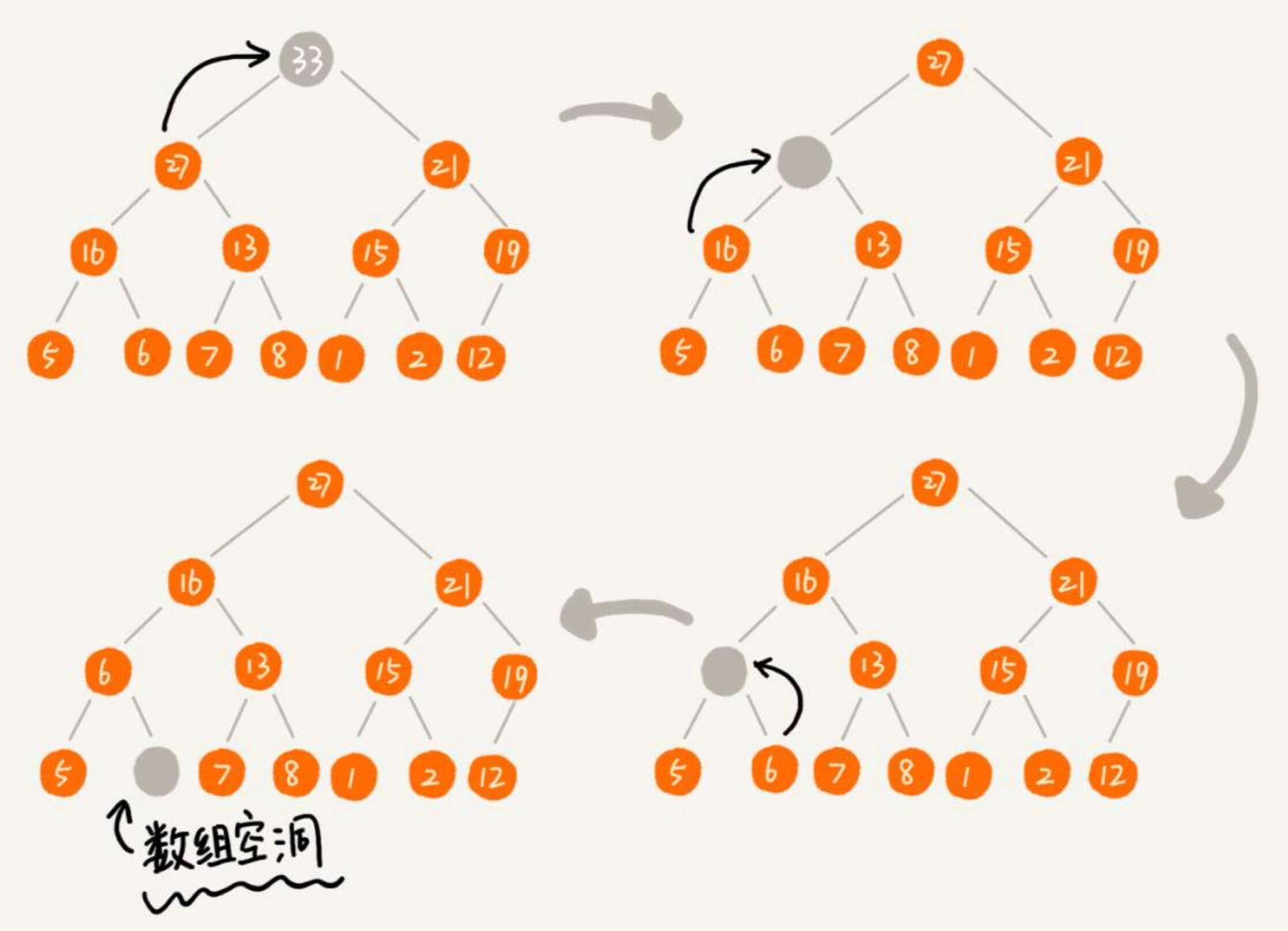
一、堆必须是一个完全二叉树。
所以，新增的元素需要在数组的尾部。
堆

二、堆中每一个节点的值都必须大于等于(或小于等于)其子树中每个节点的值。
所以，新增的元素还需要调整其位置，这个过程叫做堆化(heapify)。
堆化

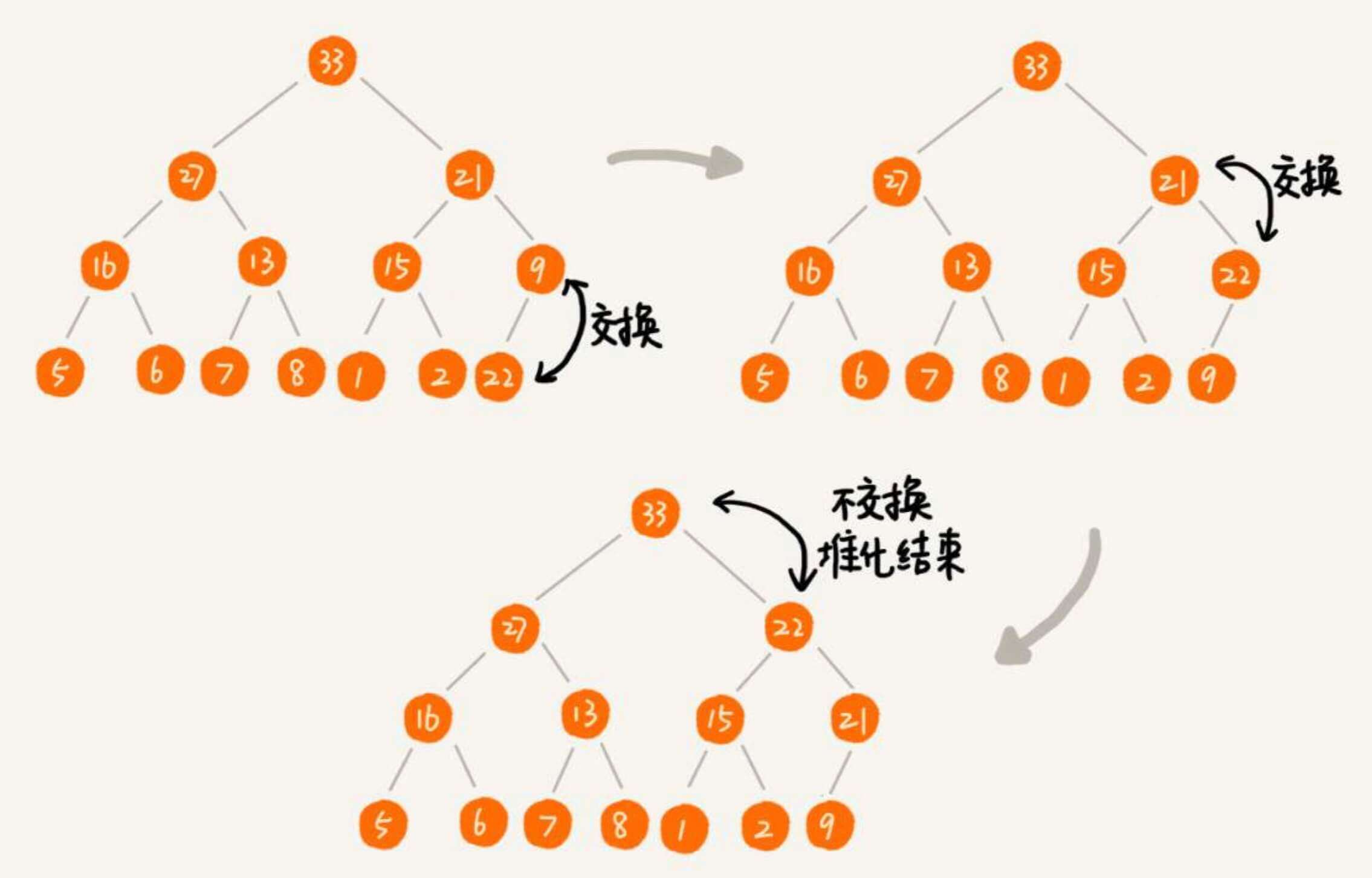
删除

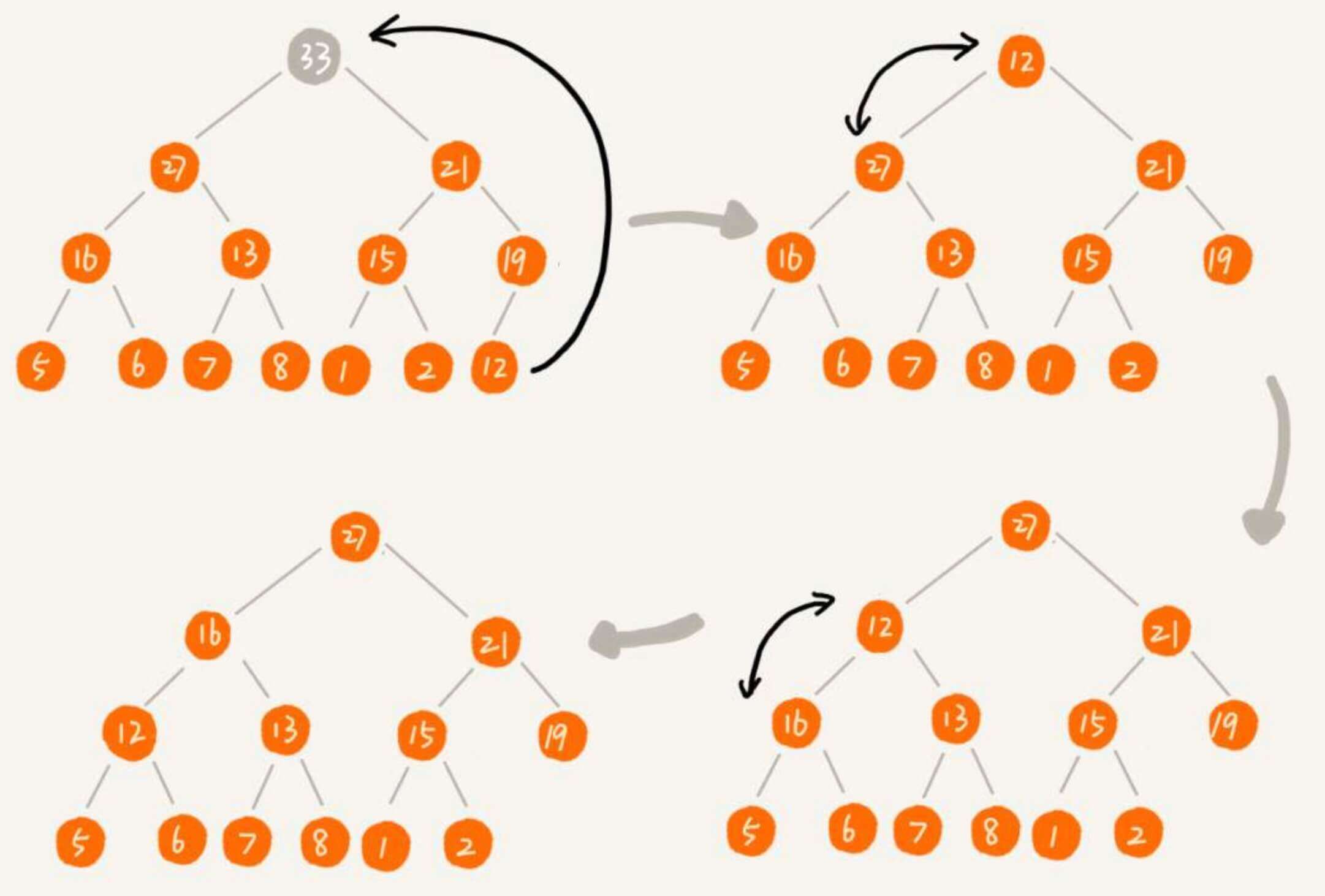
对于删除，我们把一个元素删除之后，需要把其子节点中的最大元素移上来，然后我们还需要迭代的子节点的子节点中最大的元素移上来。
删除方法

如此操作，直到出现BUG。
BUG

那么，我们换一个思路。我们把最后一个元素覆盖需要删除的元素，然后再调整元素，做堆化处理。
删除

比如在上例中，是以删除堆顶的元素为例。我们在接下来的实现代码中，会专门实现一个删除堆顶元素的方法 pop_top。

实现

示例代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
package ch09;

public class Heap {

    // 数组,从下标1开始存储数据
    private int[] a;
    // 堆可以存储的最大数据个数
    private int capacity;
    // 堆中已经存储的数据个数
    private int count;

    public Heap(int c) {
        // 0位置不放内容
        a = new int[c + 1];
        capacity = c;
        count = 0;
    }

    public void swap(int[] a,int i,int j){
        int temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }

    public void find(int data){
        for (int i = 1; i < count; i++) {
            if (a[i] == data){
                System.out.println(i);
                return;
            }
        }
        System.out.println(-1);
    }

    public boolean insert(int data) {
        // 堆满了
        if (count >= capacity)
            return false;
        count = count+1;
        a[count] = data;
        int i = count;
        // i/2 > 0 ：说明有父节点
        // a[i] > a[i/2] ：说明该节点比父节点还大
        while (i/2 > 0 && a[i] > a[i/2])
        {
            // swap()函数作用:交换下标为i和i/2的两个元素
            swap(a, i, i/2);
            i = i/2;
        }
        return true;
    }

    public boolean remove(int data){
        // 堆中没有数据
        if (count == 0)
            return false;
        int index = -1;
        for (int i = 1; i < a.length; i++) {
            if (a[i] == data){
                index = i;
                break;
            }
        }
        // 没有要删除的数据
        if (index == -1){
            return false;
        }
        // 换位置
        a[index] = a[count];
        count = count-1;

        while (true) {
            // 最大值的位置
            int maxPos = index;
            // 判断左子节点
            // 如果有左子节点，且小于左子节点
            if (index*2 <= count && a[maxPos] < a[index*2])
                // 左子节点作为最大的位置
                maxPos = index*2;
            // 判断右子节点
            // 如果有右子节点，且最大位置的节点小于右子节点
            if (index*2+1 <= count && a[maxPos] < a[index*2+1])
                // 那么，右子节点的作为最大的位置
                maxPos = index*2+1;
            // 如果左右节点都比较过了，index就是最大位置，那么说明完成。
            if (maxPos == index)
                break;
            // 互换
            swap(a, index, maxPos);
            // 迭代
            index = maxPos;
        }
        return true;
    }

    public int pop_top() throws Exception {
        if (count == 0){
            throw new Exception("Heap has no element");
        }

        int index = 1;
        int rnt = a[index];
        // 换位置
        a[index] = a[count];
        count = count-1;

        while (true) {
            // 最大值的位置
            int maxPos = index;
            // 判断左子节点
            // 如果有左子节点，且小于左子节点
            if (index*2 <= count && a[maxPos] < a[index*2])
                // 左子节点作为最大的位置
                maxPos = index*2;
            // 判断右子节点
            // 如果有右子节点，且最大位置的节点小于右子节点
            if (index*2+1 <= count && a[maxPos] < a[index*2+1])
                // 那么，右子节点的作为最大的位置
                maxPos = index*2+1;
            // 如果左右节点都比较过了，index就是最大位置，那么说明完成。
            if (maxPos == index)
                break;
            // 互换
            swap(a, index, maxPos);
            // 迭代
            index = maxPos;
        }
        return rnt;

    }

    public void print(){
        String rnt = "";
        for (int i = 1; i <= count; i++) {
            rnt = rnt + a[i] + ",";
        }
        if (rnt.length() > 1){
            rnt = rnt.substring(0,rnt.length() -1);
        }
        System.out.println(rnt);
    }

    public static void main(String[] args) throws Exception {
        Heap heap = new Heap(10);
        heap.insert(9);
        heap.insert(8);
        heap.insert(7);
        heap.insert(6);
        heap.insert(4);
        heap.insert(3);
        heap.insert(2);
        heap.insert(1);
        heap.insert(0);
        heap.print();

        heap.insert(5);
        heap.print();

        heap.remove(10);
        heap.print();

        heap.find(3);

        heap.remove(3);
        heap.print();

        heap.find(3);

        System.out.println(heap.pop_top());
        System.out.println(heap.pop_top());
        System.out.println(heap.pop_top());
        System.out.println(heap.pop_top());
        System.out.println(heap.pop_top());
        System.out.println(heap.pop_top());
        System.out.println(heap.pop_top());
        System.out.println(heap.pop_top());
        System.out.println(heap.pop_top());

    }
}
运行结果： 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
9,8,7,6,4,3,2,1,0
9,8,7,6,5,3,2,1,0,4
9,8,7,6,5,3,2,1,0,4
6
9,8,7,6,5,4,2,1,0
-1
9
8
7
6
5
4
2
1
0

示例代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
class Heap:

    def __init__(self, c):
        self.a = [None] * (c + 1)
        self.capacity = c
        self.count = 0

    def find(self, data):
        for index in range(1, self.count):
            if self.a[index] == data:
                print(index)
                return

        print(-1)

    def insert(self, data):
        # 堆满了
        if self.count >= self.capacity:
            return False
        self.count = self.count + 1
        self.a[self.count] = data
        i = self.count
        # i/2 > 0 ：说明有父节点
        # a[i] > a[i/2] ：说明该节点比父节点还大
        while i // 2 > 0 and self.a[i] > self.a[i // 2]:
            self.a[i], self.a[i // 2] = self.a[i // 2], self.a[i]
            i = i // 2
        return True

    def remove(self, data):
        # 堆中没有数据
        if self.count == 0:
            return False
        index = -1
        for i in range(1, self.count):
            if self.a[i] == data:
                index = i
                break
        # 没有要删除的数据
        if index == -1:
            return False
        # 换位置
        self.a[index] = self.a[self.count]
        self.count = self.count - 1
        while True:
            # 最大值的位置
            max_pos = index
            # 判断左子节点
            # 如果有左子节点，且小于左子节点
            if index * 2 <= self.count and self.a[max_pos] < self.a[index * 2]:
                # 左子节点作为最大的位置
                max_pos = index * 2
                # 判断右子节点
                # 如果有右子节点，且最大位置的节点小于右子节点
            if index * 2 + 1 <= self.count and self.a[max_pos] < self.a[index * 2 + 1]:
                # 那么，右子节点的作为最大的位置
                max_pos = index * 2 + 1
            # 如果左右节点都比较过了，index就是最大位置，那么说明完成。
            if max_pos == index:
                break
            self.a[index], self.a[max_pos] = self.a[max_pos], self.a[index]
            index = max_pos

        return True

    def print(self):
        print(self.a[1:self.count + 1])

    def pop_top(self):
        if self.count == 0:
            raise Exception("Heap has no element")
        index = 1
        rnt = self.a[index]
        # 换位置
        self.a[index] = self.a[self.count]
        self.count = self.count - 1
        while True:
            # 最大值的位置
            max_pos = index
            # 判断左子节点
            # 如果有左子节点，且小于左子节点
            if index * 2 <= self.count and self.a[max_pos] < self.a[index * 2]:
                # 左子节点作为最大的位置
                max_pos = index * 2
                # 判断右子节点
                # 如果有右子节点，且最大位置的节点小于右子节点
            if index * 2 + 1 <= self.count and self.a[max_pos] < self.a[index * 2 + 1]:
                # 那么，右子节点的作为最大的位置
                max_pos = index * 2 + 1
            # 如果左右节点都比较过了，index就是最大位置，那么说明完成。
            if max_pos == index:
                break
            self.a[index], self.a[max_pos] = self.a[max_pos], self.a[index]
            index = max_pos

        return rnt


if __name__ == '__main__':
    heap = Heap(10)
    heap.insert(9)
    heap.insert(8)
    heap.insert(7)
    heap.insert(6)
    heap.insert(4)
    heap.insert(3)
    heap.insert(2)
    heap.insert(1)
    heap.insert(0)
    heap.print()

    heap.insert(5)
    heap.print()

    heap.remove(10)
    heap.print()

    heap.find(3)

    heap.remove(3)
    heap.print()

    heap.find(3)

    print(heap.pop_top())
    print(heap.pop_top())
    print(heap.pop_top())
    print(heap.pop_top())
    print(heap.pop_top())
    print(heap.pop_top())
    print(heap.pop_top())
    print(heap.pop_top())
    print(heap.pop_top())
运行结果： 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
[9, 8, 7, 6, 4, 3, 2, 1, 0]
[9, 8, 7, 6, 5, 3, 2, 1, 0, 4]
[9, 8, 7, 6, 5, 3, 2, 1, 0, 4]
6
[9, 8, 7, 6, 5, 4, 2, 1, 0]
-1
9
8
7
6
5
4
2
1
0

堆排序

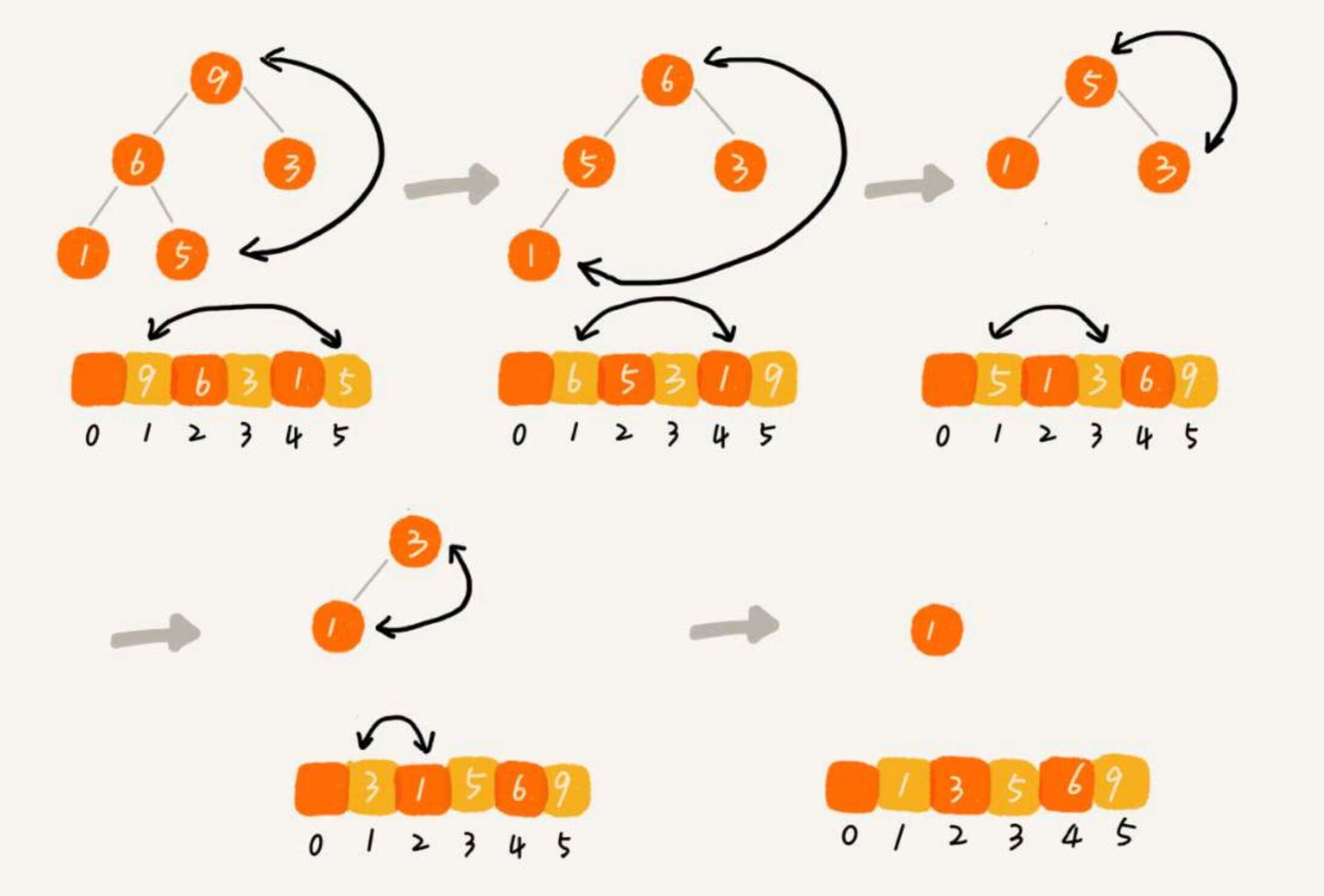
现在，观察一下上面的代码，尤其是 pop_top，元素从到小依此弹出？排序？

排序

再想一下，堆有什么特点。
对于大顶堆，顶部的元素一定是整个堆中堆大的。
对于小顶堆，顶部的元素一定是整个堆中最小的。

那么如果我们迭代从堆中"弹出"顶部的元素，是不是就实现了排序？
时间复杂度O(nlog⁡n)O(n \log n)。
思路就是这么简单，但是在具体实现上，我们为了做到原地排序，可以这么做。
最堆顶的元素和堆的最后一个元素互换，然后剩下的元素重新堆化成新的堆。
排序

建堆

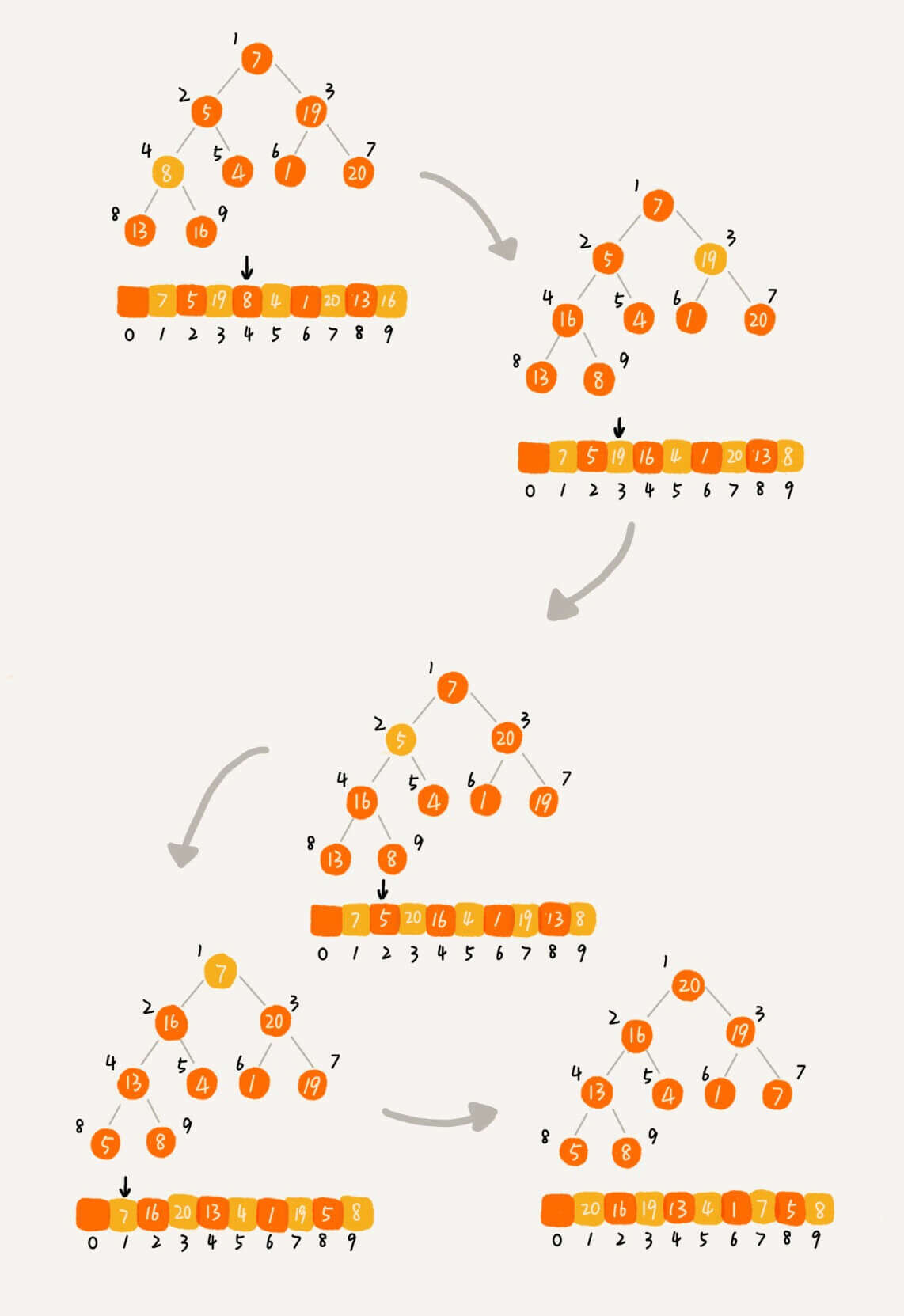
现在有一个问题了，我们上面那个排序算法基于了一个前提条件：数据已经组成了一个堆结构。
可是，没这个条件啊。
创造条件

那我们就来创造条件，建堆。
我们循环迭代调用上文中的insert方法。
那么时间复杂就是O(nlog⁡n)O(n \log n)

在这里，我们讨论另一种方法。
所有的元素组成一个完全二叉树，然后我们从完全二叉树的最后一个非叶子节点开始一直到根节点，循环迭代做堆化操作。
建堆

实现

需要特别注意的是，因为参与堆排序的数组通常是从0位置开始，所以在这份代码中，我们的堆也从0位置开始。

示例代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
package ch09;

import java.util.Arrays;

public class HeapSort {

    public static void swap(int[] a, int i, int j){
        int temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }

    /**
     *
     * @param arr
     * @return
     */
    public static int[] heapSort(int[] arr) {
        if (arr.length <= 1) {
            return arr;
        }

        // 1、建堆
        for (int i = (arr.length - 1) / 2; i >= 0; i--) {
            heapify(arr, arr.length - 1, i);
        }

        // 2、排序
        int k = arr.length - 1;
        while (k > 0) {
            // 将堆顶元素（最大）与最后一个元素交换位置
            swap(arr, 0, k);
            // 将剩下元素重新堆化，堆顶元素变成最大元素
            k = k - 1;
            heapify(arr, k, 0);
        }
        return arr;
    }

    private static void heapify(int[] arr, int n, int i) {
        while (true) {
            // 最大值位置
            int maxPos = i;
            // 与左子节点（i * 2 + 1）比较，获取最大值位置
            if (i * 2 + 1 <= n && arr[i] < arr[i * 2 + 1]) {
                maxPos = i * 2 + 1;
            }
            // 最大值与右子节点（i * 2 + 2）比较，获取最大值位置
            if (i * 2 + 2 <= n && arr[maxPos] < arr[i * 2 + 2]) {
                maxPos = i * 2 + 2;
            }
            // 最大值是当前位置结束循环
            if (maxPos == i) {
                break;
            }
            // 与子节点交换位置
            swap(arr, i, maxPos);
            // 以交换后子节点位置接着往下查找
            i = maxPos;
        }
    }


    public static void main(String[] args) {
        int[] arr = {3,44,38,5,47,15,36,26,27,2,46,4,19,50,48};
        System.out.println(Arrays.toString(arr));
        // 只有数组不为空，并且数组的长度大于1，这时候的排序才有意义
        if (null != arr && arr.length > 1){
            heapSort(arr);
        }
        System.out.println(Arrays.toString(arr));
    }
}
运行结果： 
1
2
[3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]
[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

示例代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
def heap_sort(arr):
    if len(arr) <= 1:
        return arr

    # 1、建堆
    for i in range((len(arr) - 1) // 2, -1, -1):
        arr = heapify(arr, len(arr) - 1, i)

    # 2、排序
    k = len(arr) - 1
    while k > 0:
        # 将堆顶元素（最大）与最后一个元素交换位置
        arr[0], arr[k] = arr[k], arr[0]
        # 将剩下元素重新堆化，堆顶元素变成最大元素
        k = k - 1
        arr = heapify(arr, k, 0)
    return arr


def heapify(arr, n, i):
    while (True):
        # 最大值位置
        max_pos = i
        # 与左子节点（i * 2 + 1）比较，获取最大值位置
        if i * 2 + 1 <= n and arr[i] < arr[i * 2 + 1]:
            max_pos = i * 2 + 1
        # 最大值与右子节点（i * 2 + 2）比较，获取最大值位置
        if i * 2 + 2 <= n and arr[max_pos] < arr[i * 2 + 2]:
            max_pos = i * 2 + 2
        # 最大值是当前位置结束循环
        if max_pos == i:
            break
        # 与子节点交换位置
        arr[i], arr[max_pos] = arr[max_pos], arr[i]
        # 以交换后子节点位置接着往下查找
        i = max_pos
    return arr


if __name__ == '__main__':
    arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]
    print(arr)
    print(heap_sort(arr))
运行结果： 
1
2
[3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]
[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

优先队列

在第二章的时候，我们讨论了"队列"，其特点是先进先出，排队。
那么，现在，这种情况怎么办？
医院排队

医院排队，这种情况是不是要让严重的患者先看病？
这就是优先队列，优先级高的先出队。

那么怎么实现优先队列？
再观察一下我们上文的堆的实现，特别是 pop_top，弹出堆顶的元素，这个就是我们的出队方法。
优先队列的原理就是堆，在Java中是PriorityQueue(优先队列)；在Python中，则毫不掩饰的告诉你他的原理，heapq(堆队列)。

接下来，我们具体来看看PriorityQueue和heapq。

示例代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
package ch09;

import java.util.PriorityQueue;

public class PriorityQueueTest {

    public static void main(String[] args) {
        PriorityQueue<Integer> q = new PriorityQueue<Integer>();
        q.offer(3);
        q.offer(1);
        q.offer(4);
        q.offer(1);
        q.offer(5);
        q.offer(9);
        q.offer(2);
        q.offer(6);

        System.out.println(q.poll());
        System.out.println(q.poll());
        System.out.println(q.poll());
        System.out.println(q.poll());

    }
}
运行结果： 
1
2
3
4
1
1
2
3

示例代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import heapq

q = []
heapq.heappush(q, 3)
heapq.heappush(q, 1)
heapq.heappush(q, 4)
heapq.heappush(q, 1)
heapq.heappush(q, 5)
heapq.heappush(q, 9)
heapq.heappush(q, 2)
heapq.heappush(q, 6)

print(heapq.heappop(q))
print(heapq.heappop(q))
print(heapq.heappop(q))
print(heapq.heappop(q))
运行结果： 
1
2
3
4
1
1
2
3

那么，现在有一个问题了。
这个优先队列都是让小的数字先出对列，如果我想要大的数先出队列呢？

而且，如果队列中的元素不是那些可以比较的基础类型呢？比如，我们自己定义的一个类，学生类，股票类。

千万次的问

这已经不是第一次我们问自己这个问题了，在第七章，讨论TreeMap有序表的时候，有提出了类似的问题。
如果在TreeMap中，如果我们的key不是那些可以比较的基础类型呢？比如，我们自己定义的一个类，学生类，股票类。

比较器

那我就自行定义他们之间的大小关系，这就是比较器。

优先队列的比较器

在Java中

在Java中，我们自定义一个比较器就OK了。
示例代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
package ch09;

import java.util.Comparator;
import java.util.PriorityQueue;

public class PriorityQueueComparator {

    public static class C {
        public String k;
        public Integer v;
        public C(String key, int value){
            k = key;
            v = value;
        }

        @Override
        public String toString() {
            return "C{" +
                    "k='" + k + '\'' +
                    ", v=" + v +
                    '}';
        }
    }

    static class com implements Comparator<C> {

        @Override
        public int compare(C o1, C o2) {
            return o2.v - o1.v;
        }
    }

    public static void main(String[] args) {
        PriorityQueue<C> q = new PriorityQueue<C>(new com());
        q.offer(new C("c1",3));
        q.offer(new C("c2",1));
        q.offer(new C("c3",4));
        q.offer(new C("c4",5));
        q.offer(new C("c5",9));

        System.out.println(q.poll().toString());
        System.out.println(q.poll().toString());
        System.out.println(q.poll().toString());
        System.out.println(q.poll().toString());
        System.out.println(q.poll().toString());

    }
}

运行结果：

1
2
3
4
5
C{k='c5', v=9}
C{k='c4', v=5}
C{k='c3', v=4}
C{k='c1', v=3}
C{k='c2', v=1}

在Python中

在Python中，有一个麻烦是 heapq本身不支持自定义比较函数。
但是，如果我们查看heapq的源代码，会看到这么一段。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 'heap' is a heap at all indices >= startpos, except possibly for pos.  pos
# is the index of a leaf with a possibly out-of-order value.  Restore the
# heap invariant.
def _siftdown(heap, startpos, pos):
    newitem = heap[pos]
    # Follow the path to the root, moving parents down until finding a place
    # newitem fits.
    while pos > startpos:
        parentpos = (pos - 1) >> 1
        parent = heap[parentpos]
        if newitem < parent:
            heap[pos] = parent
            pos = parentpos
            continue
        break
    heap[pos] = newitem

是通过if newitem < parent:来实现的。
所以，我们的思路是重写对象的__lt__()。

示例代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
import heapq

class C:
    def __init__(self, key, value):
        self.k = key
        self.v = value

    def __lt__(self, other):
        if self.v < other.v:
            return False
        else:
            return True

    def p(self):
        print(self.k, self.v)


c1 = C("c1", 3)
c2 = C("c2", 1)
c3 = C("c3", 4)
c4 = C("c4", 5)
c5 = C("c5", 9)

h = []
heapq.heappush(h, c1)
heapq.heappush(h, c2)
heapq.heappush(h, c3)
heapq.heappush(h, c4)
heapq.heappush(h, c5)
heapq.heappop(h).p()
heapq.heappop(h).p()
heapq.heappop(h).p()
heapq.heappop(h).p()
heapq.heappop(h).p()

运行结果：

1
2
3
4
5
c5 9
c4 5
c3 4
c1 3
c2 1

TreeMap的比较器

最后，我们解答一下在第七章我们留下的一个问题，如果在TreeMap中，如果我们的key不是那些可以比较的基础类型呢？

示例代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
package ch09;

import java.util.Comparator;
import java.util.TreeMap;

public class TreeMapComparator {

    public static class C {
        public String k;
        public Integer v;
        public C(String key, int value){
            k = key;
            v = value;
        }

        @Override
        public String toString() {
            return "C{" +
                    "k='" + k + '\'' +
                    ", v=" + v +
                    '}';
        }
    }

    static class com implements Comparator<C> {

        @Override
        public int compare(C o1, C o2) {
            return o2.v - o1.v;
        }
    }

    public static void main(String[] args) {
        TreeMap<C,String> treeMap = new TreeMap<C,String>(new com());
        treeMap.put(new C("c1",3),"三");
        treeMap.put(new C("c2",1),"一");
        treeMap.put(new C("c3",4),"四");
        treeMap.put(new C("c4",5),"五");
        // treeMap.put(new C("c5",9),"九");
        treeMap.put(new C("c6",2),"二");
        treeMap.put(new C("c7",6),"六");

        System.out.println(treeMap.firstKey());
        System.out.println(treeMap.lastKey());

        System.out.println(treeMap.floorKey(new C("c5",9)));
        System.out.println(treeMap.ceilingKey(new C("c5",9)));

    }


}

运行结果：

1
2
3
4
C{k='c7', v=6}
C{k='c2', v=1}
null
C{k='c7', v=6}
文章作者: Kaka Wan Yifan
文章链接: https://kakawanyifan.com/10609
版权声明: 本博客所有文章版权为文章作者所有，未经书面许可，任何机构和个人不得以任何形式转载、摘编或复制。
评论区