二叉树的应用非常广泛。在金融中也有,作为期权定价的一种方法。
不过,和这个问题密切相关。
MySQL的索引是怎么实现的? 树开始。
树
在生活中,我们随处可见树。
而我们要讨论的计算机中的树,就和这个类似。
树的节点
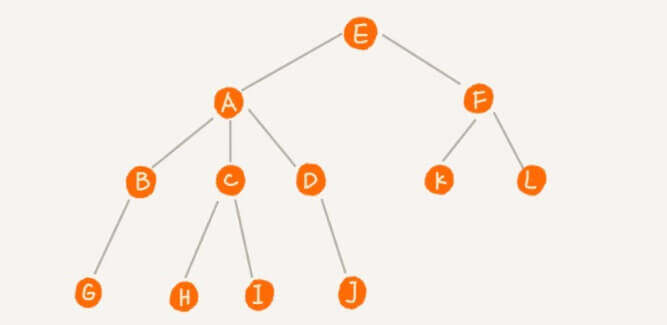
就以上文的那颗树为例。根节点 ,在这里E是根节点。叶子节点 ,G、H、I、J、K、L都是叶子节点。兄弟节点 ,比如B、C和D互为兄弟节点,他们的父节点都是A。
高度、深度与层
在讨论树的时候,我们还会提到树的高度、深度和层数。这三个概念,容易混淆,这里我们辨析一下。
节点的高度: 节点的深度: 节点的层数: 树的高度: 在这里,容易记错的是高度 和深度 ,记住这么一个成语:根深蒂固
为什么节点的高度要强调最长路径(最大边数),但深度不用强调?最长路径(最大边数),因为一个节点到根节点,必然只有一条路径,只存在一个边数。
我们以上文的树为例,找几个节点,计算其高度、深度和层。
高度 深度 层
E3
0
1
A2
1
2
F1
1
1
C1
2
3
K0
2
3
I0
3
4
二叉树
在讨论树之后,我们讨论一种常见又特殊的树,二叉树 。
二叉树的定义
常见在哪里?常见就在于我们真的经常会见到。最多 有两个子节点,分别是左子节点 和右子节点 。最多 有两个。
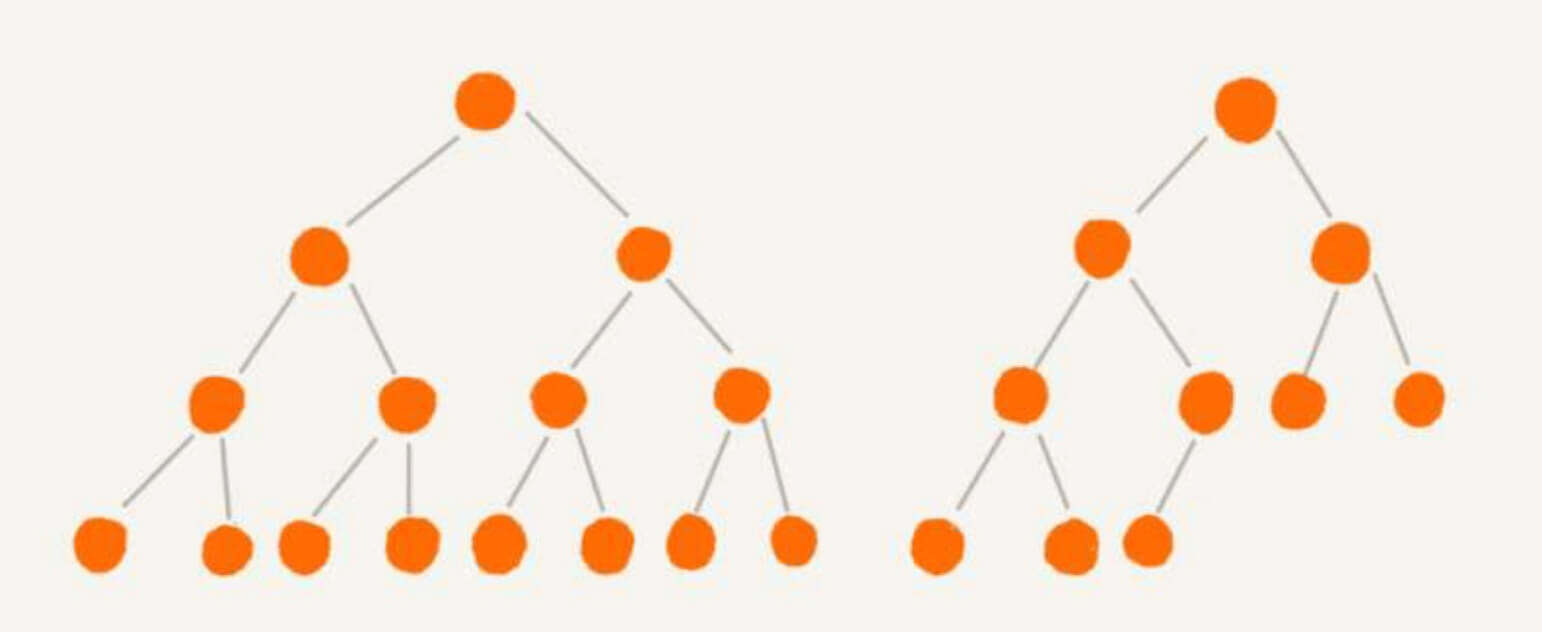
比如,这两颗树,就是二叉树,但是右边的树,有一个节点,只有一个子节点。
满二叉树和完全二叉树
而这两棵二叉树,又有不一样的地方。
左边那颗,我们称之为满二叉树 ,有两个特点:
最后一层的节点都是叶子节点。
其它各层的所有节点都具有左右两个子节点。
右边的是完全二叉树 ,特点是:
所以,满二叉树一定是完全二叉树,但是完全二叉树不一定是满二叉树。
不同的观点
其实,关于这一部分,或许因为翻译的存在偏差,或许因为其他历史原因。在名字方面,还存在争议,有不同的名字,而这种名字主要存在于欧美。
满二叉树(Full Binary Tree):完全二叉树(Complete Binary Tree):完美二叉树(Perfect Binary Tree):
在欧美,他们所指的满二叉树(Full Binary Tree)是指树上的所有节点,要么是叶子节点,要么同时具有左右子树。满二叉树(Full Binary Tree)。
但在我们的观点中,哈夫曼树不是满二叉树。满二叉树,他们称之为完美二叉树(Perfect Binary Tree)。
对应关系如下:
我们
欧美
满二叉树
完美二叉树
完全二叉树
完全二叉树
满二叉树
其实只是名字的不同。
但现在,似乎有一个名不副实的家伙。完全二叉树。
二叉树的存储方式
二叉树有两种存储方式:
链表存储法(也称,链式存储法)
数组存储法(也称,顺序存储法)
链表存储法
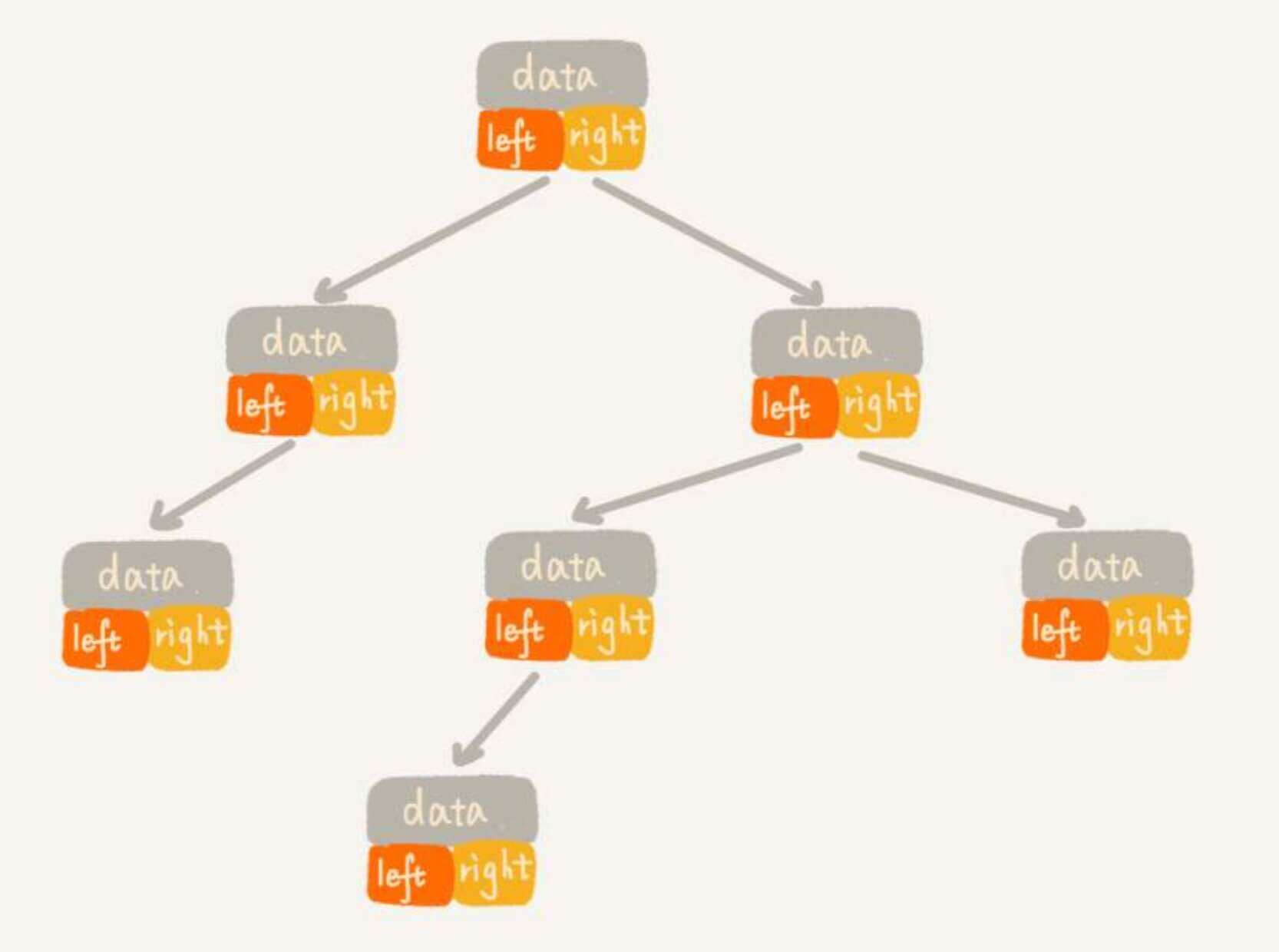
链表存储法,顾名思义,就是用一个链表来存储二叉树。
数组存储法
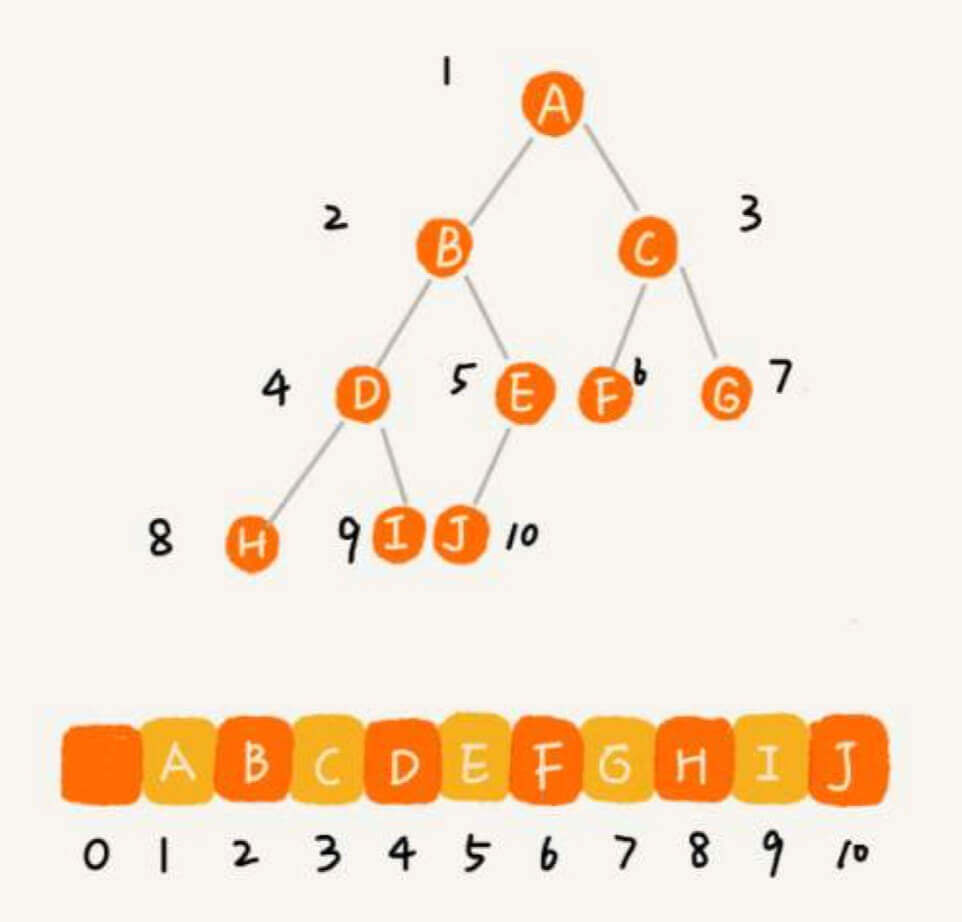
数组存储法,就是用一个数组来存储二叉树。0位置空着,我们根节点放在1位置。在2*1位置放根节点的左子节点,在2*1+1位置放根节点的右子节点。类似的,如果一个节点在i位置,那么我们在2*i位置放该节点的左子节点,在2*i+1位置放该节点的右子节点。
对于一颗完全二叉树,在数组存储中,我们有:
这就是完全二叉树的"完全"所在。
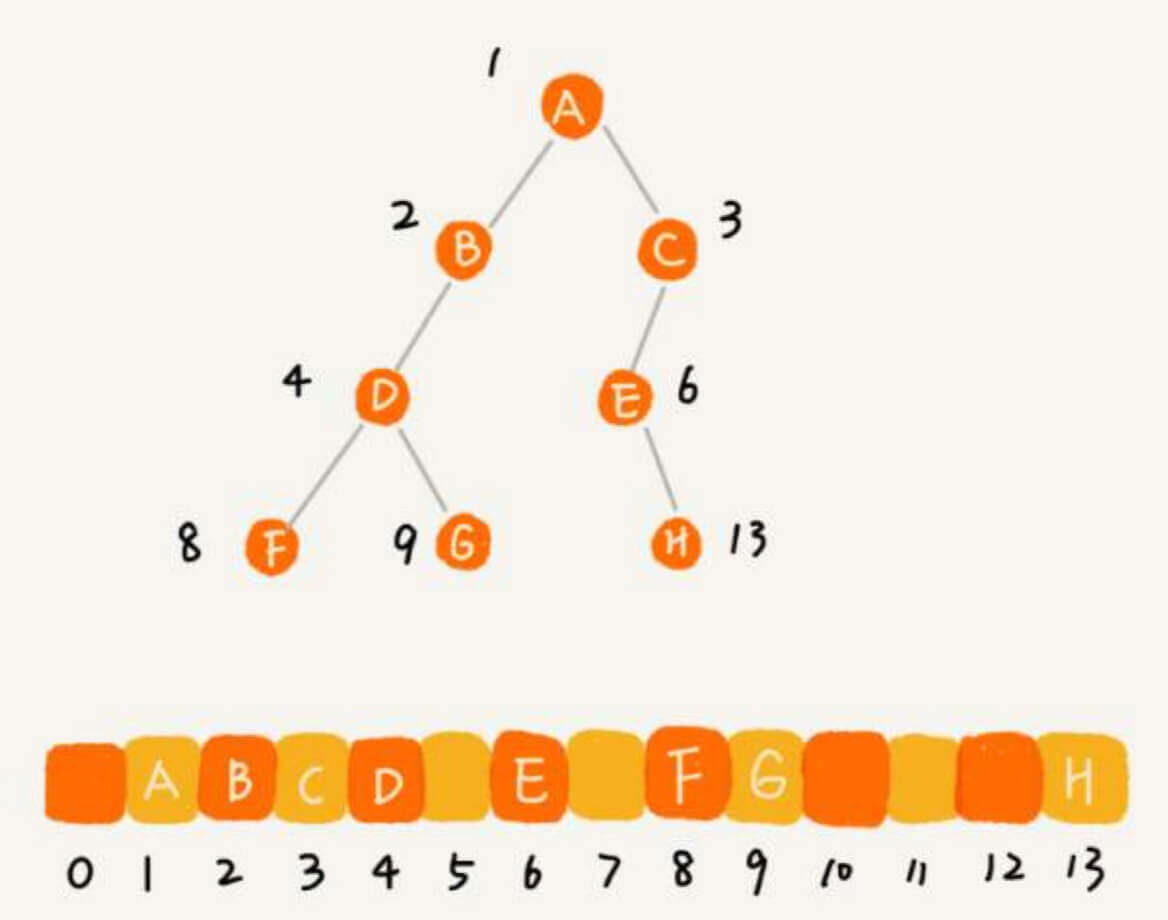
非完全二叉树就存在空间的浪费了。
二叉树的遍历
前序、中序和后序遍历
前序、中序和后序遍历,其实都属于深度优先遍历。
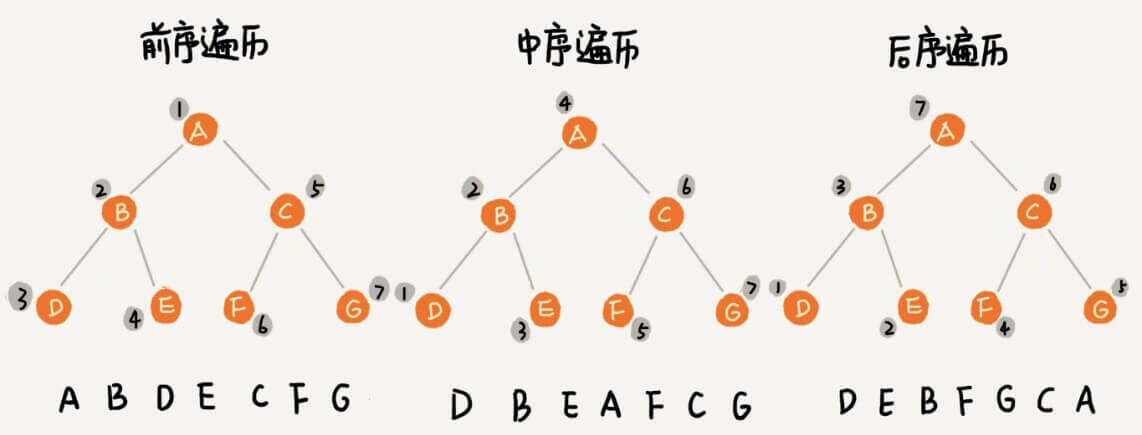
前序遍历 :对于树中的任何一个节点:节点本身 ,节点的左子树 ,节点的右子树 。中序遍历 :对于树中的任何一个节点:节点的左子树 ,节点本身 ,节点的右子树 。后序遍历 :对于树中的任何一个节点:节点的左子树 ,节点的右子树 ,节点本身 。
特别注意:是 左子树右子树左节点右节点
也有一些资料会把前序遍历称作先序遍历,这两种除了名字不一样,没有任何区别。
遍历的实现
现在,我们对这么一颗二叉树进行遍历。
这个二叉树有一个特点:对于树中的每一个节点,其左子树中的每个节点的值都要小于这个节点的值,而右子树的每个节点的值都大于这个节点的值。
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 package ch08;import java.util.ArrayList;public class TraverseBinaryTree public static class Node public int value; public Node left; public Node right; public Node (int v) value = v; } } public static ArrayList<Integer> pre (Node root) ArrayList<Integer> rnt = new ArrayList<>(); if (root == null ){ return rnt; } rnt.add(root.value); rnt.addAll(pre(root.left)); rnt.addAll(pre(root.right)); return rnt; } public static ArrayList<Integer> mid (Node root) ArrayList<Integer> rnt = new ArrayList<>(); if (root == null ){ return rnt; } rnt.addAll(mid(root.left)); rnt.add(root.value); rnt.addAll(mid(root.right)); return rnt; } public static ArrayList<Integer> pos (Node root) ArrayList<Integer> rnt = new ArrayList<>(); if (root == null ){ return rnt; } rnt.addAll(pos(root.left)); rnt.addAll(pos(root.right)); rnt.add(root.value); return rnt; } public static void main (String[] args) Node root = new Node(6 ); root.left = new Node(4 ); root.right = new Node(8 ); root.left.left = new Node(2 ); root.left.right = new Node(5 ); root.right.left = new Node(7 ); root.right.right = new Node(9 ); root.left.left.left = new Node(1 ); root.left.left.right = new Node(3 ); System.out.println("pre:" ); System.out.println(pre(root)); System.out.println("mid:" ); System.out.println(mid(root)); System.out.println("pos:" ); System.out.println(pos(root)); } }
运行结果:
1 2 3 4 5 6 pre: [6, 4, 2, 1, 3, 5, 8, 7, 9] mid: [1, 2, 3, 4, 5, 6, 7, 8, 9] pos: [1, 3, 2, 5, 4, 7, 9, 8, 6]
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 class Node : def __init__ (self, v) : self.left = None self.right = None self.value = v def pre (r) : rnt = [] if r is None : return rnt rnt.append(r.value) rnt.extend(pre(r.left)) rnt.extend(pre(r.right)) return rnt def mid (r) : rnt = [] if r is None : return rnt rnt.extend(mid(r.left)) rnt.append(r.value) rnt.extend(mid(r.right)) return rnt def pos (r) : rnt = [] if r is None : return rnt rnt.extend(pos(r.left)) rnt.extend(pos(r.right)) rnt.append(r.value) return rnt if __name__ == '__main__' : root = Node(6 ) root.left = Node(4 ) root.right = Node(8 ) root.left.left = Node(2 ) root.left.right = Node(5 ) root.right.left = Node(7 ) root.right.right = Node(9 ) root.left.left.left = Node(1 ) root.left.left.right = Node(3 ) print('pre:' ) print(pre(root)) print('mid:' ) print(mid(root)) print('pos:' ) print(pos(root))
运行结果:
1 2 3 4 5 6 pre: [6, 4, 2, 1, 3, 5, 8, 7, 9] mid: [1, 2, 3, 4, 5, 6, 7, 8, 9] pos: [1, 3, 2, 5, 4, 7, 9, 8, 6]
递归序
特别的,我们还可以来分析一下上述代码的运行过程。
6进入pre(),pre(6)。6左节点4进入递归,pre(4)。4的左节点2进入递归,pre(2)。2的左节点1进入递归,pre(1)。1的左节点进入递归,左节点是空的,返回,回到pre(1)。1的右节点进入递归,右节点是空的,返回,回到pre(1)。1返回,回到pre(2)。2的右节点3进入递归,pre(3)。3的左节点进入递归,左节点是空的,返回,回到pre(3)。3的右节点进入递归,右节点是空的,返回,回到pre(3)。3返回,回到pre(2)。2返回,回到pre(4)。4的右节点5进入递归,pre(5)。5的左右节点都是空,所以会先后两次回到pre(5)5返回,回到pre(4)。4返回,回到pre(6)。6的右节点8进入递归,pre(8)。…
即每个节点,都会到达三次。
我们还可以把这个过程打印出来。
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 package ch08;public class RecurBinaryTree public static class Node public int value; public Node left; public Node right; public Node (int v) value = v; } } public static void recur (Node root) if (null == root){ return ; } System.out.print(root.value); recur(root.left); System.out.print(root.value); recur(root.right); System.out.print(root.value); } public static void main (String[] args) Node root = new Node(6 ); root.left = new Node(4 ); root.right = new Node(8 ); root.left.left = new Node(2 ); root.left.right = new Node(5 ); root.right.left = new Node(7 ); root.right.right = new Node(9 ); root.left.left.left = new Node(1 ); root.left.left.right = new Node(3 ); recur(root); } }
运行结果:
1 642111233324555468777899986
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 class Node : def __init__ (self, v) : self.left = None self.right = None self.value = v def recur (r) : if r is None : return print(r.value, end='' ) recur(r.left) print(r.value, end='' ) recur(r.right) print(r.value, end='' ) if __name__ == '__main__' : root = Node(6 ) root.left = Node(4 ) root.right = Node(8 ) root.left.left = Node(2 ) root.left.right = Node(5 ) root.right.left = Node(7 ) root.right.right = Node(9 ) root.left.left.left = Node(1 ) root.left.left.right = Node(3 ) recur(root)
运行结果:
1 642111233324555468777899986
而前序优先遍历是节点第一次到达的时候就打印,中序优先遍历是节点第二次到达的时候打印,后序优先遍历则是节点第三次到达的时候才打印。
层序遍历
我们刚刚讨论的前序、中序和后序三种遍历方法都属于深度优先。除了这种遍历方法,还有一种方法,广度优先。层序遍历 。左节点和右节点依次加入队列。然后按照先进先出的出队顺序遍历下一层。
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 package ch08;import java.util.ArrayList;import java.util.LinkedList;import java.util.Queue;public class TraverseBinaryTree_Layer public static class Node public int value; public Node left; public Node right; public Node (int v) value = v; } } public static ArrayList<Integer> layer (Node root) ArrayList<Integer> rnt = new ArrayList<>(); if (null == root){ return rnt; } Queue<Node> queue = new LinkedList<Node>(); queue.offer(root); while (!queue.isEmpty()){ Node node = queue.poll(); rnt.add(node.value); if (null != node.left){ queue.offer(node.left); } if (null != node.right){ queue.offer(node.right); } } return rnt; } public static void main (String[] args) Node root = new Node(6 ); root.left = new Node(4 ); root.right = new Node(8 ); root.left.left = new Node(2 ); root.left.right = new Node(5 ); root.right.left = new Node(7 ); root.right.right = new Node(9 ); root.left.left.left = new Node(1 ); root.left.left.right = new Node(3 ); System.out.println(layer(root)); } }
运行结果:
1 [6, 4, 8, 2, 5, 7, 9, 1, 3]
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 from queue import Queueclass Node : def __init__ (self, v) : self.value = v self.left = None self.right = None def layer (r) : rnt = [] if r is None : return r q = Queue() q.put(r) while q.empty() is False : n = q.get() rnt.append(n.value) if n.left is not None : q.put(n.left) if n.right is not None : q.put(n.right) return rnt if __name__ == '__main__' : root = Node(6 ) root.left = Node(4 ) root.right = Node(8 ) root.left.left = Node(2 ) root.left.right = Node(5 ) root.right.left = Node(7 ) root.right.right = Node(9 ) root.left.left.left = Node(1 ) root.left.left.right = Node(3 ) print(layer(root))
运行结果:
1 [6, 4, 8, 2, 5, 7, 9, 1, 3]
二叉查找树
在刚刚的代码中,我们还发现一个神奇的现象,在中序优先遍历中。
1 2 mid: [1, 2, 3, 4, 5, 6, 7, 8, 9]
恰好是按大小顺序打印的。
二叉查找树(Binary Search Tree,二叉搜索树)。对于树中的每一个节点,其左子树中的每个节点的值都要小于这个节点的值,而右子树的每个节点的值都大于这个节点的值。
与之前讨论哈希表以及栈和队列一样,我们来讨论二叉查找树的"增删改查"。
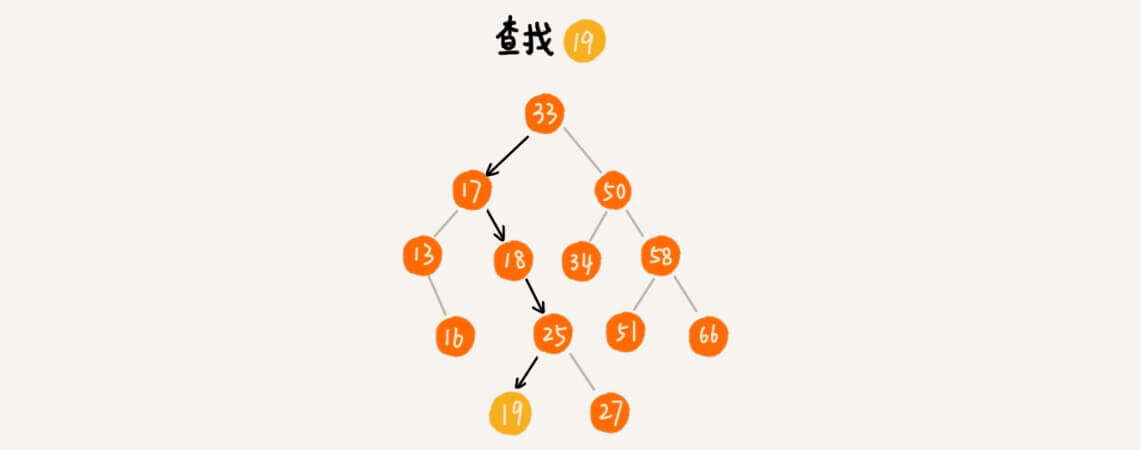
查找
我们从根节点开始,如果需要查找的数大于根节点,就进入根节点的左子树,从左子树递归查找;如果需要查找的数小于根节点,就进入根节点的右子树,从右子树递归查找;如果恰好等于根节点,那么就返回找到了。如果都到叶子节点了还没找到呢?那就是没找到。
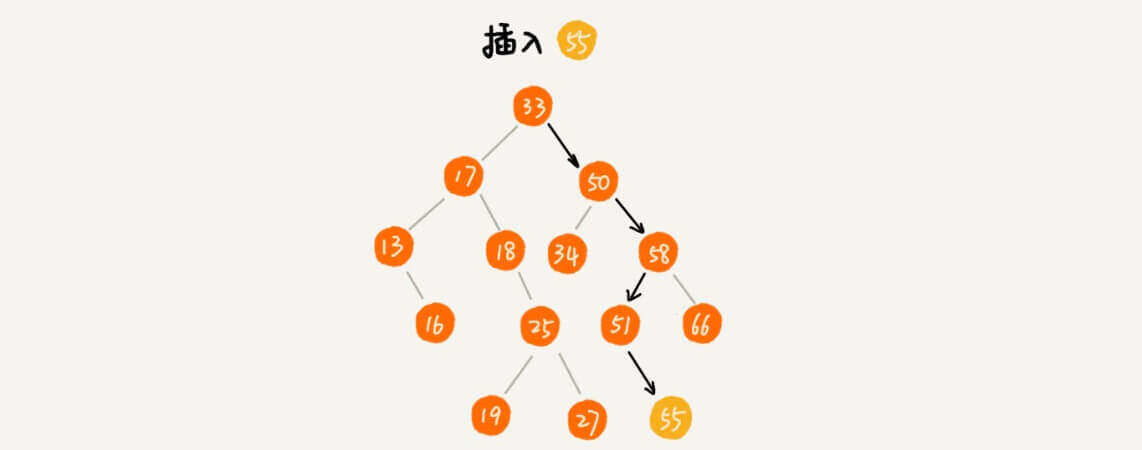
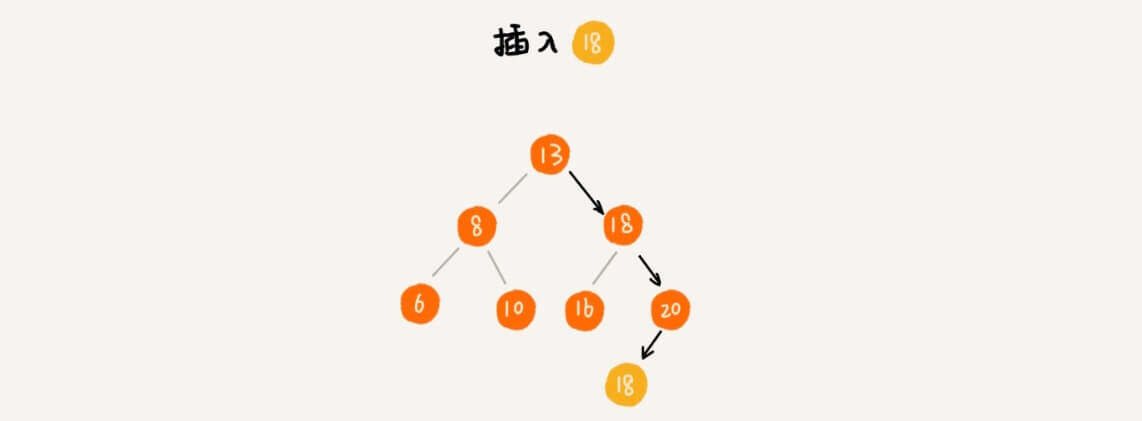
插入
二叉查找树的插入过程有点类似查找操作。
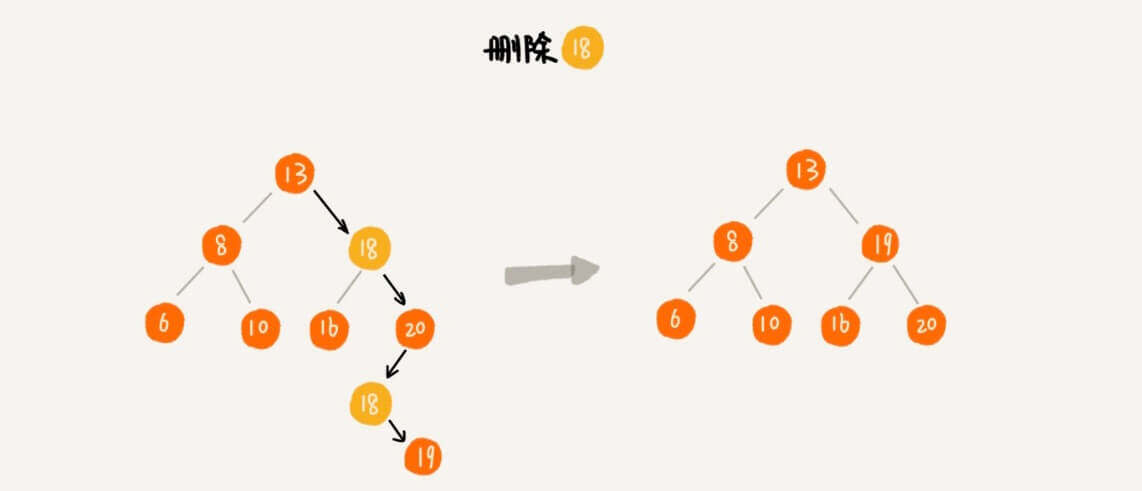
删除
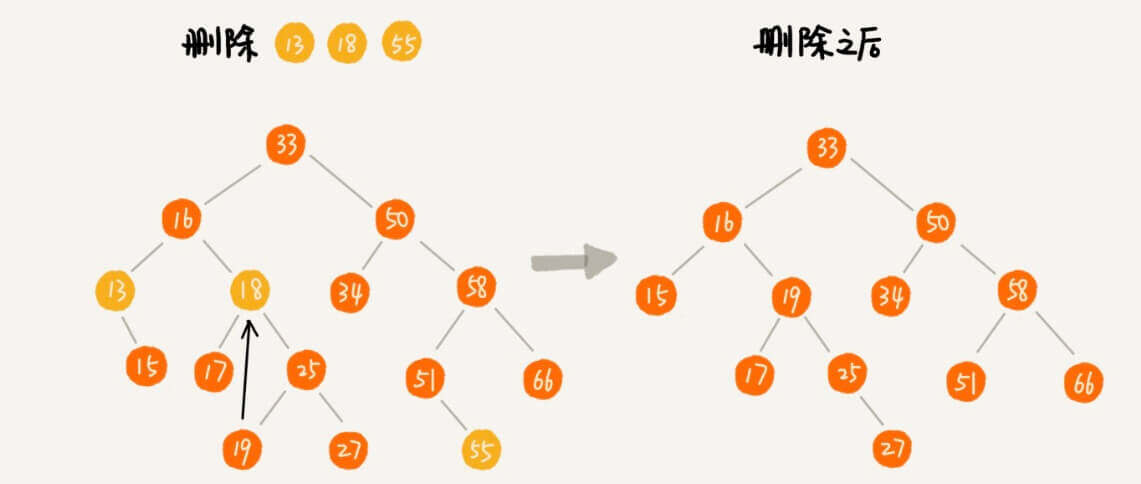
删除的话,就比较麻烦了。我们分情况讨论。
被删除的节点是叶子节点 55。
被删除的节点只有一个子节点 13。
被删除的节点有两个子节点 18,这个节点有两个子节点,我们找到其右子树中的最小节点19,然后把被删除节点的值改为19,再删除节点19。
那么选左子树中的最大节点,可以吗?当然也可以。
其实呢,关于删除,还有一个取巧的办法。
我们不真的去删除,只是打上deleted标签。
修改
修改我们理解为先删除再新增。
相比哈希表的优点
因为专业,所以卓越。不仅仅是"比亚迪·秦",还有二叉查找树。
虽然二叉查找树的插入、查找和修改的时间复杂度都是O ( log n ) O(\log n) O ( log n ) O ( 1 ) O(1) O ( 1 )
查找最小和最大值
这个在哈希表中怎么做?只有一个办法,遍历哈希表中的所有数据,时间复杂度O ( n ) O(n) O ( n ) O ( log n ) O(\log n) O ( log n )
区间查找
这个我们也经常用,比如查找20岁到35岁之间的候选者。在哈希表中怎么做?也只有遍历,时间复杂度O ( n ) O(n) O ( n )
如果根节点属于20到35之间,记下根节点。
如果根节点大于等于20,那么从根节点的左节点开始,递归。
如果根节点小于等于35,那么从根节点的右节点开始,递归。
这个时间复杂度虽然也是O ( n ) O(n) O ( n )
其实呢,二叉查找树的效率还是有限,在后面我们会讨论B+树,效率更高。
实现
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 package ch08;import java.util.ArrayList;public class BinarySearchTree public static class Node public int value; public Node left; public Node right; public Node (int v) value = v; } } public static Node insert (Node tree,int data) if (tree == null ) { tree = new Node(data); return tree; } Node curr = tree; while (curr != null ) { if (data > curr.value) { if (null == curr.right) { curr.right = new Node(data); break ; } else { curr = curr.right; } } else { if (null == curr.left) { curr.left = new Node(data); break ; } else { curr = curr.left; } } } return tree; } public static Boolean find (Node tree,int data) Node curr = tree; while (curr != null ){ if (data < curr.value){ curr = curr.left; }else if (data > curr.value){ curr = curr.right; }else { return true ; } } return false ; } public static Node delete (Node tree,int data) Node curr = tree; Node currFather = null ; while (null != curr){ if (curr.value == data){ break ; } currFather = curr; if (curr.value > data){ curr = curr.left; }else { curr = curr.right; } } if (curr == null ){ return tree; } if (null == curr.left || null == curr.right){ Node child = null ; if (null != curr.left){ child = curr.left; }else if (null != curr.right){ child = curr.right; }else { child = null ; } if (currFather == null ){ tree = child; }else if (currFather.left == curr){ currFather.left = child; }else { currFather.right = child; } }else { Node min = curr.right; Node minFather = null ; while (null != min.left){ minFather = min; min = min.left; } curr.value = min.value; if (minFather.left == min){ minFather.left = null ; }else { minFather.right = null ; } } return tree; } public static ArrayList<Integer> findInterval (Node root, int min, int max) ArrayList<Integer> rnt = new ArrayList<>(); if (null == root){ return rnt; } if (root.value >= min && root.value <= max){ rnt.add(root.value); } if (root.value > min){ rnt.addAll(findInterval(root.left,min,max)); } if (root.value < max){ rnt.addAll(findInterval(root.right,min,max)); } return rnt; } public static Integer findMax (Node tree) Integer max = null ; Node curr = tree; while (null != curr){ max = curr.value; curr = curr.right; } return max; } public static Integer findMin (Node tree) Integer min = null ; Node curr = tree; while (null != curr){ min = curr.value; curr = curr.left; } return min; } public static ArrayList<Integer> mid (Node root) ArrayList<Integer> rnt = new ArrayList<>(); if (root == null ){ return rnt; } rnt.addAll(mid(root.left)); rnt.add(root.value); rnt.addAll(mid(root.right)); return rnt; } public static void main (String[] args) Node tree = null ; tree = insert(tree,0 ); tree = insert(tree,1 ); tree = insert(tree,2 ); tree = insert(tree,3 ); tree = insert(tree,4 ); tree = insert(tree,5 ); tree = insert(tree,6 ); tree = insert(tree,7 ); tree = insert(tree,8 ); tree = insert(tree,9 ); System.out.println(tree.value); System.out.println(mid(tree)); System.out.println(find(tree,10 )); System.out.println(find(tree,1 )); tree = delete(tree,10 ); tree = delete(tree,1 ); System.out.println(find(tree,10 )); System.out.println(find(tree,1 )); System.out.println(findInterval(tree,3 ,6 )); tree = delete(tree,5 ); System.out.println(findInterval(tree,3 ,6 )); System.out.println(findMax(tree)); System.out.println(findMin(tree)); tree = delete(tree,0 ); tree = delete(tree,9 ); System.out.println(findMax(tree)); System.out.println(findMin(tree)); } }
运行结果:
1 2 3 4 5 6 7 8 9 10 11 12 0 [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] false true false false [3, 4, 5, 6] [3, 4, 6] 9 0 8 2
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 class Node : def __init__ (self, v) : self.value = v self.left = None self.right = None def insert (tree, data) : """ 插入 :param tree: :param data: :return: """ if tree is None : tree = Node(data) return tree curr = tree while curr is not None : if data > curr.value: if curr.right is None : curr.right = Node(data) break else : curr = curr.right else : if curr.left is None : curr.left = Node(data) break else : curr = curr.left; return tree def find (tree, data) : curr = tree while curr is not None : if data < curr.value: curr = curr.left elif data > curr.value: curr = curr.right else : return True return False def delete (tree, data) : curr = tree curr_father = None while curr is not None : if curr.value == data: break curr_father = curr if curr.value > data: curr = curr.left else : curr = curr.right if curr is None : return tree if curr.left is None or curr.right is None : child = None if curr.left is not None : child = curr.left elif curr.right is not None : child = curr.right else : child = None if curr_father is None : tree = child elif curr_father.left == curr: curr_father.left = child else : curr_father.right = child else : min = curr.right min_father = None while min.left is not None : min_father = min min = min.left curr.value = min.value if min_father.left == min: min_father.left = None else : min_father.right = None return tree def find_interval (root, min, max) : rnt = [] if root is None : return rnt if min <= root.value <= max: rnt.append(root.value) if root.value > min: rnt.extend(find_interval(root.left, min, max)) if root.value < max: rnt.extend(find_interval(root.right, min, max)) return rnt def find_max (tree) : max = None curr = tree while curr is not None : max = curr.value curr = curr.right return max def find_min (tree) : min = None curr = tree while curr is not None : min = curr.value curr = curr.left return min def mid (r) : rnt = [] if r is None : return rnt rnt.extend(mid(r.left)) rnt.append(r.value) rnt.extend(mid(r.right)) return rnt if __name__ == '__main__' : t = None t = insert(t, 0 ) t = insert(t, 1 ) t = insert(t, 2 ) t = insert(t, 3 ) t = insert(t, 4 ) t = insert(t, 5 ) t = insert(t, 6 ) t = insert(t, 7 ) t = insert(t, 8 ) t = insert(t, 9 ) print(t.value) print(mid(t)) print(find(t, 10 )) print(find(t, 1 )) t = delete(t, 10 ) t = delete(t, 1 ) print(find(t, 10 )) print(find(t, 1 )) print(find_interval(t, 3 , 6 )) t = delete(t, 5 ) print(find_interval(t, 3 , 6 )) print(find_max(t)) print(find_min(t)) t = delete(t, 0 ) t = delete(t, 9 ) print(find_max(t)) print(find_min(t))
运行结果:
1 2 3 4 5 6 7 8 9 10 11 12 0 [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] False True False False [3, 4, 5, 6] [3, 4, 6] 9 0 8 2
重复数据的处理
在上文中我们举的二叉树的例子,有意避免了重复数据。
基于链表的实现
我想我们可以把每一个节点都改成链表的形式,有新的重复数据加入,就在链表的后面加。
即,我们修改Node Class,新增一个属性nextEqual。
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 public static class Node public int value; public Node left; public Node right; public Node nextEqual; public Node (int v) value = v; } }
示例代码:
1 2 3 4 5 6 class Node : def __init__ (self, v) : self.value = v self.left = None self.right = None self.next_equal = None
这样的话。nextEqual,找出所有相等的元素。nextEqual,把新增的元素放在后面。nextEqual指向空。
等于和大于合为大于等于
第二种方法,我们把节点左边的设置为小于,右边的设置为大于等于。
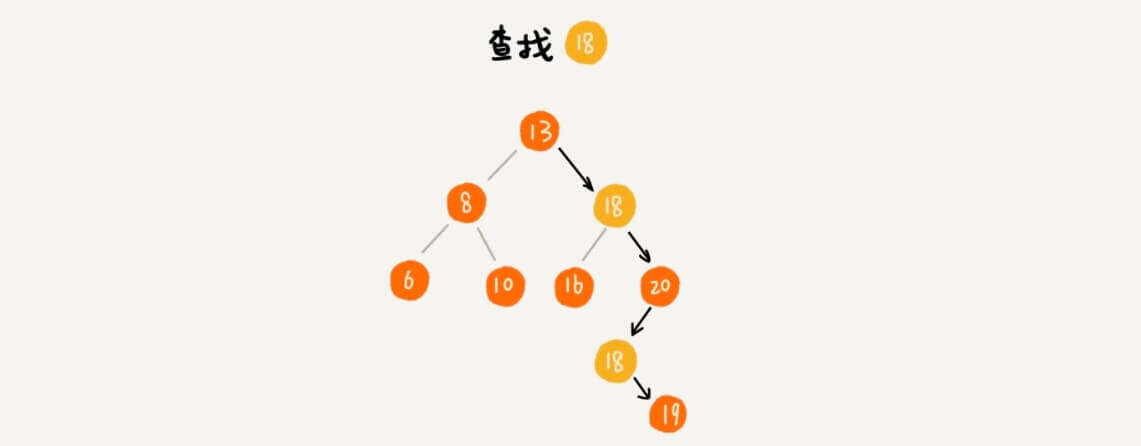
查找
对于查找,我们需要一直找,直到已经到达叶子节点为止。
插入
插入就很简单了,之前在大于的时候我们怎么做的,这次在大于等于也怎么做。并无区别。
删除
麻烦的是删除。
平衡二叉树
再来看看我们上文中的例子,我们二叉树的结构是怎么样的?0节点插入二叉树;然后1节点插入二叉树,作为0节点的右子节点;之后以此是2节点、3节点等等。
时间复杂度退化到O ( n ) O(n) O ( n )
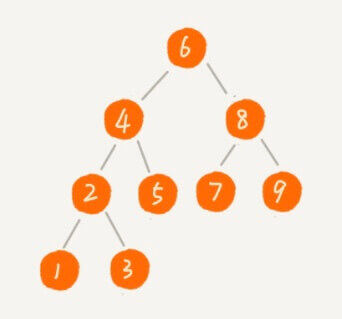
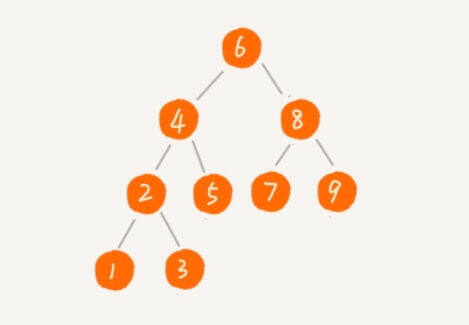
但是,如果我们能表示成下图这种形式,是不是就会好很多?
这就是平衡二叉树,也被成为平衡二叉查找树。平衡的含义是,让整棵树左右看起来比较"对称"、比较"平衡",不要出现左子树很高、右子树很矮的情况。这样就能让整棵树的高度相对来说低一些,相应的插入、删除、查找等操作的效率高一些。
不过,也有一些资料关于平衡二叉树的定义会更严格,认为平衡二叉树的任何节点的左右子树高度差的绝对值小于等于1
但通常我们认为红黑树就是平衡二叉树的典型代表。
但关于红黑树,我们不作太多讨论。
三种索引的比较
截至目前,带有索引功能的数据结构,我们一共讨论了三种。
哈希表
有序数组(特殊的哈希表)
平衡二叉树
那么,谁会是MySQL的索引的原理呢?
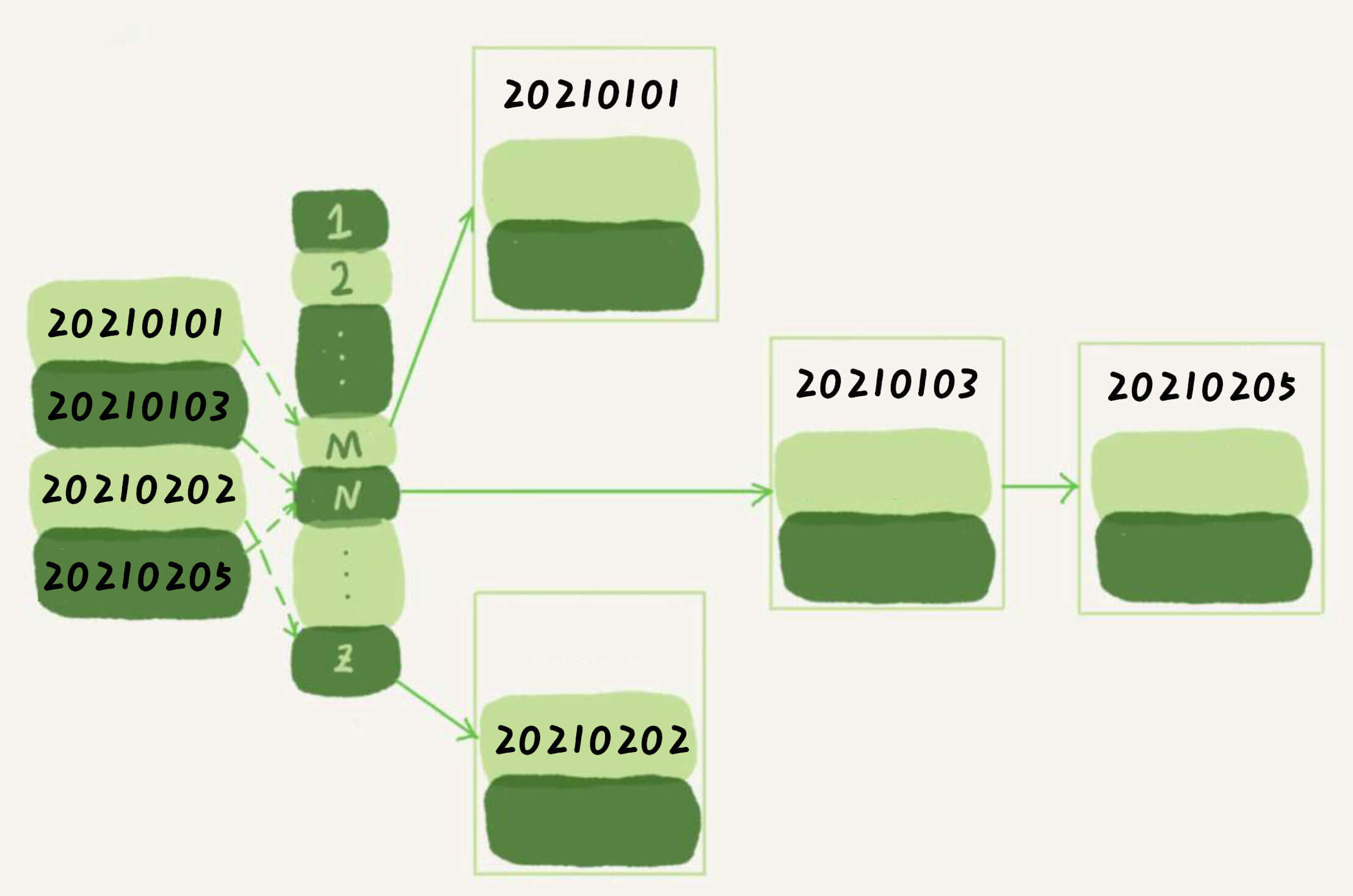
会是哈希表吗?
SQL,单一查找的时候,用哈希表没有问题。
1 select * from stock where ann_date = '20210205'
但如果我们是查找一个区间的呢?
1 select * from stock where ann_date between '20210101' and '20210205'
那么,哈希表只能遍历,显然不够优秀。
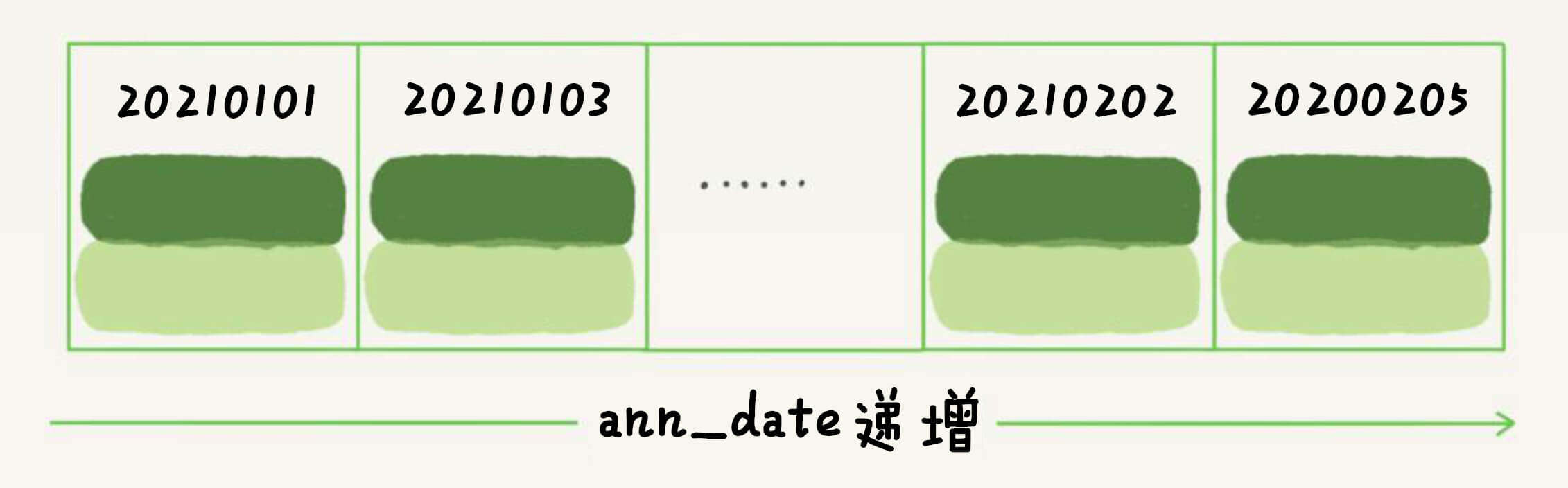
会是有序数组吗?
那么,会是有序数组吗?(其实有序数组可以理解为一种特殊的哈希表)
有序数组的话,无论单一查找
1 select * from stock where ann_date = '20210205'
还是区间查找
1 select * from stock where ann_date between '20210101' and '20210205'
利用二分法,我们都可以做到效率很高。
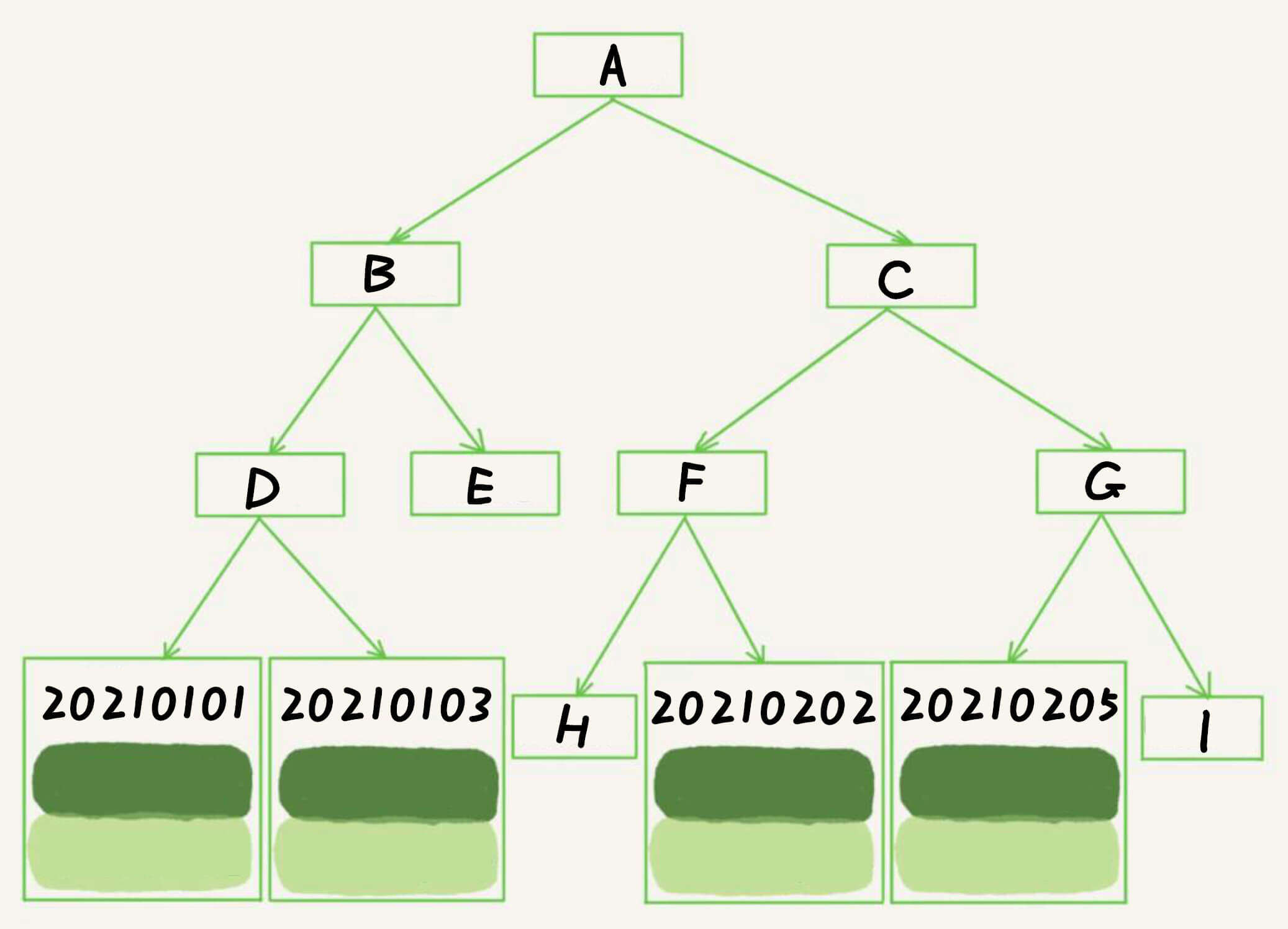
会是平衡二叉树吗?
也不是。
1 select * from stock where ann_date = '20210205'
的效率比较高。
但同样是区间查找麻烦。
1 select * from stock where ann_date between '20210101' and '20210205'
要先找到20210101,然后一个一个回旋,直到20210205。
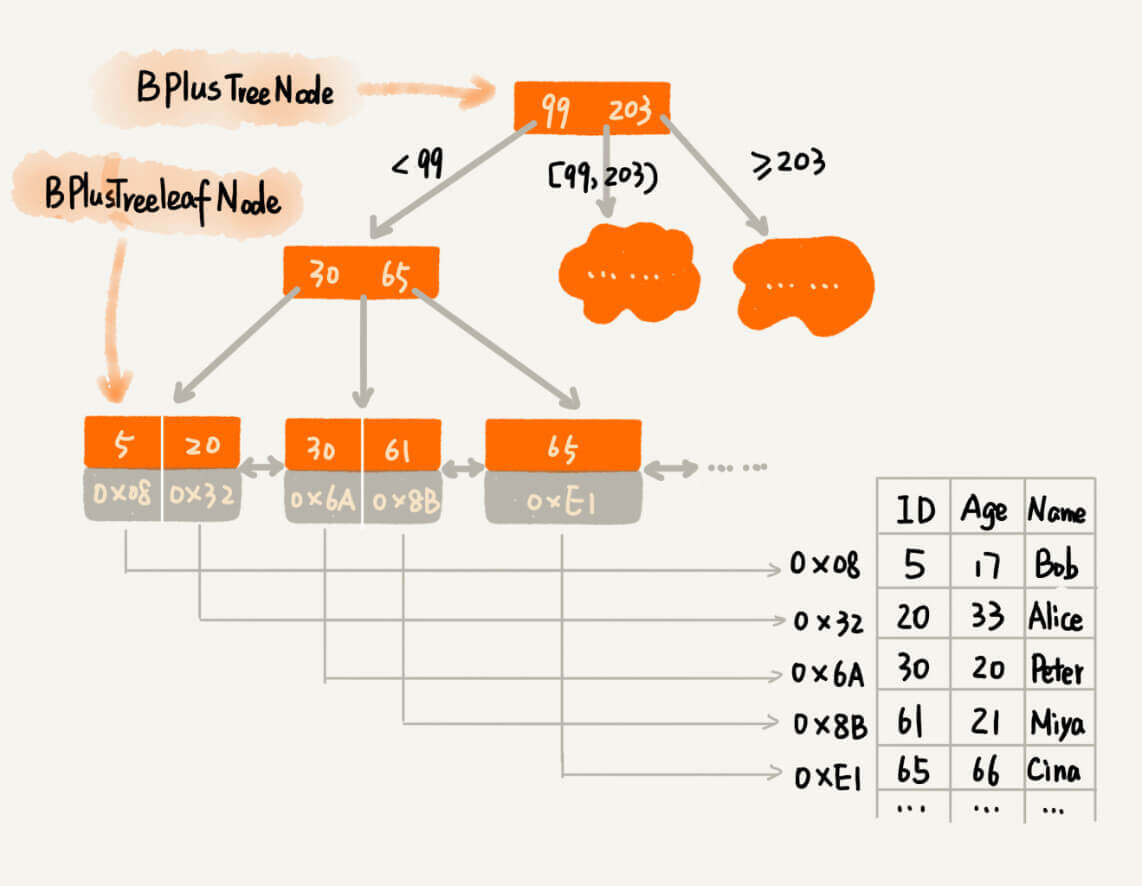
B+树
这种数据结构的特点是:
一个节点可以存储两个值。用以降低树的高度。
叶子节点通过指针串成了一个链表,而且是有序链表。从而解决了区间查找时候的"回旋问题"。
非叶子节点只存储key,不存储具体内容。具体内容通过叶子节点中的一个指针指向。
注意
关于MySQL索引的结构,我们在《MySQL从入门到实践:4.结构》 中有更多的讨论。 实际上,哈希表,也可能是MySQL的索引,只是一般情况下,我们说的MySQL的索引,都是说InnoDB中的BTREE索引。
二叉树的递归方法
在本章的最后,我们来讨论一下二叉树的递归方法,这种方法主要用于解决树型动态规划。关于具体什么是动态规划,我们还没讨论。但我想,这并不影响我们讨论接下来的内容。
是不是平衡二叉树
在上文中,我们讨论了平衡二叉树。严格的 平衡二叉树?
那么,我们需要哪些信息才能判断是不是严格的 平衡二叉树呢?严格的 平衡二叉树呢?
平衡二叉树,需要三个条件:
左子树是平衡的。 右子树是平衡的。 左右子树的高度差不大于1。
所以,我们需要左右子树提供的信息是:
是否平衡 高度多少
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 package ch08;public class IsBalance public static class Node public int value; public Node left; public Node right; public Node (int v) value = v; } } public static class Info public boolean isBalance; public int height; public Info (boolean b,int h) isBalance = b; height = h; } } public static Info process (Node root) if (null == root){ return new Info(true ,0 ); } Info leftInfo = process(root.left); Info rightInfo = process(root.right); int height = Math.max(leftInfo.height,rightInfo.height) + 1 ; boolean isBalance = false ; if (leftInfo.isBalance && rightInfo.isBalance && (Math.abs(leftInfo.height - rightInfo.height) <= 1 )){ isBalance = true ; } return new Info(isBalance,height); } public static void main (String[] args) Node root = new Node(6 ); root.left = new Node(4 ); root.right = new Node(8 ); root.left.left = new Node(2 ); root.left.right = new Node(5 ); root.right.left = new Node(7 ); root.right.right = new Node(9 ); root.left.left.left = new Node(1 ); root.left.left.right = new Node(3 ); System.out.println(process(root).isBalance); } }
运行结果:
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 class Node : def __init__ (self, v) : self.value = v self.left = None self.right = None class Info : def __init__ (self, b, h) : self.is_balance = b self.height = h def process (r) : if r is None : return Info(True , 0 ) left_info = process(r.left) right_info = process(r.right) height = max(left_info.height, right_info.height) + 1 is_balance = False if left_info.is_balance and right_info.is_balance and abs(left_info.height - right_info.height) <= 1 : is_balance = True return Info(is_balance, height) if __name__ == '__main__' : root = Node(6 ) root.left = Node(4 ) root.right = Node(8 ) root.left.left = Node(2 ) root.left.right = Node(5 ) root.right.left = Node(7 ) root.right.right = Node(9 ) root.left.left.left = Node(1 ) root.left.left.right = Node(3 ) print(process(root).is_balance)
运行结果:
网络拓扑图的最长距离
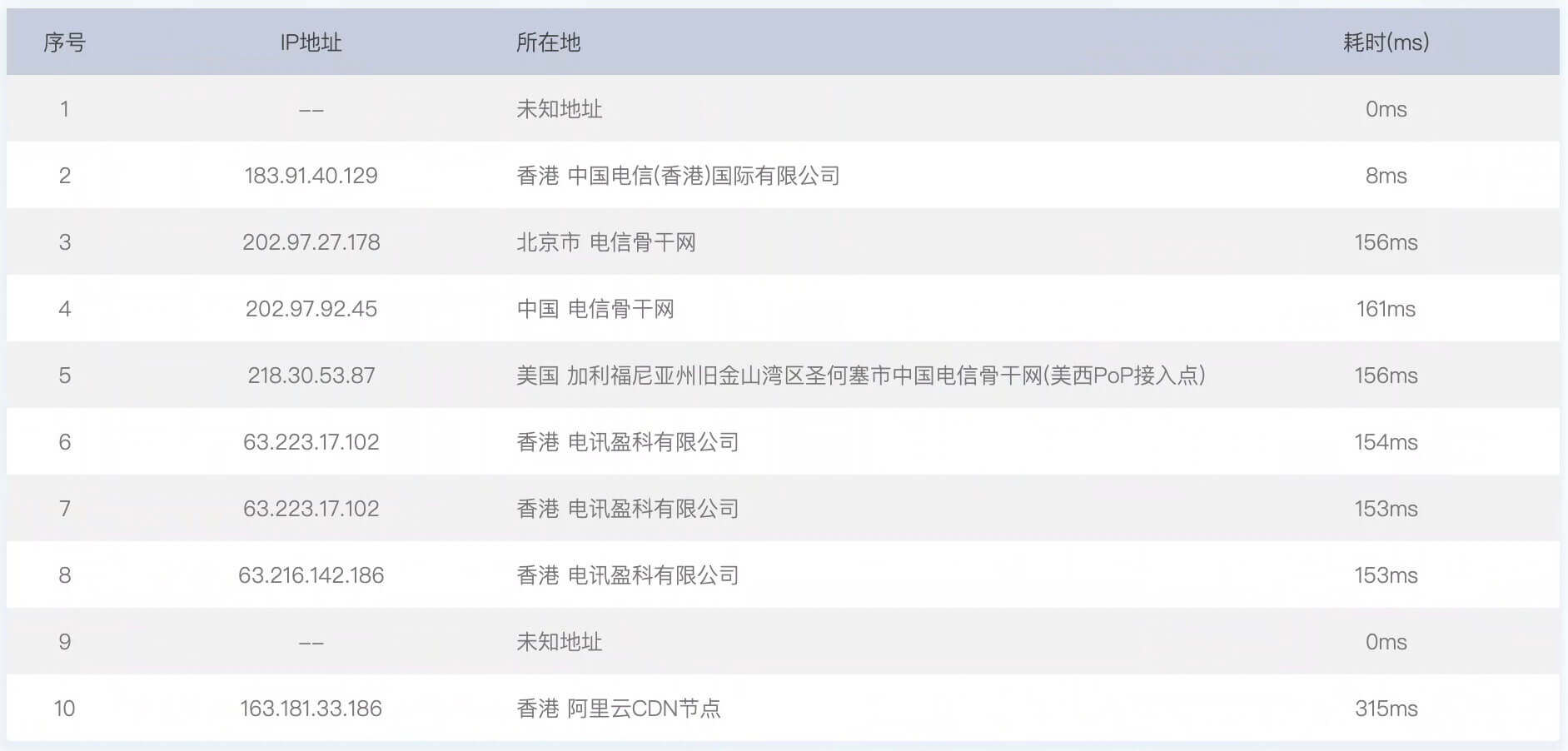
接下来,我们来看一个有意思的事情。中国电信(香港)访问kakawanyifan.com的链路。
我们看到要先从中国电信(香港)去北京,然后从国际线路出去到达美国,再从美国发到香港电讯盈科,最后到达香港阿里云CDN节点。
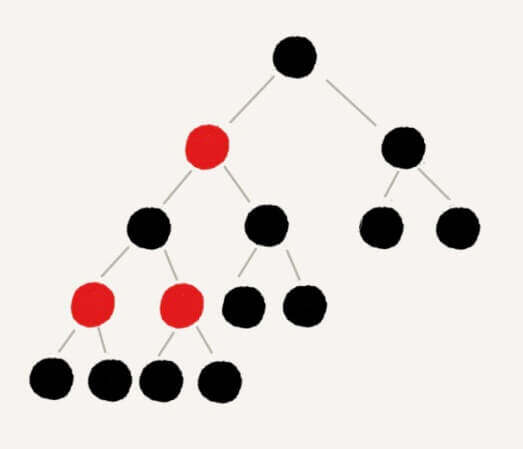
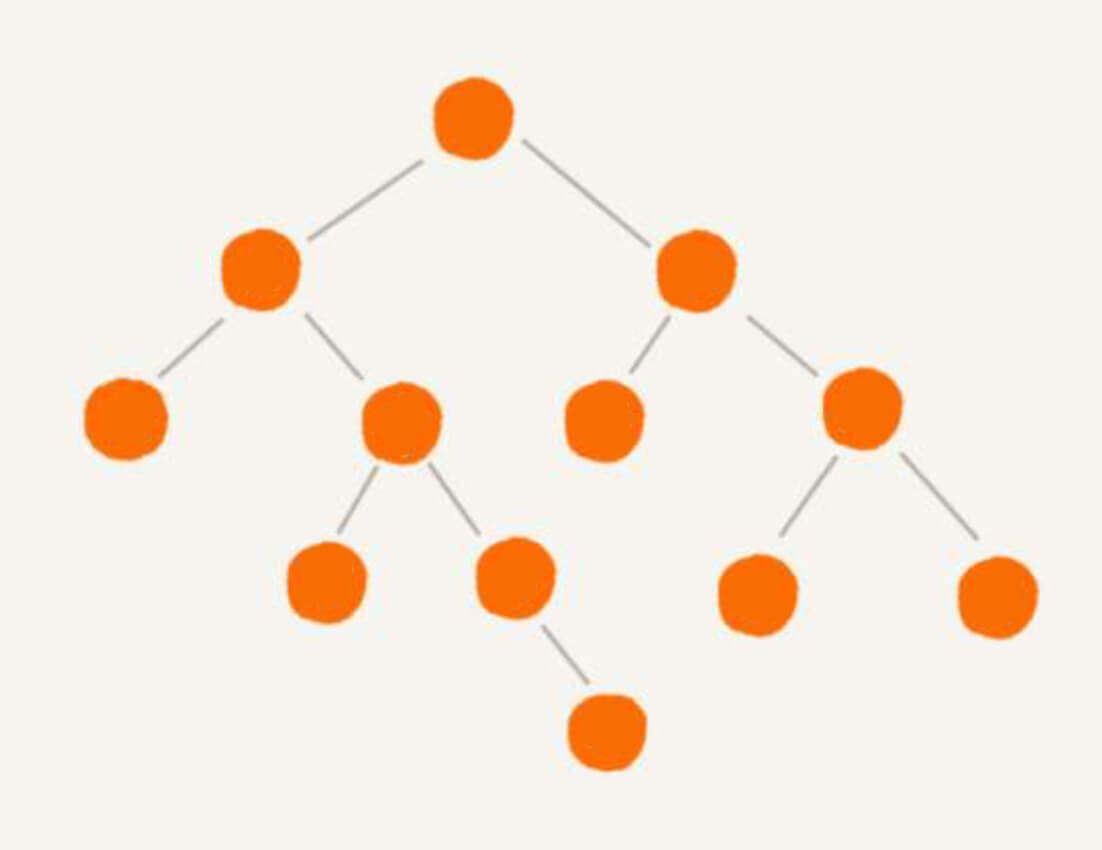
现在有这么一个二叉树形式的网络拓扑图。
在这里任何两个节点之间都存在距离,现在我们需要知道整个二叉树的最大距离,以此作为对网络拓扑的评价指标。
怎么做?
我们来具体分析一下这个问题。
现在给定出一个节点,我们需要哪些信息才能知道最大距离呢?
有这么两种情况。
最大距离不经过当前节点: 最大距离经过当前节点:
那么,我们需要左右子树提供的信息是:
最大距离 高度多少
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 package ch08;public class MaxDistance public static class Node public int value; public Node left; public Node right; public Node (int v) value = v; } } public static class Info public int maxDistance; public int height; public Info (int d,int h) maxDistance = d; height = h; } } public static Info process (Node root) if (null == root){ return new Info(0 ,0 ); } Info leftInfo = process(root.left); Info rightInfo = process(root.right); int height = Math.max(leftInfo.height,rightInfo.height) + 1 ; int maxDistance = Math.max(Math.max(leftInfo.maxDistance,rightInfo.maxDistance),leftInfo.height + rightInfo.height); return new Info(maxDistance,height); } public static void main (String[] args) Node root = new Node(6 ); root.left = new Node(4 ); root.right = new Node(8 ); root.left.left = new Node(2 ); root.left.right = new Node(5 ); root.right.left = new Node(7 ); root.right.right = new Node(9 ); root.left.left.left = new Node(1 ); root.left.left.right = new Node(3 ); System.out.println(process(root).maxDistance); } }
运行结果:
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 class Node : def __init__ (self, v) : self.value = v self.left = None self.right = None class Info : def __init__ (self, d, h) : self.max_distance = d self.height = h def process (r) : if r is None : return Info(True , 0 ) left_info = process(r.left) right_info = process(r.right) height = max(left_info.height, right_info.height) + 1 max_distance = max(left_info.max_distance, right_info.max_distance, left_info.height + right_info.height) return Info(max_distance, height) if __name__ == '__main__' : root = Node(6 ) root.left = Node(4 ) root.right = Node(8 ) root.left.left = Node(2 ) root.left.right = Node(5 ) root.right.left = Node(7 ) root.right.right = Node(9 ) root.left.left.left = Node(1 ) root.left.left.right = Node(3 ) print(process(root).max_distance)
运行结果:
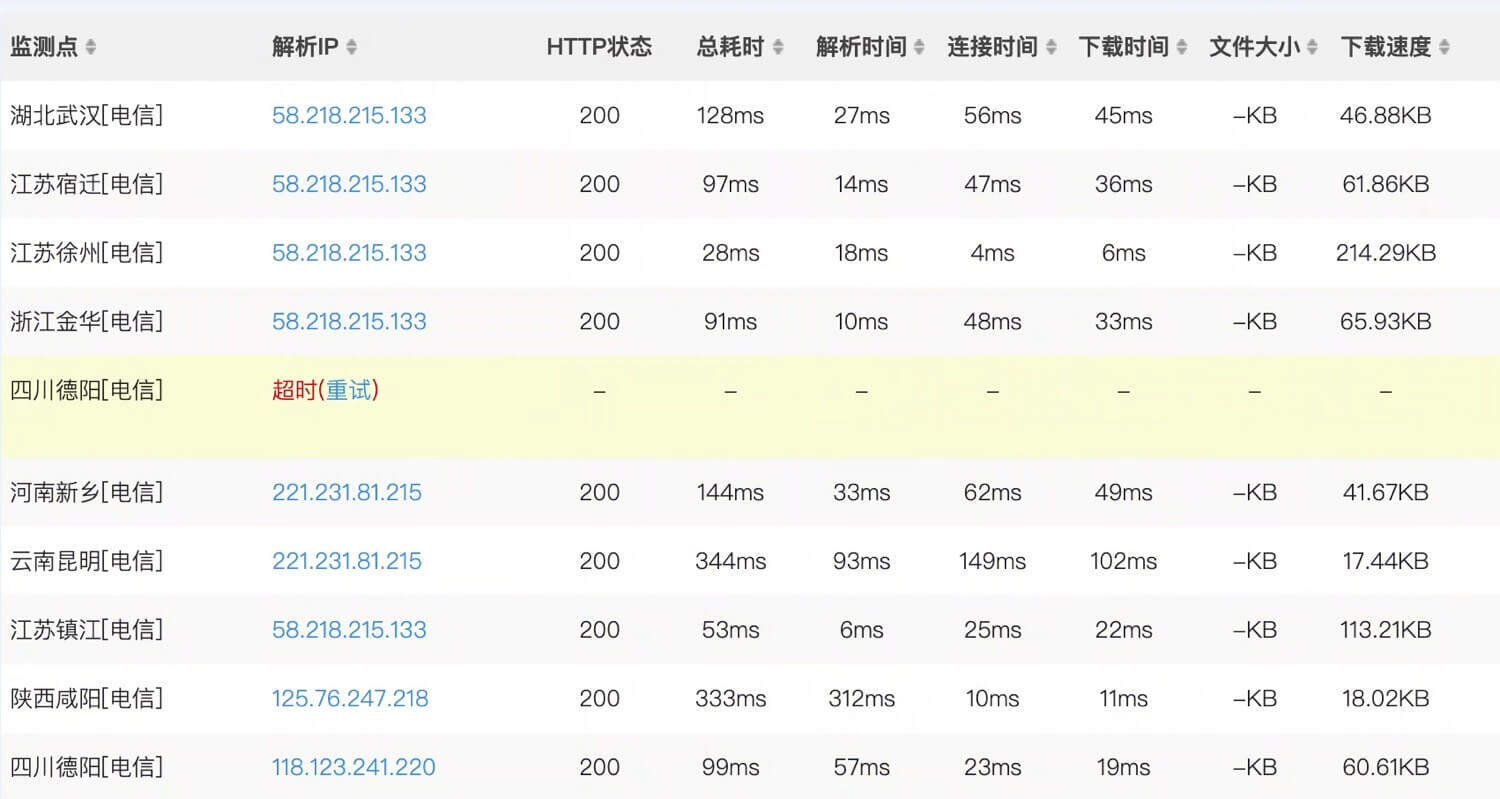
网络故障的处理
继续以网络拓扑图为例。四川德阳访问kakawanyifan.com存在超时,那么一定是中间有一个或几个节点故障了。
找到四川德阳和kakawanyifan.com之间的最低公共节点
如果公共节点有故障,处理公共节点。四川德阳到公共节点之间的线路、kakawanyifan.com到公共节点之间的线路。
现在,我们做第一步:找到四川德阳和kakawanyifan.com之间的最低公共节点。
现在给出根节点X,已经故障节点A和B。
分情况讨论:
A和B就不在以X为根节点的树上。A和B有且仅有一个以X为根节点的树上。A和B都在以X为根节点的树上。左子树和右子树各有一个 都在左子树上 都在右子树上 X就是A或者B
那么,我们需要左右子树提供的信息是:
A和B的最低公共节点是谁?不知道就回答不知道,返回空。在以你为根节点的树上,你有没有发现A? 在以你为根节点的树上,你有没有发现B?
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 package ch08;public class LowestCommonNode public static class Node public int value; public Node left; public Node right; public Node (int v) value = v; } } public static class Info public Node ans; public boolean findA; public boolean findB; public Info (Node f,boolean a,boolean b) ans = f; findA = a; findB = b; } } public static Info process (Node x,Node a,Node b) if (null == x){ return new Info(null ,false ,false ); } Info leftInfo = process(x.left,a,b); Info rightInfo = process(x.right,a,b); boolean findA = (x == a || leftInfo.findA || rightInfo.findA); boolean findB = (x == b || leftInfo.findB || rightInfo.findB); Node ans = null ; if (null != leftInfo.ans){ ans = leftInfo.ans; } if (null != rightInfo.ans){ ans = rightInfo.ans; } if (null == ans){ if (findA && findB){ ans = x; } } return new Info(ans,findA,findB); } public static void main (String[] args) Node root = new Node(6 ); Node a = new Node(5 ); Node b = new Node(1 ); root.left = new Node(4 ); root.right = new Node(8 ); root.left.left = new Node(2 ); root.left.right = a; root.right.left = new Node(7 ); root.right.right = new Node(9 ); root.left.left.left = b; root.left.left.right = new Node(3 ); System.out.println(process(root,a,b).ans.value); } }
运行结果:
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 class Node : def __init__ (self, v) : self.value = v self.left = None self.right = None class Info : def __init__ (self, f, a, b) : self.ans = f self.find_a = a self.find_b = b def process (x, a, b) : if x is None : return Info(None , False , False ) left_info = process(x.left, a, b) right_info = process(x.right, a, b) find_a = (x == a or left_info.find_a or right_info.find_a) find_b = (x == b or left_info.find_b or right_info.find_b) ans = None if left_info.ans is not None : ans = left_info.ans if right_info.ans is not None : ans = right_info.ans if ans is None : if find_a and find_b: ans = x return Info(ans, find_a, find_b) if __name__ == '__main__' : root = Node(6 ) a = Node(5 ) b = Node(1 ) root.left = Node(4 ) root.right = Node(8 ) root.left.left = Node(2 ) root.left.right = a root.right.left = Node(7 ) root.right.right = Node(9 ) root.left.left.left = b root.left.left.right = Node(3 ) print(process(root, a, b).ans.value)
运行结果:
现在,我们已经找到了四川德阳和kakawanyifan.com之间的最低公共节点,那么接下来怎么办?
小结
关于二叉树的递归方法,我们一共举了三个例子,其实都是差不多的步骤。
审题,确定需要左子树和右子树提供信息,具体什么信息再讨论。
分析可能存在哪些情况。
这些情况都需要左子树和右子树提供哪些信息。