7.哈希表

在第四章讨论递归的时候，我们多次提到了哈希表。

1. 在讨论子序列的时候，我们提到了不要出现重复字面值。当时我们说可以用哈希表来实现。
2. 在讨论排列的时候，我们提到了不要重复排列。当时我们说可以用哈希表来实现。
3. 在讨论跳台阶问题的时候，我们提到了递归的一个缺点是重复计算，当时我们说可以用哈希表可以克服这个缺点。

这一章，我们讨论哈希表。

但在开始之前，我们先来看看电影《让子弹飞》中的一个片段。

张(从袖口中甩出一把枪来，拍案，卷袖)：这个能不能挣钱？
汤：能挣，山里。
张(惊堂木拍案)：这个能不能挣钱？
汤：能挣，跪着。
张：这个加上这个，能不能站着把钱赚了？
汤：敢问九筒大哥何方神圣？
张：鄙人，张麻子！

我们这一章的主题，哈希表(Hash Table,散列表)，就是这样。
数组读取很快，但是插入和删除很慢。
链表插入和删除很快，但是读取很快。
那么如果把数组和链表结合起来呢？

链表法哈希表

第一版

在第一版，我们这么做。
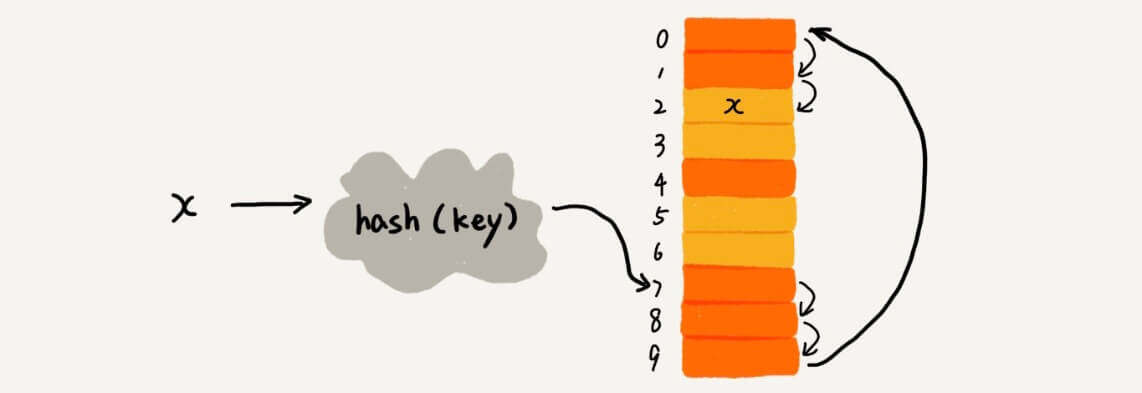
定义一个哈希函数，入参是key，出参是数组的下标。
在这里我们的每一个元素都是数字，我们直接把数字作为key。
而我们的哈希函数就是求余函数。
我们来看看怎么做增删改查。

新增
现在有11这个数字要进入哈希表了。
首先11对11求余，余数是0，所以我们放在0位置。
但我们不直接往0位置放，这么做，从0位置引出一根指针，把11放在指针所指向的区域。
对于其他的数字，我们用一样的方法进行存储。

查询
接下来我们查询哈希表中是否存在12这个数字。
同样，12对11求余，余数是1。然后我们找到1位置，一看指针指向null，
所以，没有。

删除
删除类似，也是先根据哈希函数去找位置。
比如，删除20。
20是key，hash(20)，结果是9，找到9位置，把指针所指向的区域赋值为null。

修改
而修改操作可以理解为先删除，再新增。

而且！
增删改查，修改的时间复杂度都是$O(1)$。

趁热打铁，我们再来新增一个数字。

$$22$$

22作为key，进入hash(key)，对11求余，余数是0。
所以我们找到0位置，把22放在0位置的指针所指向的区域。
一看，哟，已经有东西了，11已经在0位置了。

第二版

我们还有链表还没用上呢！

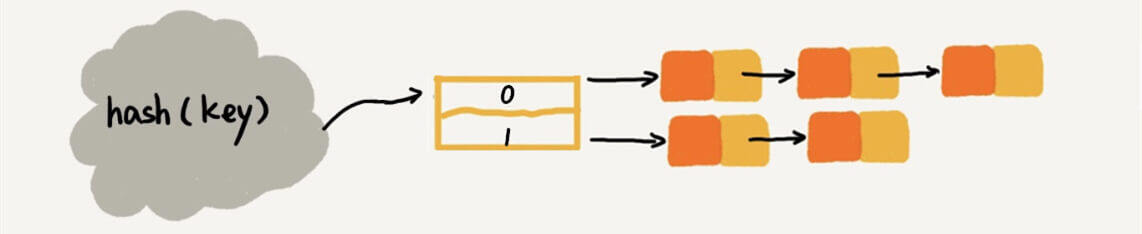
如图，是我们的第二版。
数组中每一指针都指向一个链表。当22要进入哈希表的时候，根据哈希函数，找到了0位置，然后继续从0位置所指向的链表找。
查询，删除，修改也都类似。

这种基于链表的方法就被称为链表法，是在实际中最常用的一种方法。(也有些资料称之为拉链法)
是哈希冲突已经发生了的一个解决方法。

开放地址法

我们再来讨论第二个方法，开放地址法。同样是哈希冲突已经发生了的一种解决方法。
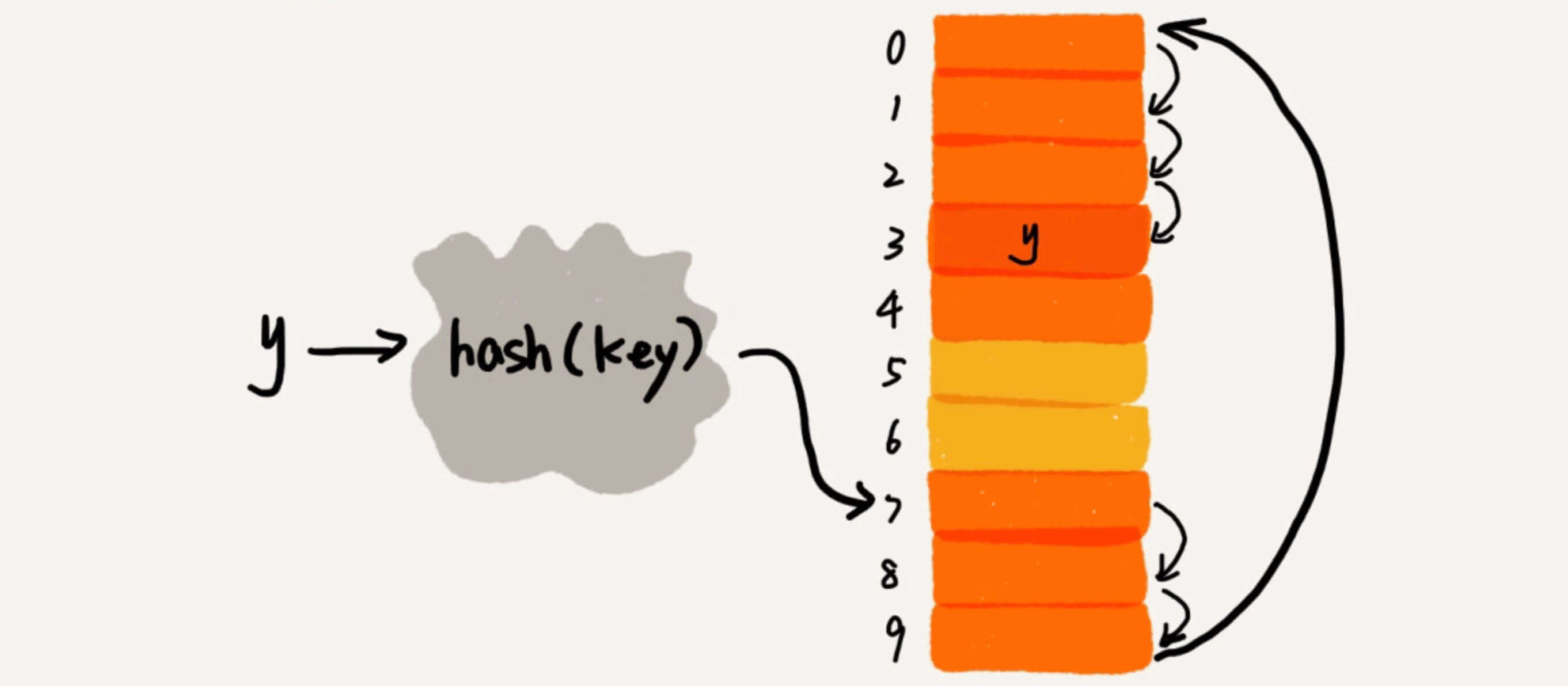
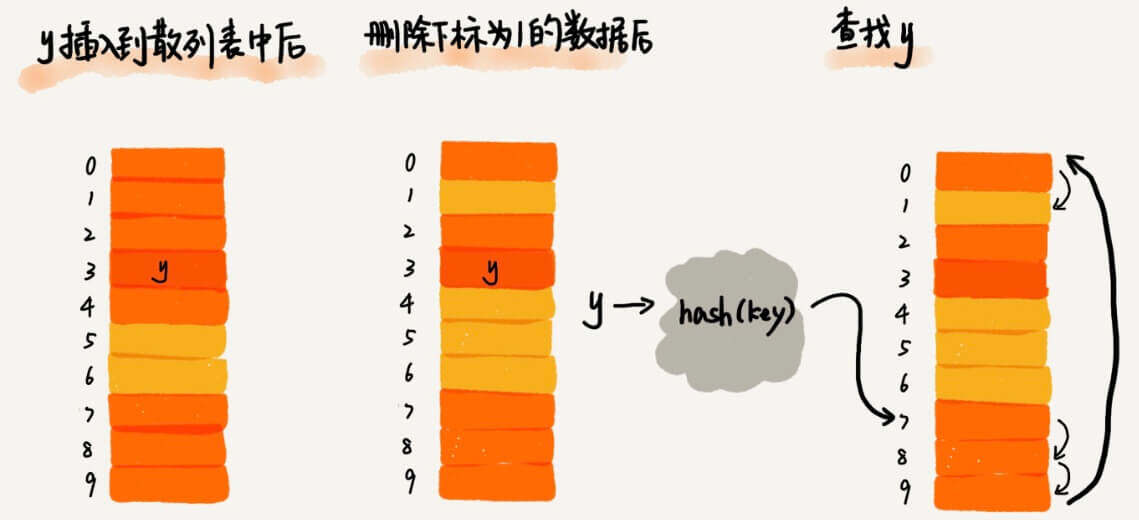
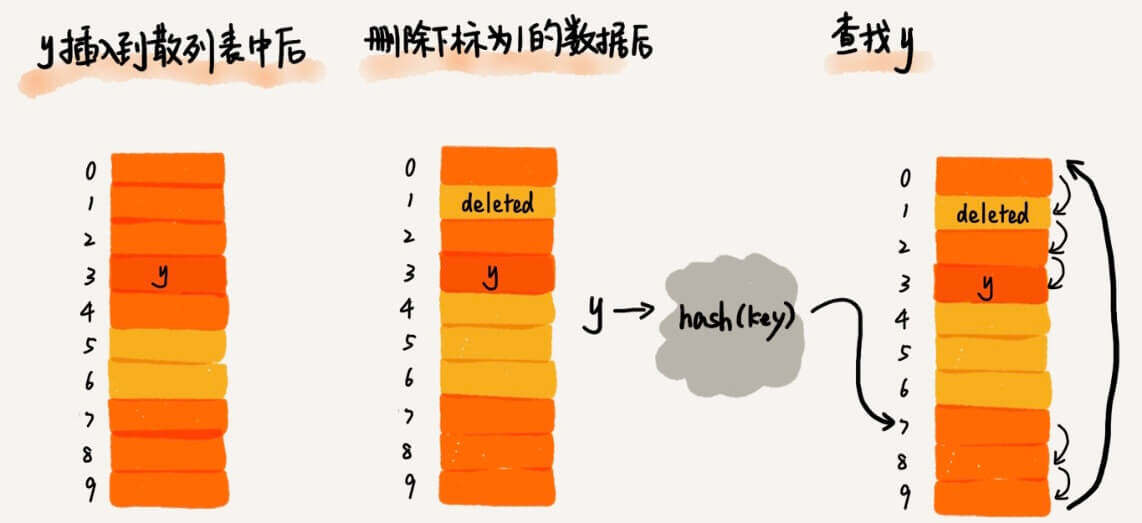
当我们往哈希表中插入数据时，如果某个数据经过哈希函数之后，存储位置已经被占用了，我们就从当前位置开始，依次往后查找，看是否有空闲位置，直到找到为止。

新增

我们用黄色的表示空闲的区域，用橙色的表现已经填了数字的区域。
现在有一个数字，x，x做为key，进入哈希函数，地址是7。
一看，7位置已经满了。所以从7位置开始，往后面找，一直找到2位置是空闲的，把x放进去。

查找
那我们怎么查找一个元素存在不存在呢？
类似的，从第一个位置开始找，如果找到空了，都没找到指定的元素，那么就是不存在。

如果在中途找到了，那就是存在。

删除

那么，删除怎么做呢？
从第一位置，一直往下找，找到元素所在位置后，将其置为空。
这样有没有问题？
这样的话，就可能会找不到实际存在的元素，然后返回空。

那我们这么做，对于删除的元素，我们不将其置为空。我们打上一个标签，比如deleted。

这样的话，就解决这个问题了。

修改，类似。我们可以理解成先删除，再新增。

但其实，开放地址法存在很大问题。当哈希表中插入的数据越来越多时，哈希冲突发生的可能性就会越来越大，空闲位置会越来越少，时间就会越来越久。极端情况下，我们可能需要遍历整个散列表，所以最坏情况下的时间复杂度为$O(n)$。同理，在删除和查找时，也有可能会遍历整张散列表，才能找到要查找或者删除的数据。

但并不是说开放寻址法就一点作用也没有。当数据量比较小、装载因子小的时候，适合采用开放寻址法。比如Java中的ThreadLocalMap

总体上，还是第一种结构更常用。接下来，我们主要基于第一种结构展开讨论。

哈希表的改进

在上一节中，我们已经讨论了哈希表的基本原理。但是为了让我们的哈希表更健壮，还有很多改进的空间。

哈希函数的改进

现在有这一个链表法哈希表。

所有的元素都集中在0位置。
查询性能急剧退化到$O(n)$。

因为我们的哈希函数是

$$X\text{对}\bold{1}\text{求余}$$

简单。
我们换一个均匀分布的哈希函数，轻松搞定。

$$X\text{对}1\text{求余，循环}11\text{次，}11\text{次的结果叠加}$$

这样的话，我们哈希函数生成的值就会随机均匀分布。

这样可以吗
当然可以，但是，是不是有点慢？

$$X\text{对}11\text{求余}$$

这样的话，我们哈希函数不会太复杂。

这就是我们对哈希函数的两个要求。

1. 生成的值要均匀分布
2. 函数不能太复杂

动态扩容

在讨论动态扩容之前，我们先讨论一下，装载因子。

$$\text{装载因子} = \frac{\text{填入表中的元素个数}}{\text{数组的长度}}$$

现在，我们有这么一个哈希表。

我们的哈希函数是

$$\text{对}2\text{求余}$$

这个哈希函数没有任何问题。均匀分布，而且也不复杂。
但是呢，这个哈希表，只要数据一多，就会很慢，甚至时间复杂度又会退到$O(n)$

其实这个也简单。
那别让装载因子别那么大不就行了，数组设置大一点嘛。

这个的确可以，那数组设置多大合适呢？
16？
万一，不够用怎么办？
那就1个G？
万一，太大了浪费怎么办？

$$\text{动态扩容}$$

这就是我们的解决方法。
在Java中，最大装载因子默认是$0.75$，超过这个就进行扩容。
在Python中，最大装载因子默认是$\frac{2}{3}$。

但是扩容的话呢，在到达最大装载因子的那一瞬间，数组扩容了，那么哈希表中的所有元素是不是要搬移？
如果哈希表本身已经足够大了，扩容，搬移，在总有那么一瞬间，会有明显的卡顿。
那这么办？

那就不要一次性搬移。

当装载因子触达阈值之后，我们只申请新空间，但并不把老的数据搬移到新哈希表中。
当有新数据要插入时，我们将新数据插入新哈希表中，并且从老的哈希表中拿出一个数据放入到新哈希表。
每次插入一个数据到哈希表，经过足够多次插入操作之后，老的哈希表中的数据就一点一点全部搬移到新哈希表中了。
这样没有了集中的一次性数据搬移，插入操作就都变得很快了。

可是，查询怎么办呢？我怎么知道应该去哪个哈希表中找数据？
一共也就新老两个哈希表，试一下呗。
对于查询操作，为了兼容了新、老哈希表中的数据，我们先从新哈希表中查找，如果没有找到，再去老的哈希表中查找。

不一次性搬移数据，这也是动态扩容中动态两个字的含义。

即，第二个改进方法是，设置合理的初始大小和最大装载因子，然后动态进行扩容。

在JDK1.8中，还有一种方法，引入红黑树。

关于红黑树我们不会讨论太多，但是在下一章我们会讨论红黑树所属于的大分支二叉树。

Java中的哈希表

Java中的哈希表有两种形式

1. HashMap
2. HashSet

其实这两种的实现机制几乎是一样的，都是基于我们刚刚讨论的哈希表。
只是在HashMap中有了一个永远跟着key的value，而在HashSet中只有key。

传值和传址

关于"传值和传址"，其实是一个很常见的现象，很多编程语言都有这个现象，在这些文章中有讨论。

• Java：《基于Java的后端开发入门：1.基础语法》，关于"基本数据类型"、"数组"和"方法"的讨论。
• Python：《基于Python的后端开发入门：1.基础语法》，关于"不可变数据类型"和"可变数据类型"的讨论。
• Python：《基于Python的后端开发入门：3.拷贝、类型注解、闭包、装饰器和一些常用的包》，关于"拷贝和深拷贝"的讨论。
• JavaScript：《基于JavaScript的前端开发入门：1.基础语法》，关于"内存分配"的讨论。

我们主要讨论一下HashMap中的一些现象。

我们知道在Java中有基础类型。int、double和float，他们也都有对应的Integer、Doubel和Float。
那么，除了名字不同，这些有什么区别呢？
int、double和float是传值。
Integer、Doubel和Float是"传址"。
(在Java中，更规范的说法是"传引用"。)

先来看 int
示例代码：

int a = 1000;
int b = 1000;
System.out.println(a == b);

运行结果：

true

这个没有任何疑问。

再来看 Integer
示例代码：

Integer a = 1000;
Integer b = 1000;
System.out.println(a == b);

运行结果：

false

居然是false，这是因为Integer、Doubel和Float是"传址"。
如果要去比较值是否相等，我们可以用equals()。

但不总是这样
示例代码：

Integer a = 127;
Integer b = 127;
System.out.println(a == b);

运行结果：

true

因为在$[-128,127]$这个区间，又回到按值传递，只有不在这个区间是"按址"。
具体原因，我们在《基于Java的后端开发入门：3.最常用的Java自带的类》中，讨论基本数据类型的包装类的时候，有详细的讨论。

但是！
在HashMap中，没有那么多弯弯绕，所有的Integer、Doubel和Float，都是传值。

那么，在HashMap中，是不是总是"传值"呢？
不是。
对于非基础类型，一般都是"传址"，比如，我们自己定义的类。
(上述特例除外)

TreeMap

TreeMap：有序表，顾名思义，在TreeMap中，所有的key都是排序好的。

所以，相比HashMap，主要多了这么4个功能。

1. firstKey()：第一个key
2. lastKey()：最后一个key
3. floorKey()：最近的小于等于某个key
4. ceilingKey()：最近的大于等于某个key

功能强大的同时，牺牲了性能，时间复杂度都是$O(\log n)$。

示例代码：

package ch07;

import java.util.TreeMap;

public class TreeMapTest {

    public static void main(String[] args) {
        TreeMap<Integer,String> treeMap = new java.util.TreeMap<Integer,String>();
        treeMap.put(3,"三");
        treeMap.put(1,"一");
        treeMap.put(4,"四");
        // treeMap.put(5,"五");
        treeMap.put(9,"九");
        treeMap.put(2,"二");
        treeMap.put(6,"六");

        System.out.println(treeMap.firstKey());
        System.out.println(treeMap.lastKey());

        System.out.println(treeMap.floorKey(5));
        System.out.println(treeMap.ceilingKey(5));

    }

}

运行结果：

1
9
4
6

那么，如果在TreeMap中，如果我们的key不是那些可以比较的基础类型呢？
比如，我们自己定义的一个类，学生类，股票类。
怎么个有序法？
这就涉及到比较器了。我们会在讨论堆的时候再讨论。

Python中的哈希表

Python中的哈希表有两种形式

1. dict
2. set

其实这两种的实现机制几乎是一样的，都是基于我们刚刚讨论的哈希表。
只是在dict中有了一个永远跟着key的value，而在set中只有key。

dict中key的比较

我们先来看现象。
示例代码：

d = {}
d[0] = '零'
d[1] = '一'
d[1.0] = '壹'
d[False] = '〇'

print(d[0])
print(d[1])
print(d[1.0])
print(d[False])

运行结果：

〇
壹
壹
〇

居然不是

零
一
壹
〇

因为：
在Python中，dict通过检查键值是否相等和比较哈希值来确定两个键是否相同.

而具有相同值的不可变对象在Python中始终具有相同的哈希值.
示例代码：

print(5 == 5.0)
print(hash(5) == hash(5.0))

运行结果：

True
True

那么都是输出〇又怎么解释？
因为：
布尔值是int的子类，True的整数值是1，而False的整数值是0
示例代码

print(isinstance(True, int))
print(isinstance(False, int))
print(True == 1 == 1.0 and False == 0 == 0.0)

运行结果：

True
True
True

原地修改

同样，我们先来看现象。
示例代码：

d = {1: '一', 2: '二'}
d.update({3: '三'})
print(d)
d = d.update({4: '四'})
print(d)

运行结果：

{1: '一', 2: '二', 3: '三'}
None

因为：
d.update()是原地修改对象并返回None。

Python这么做是为了提高性能，避免创建对象的副本。

其实，大多数修改序列/映射对象的方法，比如list.append，list.sort 等等，都是原地修改，返回None。

哈希表在递归中的应用

分支界限

那么，怎么在子序列问题中，实现不要出现重复字符面值呢？怎么在排列问题中，实现不要重复排列呢？
set。
这个方法也是最简单的。但是我们现在来讨论一个复杂的。
我们在递归的时候就进行处理，这个叫做分支界限。
每个分支在遍历之前检查一下之前是否遍历过，如果没遍历过则遍历，并记录下来；如果遍历过，则直接跳过。
我们以排列为例。

• Java
• Python

示例代码：

package ch07;

import java.util.ArrayList;
import java.util.HashMap;

public class Permutation2nd {
    /**
     * @param str   固定参数
     * @param index 来到了str[index]字符，index是位置
     * @param ans
     * @param path  之前已经决定的不能改变，即使path
     * @return
     */
    public static void process(ArrayList<Character> str, ArrayList<String> ans, String path) {
        if (str.isEmpty()) {
            ans.add(path);
            return;
        }
        // 假设就甲乙丙三人
        HashMap<Character,Boolean> visit = new HashMap<>();
        visit.put('甲',false);
        visit.put('乙',false);
        visit.put('丙',false);
        for (int i = 0; i < str.size(); i++) {
            // 如果没有出现过
            if (visit.get(str.get(i)) == false){
                visit.put(str.get(i),true);
                ArrayList<Character> temp = (ArrayList<Character>) str.clone();
                temp.remove(i);
                process(temp, ans, path + String.valueOf(str.get(i)));
            }
        }
    }


    public static void main(String[] args) {
        ArrayList<Character> l = new ArrayList<>();
        l.add('甲');
        l.add('甲');
        l.add('乙');
        ArrayList<String> ans = new ArrayList<>();
        String path = "";
        process(l, ans, path);
        System.out.println(ans);
    }
}

运行结果：

[甲甲乙, 甲乙甲, 乙甲甲]

示例代码：

def process(s, ans, path):
    if len(s) == 0:
        ans.append(path)
        return
    # 假设就甲乙丙三人
    visit = dict()
    visit['甲'] = False
    visit['乙'] = False
    visit['丙'] = False

    for i in range(len(s)):
        # 如果没有出现过
        if not visit[s[i]]:
            visit[s[i]] = True
            temp = s.copy()
            temp.pop(i)
            process(temp, ans, path + s[i])


if __name__ == '__main__':
    l = ['甲', '甲', '乙']
    ans = []
    path = ""
    process(l, ans, path)
    print(ans)

运行结果：

['甲甲乙', '甲乙甲', '乙甲甲']

记忆化搜索

最后，我们再讨论一下怎么用哈希表克服递归的重复计算。
其实很简单，因为哈希表的增删改查的时间复杂度都是$O(1)$，我们在每次计算前，都去哈希表里查一下。在每次新计算之后，都把结果存入哈希表。
这种方法，还有一个很时髦的名字，记忆化搜索。

• Java
• Python

示例代码：

package ch07;

import java.util.HashMap;

public class HashSteps {

    public static HashMap<Integer, Integer> hashSteps = new HashMap<>();
    /**
     * 跳
     * @param n
     * @return 方法数
     */
    public static int jump(int n){
        if (n == 1){
            return 1;
        }
        if (n == 2){
            return 2;
        }
        if (hashSteps.containsKey(n)){
            return hashSteps.get(n);
        }
        int res= jump(n-1) + jump(n-2);
        hashSteps.put(n,res);
        return res;
    }

    public static void main(String[] args) {
        int total = jump(6);
        System.out.println(total);
    }
}

运行结果：

13

示例代码：

hash_steps = {}


def jump(n):
    """
    跳
    :param n:
    :return:
    """
    if n == 1:
        return 1
    if n == 2:
        return 2
    if hash_steps.__contains__(n):
        return hash_steps[n]

    res = jump(n - 1) + jump(n - 2)
    hash_steps[n] = res
    return res


if __name__ == '__main__':
    total = jump(6)
    print(total)

运行结果：

13