这一章,我们会讨论两个特别有意思的问题:
用算法做投资决策
用算法玩扑克游戏
但,在讨论这两个问题之前,我们先来讨论一个之前我们提到了,但是没讨论的问题,换零钱 。动态规划 的"公式套路"。
换零钱
在《4.递归》 这一章的最后,我们讨论了跳台阶 这个问题。
【排列】 现在有N阶台阶,每次只能跳1阶或者2阶,有多少种方法?
通过这个问题,我们引出了递归的一个缺点:重复计算 。《7.哈希表》 这一章中,讨论了如何用哈希表克服这个缺点。
另外,在《4.递归》 中,我们还提到了这么一个问题:
【组合】 现在有N元钱,要换成1元的或者2元的,有多少种方法?
现在,我们来讨论换零钱。100 100 1 0 0
[ 1 , 2 , 5 , 10 , 20 , 50 ] [1,2,5,10,20,50]
[ 1 , 2 , 5 , 1 0 , 2 0 , 5 0 ]
有多少种方法?
暴力递归
我们来穷举,遍历。0 0 0 1 1 1 2 2 2 100 1 \frac{100}{1} 1 1 0 0 M M M 0 0 0 1 1 1 100 − M ∗ 1 2 \frac{100 - M*1}{2} 2 1 0 0 − M ∗ 1
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 package ch11;public class PocketMoneyRecur public static int process (int [] arr,int index,int rest) if (index == arr.length){ return rest == 0 ? 1 :0 ; } int ways = 0 ; for (int zhang = 0 ; zhang * arr[index] <= rest; zhang++) { ways = ways + process(arr,index+1 ,rest-(zhang*arr[index])); } return ways; } public static void main (String[] args) int [] arr = {1 ,2 ,5 ,10 ,20 ,50 }; int total = 100 ; System.out.println(process(arr,0 ,total)); } }
运行结果:
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 def process (arr, index, rest) : if index == len(arr): return 1 if rest == 0 else 0 ways = 0 zhang = 0 while zhang * arr[index] <= rest: ways = ways + process(arr, index + 1 , rest - (zhang * arr[index])) zhang = zhang + 1 return ways if __name__ == '__main__' : a = [1 , 2 , 5 , 10 , 20 , 50 ] total = 100 print(process(a, 0 , total))
运行结果:
记忆化搜索
在讨论跳台阶 的时候,我们说递归会有重复计算。那么换零钱 问题会有重复计算吗?
我们用了2张一元的,0张两元的。那么我们是从2位置的货币开始,换98元。
我们用了0张一元的,1张两元的。那么我们也是从2位置的货币开始,换98元。
对症下药。《7.哈希表》 中,我们用哈希表去处理跳台阶重复计算问题的方法,就是记忆化搜索。
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 package ch11;public class PocketMoneyMemory public static int process (int [] arr,int index,int rest,int [][] memory) if (memory[index][rest] != -1 ){ return memory[index][rest]; } if (index == arr.length){ memory[index][rest] = rest == 0 ? 1 :0 ; return memory[index][rest]; } int ways = 0 ; for (int zhang = 0 ; zhang * arr[index] <= rest; zhang++) { ways = ways + process(arr,index+1 ,rest-(zhang*arr[index]),memory); } memory[index][rest] = ways; return memory[index][rest]; } public static void main (String[] args) int [] arr = {1 ,2 ,5 ,10 ,20 ,50 }; int total = 100 ; int [][] memory = new int [arr.length + 1 ][total+1 ]; for (int i = 0 ; i < memory.length; i++) { for (int j = 0 ; j < memory[i].length; j++) { memory[i][j] = -1 ; } } System.out.println(process(arr,0 ,total,memory)); } }
运行结果:
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 def process (arr, index, rest, memory) : if memory[index][rest] is not None : return memory[index][rest] if index == len(arr): memory[index][rest] = 1 if rest == 0 else 0 return memory[index][rest] ways = 0 zhang = 0 while zhang * arr[index] <= rest: ways = ways + process(arr, index + 1 , rest - (zhang * arr[index]), memory) zhang = zhang + 1 memory[index][rest] = ways return memory[index][rest] if __name__ == '__main__' : a = [1 , 2 , 5 , 10 , 20 , 50 ] total = 100 memory = [[None ] * (total + 1 ) for i in range(len(a) + 1 )] print(process(a, 0 , total, memory))
运行结果:
动态规划
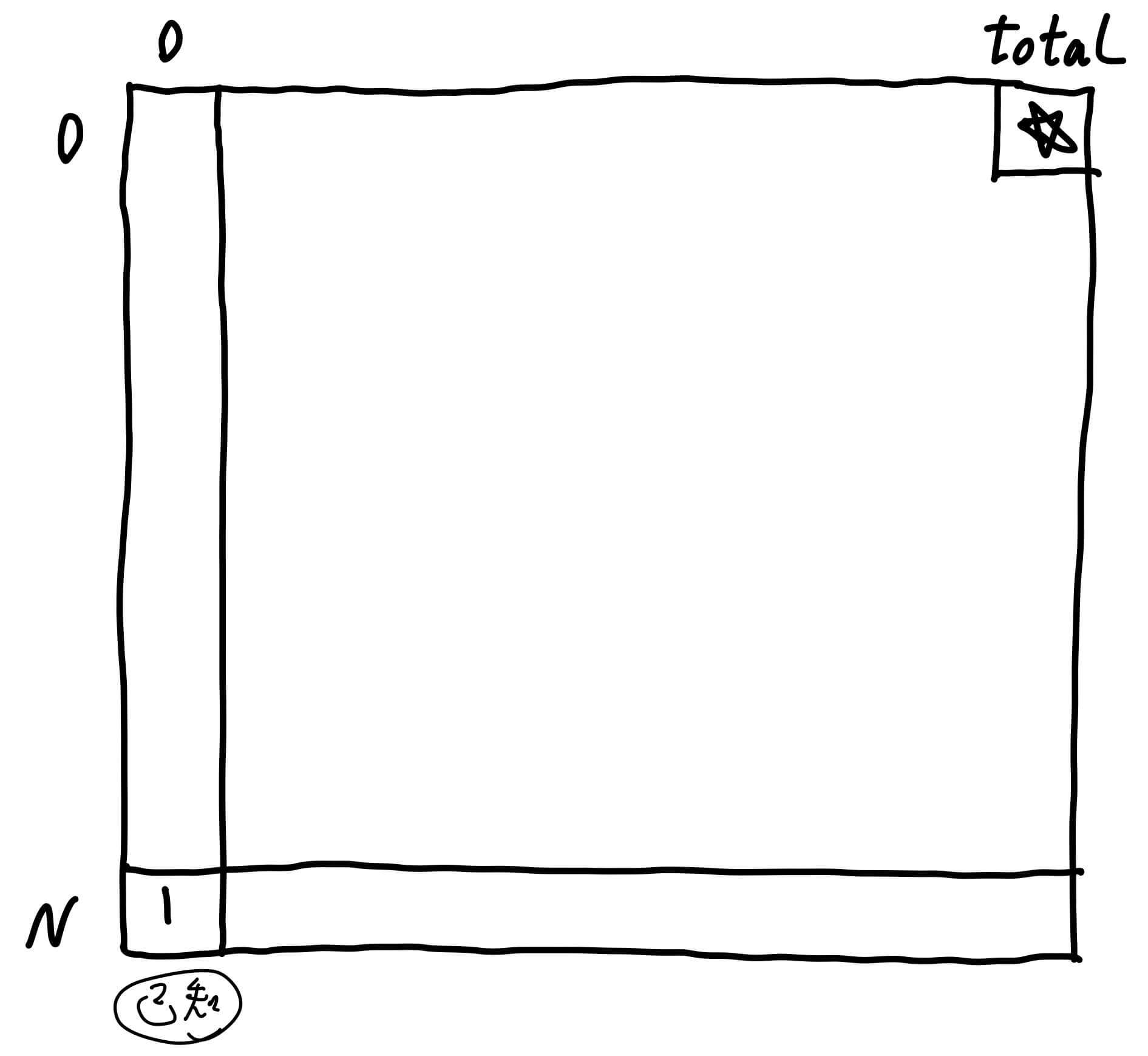
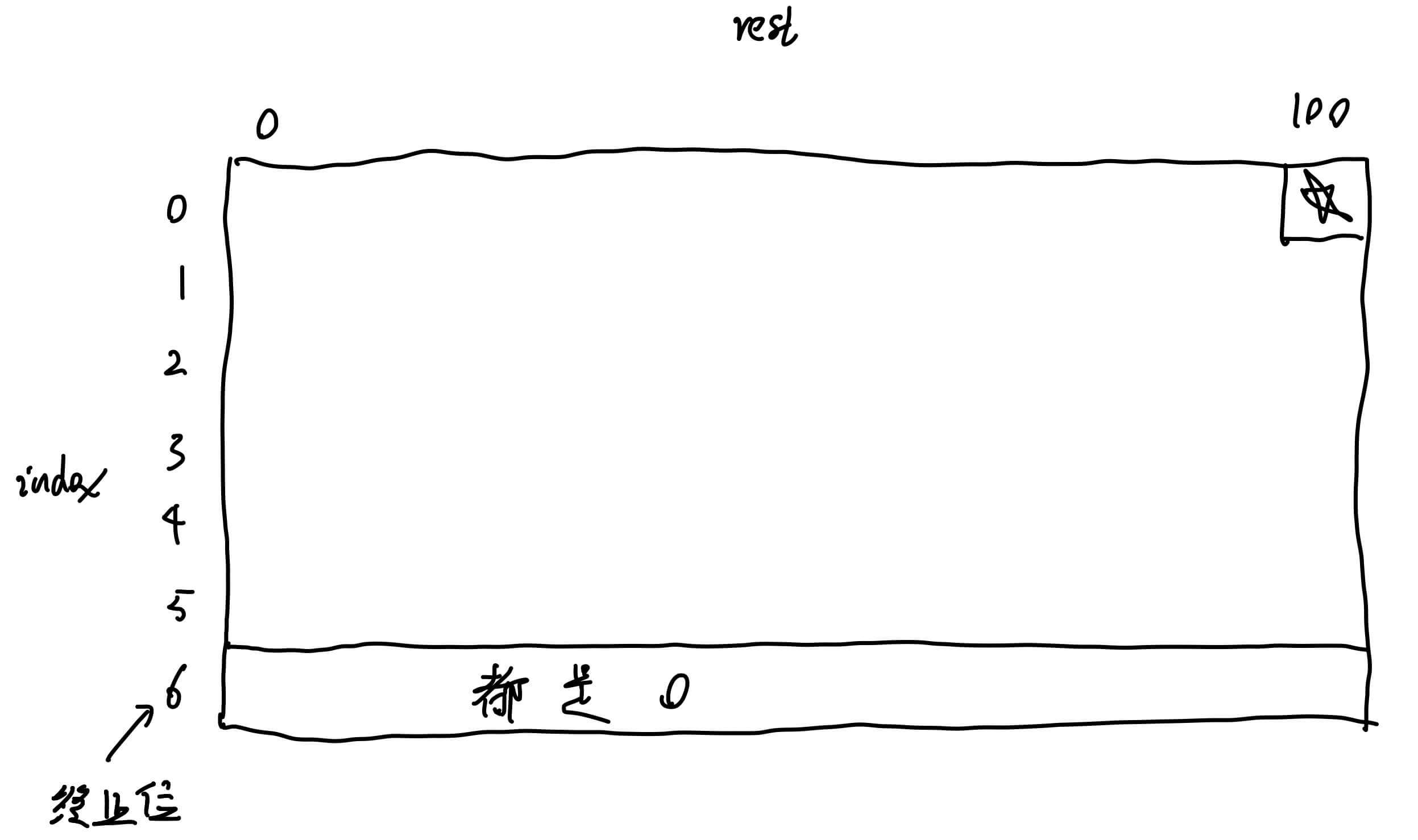
第三步,我们来做动态规划。index == arr.length且rest == 0的时候,返回1 1 1 index == arr.length都是返回0 0 0
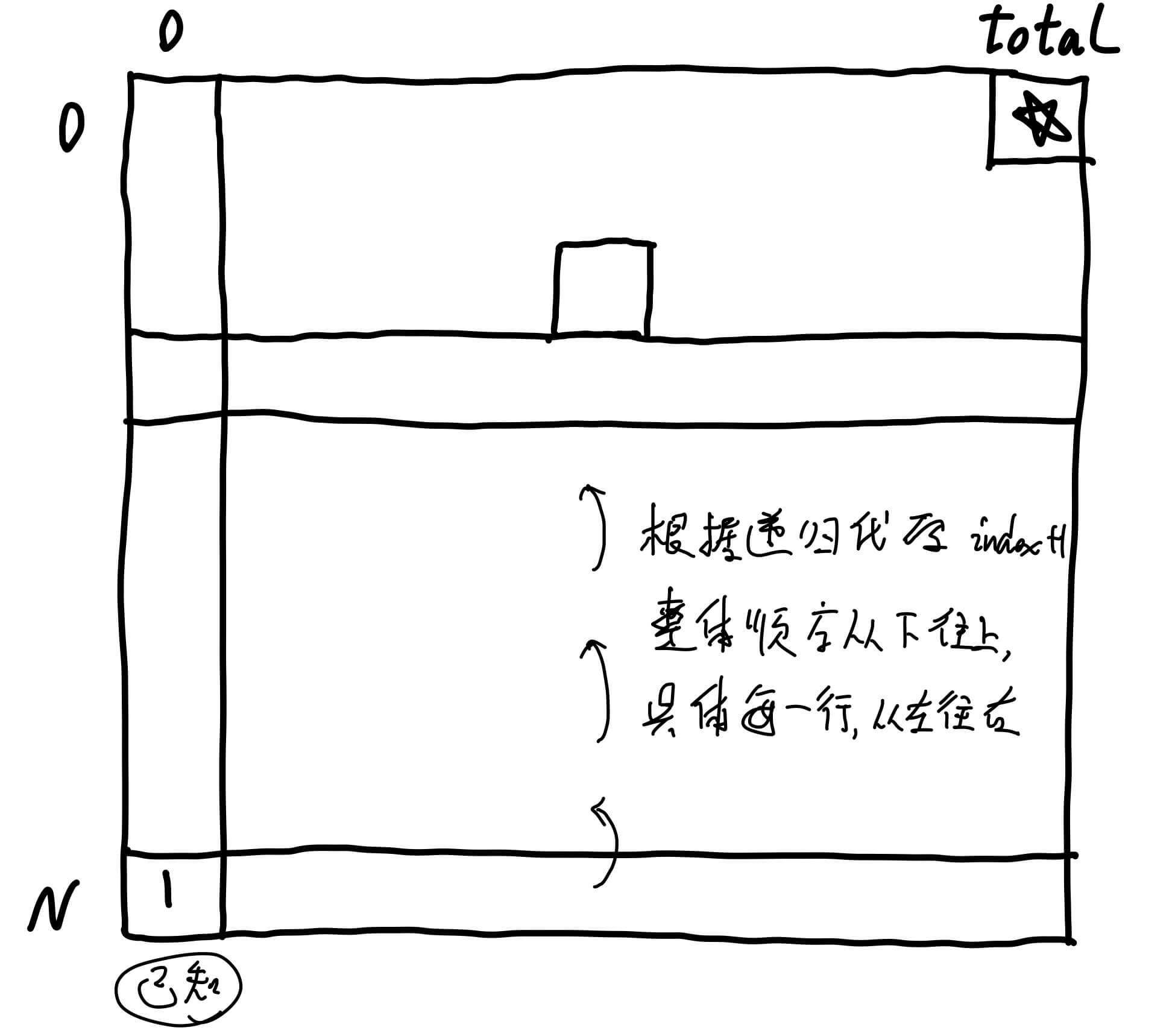
我们要求的值就是画五角星的地方。index + 1,且我们已经知道了第N行的值。
接下来,就根据这个过程写代码。
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 package ch11;public class PocketMoneyDP public static void main (String[] args) int [] arr = {1 ,2 ,5 ,10 ,20 ,50 }; int total = 100 ; int [][] dp = new int [arr.length + 1 ][total+1 ]; dp[arr.length][0 ] = 1 ; for (int index = arr.length-1 ;index >= 0 ;index--){ for (int rest = 0 ; rest <= total; rest++) { int ways = 0 ; for (int zhang = 0 ; zhang * arr[index] <= rest; zhang++) { ways = ways + dp[index+1 ][rest - (zhang * arr[index])]; } dp[index][rest] = ways; } } System.out.println(dp[0 ][total]); } }
运行结果:
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 arr = [1 , 2 , 5 , 10 , 20 , 50 ] total = 100 dp = [[0 ] * (total + 1 ) for i in range(len(arr) + 1 )] dp[len(arr)][0 ] = 1 for index in range(len(arr) - 1 , -1 , -1 ): for rest in range(0 , total + 1 , 1 ): ways = 0 zhang = 0 while zhang * arr[index] <= rest: ways = ways + dp[index + 1 ][rest - (zhang * arr[index])] zhang = zhang + 1 dp[index][rest] = ways print(dp[0 ][total])
运行结果:
代码的形式非常像"暴力递归"和"记忆化搜索"的一个整合
继续优化
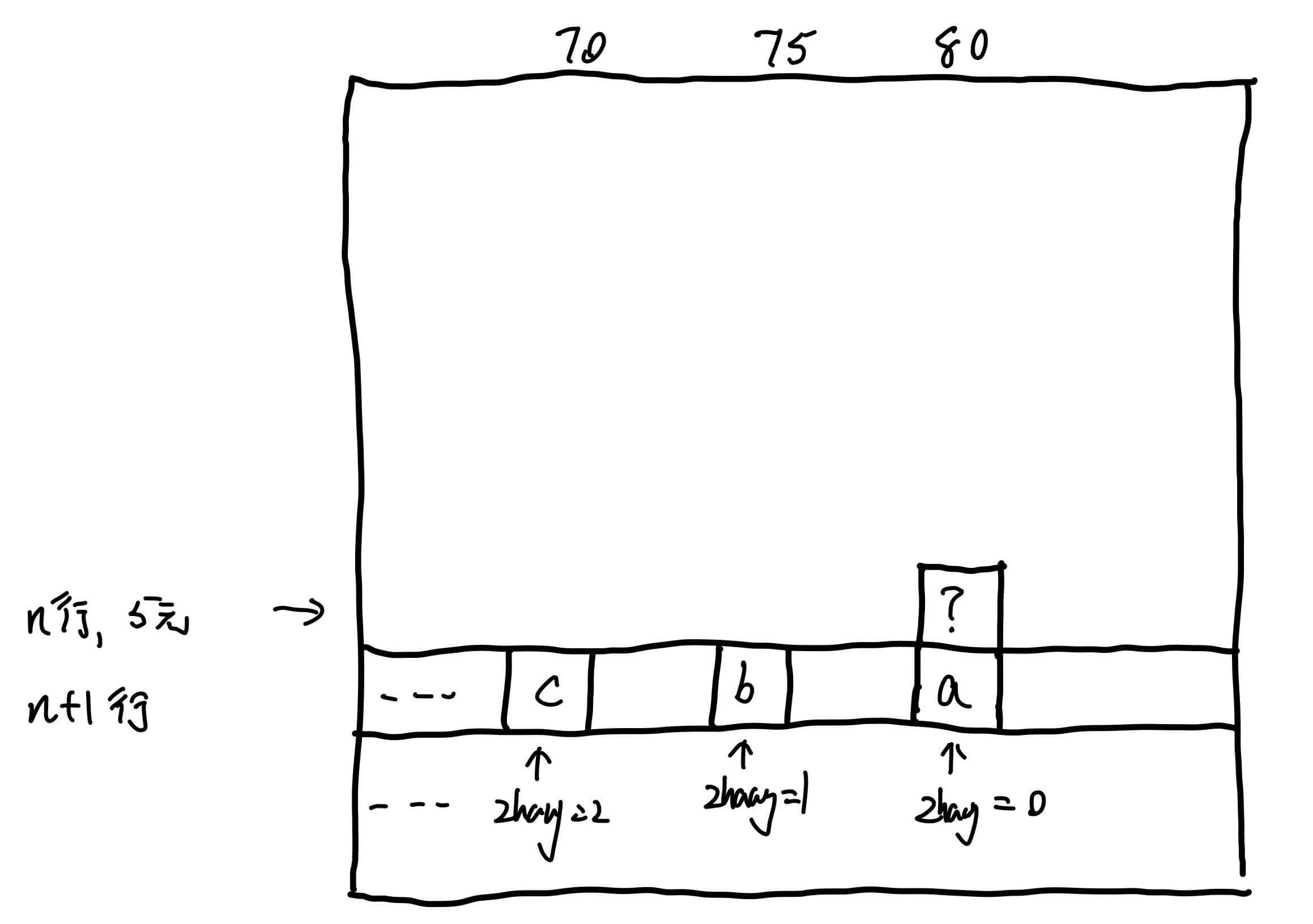
根据上面的代码,我们还可以得到如图所示的一个关系。
问号 = a + b + c + ⋯ \text{问号} = a + b + c + \cdots
问号 = a + b + c + ⋯
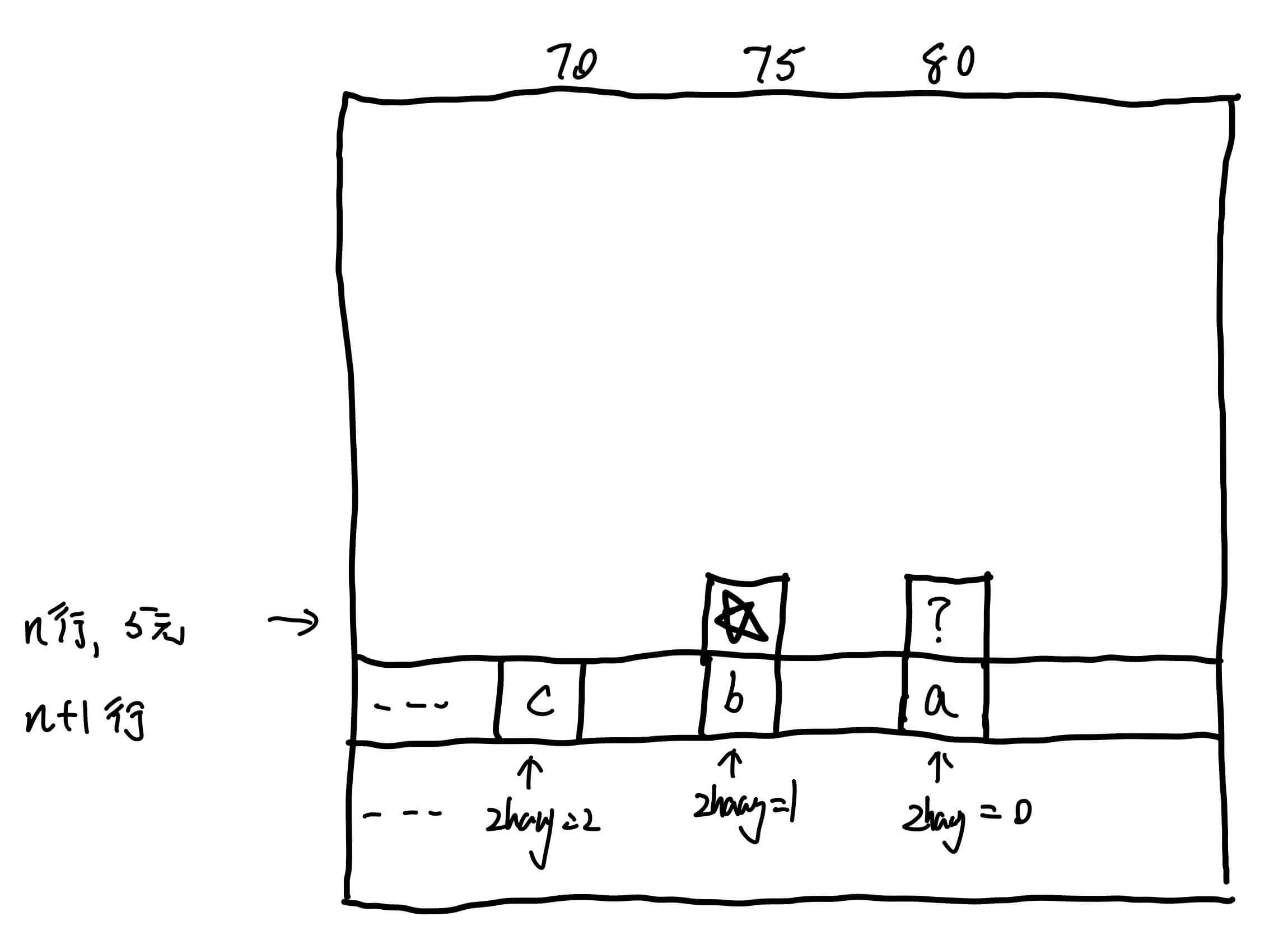
再来看,从左往右计算,我们是不是先计算 星号问号
那么星号等于多少?
星号 = b + c + ⋯ \text{星号} = b + c + \cdots
星号 = b + c + ⋯
所以,我们有:
问号 = 星号 + a \text{问号} = \text{星号} + a
问号 = 星号 + a
这就是我们继续优化后的动态规划。
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 package ch11;public class PocketMoneyDP2nd public static void main (String[] args) int [] arr = {1 ,2 ,5 ,10 ,20 ,50 }; int total = 100 ; int [][] dp = new int [arr.length + 1 ][total+1 ]; dp[arr.length][0 ] = 1 ; for (int index = arr.length-1 ;index >= 0 ;index--){ for (int rest = 0 ; rest <= total; rest++) { dp[index][rest] = dp[index + 1 ][rest]; if (rest - arr[index] >= 0 ){ dp[index][rest] = dp[index][rest] + dp[index][rest-arr[index]]; } } } System.out.println(dp[0 ][total]); } }
运行结果:
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 arr = [1 , 2 , 5 , 10 , 20 , 50 ] total = 100 dp = [[0 ] * (total + 1 ) for i in range(len(arr) + 1 )] dp[len(arr)][0 ] = 1 for index in range(len(arr) - 1 , -1 , -1 ): for rest in range(0 , total + 1 , 1 ): dp[index][rest] = dp[index + 1 ][rest] if rest - arr[index] >= 0 : dp[index][rest] = dp[index][rest] + dp[index][rest-arr[index]] print(dp[0 ][total])
运行结果:
公式套路
我们来小结一下上述过程:
首先,我们用暴力递归的方法,发现存在重复计算。
于是,我们改成记忆化搜索。
然后,我们把再做精细化组织,就是我们的动态规划。
最后,我们发现还可以再优化,那就再优化。
而,我们动态规划的代码形式非常像"暴力递归"和"记忆化搜索"的一个整合之后,我们再遇到类似的问题,也可以按照上面的公式套路,一步一步来。
背包问题
背包问题是一类问题的代表,其实有很多种形式。N N N W N W_N W N P N P_N P N M M M
那么,我们怎么做?Kruskal,贪心。
项目
一
二
三
四
五
六
资金
9
2
2
2
2
2
回报
10
2.1
2.1
2.1
2.1
2.1
现在我们的可用资金是10 10 1 0 10 9 ≈ 1.11 \frac{10}{9} \approx 1.11 9 1 0 ≈ 1 . 1 1 2.1 1 = 1.05 \frac{2.1}{1} = 1.05 1 2 . 1 = 1 . 0 5 1 1 1 10 10 1 0 10.5 10.5 1 0 . 5
暴力递归
现在,让我们按公式套路来解决问题,首先暴力递归。
穷举,比较大小。
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 package ch11;public class KnapsackRecur public static double process (double [] wArr , double [] pArr, int index, double rest) if (rest < 0 ) { return -1 ; } if (index == wArr.length) { return 0 ; } double p1 = 0 ; double next = process(wArr, pArr, index + 1 , rest - wArr[index]); if (next != -1 ) { p1 = pArr[index] + next; } double p2 = process(wArr, pArr, index + 1 , rest); return Math.max(p1, p2); } public static void main (String[] args) double [] wArr = {9.0 ,2.0 ,2.0 ,2.0 ,2.0 ,2.0 }; double [] pArr = {10.0 ,2.1 ,2.1 ,2.1 ,2.1 ,2.1 }; System.out.println(process(wArr,pArr,0 ,10 )); } }
运行结果:
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 def process (w_arr, p_arr, index, rest) : if rest < 0 : return -1 if index == len(w_arr): return 0 p1 = 0 next = process(w_arr, p_arr, index + 1 , rest - w_arr[index]) if next != -1 : p1 = p_arr[index] + next p2 = process(w_arr, p_arr, index + 1 , rest) return max(p1, p2) if __name__ == '__main__' : w_arr = [9.0 , 2.0 , 2.0 , 2.0 , 2.0 , 2.0 ] p_arr = [10.0 , 2.1 , 2.1 , 2.1 , 2.1 , 2.1 ] print(process(w_arr, p_arr, 0 , 10 ))
运行结果:
记忆化搜索
那么,在上述过程中,有重复计算吗?
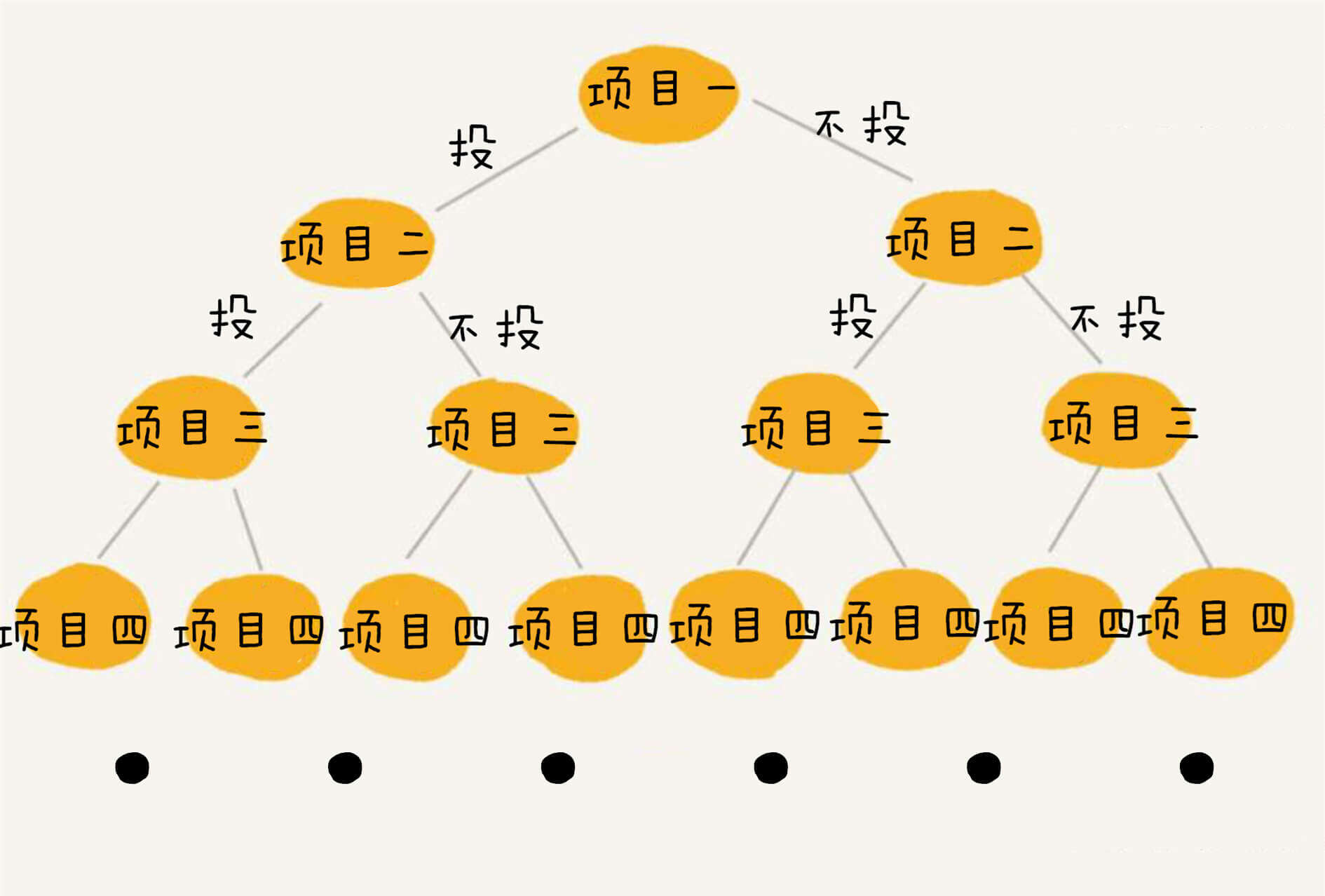
项目一不投,项目二投,项目三不投:
项目一不投,项目二不投,项目三投:
既然这样的话,我们就可以改成记忆化搜索。
与上例不同的在于,我们的资金,我们的收益,都是浮点数。
第一种方法: key = index + "-" + rest。
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 package ch11;import java.util.HashMap;public class KnapsackMemory public static double process (double [] wArr , double [] pArr, int index, double rest,HashMap<String,Double> memory) String key = index + "-" + rest; if (memory.containsKey(key)){ return memory.get(key); } if (rest < 0 ) { return -1 ; } if (index == wArr.length) { memory.put(key, 0.0 ); return memory.get(key); } double p1 = 0 ; double next = process(wArr, pArr, index + 1 , rest - wArr[index],memory); if (next != -1 ) { p1 = pArr[index] + next; } double p2 = process(wArr, pArr, index + 1 , rest,memory); memory.put(key,Math.max(p1, p2)); return memory.get(key); } public static void main (String[] args) double [] wArr = {9.0 ,2.0 ,2.0 ,2.0 ,2.0 ,2.0 }; double [] pArr = {10.0 ,2.1 ,2.1 ,2.1 ,2.1 ,2.1 }; HashMap<String,Double> memory = new HashMap<>(); System.out.println(process(wArr,pArr,0 ,10 ,memory)); } }
运行结果:
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 def process (w_arr, p_arr, index, rest, memory) : key = str(index) + '-' + str(rest) if key in memory.keys(): return memory[key] if rest < 0 : memory[key] = -1 return memory[key] if index == len(w_arr): memory[key] = 0 return memory[key] p1 = 0 next = process(w_arr, p_arr, index + 1 , rest - w_arr[index], memory) if next != -1 : p1 = p_arr[index] + next p2 = process(w_arr, p_arr, index + 1 , rest, memory) memory[key] = max(p1, p2) return memory[key] if __name__ == '__main__' : w = [9.0 , 2.0 , 2.0 , 2.0 , 2.0 , 2.0 ] p = [10.0 , 2.1 , 2.1 , 2.1 , 2.1 , 2.1 ] m = dict() print(process(w, p, 0 , 10 , m))
运行结果:
第二种方法:
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 package ch11;public class KnapsackMemory2nd public static int process (int [] wArr , int [] pArr, int index, int rest,int [][] memory) if (rest < 0 ) { return -1 ; } if (memory[index][rest] != -1 ){ return memory[index][rest]; } if (index == wArr.length) { memory[index][rest] = 0 ; return memory[index][rest]; } int p1 = 0 ; int next = process(wArr, pArr, index + 1 , rest - wArr[index],memory); if (next != -1 ) { p1 = pArr[index] + next; } int p2 = process(wArr, pArr, index + 1 , rest,memory); memory[index][rest] = Math.max(p1, p2); return memory[index][rest]; } public static void main (String[] args) double [] wArr = {9.0 ,2.0 ,2.0 ,2.0 ,2.0 ,2.0 }; double [] pArr = {10.0 ,2.1 ,2.1 ,2.1 ,2.1 ,2.1 }; int [] wArr_int = new int [wArr.length]; for (int i = 0 ; i < wArr.length; i++) { wArr_int[i] = (int ) (wArr[i] * 10 ); } int [] pArr_int = new int [pArr.length]; for (int i = 0 ; i < pArr.length; i++) { pArr_int[i] = (int ) (pArr[i] * 10 ); } int rest = 10 * 10 ; int [][] memory = new int [wArr.length + 1 ][rest + 1 ]; for (int i = 0 ; i < memory.length; i++) { for (int j = 0 ; j < memory[i].length; j++) { memory[i][j] = -1 ; } } System.out.println(process(wArr_int,pArr_int,0 ,rest,memory)/10.0 ); } }
运行结果:
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 def process (w_arr, p_arr, index, rest, memory) : if rest < 0 : return -1 if memory[index][rest] is not None : return memory[index][rest] if index == len(w_arr): memory[index][rest] = 0 return memory[index][rest] p1 = 0 next = process(w_arr, p_arr, index + 1 , rest - w_arr[index], memory) if next != -1 : p1 = p_arr[index] + next p2 = process(w_arr, p_arr, index + 1 , rest, memory) memory[index][rest] = max(p1, p2) return memory[index][rest] if __name__ == '__main__' : w = [9.0 , 2.0 , 2.0 , 2.0 , 2.0 , 2.0 ] p = [10.0 , 2.1 , 2.1 , 2.1 , 2.1 , 2.1 ] w_10 = [int(i * 10 ) for i in w] p_10 = [int(i * 10 ) for i in p] rest = 10 * 10 m = [[None ] * (rest + 1 ) for i in range(len(w_10) + 1 )] print(process(w_10, p_10, 0 , rest, m)/10.0 )
运行结果:
动态规划
按照公式套路,第三步,我们要改动态规划了。
当index == 6,无论rest等于多少,都是0。
我们需要的是0,100位置的值。
即:
那么,我们如何一步一步的推到0,100呢?
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 package ch11;public class KnapsackDP public static void main (String[] args) double [] wArr = {9.0 , 2.0 , 2.0 , 2.0 , 2.0 , 2.0 }; double [] pArr = {10.0 , 2.1 , 2.1 , 2.1 , 2.1 , 2.1 }; int [] wArr_int = new int [wArr.length]; for (int i = 0 ; i < wArr.length; i++) { wArr_int[i] = (int ) (wArr[i] * 10 ); } int [] pArr_int = new int [pArr.length]; for (int i = 0 ; i < pArr.length; i++) { pArr_int[i] = (int ) (pArr[i] * 10 ); } int rest = 10 * 10 ; int [][] dp = new int [wArr_int.length + 1 ][rest + 1 ]; for (int index = wArr_int.length - 1 ; index >= 0 ; index--) { for (int r = 0 ; r <= rest; r++) { int p1 = dp[index + 1 ][r]; int p2 = 0 ; int next = r - wArr_int[index] < 0 ? -1 : dp[index + 1 ][r - wArr_int[index]]; if (next != -1 ) { p2 = pArr_int[index] + next; } dp[index][r] = Math.max(p1, p2); } } System.out.println(dp[0 ][rest] / 10.0 ); } }
运行结果:
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 w = [9.0 , 2.0 , 2.0 , 2.0 , 2.0 , 2.0 ] p = [10.0 , 2.1 , 2.1 , 2.1 , 2.1 , 2.1 ] w_10 = [int(i * 10 ) for i in w] p_10 = [int(i * 10 ) for i in p] rest = 10 * 10 dp = [[0 ] * (rest + 1 ) for i in range(len(w_10) + 1 )] for index in range(len(w_10) - 1 , -1 , -1 ): for r in range(0 , rest + 1 , 1 ): p1 = dp[index + 1 ][r] p2 = 0 next = -1 if r - w_10[index] < 0 else dp[index + 1 ][r - w_10[index]] if next != -1 : p2 = p_10[index] + next dp[index][r] = max(p1, p2) print(dp[0 ][rest] / 10.0 )
运行结果:
预测赢家
在电影《决胜21点》中,一个由MIT的教授和学生组成的团队,靠数学在拉斯维加斯的赌场上赚钱。这个过程和量化投资极为相似(当然,金融市场不是赌场,但同样充满了不确定性),因此这部电影甚至被看作是一部和量化投资有关的电影。
现在我们就来做这么一件事情。
7 , K , A , 5 7,K,A,5
7 , K , A , 5
玩家一先拿牌,如果玩家一拿7 7 7 K K K 玩家二就可以拿K K K 玩家一为了不让玩家二拿到K K K 5 5 5 玩家二无论拿A A A 7 7 7 K K K 玩家二选择拿7 7 7 玩家一拿K K K 玩家二拿A A A 玩家一获胜,K + 5 = 18 K+5=18 K + 5 = 1 8 7 + A = 8 7+A=8 7 + A = 8
那么,这个游戏是不是先手一定会赢呢?不是。比如:
A , K , A A,K,A
A , K , A
现在,我们假设所有的玩家都知道了这个游戏的技巧,这将会是一个强有效市场,输赢从牌发下来那一刻就已经注定了。所以直接参与这个游戏,很有可能就是一个输赢各一半的游戏。
接下来,我们就讨论如何预测赢家。
A , 5 , 8 , 6 A,5,8,6
A , 5 , 8 , 6
暴力递归
同样,第一个方法是暴力递归。
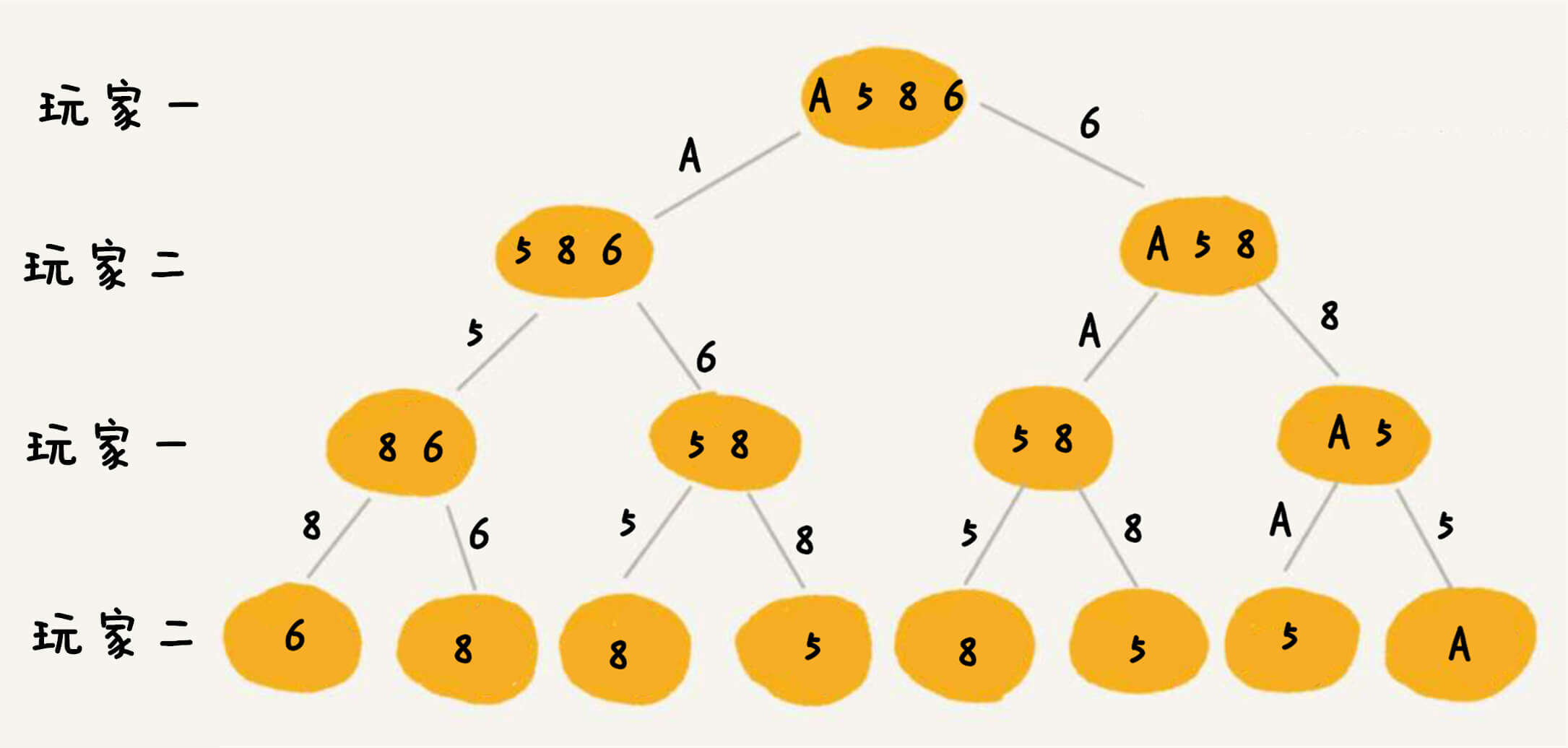
从下向上进行分析。
对于玩家一:
如果现在有8,6两张牌,如果选8的话,玩家二就会选6,赢面是2;如果选6的话,玩家二就会选8,赢面是-2。那么玩家一肯定会选8,即8,6,玩家一的赢面是2。
同理,对于5,8,玩家一肯定会选8,赢面是3。
对于5,8,玩家一的赢面是3。
对于A,5,玩家一的赢面是4。
往上,对于玩家二:
现在有5,8,6,如果选5,玩家一的赢面是2,玩家二是赢面就是3,如果选6,玩家一的赢面是3,玩家二的赢面也是3,所以在5,8,6中,玩家二的赢面是3。
同理,对于1,5,8,玩家二的赢面是4。
回到顶部:
如果玩家一选1,赢面是-2。
如果玩家一选6,赢面是2。
所以要判断玩家一是否获胜,只需要考虑max(-2,2)是否大于0。
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 package ch11;public class PredictWinnerRecur public static int predictWinner (int [] arr,int L,int R) if (L == R){ return arr[L]; } return Math.max(arr[L] - predictWinner(arr,L+1 ,R),arr[R] - predictWinner(arr,L,R-1 )); } public static void main (String[] args) int [] arr = {1 ,5 ,8 ,6 }; if (predictWinner(arr,0 ,arr.length-1 ) >= 0 ){ System.out.println("玩家一获胜" ); }else { System.out.println("玩家二获胜" ); } arr = new int []{7 , 13 , 1 , 5 }; if (predictWinner(arr,0 ,arr.length-1 ) >= 0 ){ System.out.println("玩家一获胜" ); }else { System.out.println("玩家二获胜" ); } arr = new int []{1 , 13 , 1 }; if (predictWinner(arr,0 ,arr.length-1 ) >= 0 ){ System.out.println("玩家一获胜" ); }else { System.out.println("玩家二获胜" ); } } }
运行结果:
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 def predict_winner (arr, l, r) : if l == r: return arr[l] return max(arr[l] - predict_winner(arr, l + 1 , r), arr[r] - predict_winner(arr, l, r - 1 )); if __name__ == '__main__' : a = [1 , 5 , 8 , 6 ] if predict_winner(a, 0 , len(a) - 1 ) >= 0 : print("玩家一获胜" ) else : print("玩家二获胜" ) a = [7 , 13 , 1 , 5 ] if predict_winner(a, 0 , len(a) - 1 ) >= 0 : print("玩家一获胜" ) else : print("玩家二获胜" ) a = [1 , 13 , 1 ] if predict_winner(a, 0 , len(a) - 1 ) >= 0 : print("玩家一获胜" ) else : print("玩家二获胜" )
运行结果:
记忆化搜索
那么这个问题有重复计算吗?5,8。
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 package ch11;public class PredictWinnerMemory public static int predictWinner (int [] arr,int L,int R,Integer[][] memory) if (null != memory[L][R]){ return memory[L][R]; } if (L == R){ memory[L][R] = arr[L]; return memory[L][R]; } int a = 0 ; if (null != memory[L+1 ][R]){ a = memory[L+1 ][R]; }else { a = predictWinner(arr,L+1 ,R,memory); } int b = 0 ; if (null != memory[L][R-1 ]){ b = memory[L][R-1 ]; }else { b = predictWinner(arr,L,R-1 ,memory); } memory[L][R] = Math.max(arr[L] - a,arr[R] - b); return memory[L][R]; } public static void main (String[] args) int [] arr = {1 ,5 ,8 ,6 }; Integer[][] memory = new Integer[arr.length][arr.length]; if (predictWinner(arr,0 ,arr.length-1 ,memory) >= 0 ){ System.out.println("玩家一获胜" ); }else { System.out.println("玩家二获胜" ); } arr = new int []{7 , 13 , 1 , 5 }; memory = new Integer[arr.length][arr.length]; if (predictWinner(arr,0 ,arr.length-1 ,memory) >= 0 ){ System.out.println("玩家一获胜" ); }else { System.out.println("玩家二获胜" ); } arr = new int []{1 , 13 , 1 }; memory = new Integer[arr.length][arr.length]; if (predictWinner(arr,0 ,arr.length-1 ,memory) >= 0 ){ System.out.println("玩家一获胜" ); }else { System.out.println("玩家二获胜" ); } } }
运行结果:
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 def predict_winner (arr, l, r, memory) : if memory[l][r] is not None : return memory[l][r] if l == r: memory[l][r] = arr[l] return memory[l][r] a = 0 if memory[l + 1 ][r] is not None : a = memory[l + 1 ][r] else : a = predict_winner(arr, l + 1 , r,memory) b = 0 if memory[l][r - 1 ] is not None : b = memory[l][r - 1 ] else : b = predict_winner(arr, l, r - 1 ,memory) return max(arr[l] - a, arr[r] - b) if __name__ == '__main__' : a = [1 , 5 , 8 , 6 ] m = [[None ] * (len(a) + 1 ) for i in range(len(a) + 1 )] if predict_winner(a, 0 , len(a) - 1 , m) >= 0 : print("玩家一获胜" ) else : print("玩家二获胜" ) a = [7 , 13 , 1 , 5 ] if predict_winner(a, 0 , len(a) - 1 , m) >= 0 : print("玩家一获胜" ) else : print("玩家二获胜" ) a = [1 , 13 , 1 ] if predict_winner(a, 0 , len(a) - 1 , m) >= 0 : print("玩家一获胜" ) else : print("玩家二获胜" )
运行结果:
动态规划
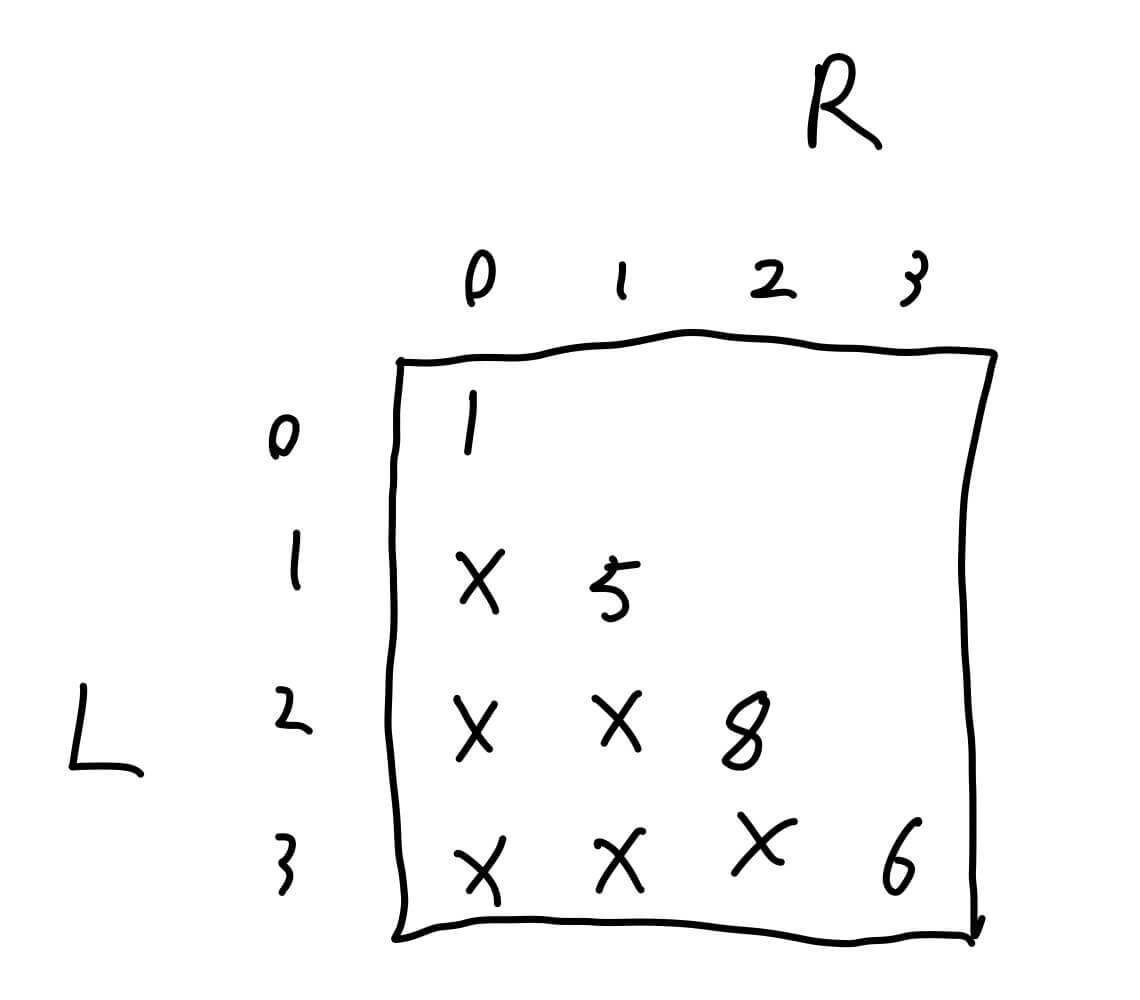
第三步,动态规划。1 5 8 6为例。
L > R,没有意义,用X表示L = R,取arr[L],在这个例子中是1 5 8 6。
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 package ch11;public class PredictWinnerDP public static int predictWinner (int [] arr) Integer[][] dp = new Integer[arr.length][arr.length]; for (int i = 0 ; i < arr.length; i++) { dp[i][i] = arr[i]; } for (int i = arr.length-1 ; i >= 0 ; i--) { for (int j = i+1 ;j< arr.length;j++){ dp[i][j]=Math.max(arr[i]-dp[i+1 ][j],arr[j]-dp[i][j-1 ]); } } return dp[0 ][arr.length-1 ]; } public static void main (String[] args) int [] arr = {1 ,5 ,8 ,6 }; if (predictWinner(arr) >= 0 ){ System.out.println("玩家一获胜" ); }else { System.out.println("玩家二获胜" ); } arr = new int []{7 , 13 , 1 , 5 }; if (predictWinner(arr) >= 0 ){ System.out.println("玩家一获胜" ); }else { System.out.println("玩家二获胜" ); } arr = new int []{1 , 13 , 1 }; if (predictWinner(arr) >= 0 ){ System.out.println("玩家一获胜" ); }else { System.out.println("玩家二获胜" ); } } }
运行结果:
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 def predict_winner (arr) : dp = [[None ] * (len(arr) + 1 ) for i in range(len(arr) + 1 )] for i in range(len(a)): dp[i][i] = arr[i] for i in range(len(arr) - 1 , -1 , -1 ): for j in range(i + 1 , len(arr), 1 ): dp[i][j] = max(arr[i] - dp[i + 1 ][j], arr[j] - dp[i][j - 1 ]) return dp[0 ][len(arr) - 1 ] if __name__ == '__main__' : a = [1 , 5 , 8 , 6 ] if predict_winner(a) >= 0 : print("玩家一获胜" ) else : print("玩家二获胜" ) a = [7 , 13 , 1 , 5 ] if predict_winner(a) >= 0 : print("玩家一获胜" ) else : print("玩家二获胜" ) a = [1 , 13 , 1 ] if predict_winner(a) >= 0 : print("玩家一获胜" ) else : print("玩家二获胜" )
运行结果: