10.自编码器和变分自编码器

在《无间道》这部电影，有一个细节特别有意思，那就是卧底陈永仁和警司黄志诚的沟通方式，是一种类似于摩斯密码的编码方式。
其中卧底陈永仁把情报通过敲击音节传给警司黄志诚，这个过程叫做编码，卧底陈永仁就是编码器。警司黄志诚收到敲击音节后，再还原回情报，这个过程叫做解码，警司黄志诚称之为解码器。

而编码器和解码器，将会贯穿我们这一章。

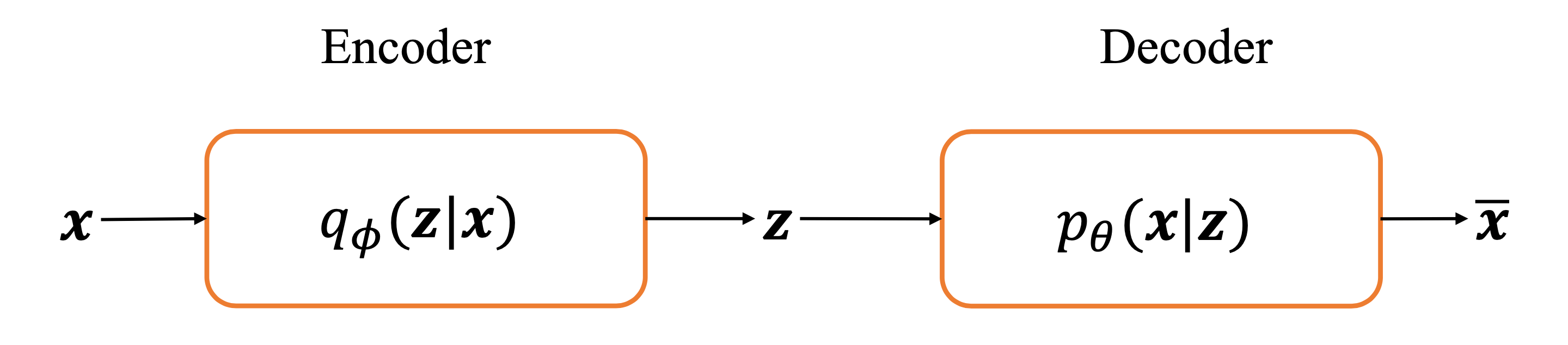
自编码器的原理

情报$\bold{x}$会被编码器编码成$\bold{z}$，$\bold{z}$又会被解码器解码成$\bold{\widehat{x}}$。这是一个非常简单的过程，但我们要注意，$\bold{\widehat{x}}$要等于$\bold{x}$，如果做不到等于的话，那也要约等于。

我们对上面的过程，再进行数学抽象。

• 函数$f()$是编码器，$\bold{z} = f(\bold{x})$。
• 函数$g()$是解码器，$\bold{\widehat{x}} = g(\bold{z}) = g(f(\bold{x}))$。
• 损失函数$loss = dist(\bold{x},\bold{\widehat{x}})$。
• 通常，我们用欧式距离(两点间的距离)来度量$\bold{x}$和$\bold{\widehat{x}}$之间的距离。也有时候不开根号，用欧式距离的平方。

那么现在，规则已经都清楚了，就差卧底陈永仁和警司黄志诚。
其实这个已经有了。

回想一下我们在《循环神经网络》这一章讨论的Word Embedding。这是不是就是一种编码方式？

$$\begin{pmatrix}1 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 \end{pmatrix}\begin{pmatrix}w_{11} & w_{12} & w_{13}\\ w_{21} & w_{22} & w_{23}\\ w_{31} & w_{32} & w_{33}\\ w_{41} & w_{42} & w_{43}\\ w_{51} & w_{52} & w_{53}\\ w_{61} & w_{62} & w_{63}\end{pmatrix}=\begin{pmatrix}w_{11} & w_{12} & w_{13}\\ w_{21} & w_{22} & w_{23}\end{pmatrix}$$

• One-Hot编码的不同行，代表不同的词语。

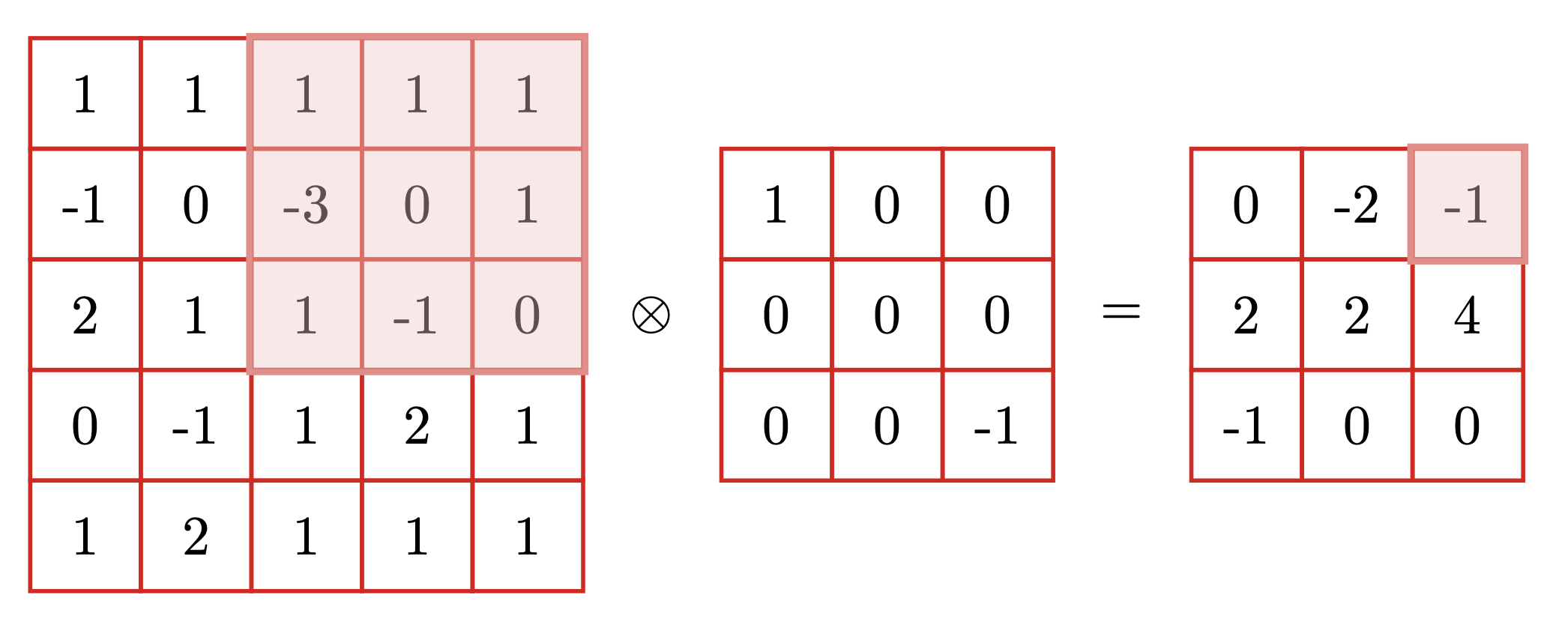
再比如，卷积神经网络中。我们的卷积运算。

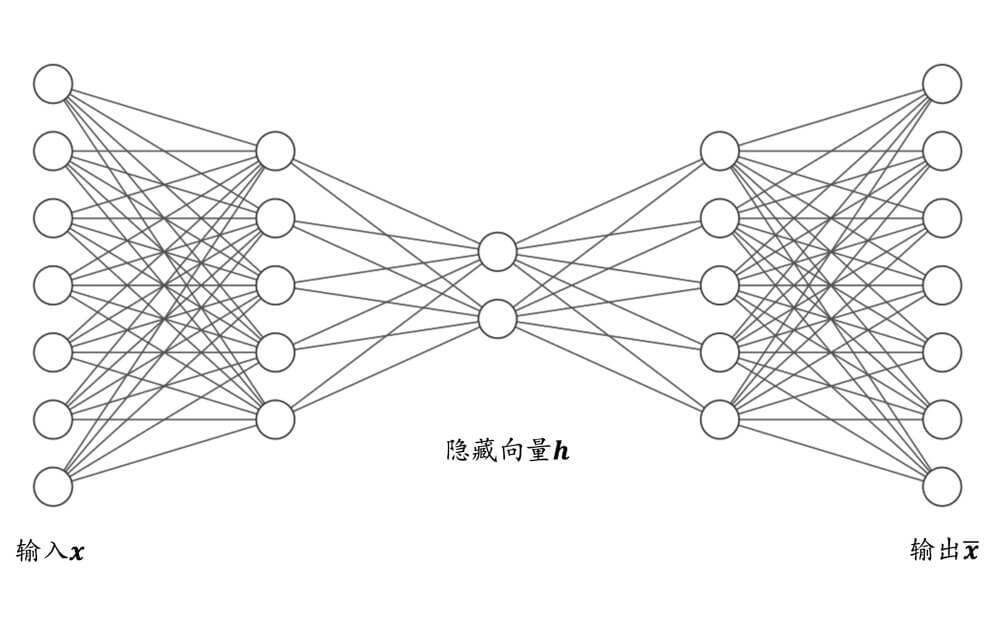
又或者，我们的全连接层网络。

接下来，我们实现一个基于全连接神经网络的自编码器。

自编码器的实现

完整可运行代码见：
https://github.com/KakaWanYifan/deep-learning-for-blog/blob/master/Ch10/Ch10-1.py

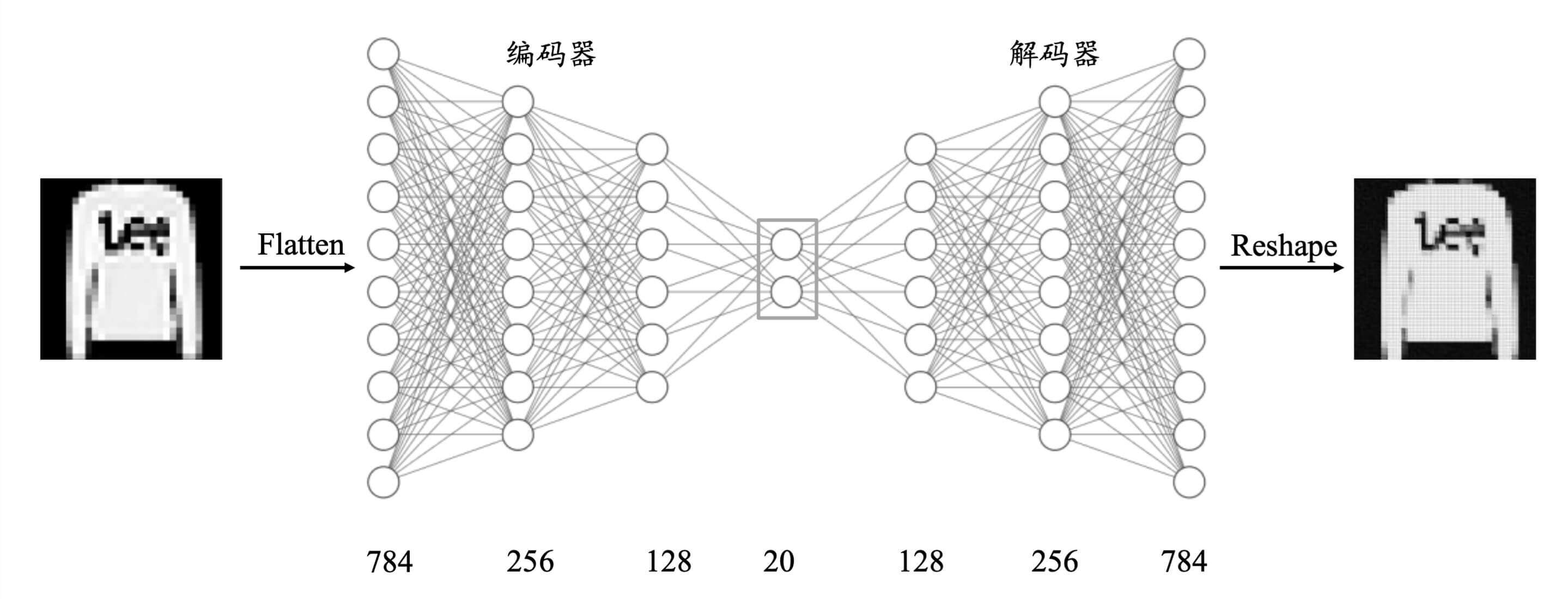
我们以Fashion MNIST的编码解码为例。
如图所示，是Fashion MNIST数据集。

神经网络模型如下：

编码器

首先，我们需要编码器(卧底陈永仁)。
三层的全连接层。
示例代码：

encoder = Sequential([
    layers.Dense(256,activation=tf.nn.relu),
    layers.Dense(128,activation=tf.nn.relu),
    layers.Dense(20)
])

解码器

然后我们需要解码器(警司黄志诚)。
示例代码：

decoder = Sequential([
    layers.Dense(128,activation=tf.nn.relu),
    layers.Dense(256,activation=tf.nn.relu),
    layers.Dense(784)
])

自编码器

编码器和解码器就合成了我们的自编码器。
这里的初始化方法和前向计算都很简单，不赘述。
示例代码：

class AE(Model):
    # 包含了Encoder和Decoder
    def __init__(self):
        super(AE, self).__init__()

        # 创建Encoders网络
        self.encoder = Sequential([
            layers.Dense(256, activation=tf.nn.relu),
            layers.Dense(128, activation=tf.nn.relu),
            layers.Dense(h_dim)
        ])
        # 创建Decoders网络 
        self.decoder = Sequential([
            layers.Dense(128, activation=tf.nn.relu), 
            layers.Dense(256, activation=tf.nn.relu),
            layers.Dense(784) 
        ])
    
    def call(self, inputs, training=None): 
        # 前向传播函数
        # 编码获得隐藏向量h,[b, 784] => [b, 20] 
        h = self.encoder(inputs)
        # 解码获得重建图片，[b, 20] => [b, 784] 
        x_hat = self.decoder(h)
        
        return x_hat

加载数据

示例代码：

# 加载Fashion MNIST图片数据集
(x_train, y_train), (x_test, y_test) = datasets.fashion_mnist.load_data()
# 归一化
x_train, x_test = x_train.astype(np.float32) / 255., x_test.astype(np.float32) / 255.
# 只需要通过图片数据即可构建数据集对象，不需要标签
train_db = tf.data.Dataset.from_tensor_slices(x_train)
train_db = train_db.shuffle(128 * 5).batch(128)
# 构建测试集对象
test_db = tf.data.Dataset.from_tensor_slices(x_test)
test_db = test_db.batch(128)

for step, x in enumerate(train_db):
    if step > 3:
        break;
    print(x.shape)

print('\n')

for step, x in enumerate(test_db):
    if step > 3:
        break;
    print(x.shape)

运行结果：

(128, 28, 28)
(128, 28, 28)
(128, 28, 28)
(128, 28, 28)


(128, 28, 28)
(128, 28, 28)
(128, 28, 28)
(128, 28, 28)

网络训练

示例代码：

model = AE()
model.build(input_shape=(None, 784))
model.summary()

optimizer = tf.optimizers.Adam(lr=0.01)

for epoch in range(5):
    for step, x in enumerate(train_db):
        # [b, 28, 28] => [b, 784]
        x = tf.reshape(x, [-1, 784])

        with tf.GradientTape() as tape:
            x_rec_logits = model(x)

            rec_loss = tf.losses.binary_crossentropy(x, x_rec_logits, from_logits=True)
            rec_loss = tf.reduce_mean(rec_loss)

        grads = tape.gradient(rec_loss, model.trainable_variables)
        optimizer.apply_gradients(zip(grads, model.trainable_variables))

        if step % 100 == 0:
            print(epoch, step, float(rec_loss))

运行结果：

Model: "ae"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
sequential (Sequential)      (None, 20)                236436    
_________________________________________________________________
sequential_1 (Sequential)    (None, 784)               237200    
=================================================================
Total params: 473,636
Trainable params: 473,636
Non-trainable params: 0
_________________________________________________________________
0 0 0.6935020685195923
0 100 0.3264176845550537
0 200 0.30031147599220276
0 300 0.2973533570766449
0 400 0.29836705327033997

【部分运行结果略】

4 0 0.2900039553642273
4 100 0.26454201340675354
4 200 0.2719815671443939
4 300 0.28770673274993896
4 400 0.2869689464569092

模型评估

比如对于图片重建，一般依赖于人工主观评价图片生成的质量，或利用某些图片逼真度计算方法(如 Inception Score 和 Frechet Inception Distance)来辅助评估。

我们这里对图片进行重建，并进行主观评估。
示例代码：

# evaluation
x = next(iter(test_db))
logits = model(tf.reshape(x, [-1, 784]))
x_hat = tf.sigmoid(logits)
# [b, 784] => [b, 28, 28]
x_hat = tf.reshape(x_hat, [-1, 28, 28])

# [b, 28, 28] => [2b, 28, 28]
# 输入的前 50 张+重建的前 50 张图片合并
x_concat = tf.concat([x[:10], x_hat[:10]], axis=0)
# 恢复为 0-255 的范围
x_concat = x_concat.numpy() * 255.
# 转换为整型
x_concat = x_concat.astype(np.uint8)

通过上面的代码，我们获得编码前的$\bold{x}$和编码后的$\bold{\widehat{x}}$。然后我们再将其绘制成图片。
示例代码：

def printImage(images):
    plt.figure(figsize=(10.0, 8.0))
    for i in range(20):
        plt.subplot(4, 5, i + 1)
        plt.xticks([])
        plt.yticks([])
        plt.grid(False)
        plt.imshow(images[i], cmap=plt.cm.binary)

    plt.show()

printImage(x_concat)

运行结果：

上面两行是$\bold{x}$，下面两行是$\bold{\widehat{x}}$。当然，因为我们只迭代了5个epoch，所以效果有限。

KL散度

刚刚我们已经体会到了，自编码器就是学习输入$\bold{x}$和隐藏变量$\bold{z}$之间映射关系。那么，如果我们给定隐藏变量$\bold{z}$的随机分布$p(\bold{z})$，如果可以学习到条件概率分布$p(\bold{x}|\bold{z})$，并通过对联合概率分布$p(\bold{x},\bold{z}) = p(\bold{x}|\bold{z})p(\bold{z})$进行采样。
这样我们是不是可以反向生成样本了呢？

如果这么做的话，我们需要有一个东西，来度量两个分布之间的距离，以此来做损失函数。KL散度。

我们决定按照这个顺序讨论，把这几个串起来。

$$\text{信息熵} \quad \longrightarrow \text{交叉熵} \quad \longrightarrow \text{KL散度}$$

信息熵

假设，现在有4个西瓜，而且4个西瓜中只有一个是好瓜。而我们对西瓜完全不了解，只能猜。这时候卖西瓜的和我们玩一个游戏，猜一次一块钱。
那么，成本最小的方式是：

graph LR 1-2{在1-2中?} 1{1?} 3{3?} g1(瓜-1) g2(瓜-2) g3(瓜-3) g4(瓜-4) 1-2 -- 是 --> 1 1-2 -- 否 --> 3 1 -- 是 --> g1 1 -- 否 --> g2 3 -- 是 --> g3 3 -- 否 --> g4

按照这个策略，我们只需要猜两次，就可以选中最好的西瓜。

那么，我们还会发现。
有4个西瓜，只有1个好瓜。而且对我们来说，每个西瓜是好瓜的概率是相等的。

$$\log_2 4 = 2\text{比特}$$

而这个$2\text{比特}$就是信息量。
其中每个西瓜的信息量是$- \log_2 \frac{1}{4}$
那么四个西瓜的信息量就是

$$-\bigg (\sum_{i=1}^{4} \frac{1}{4} * \log_2 \frac{1}{4} \bigg ) = 2$$

即确定一个有$n$种等可能情况的概率需要$\log_2 n$的信息。
换句话说，一个事件发生的概率是$\frac{1}{n}$的话，为了消除不确定，需要的信息量是：

$$\quad -\bigg (\sum_{i=1}^{n} \frac{1}{n} * \log_2 \frac{1}{n} \bigg ) \quad$$

现在改一下。我们对西瓜也略知一二。
我们认为每个西瓜是好瓜的概率如下：

1	2	3	4
0.4	0.3	0.2	0.1

那么，这时候，我们需要多少信息量去挑选好瓜呢？或者我们需要多少信息量去消除不确定呢？

$$(-{0.4}\log_2{0.4}) + (-\log{0.3}\log_2{0.3}) + (-{0.2}\log_2{0.2}) + (-{0.1}\log_2{0.1})$$

这就是我们的信息熵的公式：

$$H(X) = - \sum_{i\in X} p(i) * \log_2 p(i)$$

交叉熵

我们把信息熵的公式改一下。

$$H(X) = - \sum_{i\in X} p(i) * \log_2 q(i)$$

• 把$\log_2 p(i)$换成$\log_2 q(i)$。

这就是交叉熵的公式，用于度量两个概率分布间的差异性信息。

提起交叉熵，我们很容易会联想到一个损失函数：交叉熵损失。
交叉熵的公式：

$$H(\bold{p}||\bold{q}) = - \sum_i p_i \log_2 q_i$$

KL散度

KL散度又被称为相对熵，那么既然是熵呢，肯定也和信息熵、交叉熵一样，是衡量混乱程度的。

$$\begin{aligned} D_{KL}(\bold{p}||\bold{q}) &= H(\bold{p}||\bold{q}) - H(\bold{p}) \\ &= \text{p和q的交叉熵} - \text{p的熵} \end{aligned}$$

特别需要注意的是：

• $D_{KL}(\bold{p}||\bold{q}) \neq D_{KL}(\bold{q}||\bold{p})$
• $H(\bold{p}||\bold{q}) \neq H(\bold{q}||\bold{p})$

这个被称为不对称性。

为什么是交叉熵损失

再讨论一个问题。为什么之前我们的损失函数都是交叉熵损失，不是KL散度？
当$\bold{p}$固定时，那么最小化KL散度$D_{KL}(\bold{p}||\bold{q})$，等价于最小化交叉熵$H(\bold{p}||\bold{q})$。
我们通过公式也可以看出来。

$$D_{KL}(\bold{p}||\bold{q}) = H(\bold{p}||\bold{q}) - H(\bold{p})$$

$\bold{p}$都固定了，最小化$D_{KL}(\bold{p}||\bold{q})$，不就是在最小化$H(\bold{p}||\bold{q})$吗？

那么既然两者等价呢，我们何必再折腾去减个$H(\bold{p})$呢？直接用交叉熵损失。

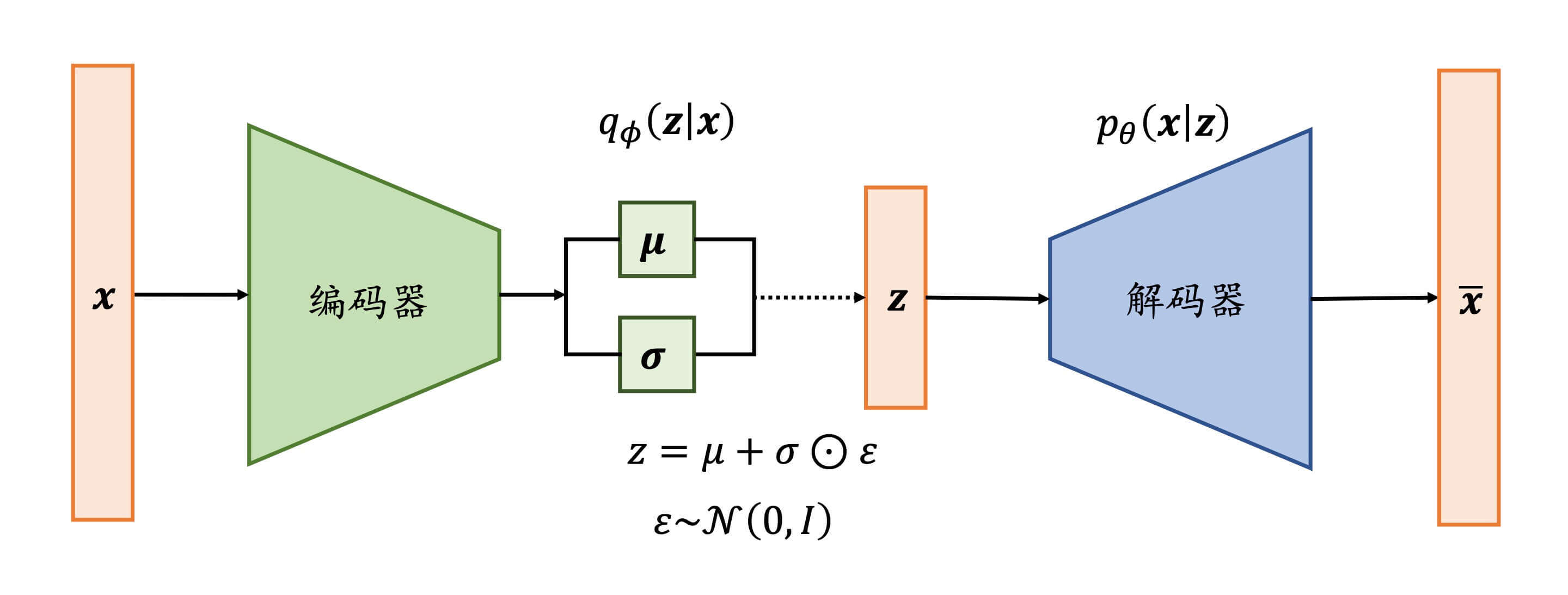
变分自编码器的原理

如图，是变分自编码起的网络结构。

编码器把$\bold{x}$编码为$\bold{z}$，解码器把$\bold{z}$解码为$\bold{\widetilde{x}}$。唯一不同的地方，我们对$\bold{z}$增加约束，希望$\bold{z}$符合某个分布$p(\bold{z})$。这样的话，对于一个给定的$\bold{z}$，我们可以通过分布$p(\bold{x}|\bold{z})$生成一系列的样本。

那么，这时候我们需要一个分布$q_{\phi}(\bold{z}|\bold{x})$来逼近$p(\bold{z}|\bold{x})$。用什么来衡量逼近的程度呢？就是我们之前讨论的KL散度。

损失函数

$$\min_{\phi} D_{KL}(q_{\phi}(\bold{z}|\bold{x})||p(\bold{z}|\bold{x}))$$

这就是$q_{\phi}(\bold{z}|\bold{x})$的$p(\bold{z}|\bold{x})$KL散度的表达式，我们用KL散度的公式，进行展开。

$$D_{KL}(q_{\phi}(\bold{z}|\bold{x})||p(\bold{z}|\bold{x})) = \sum_z q_{\phi}(\bold{z}|\bold{x}) \log \frac{q_{\phi}(\bold{z}|\bold{x})}{p(\bold{z}|\bold{x})}$$

我们知道$p(\bold{z}|\bold{x}) \cdot p(\bold{x}) = p(\bold{x},\bold{z})$，则有

$$\begin{aligned} D_{KL}(q_{\phi}(\bold{z}|\bold{x})||p(\bold{z}|\bold{x})) &= \sum_z q_{\phi}(\bold{z}|\bold{x}) \log \frac{q_{\phi}(\bold{z}|\bold{x}) p(\bold{x})}{p(\bold{x},\bold{z})} \\ &= \sum_z q_{\phi}(\bold{z}|\bold{x}) \log \frac{q_{\phi}(\bold{z}|\bold{x})}{p(\bold{x},\bold{z})} + \sum_z q_{\phi}(\bold{z}|\bold{x}) \log p(\bold{x}) \\ &= -\bigg( - \sum_z q_{\phi}(\bold{z}|\bold{x}) \log \frac{q_{\phi}(\bold{z}|\bold{x})}{p(\bold{x},\bold{z})} \bigg) + \log p(\bold{x}) \end{aligned}$$

我们把$\Big( - \sum_z q_{\phi}(\bold{z}|\bold{x}) \log \frac{q_{\phi}(\bold{z}|\bold{x})}{p_{\theta}(\bold{x},\bold{z})} \Big)$记做$L(\phi,\theta)$。
因此

$$D_{KL}(q_{\phi}(\bold{z}|\bold{x})||p(\bold{z}|\bold{x})) = - L(\phi,\theta) + \log p(\bold{x})$$

我们知道$D_{KL}(q_{\phi}(\bold{z}|\bold{x})||p(\bold{z}|\bold{x})) \ge 0$，要使得$D_{KL}(q_{\phi}(\bold{z}|\bold{x})||p(\bold{z}|\bold{x}))$最小，就要$L(\phi,\theta)$最大。

所以：

$$\text{损失函数从} \min_{\phi} D_{KL}(q_{\phi}(\bold{z}|\bold{x})||p(\bold{z}|\bold{x})) \quad \longrightarrow \quad \max L(\phi,\theta)$$

那么，如何使得$L(\phi,\theta)$最大呢？
我们把$L(\phi,\theta)$进行展开变换

$$\begin{aligned} L(\phi,\theta) &= \sum_z q_{\phi}(\bold{z}|\bold{x}) \log \frac{p(\bold{x},\bold{z})}{q_{\phi}(\bold{z}|\bold{x})} \\ &= \sum_z q_{\phi}(\bold{z}|\bold{x}) \log \frac{p(\bold{z})p_{\theta}(\bold{x}|\bold{z})}{q_{\phi}(\bold{z}|\bold{x})} \end{aligned}$$

再进行变换操作，最后

$$L(\phi,\theta) = - D_{KL}\bigg(q_{\phi}(\bold{z}|\bold{x})||p(\bold{z})\bigg) + \mathbf{E}_{z \sim q}\bigg[ \log p_{\theta}(\bold{x}|\bold{z})\bigg]$$

所以：

$$\text{损失函数从} \max L(\phi,\theta) \quad \longrightarrow \quad \begin{cases} \min D_{KL}(q_{\phi}(\bold{z}|\bold{x})||p(\bold{z})) \\ \max \mathbf{E}_{z \sim q}[ \log p_{\theta}(\bold{x}|\bold{z})] \end{cases}$$

小结：

$$\min_{\phi} D_{KL}(q_{\phi}(\bold{z}|\bold{x})||p(\bold{z}|\bold{x})) \ \longrightarrow \ \max L(\phi,\theta) \quad \longrightarrow \quad \begin{cases} \min D_{KL}(q_{\phi}(\bold{z}|\bold{x})||p(\bold{z})) \\ \max \mathbf{E}_{z \sim q}[ \log p_{\theta}(\bold{x}|\bold{z})] \end{cases}$$

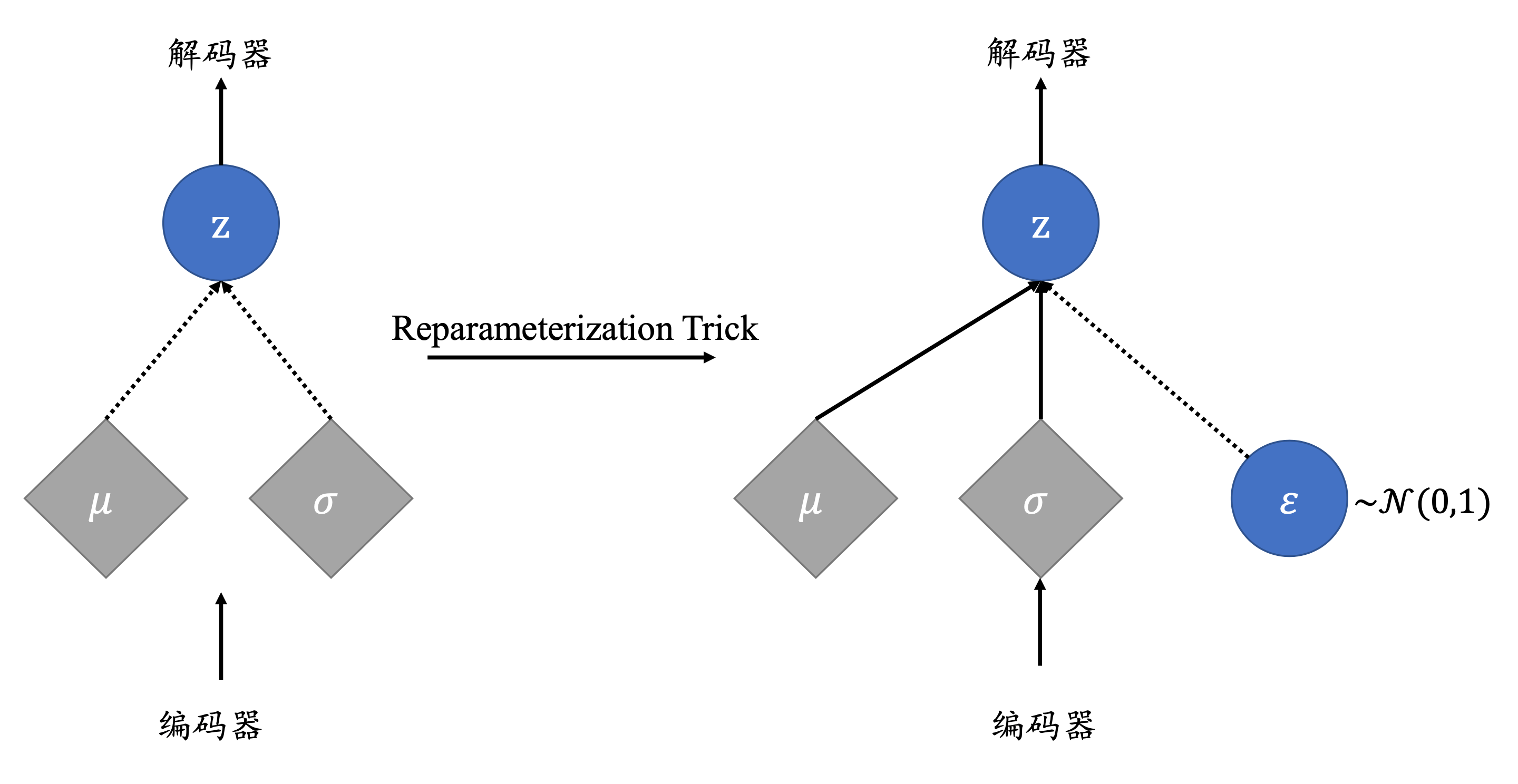
Reparameterization Trick

现在，再让我们看一下这个过程。我们预设$\bold{z}$符合某个分布$p(\bold{z})$，比如$\bold{N}(\mu,\sigma^2)$，然后我们每次从这个分布中进行抽样。
抽样有什么问题？抽样本身当然没问题，肯定要进行抽样。问题是这样反向传播，是没法传到到$\mu$和$\sigma^2$的，毕竟抽样是随机的，抽样这个过程是不可以进行微分的。
那怎么办呢？

我们通过$z = \mu + \sigma \odot \varepsilon$进行抽样，$\varepsilon \sim \bold{N}(0,1)$。
这样的话，$\bold{z}$依旧服从分布$\bold{N}(\mu,\sigma^2)$。
这样的话，$\frac{\partial z}{\partial \mu}$是可导的，$\frac{\partial z}{\partial \sigma}$也是可导的。
有一个不可导，$\frac{\partial z}{\partial \varepsilon}$，但是这个不可导，又有什么关系呢，$\varepsilon \sim \bold{N}(0,1)$，我们并不会去更新这一部分的参数。

这个操作叫做Reparameterization Trick。

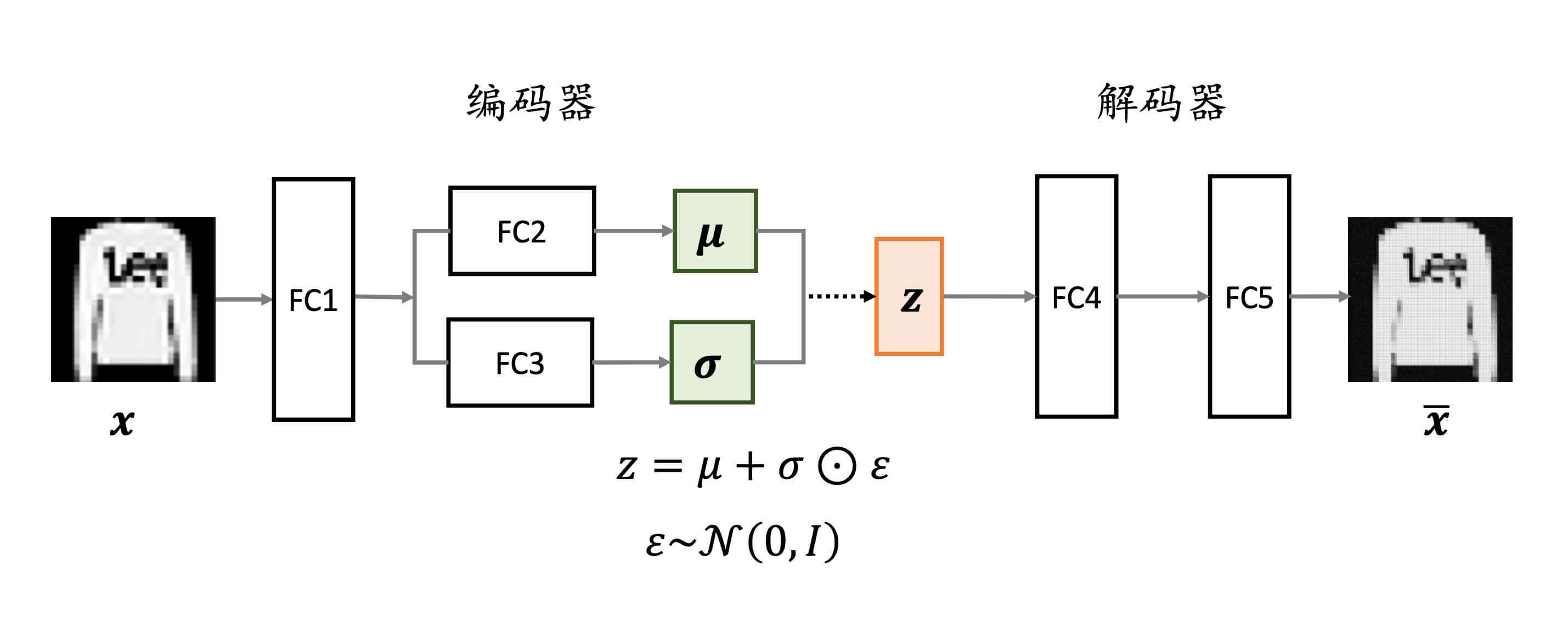
整个网络的结构如下：

• 通常解码器网络层输出的是$\log \sigma^2$，而不是$\sigma$，这么做的原因是$\log \sigma^2$$(-\infty,+\infty)$，而$\sigma^2$的值域是$[0,+\infty)$。相当于自带激活函数。后面再把$\log \sigma^2$还原回$\sigma$。

变分自编码器的实现

完整可运行代码见：
https://github.com/KakaWanYifan/deep-learning-for-blog/blob/master/Ch10/Ch10-2.py

我们继续以Fashion MNIST的编码解码为例。

初始化方法

示例代码：

class VAE(Model):

    def __init__(self):
        super(VAE, self).__init__()

        # 编码器
        self.fc1 = layers.Dense(128)
        # 均值
        self.fc2 = layers.Dense(10)
        # 方差
        self.fc3 = layers.Dense(10)
        
        # 解码器
        self.fc4 = layers.Dense(128)
        self.fc5 = layers.Dense(784)

前向计算

接下来，我们来实现前向计算。

1、编码器的前向计算
正如之前的讨论，通常得到的是$\log \sigma^2$，而不是$\sigma$。
示例代码：

def encoder(self, x):

    h = tf.nn.relu(self.fc1(x))
    # 均值
    mu = self.fc2(h)
    # 方差的log
    log_var = self.fc3(h)

    return mu, log_var

2、解码器的前向计算
示例代码：

def decoder(self, z):

    out = tf.nn.relu(self.fc4(z))
    out = self.fc5(out)

    return out

3、Reparameterization Trick
在这里我们会把$\log \sigma^2$还原回$\sigma$。
示例代码：

def reparameterize(self, mu, log_var):

    eps = tf.random.normal(log_var.shape)
    std = tf.exp(log_var)**0.5
    z = mu + std * eps

    return z

4、call方法
示例代码：

def call(self, inputs, training=None):

    # [b, 784] => [b, 10], [b, 10]
    mu, log_var = self.encoder(inputs)
    # Reparameterization Trick
    z = self.reparameterize(mu, log_var)

    x_hat = self.decoder(z)

    return x_hat, mu, log_var

模型训练

示例代码：

model = VAE()
model.build(input_shape=(4, 784))
model.summary()

optimizer = tf.optimizers.Adam(lr=0.01)

for epoch in range(5):
    for step, x in enumerate(train_db):
        # [b, 28, 28] => [b, 784]
        x = tf.reshape(x, [-1, 784])

        with tf.GradientTape() as tape:
            x_rec_logits, mu, log_var = model(x)

            rec_loss = tf.nn.sigmoid_cross_entropy_with_logits(labels=x, logits=x_rec_logits)
            rec_loss = tf.reduce_sum(rec_loss) / x.shape[0]

            kl_div = -0.5 * (log_var + 1 - mu ** 2 - tf.exp(log_var))
            kl_div = tf.reduce_sum(kl_div) / x.shape[0]

            loss = rec_loss + 1. * kl_div

        grads = tape.gradient(loss, model.trainable_variables)
        optimizer.apply_gradients(zip(grads, model.trainable_variables))

        if step % 100 == 0:
            print(epoch, step, 'kl div:', float(kl_div), 'rec loss:', float(rec_loss))

运行结果：

Model: "vae"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense (Dense)                multiple                  100480    
_________________________________________________________________
dense_1 (Dense)              multiple                  1290      
_________________________________________________________________
dense_2 (Dense)              multiple                  1290      
_________________________________________________________________
dense_3 (Dense)              multiple                  1408      
_________________________________________________________________
dense_4 (Dense)              multiple                  101136    
=================================================================
Total params: 205,604
Trainable params: 205,604
Non-trainable params: 0
_________________________________________________________________
0 0 kl div: 2.082995891571045 rec loss: 545.6994018554688
0 100 kl div: 14.052530288696289 rec loss: 256.65277099609375
0 200 kl div: 14.115103721618652 rec loss: 253.49703979492188
0 300 kl div: 12.919075012207031 rec loss: 245.1560821533203
0 400 kl div: 12.998880386352539 rec loss: 243.81082153320312

【部分运行结果略】

4 0 kl div: 13.248461723327637 rec loss: 237.49778747558594
4 100 kl div: 12.899820327758789 rec loss: 232.00466918945312
4 200 kl div: 13.066536903381348 rec loss: 235.38673400878906
4 300 kl div: 13.595346450805664 rec loss: 234.9623260498047
4 400 kl div: 13.309326171875 rec loss: 240.35516357421875

评估模型

我们要发挥变分自编码器的优势，做点自编码器不能做的事情。比如：生成样本。
示例代码：

z = tf.random.normal((128, 10))
logits = model.decoder(z)
x_hat = tf.sigmoid(logits)
x_hat = tf.reshape(x_hat, [-1, 28, 28]).numpy() *255.
x_hat = x_hat.astype(np.uint8)
printImage(x_hat)

运行结果：

我们看到衣服和鞋子的模样已经画出来了。但这只是一个demo，我们的epoch设置得很低。如果想获得更好的效果，可以调整参数、学习率等。
但即便如此，效果还是有限。

如果想获得更好的效果，那需要新的模型。
生成对抗网络

下一章，我们讨论生成对抗网络。