2.numpy

关于通过np.array()所创建的，到底是应该被称为数组，还是矩阵，其实各有优劣。

• 从字面意思上，似乎应该是数组，但是其有能进行很多矩阵才有的运算。
• 如果称其为矩阵的话，那么拼接、分割和排序这些，似乎又是数组才有的特性。

本文，结合具体讨论的内容，矩阵和数组，两个名词，会进行穿插，

numpy

numpy，一款在Python中做科学计算的基础库，也是大部分Python科学计算库的基础库。

官网：https://numpy.org

创建数组

array()

np.array()用以创建numpy中的数组。

示例代码：

import numpy as np

a = np.array([1,2,3,4,5])
b = np.array((range(1,6)))

print(a)
print(b)

运行结果：

[1 2 3 4 5]
[1 2 3 4 5]

示例代码：

import numpy as np

l = [[1, 2], [1, 1]]
print(l)

a = np.array(l)
print(a)

print(type(a))

运行结果：

[[1, 2], [1, 1]]
[[1 2]
 [1 1]]
<class 'numpy.ndarray'>

其他方法

arange()

numpy.arange()：

arange([start,] stop[, step,], dtype=None)

示例代码：

import numpy as np
a = np.arange(1,6,2)
print(a)

运行结果：

[1 3 5]

mat()

利用mat()创建数组，示例代码：

import numpy as np

l = [[1, 2], [1, 1]]
print(l)

am = np.mat(l)
print(am)

print(type(am))

运行结果：

[[1, 2], [1, 1]]
[[1 2]
 [1 1]]
<class 'numpy.matrix'>

array()和mat()的区别

通过打印的type，我们能看出一些区别。

• 通过array()方法创建的，类型是<class 'numpy.ndarray'>
• 通过mat()方法创建的，类型是<class 'numpy.matrix'>

在计算速度方面，<class 'numpy.ndarray'>的计算速度要快过<class 'numpy.matrix'>。

有些资料说：

• <class 'numpy.matrix'>，可以通过运算符直接进行运算。
• <class 'numpy.ndarray'>，不能直接通过运算符进行运算。

可能对于老版本的Numpy是这样的，但是对于新版本的不是这样( 但是！需要注意矩阵相乘运算。 )。

<class 'numpy.matrix'>，可以通过运算符直接进行运算，示例代码：

print(am + am)
print(am - am)
print(am * am)
print(am / am)

运行结果：

[[2 4]
 [2 2]]
[[0 0]
 [0 0]]
[[3 4]
 [2 3]]
[[1. 1.]
 [1. 1.]]

<class 'numpy.ndarray'>，也可以通过运算符直接进行运算，示例代码：
示例代码：

print(a + a)
print(a - a)
print(a * a)
print(a @ a)
print(a / a)

运行结果：

[[2 4]
 [2 2]]
[[0 0]
 [0 0]]
[[1 4]
 [1 1]]
[[3 4]
 [2 3]]
[[1. 1.]
 [1. 1.]]

特别注意！a * a和a @ a。

关于矩阵相乘，在下文会进行更多的讨论。

创建特殊的数组

除了上述的用numpy.array()来创建数组外，还有这些方法：

1. 创建未初始化的数组：numpy.empty()。
2. 创建各元素都是0的数组：numpy.zeros()。
3. 创建各元素都是1的数组：numpy.ones()。
4. 创建对角线元素是1的数组(单位矩阵)：numpy.eye()。
5. 创建对角矩阵：np.diag()。

创建未初始化的数组

创建未初始化的数组：numpy.empty()。

示例代码：

import numpy as np 
a = np.empty([2,2,3])
print(a)

运行结果：

[[[1.50692040e-312 0.00000000e+000 8.76794447e+252]
  [2.15895723e+227 6.48224638e+170 3.67145870e+228]]

 [[9.45337822e-096 9.03292329e+271 9.08366793e+223]
  [1.41075687e+232 1.16070543e-028 4.05919345e-317]]]

创建各元素都是0的数组

创建各元素都是0的数组：numpy.zeros()。

示例代码：

import numpy as np 
a = np.zeros([2,2,3]) 
print(a)

运行结果：

[[[0. 0. 0.]
  [0. 0. 0.]]

 [[0. 0. 0.]
  [0. 0. 0.]]]

创建各元素都是1的数组

创建各元素都是1的数组：numpy.ones()。

示例代码：

import numpy as np 
a = np.ones([2,2,3]) 
print(a)

运行结果：

[[[1. 1. 1.]
  [1. 1. 1.]]

 [[1. 1. 1.]
  [1. 1. 1.]]]

创建对角线元素是1的数组(单位矩阵)

创建对角线元素是1的数组：numpy.eye()。

该方法创建对角线元素是1的数组，当然只针对二维的数组。
示例代码：

import numpy as np

a = np.eye(3)
print(a)

运行结果：

[[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]

这种矩阵(数组)，也被称为单位矩阵，单位矩阵和任何矩阵相乘，运算结果都是原矩阵。

示例代码：

import numpy as np

l = [[1, 2], [1, 1]]

a = np.array(l)
print(a)

e = np.eye(2)
print(e)

print(a @ e)

运行结果：

[[1 2]
 [1 1]]
[[1. 0.]
 [0. 1.]]
[[1. 2.]
 [1. 1.]]

创建对角矩阵

创建对角矩阵，np.diag()，示例代码：

a = np.diag([1,2,3,4,5])
print(a)

运行结果：

[[1 0 0 0 0]
 [0 2 0 0 0]
 [0 0 3 0 0]
 [0 0 0 4 0]
 [0 0 0 0 5]]

对角线向上偏移一位，示例代码：

a = np.diag([1,2,3,4,5], 1)
print(a)

运行结果：

[[0 1 0 0 0 0]
 [0 0 2 0 0 0]
 [0 0 0 3 0 0]
 [0 0 0 0 4 0]
 [0 0 0 0 0 5]
 [0 0 0 0 0 0]]

对角线向下偏移一位，示例代码：

a = np.diag([1,2,3,4,5], -1)
print(a)

运行结果：

[[0 0 0 0 0 0]
 [1 0 0 0 0 0]
 [0 2 0 0 0 0]
 [0 0 3 0 0 0]
 [0 0 0 4 0 0]
 [0 0 0 0 5 0]]

数组的数据类型

数组类名和数据类型

首先，我们讨论一下数组类名和数据类型。
示例代码：

import numpy as np
a = np.array([[1,2,3],[2,3,4]])
print(a)
print('数组类名')
print(type(a))
print('数据类型')
print(a.dtype)

运行结果：

[[1 2 3]
 [2 3 4]]
数组类名
<class 'numpy.ndarray'>
数据类型
int32

• 数组的类名是numpy.ndarray。
• 数组的数据类型是int32。

numpy中常见的数据类型

数组的数据类型有非常多种。

类型	类型代码	说明
int8,uint8	i1,u1	有符号和无符号的8位（1个字节）整型
int16,uint16	i2,u2	有符号和无符号的16位（2个字节）整型
int32,uint32	i4,u4	有符号和无符号的32位（4个字节）整型
int64,uint64	i8,u8	有符号和无符号的64位（8个字节）整型
float16	f2	半精度浮点数
float32	f4或f	单精度浮点数
float64	f8或d	双精度浮点数
float128	f16或g	拓展精度浮点数
complex64,complex128,complex256	c8,c16,c32	分别用两个32位、64位和128位浮点数表示的复数
bool	?	布尔类型

在数据较大或者内存不够的时候，可以考虑指定或者修改数据类型。
我们还可以用ndarray.itemsize查看每个元素的字节数。

指定数据类型

上面我们讨论了创建数组多个方法，这些方法都有一个参数dtype。

dtype：数据类型，默认是所需的最小类型。可以给dtype赋值np.XXX或字符串，以指定数据类型。

示例代码：

import numpy as np
a = np.array([1,2,3,4,5],dtype=np.int8)
print("dtype=np.int8")
print(a.dtype)
print(a.itemsize)
b = np.array([0,1,0,1],dtype=np.bool)
print("dtype=np.bool")
print(b.dtype)
print(b.itemsize)
c = np.array([1,2,3],dtype='int64')
print("dtype='int64'")
print(c.dtype)
print(c.itemsize)
d = np.array([1,2,3],dtype='i4')
print("dtype='i4'")
print(d.dtype)
print(d.itemsize)

运行结果：

dtype=np.int8
int8
1
dtype=np.bool
bool
1
dtype='int64'
int64
8
dtype='i4'
int32
4

修改数据类型

修改数据类型的方法为ndarray.astype()。
可以传入参数np.XXX或字符串，以指定数据类型。
示例代码：

import numpy as np
a = np.array([0,1,0,1],dtype=np.bool)
print('修改之前')
print(a)
print(a.dtype)
print(a.itemsize)
print('指定为np.int8')
a = a.astype(np.int8)
print(a)
print(a.dtype)
print(a.itemsize)
print('指定为i8')
a = a.astype("i8")
print(a)
print(a.dtype)
print(a.itemsize)

运行结果：

修改之前
[False  True False  True]
bool
1
指定为np.int8
[0 1 0 1]
int8
1
指定为i8
[0 1 0 1]
int64
8

数组的维度

查看数组的维度

ndarray.shape表示数组的维度，返回一个元组，这个元祖就是数组的维度。
示例代码：

import numpy as np
a = np.array([[1,3,5],[2,4,6]])
print(a)
print('数组的维数')
print(a.shape)
print('数组的维数的长度')
print(len(a.shape))

运行结果：

[[1 3 5]
 [2 4 6]]
数组的维数
(2, 3)
数组的维数的长度
2

修改数组的维度

numpy.reshape()方法可以在不改变数据的条件下修改数组的维度。
该方法有一个参数order，取值及含义如下：

• C：按行
• F：按列
• A：原顺序
• k：元素在内存中的出现顺序
• 默认值是C

示例代码：

import numpy as np
a = np.array([[1,3,5],[2,4,6]])
print('reshape之前')
print(a)
print("reshape(1,6)")
print(a.reshape(1,6))
print("reshape(1,6,order='C')")
print(a.reshape(1,6,order='C'))
print("reshape(1,6,order='F')")
print(a.reshape(1,6,order='F'))

运行结果：

reshape之前
[[1 3 5]
 [2 4 6]]
reshape(1,6)
[[1 3 5 2 4 6]]
reshape(1,6,order='C')
[[1 3 5 2 4 6]]
reshape(1,6,order='F')
[[1 2 3 4 5 6]]

平铺数组

ndarray.flatten返回平铺后的一维数组，该方法有一个参数order，取值及含义如下：

• C：按行
• F：按列
• A：原顺序
• k：元素在内存中的出现顺序
• 默认值是C

示例代码：

import numpy as np
a = np.array([[1,3,5],[2,4,6]])
print("flatten之前")
print(a)
print("flatten()")
print(a.flatten())
print("flatten(order='C')")
print(a.flatten(order='C'))
print("flatten(order='F')")
print(a.flatten(order='F'))

运行结果：

flatten之前
[[1 3 5]
 [2 4 6]]
flatten()
[1 3 5 2 4 6]
flatten(order='C')
[1 3 5 2 4 6]
flatten(order='F')
[1 2 3 4 5 6]

数组的拼接和分割

数组的拼接

数组的拼接有四种方法。

1. concatenate()：连接沿现有轴的数组序列
2. stack()：沿着新的轴加入一系列数组
3. hstack()：水平堆叠序列中的数组(列方向)
4. vstack()：竖直堆叠序列中的数组(行方向)

concatenate

numpy.concatenate()方法用于沿指定轴连接相同形状的两个或多个数组，格式如下：

numpy.concatenate((a1, a2, ...), axis)

其中axis代表连接数组的轴，默认为0。
示例代码：

import numpy as np

a = np.array([[1, 3, 5], [2, 4, 6]])
print('a')
print(a)
print(a.shape)

b = np.array([[11, 13, 15], [12, 14, 16]])
print('b')
print(b)
print(b.shape)

print("concatenate((a,b)")
print(np.concatenate((a, b)))

print("np.concatenate((a,b),axis = 1)")
print(np.concatenate((a, b), axis=1))

print("np.concatenate((a,b),axis = 0)")
print(np.concatenate((a, b), axis=0))

运行结果：

a
[[1 3 5]
 [2 4 6]]
(2, 3)
b
[[11 13 15]
 [12 14 16]]
(2, 3)
concatenate((a,b)
[[ 1  3  5]
 [ 2  4  6]
 [11 13 15]
 [12 14 16]]
np.concatenate((a,b),axis = 1)
[[ 1  3  5 11 13 15]
 [ 2  4  6 12 14 16]]
np.concatenate((a,b),axis = 0)
[[ 1  3  5]
 [ 2  4  6]
 [11 13 15]
 [12 14 16]]

stack

numpy.stack函数用于沿新轴堆叠数组，格式如下：

numpy.stack(arrays, axis)

示例代码：

import numpy as np

a = np.array([[1, 3, 5], [2, 4, 6]])
print('a')
print(a)
print(a.shape)

b = np.array([[11, 13, 15], [12, 14, 16]])
print('b')
print(b)
print(b.shape)

print("stack((a,b)")
print(np.stack((a, b)))
print(np.stack((a, b)).shape)

print("np.stack((a,b),axis = 1)")
print(np.stack((a, b), axis=1))
print(np.stack((a, b), axis=1).shape)

print("np.stack((a,b),axis = 0)")
print(np.stack((a, b), axis=0))
print(np.stack((a, b), axis=0).shape)

运行结果：

a
[[1 3 5]
 [2 4 6]]
(2, 3)
b
[[11 13 15]
 [12 14 16]]
(2, 3)
stack((a,b)
[[[ 1  3  5]
  [ 2  4  6]]

 [[11 13 15]
  [12 14 16]]]
(2, 2, 3)
np.stack((a,b),axis = 1)
[[[ 1  3  5]
  [11 13 15]]

 [[ 2  4  6]
  [12 14 16]]]
(2, 2, 3)
np.stack((a,b),axis = 0)
[[[ 1  3  5]
  [ 2  4  6]]

 [[11 13 15]
  [12 14 16]]]
(2, 2, 3)

hstack

numpy.hstack()，沿着水平方向堆叠数组。
示例代码：

import numpy as np

a = np.array([[1, 3, 5], [2, 4, 6]])
print('a')
print(a)
print(a.shape)

b = np.array([[11, 13, 15], [12, 14, 16]])
print('b')
print(b)
print(b.shape)

print("hstack((a,b)")
print(np.hstack((a, b)))
print(np.hstack((a, b)).shape)

运行结果：

a
[[1 3 5]
 [2 4 6]]
(2, 3)
b
[[11 13 15]
 [12 14 16]]
(2, 3)
hstack((a,b)
[[ 1  3  5 11 13 15]
 [ 2  4  6 12 14 16]]
(2, 6)

vstack

numpy.vstack，沿着竖直方向堆叠数组。
示例代码：

import numpy as np

a = np.array([[1, 3, 5], [2, 4, 6]])
print('a')
print(a)
print(a.shape)

b = np.array([[11, 13, 15], [12, 14, 16]])
print('b')
print(b)
print(b.shape)

print("vstack((a,b)")
print(np.vstack((a, b)))
print(np.vstack((a, b)).shape)

运行结果：

a
[[1 3 5]
 [2 4 6]]
(2, 3)
b
[[11 13 15]
 [12 14 16]]
(2, 3)
vstack((a,b)
[[ 1  3  5]
 [ 2  4  6]
 [11 13 15]
 [12 14 16]]
(4, 3)

数组的分割

常见的数组的分割方法有三种。

1. split()
2. hsplit()
3. vsplit()

split

指定子数组数量进行分割

numpy.split()方法沿指定的轴将数组分割为子数组，格式如下：

numpy.split(ary, indices_or_sections, axis)

示例代码：

import numpy as np

a = np.array([[1, 3, 5], [2, 4, 6]])
print('a')
print(a)
print("np.split(a,2)")
print(np.split(a, 2))
print("np.split(a,3,axis=1)")
print(np.split(a, 3, axis=1))
print("np.split(a,2,axis=0)")
print(np.split(a, 2, axis=0))

运行结果：

a
[[1 3 5]
 [2 4 6]]
np.split(a,2)
[array([[1, 3, 5]]), array([[2, 4, 6]])]
np.split(a,3,axis=1)
[array([[1],
       [2]]), array([[3],
       [4]]), array([[5],
       [6]])]
np.split(a,2,axis=0)
[array([[1, 3, 5]]), array([[2, 4, 6]])]

指定分割位置进行分割

除了指定子数组数量，还可以指定分割位置。
示例代码：

import numpy as np
 
a = np.array([[1,3,5],[2,4,6]])
print('a')
print(a)
print("np.split(a,[2],axis=1)")
print(np.split(a,[2],axis=1))

运行结果：

a
[[1 3 5]
 [2 4 6]]
np.split(a,[2],axis=1)
[array([[1, 3],
       [2, 4]]), array([[5],
       [6]])]

hsplit

numpy.hsplit()

该方法将一个数组水平分割为多个子数组（按列）。
示例代码：

import numpy as np
 
a = np.array([[1,3,5],[2,4,6]])
print('a')
print(a)
print("np.hsplit(a,[2])")
print(np.hsplit(a,[2]))
print("np.hsplit(a,3)")
print(np.hsplit(a,3))

运行结果：

a
[[1 3 5]
 [2 4 6]]
np.hsplit(a,[2])
[array([[1, 3],
       [2, 4]]), array([[5],
       [6]])]
np.hsplit(a,3)
[array([[1],
       [2]]), array([[3],
       [4]]), array([[5],
       [6]])]

vsplit

numpy.vsplit()

该方法将一个数组竖直分割为多个子数组（按行）。
示例代码：

import numpy as np
 
a = np.array([[1,3,5],[2,4,6]])
print('a')
print(a)
print("np.vsplit(a,[0])")
print(np.vsplit(a,[0]))
print("np.vsplit(a,2)")
print(np.vsplit(a,2))

运行结果：

a
[[1 3 5]
 [2 4 6]]
np.vsplit(a,[0])
[array([], shape=(0, 3), dtype=int32), array([[1, 3, 5],
       [2, 4, 6]])]
np.vsplit(a,2)
[array([[1, 3, 5]]), array([[2, 4, 6]])]

数组的索引

我们可以通过索引获取单个元素，也可以用来获取子数组。后者也被称为数组的切片。

获取单个元素

示例代码：

import numpy as np
 
a = np.array([1,3,5,2,4,6])
print("a")
print(a)
print("a[2]  获取索引为2的元素")
print(a[2])
print("a[-1]  获取最后一个索引对应的元素")
print(a[-1])
a = a.reshape(2,3)
print("a.reshape(2,3)")
print(a)
print("a[1,1]  获取行索引为1，列索引为1的元素")
print(a[1,1])
print("a[0,-1]  获取行索引为0，列索引是最后一个的元素")
print(a[0,-1])

运行结果：

a
[1 3 5 2 4 6]
a[2]  获取索引为2的元素
5
a[-1]  获取最后一个索引对应的元素
6
a.reshape(2,3)
[[1 3 5]
 [2 4 6]]
a[1,1]  获取行索引为1，列索引为1的元素
4
a[0,-1]  获取行索引为0，列索引是最后一个的元素
5

获取子数组

示例代码：

import numpy as np
 
a = np.array([1,3,5,2,4,6])
print("a")
print(a)
print("a[:5]  前5个")
print(a[:5])
print("a[5:]  索引5之后")
print(a[5:])
print("a[2:5]  索引2到索引5")
print(a[2:5])
print("a[::2]  每间隔一个")
print(a[::2])
print("a[1::2]  每间隔一个，从索引1开始")
print(a[1::2])
print("a[::-1]  所有元素，逆序")
print(a[::-1])
a = a.reshape(2,3)
print("a.reshape(2,3)")
print(a)
print("a[:2,:2]  前2行，前2列")
print(a[:2,:2])
print("a[:2,::2]  前2行，间隔一列")
print(a[:2,::2])
print("a[::-1,::-1]  行逆序，列逆序")
print(a[::-1,::-1])
print("a[:,1]  第二列")
print(a[:,1])
print("a[1,:]  第二行")
print(a[1,:])
print("a[1]  获取行的简洁写法")
print(a[1])

运行结果：

a
[1 3 5 2 4 6]
a[:5]  前5个
[1 3 5 2 4]
a[5:]  索引5之后
[6]
a[2:5]  索引2到索引5
[5 2 4]
a[::2]  每间隔一个
[1 5 4]
a[1::2]  每间隔一个，从索引1开始
[3 2 6]
a[::-1]  所有元素，逆序
[6 4 2 5 3 1]
a.reshape(2,3)
[[1 3 5]
 [2 4 6]]
a[:2,:2]  前2行，前2列
[[1 3]
 [2 4]]
a[:2,::2]  前2行，间隔一列
[[1 5]
 [2 6]]
a[::-1,::-1]  行逆序，列逆序
[[6 4 2]
 [5 3 1]]
a[:,1]  第二列
[3 4]
a[1,:]  第二行
[2 4 6]
a[1]  获取行的简洁写法
[2 4 6]

布尔索引

布尔索引，顾名思义，以布尔值作为索引。
示例代码：

a = np.array([1,3,5,2,4,6])
print([a>5])
print(a[a>5])

运行结果：

[array([False, False, False, False, False,  True])]
[6]

花式索引

利用整数数组进行索引就是花式索引

一维整型数组作为索引

对于使用一维整型数组作为索引：

• 如果目标是一维数组，那么就是对应位置的元素。
• 如果目标是二维数组，那么就是对应下标的行。

示例代码：

import numpy as np
 
a = np.array([1,3,5,2,4,6])
print('a')
print(a)
print("a[[0]]")
print(a[[0]])
a = a.reshape(2,3)
print("a.reshape(2,3)")
print(a)
print("a[[0]]")
print(a[[0]])

运行结果：

a
[1 3 5 2 4 6]
a[[0]]
[1]
a.reshape(2,3)
[[1 3 5]
 [2 4 6]]
a[[0]]
[[1 3 5]]

多维整型数组作为索引

多维整型数组作为索引要使用np.ix_()
示例代码：

import numpy as np
 
x=np.arange(32).reshape((8,4))
print(x)
print (x[np.ix_([1,5,7,2],[0,3,1])])

运行结果：

[[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]
 [12 13 14 15]
 [16 17 18 19]
 [20 21 22 23]
 [24 25 26 27]
 [28 29 30 31]]
[[ 4  7  5]
 [20 23 21]
 [28 31 29]
 [ 8 11  9]]

数组(矩阵)的运算

转置

矩阵的转置：每个元素行列位置互换。

有两种方法：

• .T
• .transpose()

示例代码：

import numpy as np

l = [[1, 2], [3, 4]]

a = np.array(l)
print(a)

at = a.T
print(at)

atr = a.transpose()
print(atr)

运行结果：

[[1 2]
 [3 4]]
[[1 3]
 [2 4]]
[[1 3]
 [2 4]]

取上(下)三角矩阵

• np.triu(a)，取矩阵a中的上三角矩阵。
• np.tril(a)，取矩阵a中的下三角矩阵。

示例代码：

import numpy as np

l = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]

a = np.array(l)
print(a)

atriu = np.triu(a)
print(atriu)

atril = np.tril(a)
print(atril)

运行结果：

[[1 2 3]
 [4 5 6]
 [7 8 9]]
[[1 2 3]
 [0 5 6]
 [0 0 9]]
[[1 0 0]
 [4 5 0]
 [7 8 9]]

数组的四则运算

四则运算

注意！这里讨论的，都是+、-、*、/，四则运算。
不包括，点积、矩阵相乘等。

数组和数的四则运算

数组中的每个元素都和这个数字进行运算。

示例代码：

import numpy as np
a = np.array([[1,3,5],[2,4,6]])
print('a')
print(a)
print('+ 2')
print(a + 2)
print('- 2')
print(a - 2)
print('* 2')
print(a * 2)
print('/ 2')
print(a / 2)

运行结果：

a
[[1 3 5]
 [2 4 6]]
+ 2
[[3 5 7]
 [4 6 8]]
- 2
[[-1  1  3]
 [ 0  2  4]]
* 2
[[ 2  6 10]
 [ 4  8 12]]
/ 2
[[0.5 1.5 2.5]
 [1.  2.  3. ]]

特别的，如果数组除以0，会有警告，但是仍可以得到结果。

示例代码：

import numpy as np
a = np.array([[1,3,5],[2,4,6]])
print('a')
print(a)
print('/ 0')
print(a / 0)

运行结果：

a
[[1 3 5]
 [2 4 6]]
/ 0
[[inf inf inf]
 [inf inf inf]]

RuntimeWarning: divide by zero encountered in true_divide

解释说明：

• nan：not a number
• inf：infinity

数组和数组的四则运算

当数组形状相同的运算

数组的对应元素进行运算。

示例代码：

import numpy as np
a = np.array([[1,3,5,7,9,11],[2,4,6,8,0,10]])
print(a)
b = np.arange(1,13).reshape(2,6)
print(b)
print('+')
print(a + b)
print('-')
print(a - b)
print('*')
print(a * b)
print('/')
print(a / b)

运行结果：

[[ 1  3  5  7  9 11]
 [ 2  4  6  8  0 10]]
[[ 1  2  3  4  5  6]
 [ 7  8  9 10 11 12]]
+
[[ 2  5  8 11 14 17]
 [ 9 12 15 18 11 22]]
-
[[  0   1   2   3   4   5]
 [ -5  -4  -3  -2 -11  -2]]
*
[[  1   6  15  28  45  66]
 [ 14  32  54  80   0 120]]
/
[[1.         1.5        1.66666667 1.75       1.8        1.83333333]
 [0.28571429 0.5        0.66666667 0.8

当数组性形状不同的时候

我们以多维数组和一维数组的运算为例，有如下几种情况：

1. 每一行的维数一样
   多维数组的每一行和一维数组的每一行进行运算。
2. 每一列的维数一样
   多维数组的每一列和一维数组的每一列进行运算。
3. 行的维数不一样，列的维数也不一样
   无法进行运算。

每一行的维数一样的时候，多维数组的每一行和一维数组的每一行进行运算。

示例代码：

import numpy as np
a = np.array([[1,3,5,7,9,11],[2,4,6,8,0,10]])
print('a')
print(a)
b = np.array([1,2,3,4,5,6])
print('b')
print(b)
print('+')
print(a + b)
print('-')
print(a - b)
print('*')
print(a * b)
print('/')
print(a / b)

运行结果：

a
[[ 1  3  5  7  9 11]
 [ 2  4  6  8  0 10]]
b
[1 2 3 4 5 6]
+
[[ 2  5  8 11 14 17]
 [ 3  6  9 12  5 16]]
-
[[ 0  1  2  3  4  5]
 [ 1  2  3  4 -5  4]]
*
[[ 1  6 15 28 45 66]
 [ 2  8 18 32  0 60]]
/
[[1.         1.5        1.66666667 1.75       1.8        1.83333333]
 [2.         2.         2.         2.

每一列的维数一样的时候，多维数组的每一列和一维数组的每一列进行运算。

示例代码：

import numpy as np
a = np.array([[1,3,5,7,9,11],[2,4,6,8,0,10]])
print('a')
print(a)
b = np.array([[1],[2]])
print('b')
print(b)
print('+')
print(a + b)
print('-')
print(a - b)
print('*')
print(a * b)
print('/')
print(a / b)

运行结果：

a
[[ 1  3  5  7  9 11]
 [ 2  4  6  8  0 10]]
b
[[1]
 [2]]
+
[[ 2  4  6  8 10 12]
 [ 4  6  8 10  2 12]]
-
[[ 0  2  4  6  8 10]
 [ 0  2  4  6 -2  8]]
*
[[ 1  3  5  7  9 11]
 [ 4  8 12 16  0 20]]
/
[[ 1.  3.  5.  7.  9. 11.]
 [ 1.  2.  3.  4.  0.  5.]]

行的维数不一样，列的维数也不一样，当行的维数不一样，列的维数也不一样时，无法进行运算。

广播原则

如果两个数组的后缘维度（trailing dimension，即从末尾开始算起的维度）的轴长度相符或其中一方的长度为1，则认为它们是广播兼容的。
广播会在缺失的维度或长度为1的维度上进行。

广播兼容：

shape(3,3,2)和shape(3,2)进行比较，其后缘维度是(3,2)，可以进行计算。

shape(3,3,2)和shape(3,1)进行比较，有一个维度是(1)，可以进行计算。

缺失的维度：
比如

a
[[ 1  3  5  7  9 11]
 [ 2  4  6  8  0 10]]
b
[[1]
 [2]]

在行的维度上有缺失，则在行的维度上进行运算。

点积

什么是点积

点积，也被称为内积，指的是向量或矩阵对应位置元素相乘后相加。

向量点积

向量点积有三种实现方法：

• dot
• vdot
• ineer

示例代码：

import numpy as np

a = np.arange(4)
print(a)

print(np.dot(a, a))
print(a.dot(a))

print(np.vdot(a, a))

print(np.inner(a, a))

print((a * a).sum())

运行结果：

[0 1 2 3]
14
14
14
14
14

矩阵点积

矩阵点积，有且仅有一个方法，vdot。

示例代码：

import numpy as np

l = [[1, 2], [3, 4]]

a = np.array(l)
print(a)

print(np.vdot(a, a))

运行结果：

[[1 2]
 [3 4]]

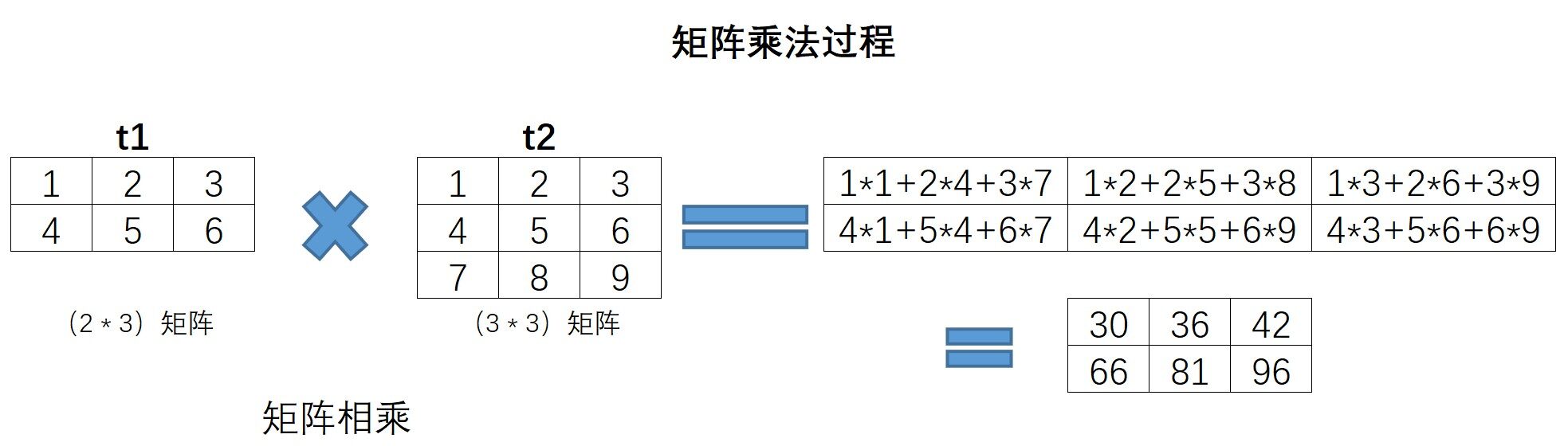
矩阵相乘

什么是矩阵相乘

注意！这里的矩阵相乘，指的不是数组的四则运算中的乘法。

矩阵相乘的过程如下：

• 矩阵相乘，要求左乘矩阵列数和右乘矩阵行数相同。
• 而内积计算过程则严格要求两个矩阵(向量)形状完全一致。

实现

实现矩阵相乘的方法有：

• dot
• @
• matmul

示例代码：

a1 = np.arange(1, 7).reshape(2, 3)
print(a1)

a2 = np.arange(1, 10).reshape(3, 3)
print(a2)

print(a1.dot(a2))
print(a1 @ a2)
print(np.matmul(a1,a2))

运行结果：

[[1 2 3]
 [4 5 6]]
[[1 2 3]
 [4 5 6]
 [7 8 9]]
[[30 36 42]
 [66 81 96]]
[[30 36 42]
 [66 81 96]]
[[30 36 42]
 [66 81 96]

矩阵的线性代数运算

矩阵的迹(trace)

什么是矩阵的迹

矩阵的迹，矩阵对角线元素之和

trace

可以使用trace()进行计算。

示例代码：

import numpy as np

a = np.array([[1, 2], [3, 4]])
print(a)

print(np.trace(a))

运行结果：

[[1 2]
 [3 4]]
5

注意，对于矩阵的迹，计算不需要是方阵。示例代码：

import numpy as np

a = np.array([[1, 2, 3], [3, 4, 5]])
print(a)

print(np.trace(a))

运行结果：

[[1 2 3]
 [3 4 5]]
5

矩阵的秩(rank)

什么是矩阵的秩

矩阵的秩(rank），是指矩阵中行或列的极大线性无关数，且矩阵中行、列极大无关数总是相同的，任何矩阵的秩都是唯一值。

满秩指的是方阵(行数和列数相同的矩阵)中行数、列数和秩相同，满秩矩阵有线性唯一解等重要特性，而其他矩阵也能通过求解秩来降维，同时，秩也是奇异值分解等运算中涉及到的重要概念。

matrix_rank

示例代码：

import numpy as np

a = np.array([[1, 2, 3], [1, 2, 3], [1, 3, 5]])
print(a)

print(np.linalg.matrix_rank(a))

运行结果：

[[1 2 3]
 [1 2 3]
 [1 3 5]]
2

解释说明：第一行可以通过第二行线性标识，因此极大线性无关组只有两行，秩为2。

矩阵的逆

什么是矩阵的逆

如果矩阵B和矩阵A相乘能够得到单位矩阵，即：

$$B \cdot A = E$$

则称$B$为$A$的逆矩阵，也可将B写作$A^{-1}$。当然，逆矩阵的性质是相互的，我们也可称$A$为$B$的逆矩阵，或者$A$和$B$互为逆矩阵。

inv

示例代码：

import numpy as np

a = np.array([[1, 1], [3, 1]])
print(a)

b = np.linalg.inv(a)
print(b)

print(a.dot(np.linalg.inv(a)))

运行结果：

[[1 1]
 [3 1]]
[[-0.5  0.5]
 [ 1.5 -0.5]]
[[1.00000000e+00 1.11022302e-16]
 [2.22044605e-16 1.00000000e+00]]

应用：矩阵方程求解

转换为矩阵方程

我们假设存在一个线性方程如下：

$$y = wx + b$$

现在，存在两个点：(1,2)，(2,3)。
通过消元法，我们很容易得到这个方程的w和b。这里我们讨论矩阵方程的方法。

有方程组如下：

$$\begin{aligned} 1 w + b & = 2 \\ 2 w + b & = 3 \end{aligned}$$

令：

$$A = \left [ \begin{array}{cccc} 1 & 1 \\ 2 & 1 \\ \end{array} \right]$$

$$B = \left [ \begin{array}{cccc} 2 \\ 3 \\ \end{array} \right]$$

$$X = \left[ \begin{array}{cccc} w \\ b \\ \end{array} \right]$$

其中$X$为参数向量，上述方程组可等价表示为：

$$A \cdot X - B = 0$$

即

$$A \cdot X = B$$

至此我们就将方程组转化为了矩阵方程。

求解

思路

只需要在矩阵方程左右两端同时左乘其逆矩阵，即可解出$X$的取值

$$\begin{aligned} A^{-1}AX & = A^{-1}B \\ X & = A^{-1}B \end{aligned}$$

实现

首先创建二维张量去表示上述矩阵方程中的$A$和$B$，示例代码：

import numpy as np

A = np.array([[1, 1], [2, 1]])
B = np.array([[2, 3]]).T

print(A)
print(B)

运行结果：

[[1 1]
 [2 1]]
[[2]
 [3]]

验证A是否满秩，示例代码：

print(np.linalg.matrix_rank(A))

运行结果：

2

对于满秩矩阵，我们可以求其逆矩阵，示例代码：

A_1 = np.linalg.inv(A)
print(A_1)

运行结果：

[[-1.  1.]
 [ 2. -1.]]

计算$A^{-1}B$，示例代码：

print(np.matmul(A_1, B))

运行结果：

[[1.]
 [1.]]

即

$$X = \left[ \begin{array}{cccc} w \\ b \\ \end{array} \right] = \left[ \begin{array}{cccc} 1 \\ 1 \\ \end{array} \right]$$

numpy中提供了一种求解矩阵方程的函数，类似于上述$A*X^T=B$的矩阵方程，我们还可以通过np.linalg.solve()求解。
示例代码：

print(np.linalg.solve(A, B))

运行结果：

[[1.]
 [1.]]

数组中元素的遍历

numpy.nditer()

用numpy.nditer()对其进行遍历，默认采用行序优先。
示例代码

import numpy as np
a = np.array([[1,3,5],[2,4,6]])
print(a)
for x in np.nditer(a):
    print (x,end=',')

运行结果：

[[1 3 5]
 [2 4 6]]
1,3,5,2,4,6,

控制遍历顺序

numpy.nditer()中的参数order用以控制遍历顺序，取值及含义如下：

• C：按行
• F：按列
• A：原顺序
• K：元素在内存中的出现顺序
• 默认值是C

示例代码：

import numpy as np
a = np.array([[1,3,5],[2,4,6]])
print('原数组')
print(a)
print('\n')
print("nditer(a)")
for x in np.nditer(a):
    print (x,end=',')
print('\n')
print("nditer(a,order='C')")
for x in np.nditer(a,order='C'):
    print (x,end=',')
print('\n')
print("nditer(a,order='F')")
for x in np.nditer(a,order='F'):
    print (x,end=',')

运行结果：

原数组
[[1 3 5]
 [2 4 6]]


nditer(a)
1,3,5,2,4,6,

nditer(a,order='C')
1,3,5,2,4,6,

nditer(a,order='F')
1,2,3,4,5,6,

遍历修改数组中的元素

nditer方法有另一个可选参数op_flags。
op_flags的默认值是['readonly']，需要将其修改为['readwrite']或者['writeonly']。
示例代码：

import numpy as np
a = np.array([[1,2,3,4],[2,3,4,5]])
print(a)
print('\n')
for x in np.nditer(a,op_flags=['readwrite']):
    x[...] = x + 10
print(a)

运行结果：

[[1 2 3 4]
 [2 3 4 5]]


[[11 12 13 14]
 [12 13 14 15]]

特别注意：是x[...] = x + 10，而不是x = x + 10。

数组的排序

对数组进行排序，有两种方法

• numpy中的sort()
• Python内置的sorted()

对一维数组进行排序，示例代码：

import numpy as np

# 创建一个一维的numpy数组
arr = np.array([3, 1, 4, 1, 5, 9, 2, 6, 5, 3])

# 使用numpy中的sort()函数对数组进行升序排序
sorted_arr = np.sort(arr)

# 使用Python内置的sorted()函数对数组进行升序排序
py_sorted_arr = sorted(arr)

print("原始数组:", arr)
print("numpy中的sort()函数排序后的数组:", sorted_arr)
print("Python内置的sorted()函数排序后的数组:", py_sorted_arr)

运行结果：

原始数组: [3 1 4 1 5 9 2 6 5 3]
numpy中的sort()函数排序后的数组: [1 1 2 3 3 4 5 5 6 9]
Python内置的sorted()函数排序后的数组: [1, 1, 2, 3, 3, 4, 5, 5, 6, 9]

时间处理

datetime64

创建时间

使用日期时间格式的字符串，通过构造方法创建时间。示例代码：

import numpy as np

d = np.datetime64('2005-02-25')

print(d)
print(type(d))

运行结果：

2005-02-25
<class 'numpy.datetime64'>

仅指定月份，示例代码：

import numpy as np

d = np.datetime64('2005-02')

print(d)
print(type(d))

运行结果：

2005-02
<class 'numpy.datetime64'>

仅指定月份，但强制使用"天"单位。示例代码：

import numpy as np

d = np.datetime64('2005-02', 'D')

print(d)
print(type(d))

运行结果：

2005-02-01
<class 'numpy.datetime64'>

精确到小时分钟。示例代码：

import numpy as np

d = np.datetime64('2005-02-25T03:30')

print(d)
print(type(d))

运行结果：

2005-02-25T03:30
<class 'numpy.datetime64'>

NAT(不是时间)，示例代码：

import numpy as np

d = np.datetime64('nat')

print(d)
print(type(d))

运行结果：

NaT
<class 'numpy.datetime64'>

创建时间数组

还可以创建一个时间数组，dtype='datetime64'。示例代码：

import numpy as np

na = np.array(['2007-07-13', '2006-01-13', '2010-08-13'], dtype='datetime64')

print(na)

运行结果：

['2007-07-13' '2006-01-13' '2010-08-13']

当两个时间的精度不一致时，会自动填充至高精度。示例代码：

import numpy as np

na = np.array(['2001-01-01T12:00', '2002-02-03T13:56:03.172'], dtype='datetime64')

print(na)

运行结果：

['2001-01-01T12:00:00.000' '2002-02-03T13:56:03.172']

还可以利用np.arange，用于生成日期范围。示例代码：

import numpy as np

nar = np.arange('2005-02', '2005-03', dtype='datetime64[D]')

print(nar)

运行结果：

['2005-02-01' '2005-02-02' '2005-02-03' '2005-02-04' '2005-02-05'
 '2005-02-06' '2005-02-07' '2005-02-08' '2005-02-09' '2005-02-10'
 '2005-02-11' '2005-02-12' '2005-02-13' '2005-02-14' '2005-02-15'
 '2005-02-16' '2005-02-17' '2005-02-18' '2005-02-19' '2005-02-20'
 '2005-02-21' '2005-02-22' '2005-02-23' '2005-02-24' '2005-02-25'
 '2005-02-26' '2005-02-27' '2005-02-28']

datetime64的存储方式

先看现象。示例代码：

import numpy as np

n1 = np.datetime64('2005')
n2 = np.datetime64('2005-01-01')

n3 = np.datetime64('2010-03-14T15')
n4 = np.datetime64('2010-03-14T15:00:00.00')

print(n1)
print(n2)
print(n1 == n2)

print(n3)
print(n4)
print(n3 == n4)

运行结果：

2005
2005-01-01
True
2010-03-14T15
2010-03-14T15:00:00.000
True

我们可以理解为，np.datetime64的存储分为两部分，一部分以一种类似于时间戳的格式进行存储原始数据，另一部分存储显示格式。

timedelta64

创建时间差

timedelta64，用一个数字和一个单位，表示时间差值。也可以用字符串NAT表示创建非时间差。

单位有：

• D days
• M months
• Y years
• h hours
• m minutes
• s seconds

示例代码：

import numpy as np

td1 = np.timedelta64(1, 'D')
td2 = np.timedelta64(4, 'h')
td3 = np.timedelta64('nAt')

print(td1)
print(type(td1))
print(td2)
print(type(td2))
print(td3)
print(type(td3))

运行结果：

1 days
<class 'numpy.timedelta64'>
4 hours
<class 'numpy.timedelta64'>
NaT
<class 'numpy.timedelta64'>

日期时间计算

datetime64和timedelta64一起工作，能够进行日期时间的计算。示例代码：

import numpy as np

v1 = np.datetime64('2009-01-01') - np.datetime64('2008-01-01')
v2 = np.datetime64('2009') + np.timedelta64(20, 'D')
v3 = np.datetime64('2011-06-15T00:00') + np.timedelta64(12, 'h')
v4 = np.timedelta64(1, 'W') / np.timedelta64(1, 'D')
v5 = np.timedelta64(1, 'W') % np.timedelta64(10, 'D')
v6 = np.datetime64('nat') - np.datetime64('2009-01-01')
v7 = np.datetime64('2009-01-01') + np.timedelta64('nat')

print(v1)
print(type(v1))

print(v2)
print(type(v2))

print(v3)
print(type(v3))

print(v4)
print(type(v4))

print(v5)
print(type(v5))

print(v6)
print(type(v6))

print(v7)
print(type(v7))

运行结果：

366 days
<class 'numpy.timedelta64'>
2009-01-21
<class 'numpy.datetime64'>
2011-06-15T12:00
<class 'numpy.datetime64'>
7.0
<class 'numpy.float64'>
7 days
<class 'numpy.timedelta64'>
NaT
<class 'numpy.timedelta64'>
NaT
<class 'numpy.datetime64'>

有两处要特别注意：

1. 每年有多少天，是不固定的。
2. 每月有多少天，是不固定的。

每年有多少天，是不固定的。示例代码：

import numpy as np

a = np.timedelta64(1, 'Y')
print(a)

am = np.timedelta64(a, 'M')
print(am)

ad = np.timedelta64(a, 'D')
print(ad)

运行结果：

1 years
12 months
TypeError: Cannot cast NumPy timedelta64 scalar from metadata [Y] to [D] according to the rule 'same_kind'

每月有多少天，是不固定的。示例代码：

import numpy as np

a = np.timedelta64(1, 'M')
print(a)

ad = np.timedelta64(a, 'D')
print(ad)

运行结果：

1 months
TypeError: Cannot cast NumPy timedelta64 scalar from metadata [M] to [D] according to the rule 'same_kind'

日期时间单位

但是，我们通过astype方法，可以将年转换成天。示例代码：

import numpy as np

a = np.timedelta64(1, 'Y')
print(a)

ad = a.astype('timedelta64[D]')

print(ad)

运行结果：

1 years
365 days

日期单位：

• Y，年
• M，月
• W，周
• D，天

时间单位：

• h，小时
• m，分钟
• s，秒
• ms，毫秒
• us，微秒
• ns，纳秒

题外话

• 大写字母是date units
• 小写字母是time units

但，这个不是惯例。比如

import time

ts = 1600000000
dt = time.strftime("%Y-%m-%d %H:%M:%S", time.localtime(ts))
print(dt)

运行结果：

2020-09-13 20:26:40

astype

可以使用astype进行类型转化。示例代码：

import numpy as np

t1 = np.datetime64('2022-05-02 22:01:27')
t2 = np.datetime64('2022-01-03 02:31:52')

td = t1 - t2

print(td)
print(type(td))

print(td.astype('timedelta64[s]'))
print(td.astype('timedelta64[h]'))
print(td.astype('timedelta64[D]'))
print(td.astype('timedelta64[M]'))
print(td.astype('timedelta64[Y]'))

print(td.astype('timedelta64[s]').astype('int'))
print(td.astype('timedelta64[h]').astype('int'))
print(td.astype('timedelta64[D]').astype('int'))
print(td.astype('timedelta64[M]').astype('int'))
print(td.astype('timedelta64[Y]').astype('int'))

运行结果：

10351775 seconds
<class 'numpy.timedelta64'>
10351775 seconds
2875 hours
119 days
3 months
0 years
10351775
2875
119
3
0

可以使用astype方法对数组的数据进行类型转换。

字符串类型转换为时间类型，示例代码：

import numpy as np

s = np.array(['2020-01-01', '2020-01-02', '2020-01-03'], dtype=str)
print(type(s[0]))
t = s.astype(np.datetime64)
print(type(t[0]))
print(t)

运行结果：

<class 'numpy.str_'>
<class 'numpy.datetime64'>
['2020-01-01' '2020-01-02' '2020-01-03']

将时间类型转换为整型。示例代码：

import numpy as np

t = np.array(['2020-01-01', '2020-01-02', '2020-01-03'], dtype=np.datetime64)
print(type(t[0]))
i = t.astype(int)
print(type(i[0]))
print(i)

print(np.datetime64('2020-01-01') - np.datetime64('1970-01-01'))

运行结果：

<class 'numpy.datetime64'>
<class 'numpy.int64'>
[18262 18263 18264]
18262 days

解释说明：其转换的是距离1970-01-01的天数。

busday

busday，包含一系列的相关函数：

• np.is_busday，判断是否为工作日
• np.busday_offset，找到偏移的工作日
• np.busday_count，合计有多少个工作日

在有些资料，说的不是"工作日"，而是"有效日期"。
这种说法非常准确，因为只需要对weekmask和holidays等进行一定的设定，完全可以用来判断某些场景下的有效日期，比如，可以用来判断是不是节假日、是不是交易日等。

但是，"工作日"这个措辞，容易理解。

定义假期

以np.is_busday为例：

is_busday(dates, weekmask='1111100', holidays=None, busdaycal=None, out=None)

默认weekmask='1111100'，其含义是周六和周日，不是工作日。holidays=None，没有定义节假日。我们可以据此定义节假日。

示例代码：

import numpy as np

# 定义一个日期数组
dates = np.array(['2021-07-01', '2021-07-02', '2021-07-03', '2021-07-04', '2021-07-05'], dtype=np.datetime64)

# 定义一个节假日数组
holidays = np.array(['2021-07-01', '2021-07-04'], dtype=np.datetime64)

# 判断日期数组中的每个日期是否是工作日
is_busday = np.is_busday(dates, holidays=holidays)

print(is_busday)

运行结果：

[False  True False False  True]

解释说明：2021-07-01、2021-07-02和2021-07-05，分别是周四、周五和周一；2021-07-03和2021-07-04，分别是周六和周日；定义2021-07-01, 2021-07-04为节假日。所以运行结果为2021-07-01、2021-07-03和2021-07-04不是工作日。

np.is_busday()

np.is_busday()，用于判断是否为工作日。
除了判断日期数组，还可以用于判断某个日期是否为工作日。

示例代码：

import numpy as np

print(np.is_busday(np.datetime64('2021-07-01')))

运行结果：

True

np.busday_offset()

np.busday_offset()，找到偏移的工作日。

示例代码：

import numpy as np

dates = np.datetime64('2021-07-01')

holidays = np.array(['2021-07-04'], dtype=np.datetime64)

busday_offset = np.busday_offset(dates, offsets=1, holidays=holidays)

print(busday_offset)

运行结果：

2021-07-02

但是，如果2021-07-01，不是工作日，就会报错。示例代码：

import numpy as np

dates = np.datetime64('2021-07-01')

holidays = np.array(['2021-07-01', '2021-07-04'], dtype=np.datetime64)

busday_offset = np.busday_offset(dates, offsets=1, holidays=holidays)

print(busday_offset)

运行结果：

ValueError: Non-business day date in busday_offset

我们可以通过参数roll，进行定义：

• raise：对于非工作日，抛异常。
• nat：对于非工作日，返回NaT(不是时间)。
• forward和following，取时间轴上后面的第一个工作日。
• backward和preceding，取时间轴上前面的第一个工作日。
• modifiedfollowing，取时间轴上后面的第一个工作日。但是如果跨越了一个月的边界，取时间轴上前面的第一个工作日。
• modifiedpreceding，取时间轴上前面的第一个工作日。但是如果跨越了一个月的边界，取时间轴上后面的第一个工作日。

示例代码：

import numpy as np

dates = np.datetime64('2021-07-01')

holidays = np.array(['2021-07-01', '2021-07-04'], dtype=np.datetime64)

busday_offset_forward = np.busday_offset(dates, offsets=1, roll='forward', holidays=holidays)

print(busday_offset_forward)


busday_offset_backward = np.busday_offset(dates, offsets=1, roll='backward', holidays=holidays)

print(busday_offset_backward)

运行结果：

2021-07-05
2021-07-02

母亲节是在五月的第二个星期天，可以使用自定义的周掩码来计算。示例代码：

import numpy as np


mothers_day = np.busday_offset('2012-05', 1, roll='forward', weekmask='Sun')

print(mothers_day)

运行结果：

2012-05-13

np.busday_count()

np.busday_count()，用于统计工作日的数量。常用参数有：

• begindates
• enddates
• weekmask
• holidays

对于begindates和enddates，没有必须为工作日的限制。示例代码：

import numpy as np

holidays = np.array(['2021-07-01', '2021-07-04'], dtype=np.datetime64)

busday_count = np.busday_count(begindates=np.datetime64('2021-07-01'), enddates=np.datetime64('2021-07-05'))

print(busday_count)

运行结果：

2

begindates本身加入统计，enddates不加入统计。示例代码：

import numpy as np

holidays = np.array(['2021-07-01', '2021-07-04'], dtype=np.datetime64)

busday_count = np.busday_count(begindates=np.datetime64('2021-07-02'), enddates=np.datetime64('2021-07-05'))

print(busday_count)

运行结果：

1

统计2011年01月的工作日的数量，示例代码：

np.busday_count('2011-01', '2011-02')

统计2011年的工作日的数量，示例代码：

np.busday_count('2011', '2012')

统计2011年的星期六的数量，示例代码：

np.busday_count('2011', '2012', weekmask='Sat')

常用统计函数

1. 求和：t.sum(axis=None)
2. 均值：t.mean(axis=None)
3. 最大值：t.max(axis=None)
4. 最小值：t.min(axis=None)
5. 标准差：t.std(axis=None)
6. 值的范围(最大值和最小值的差)：np.ptp(t,axis=None)
7. 中位数：np.median(t,axis=None)

默认返回多维数组的全部的统计结果,如果指定axis则返回一个当前轴上的结果

示例代码：

import numpy as np

a = np.array([[1,3,5],[2,5,6]])
print("a")
print(a)
print("求和")
print(a.sum())
print(a.sum(axis=0))
print(a.sum(axis=1))
print("均值")
print(a.mean())
print(a.mean(axis=0))
print(a.mean(axis=1))
print("最大值")
print(a.max())
print(a.max(axis=0))
print(a.max(axis=1))
print("最小值")
print(a.min())
print(a.min(axis=0))
print(a.min(axis=1))
print("标准差")
print(a.std())
print(a.std(axis=0))
print(a.std(axis=1))
print("值的范围")
print(np.ptp(a))
print(np.ptp(a,axis=0))
print(np.ptp(a,axis=1))
print("中位数")
print(np.median(a))
print(np.median(a,axis=0))
print(np.median(a,axis=1))

运行结果：

a
[[1 3 5]
 [2 5 6]]
求和
22
[ 3  8 11]
[ 9 13]
均值
3.6666666666666665
[1.5 4.  5.5]
[3.         4.33333333]
最大值
6
[2 5 6]
[5 6]
最小值
1
[1 3 5]
[1 2]
标准差
1.7950549357115015
[0.5 1.  0.5]
[1.63299316 1.69967317]
值的范围
5
[1 2 1]
[4 4]
中位数
4.0
[1.5 4.  5.5]
[3. 5.]

视图与拷贝

现象

切片方式创建数组

创建一个Numpy数组。示例代码：

import numpy as np

arr = np.array([1, 2, 4, 8, 16, 32])
print(arr)

运行结果：

[ 1  2  4  8 16 32]

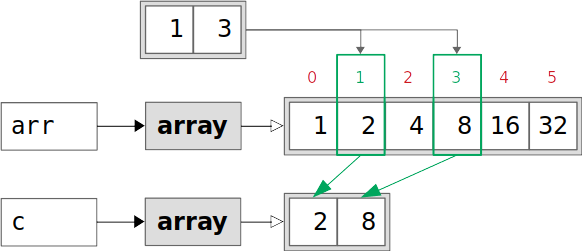
然后我们此基础，通过切片的方式，再创建一个数组。示例代码：

arr_1 = arr[1:4:2]
print(arr_1)

运行结果：

[2 8]

列表方式创建数组

再通过列表方式，创建一个数组。示例代码：

arr_2 = arr[[1, 3]]
print(arr_2)

运行结果：

[2 8]

比较

比较type和id

type是一样的，id是不一样的。这个没有任何问题。

示例代码：

print(type(arr))
print(type(arr_1))
print(type(arr_2))

print(id(arr))
print(id(arr_1))
print(id(arr_2))

运行结果：

<class 'numpy.ndarray'>
<class 'numpy.ndarray'>
<class 'numpy.ndarray'>
140224660296304
140224660630960
140224683551984

base

ndarray.base用于判断数组中的数据是否来自于别的数组。

我们通过切片方式创建的数组，base有值；但是通过列表创建的，没有base。

示例代码：

print(arr.base)
print(arr_1.base)
print(arr_2.base)

运行结果：

None
[ 1  2  4  8 16 32]
None

flags.owndata

ndarray.flags.owndata用于判断数组是否是数据的所有者。

我们通过切片方式创建的数组，不是数据的所有者；但是通过列表创建的，是数据的所有者。

示例代码：

print(arr.flags.owndata)
print(arr_1.flags.owndata)
print(arr_2.flags.owndata)

运行结果：

True
False
True

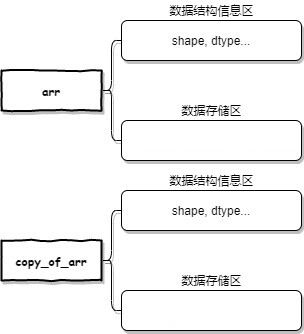
数据结构

如果要解释上述现象，就涉及到Numpy中数组的数据结构了。
Numpy中数组大致可以分为两部分：

• 结构信息区
  结构信息区中有数组的形状(shape)以及数据类型(data-type)等信息
• 数据存储区
  而数据存储区则是用于存储数组的数据

这么设计的原因是，Numpy中数组中的数据可以指向其它数组中的数据，这样多个数组可以共用同一个数据。

视图

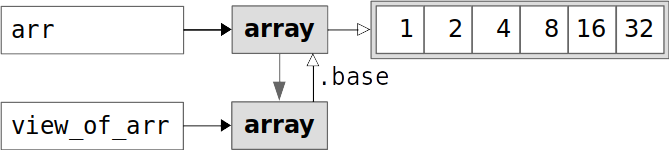
view()

切片(arr[1:4:2])返回的是视图，其实只修改了结构信息区的内容，和原数组共用一个数据存储区。

我们可以用.view()方法创建数组的视图。示例代码：

view_of_arr = arr.view()
print(view_of_arr)
print(view_of_arr.base)
print(id(view_of_arr.base))
print(id(arr))
print(view_of_arr.flags.owndata)

运行结果：

[ 1  2  4  8 16 32]
[ 1  2  4  8 16 32]
140565949764208
140565949764208
False

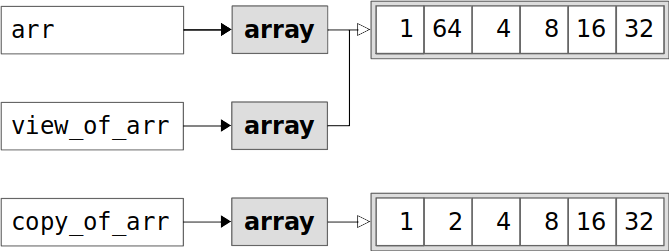
view_of_arr和arr之间的关系如图所示

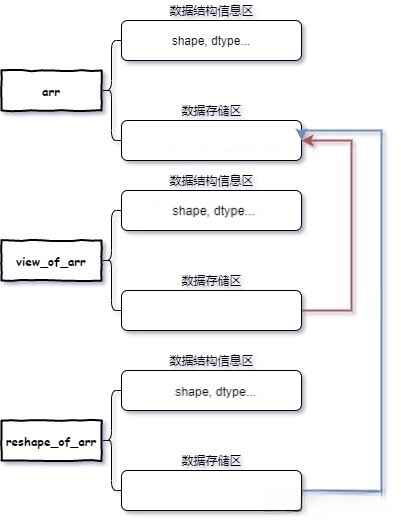
reshape()

reshape()，也是一个改变结构信息区的方法。

示例代码：

reshape_of_arr = view_of_arr.reshape((2, 3))
print(reshape_of_arr)
print(reshape_of_arr.base)
print(id(reshape_of_arr.base))
print(id(arr))
print(reshape_of_arr.flags.owndata)

运行结果：

[[ 1  2  4]
 [ 8 16 32]]
[ 1  2  4  8 16 32]
140556379411056
140556379411056
False

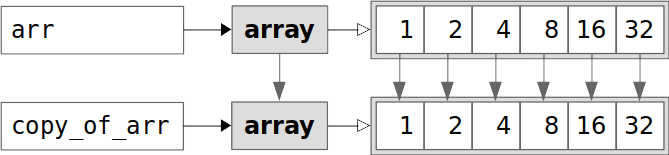
拷贝

不但有自己的结构信息区，还有自己的数据存储区，则被称为拷贝。

我们可以利用.copy()方法来演示拷贝。

示例代码：

copy_of_arr = arr.copy()
print(copy_of_arr)
print(copy_of_arr.base)
print(copy_of_arr.flags.owndata)

运行结果：

[ 1  2  4  8 16 32]
None
True

copy_of_arr没有base属性，flags.owndata的返回值是True。

拷贝过程：

copy_of_arr和arr之间的关系：

其他现象

接下来，我们看看因为上述的区别，而导致的其他现象。

所占用的内存空间大小

sys.getsizeof()，计算所占用的内存空间大小。

示例代码：

print(sys.getsizeof(arr))
print(sys.getsizeof(view_of_arr))
print(sys.getsizeof(copy_of_arr))

运行结果：

160
112
160

我们看到view_of_arr的大小少了48个字节。

而这48个字节，恰好就是数组中所有数据占用的字节数。示例代码：

print(arr.nbytes)
print(view_of_arr.nbytes)
print(copy_of_arr.nbytes)

运行结果：

48
48
48

这个例子，也佐证了 nbytes属性是数组中的所有数据消耗掉的字节数，不是数组的开销，数组整体占用的空间会更大。

对原数组进行修改

对原数组进行修改，视图会受影响，但是拷贝不会受影响。
示例代码：

arr[1] = 64
print(arr)
print(view_of_arr)
print(copy_of_arr)

运行结果：

[ 1 64  4  8 16 32]
[ 1 64  4  8 16 32]
[ 1  2  4  8 16 32]

小结

切片，得到的是视图。

列表，的到的是拷贝。