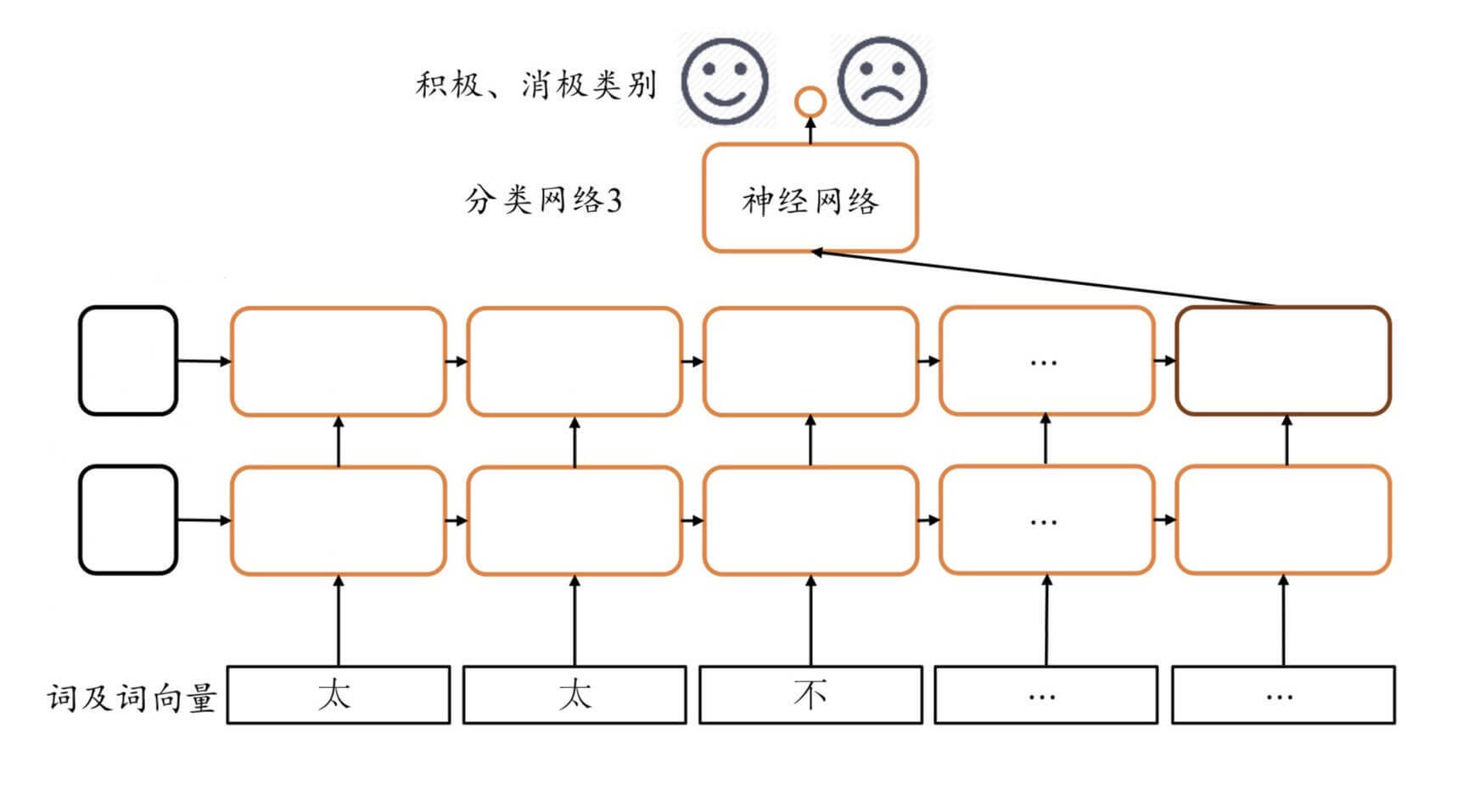
《东邪西毒》是一部非常经典的电影,王家卫导演挪用了金庸先生的故事以及武侠片的形式,上演了另一个主题:回忆 。
而相比中文名,电影的英文名"Ashes of Time(时间的灰烬)"或许更贴近影片主题。
以前发生过的事情留在回忆里,像是时间被燃烧成灰烬一样,而且回忆会淡去,就像灰烬会随风扬尽。
在影片最后,还有这么一段话。
我们这一章要讨论的LSTM和GRU,就和这个有关,令自己不要忘记 。
RNN的遗忘
在影片开头,讲述了一个关于"遗忘"的故事。
我们也先讨论"遗忘"。
h t = tanh ( W x h x t + W h h h t − 1 + b ) \bold{h}_t = \tanh(\bold{W}_{xh}\bold{x}_t + \bold{W}_{hh}\bold{h}_{t-1} + b)
h t = tanh ( W x h x t + W h h h t − 1 + b )
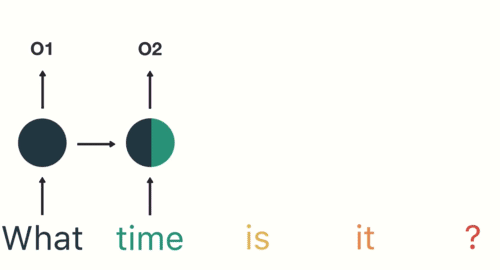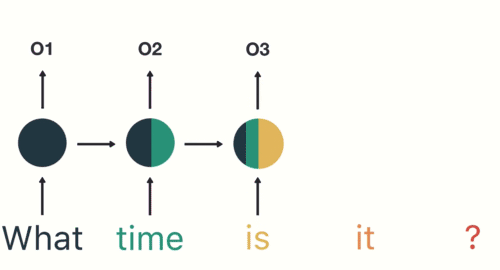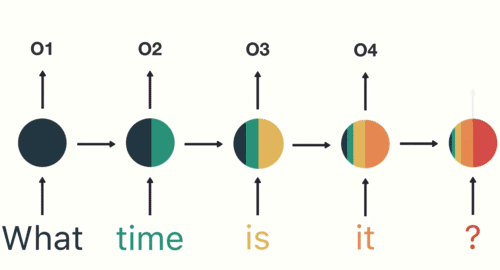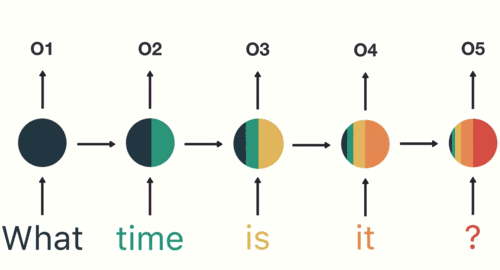
如图和公式所示,在循环迭代多次后,最初的那个x 0 \bold{x}_0 x 0 x 1 \bold{x}_1 x 1
但x 0 \bold{x}_0 x 0 x 1 \bold{x}_1 x 1
那么,就不得不讨论长短期记忆神经网络。
LSTM的结构
LSTM,长短期记忆神经网络(Long Short-Term Memory)。
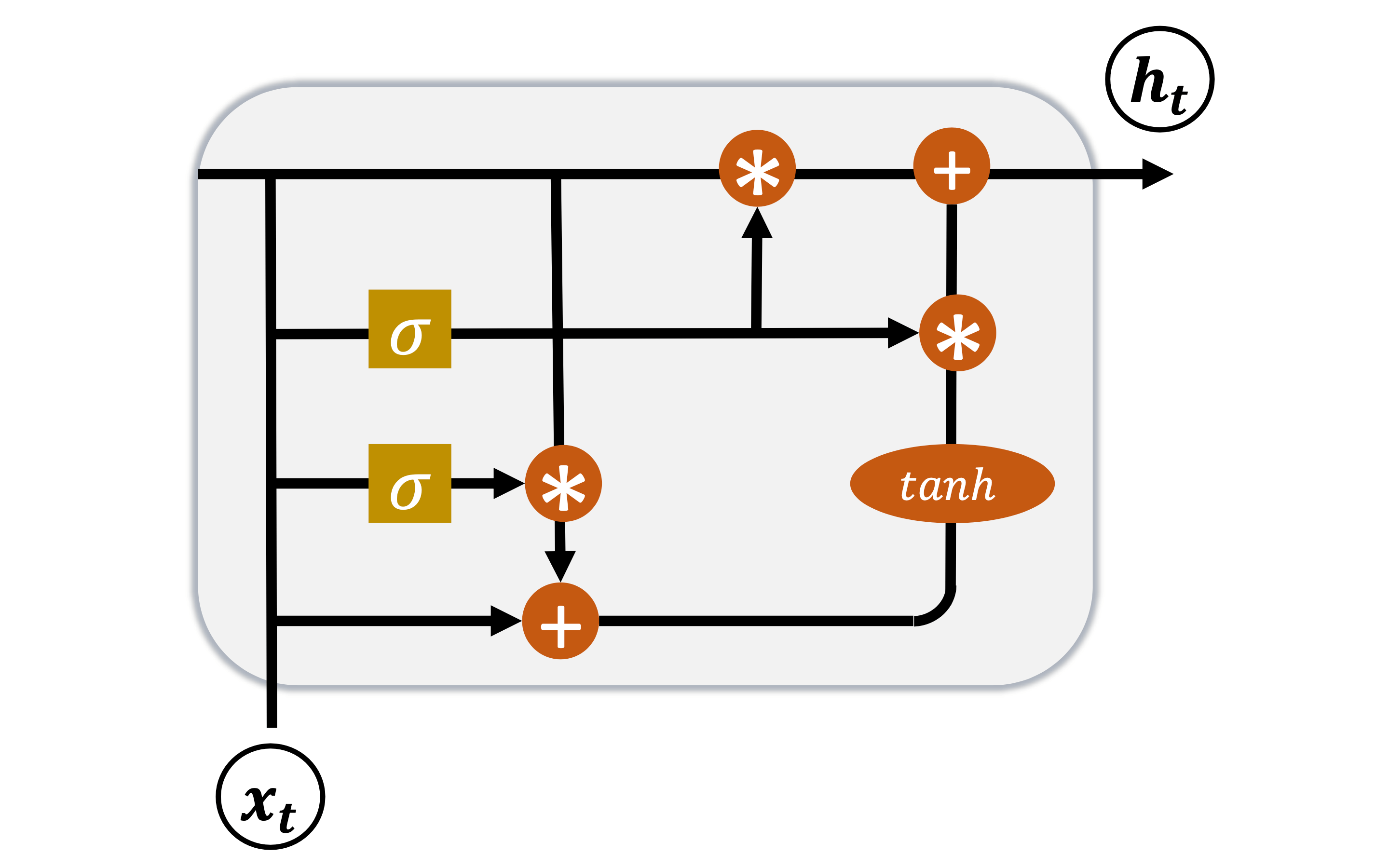
如图所示,就是长短期记忆神经网络的结构。我们为了记住过去,新增了一个状态量c 。
可是正如影片中所述,
我们也不能所有的事情都记住,有些需要忘记。
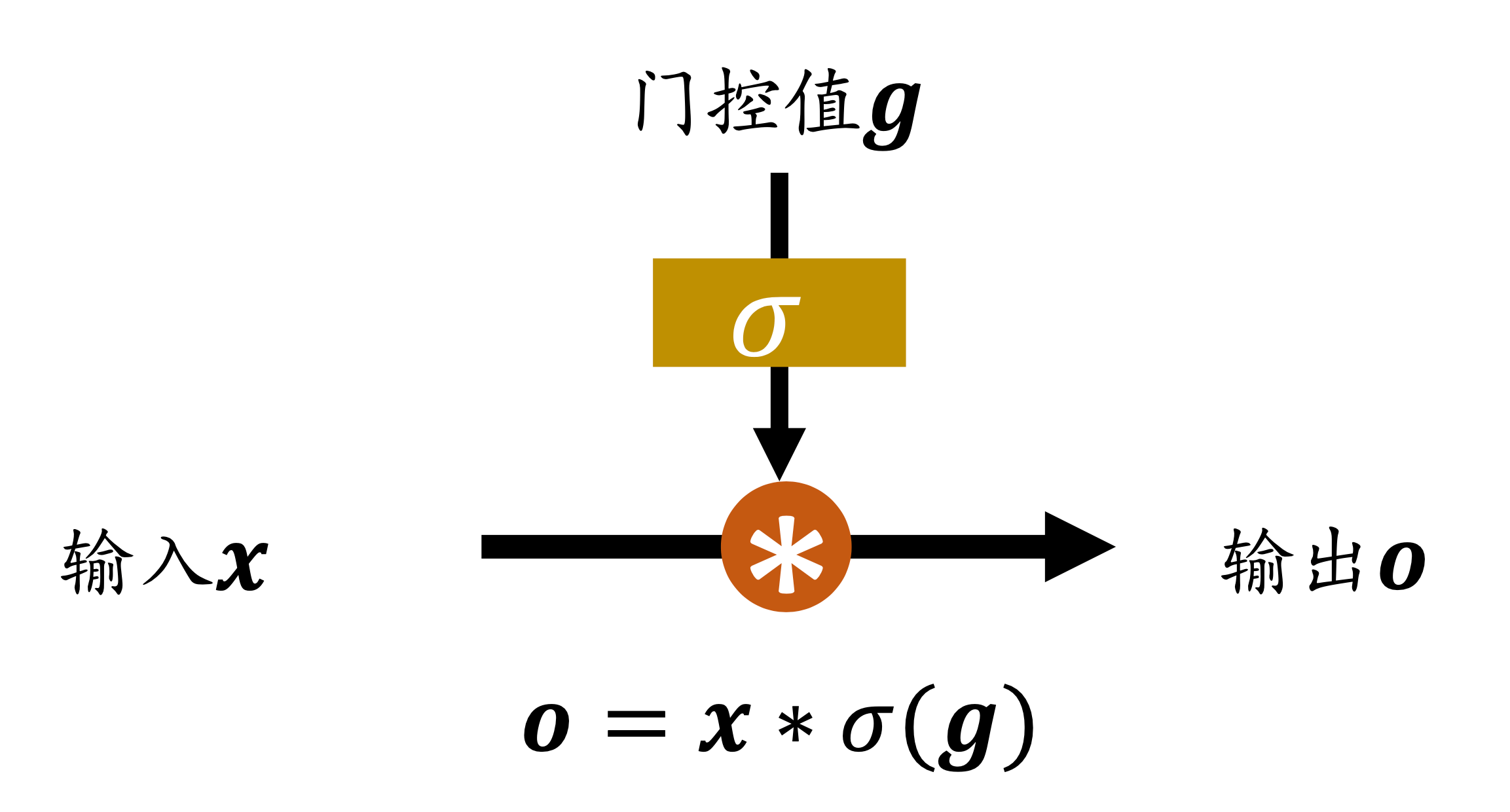
门控机制
我们通过门来忘记。门呢,要么开,要么关,再要么就是虚掩。总之总是在0和1之间,所以,我们需要一个函数,再把这个函数套在合适的激活函数里面,这样就输出[ 0 , 1 ] [0,1] [ 0 , 1 ]
激活函数
值域
备注
阶跃函数
0 0 0 1 1 1 不可以用梯度下降
sigmoid
[ 0 , 1 ] [0,1] [ 0 , 1 ]
tanh
[ − 1 , 1 ] [-1,1] [ − 1 , 1 ]
ReLU
[ 0 , + ∞ ) [0,+\infty) [ 0 , + ∞ )
SoftMax
[ 0 , 1 ] [0,1] [ 0 , 1 ] 多个输出值,所有输出值之和为1
显然,我们决定用sigmoid作为激活函数。
当σ ( g ) = 0 \sigma(\bold{g}) = 0 σ ( g ) = 0
当σ ( g ) = 1 \sigma(\bold{g}) = 1 σ ( g ) = 1
当σ ( g ) ∈ ( 0 , 1 ) \sigma(\bold{g}) \in (0,1) σ ( g ) ∈ ( 0 , 1 )
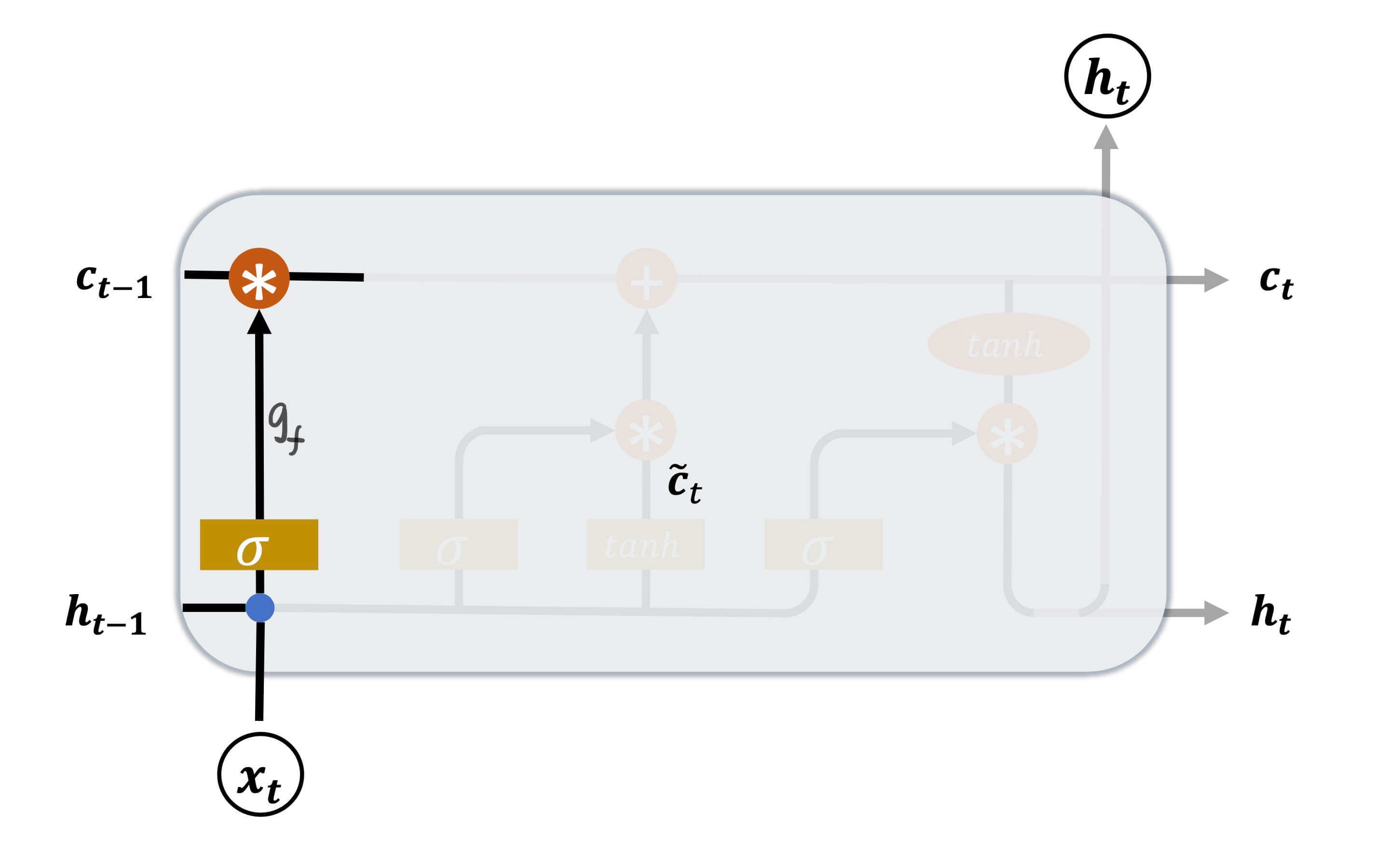
遗忘门
正如之前的讨论,c c c sigmoid函数用来做门控函数最外面一层的激活函数。
g f = σ ( W f ⋅ [ h t − 1 , x t ] + b f ) \bold{g}_f = \sigma(\bold{W}_f \cdot [ \bold{h}_{t-1},\bold{x}_t ] + \bold{b}_f)
g f = σ ( W f ⋅ [ h t − 1 , x t ] + b f )
W f \bold{W}_f W f b f \bold{b}_f b f σ \sigma σ sigmoid。
通过这个操作,可以得到[ 0 , 1 ] [0,1] [ 0 , 1 ] c t − 1 \bold{c}_{t-1} c t − 1 g f c t − 1 \bold{g}_f\bold{c}_{t-1} g f c t − 1
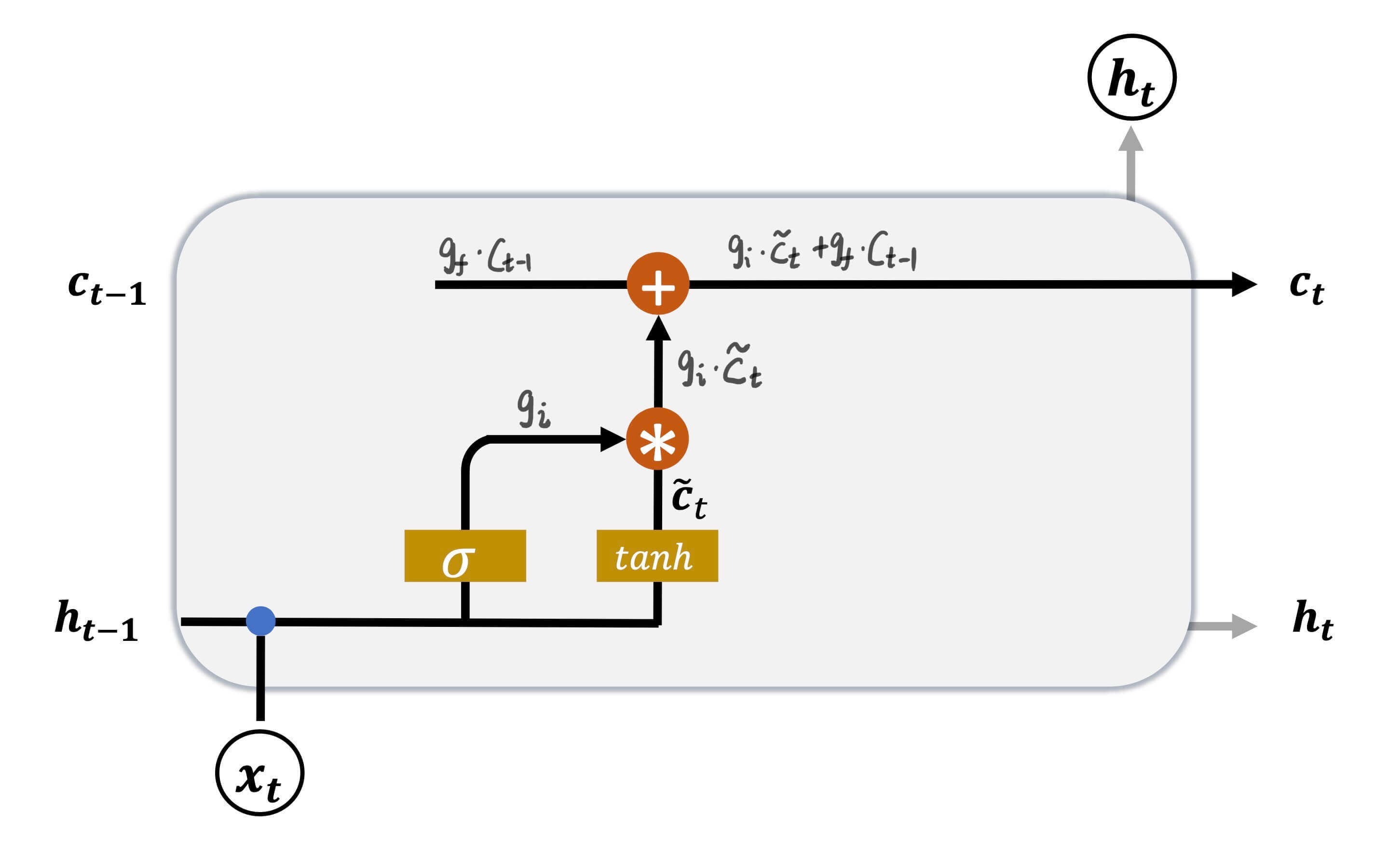
输入门
通过遗忘门,可以忘记过去,或者部分忘记过去。但是总有新的事情会发生,新的事情也不一定都要记住。这就是输入门。
c ~ t = tanh ( W c ⋅ [ h t − 1 , x t ] + b c ) \bold{\tilde{c}}_t = \tanh(\bold{W}_c \cdot [ \bold{h}_{t-1},\bold{x}_t ] + \bold{b}_c)
c ~ t = tanh ( W c ⋅ [ h t − 1 , x t ] + b c )
W c \bold{W}_c W c b c \bold{b}_c b c tanh \tanh tanh [ − 1 , 1 ] [-1,1] [ − 1 , 1 ]
g i = σ ( W i ⋅ [ h t − 1 , x t ] + b i ) \bold{g}_i = \sigma(\bold{W}_i \cdot [ \bold{h}_{t-1},\bold{x}_t ] + \bold{b}_i)
g i = σ ( W i ⋅ [ h t − 1 , x t ] + b i )
W i \bold{W}_i W i b i \bold{b}_i b i σ \sigma σ sigmoid。
然后将两者相乘。
g i ⋅ c ~ t \bold{g}_i \cdot \bold{\tilde{c}}_t
g i ⋅ c ~ t
如此对现在的输入实现门控。
最后
c t = g i c ~ t + g f c t − 1 \bold{c}_t = \bold{g}_i \bold{\tilde{c}}_t + \bold{g}_f \bold{c}_{t-1}
c t = g i c ~ t + g f c t − 1
通过这个方法,刷新记忆。
根据c t \bold{c}_t c t
遗忘门控
输入门控
LSTM行为
1
0
只有记忆
1
1
综合输入和记忆
0
0
清空所有,新的开始
0
1
忘记过去,只记今朝
在影片中,还给我们讲了一个极端的情况。每一个神经元的遗忘门控和输入门控都是0。
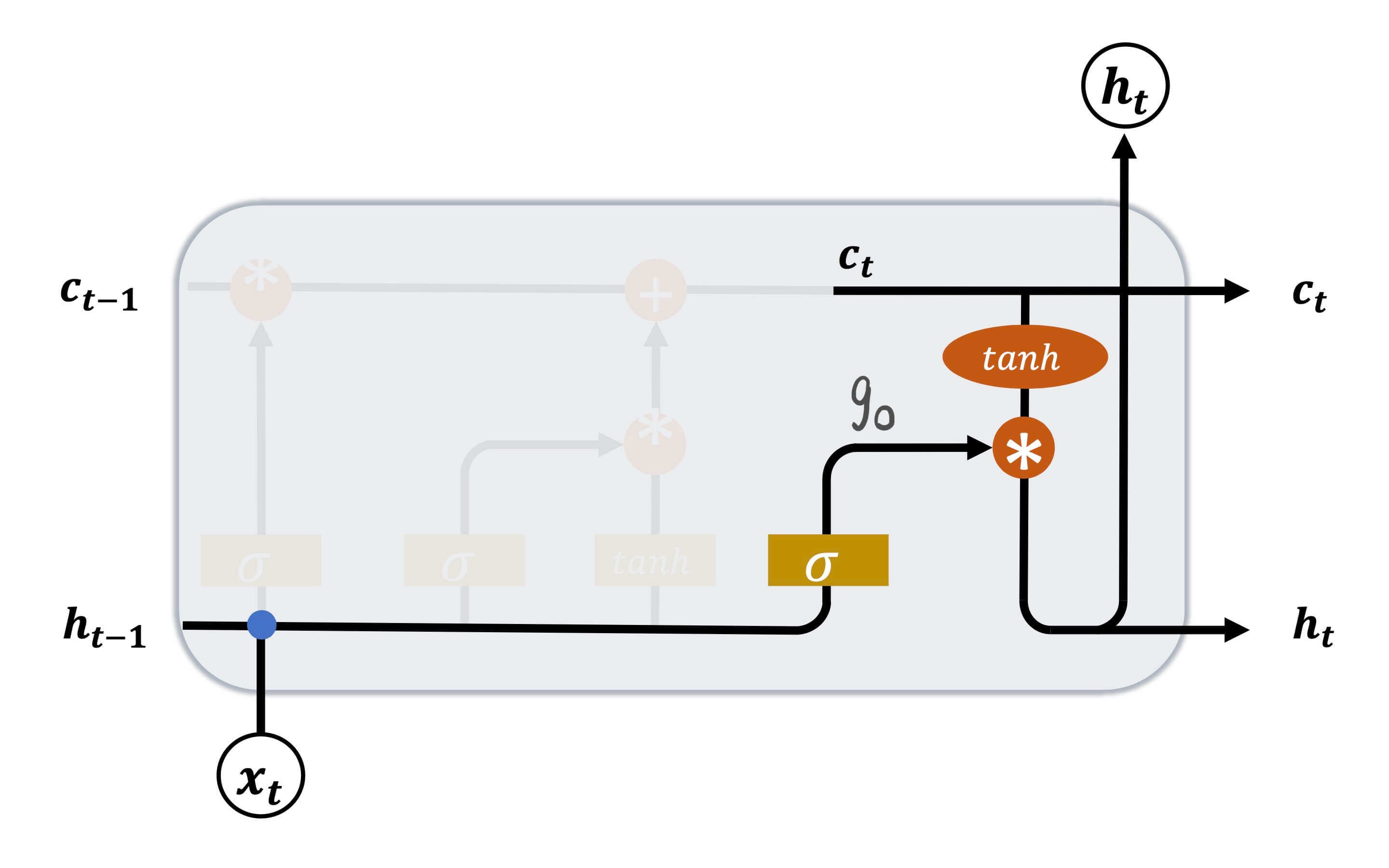
输出门
到目前位置,LSTM都是只对过去和现在的输入进行处理,从而形成记忆。
g o = σ ( W o ⋅ [ h t − 1 , x t ] + b o ) \bold{g}_o = \sigma(\bold{W}_o \cdot [ \bold{h}_{t-1},\bold{x}_t ] + \bold{b}_o)
g o = σ ( W o ⋅ [ h t − 1 , x t ] + b o )
W o \bold{W}_o W o b o \bold{b}_o b o σ \sigma σ sigmoid。
h t = g o ∗ tanh ( c t ) \bold{h}_t = \bold{g}_o * \tanh(\bold{c}_t)
h t = g o ∗ tanh ( c t )
即当前的记忆c t \bold{c}_t c t tanh \tanh tanh g o \bold{g}_o g o h t \bold{h}_t h t
因为g o \bold{g}_o g o sigmoid函数,所以其值域是[ 0 , 1 ] [0,1] [ 0 , 1 ] tanh \tanh tanh [ − 1 , 1 ] [-1,1] [ − 1 , 1 ] h t ∈ [ − 1 , 1 ] \bold{h}_t \in [-1,1] h t ∈ [ − 1 , 1 ]
小结
最后我们进行一个小结。
g f = σ ( W f ⋅ [ h t − 1 , x t ] + b f ) g i = σ ( W i ⋅ [ h t − 1 , x t ] + b i ) g o = σ ( W o ⋅ [ h t − 1 , x t ] + b o ) \begin{aligned}
\bold{g}_f &= \sigma(\bold{W}_f \cdot [ \bold{h}_{t-1},\bold{x}_t ] + \bold{b}_f) \\
\bold{g}_i &= \sigma(\bold{W}_i \cdot [ \bold{h}_{t-1},\bold{x}_t ] + \bold{b}_i) \\
\bold{g}_o &= \sigma(\bold{W}_o \cdot [ \bold{h}_{t-1},\bold{x}_t ] + \bold{b}_o)
\end{aligned}
g f g i g o = σ ( W f ⋅ [ h t − 1 , x t ] + b f ) = σ ( W i ⋅ [ h t − 1 , x t ] + b i ) = σ ( W o ⋅ [ h t − 1 , x t ] + b o )
而这三个门都是由h t − 1 \bold{h}_{t-1} h t − 1 x t \bold{x}_t x t
一个中间状态:
c ~ t = tanh ( W c ⋅ [ h t − 1 , x t ] + b c ) \bold{\tilde{c}}_t = \tanh(\bold{W}_c \cdot [ \bold{h}_{t-1},\bold{x}_t ] + \bold{b}_c)
c ~ t = tanh ( W c ⋅ [ h t − 1 , x t ] + b c )
两个输出:
c t = g i c ~ t + g f c t − 1 h t = g o ∗ tanh ( c t ) \begin{aligned}
\bold{c}_t &= \bold{g}_i \bold{\tilde{c}}_t + \bold{g}_f \bold{c}_{t-1} \\
\bold{h}_t &= \bold{g}_o * \tanh(\bold{c}_t)
\end{aligned}
c t h t = g i c ~ t + g f c t − 1 = g o ∗ tanh ( c t )
也有些时候,我们会写成这种形式。
LSTM梯度
现在我们来讨论LSTM的梯度。l o s s loss l o s s h t \bold{h}_t h t ∂ l o s s ∂ h t \frac{\partial loss}{\partial \bold{h}_t} ∂ h t ∂ l o s s
h t = g o ∗ tanh ( c t ) ∂ h t ∂ W = ( g o ) ′ ( tanh ( c t ) ) + ( g o ) ( tanh ( c t ) ) ′ \begin{aligned}
\bold{h}_t &= \bold{g}_o * \tanh(\bold{c}_t) \\
\frac{\partial \bold{h}_t}{\partial \bold{W}} &= (\bold{g}_o)'(\tanh(\bold{c}_t)) + (\bold{g}_o)(\tanh(\bold{c}_t))'
\end{aligned}
h t ∂ W ∂ h t = g o ∗ tanh ( c t ) = ( g o ) ′ ( tanh ( c t ) ) + ( g o ) ( tanh ( c t ) ) ′
而g o = σ ( W o ⋅ [ h t − 1 , x t ] + b o ) \bold{g}_o = \sigma(\bold{W}_o \cdot [ \bold{h}_{t-1},\bold{x}_t ] + \bold{b}_o) g o = σ ( W o ⋅ [ h t − 1 , x t ] + b o ) ( g o ) ′ (\bold{g}_o)' ( g o ) ′
c t = g i c ~ t + g f c t − 1 \bold{c}_t = \bold{g}_i \bold{\tilde{c}}_t + \bold{g}_f \bold{c}_{t-1}
c t = g i c ~ t + g f c t − 1
且g i \bold{g}_i g i c ~ t \bold{\tilde{c}}_t c ~ t g f \bold{g}_f g f h t − 1 \bold{h}_{t-1} h t − 1 h t − 1 \bold{h}_{t-1} h t − 1 c t − 1 \bold{c}_{t-1} c t − 1 c t \bold{c}_{t} c t c t − 1 \bold{c}_{t-1} c t − 1
在循环神经网络中: h t = tanh ( W x h x t + W h h h t − 1 + b ) \text{在循环神经网络中:}\bold{h}_t = \tanh(\bold{W}_{xh}\bold{x}_t + \bold{W}_{hh}\bold{h}_{t-1} + b)
在循环神经网络中: h t = tanh ( W x h x t + W h h h t − 1 + b )
又是t − 1 t-1 t − 1 t t t
∂ c t ∂ c t − 1 = ( g i ) ′ ( c ~ t ) + ( g i ) ( c ~ t ) ′ + ( g f ) ′ ( c t − 1 ) + ( g f ) ( c t − 1 ) ′ \frac{\partial \bold{c}_t}{\partial \bold{c}_{t-1}} = (\bold{g}_i)'(\bold{\tilde{c}}_t) + (\bold{g}_i)(\bold{\tilde{c}}_t)' + (\bold{g}_f)'(\bold{c}_{t-1}) + (\bold{g}_f)(\bold{c}_{t-1})'
∂ c t − 1 ∂ c t = ( g i ) ′ ( c ~ t ) + ( g i ) ( c ~ t ) ′ + ( g f ) ′ ( c t − 1 ) + ( g f ) ( c t − 1 ) ′
我们注意到最后一部分。
( g f ) ( c t − 1 ) ′ = g f (\bold{g}_f)(\bold{c}_{t-1})' = \bold{g}_f
( g f ) ( c t − 1 ) ′ = g f
g f \bold{g}_f g f g f = 1 \bold{g}_f = 1 g f = 1 g f ≈ 1 \bold{g}_f \approx 1 g f ≈ 1
所以,LSTM不容易出现梯度弥散。
LSTM层的实现
与RNN一样,在TensorFlow中,LSTM层同样有两种方法。
keras.layers.LSTMCell
keras.layers.LSTM
LSTMCell
方法:
LSTMCell的trainable_variables
我们将LSTMCell和SimpleRNNCell进行比较。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 from tensorflow.keras import layerslstmcell = layers.LSTMCell(5 ) rnncell = layers.SimpleRNNCell(5 ) lstmcell.build(input_shape=(None ,10 )) rnncell.build(input_shape=(None ,10 )) for var in zip(lstmcell.trainable_variables,rnncell.trainable_variables): print(var[0 ].name,var[0 ].shape,var[0 ].dtype) print(var[1 ].name,var[1 ].shape,var[1 ].dtype) print('\n' )
运行结果:
1 2 3 4 5 6 7 8 9 10 kernel:0 (10, 20) <dtype: 'float32'> kernel:0 (10, 5) <dtype: 'float32'> recurrent_kernel:0 (5, 20) <dtype: 'float32'> recurrent_kernel:0 (5, 5) <dtype: 'float32'> bias:0 (20,) <dtype: 'float32'> bias:0 (5,) <dtype: 'float32'>
我们发现LSTMCell的参数量是SimpleRNNCell的四倍。哪四倍呢?
W f \bold{W}_f W f W i \bold{W}_i W i W o \bold{W}_o W o W c \bold{W}_c W c
前向计算
对于前向计算,我们需要初始化的状态有两个:h 0 \bold{h}_0 h 0 c 0 \bold{c}_0 c 0
1 2 3 4 5 6 7 8 9 10 11 state0 = [tf.zeros([4 , 5 ]),tf.zeros([4 , 5 ])] x = tf.random.normal([4 , 7 , 10 ]) xt = x[:,0 ,:] out, state1 = lstmcell(xt, state0) print(out.shape, state1[0 ].shape,state1[1 ].shape) print(id(out),id(state1[0 ]),id(state1[1 ]))
运行结果:
1 2 (4, 5) (4, 5) (4, 5) 140528518879184 140528518879184 140528544545600
正如运行结果所示,返回的输出o u t \bold{out} o u t h t \bold{h}_t h t
串联成LSTM层
我们可以发挥循环神经网络的精髓。x t \bold{x}_t x t h t \bold{h}_t h t o t \bold{o}_t o t
示例代码:
1 2 3 4 5 6 state = state0 for xt in tf.unstack(x, axis=1 ): out, state = lstmcell(xt, state) print(out.shape,state[0 ].shape,state[1 ].shape)
运行结果:
1 2 3 4 5 6 7 (4, 5) (4, 5) (4, 5) (4, 5) (4, 5) (4, 5) (4, 5) (4, 5) (4, 5) (4, 5) (4, 5) (4, 5) (4, 5) (4, 5) (4, 5) (4, 5) (4, 5) (4, 5) (4, 5) (4, 5) (4, 5)
LSTM层
除了串联LSTMCell,我们还有更简洁的方法。
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 import tensorflow as tffrom tensorflow.keras import layerslayer = layers.LSTM(5 ) x = tf.random.normal([4 , 7 , 10 ]) out = layer(x) print(out) print('\n' ) for var in layer.trainable_variables: print(var.name,var.shape,var.dtype)
运行结果:
1 2 3 4 5 6 7 8 9 10 tf.Tensor( [[-0.10342102 0.01817901 -0.47463024 0.14861609 -0.07993239] [ 0.26894122 -0.02338248 0.38075954 0.21347676 0.20355701] [ 0.03350078 -0.06494962 0.08367281 -0.09063848 -0.07871907] [ 0.1321046 0.42025885 0.19594304 0.03045102 0.06093809]], shape=(4, 5), dtype=float32) lstm/lstm_cell/kernel:0 (10, 20) <dtype: 'float32'> lstm/lstm_cell/recurrent_kernel:0 (5, 20) <dtype: 'float32'> lstm/lstm_cell/bias:0 (20,) <dtype: 'float32'>
在上面的代码中,我们还专门看了一下layer的trainable_variables,和LSTMCell的trainable_variables是一样的,即做了权值共享。
和RNNCell一样,如果需要每一个LSTMCell都输出,可以通过设置return_sequences=True来实现。
1 2 3 4 5 6 layer = layers.LSTM(5 ,return_sequences=True ) x = tf.random.normal([4 , 7 , 10 ]) out = layer(x) print(out.shape)
运行结果:
当然,我们也堆叠多个LSTM层。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 import tensorflow as tffrom tensorflow.keras import layers,Sequentialnet = Sequential([ layers.LSTM(5 , return_sequences=True ), layers.LSTM(5 ), ]) x = tf.random.normal([4 , 7 , 10 ]) out = net(x) print(out) for var in net.trainable_variables: print(var.name,var.shape,var.dtype)
运行结果:
1 2 3 4 5 6 7 8 9 10 11 tf.Tensor( [[ 0.01342524 -0.03180564 0.05031351 0.01574086 0.12032484] [-0.03389003 0.03127829 0.07479815 0.06893347 0.13489318] [-0.02699067 0.04662055 0.02154445 0.15134797 -0.03523358] [-0.09501531 0.12560178 0.1094329 0.14707239 0.08788656]], shape=(4, 5), dtype=float32) lstm_1/lstm_cell_1/kernel:0 (10, 20) <dtype: 'float32'> lstm_1/lstm_cell_1/recurrent_kernel:0 (5, 20) <dtype: 'float32'> lstm_1/lstm_cell_1/bias:0 (20,) <dtype: 'float32'> lstm_2/lstm_cell_2/kernel:0 (5, 20) <dtype: 'float32'> lstm_2/lstm_cell_2/recurrent_kernel:0 (5, 20) <dtype: 'float32'> lstm_2/lstm_cell_2/bias:0 (20,) <dtype: 'float32'>
LSTM的实现
还是以IMDB电影评论的积极消极分类为例。
基于LSTMCell的实现
只需要在基于RNNCell的RNN实现的基础上,对初始化方法做非常简单的修改。
需要提供h 0 \bold{h}_0 h 0 c 0 \bold{c}_0 c 0
把SimpleRNNCell换成LSTMCell。
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 def __init__ (self, units) : super(LSTM, self).__init__() self.state0 = [tf.zeros([batch_size, units]), tf.zeros([batch_size, units])] self.state1 = [tf.zeros([batch_size, units]), tf.zeros([batch_size, units])] self.embedding = layers.Embedding(input_dim=total_words, output_dim=embedding_len, input_length=max_review_len) self.rnn_cell0 = layers.LSTMCell(units, dropout=0.5 ) self.rnn_cell1 = layers.LSTMCell(units, dropout=0.5 ) self.out = layers.Dense(1 )
基于LSTM层的实现
只需要在基于RNN层的RNN实现的基础上,对初始化方法做非常简单的修改。
示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 def __init__ (self, units) : super(LSTM, self).__init__() self.embedding = layers.Embedding(total_words, embedding_len, input_length=max_review_len) self.lstmlayer = keras.Sequential([ layers.LSTM(units, dropout=0.5 , return_sequences=True , unroll=True ), layers.LSTM(units, dropout=0.5 , unroll=True ) ]) self.outlayer = layers.Dense(1 )
LSTM的优缺点
和RNN相比。
优点有:
具有更长的记忆能力
不容易出现梯度弥散现象
缺点有:
LSTM结构相对复杂,计算代价较高,模型参数量较大。
那么,有没有具有更长的记忆能力,不容易出现梯度弥散。结构还简单的网络模型呢?
GRU的结构
GRU,门控循环网络(Gated Recurrent Unit)。
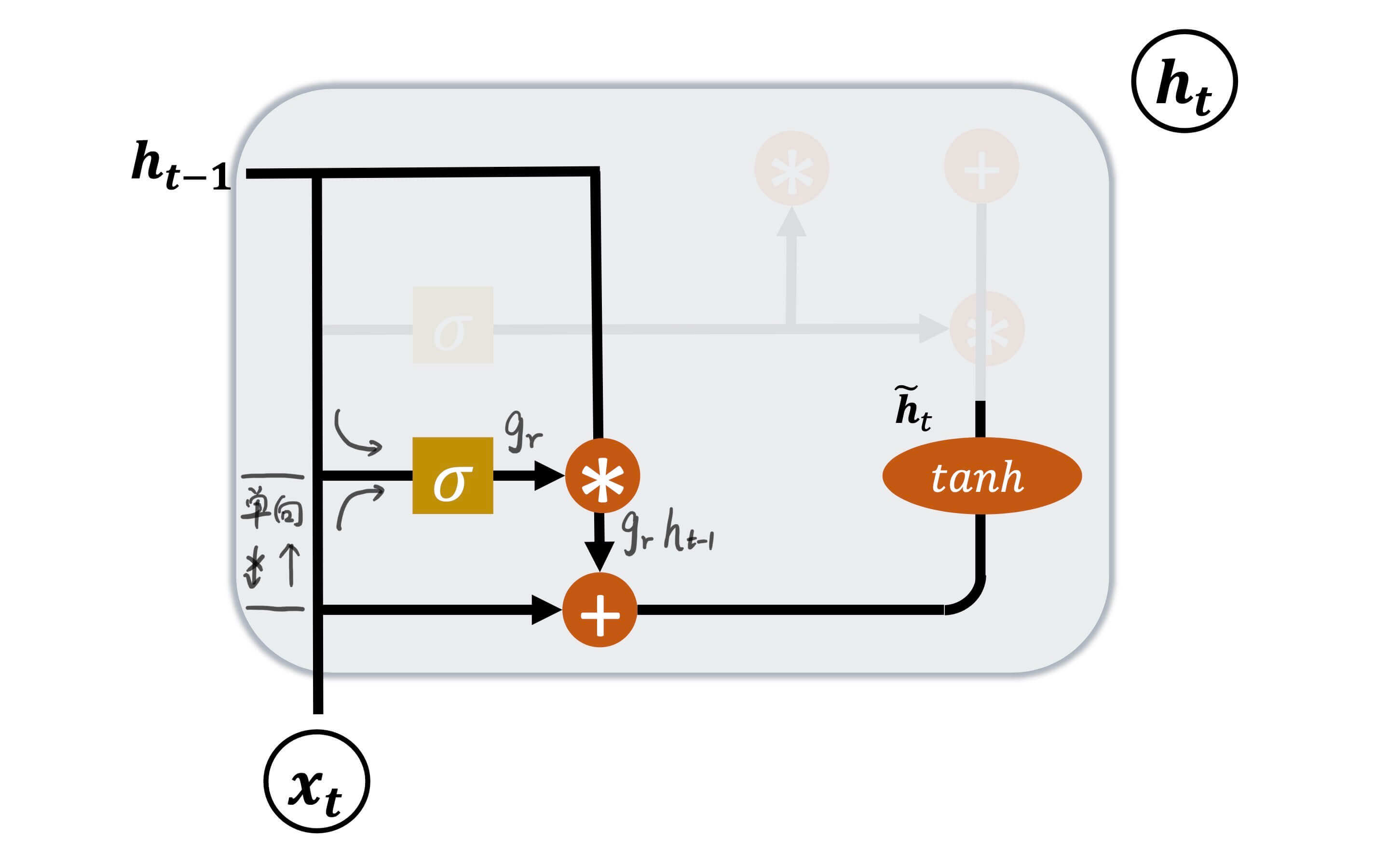
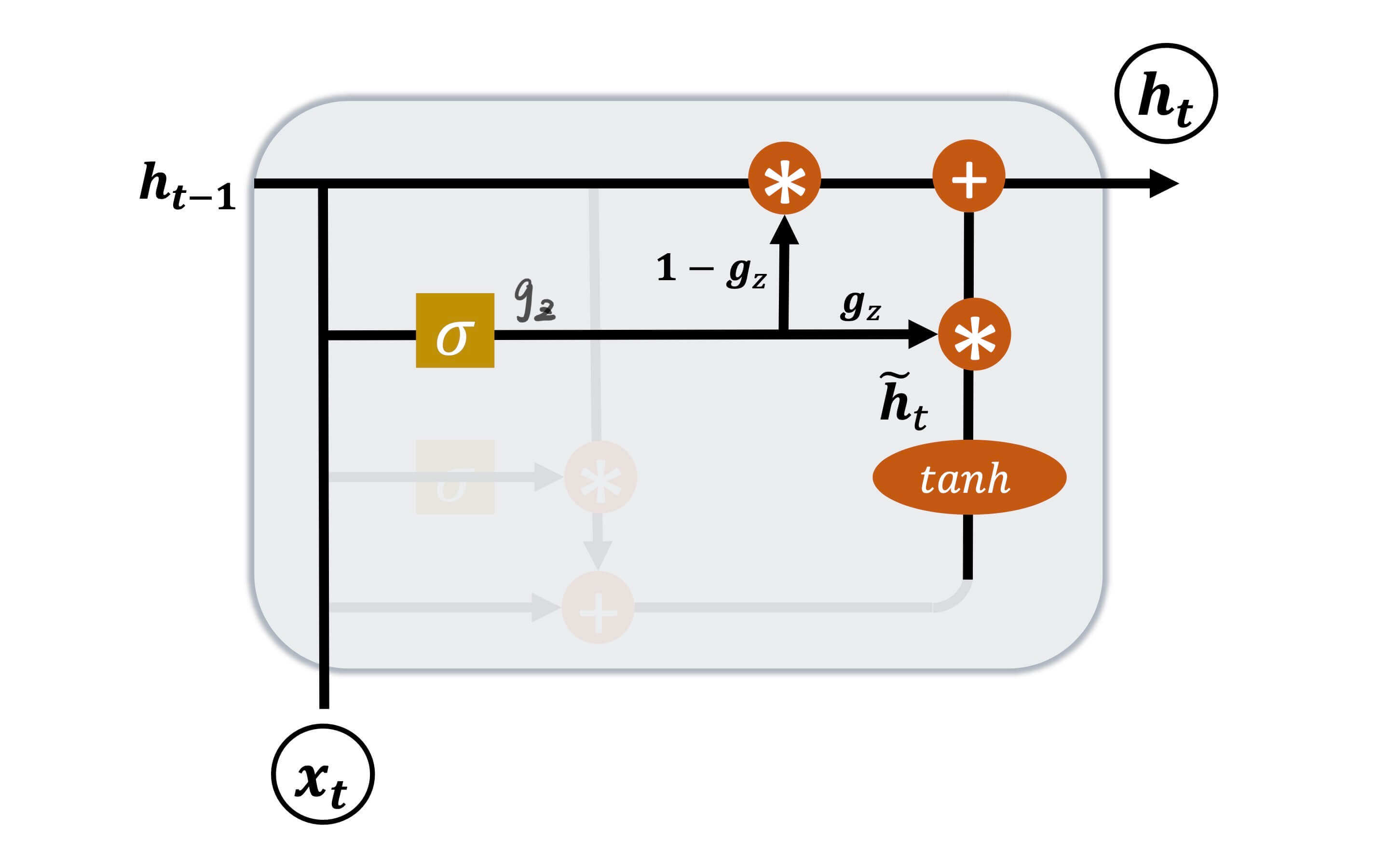
在GRU中c \bold{c} c h \bold{h} h h \bold{h} h
复位门(Reset Gate)
更新门(Update Gate)
复位门
复位门用于控制上一个GRU神经元的h t − 1 \bold{h}_{t-1} h t − 1
g r = σ ( W r [ h t − 1 , x t ] + b r ) \bold{g}_r = \sigma(\bold{W}_r[\bold{h}_{t-1},\bold{x}_t] + \bold{b}_r)
g r = σ ( W r [ h t − 1 , x t ] + b r )
W r \bold{W}_r W r b r \bold{b}_r b r σ \sigma σ sigmoid。
h ~ t = tanh ( W h ⋅ [ g r h t − 1 , x t ] + b h ) \bold{\tilde{h}}_t = \tanh(\bold{W}_h \cdot [ \bold{g}_r \bold{h}_{t-1},\bold{x}_t] + \bold{b}_h)
h ~ t = tanh ( W h ⋅ [ g r h t − 1 , x t ] + b h )
即,门控向量g r \bold{g}_r g r h t − 1 \bold{h}_{t-1} h t − 1 x t \bold{x}_t x t
更新门
更新门则是控制当前GRU神经元输出至下一个神经元的h t \bold{h}_t h t
g z = σ ( W z [ h t − 1 , x t ] + b z ) \bold{g}_z = \sigma(\bold{W}_z[\bold{h}_{t-1},\bold{x}_t] + \bold{b}_z)
g z = σ ( W z [ h t − 1 , x t ] + b z )
W z \bold{W}_z W z b z \bold{b}_z b z σ \sigma σ sigmoid。
h t = ( 1 − g z ) h t − 1 + g z h ~ t \bold{h}_t = (1-\bold{g}_z) \bold{h}_{t-1} + \bold{g}_z \bold{\tilde{h}}_t
h t = ( 1 − g z ) h t − 1 + g z h ~ t
即,g z \bold{g}_z g z h ~ t \bold{\tilde{h}}_t h ~ t 1 − g z 1-\bold{g}_z 1 − g z h t − 1 \bold{h}_{t-1} h t − 1 g z \bold{g}_z g z h ~ t \bold{\tilde{h}}_t h ~ t h t − 1 \bold{h}_{t-1} h t − 1
至于GRU层的实现和GRU神经网络的实现,和之前讨论的"RNN"以及"LSTM"类似,这里不再赘述。