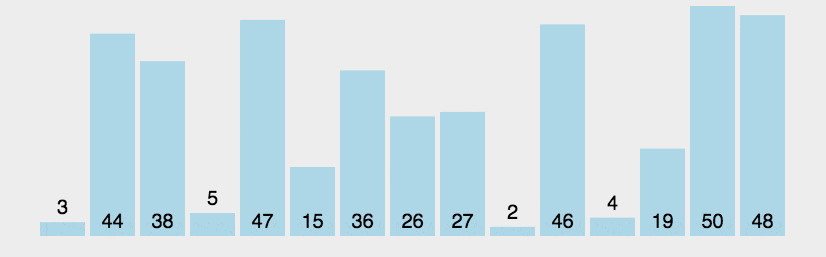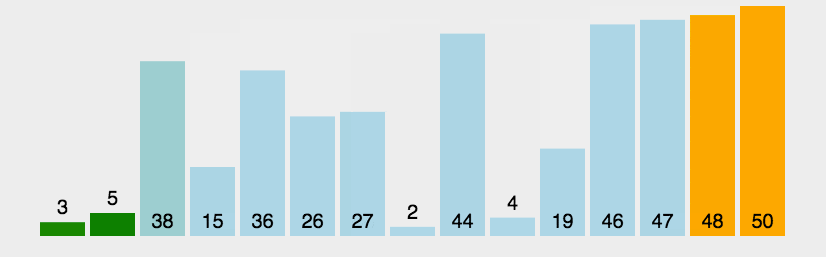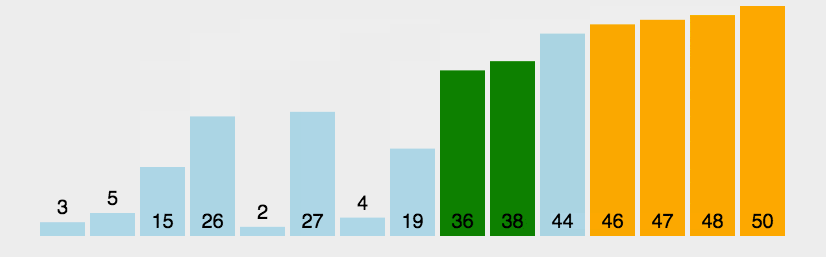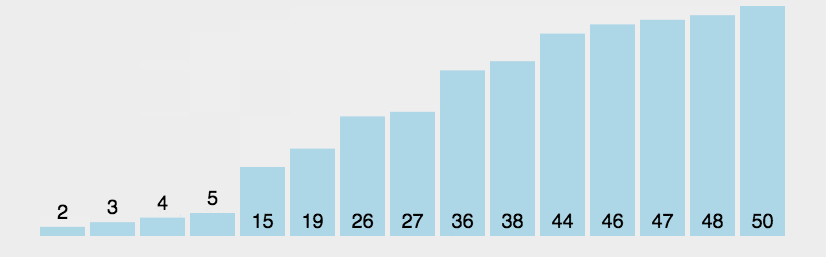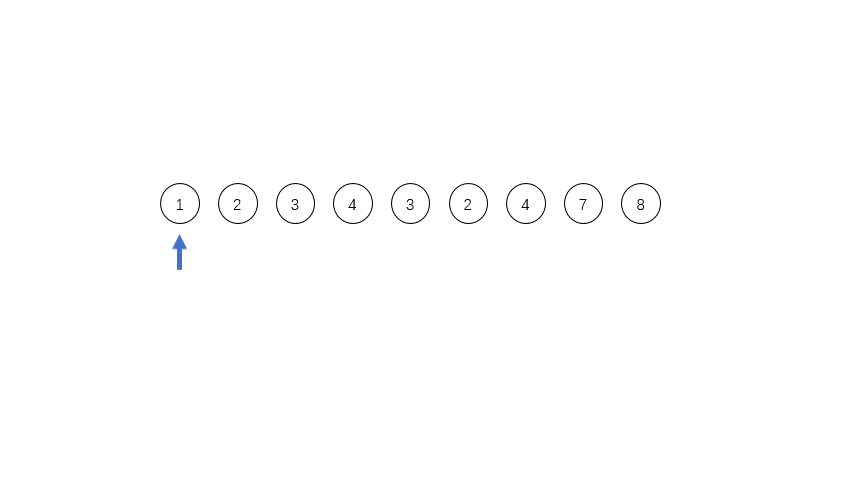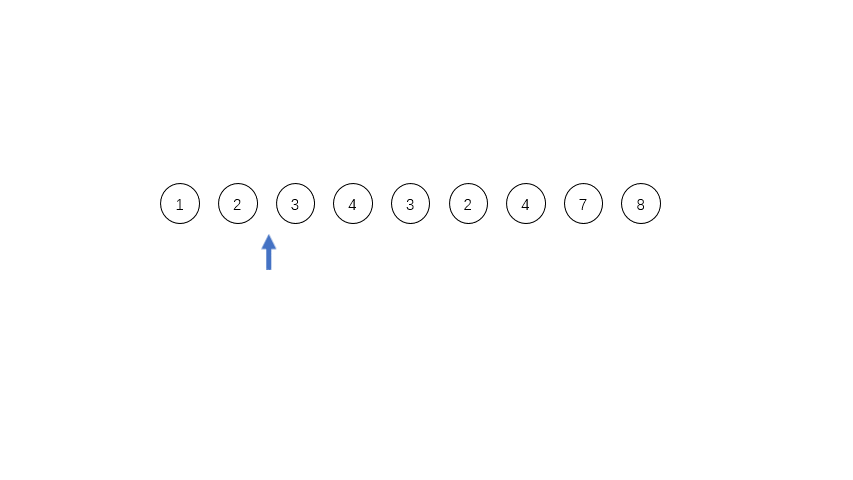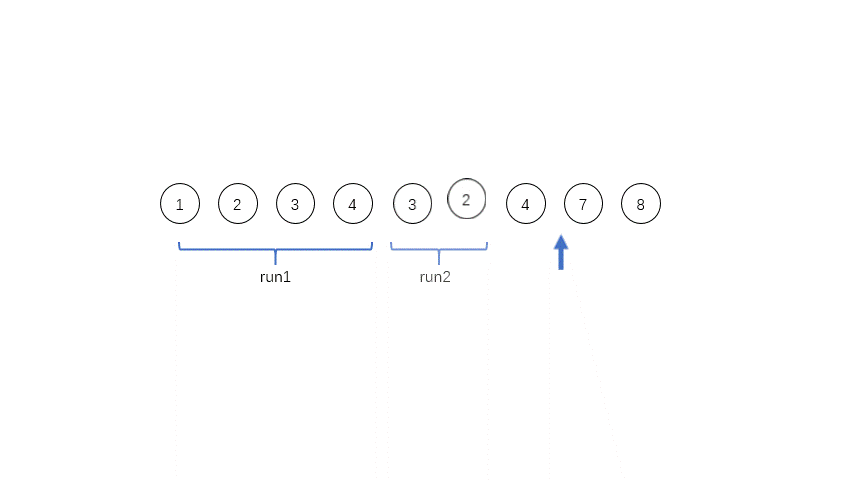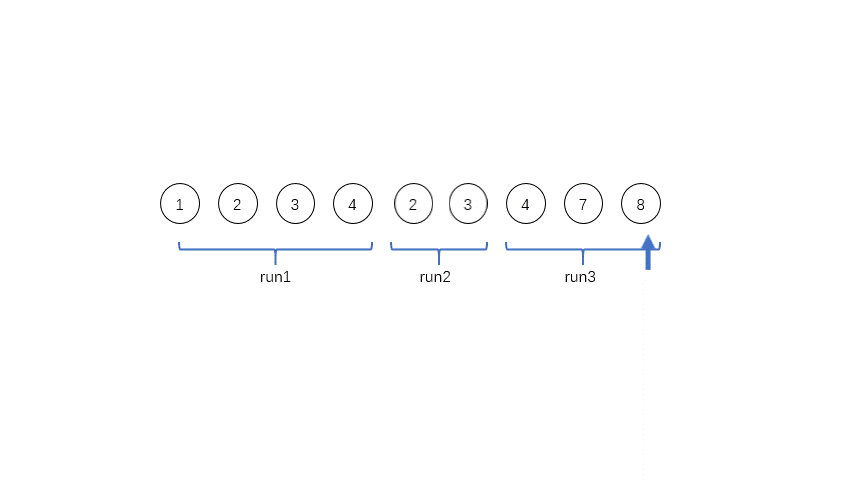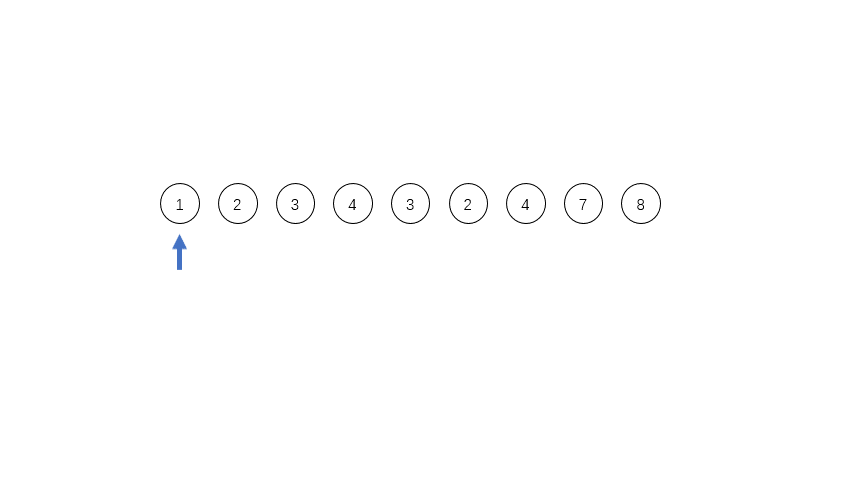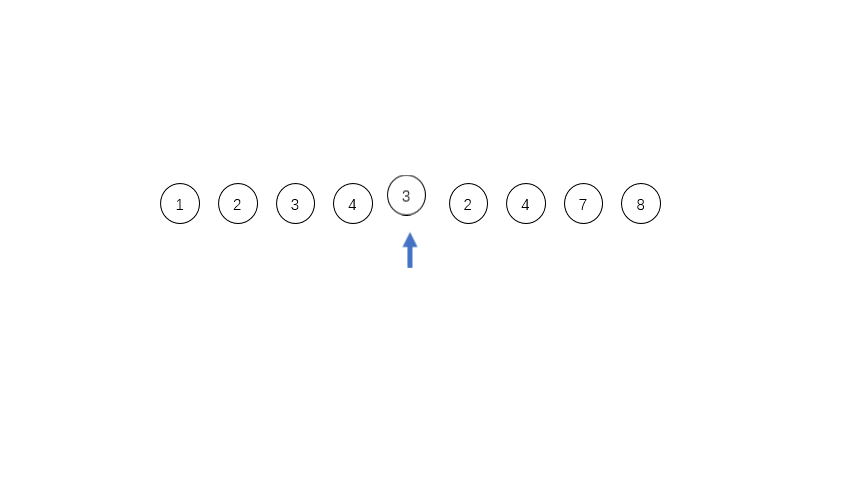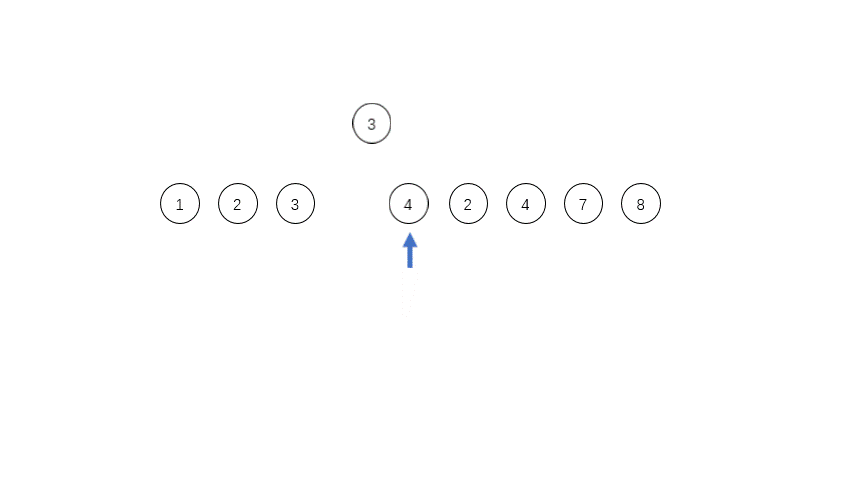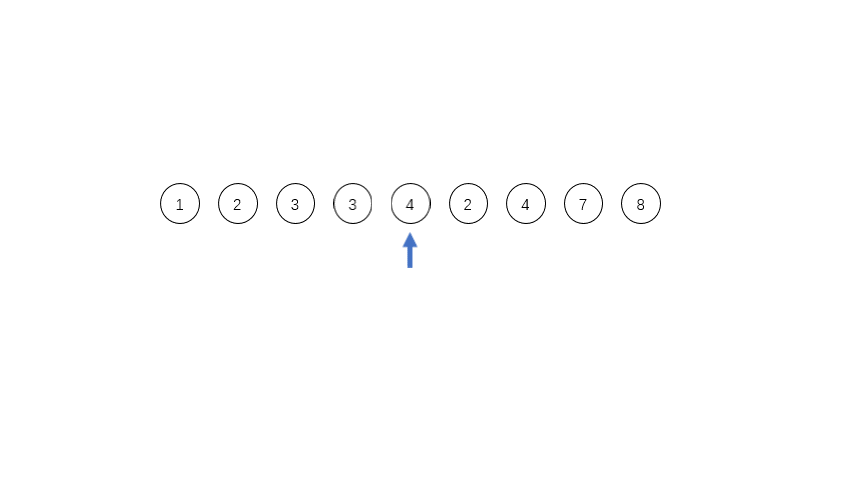5.排序

排序，这个我们太常用了。而且估计99%的编程语言都内置了排序算法。

• Java
• Python

示例代码：

int[] a = {3, 1, 4, 5, 9, 2, 6};
Arrays.sort(a);
System.out.println(Arrays.toString(a));

运行结果：

[1, 2, 3, 4, 5, 6, 9]

示例代码：

a = [3, 1, 4, 5, 9, 2, 6]
a.sort()
print(a)

运行结果：

[1, 2, 3, 4, 5, 6, 9]

那些编程语言内置的排序算法是什么？

如何评价一个排序算法

那些创造编程语言的人，才是真正的顶级软件工程师。
而能够作为编程语言的内置的排序算法，也必然是工业级的，评价最好的排序算法。

所以，我们讨论的第一个问题是，如何评价一个排序算法？

关于如何评价一个算法，这个我们讨论过了，两个指标，时间复杂度和空间复杂度。
而关于排序算法，我们还有几个特别的评价指标。

1. 原地排序
2. 稳定性

原地排序

原地排序(Sorted in place)，特指空间复杂度是$O(1)$。

稳定性

如果待排序的序列中存在值相等的元素，经过排序之后，相等的元素之间的原有先后顺序不变。我们就说这个排序算法是稳定的。

举个例子。
现在有这么一组数据。3,1,4,1,5,9,2,6，其中第一个1的内存位置是a，第二个1的内存位置是b。在经过某个排序算法排序之后，是1,1,2,3,4,5,6,9，并且内存地址为a的1依旧在前面，内存地址为b的1依旧在后面。那么，我们说这个排序算法是稳定的了。

如果b在前，a在后呢？那就不稳定了。

再举个例子
现在我们要对市场的股票进行排序，先按涨跌幅进行排序，对于涨跌幅相同的股票，再按照成交量进行排序。
那我们怎么做？

方案一：
第一步、按照涨跌幅排序
第二步、按照成交量排序

完了，如果排序算法不稳定的话，第二步会把第一步按涨跌幅排好的顺序给弄乱了。

方案二：
我们先按照涨跌幅进行排序，对于涨跌幅相同的股票，再按照成交量进行排序。
这么做当然可以，但，不嫌麻烦？不嫌慢？

方案三：
我们先按照成交量，在按照成交量排序完成之后，再用稳定的排序算法，按照涨跌幅进行排序。这样两遍排序，完成。
稳定的排序可以保持成交量相同的两只股票，在排序之后的前后顺序不变。

这就是为什么我们要求排序算法稳定。

选择排序

接下来，我们来依次讨论八大排序算法。
首先是选择排序。

选择排序的过程

在第一章讨论时间复杂度的时候，我们已经讨论过了选择排序。当时我们以选择排序为例，讨论了计算时间复杂度的第一个规则：把整个流程拆分为一个个不可以再拆分的常数操作，只考虑最高阶。

现在，我们复习一下选择排序。

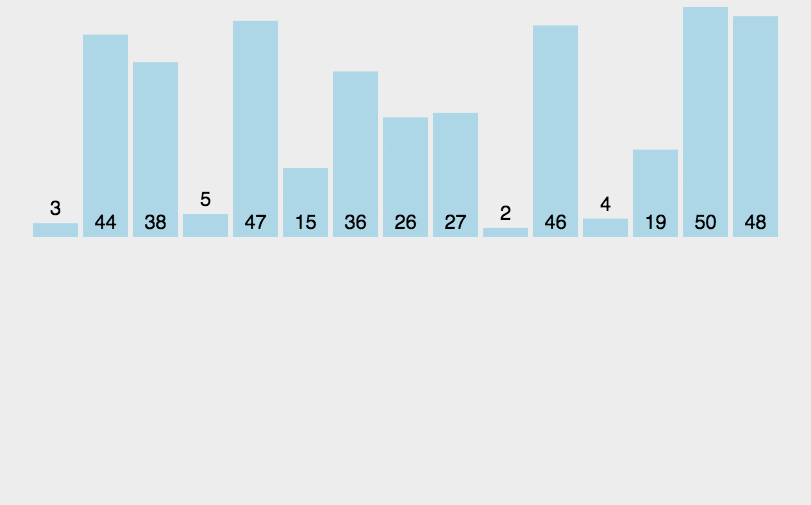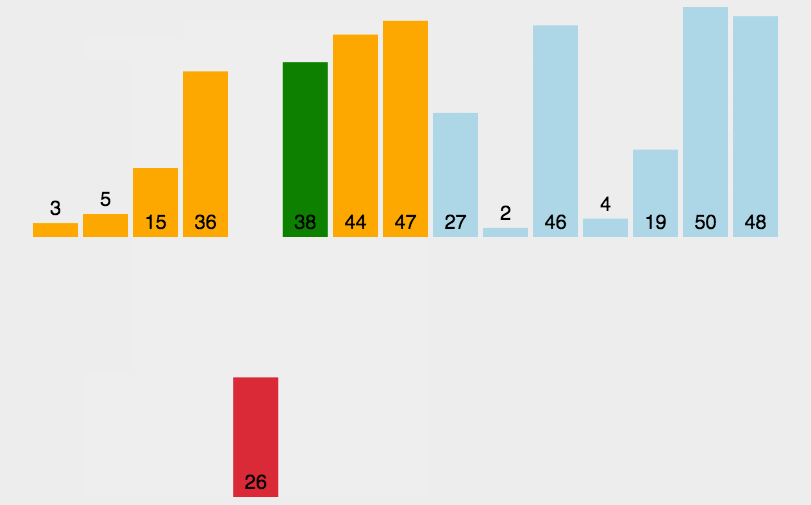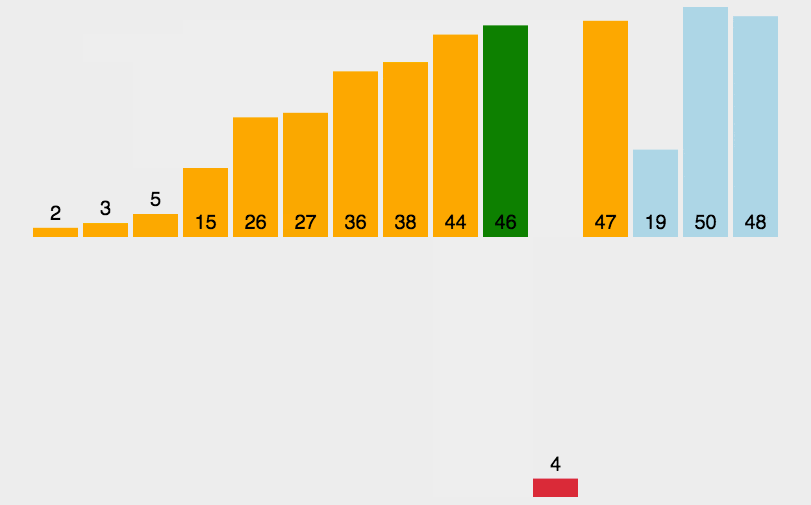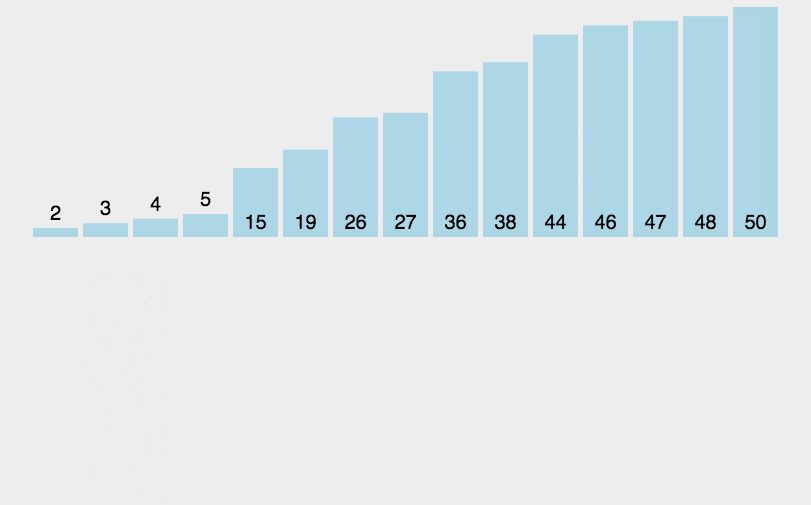
排序之前：

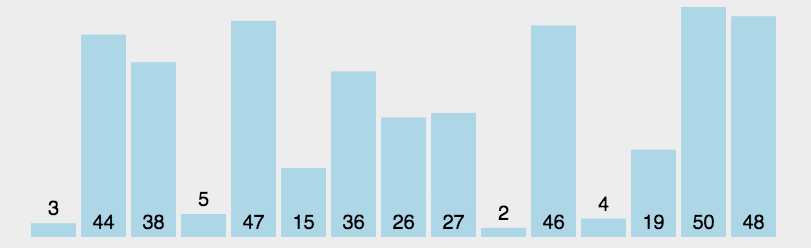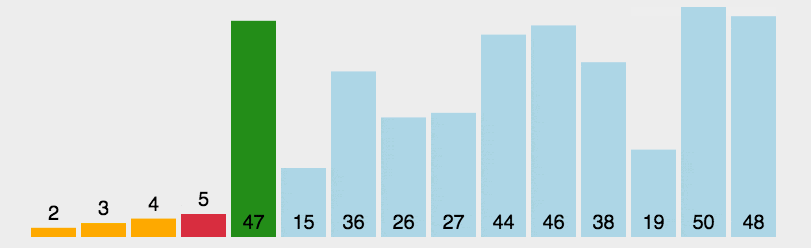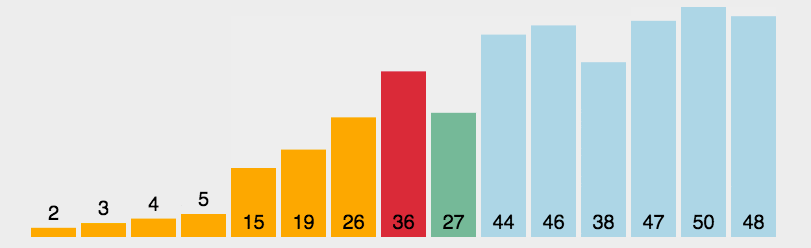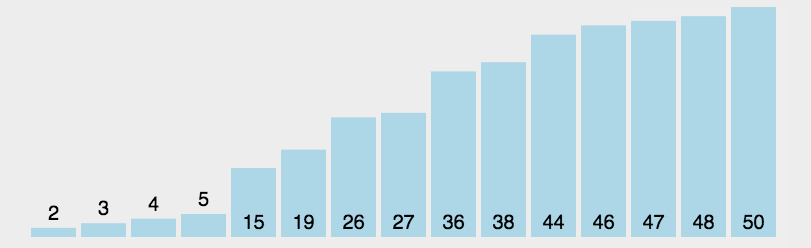
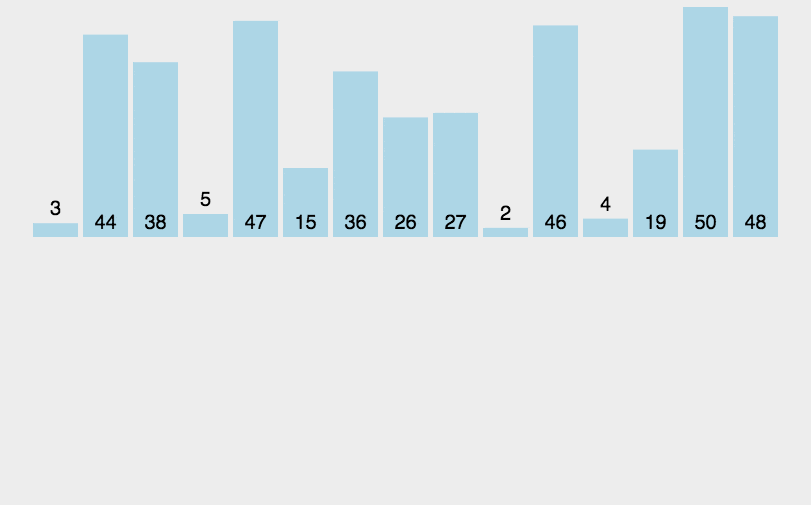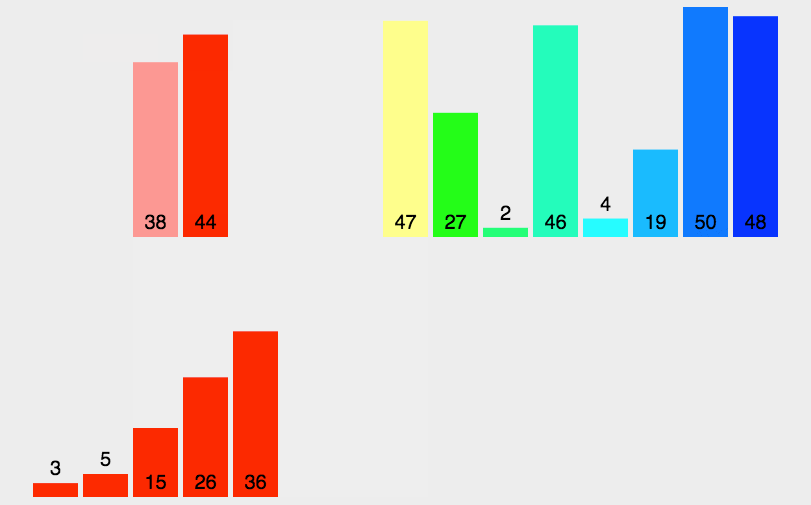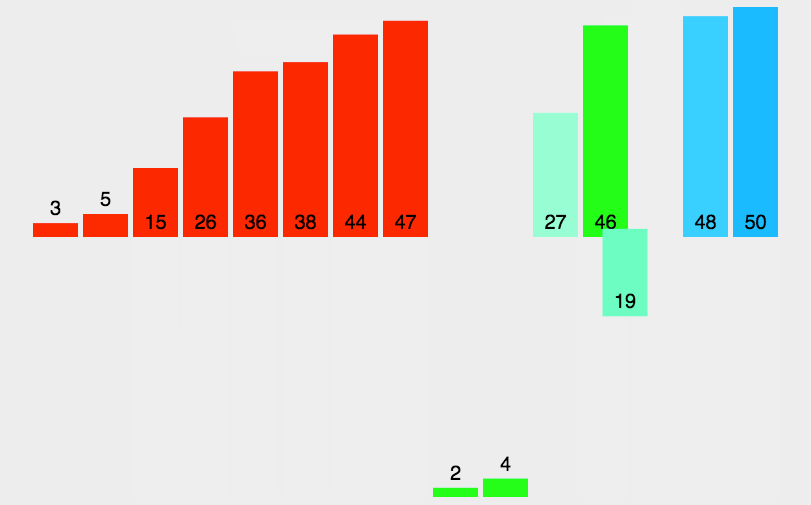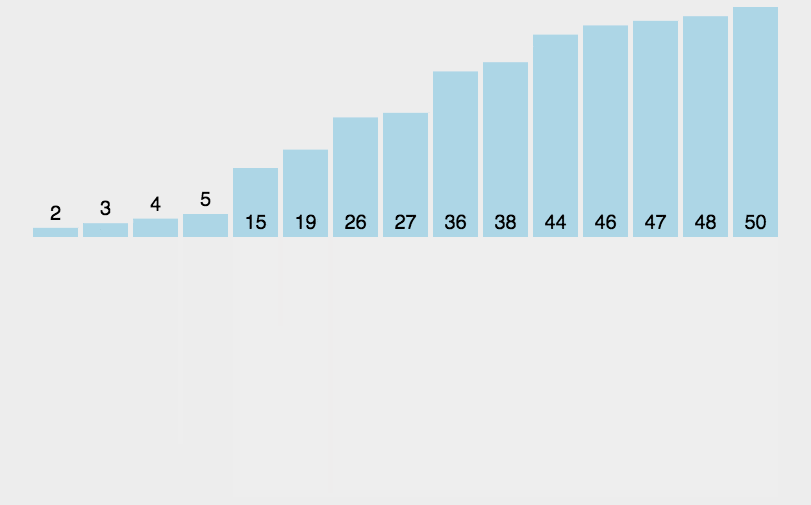
[3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]

第一轮
我们把从index为0的数字到index为n-1的数字进行比较，记住最小值的index。

1. 3和44相比，3最小，记住最小值的index
2. 3和38相比，3最小，记住最小值的index
3. 3和5相比，3最小，记住最小值的index
4. ······

最后，我们把最小值移到前部，和0位置的数字进行互换。
第一轮结束，我们会得到

[2,44,38,5,47,15,36,26,27,3,46,4,19,50,48]

第二轮
我们把从index为1的数字到index为n-1的数字进行比较，并把最小的数字，通过互换的方式移到前部。
最后会得到

[2,3,38,5,47,15,36,26,27,44,46,4,19,50,48]

如此迭代循环，每一轮都选择当前轮的最小数，通过互换移到前面，最后完成排序过程。

选择排序的实现

这个参考第一章的代码，不再赘述。

选择排序的特点

我们从三个角度去讨论选择排序的特点。
之后所有的排序算法，也都是从这三个角度去讨论。

1. 时间复杂度
2. 是否原地排序(空间复杂度)
3. 是否稳定

时间复杂度

$O(n^2)$

是否原地排序

是原地排序。选择排序只涉及到数据交换，只需要常量级别的额外空间，空间复杂度为$O(1)$。

是否稳定

不稳定
我们这里举一个反例。
有这么一串数字：

$$20\widehat{\bold{2}}1$$

• 为了以示区分，第二个2，我们写作$\widehat{\bold{2}}$。

第一轮，当前轮的最小数是$0$，和0位置的数互换，和$2$互换。

$$02\widehat{\bold{2}}1$$

第二轮，当前轮的最小数是$1$，和1位置的数互换，和$2$互换。

$$01\widehat{\bold{2}}2$$

乱了，乱了，乱了。2的位置不对了。
刚刚还是$2$在$\widehat{\bold{2}}$的前面，现在成了$\widehat{\bold{2}}$在$2$的前面了。

冒泡排序

接下来，我们讨论第二个排序算法：冒泡排序。
这是一个"不会乱"的排序算法。

冒泡排序的过程

在第一章，我们以冒泡排序算法为例，讨论了计算时间复杂度的第二个规则：最有参考价值的是最坏时间复杂度。
现在，我们复习一下冒泡排序。

排序之前：

[3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]

冒泡过程：
index为0的数字和index为1的数字进行比较，3和44比较，右边(index为1)的数大，不交换。
index为1的数字和index为2的数字进行比较，44和38比较，左边(index为1)的数大，交换。(冒泡)
得到

[3,38,44,5,47,15,36,26,27,2,46,4,19,50,48]

继续，index为2的数字和index为3的数字进行比较，44和5比较，左边(index为2)的的数大，交换。(冒泡)得到

[3,38,5,44,47,15,36,26,27,2,46,4,19,50,48]

最后，当我们index为n-1的数字和index为n的数字进行比较，并按条件进行交换之后，一定是最大的数在最右边。然后我们再进行一轮，这样第二大的数会在从右往左第二个。

如此迭代循环，大的数就像冒泡一样，一个一个冒上去。

• 需要注意的是：当两个元素大小相等的时候，我们不交换。这样才能保证冒泡排序的稳定性。

冒泡排序的实现

这个参考第一章的代码，不再赘述。

冒泡排序的特点

时间复杂度

最坏时间复杂度：$O(n^2)$

• 例如：[9 8 7 6 5 4 3 2 1 0]

最好时间复杂度：$O(n)$

• 例如：[0 1 2 3 4 5 6 7 8 9]

是否原地排序

是原地排序。冒泡排序同样只涉及到数据交换，只需要常量级别的额外空间，空间复杂度为$O(1)$。

是否稳定

稳定
冒泡的时候，相同的元素别交换就行。

这回不乱了。

插入排序

第三个排序算法，插入排序。

插入排序的过程

“酒一口一口喝，路一步一步走。”
这就是插入排序的特点。
我们先做到前两个数字是有序的，在前两个数有序的基础上，我们做到前三个数有序，再做到前四个数有序。最后，我们做到整体有序。
具体过程如下图

排序之前：

[3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]

第一步：
我们做到前两个数是有序的。
把index为1的数字抽出来，和index为0的数字比较。44和3比较，44比3大，有序，不做操作。

第二步：
我们做到前三个数是有序的。
把index为2的数字抽出来，和index为1的数字比较。38和44比较，33比44小，互换。
得到：

[3,38,44,5,47,15,36,26,27,2,46,4,19,50,48]

index为1的数再和index为0的数比较，38个2比较，38比3大，有序，不做操作。

第三步：
我们做到前四个数是有序的。
把index为3的数字抽出来，和index为2的数字比较。5和44比较，5比44小，互换。
得到

[3,38,5,44,47,15,36,26,27,2,46,4,19,50,48]

index为2的数字和index为1的数字比较，5比38小，互换。得到

[3,5,38,44,47,15,36,26,27,2,46,4,19,50,48]

再把index为1的数字和index为0的数字比较，5和3比较，有序，不做操作。

按照上述的操作迭代，按顺序插入，先部分有序，最后整体有序。

插入排序的实现

• Java
• Python

示例代码：

package ch05;

import java.util.Arrays;

/**
 * 插入排序
 */
public class InsertionSort {

    public static void main(String[] args) {
        int[] arr = {3,44,38,5,47,15,36,26,27,2,46,4,19,50,48};
        System.out.println(Arrays.toString(arr));
        // 只有数组不为空，并且数组的长度大于1，这时候的排序才有意义
        if (null != arr && arr.length > 1){
            arr = insertionSort(arr);
        }
        System.out.println(Arrays.toString(arr));
    }

    /**
     * 插入排序
     * @param arr
     * @return
     */
    public static int[] insertionSort(int[] arr){
        // i从1开始，先做到前2个数有序。
        // 为什么不是先做到前1个数有序？一个数字，不用排序了。
        for (int i = 1; i < arr.length; i++) {
            // maxIndex
            int maxIndex = i;

            for (int j = maxIndex; j > 0; j--) {
                if (arr[j] < arr[j-1]){
                    swap(arr,j,j-1);
                }else{
                    break;
                }
            }
        }
        return arr;
    }

    /**
     * 互换
     * @param arr 数组
     * @param i 需要互换的元素的index
     * @param j 需要互换的元素的index
     */
    public static void swap(int[] arr,int i,int j){
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }

}

运行结果：

[3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]
[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

特别注意：
一定是

if (arr[j] < arr[j-1])

一定不能是

if (arr[j] <= arr[j-1])

否则就不稳定了。

示例代码：

def insertionSort(arr_args):
    """
    插入排序
    :param arr_args: 需要排序的数组
    :return: 排序之后的数组
    """
    for i in range(1, len(arr_args)):
        # i从1开始，先做到前2个数有序。
        # 为什么不是先做到前1个数有序？一个数字，不用排序了。
        maxIndex = i
        for j in range(maxIndex, 0, -1):
            if arr_args[j] < arr_args[j - 1]:
                arr_args[j], arr_args[j - 1] = arr_args[j - 1], arr_args[j]
            else:
                break

    return arr_args


if __name__ == '__main__':
    arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]
    print(arr)
    print(insertionSort(arr))

运行结果：

[3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]
[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

特别注意：
一定是

if arr_args[j] < arr_args[j - 1]

一定不能是

if arr_args[j] <= arr_args[j - 1]

否则就不稳定了。

插入排序的特点

时间复杂度

最坏时间复杂度：$O(n^2)$

• 例如：[9 8 7 6 5 4 3 2 1 0]

最好时间复杂度：$O(n)$

• 例如：[0 1 2 3 4 5 6 7 8 9]

是否原地排序

是原地排序。

是否稳定

稳定
在插入排序中，对于值相同的元素，我们会把后面出现的元素，插入到前面出现元素的后面，这样就可以保持原有的前后顺序不变。

对数器

截止目前，我们已经实现了三个排序算法。
现在有一个问题，我怎么知道写的对不对。
对个答案。
我们用足够多组的无序数据，去排序，再和我们已知的算法或者已知的方法进行比较。
这就是对数器。

例如，对我们写的选择排序算法进行核验，和Java或者Python自带的排序方法进行比较。

• Java
• Python

示例代码：

package ch05;

import java.util.Arrays;

/**
 * 对数器
 */
public class Comparator {

    public static void main(String[] args) throws Exception {
        int testTimes = 5000;
        int maxSize = 100;
        int maxValue = 100;
        boolean isSuccess = true;
        for (int i = 0; i < testTimes; i++) {
            int[] arr1 = genRandomArr(maxSize,maxValue);
            int[] arr2 = copyArr(arr1);
            // 用已知方法对数组进行排序
            knownFunc(arr1);
            // 选择排序
            InsertionSort.insertionSort(arr2);
            if (isEqual(arr1,arr2) == false){
                // 只要有一个测试没过，就失败。
                isSuccess = false;
                break;
            }
        }
        System.out.print(isSuccess);
    }

    /**
     * 生成随机长度的随机无序数组
     * @param maxSize 数组的最大长度
     * @param maxValue 数组的最大值
     * @return 随机长度的随机无序数组
     */
    public static int[] genRandomArr(int maxSize,int maxValue){
        int[] arr = new int[(int)(Math.random() * maxSize)];
        for (int i = 0; i < arr.length; i++) {
            arr[i] = (int)(Math.random() * maxValue);
        }
        return arr;
    }

    /**
     * 复制数组
     * @param arr
     * @return
     */
    public static int[] copyArr(int[] arr){
        if (null == arr){
            return null;
        }

        int[] rnt = new int[arr.length];
        for (int i = 0; i < arr.length; i++) {
            rnt[i] = arr[i];
        }
        return rnt;
    }

    /**
     * 已知函数，这里用Java自带的方法
     * @param arr 需要排序的数组
     */
    public static void knownFunc(int[] arr){
        Arrays.sort(arr);
    }

    /**
     * 判断arr1和arr2是否一致
     * @param arr1 参与比较的数组一
     * @param arr2 参与比较的数组二
     * @return 比较结果
     */
    public static boolean isEqual(int[] arr1,int[] arr2){
        // 先做null的判断
        if ((null == arr1 && null != arr2) || (null != arr1 && null == arr2)){
            return false;
        }
        if (null == arr1 && null == arr2){
            return true;
        }

        // 再做长度的判断
        if (arr1.length != arr2.length){
            return false;
        }

        for (int i = 0; i < arr1.length; i++) {
            // 只要有一个不相等，就false
            if (arr1[i] != arr2[i]){
                return false;
            }
        }

        return true;
    }
}

运行结果：

true

示例代码：

import random

from ch05 import InsertionSort


def knownFunc(arr_args):
    """
    已经知道的方法
    :param arr_args: 需要排序的数组
    :return: 排序好的数组
    """
    list.sort(arr_args)
    return arr_args


def genRandomArr(max_size, max_value):
    """
    生成一个随机的数组
    :param max_size: 生成的随机数组的最大长度
    :param max_value: 生成的随机数组的最大值
    :return: 生成的随机数组
    """
    arr_rnt = []
    randomSize = random.randint(0, max_size)
    for i in range(randomSize):
        arr_rnt.append(random.randint(0, max_value))

    return arr_rnt


if __name__ == '__main__':
    testTimes = 5000
    maxSize = 100
    maxValue = 100
    isSuccess = True

    for i in range(testTimes):
        arr1 = genRandomArr(maxSize, maxValue)
        arr2 = arr1.copy()
        arr1 = knownFunc(arr1)
        arr2 = InsertionSort.insertionSort(arr2)
        if arr1 != arr2:
            isSuccess = False
            break

    print(isSuccess)

运行结果：

True

归并排序

接下来，我们讨论归并排序。
归并排序，以及下一节的快速排序。其实都用到了一个思想，分治。

归并排序的过程

排序之前：

[3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]

准备操作

1. 把数据平均的分成两组。前8个数字为一组，3到26；后7个数字为一组，27到48。
2. 对于这两组数字再进行拆分。第一组的前4个数字为一组，后4个数字为一组。第二组的前4个数字为一组，后3个数字为一组。
3. 如此，一直进行拆分，直到不可分。

归并操作 第一步

1. 现在3和44是两个独立的小组，两个小组均有一个指针，指针指向第一个元素。指针所指的元素进行比较，3和44比较，3比44小，先排3，再排44。两个小组都空了，合并成一个新的小组。
2. 38和5是两个独立的小组，两个小组均有一个指针，指针指向第一个元素。指针所指的元素进行比较，38和5大比较，5比38小，先排5，再排38。两个小组都空了，合并成一个小组。

归并操作 第二步
经过第一步，我们有两个小组了。[3,44]、[5，38]。两个小组均有一个指针，指针指向第一个元素。

1. 指针所指的元素进行比较。3和5比较，3比5小。排3，再排谁还要再比较。
2. [3,44]的指针后移，[5,38]的指针保持不动。指针所指向的元素进行比较。44和5比较，5比44小，排5，再排谁还要再比较
3. [5,38]的指针后移，[3,44]的指针保持不懂。指针所指向的元素进行比较。44和38比较，38比44小。排38，再排44。两个小组都空了，合并成一个小组。

如此迭代循环，通过递归，按顺序合并的方法，最后完成排序操作。

归并排序的实现

• Java
• Python

示例代码：

package ch05;

import java.util.Arrays;

public class MergeSort {

    /**
     * 归并排序
     * @param arr 参与归并排序的数组
     * @param L 左指针【两个指针其实在这里起到了分组的作用】
     * @param R 右指针【两个指针其实在这里起到了分组的作用】
     * @return 排序之后的数组
     */
    public static int[] mergeSort(int[] arr,int L,int R) throws Exception {

        // 如果左指针等于右指针，说明已经拆分到不可以拆分了，这时候arr就是只有一个元素的数组
        // 递归中的BaseCase
        if (L == R){
            return arr;
        }

        // 如果L不等于R，说明不止一个数，那么，递归吧
        // 中间
        int M = (L+R)/2;
        // 递归
        mergeSort(arr, L, M);
        mergeSort(arr,M+1,R);
        // 合并操作
        merge(arr, L, M, R);
        return arr;
    }

    /**
     * 归并操作
     * @param arr
     * @param L L到M 左侧
     * @param M M+1到R 右侧
     * @param R
     */
    private static void merge(int[] arr, int L, int M, int R) {
        // 辅助数组 大小是 R-L+1，即归并之后的数组的大小
        int[] help = new int[R - L + 1];
        // 辅助数组的指针
        int helpPoint = 0;

        // 指针一，第一个数组的指针
        int p1 = L;
        // 指针二，第二个数组的指针
        int p2 = M + 1;
        // 如果指针一和指针二都没结束
        while (p1 <= M && p2 <= R) {
            // 谁小放谁
            // 这里就有一个`i++`的技巧
            help[helpPoint++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];
        }

        // 要么p1越界了，要么p2越界了
        while (p1 <= M) {
            help[helpPoint++] = arr[p1++];
        }

        while (p2 <= R) {
            help[helpPoint++] = arr[p2++];
        }

        // 归并之后，把数据从辅助数组中塞回去
        for (int i = 0; i < help.length; i++) {
            arr[L + i] = help[i];
        }
    }

    public static void main(String[] args) throws Exception {
        int[] arr = {3,44,38,5,47,15,36,26,27,2,46,4,19,50,48};
        System.out.println(Arrays.toString(arr));
        // 只有数组不为空，并且数组的长度大于1，这时候的排序才有意义
        if (null != arr && arr.length > 1){
            arr = mergeSort(arr,0,arr.length-1);
        }
        System.out.println(Arrays.toString(arr));
    }

}

运行结果：

[3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]
[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

示例代码：

def mergeSort(arr, L, R):
    # 如果左指针等于右指针，说明已经拆分到不能拆分了。
    if L == R:
        return arr
    # 如果L不等于R，说明不止一个数，那么，递归吧
    # 中间
    M = (L + R) // 2
    # 递归
    mergeSort(arr, L, M)
    mergeSort(arr, M + 1, R)
    # 合并操作
    merge(arr, L, M, R)
    return arr


def merge(arr, L, M, R):
    # 辅助数组 大小是 R - L + 1，即归并之后的数组的大小
    helpArr = [None] * (R - L + 1)
    # 辅助数组的指针
    helpPoint = 0
    # 指针一，第一个数组的指针
    p1 = L
    # 指针二，第二个数组的指针
    p2 = M + 1
    # 如果指针一和指针二都没结束
    while p1 <= M and p2 <= R:
        # 谁小放谁
        if arr[p1] <= arr[p2]:
            helpArr[helpPoint] = arr[p1]
            p1 = p1 + 1
        else:
            helpArr[helpPoint] = arr[p2]
            p2 = p2 + 1
        helpPoint = helpPoint + 1
    # 要么p1越界了，要么p2越界了
    while p1 <= M:
        helpArr[helpPoint] = arr[p1]
        helpPoint = helpPoint + 1
        p1 = p1 + 1

    while p2 <= R:
        helpArr[helpPoint] = arr[p2]
        helpPoint = helpPoint + 1
        p2 = p2 + 1

    # 归并之后，把数据从辅助数组中塞回去
    for i in range(len(helpArr)):
        arr[L + i] = helpArr[i]


if __name__ == '__main__':
    a = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]
    print(a)
    # 只有数组不为空，并且数组的长度大于1，这时候的排序才有意义
    if a is not None and len(a) > 1:
        a = mergeSort(a, 0, len(a) - 1)
    print(a)

运行结果：

[3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]
[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

归并排序的特点

时间复杂度

时间复杂度的计算

归并排序的时间复杂度比较复杂，因为涉及到递归。我们再来捋一下递归的过程。
在递归中，我们把一个大问题，分解成了若干个子问题。
在归并排序中，我们的确分解成了两个小问题。那么，我们可以说一个大问题的的时间等于两个小问题的时间。即

$$T(\text{大问题}) = T(\text{小问题一}) + T(\text{小问题二}) + K$$

• K是merge的时间，$O(n)$

小问题又可以拆成两个小小问题，一直拆分。所以，归并排序的时间复杂度是$O(n \log n)$。

而我们之前讨论的排序算法，时间复杂度都是$O(n^2)$。那么这两个时间复杂度，谁大谁小呢？

求个极限

$$\lim_{n \rightarrow \infty} \frac{n \log n}{n^2} = \lim_{n \rightarrow \infty} \frac{\log n}{n} = 0$$

• 分别画一下$\log n$和$n$的函数图像，就可以知道了。
  即

$$O(n \log n) < O(n^2)$$

为什么归并排序的时间复杂度小

那么为什么归并排序排序的时间复杂度更小呢？归并排序和之前讨论的排序算法，相比之下具体优势在哪里呢？

选择排序
在选择排序中，我们把0到n-1位置的数拿出来比较，比较一轮之后，确定了最小的数，放在0位置上。然后把1到n-1位置的数在拿出来比较，比较一轮之后，确定了最小的数，放在1位置上。在这个过程中，比如n-4与n-3这两个位置的数，在第一轮已经进行比较了，在第二轮可能再进行比较。
浪费比较行为！

冒泡排序
冒泡排序中同样存在类似的问题，浪费比较行为，已经比较过的数，在下一轮可能还会进行比较。

插入排序
插入排序就不一样了。
在插入排序中，已经比较的过的数，的确不会再进行比较，不存在浪费比较行为。
在插入排序中，我们要插入一个数，需要和前面已经有序的数组进行比较。注意，有序，所以，我们甚至可以用二分法来确定这个数要插入的位置。(二分法会在下一章进行讨论)
插入排序的麻烦，就在于插入，每插入一个数，后面所有的数都要后移。
所以，即使我们用了二分法，最坏时间复杂度依旧是$O(n^2)$。

归并排序
那么归并排序呢？
比如9 5 2 7。
9和5进行比较，得到5 9，顺序已经固定了。
2和7进行比较，得到2 7，顺序也已经固定了。
5 9和2 7进行比较，得到2 5 7 9，顺序也固定了。
所以，在归并排序中，每一次比较行为都没有浪费。
而且，在归并排序中，因为我们牺牲了空间复杂度，用了一个临时数组来辅助归并操作。所以每一次的归并操作，并不需要后面的N个数字后移。

是否原地排序

当然不是原地排序。都用到了辅助数组了，怎么会是原地。
那么，空间复杂度是多少呢？
一个问题拆成多个小问题，所以空间复杂度也需要加起来？
不是的。
如果100个数的话，最多只需要准备长度为100的临时数组即可。
所以空间复杂度$O(n)$

是否稳定

稳定。
因为左边的数小于或等于右边的数的时候，我们先排左边的数。

快速排序

接下来，讨论快速排序。
在讨论快速排序之前，我们先讨论"Partition过程"和"荷兰国旗问题"，借此引出快速排序。

Partition过程

给定一个数组Arr，和一个数字Num。把小于等于Num的数放在数组的左边，大于Num的数放在数组右边。
要求：时间复杂度是$O(n)$。

这个问题太简单了，我们创建两个数组，小于等于数组和大于数组，Arr中的每个数都和Num进行比较，小于等于Num的插入小于等于数组，大于Num的插入大于数组。插入的时候注意，不要往头部插入，从尾部插入，因为从头部插入每次插入后面的数字都要后移。
最后小于等于数组和大于数组两个数组拼接一下。
搞定。时间复杂度是$O(n)$。

现在，我们再加一个要求。
除了时间复杂度是$O(n)$，我们还要求空间复杂度是$O(1)$。

我们这么做。
比如：
Arr是

[3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]

Num是21。
我们定义两个指针：

1. 第一个指针是i，用来遍历数组。初始值为0。
2. 第二个指针是小于等于边界，用来记录小于等于的边界。初始值为-1。
   (在Python中，-1是数组的最后一个元素，但在这里不是这个含义。)

我们解决方案的核心就两点：

1. 如果Arr[i]小于或等于Num，Arr[i]和小于等于边界的下一个位置的数进行交换。然后i ++，小于等于边界也 ++
2. 如果Arr[i]大于Num，只有i ++。

在上例中。

1. Arr[0]和Num比较，3小于或等于21，3和小于等于边界的下一个位置的数进行交换，小于等于边界的下一个位置就是0位置，所以3的位置不动。i ++，小于等于边界也 ++。此时i等于1，小于等于边界等于0。
   得到：

   [3] [44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]

2. Arr[1]和Num比较，44大于21，只有i ++。i等于2。
3. Arr[2]和Num比较，38大于21，只有i ++。i等于3。
4. Arr[3]和Num比较，5小于或等于21，5和小于等于边界的下一个位置的数进行交换，即5和44进行交换。然后i ++，小于等于边界也 ++。此时i等于4，小于等于边界等于1。
   得到

   [3 ,5] [38, 44, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]

5. 如此迭代循环，完成。

荷兰国旗问题

现在，我们把问题升级一下。
小于Num的放左边，大于Num的放右边，等于Num的放中间。
这个是什么？

美国大选？
法国国旗？

这个问题，更为人知的一个名字是荷兰国旗。

但是，叫什么名字无所谓。

我们把代号拿掉，关注问题本身。
我们现在定义三个指针：

1. 第一个指针依旧是i，用来遍历数组。初始值为0。
2. 第二个指针是小于边界，用来记录小于的边界。初始值为-1。
   (在Python中，-1是数组的最后一个元素，但在这里不是这个含义。)
3. 第三个指针是大于边界，用来记录大于的边界。初始指为数组的长度。

我们解决方案的核心就三点：

1. 如果Arr[i]等于Num，i ++。
2. 如果Arr[i]小于Num，Arr[i]与小于边界右一个交换，小于边界右移，i ++。
3. 如果Arr[i]大于Num，Arr[i]与大于边界左一个交换，大于边界左移。i不动。

继续以刚刚的数组为例，现在我们假设Num是19。

1. Arr[0]和Num比较，3小于19，3和小于边界右一个位置的数进行交换，小于边界的右一个位置就是0位置，所以3的位置不动。i ++，小于边界右扩，也 ++。此时i等于1，小于等于边界等于0。

   [3] [44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]

2. Arr[1]和Num比较，44大于19，44和大于边界左一个位置的数进行交换，大于边界的左一个位置的数是48，44和48交换。大于边界左扩，i不动。此时i依旧等于1，大于边界是14。

   [3] [48, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50] [44]

3. Arr[1]和Num比较，48大于19，48和大于边界左一个位置的数进行交换，大于边界的左一个位置的数是50，48和50交换。大于边界左扩，i不动。此时i依旧等于1，大于边界是13。

   [3] [50, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19] [48, 44]

4. Arr[1]和Num比较，50大于19，50和大于边界左一个位置的数进行交换，大于边界的左一个位置的数是19，50和19交换。大于边界左扩，i不动。此时i依旧等于1，大于边界是12。

   [3] [19, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4] [50, 48, 44]

5. Arr[1]和Num比较，19等于19。i ++。

   [3] [19, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4] [50, 48, 44]

6. 如此迭代循环，完成。

基于荷兰国旗问题的快排

现在，我们把荷兰国旗问题做一些微小的改动。
我们不指定Num了，Arr的最后一个元素就是Num。
保持最后一个元素不动，我们先做一次荷兰国旗过程。
这样的话，小于边界内的元素都是小于Num的，中间的元素都是等于Num的，大于边界内的元素都是大于Num的，再把最后一个元素和大于边界的第一个元素交换，大于边界右移。
这样的话，左边的元素都是小于Num的，中间的元素都是等于Num的，右边的元素都是大于Num的。
如果对于左边和右边的元素，我们递归做荷兰国旗过程呢？
最后是不是排序完成？
这就是基于荷兰国旗过程的快速排序。

代码实现如下：

• Java
• Python

示例代码：

package ch05;

import java.util.Arrays;

public class NetherlandsFlag_QuickSort {


    /**
     * 荷兰国旗过程
     * @param arr 需要进行荷兰国旗过程的数组
     * @param L 左边界
     * @param R 右边界
     * @return 荷兰国旗过程之后的新的边界
     */
    public static int[] netherlandsFlag(int[] arr,int L,int R){

        // 小于边界
        // 小于边界的起始位置在左边界的左
        int less = L - 1;
        // 大于边界
        // 大于边界本来是应该在右边界的右，我们这里，暂时把Arr[R]包裹进去，后面再换一下。
        int more = R;
        // index指针，用来遍历
        int index = L;
        // index只能没有和大于边界相遇
        while (index < more) {
            // 这一段过程就是荷兰国旗过程了
            // 对着逻辑敲代码
            if (arr[index] == arr[R]) {
                index = index + 1;
            } else if (arr[index] < arr[R]) {
                swap(arr, less + 1, index);
                less = less + 1;
                index = index + 1;
            } else {
                swap(arr, index, more-1);
                more = more - 1;
            }
        }
        // 把Arr[R]移过去
        swap(arr, more, R);

        return new int[] { less + 1, more };
    }

    /**
     * 互换
     * @param arr 数组
     * @param i 需要互换的元素的index
     * @param j 需要互换的元素的index
     */
    public static void swap(int[] arr,int i,int j){
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }

    /**
     * 快速排序
     * @param arr 参与排序的数组
     * @param L 左边界
     * @param R 右边界
     */
    public static int[] quickSort(int[] arr, int L, int R) {
        if (L >= R) {
            return arr;
        }
        int[] equalArea = netherlandsFlag(arr, L, R);
        quickSort(arr, L, equalArea[0] - 1);
        quickSort(arr, equalArea[1] + 1, R);
        return arr;
    }

    public static void main(String[] args) {
        int[] arr = {3,44,38,5,47,15,36,26,27,2,46,4,19,50,48};
        System.out.println(Arrays.toString(arr));
        // 只有数组不为空，并且数组的长度大于1，这时候的排序才有意义
        if (null != arr && arr.length > 1){
            arr = quickSort(arr,0,arr.length-1);
        }
        System.out.println(Arrays.toString(arr));
    }
}

运行结果：

[3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]
[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

示例代码：

def netherlandsFlag(arr, L, R):
    """
    荷兰国旗过程
    :param arr: 参与荷兰过程过程的数组 
    :param L: 左边界
    :param R: 右边界
    :return: 荷兰国旗过程之后的新的边界
    """
    # 小于边界
    # 小于边界的起始位置在左边界的左
    less = L - 1
    # 大于边界
    # 大于边界本来是应该在右边界的右，我们这里，暂时把Arr[R]包裹进去，后面再换一下。
    more = R
    # index指针，用来遍历
    index = L
    # index只要没有和大于边界相遇
    while index < more:
        # 这一段过程就是荷兰国旗过程了
        # 对着逻辑敲代码
        if arr[index] == arr[R]:
            index = index + 1
        elif arr[index] < arr[R]:
            arr[less + 1], arr[index] = arr[index], arr[less + 1]
            less = less + 1
            index = index + 1
        else:
            arr[index], arr[more - 1] = arr[more - 1], arr[index]
            more = more - 1

    # 把Arr[R]移过去
    arr[more], arr[R] = arr[R], arr[more]
    return [less + 1, more]


def quickSort(arr, L, R):
    if L >= R:
        return arr
    equalArea = netherlandsFlag(arr, L, R)
    quickSort(arr, L, equalArea[0] - 1)
    quickSort(arr, equalArea[1] + 1, R)
    return arr


if __name__ == '__main__':
    a = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]
    print(a)
    print(quickSort(a, 0, len(a) - 1))

运行结果：

[3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]
[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

那么，现在有一个问题。基于荷兰国旗问题的快排，最坏的时间复杂度是多少？
举个特例，这么一个数组

[0 1 2 3 4 5 6 7 8 9]

每一轮的荷兰国旗过程，大于边界都要一步一步的从右推到最左边，然后才能确定一个数的位置。有N个数，就需要N轮。显然

$$O(n^2)$$

随机荷兰国旗快排

那么，现在有一个疑问了。
大家都是排序算法，你的时间复杂度还是$O(n^2)$。你怎么好意思称自己是快速排序？

别急，画龙就差最后一下"点睛"了。

我们在每一次荷兰国旗过程之前，都把Arr[R]和其他位置的任意一个数交换。

• Java
• Python

对于Java，我们在quickSort方法中添加这么一行。

swap(arr,L + (int) (Math.random() * (R - L + 1)), R);

对于Python，我们在quickSort方法中添加这么两行。

andomVal = randint(L, R)
arr[randomVal], arr[R] = arr[R], arr[randomVal]

这样就是快速排序了。

来，我们分析一下。
好情况是什么？
好情况是我们选择一个Num之后，Num处在中间的位置，而且这时候左右两侧的规模差不多。

如果Num处在中间的位置。这时候的时间复杂度是

$$\begin{aligned} T(n) &= T(\frac{n}{2}) + T(\frac{n}{2}) + O(n) \\ &=O(n \log n) \end{aligned}$$

而差的情况就是Num很偏，让左右两侧规模悬殊。

那么，我们随机选一个数。
有几种情况？
Num有可能在$\frac{n}{3}$的位置。

$$T(n) = T(\frac{n}{3}) + T(\frac{2}{3}n) + O(n)$$

Num有可能个在$\frac{n}{5}$的位置

$$T(N) = T(\frac{n}{5}) + T(\frac{4}{5}n) + O(n)$$

Num有可能个在$\frac{N}{6}$的位置
Num有可能个在$\frac{N}{7}$的位置
Num有可能个在$\frac{N}{8}$的位置
Num有可能个在$\frac{N}{9}$的位置
Num有可能个在$\frac{N}{10}$的位置

各种可能。

概率累加。
期望就是

$$O(n \log n)$$

有点乱，有点乱。
说好的时间复杂度要以最坏时间复杂度衡量，怎么这里成了平均时间复杂度呢？
因为在这里，即使我们给出了一个

[0 1 2 3 4 5 6 7 8 9]

最差的情况命中的概率也非常的小。
但是对于其他的算法不是这样的，比如在冒泡和插入排序中，给出

[9 8 7 6 5 4 3 2 1 0]

最坏的情况必命中。

快速排序
果然名不虚传

快速排序的特点

时间复杂度

• 最好时间复杂度：$O(n \log n)$
• 最坏时间复杂度：$O(n^2)$
• 平均时间复杂度：$O(n \log n)$
• 通常所指的快速排序的时间复杂度是平均时间复杂度。

是否原地排序

正如我们之前讨论的，快速排序是基于荷兰国旗过程的，而荷兰国旗过程的空间复杂度就是$O(1)$，那么快速排序是不是空间复杂度为$O(1)$的原地排序呢？

不是。因为要递归啊，递归的时候调用信息不得一个一个入栈？

那既然是递归呢，那就有不用递归的方法实现。
所以，空间复杂度还是$O(1)$。

也不是，因为每一轮递归或者每一轮循环，我们都要记两个东西，L和R。当然咯，我们可以用一个变量，记完L，释放，再记R。
但无论如何，空间复杂度是

$$O(\log n)$$

这就是快速排序的空间复杂度。

$$O(\log n)$$

有部分资料说快速排序的空间复杂度是$O(1)$，大家可以一起讨论，一起进步啊。

是否稳定

不稳定。
例如：

$$57\widehat{\bold{7}}81$$

我们首先，随机选一个数和最后一个交换，比如选择了$7$，得到

$$51\widehat{\bold{7}}87$$

然后进行荷兰国旗过程，依旧是

$$51\widehat{\bold{7}}87$$

再把7和大于边界的最左边的一个数交换。

$$51\widehat{\bold{7}}78$$

乱了，乱了，乱了。
刚刚还是$7$在$\widehat{\bold{7}}$的前面，现在成$\widehat{\bold{7}}$在$7$的前面了。

桶排序

最后，我们再讨论三个排序算法：桶排序、计数排序和基数排序。这三个排序算法的时间复杂度都是线性的，即$O(n)$，因为也被成为线性排序。
首先，桶排序。

桶排序的过程

桶排序的核心思想是将要排序的数据分到几个有序的桶里，每个桶里的数据再单独进行排序。桶内排完序之后，再把每个桶里的数据按照顺序依次取出，组成的序列就是有序的了。

桶排序的特点

时间复杂度

假定要排序的数据有$n$个，我们把它们均匀地划分到$m$个桶内，每个桶里就有$k=\frac{n}{m}$个元素。
每个桶内部使用快速排序，时间复杂度为$O(k \log k)$。$m$个桶排序的时间复杂度就是$O(m*k \log k)$。
而$k=\frac{n}{m}$，所以整个桶排序的时间复杂度就是$O(n \log (\frac{n}{m}))$。
当我们的桶个数足够多，$m \rightarrow n$时，$\log(\frac{n}{m}) \rightarrow 1$。
这时候，桶排序的时间复杂度接近$O(n)$。

妙啊，居然还有这么优秀的排序算法。
但是呢，桶排序基于两个假设：

1. 你要有已经排好序的而且足够多的桶。
   所以，桶排序适用于量大但是范围小的问题。
2. 数据在各个桶之间的分布是均匀的。如果数据经过桶的划分之后，有些桶里的数据非常多，有些非常少。例如，如果数据都被划分到一个桶里，那时间复杂度就是$O(n \log n)$。

是否原地排序

不是
桶需要大于$O(1)$的空间。

是否稳定

稳定
每个桶内部的排序算法，都用稳定的排序算法。那么桶排序就稳定。

计数排序

计数排序的过程

计数排序其实和桶排序非常的类似，只是桶的大小粒度不一样。可以理解为一种特殊的桶排序。
在计数排序中，每个桶的大小都是最小单位。
比如，高考成绩排序，我们假定最小单位是1分。那么就有0到750，一共751个桶。

计数排序的特点

时间复杂度

$O(n+k)$

• k是数据范围

是否原地排序

不是

是否稳定排序

是
进入每一个计数桶的时候控制其稳定，就能是稳定的排序。

计数排序同样适用于量大但是范围小的问题。

基数排序

基数排序的过程

假如数据量大，范围又大呢？
比如，对全国人民的身份证号进行排序。

这时候就是基数排序了。

比如：

$$\begin{aligned}& 130928198905281793 \\& 130532197901235712 \\& 513221197102183838 \\& 610523198305134774 \\& 230111197104266110 \\& 510422198603243893 \end{aligned}$$

我们用稳定的排序算法，从最小的一位开始排序

$$\begin{aligned}& 23011119710426611 \widehat{\bold{0}} \\& 13053219790123571 \widehat{\bold{2}} \\& 13092819890528179 \widehat{\bold{3}} \\& 51042219860324389 \widehat{\bold{3}} \\& 61052319830513477 \widehat{\bold{4}} \\& 51322119710218383 \widehat{\bold{8}} \end{aligned}$$

然后再用稳定的排序算法，对倒数第二位进行排序。

$$\begin{aligned}& 2301111971042661 \widehat{\bold{1}} \widehat{\bold{0}} \\& 1305321979012357 \widehat{\bold{1}} \widehat{\bold{2}} \\& 5132211971021838 \widehat{\bold{3}} \widehat{\bold{8}} \\& 6105231983051347 \widehat{\bold{7}} \widehat{\bold{4}} \\& 1309281989052817 \widehat{\bold{9}} \widehat{\bold{3}} \\& 5104221986032438 \widehat{\bold{9}} \widehat{\bold{3}} \end{aligned}$$

再对第三位进行排序。

$$\begin{aligned}& 230111197104266 \widehat{\bold{1}} \widehat{\bold{1}} \widehat{\bold{0}} \\& 130532197901235 \widehat{\bold{7}} \widehat{\bold{1}} \widehat{\bold{2}} \\& 610523198305134 \widehat{\bold{7}} \widehat{\bold{7}} \widehat{\bold{4}} \\& 130928198905281 \widehat{\bold{7}} \widehat{\bold{9}} \widehat{\bold{3}} \\& 513221197102183 \widehat{\bold{8}} \widehat{\bold{3}} \widehat{\bold{8}} \\& 510422198603243 \widehat{\bold{8}} \widehat{\bold{9}} \widehat{\bold{3}} \end{aligned}$$

以此类推，最后我们完成全国人民身份证号的排序。

妙啊，居然还有这么优秀的排序算法。

• 但是基数排序要求数据能分割出独立的"位"，而且"位"与"位"之间要有递进关系。
• 如果每个数据的长度不一，比如单词排序，我们还需要在不足的单词上补特殊的字符，例如"0"。
• 而且位之间还要排序，在基数排序中，位排序通常基于桶排序或者计数排序。

基数排序的特点

时间复杂度

$O(dn)$

• $d$是数据维度。
• 需要基于计数排序或者桶排序，否则没法做到$O(dn)$

是否原地排序

不是

是否稳定

是。
对每一位进行排序的时候，用稳定的排序算法，就是稳定。

八大排序算法的比较

现在，回到我们开篇的那个问题。

$$\text{那些编程语言内置的排序算法是什么？}$$

我们把八大排序算法都找出来，大家来比赛。

接下来，会用比赛解说的模式。

时间复杂度

欢迎大家来到八大排序算法争夺编程语言内置排序算法的比赛现场。
我们这次比赛一共会进行三轮，分别是时间复杂度、是否原地排序和是否稳定。
现在是第一轮，时间复杂度，比的是谁花的时间最少。

1. 首先登场的是选择排序，这也是我们认识的第一个排序算法，他的时间复杂度是$O(n^2)$。
2. 第二个登场的是冒泡排序，这个排序算法的特点就是像冒泡一样，他的时间复杂度是多少呢？居然也是$O(n^2)$。
3. 第三个排序算法登场了，插入排序，他的时间复杂度会也是$O(n^2)$吗？果然！也是$O(n^2)$。
   三个排序算法的时间复杂度都是$O(n^2)$，比赛才刚开始，就陷入了焦灼状态，会有排序算法打破$O(n^2)$吗？
4. 第四个排序算法，归并排序。时间复杂度！打破了！打破了$O(n^2)$！归并排序的时间复杂度是$O(n \log n)$！
   现在场上是归并排序暂时领先。
5. 第五个排序算法来了，这个排序算法名字就好听，快速排序，看来这个排序算法就是主打快啊。他的时间复杂度是？$O(n^2)$，我的天啊！号称快速排序的排序算法，时间复杂居然是$O(n^2)$。
   等等，这时候裁判居然示意，快速排序的时间复杂度是$O(n \log n)$。裁判给出的理由是，快速排序极难命中最坏的情况$O(n^2)$，应该按平均时间复杂度计算。
   裁判的这次裁决，让比赛再次陷入焦灼状态。
6. 接下来登场的是线性排序俱乐部的成员，线性排序作为针对特殊场景的排序算法，主打的就是快。那么，会打破$O(n \log n)$，成为编程语言的内置排序算法吗？
   桶排序！桶排序！时间复杂度！$O(n)$！
   这一定一个不可思议的时间复杂度！
7. 第七个排序算法，计数排序，时间复杂度$O(n+k)$，略微低于桶排序。
   诶？红牌？这时候裁判居然掏出了红牌？裁判给出的理由是桶排序和计数排序都用了已经排序好的桶，属于作弊行为。成绩无效。
8. 最后一个排序算法登场了，基数排序，时间复杂度$O(dn)$。
   等等，红牌？又是红牌！裁判给出的理由是$O(dn)$的一个前提条件是要用桶排序或者计数排序对每一位进行排序。成绩无效！
9. 那么，第一轮是不是尘埃落定呢？这时候，我们看到，场上起了争执！线性排序俱乐部的成员似乎不服裁判的这次判决。组委会出来了！组委会居然登场了！组委居然补刀了，线性排序作为针对特殊场景的排序算法，没有争夺编程语言默认排序算法的资格，但是仍有资格参与比赛。

是否原地排序

好，经过短暂的休息之后，欢迎大家继续来到比赛现场。有些观众可能刚刚打开电视，对上一轮的比赛结果还不太熟悉。
上一轮是时间复杂度方面的较量，归并排序和快速排序并列第一，时间复杂度都是$O(n \log n)$，紧追其后的选择排序、冒泡排序和插入排序，他们的时间复杂度都是$O(n^2)$。而我们的线性排序俱乐部的三位选手，桶排序、计数排序和基数排序被裁判判决成绩无效，甚至被组委会取消了争夺编程语言默认排序算法的资格。但是组委会仍然允许他们参加比赛，我们看到他们也来到了现场，准备参加后续的比赛。
这一轮的比赛：是否原地排序。
这就对排序算法提出了空间复杂度方面的要求，只有空间复杂度是$O(1)$的排序算法，才能被称为原地排序。

1. 首先上场的还是选择排序，看来几个排序算法的上场顺序已经确定了。
   选择排序，他的特点是每次选一个当前最小值放前面去，那么他能做到原地排序吗？
   看！选择排序给我们展示了，他只需要一个临时变量，把选中的值放前面的那一瞬间，做交换用！原地排序！
2. 接下来上场的是冒泡排序，我们知道插入排序、冒泡排序、选择排序、归并排序和快速排序，这五个都是基于比较的排序算法。
   那么他能和选择排序一样，做到原地排序吗？果然，原地排序！冒泡排序也只需要一个临时变量，在冒泡的时候，做交换用。
3. 第三个，插入排序，没有疑问，插入排序也只需要一个临时变量，在插入的时候用。
   没想到第二轮的比赛也这么焦灼。我们看到，目前基于比较的排序算法，都是能做到原地排序，那么，归并排序和快速排序他们可以做到吗？
4. 归并排序登场了！诶，归并排序居然用了临时数组来做归并操作，而且这个临时数组的空间复杂度是$O(n)$，原地排序失败！
   看来，不是所有基于比较的排序算法，都是能做到原地排序。
5. 第五个，快速排序，他会在做到时间复杂度为$O(n \log n)$的同时，还做到原地排序吗？如果可以的话，那么他极有可能是本次比赛的冠军，成为各编程语言的内置排序算法。
   快速排序脱下了外套，我们看到里面居然穿着"荷兰国旗"，快速排序表示自己的核心其实是荷兰国旗，荷兰国旗的空间复杂度是$O(1)$。用这种方式，会得到裁判组的认同吗？
   果然，裁判不认同。裁判表示，快速排序在每一轮最少都要有一个变量记住L和R，空间复杂度是$O(\log n)$
6. 线性排序俱乐部登场了。可惜，他们都没能做到原地排序，他们都用了一个叫做桶的东西。

是否稳定

欢迎大家再回到比赛现场。在第一轮比赛中，冒泡排序、插入排序和选择排序虽然都在时间复杂度方面，以$O(n^2)$输给了归并排序和快速排序的$O(n \log n)$，但是他们都在第二轮原地排序中，赢了归并排序和快速排序。而归并排序和快速排序，很遗憾，都没有做到原地排序。
看来鱼和熊掌不可兼得啊，无法做到时间复杂和空间复杂度的双赢。
现在比赛是异常的焦灼。
第三轮，是否稳定。
这个呢，就要求相同大小的数前后顺序不能变。

1. 首先上场的依旧是选择排序，诶？不稳定！选择排序不稳定。
   让我们看看慢镜头回放。$20\widehat{\bold{2}}1 \rightarrow 02\widehat{\bold{2}}1 \rightarrow 01\widehat{\bold{2}}2$，2的位置，2的位置居然乱了。
2. 第二个，冒泡排序，他能做到稳定吗？成功了！
   当两个元素大小相等的时候，冒泡不做交换，这样就做到了稳定！成功。
3. 第三个，插入排序，插入排序也做到了稳定，
   插入排序说：对于相同的元素，我们会把后面出现的元素，插入到前面出现元素的后面，这样就可以保持原有的前后顺序不变。
4. 归并排序，归并排序如果也做到了稳定，那么他将会打破第三轮双雄争霸的局面。做到了！
   归并排序也能做到稳定！当左边的数小于或等于右边的数的时候，归并排序先排了左边的数。稳定！
5. 快速排序，身穿"荷兰国旗"的快速排序是否稳定呢？
   $57\widehat{\bold{7}}81$，快速排序先随机选一个数和最后一个交换，选择了$7$，现在是$51\widehat{\bold{7}}87$，然后快速排序开始进行荷兰国旗过程了，依旧是$51\widehat{\bold{7}}87$。已经不稳定了！但是快速排序还有最后一个步骤，最后的时刻会有奇迹发生吗？会有那扭转乾坤的临门一脚吗？快速排序把最后一个元素$7$的和大于边界的最左边的一个数交换，$51\widehat{\bold{7}}78$。于事无补，快速排序不是稳定的排序算法。
6. 线性排序俱乐部上场了，开挂三人组，他们是桶排序、计数排序和基数排序。没有任何疑问，稳定。

全场比赛结束！
在最后一轮是否稳定中，冒泡排序、插入排序和归并排序都做到了稳定，选择排序和快速排序，很遗憾，并不是稳定的排序算法。
而线性排序俱乐部，因为针对特殊场景，虽然他们都做到了稳定，但是他们并没有资格作为编程语言的内置排序算法。
那么，最后会是谁呢？能够成为编程语言的内置排序算法呢？

比赛统计表

欢迎大家再次回到比赛现场。
现在三轮比赛已经结束了，让我们来看一下目前的比赛统计表。

	时间复杂度	是否原地排序	是否稳定
选择排序	$O(n^2)$	是	否
冒泡排序	$O(n^2)$	是	是
插入排序	$O(n^2)$	是	是
归并排序	$O(n \log n)$	否	是
快速排序	$O(n \log n)$	否	否
桶排序	$O(n)$	否	是
计数排序	$O(n+k)$	否	是
基数排序	$O(n+k)$	否	是

那么，最后会是谁呢？能够成为编程语言的内置排序算法。
还是说会有几个排序算法联合起来呢？

我们看到！这时候有一个身影从天而降！
TimSort！
这是一个诞生于2002年的排序算法。
19岁的TimSort会是绝大部分变成语言内置的排序算法吗？

TimSort

我们讨论的最后一个排序算法，TimSort。
为什么叫TimSort，因为就是Tim发明的。
Tim是谁？

Tim Cook?Apple CEO，不是他。

Tim Berners-Lee？也不是他，他是在伦敦奥运会的开幕式敲代码的科学家，万维网的发明者。
是Tim Peter。
他另一项有趣的东西是The Zen of Python(Python之禅)。

大家在交互式解释器中敲入import this就可以看到Tim Peters的The Zen of Python。

在上一节，我们提到了这么一句"还是说会有几个排序算法联合起来呢？"。
TimSort就联合了两种排序算法，二分插入排序和归并排序。

• 关于插入排序我们已经讨论过了，而二分插入排序，我们在讨论归并排序的时候提到了，就是用二分法来确定要插入的位置。(二分法会在下一章进行讨论)

run

TimSort其实基于了一个事实，在现实生活中，在大多数真实的数据集中，已经有很多元素是排好序的。可能整体是无序的，但是中间的某些子串是有序的。
总之，这是一个事实，没有证明。

那么，对于已经排好序的子串，在TimSort中，有一个特别的名字，run，指一个连续上升(包括相等)或者下降(不含相等)的子串。

比如对于序列[1,2,3,4,3,2,4,7,8]，其中有三个run，第一个是[1,2,3,4]，第二个是[3,2]，第三个是[4,7,8]。这三个run都是单调的。
其中在实际程序中单调递减的run会被反转成单调递增的序列。

得到run之后，我们可以干嘛呢？
归并
但是这里就有讲究了，在TimSort中，有一个参数是minrun，表示每个run的最小长度，如果长度太短，会用二分法插入排序把run后面的元素插入到run内。
对于上面的例子，如果minrun=5，那么第一个run是不符合要求的，就会把后面的3插入到第一个run里面，变成[1,2,3,3,4]。

二分插入出现了
那么？minrun取多少合适呢？这就是TimSort的高明之处了，自适应，会根据数据的特点来进行自我调整。
但也有一个大致的取值范围。
在Python中，$\text{minrun} \in [32,64]$。
在Java中，$\text{minrun} \in [16,32]$。

合并

拿到了run就需要合并了，这个也有讲究。
在归并排序中，合并是两两分别合并，第一个和第二个合并，第三个和第四个合并。
但在TimSort中不是这样的。
在Timsort中，合并是连续的，每次计算出了一个run之后都有可能导致一次合并。

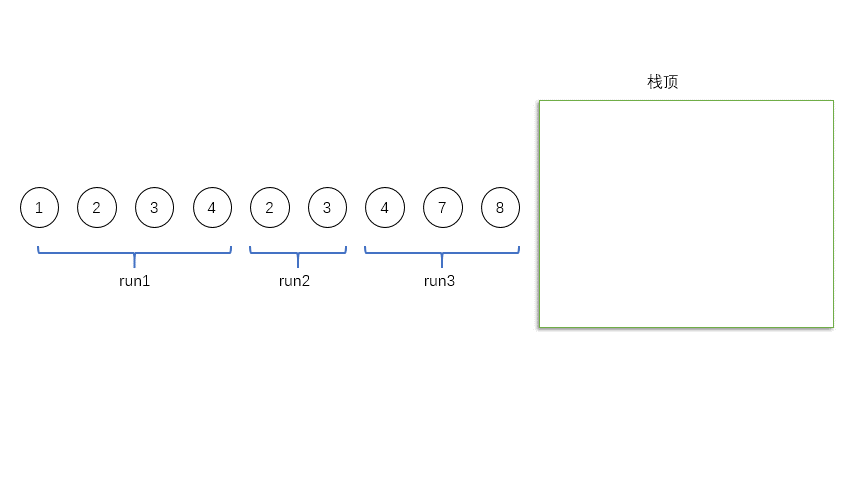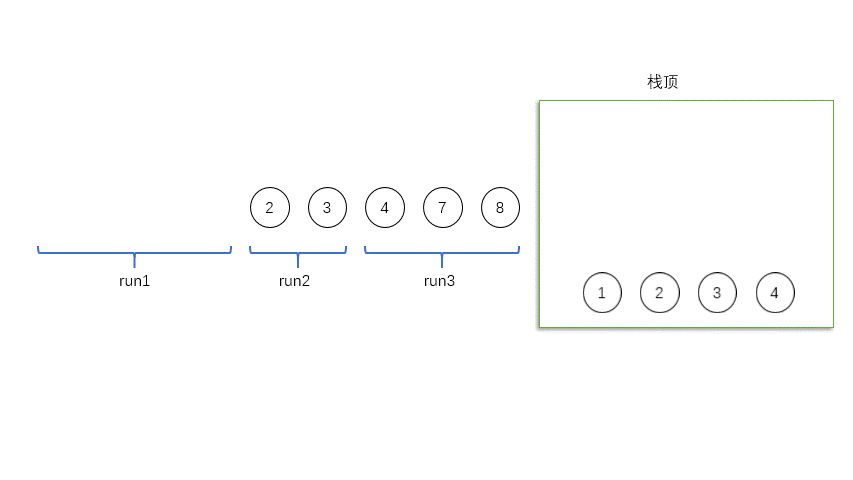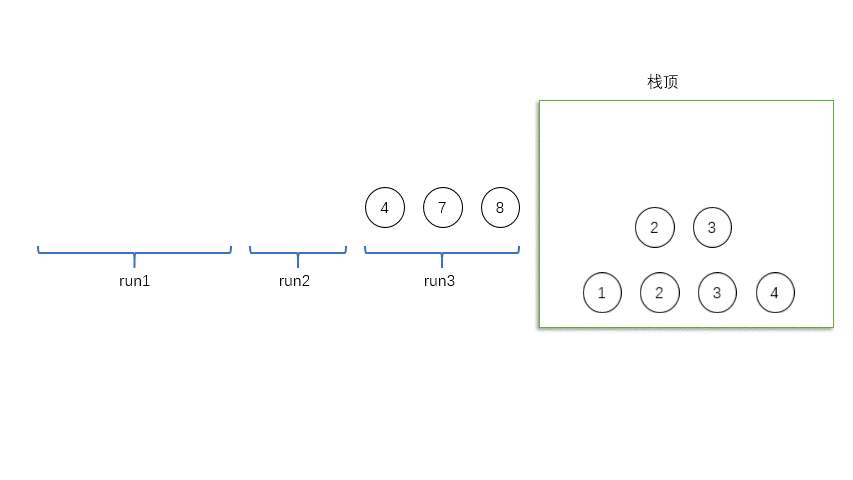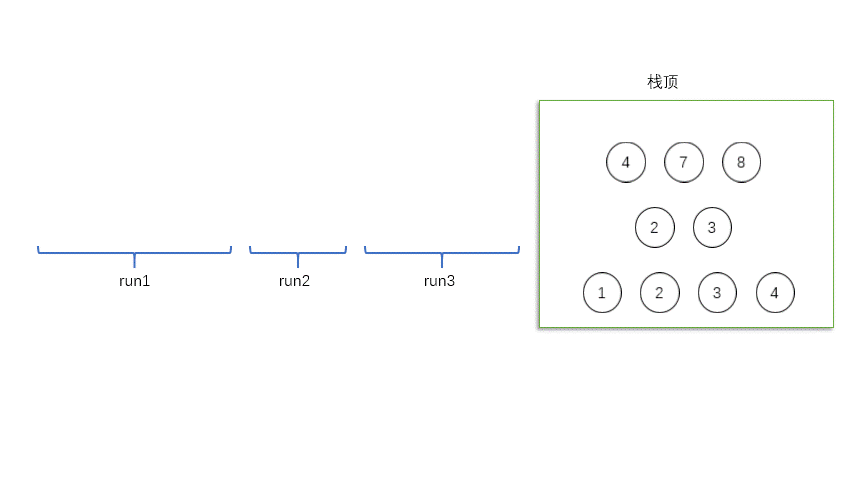
我们会有一个栈来保存每个run，比如对于上面的[1,2,3,4,3,2,4,7,8]这个例子，栈底是[1,2,3,4]，中间是[3,2]，栈顶是[4,7,8]。我们用
X、Y和Z表示他们的长度，其中X在栈顶。

如果大家玩过一款叫做《1024》合并数字的游戏就知道。这个游戏的一个技巧是，我们总是要保证最里面的数最大。

与《1024》这款游戏类似，我们必须始终维持以下的两个规则：

$$\begin{aligned} & Z > Y + X \\ & Y > X \end{aligned}$$

一旦有其中的一个条件不被满足，Y这个子序列就会和X与Z中较小的子序列合并形成一个新run，然后会再次检查栈顶的三个run看看是否仍然满足条件。如果不满足则会继续进行合并，直至栈顶的三个元素(如果只有两个run就只需要满足第二个条件)满足这两个条件。

TimSort过程

前面都是理论，现在我们举个例子，看看具体过程。
现在有这么一个数组

[8 10 15 6 18 12 7 5 4 3 20 8 11 22 9 9 17]

当然因为数据有限，我们设置minrun是4。

首先遍历数组，[8 10 15]是一个run，但是长度只有3，所以我们把第四个数6加进来，用二分法插入排序的方法，确定位置插入。得到第一个run：[6 8 10 15]，记做run_0，入栈。

此时栈里的数据是

run_0

然后我们继续找run，[18 12 7 5 4 3]，长度大于minrun，但是是单调递减的，所以反转。得到第二个run：[3 4 5 7 12 18]，记run_1，入栈。

run_1

run_0

谁是X，谁是Y？
栈顶的是X。

$$Y < X$$

所以，我们用合并，把run_0和run_1合并新的run_0，[3 4 5 6 7 8 10 12 15 18]。

继续找run，[20 8]，长度不够，再加一个，11，长度还是不够，再加一个，22。得到新的run，[8 11 20 22]，记做run_2，入栈。

run_2

run_0

$$Y > X$$

没问题，存下来。

继续找run，[9 9 17]只有三个值啊。怎么办呢？只能入栈，记作run_3。

run_3

run_2

run_0

谁是X？栈顶的是X。从上往下依次是X，Y，Z。

然后我们把最上面的两个合并，得到新的run_2，[8 9 9 11 17 20 22]。

run_2

run_0

再合并。
得到

[3 4 5 6 7 8 8 9 9 10 11 12 15 17 18 20 22]

排序完成。

TimSort的特点

时间复杂度

最坏时间复杂：$O(n \log n)$。
最好时间复杂：$O(n)$。

是否原地排序

否
空间复杂度是$O(n \log n)$

是否稳定

稳定。
因为插入排序是稳定的，归并排序也是稳定的。所以不会乱。

编程语言内置的排序算法

讨论到现在了，我们还有一个问题没回答。
编程语言内置的排序算法是什么？
之前讨论八大排序算法，现在看起来都不是。
那么会是TimSort吗？
也不是。

都不是…

答案揭晓：

• Java
• Python

在Java中：

• 当元素个数小于32的时候，是二分插入排序。
• 当元素个数大于等于32的时候，是TimSort。

在Python中：

• 当元素个数小于64的时候，是二分插入排序。
• 当元素个数大于等于64的时候，是TimSort。