一种基于强化学习的期权定价方法

整体思路

1. 明确在期权定价问题中，所确定的是期权的哪一种价格。
2. 把期权卖方的对冲过程，抽象成一个序列多步决策问题。
3. 用强化学习去解这个序列多步决策问题。
4. 设计强化学习中的奖励函数。

期权定价中的价格

在期权定价研究中，试图确定的期权价格，不是期权的成交价，不是交易所的每日结算价格，不是期权买家的预期未来回报的折现，而是期权的卖家，为了售出一个期权，在市场进行对冲所需要的资金。

我们通过举例子来说明。
假设存在一个风险资产$S$，在期初时刻，该风险资产的价格为$100$，有$0.6$的概率会在期权合约到期时刻上涨到$110$，有$0.4$的概率会在期权合约到期时刻下跌到$90$。同时存在以该风险资产$S$为标的资产的欧式看涨期权合约，假设该欧式看涨期权的行权价是$100$，不考虑货币时间价值。

如果我们从期权买家预期收益的折现角度考虑的话，期权合约的价格为

$$\begin{aligned} C_0 &= (110-100)*0.6 + 0*0.4 \\ &= 0.6 \end{aligned}$$

如果我们从期权卖家构造对冲组合的角度考虑。
在到期时，即当$t=T$时，期权的价值$C_T$为：

$$\begin{aligned} C_T &= (S_T - K)^+ \\ &= \begin{cases} (110-100)^+ = 10 \quad S_T^u = 110 \\ (90-100)^+ = 0 \quad S_T^d = 90 \end{cases} \end{aligned}$$

我们构造一个投资组合$\Phi$，$\Phi = S - 2C$。即，我们买1份标的资产，卖2份期权。在到期时，即当$t=T$时

$$V_T(\Phi) = \begin{cases} 110 - 2*10 = 90 \quad S\text{上涨} \\ 90 - 2*0 = 90 \quad S\text{下跌} \end{cases}$$

即，无论标的资产$S$是上涨或者下跌，投资组合的价值都是$90$。这个操作也被称为套期保值或对冲(Hedge)。

同时，我们假设还有另一个投资组合，这个投资组合有且只有无风险的债券$B$，并且是$90$份。在不考虑货币时间价值的情况下，在到期的时刻，

$$V_T(B) = 90$$

即，$V_T(\Phi) = V_T(B)$。

根据无套利原理，我们知道$V_0(\Phi) = V_0(B)$。

$$S_0 - 2*C_0 = B_0$$

其中，$S_0 = 100\quad B_0 = 90$，则有：

$$100 - 2*C_0 = 90$$

即

$$C_0 = 5$$

两种方法，得到的期权的价格不同。第一种方法依赖于上涨和下跌的概率。第二种方法，不依赖于上涨和下跌的概率，其中第二种方法是正确的。

期权定价研究中所试图确定的价格，和标的资产的预期收益率无关。期权定价研究所试图确定的价格不是一个预测的值，而是构建一个完全复制期权效果的资产组合所需要的资金。

虽然，对于欧式看涨期权，到期后标的资产价格越高，期权行权回报越大，在标的资产更有可能涨的情况下，看涨期权的买方更有可能盈利。但，这只能说明，期权的期望回报和标的资产的期望收益率有关。

而期权定价研究中的价格，是无套利价格，可以理解为卖方卖出期权后需要多少资金来构建对冲组合，使得期权到期时，标的资产的价格在任何位置都不会亏损，这个是不用预测未来价格走势，不用承担预测错误风险的。

这就是"风险中性"的期权定价。

序列多步决策

接下来，我们把期权卖方的对冲过程，抽象成一个序列多步决策。

假设现在我们是一个欧式期权的卖方。

该欧式期权，期时间是$T$，期权的持有者在到期时的收益是一个和$S_T$($T$时刻的标的资产的价格)有关的函数，记作$H_T(S_T)$。

我们构造一个投资组合，这个投资组合由股票和无风险债券组成。在无交易摩擦成本下，在$t$时刻($t \leq T$)，投资组合的价值$\Pi_t$为：

$$\Pi_t = u_t S_t + B_t$$

其中，$u_t$是股票的仓位，$S_t$是股票的价格，$B_t$是无风险债券的份额。

在到期时，即当$t=T$时，我们要把股票平仓，换成现金，以支付费用给期权的买方，即$u_T = 0$。
所以在$t=T$时刻，投资组合的价值$\Pi_T$

$$\begin{aligned} \Pi_T & = 0 \times S_T + B_T \\ & = B_T \\ & = H_T(S_T) \end{aligned}$$

其中$H_T(S_T)$是在到期时刻，期权的收益。

而且，这个投资组合是自融资的。即，在整个过程不会有资金加入，也不会有资金被抽走或消耗。
在这个限制下，如果我们想对股票进行调仓，就必须也对无风险债券进行调仓。想买股票，就必须卖无风险债券；想买无风险债券，就必须卖股票。

所以，对于在$t+1$时刻，对组合中的风险资产进行调仓，有如下的式子成立。

$$u_t S_{t+1} + e^{r \Delta t} B_t = u_{t+1} S_{t+1} + B_{t+1},\quad t=T-1,\cdots,0$$

其中，$\Delta t$代表一个单位的$T$，即$\Delta t = \frac{T}{N}$；$u_t$是$t$时刻的股票头寸，$u_{t+1}$是$t+1$时刻的股票头寸；$B_t$是$t$时刻的无风险债券，$B_{t+1}$是$t+1$时刻的无风险债券。

对上文的式子进行变换，则有

$$B_t = e^{-r \Delta t}[B_{t+1} + u_{t+1}S_{t+1} - u_t S_{t+1}],\quad t = T-1,\cdots,0$$

这样就得到了一个关于$B_t$的递归公式，其中$B_{t+1} + u_{t+1} S_{t+1}$就是$\Pi_{t+1}$。即

$$B_t = e^{-r \Delta t}[\Pi_{t+1} - u_t S_{t+1}],\quad t = T-1,\cdots,0$$

再把$B_t = ...$代入到式$\Pi_t = u_t S_t + B_t$，则有：

$$\begin{aligned} \Pi_t & = u_t S_t + B_t \\ & = u_t S_t + e^{-r \Delta t}[\Pi_{t+1} - u_t S_{t+1}] \\ & = u_t S_t e^{r \Delta t} e^{-r \Delta t} + e^{-r \Delta t}[\Pi_{t+1} - u_t S_{t+1}] \\ & = e^{-r \Delta t}[\Pi_{t+1} - (u_t S_{t+1} - u_t S_t e^{r \Delta t})] \\ & = e^{-r \Delta t}[\Pi_{t+1} - u_t (S_{t+1} - S_t e^{r \Delta t})] \\ \end{aligned}$$

由此，得到了一个关于$\Pi_t$的递归公式。

$$\Pi_t = e^{-r \Delta t}[\Pi_{t+1} - u_t \Delta S_t],\quad \Delta S_t = S_{t+1} - e^{r \Delta t} S_t,t = T-1,\cdots,0$$

当$t=T-1$时：

$$\Pi_{T-1} = e^{-r \Delta t}[\Pi_T - u_{T-1} \Delta S_{T-1}],\quad \Delta S_{T-1} = S_{T} - e^{r \Delta t} S_{T-1}$$

该式存在两个未知量，$\Delta S_{T-1}$和$u_{T-1}$。也就是说，标的资产的价格和对冲策略$\{u_t\}_{t=0}^T$是未知的。
如果能知道标的资产的价格和对冲策略的话，那么期权的价格也就能通过推算得出。

基于强化学习

两种方法

对于标的资产的价格，我们可以假设其服从某种随机过程，即，标的资产的运动过程是已知的。如果我们把标的资产价格的运动作为环境的话，也就意味着环境的变化过程是已知的，这在强化学习中被称为环境已知，也被称为基于模型的方法，其典型代表是动态规划。

还有一种是我们利用标的资产的历史价格，也就是说由数据驱动，我们并不知道标的资产的价格运动服从哪个随机过程。同理，如果我们把标的资产价格的运动作为环境的话，这时候意味着环境的变化过程是未知的，这在强化学习中被称为环境未知，也被称为无模型的方法。

一些关键要素

• 智能体
  期权的卖方，就是强化学习中的智能体。期权的卖方，在卖出期权后，构建对冲组合，做出调仓行为。
• 环境
  标的资产的价格运动，就是强化学习中的环境。
• 动作
  期权的卖方对对冲组合的调仓行为，就是强化学习中智能体所做出的动作。
• 状态
  某一时刻的标的资产的价格状态，就是强化学习中环境的状态。
• 策略
  状态是智能体做出动作的唯一依据。在数学上表示为状态和动作的映射关系，即$u_t = \pi(s_t)$。通俗的说，在什么状态下，做什么动作。
• 状态转移
  标的资产价格的变化，就是状态转移。

奖励函数及其设计原因

奖励函数

标的资产价格的变化，其实也就是环境对智能体的奖励。
但奖励函数需要我们自己设计，奖励函数设计如下：

$$r_t(s_t,u_t,s_{t+1}) = \begin{cases} \gamma \Pi_{t+1} - \Pi_t - H_t(s_t) \quad t < T \\ -\gamma^{T}H_T(s_T) \quad t = T \end{cases}$$

对于欧式看涨期权，$H_T(S_T) = (S_T - K)^+$；对于欧式看跌期权，$H_T(S_T) = (K - S_T)^+$；$K$表示行权价。

$\gamma$为强化学习中的折现因子，通常在$\gamma \in [0,1]$。在这里，我们把$\gamma$设置为金融中的折现率，即

$$\gamma = e^{-r \Delta T}$$

其中$r$是无风险利率。

设计原因

强化学习的目标，是去学习最优策略，评估最优策略的方法是价值函数（状态价值函数或动作价值函数）。而价值函数是由奖励函数所衍生出来的。

在期权定价的设定中，状态价值需要和期权的价格，即构建对冲组合的成本有关。奖励函数设计为上式，其衍生出来的状态价值函数，恰好和期权的价格有关，即构建对冲组合的成本有关。

状态价值函数，状态价值是指在$t$时刻的状态$s_t$下，$t$时刻的动作$a_t$还没有做，从$r_t,r_{t+1},r_{t+2}$，一直到$r_T$的奖励的之和。
基于奖励函数，则有

$$\begin{aligned} V(s_t) & = \sum_{t'=t}^T r_{t'}(s_{t'},u_{t'},s_{t'+1}) \\ & = \Bigg(\sum_{t'=t}^{T-1}\gamma^{t'}\bigg(\gamma \Pi_{t'+1} - \Pi_{t'} - H_{t'}(s_{t'})\bigg)\Bigg) - \gamma^T H_T(s_T) \\ & = \gamma^{t+1} \Pi_{t+1} - \gamma^t \Pi_t + \gamma^{t+2} \Pi_{t+2} - \gamma^{t+1}\Pi_{t+1} + \cdots + \gamma^T \Pi_{T} - \gamma^{T-1} \Pi_{T-1} - \sum_{t'=t}^T \gamma^{t'} H_{t'}(s_{t'}) \\ & = -\gamma^t\Pi_t + \gamma^T\Pi_T - \gamma^T H_T(s_T) \\ & = -\gamma^t\Pi_t \end{aligned}$$

即，当我们设计的奖励函数为上式的时候，由奖励函数所衍生出来的状态价值函数，恰好就是对冲组合价值的折现的相反数。

这也符合强化学习的设定和期权定价的设定。

强化学习是学习最优的策略，我们根据价值函数来判断策略是否最优，因为在最优策略下，价值函数的值会最大。强化学习中的所有模型都是直接或间接的使状态价值函数和动作价值函数的值最大。
但在期权定价问题的设定中，我们要力图使$\Pi_t$的值最小，最小的$\Pi_t$是期权的公允价格。

我们设计的奖励函数所衍生的状态价值，恰好是对冲组合价值的折现的相反数，同时满足了强化学习的设定和期权定价的设定。

附录：期权概述

什么是期权

期权是赋予了其持有者在未来约定的时间以约定的价格买卖约定数量和质量的某种标的资产的权利的合约。
期权的持有者具有按协议条款实施这个协议的权利，但不负有必须实施这个协议的义务。

• 约定的价格就是行权价，也被称为实施价格(exercise price)。
• 约定的时间就是行权日。
• 按期权合约规定执行购入或销售标的资产的行为就是行权，也被称为实施(exercise)。
• 期权的持有者即买方。
• 期权的买方，为了获得权利，需要支付费用给卖方，这笔费用就是期权费(premium)。

看涨期权和看跌期权

根据合约中约定的是购入还是销售标的资产来划分，期权可以分为：

• 看涨期权(call option)
• 看跌期权(put option)

看涨期权赋予期权的持有者，在约定的时间，按约定的价格购入约定的数量和质量的标的资产的权利。
看跌期权赋予期权的持有者，在约定的时间，按约定价格售出约定的数量和质量的标的资产的权利。

在英文中，call的意思是买，put的意思是卖，call option是指有买标的资产的权利的合约，put option是指有卖标的资产的权利的合约。
但是在中文翻译的时候，根据其应用场景来翻译了，当投资者认为某种资产的价格将要上涨时，就可以购买该资产的看涨期权，即将来有以约定价格买的权利。

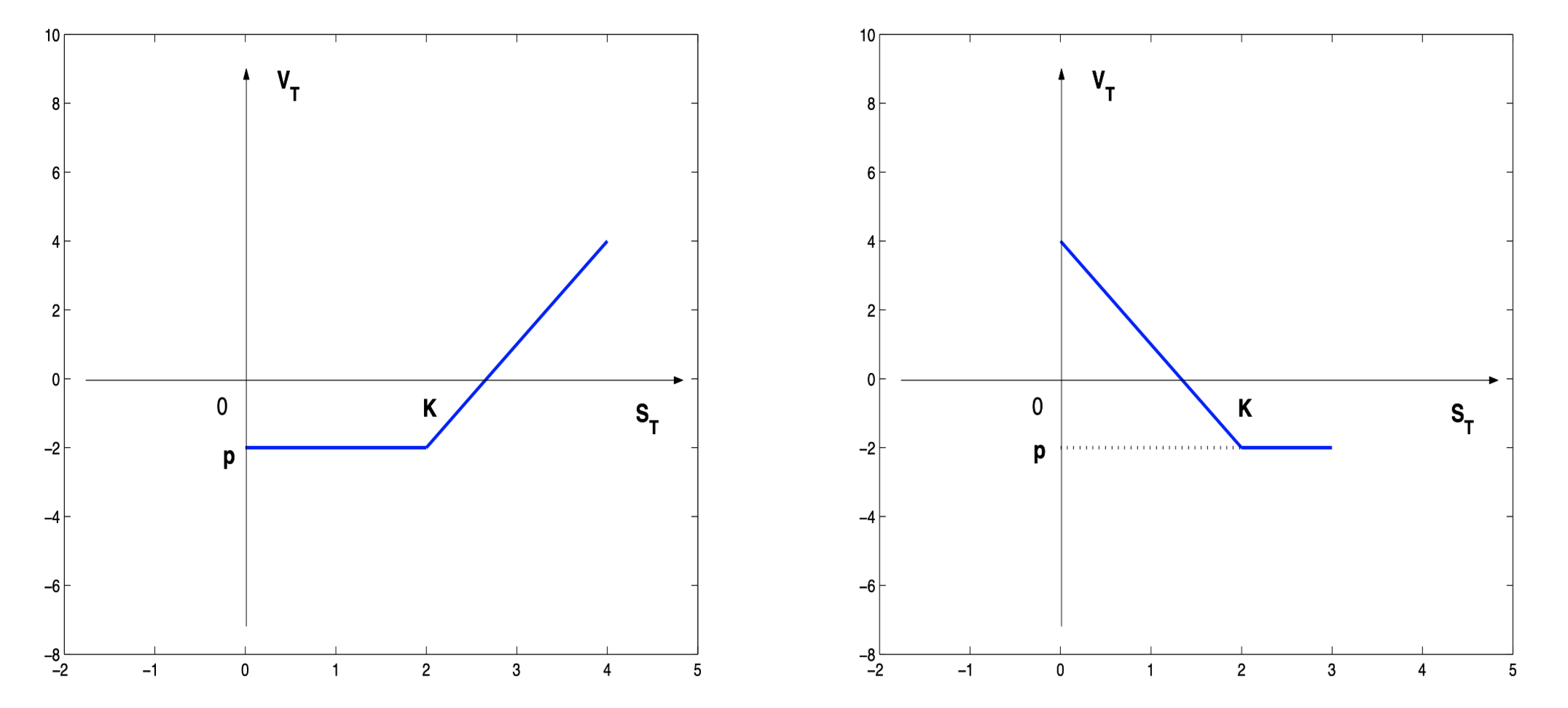
看涨期权和看跌期权的持有者，在到期时刻的收益如图所示。

左侧是看涨期权的持有者，在到期时刻的收益，当标的资产的价格小于行权价的时候，看涨期权的持有者损失期权费，当标的资产的价格大于行权价加上期权费之和时，看涨期权的持有者盈利。
右侧是看跌期权的持有者，在到期时刻的收益，当标的资产的价格小于行权价减去期权费之差时，看跌期权的持有者盈利，当标的资产的价格大于行权价时，看跌期权的持有者损失期权费。

欧式期权、美式期权及奇异期权

根据合约中有关行权的条款来划分，期权可以分为：

• 欧式期权(European options)
• 美式期权(American options)

欧式期权只能在合约规定的到期日实施；美式期权能在合约规定的到期日以及到期日之前的任何一个交易日实施。

除了上述两种，还有诸多的奇异期权，例如：

• 亚式期权，依据的是标的资产价格的平均值，而不是某一天的价格。
• 百慕大期权，既不是只在到期日可以行权，也不是每一天都可以行权，而是有好几个可以行权的区间。

BS模型

什么是BS模型

BS模型，Black-Scholes Model，是一种为金融衍生工具中的期权进行定价的数学模型。

Fischer Black和Myron Scholes（1973）提出了Black-Scholes Model；同年，Robert C. Merton（1973）对Black-Scholes Model的假定条件做了进一步削弱，并在许多重要方面进行了推广，新的模型被称为Black–Scholes–Merton Model。

BS模型的假设

假设金融资产是：

1. 无风险资产的投资回报是不变的，此回报率称作无风险利率。
2. 股票价格遵从几何布朗运动(随机游走)。
3. 股票在期权有效期内不分派红利。
4. 股票价格服从对数正态分配，即金融资产的对数收益率服从正态分配。

假设金融市场是：

1. 存在最少一种风险资产(如股票)及一种无风险资产(现金或债券)。
2. 不存在套利机会
3. 能以无风险利率借出或借入任意数量的金钱
4. 能买入及卖出任意数量的股票
5. 市场无摩擦，即不存在交易税收和交易成本

假设期权是欧式期权。

BS模型定价公式

对于欧式看涨期权：

$$C=S\times N(d_{1})-K\times e^{-r\times T}\times N(d_{2})$$

对于欧式看跌期权：

$$P=K\times e^{-r\times T}\times N(-d_{2})-S\times N(-d_{1})$$

其中：

$$d_{1}={\begin{smallmatrix}\displaystyle {\frac {\ln \displaystyle {\frac {S}{K}}+\left(r+0.5\times \sigma ^{2}\right)\times {T}}{\sigma \times {\sqrt {T}}}}\end{smallmatrix}}$$

$$d_{2}={\begin{smallmatrix}\displaystyle d_{1}-\sigma \times {\sqrt {T}}\end{smallmatrix}}$$

• $\ln$：自然对数；
• $C$：期权价格；
• $K$：行权价；
• $S$：交易所金融资产即期价格；
• $T$：期权有效期；
• $r$：连续复利计无风险利率Ｈ；
• $\sigma^2$：年度化方差；
• $N()$：正态分布变量的累积分布函数。