5.假设检验

基本概念

什么是假设检验

参数估计(parameter estimation)和假设检验(hypothesis testing)，都是利用样本对总体进行某种推断，但推断的角度不同。

• 参数估计讨论的是用样本统计量估计总体参数的方法，总体参数在估计前是未知的。
• 而在假设检验中，则是先对总体参数提出一个假设，然后利用样本信息去检验这个假设是否成立。

举个例子。

假如我们，根据统计资料得知，1989年某地新生儿的平均体重为3190克，现从1990年的新生儿中随机抽取100个，测得其平均体重为3210克。现在，问1990年的新生儿与1989年相比，体重有无显著差异？

从调查结果看，1990年新生儿的平均体重为3210克，比1989年新生儿的平均体重3190克增加了20克，但这20克的差异可能源于不同的情况。可能是抽样的随机性造成的，也可能是1990年新生儿的体重与1989年新生儿的体重相比确实有所增加。

上述问题的关键点是：20克的差异说明了什么？这个差异能不能用抽样的随机性来解释？为了回答这个问题，我们可以采取假设的方法。
假设1989年和1990年新生儿的体重没有显著差异，如果用$\mu_0$表示1989年新生儿的平均体重，$\mu$表示1990年新生儿的平均体重，我们的假设可以表示为$\mu_0 = \mu$或$\mu_0 - \mu = 0$。现要利用1990年新生儿体重的样本信息检验上述假设是否成立，如果成立，说明这两年新生儿的体重没有显著差异；如果不成立，说明1990年新生儿的体重有了明显增加。
在这里，问题是以假设的形式提出的，问题的解决方案是检验提出的假设是否成立。

所以假设检验的实质是检验我们关心的参数：1990年的新生儿总体平均体重是否等于某个我们感兴趣的数值。

原假设和备择假设

引例

例如，我们提出的命题是，1990年的新生儿与1989年的新生儿在体重上没有差异。
采用统计的语言描述原假设的话，如下：

$$H_0 : \mu_0 = \mu$$

或者

$$H_0 : \mu_0 - \mu \neq 0$$

我们$H_0$表示原假设(null hypothesis)。由于原假设($H$)的下标用$0$表示，所以也有资料称之为"零假设"。

除了原假设，还有备择假设(alternative hypothesis)，如果原假设不成立，就拒绝原假设，在备选假设中作出选择。

在我们的例子中，备择假设的表达式为：

$$\begin{aligned} H_1 & : \mu_0 \neq \mu \\ H_1 & : \mu_0 - \mu \neq 0 \end{aligned}$$

原假设与备择假设互斥，肯定原假设，意味着放弃备择假设；否定原假设，意味着接受备择假设。有些资料把备择假设称为替换假设、或者研究假设。

定义

• 原假设：待检验的假设，又称"零假设"，用$H_0$表示，是研究者想收集证据予以反对的假设。总是有符号$=$、$\geq$或$\leq$。
• 备择假设：如果原假设不成立，就要拒绝原假设，而需要在另一个假设中做出选择，用$H_1$表示，是研究者想收集证据予以支持的假设。总是有不等号($\neq$、$<$或$>$)。

两类错误

对于原假设提出的命题，我们需要作出判断，这种判断可以用"原假设正确"或"原假设错误"来表述。这种判断有可能正确，也有可能不正确，也就是说，我们面临着犯错误的可能。

所犯的错误有两种类型：

1. 第I类错误是原假设$H_0$为真却被我们拒绝了。
   犯这种错误的概率用$\alpha$表示，所以也称$\alpha$错误($\alpha$ error)或弃真错误；
   如果我们没有拒绝，则表明作出了正确的决策，其概率为$1-\alpha$。
2. 第II类错误是原假设为伪我们却没有拒绝。
   犯这种错误的概率用$\beta$表示，所以也称$\beta$错误($\beta$ error)或取伪错误；
   当$H_0$为伪，我们拒绝$H_0$，这也是正确的决策，其概率为$1-\beta$。

我们当然希望犯这两类错误的概率越小越好。但对于一定的样本量$n$，不能同时做到犯这两类错误的概率都很小。如果减少$\alpha$错误，就会增大犯$\beta$错误的机会；若减少$\beta$错误，就会增大犯$\alpha$错误的机会。

按理说，哪类错误所带来的后果更严重，危害更大，在假设检验中就应当把哪类错误作为首要的控制目标。
但在假设检验中，一般都是，首先控制犯$\alpha$错误。这样做的主要的原因在于，从实用的观点看，原假设是什么常常是明确的，而备择假设是什么则常常是模糊的。

假设检验的流程

步骤

1. 提出假设：首先提出原假设和备择假设。
2. 确定适当的检验统计量。
   在参数的假设检验中，如同在参数估计中一样，要借助样本统计量进行统计推断，这个统计量称为检验统计量。
   选择统计量的方法与参数估计相同，需考虑是大样本还是小样本，总体方差已知还是未知。
3. 规定显著性水平$\alpha$。
   原假设为真时，拒绝原假设的概率，被称为抽样分布的拒绝域，表示为$\alpha$，常用的$\alpha$值有0.01、0.05、0.10。
4. 计算检验统计量的值。
5. 作出统计决策。
   根据给定的显著性水平$\alpha$，查表得到临界值；将检验统计量的值与$\alpha$水平的临界值进行比较，得出拒绝或不拒绝原假设的结论。

案例

提出假设

在上文，我们提出了原假设和备择假设。

$$\begin{aligned} H_0 & : \mu_0 = \mu \\ H_1 & : \mu_0 - \mu \neq 0 \end{aligned}$$

确定适当的检验统计量

我们假定总体$\sigma$已知，且样本量大，考虑采用$z$统计量，计算公式为：

$$z = \frac{\bar{x} - \mu_0}{(\frac{\sigma}{\sqrt{n}})}$$

规定显著性水平

我们假设显著性水平$\alpha=0.05$。

计算检验统计量的值

假设新生儿体重的标准差为80克，即$\sigma=80$。

样本均值$\bar{x}=3210$，$\mu_0=3190$，$\sigma = 80$，$n = 100$，

$$\begin{aligned} z & = \frac{\bar{x} - \mu_0}{(\frac{\sigma}{\sqrt{n}})} \\ & = \frac{3210-3190}{(\frac{80}{\sqrt{100}})} \\ & = 2.5 \end{aligned}$$

作出统计决策

计算出的$z$值$2.5$落入拒绝域，所以拒绝原假设，认为与1989年相比，1990年新生儿的体重有显著差异。

利用P值进行决策

为什么需要P值

上文，我们根据检验统计量落入的区域作出是否拒绝原假设的决策。确定$\alpha$以后，拒绝域的位置也就相应确定了，其好处是进行决策的界限清晰，但缺陷是进行决策面临的风险是笼统的。
在上面的例子中，$z=2.5$，落入拒绝域，我们拒绝原假设，并知道犯弃真错误的概率(面临的风险)为$0.05$；如果$z=2.0$，同样落入拒绝域，我们拒绝原假设面临的风险也是$0.05$，$0.05$是一个通用的风险概率。但根据不同的样本结果进行决策，面临的风险事实上是有差别的，为了精确地反映决策的风险度，可以利用P值进行决策。

什么是P值

P值，一个概率值，当原假设为真时所得到的样本观察结果或更极端结果出现的概率。被称为观察到的(或实测的)显著性水平，表示$H_0$能被拒绝的最小值。

如果P值很小，说明这种情况发生的概率很小，P值越小，我们拒绝原假设的理由就越充分。

在左侧检验时，P值为曲线上方小于等于检验统计量部分的面积。
在右侧检验时，P值为曲线上方大于等于检验统计量部分的面积。

P值的大小取决于三个因素：

1. 样本数据与原假设之间的差异。
2. 样本量。
3. 被假设参数的总体分布。

P值的优点是反映了观察到的实际数据与原假设之间不一致的概率值，与传统的拒绝域范围相比，P是一个具体的值，这样就提供了更多的信息。

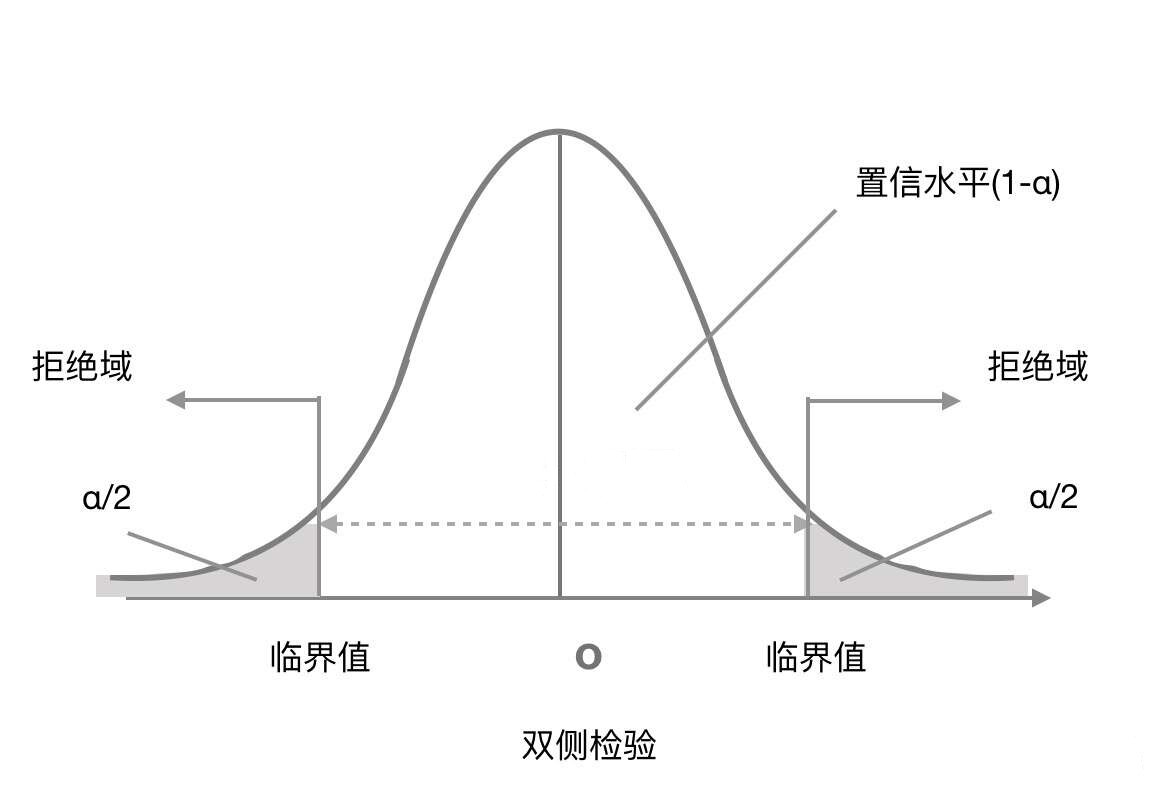
单侧检验

上文的例子，是双侧检验，不能太大，也不能太小。
除了双侧检验，还有单侧检验。

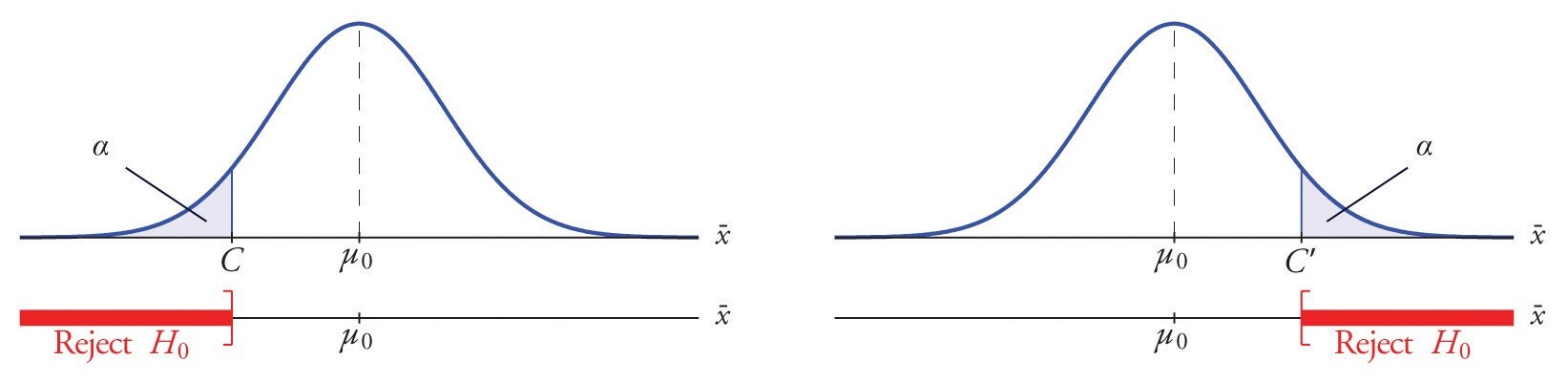
• 左单侧检验：下限检验，所考察的数值越大越好。
• 右单侧检验：上限检验，所考察的数值越小越好。

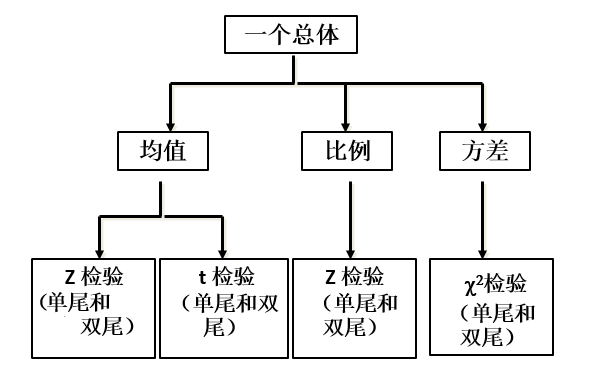
一个总体参数的检验

确定适当的检验统计量

总体均值的检验

大样本

方法

假定条件：
总体服从正态分布；
或者，可用正态分布来近似(大样本)

使用$z$统计量

如果$\sigma$已知

$$z = \frac{\bar{x}-\mu_0}{(\frac{\sigma}{\sqrt{n}})} \sim N(0,1)$$

如果$\sigma$未知，用$S$代替$\sigma$

$$z = \frac{\bar{x} - \mu_0}{(\frac{s}{\sqrt{n}})} \sim N(0,1)$$

案例

某机床厂加工一种零件，根据经验知道，该厂加工零件的椭圆度渐近服从正态分布，其总体均值为$0.081$mm，今另换一种新机床进行加工，取200个零件进行检验，得到椭圆度均值为$0.076$mm，
样本标准差为$0.025$mm，问新机床加工零件的椭圆度总体均值与以前有无显著性差别。($\alpha=0.05$）

根据题意，设置原假设和备择假设

$$\begin{aligned} H_0 & : \mu = 0.081 \quad \text{没有显著差别} \\ H_1 & : \mu \neq 0.081 \quad \text{有显著差别} \end{aligned}$$

这是一个双侧检验问题，$\mu > \mu_0$或$\mu < \mu_0$都可以拒绝原假设。

由题意可知，可知：

$$\begin{aligned} \mu_0 & = 0.081 \\ s & = 0.025 \\ \bar{x} = 0.076 \end{aligned}$$

因为$n>30$，故选用$z$统计量。

$$\begin{aligned} z & = \frac{\bar{x} - \mu_0}{(\frac{s}{\sqrt{n}})} \\ & = \frac{0.076 - 0.081}{(\frac{0.025}{\sqrt{200}})} \\ & = -2.83 \end{aligned}$$

当$\alpha=0.05$，有临界值如下：

$$z_{\frac{\alpha}{2}} = \pm 1.96$$

根据决策准侧，我们拒绝$H_0$，认为新老机床加工零件椭圆度的均值有显著性差异。

样本量小，方差已知

方法

与大样本类似，使用$z$统计量

$$z = \frac{\bar{x}-\mu_0}{(\frac{\sigma}{\sqrt{n}})} \sim N(0,1)$$

案例

假设某产品的使用寿命服从正态分布$N(1020,100^2)$。现从最近生产的一批产品中随机抽取$16$ 只，测得样本平均寿命为$1080$小时。试在$0.05$的显著性水平下判断这批产品的使用寿命是否有显著提高？

$$\begin{aligned} H_0 & : \mu \leq 1020 \\ H_1 & : \mu > 1020 \\ z & = \frac{\bar{x}-\mu_0}{(\frac{\sigma}{\sqrt{n}})} \\ & = \frac{1080-1020}{(\frac{100}{\sqrt{16}})} \\ & = 2.4 \end{aligned}$$

因为这是右侧检验，查表可以得到临界值$z_{\alpha} = z_{0.05} = 1.645$。

因为$2.4>1.645$，即有证据表明这批灯泡的使用寿命有显著提高。

样本量小，方差未知

方法

假定条件：总体为正态分布，$\sigma$未知，且小样本。

使用t统计量

$$t = \frac{\bar{x} - \mu_0}{(\frac{s}{\sqrt{n}})} \sim t(n-1)$$

案例

某机器制造出的厚度为5cm，今欲了解机器性能是否良好，随机抽取10块肥皂作为样本，测得平均厚度为5.3cm，标准差为0.3cm，试以0.05的显著性水平检验机器性能良好的假设。

如果机器性能良好，生产出的肥皂厚度将在5cm上下波动，过薄或过厚都不符合产品质量标准，所以，根据题意，这是双侧检验问题。

由于总体$\sigma$未知，且样本$n$较小，所以应采用t统计量。

已知条件为：

$$\begin{aligned} \mu & = 5 \\ \bar{x} & = 5.3 \\ \sigma & = 0.3 \\ n & = 10 \\ \alpha & = 0.05 \end{aligned}$$

原假设和备择假设如下：

$$\begin{aligned} H_0 & : \mu = 5 \\ H_1 & : \mu \neq 5 \end{aligned}$$

$$\begin{aligned} t & = \frac{\bar{x} - \mu_0}{(\frac{s}{\sqrt{n}})} \\ & = \frac{5.3 - 5}{(\frac{0.3}{\sqrt{10}})} \\ & = 3.16 \end{aligned}$$

当$\alpha=0.05$，自由度$n=10-1=9$时，$t_{\frac{\alpha}{2}} = 2.2622$。

因为$t > t_{\frac{\alpha}{2}}$，样本统计量落入拒绝域，故拒绝$H_0$，接受$H_1$，说明该机器的性能不好。

单样本t检验的效应量

特别的。
如果检验结果是拒绝原假设，则可以用效应量来分析样本统计量与假设值的差异程度。单样本t检验的效应量通常使用(Cohen)的d统计量来度量，计算公式为：

$$d = \frac{|\text{样本均值} - \text{假设的总体均值}|}{\text{样本标准差}}$$

该效应量表示样本均值与假设的总体均值的差异是多少个样本标准差。

总体比例的检验

方法

假设条件
有两类结果
并且，总体服从二项分布，可用正态分布来近似

采用$z$统计量

$$z = \frac{p - \pi_0}{\sqrt{\frac{\pi_0(1-\pi_0)}{n}}}$$

• $p$为样本比例
• $\pi_0$为总体比例$\pi$的假设值

案例

一项统计结果声称，某市老年人口(年龄在65岁以上)所占比例为$14.7\%$，该市老年人口研究会为了检验该项统计是否可靠，随机抽选了$400$名居民，发现其中有57人年龄在65岁以上。
如果$\alpha=0.05$，问调查结果是否支持该市老年人口比例为$14.7\%$的看法?

原假设和备择假设：

$$\begin{aligned} H_0 & : \pi = 14.7\% \\ H_1 & : \pi \neq 14.7\% \end{aligned}$$

根据题意有：

$$\begin{aligned} p & = \frac{57}{400} = 0.1425 \quad (14.25\%) \\ z & = \frac{p - \pi_0}{\sqrt{\frac{\pi_0(1-\pi_0)}{n}}} \\ & = \frac{0.1425 - 0.147}{\sqrt{\frac{0.147(1-0.147)}{400}}} \\ & = -0.254 \end{aligned}$$

这是一个双侧检验，当$\alpha=0.05$时，有$z_{\frac{\alpha}{2}} = \pm 1.96$。

因此，不能拒绝$H_0$，可以认为调查结果支持了该城市老年人口所占比例为$14.7\%$的看法。

总体方差的检验

方法

方差检验所使用的是$\chi^2$统计量。

$$\chi^2 = \frac{(n-1)s^2}{\sigma^2} \sim \chi^2(n-1)$$

若进行双侧检验，拒绝域分布在$\chi^2$统计量分布曲线的两边；若是单侧检验，拒绝域分布在$\chi^2$统计量分布曲线的一边。

案例

某厂商生产出一种新型的饮料装瓶机器，按设计要求，该机器装一瓶1000ml的饮料误差上下不超过 1ml。如果达到设计要求，表明机器的稳定性非常好。
现从该机器装完的产品中随机抽取25瓶，分别进行测定，然后用样本观测值分别减1000ml，得到数据：0.3、-0.4、-0.7、1.4、-0.6、-0.3、-1.5、0.6、-0.9、1.3、-1.3、0.7、1、-0.5、0、-0.6、0.7、-1.5、-0.2、-1.9、-0.5、1、-0.2、-0.6、1.1

试以$\alpha = 0.05$的显著性水平检验该机器的性能是否达到设计要求。

这里采用单侧检验，原假设和备择假设为

$$\begin{aligned} H_0 & : \sigma^2 \leq 1 \\ H_1 & : \sigma^2 > 1 \end{aligned}$$

由样本数据可以计算出$s^2 = 0.866$

对于"误差上下不超过1ml"，我们认为其含义是方差为1。

$$\begin{aligned} \chi^2 & = \frac{(n-1)s^2}{\sigma^2} \\ & = \frac{(25-1) \times 0.866}{1} \\ & = 20.8 \\ \chi_{0.05}^2(24) & = 36.415 \end{aligned}$$

故不拒绝原假设$H_0$，可以认为该机器的性能达到设计要求。

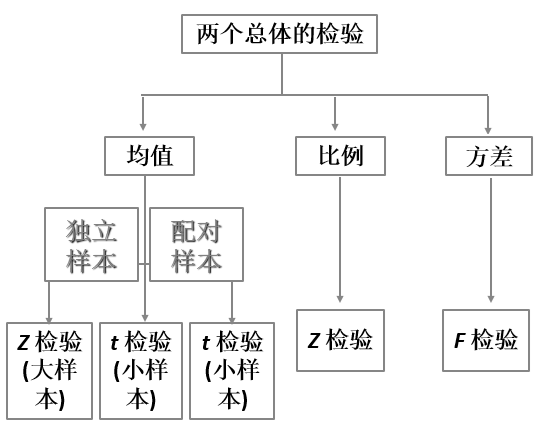
两个总体参数的检验

确定适当的检验统计量

独立样本总体均值之差的检验

方差已知

方法

假定条件：
两个样本是独立的随机样本；
并且，两个总体都是正态分布，或者满足大样本

使用正态分布统计量$z$

$$z = \frac{(\bar{x}_1 - \bar{x}_2) - (\mu_1 - \mu_2)}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}} \sim N(0,1)$$

案例

有两种方法可用于制造某种以抗拉强度为重要特征的产品。根据以往的资料得知，第一种方
法生产出的产品抗拉强度的标准差为8千克，第二种方法的标准差为10千克。从两种方法生产的
产品中各抽一个随机样本，样本容量分别为$n_1 = 32$，$n_2 = 40$，测得$\bar{x}_1 = 50$，$\bar{x}_2 = 44$。
问这两种方法生产出来的产品平均抗拉强度是否有显著差别($\alpha = 0.05$)？

由于检验两种方法生产的产品在抗拉强度上是否存在显著性差别，并未涉及方向，所以是双侧检验。

原假设和备择假设：

$$\begin{aligned} H_0 & = \mu_1 - \mu_2 = 0 \\ H_1 & = \mu_1 - \mu_2 \neq 0 \end{aligned}$$

因为$\sigma_1^2$和$\sigma_2^2$已知，考虑选用$z$作为检验统计量，即有

$$\begin{aligned} z & = \frac{(\bar{x}_1 - \bar{x}_2) - (\mu_1 - \mu_2)}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}} \\ & = \frac{(50 - 44) - 0}{\sqrt{\frac{64}{32}+\frac{100}{40}}} \\ & = 2.83 \end{aligned}$$

当$\alpha=0.05$时，$z_{\frac{\alpha}{2}} = 1.96$。

因为$z > z_{\frac{\alpha}{2}}$，所以拒绝$H_0$，即两种方法生产出来的产品其抗拉强度有显著差别。

方差未知 小样本

假定条价

假设条件：
两个样本是独立的随机样本；
并且，两个总体都是正态分布

方差相等

如果$\sigma_1^2$、$\sigma_2^2$未知且$\sigma_1^2=\sigma_2^2$

此时$\sigma_{\bar{x}_1 - \bar{x}_2}$的估计为

$$\hat{\sigma}_{\bar{x}_1 - \bar{x}_2} = s_p \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}$$

检验统计量t：

$$t = \frac{(\bar{x}_1 - \bar{x}_2) - (\mu_1 - \mu_2)}{s_p \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}} \sim t(n_1 + n_2 - 2)$$

其中

$$s_p^2 = \frac{(n_1 - s)s_1^2 + (n_2 - 1)s_2^2}{n_1 + n_2 - 2}$$

方差不相等

两个总体方差未知但不相等，即$\sigma_1^2 \neq \sigma_2^2$；

此时$\sigma_{\bar{x}_1 - \bar{x}_2}$的估计为

$$\hat{\sigma}_{\bar{x}_1 - \bar{x}_2} = \sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}$$

此时，两个样本均值之差经标准化后近似服从自由度为$f$的t分布。

自由度$f$的计算公式为：

$$f = \frac{(\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2})^2}{\frac{(\frac{s_1^2}{n_1})^2}{n_1 - 1} + \frac{(\frac{s_2^2}{n_2})^2}{n_2 - 1}}$$

检验统计量t：

$$t = \frac{(\bar{x}_1 - \bar{x}_2) - (\mu_1 - \mu_2)}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}} \sim t(f)$$

案例

“多吃谷物，将有助于减肥。”
为了验证这个假设，随机抽取了35人，询问他们早餐和午餐的通常食谱，根据他们的食谱，将其分为二类，一类为经常的谷类食用者(总体1)，一类为非经常谷类食用者(总体2)。然后测度每人午餐的大卡摄取量。经过一段时间的实验，得到两组数据。假设总体的方差不相等，检验该假设。($\alpha = 0.05$)
样本1：568、681、636、607、555、496、540、539、529、562、589、646、596、617、584
样本2：650、569、622、630、596、637、628、706、617、624、563、580、711、480、688、723、651、569、709、632

原假设和备择假设：

$$\begin{aligned} H_0 & : \mu_1 - \mu_2 \geq 0 \\ H_1 & : \mu_1 - \mu_2 < 0 \end{aligned}$$

代入公式，计算$f$

$$f = 32.34 \approx 32$$

计算$t$

$$\begin{aligned} t & = \frac{(\bar{x}_1 - \bar{x}_2) - (\mu_1 - \mu_2)}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}} \\ & = \frac{(589.67 - 629.25) - 0}{\sqrt{\frac{2431.429}{15} + \frac{3675.461}{20}}} \\ & = -2.128 \end{aligned}$$

$t_{0.05}(32)=1.694$，在给定的显著性水平下临界值为$-1.694$，$-2.128<-1.694$，落入拒绝域，没有证据表明多吃谷物将有助于减肥。

配对样本的均值差的检验

方法

配对样本的检验需要假定两个总体配对的差值服从正态分布，而且配对差值是从差值总体中随机抽取的。

对于小样本情形，配对差值经标准化后服从自由度为$n-1$的t分布，检验统计量为：

$$t = \frac{\bar{d} - (\mu_1 - \mu_2)}{(\frac{s_d}{\sqrt{n}})}$$

其中，$\bar{d}$为配对差值的均值；$s_d$为配对差值的标准差。

配对样本t检验的效应量

如果检验结果拒绝原假设，则可以计算效应量来进一步分析配对样本差值的均值与假设的总体配对差值的均值之间的差异程度。

配对样本t检验的效应量的估计由Cohen的d统计量给出。计算公式为：

$$d = \frac{|\text{配对样本差值的均值}|}{\text{配对差值的标准差}} = \frac{\bar{d}}{s_d} = \frac{|t|}{\sqrt{n}}$$

两个总体比例之差的检验

设两个总体服从二项分布，这两个总体中具有某种特征单位数的比例分别为$\pi_1$和$\pi_2$，但$\pi_1$和$\pi_2$未知，可以用样本比例$p_1$和$p_2$代替。
这时候有两种情况：

1. 检验两个总体比例之差为零的假设
2. 检验两个总体比例之差某个不为零的常数的假设

检验两个总体比例之差为零

方法

检验两个总体比例之差为零的假设，也就是，检验两个总体比例相等的假设。

该假设表达式为：$H_0 : \pi_1 - \pi_2 = 0$或$H_0 : \pi_1 = \pi_2$。

在原假设成立的条件下，最佳的方差是$p(1-p)$，其中$p$是将两个样本合并后得到的比例估计量，即

$$p = \frac{x_1 + x_2}{n_1 + n_2} = \frac{p_1 n_1 + p_2 n_2}{n_1 + n_2}$$

• $x_1$表示样本$n_1$中具有某些特征的单位数。
• $x_2$表示样本$n_2$中具有某些特征的单位数。

在大样本条件下，统计量$z$的表达式为：

$$z = \frac{p_1 - p_2}{\sqrt{p(1-p)(\frac{1}{n_1} + \frac{1}{n_2})}}$$

案例

人们普遍认为麦当劳的主要消费群体是青少年，但对市场进一步细分却发现有不同的观点。一种观点认小学生更喜欢麦当劳，另一种观点认为中学生对麦当劳的喜爱程度不亚于小学生。
某市场调查公司对此在某地区进行了一项调查，随机抽取了100名小学生和100名中学生，调查的问题是：如果有麦当劳和其他中式快餐，你会首选哪种作为经常性午餐？
调查结果如下：小学生(样本1)100人中有76人把麦当劳作为首选的经常性午餐，中学生(样本2)100人中有69人作出同样的选择。
调查结果支持哪种观点？

原假设和备择假设：

$$\begin{aligned} H_0 & : \pi_1 - \pi_2 = 0 \\ H_1 & : \pi_1 - \pi_2 \neq 0 \end{aligned}$$

根据题意有：

$$\begin{aligned} p & = \frac{x_1 + x_2}{n_1 + n_2} \\ & = \frac{76 + 69}{100 + 100} \\ & = 0.725 \\ z & = \frac{p_1 - p_2}{\sqrt{p(1-p)(\frac{1}{n_1} + \frac{1}{n_2})}} \\ & = \frac{0.76 - 0.69}{\sqrt{0.725 \times (1 - 0.725) \times (\frac{1}{100} + \frac{1}{100})}} \\ & = 1.11 \end{aligned}$$

由决策准则可知，$z=1.11$落入接受域，故调查结果支持原假设，即在该地区小学生和中学生对麦当劳的偏爱程度没有显著差异。

检验两个总体比例之差是某个不为零的常数

方法

检验两个总体比例之差是某个不为零的常数的假设，即检验$\pi_1 - \pi_2 = d_0 \quad (d_0 \neq 0)$，在这种情况下，两个样本比例之差$p_1 - p_2$，近似服从以$\pi_1 - \pi_2$为数学期望，$\frac{p_1(1-p_1)}{n1} + \frac{p_2(1-p_2)}{n_2}$为方差的正态分布，因而可以选择$z$作为检验统计量。

$$\begin{aligned} z & = \frac{(p_1 - p_2) - (\pi_1 - \pi_2)}{\sqrt{\frac{p_1(1-p_1)}{n_1} + \frac{p_2(1 - p_2)}{n_2}}} \\ & = \frac{(p_1 - p_2) - d_0}{\sqrt{\frac{p_1(1-p_1)}{n_1} + \frac{p_2(1 - p_2)}{n_2}}} \end{aligned}$$

案例

有一项研究报告说青少年经常上网聊天，男生的比例至少超过女生10个百分点，即$\pi_1 - \pi_2 \geq 10\%$($\pi_1$为男生比例，$\pi_2$为女生比例)。现对150个男生和150个女生进行上网聊天的频度调查，其中经常聊天的男生有68人，经常聊天的女生有54人。调查结果是否支持研究报告的结论($\alpha$=0.05)？

原假设和备择假设：

$$\begin{aligned} H_0 & : \pi_1 - \pi_2 \geq 10\% \\ H_1 & : \pi_1 - \pi_2 < 10\% \end{aligned}$$

由题意可知：

$$\begin{aligned} n_1 & = 150 \\ n_2 & = 150 \\ p_1 & = \frac{68}{150} = 0.45 \\ p_2 & = \frac{54}{150} = 0.36 \\ d_0 & = 10\% \end{aligned}$$

计算检验统计量$z$：

$$\begin{aligned} z & = \frac{(p_1 - p_2) - d_0}{\sqrt{\frac{p_1(1-p_1)}{n_1} + \frac{p_2(1 - p_2)}{n_2}}} \\ & = \frac{(0.45 - 0.36) - 0.1}{\sqrt{\frac{0.45(1-0.45)}{150} + \frac{0.36(1 - 0.36)}{150}}} \\ & = -0.177 \end{aligned}$$

这是一个左单侧检验，$z_{\alpha}=-1.645$，由决策准则可知$z = -0.177$，落入非拒绝域，故无法推翻原假设，调查结果支持研究报告的结论。

两个总体方差比的检验

方法

假设条件：
两个总体都服从正态分布；
并且，两个独立的随机样本

检验统计量：

$$F = \frac{(\frac{s_1^2}{\sigma_1^2})}{(\frac{s_2^2}{\sigma_2^2})} \sim F(n_1 - 1,n_2 - 1)$$

案例

假设，两个样本的方差分别为$s_1^2 = 2431.429$、$s_2^2 = 3675.461$，现以$\alpha=0.05$的显著性水平检验两总体方差是否相等。

原假设和备择假设：

$$\begin{aligned} H_0 & : \sigma_1^2 = \sigma_2^2 \\ H_1 & : \sigma_1^2 \neq \sigma_2^2 \end{aligned}$$

检验统计量$F$为：

$$\begin{aligned} F & = \frac{(\frac{s_1^2}{\sigma_1^2})}{(\frac{s_2^2}{\sigma_2^2})} \\ & = \frac{s_1^2}{s_2^2} \\ & = \frac{2431.429}{3675.461} \\ & = 0.662 \end{aligned}$$

在$\alpha=0.05$的显著性水平下，$F_{0.025}(14,19)=2.62$，$F_{0.975}(14,19)=0.352$。统计量落入接受域，不拒绝原假设。因此可以认为两总体方差没有显著差异。

正态性检验

什么是正态性检验

正态性检验(normality test)，检验样本数据是否来自正态总体就是。

正态性检验方法有图示法和检验法两大类。关于图示法我们不讨论，我们讨论检验法。

检验的原假设是总体服从正态分布；如果检验获得的P值小于指定的显著性水平，则拒绝原假设，表示总体不服从正态分布；如果P值较大而不能拒绝原假设，则可以认为总体服从正态分布。

正态性的检验方法有很多，本文讨论两种常用的检验方法：

1. S-W 检验
2. K-S 检验

S-W 检验

S-W检验，也用资料称之为W检验，用顺序统计量$W$来检验分布的正态性。

S-W检验的具体步骤如下：
首先，对研究的总体提出如下假设

$$\begin{aligned} H_0 & : \text{总体服从正态分布} \\ H_1 & : \text{总体不服从正态分布} \end{aligned}$$

然后，按下列公式计算检验统计量$W$

$$W = \frac{\sum a_i y_i^2}{\sum(y_i - \bar{y})^2}$$

其中，$y_i$为排序后的样本数据；$\bar{y}$为样本均值；$a_i$是样本量为$n$时对应的系数。可以通过《正态性检验统计量$W$的系数$a_i(n)$数值表》进行查询。

当P值小于指定显著性水平时表示总体不符合正态分布。
S-W检验适用于样本量较小的情形，一般认为样本量$[8,50]$适用。

K-S 检验

当样本量较大时，可使用K-S检验。该检验既可用于大样本，也可用于小样本，主要用于检验总体是否服从某个己知的理论分布(包括正态分布、泊松分布、均匀分布、指数分布)。

K-S检验是将某一变量的累积分布函数与特定的分布函数进行比较，检验其拟合程度。
设总体的累积分布函数为$F(x)$，已知的理论分布函数为$F_0(x)$，则检验的原假设和备择假设为：

$$\begin{aligned} H_0 & : F(x) = F_0(x) \quad \text{(总体分布与指定的理论分布差鼻不显著)} \\ H_1 & : F(x) \neq F_0(x) \quad \text{(总体分布与指定的理论分布差异显著)} \end{aligned}$$

设各样本观测值在理论分布中出现的累积概率为$F_0(x)$，各样本观测值的实际累积概率为$S(x)$，实际累积概率与理论累积概率的差值为$D(x)$，差值序列中的最大绝对差值为：

$$D = \max(|s(x_i) - F_0(x_i)|)$$

由于实际累积概率为离散值，通常做以下修正：

$$D = \max\{(|s(x_i) - F_0(x_i)|),(|s(x_{i-1} - F_0(x_i))|)\}$$

上式就是K-S检验的统计量。

在小样本情形下，统计量D服从Kolmogorov分布；在大样本情形下，则用正态分布近似，统计量为

$$z = \sqrt{n} D$$

如果$H_0$成立，每次抽样得到的D值应当不会与零偏离太远，否则就应拒绝$H_0$。
对于设定的显著性水乎$\alpha$，若检验统计量$D$(或$Z$)对应的概率小于$\alpha$，则拒绝$H_0$，表示总体分布与指定的理论分布差异显著。

K-S检验要求样本数据是连续的数值型数据，而且要求理论分布已知。比如，要检验样本数据是否来自$N(100,10^2)$的正态总体。当总体均值和方差未知时，可以用样本均值和方差来代替。

Python计算

总体均值的检验

一个总体均值的检验

大样本的检验

为了监测空气质量，某城市环保部门每隔几周对空气中的PM2.5进行一次随机测试。己知该城市过去每立方米空气中PM2.5的均值是$81$(微克/立方米)。统计了在最近一段时间的$40$次检测中，每立方米空气中的PM2.5数值。
根据最近的测量数据，能否认为该城市每立方米空气中的PM2.5均值显薯低于$81$(微克/立方米) ($\alpha = 0.05$)。

这里关心的是空气中PM2.5的均值是否显著低于过去的均值，也就是是否小于$81$(微克/立方米)，属于左侧检验。
提出的假设为：

$$\begin{aligned} H_0 & : \mu \geq 81 \\ H_1 & : \mu < 81 \end{aligned}$$

示例代码：

import pandas as pd

from statsmodels.stats.weightstats import ztest

df = pd.read_csv('XXX.csv')

z, p_value = ztest(x1=df['PM2.5值'], value=81, alternative='smaller')

print(z, p_value)

运行结果：

-1.1855576482277341 0.11789851794613643

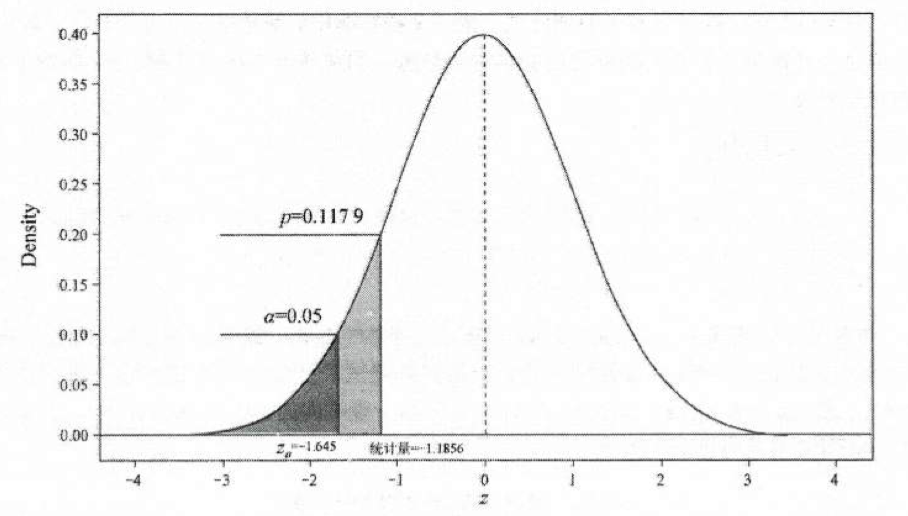
在该项检验中，$z=-1.1856$，$p=0.1179$。
因为$p>0.05$，不拒绝$H_0$，没有证据表明该城市每立方米空气中的PM2.5均值显著低于$81$(微克/立方米)。

小样本的检验

一种建筑材料的厚度要求为$5$cm，高于或低于该标准均被认为是不合格的。现对一家生产企业提供的20个样品进行检测，记录其检测结果。假定建筑材料的厚度服从正态分布，在$0.05$的显著性水平下，检验该企业生产的建筑材料的厚度是否符合要求。

依题意建立如下假设

$$\begin{aligned} H_0 & : \mu = 5 \\ H_1 & : \mu \neq 5 \end{aligned}$$

示例代码：

import pandas as pd

from scipy.stats import ttest_1samp

df = pd.read_csv('XXX.csv')

# popmean 为假设的总体均值
t, p_value = ttest_1samp(a=df['厚度'], popmean=5)

print(t, p_value)

运行结果：

-5.627314338711359 1.997624965504381e-05

在该项检验中，$t=-5.6273$，$p=1.998e-05$，由于$P<0.05$，拒绝$H_0$，即有证据显示该企业生产的建筑材料的厚度不符合要求。

两个总体均值差的检验

独立大样本的检验

为分析男女学生上网时间是否有差异，从男女学生中各随机抽取$36$人，得到每天的上网时间数据。设显著性水平为$0.05$，检验男女学生上网的平均时间是否有显著差异。

用$\mu_1$表示男生上网的平均时间，用$\mu_2$表示女生上网的平均时间。由于关心的是上网的平均时间是否有显著差异，故提出的假设为：

$$\begin{aligned} H_0 & : \mu_1 - \mu_2 = 0 \\ H_1 & : \mu_1 - \mu_2 \neq 0 \end{aligned}$$

示例代码：

import pandas as pd
from statsmodels.stats.weightstats import ztest

df = pd.read_csv('XXX.csv')

x1 = df['男生上网时间']
x2 = df['女生上网时间']

z, p_value = ztest(x1=x1, x2=x2, alternative='two-sided')

print(z, p_value)

运行结果：

1.118824633522991 0.263214960453917

在该项检验中，$z=1.1188$，$p=0.2632$，由于$P>0.05$，不拒绝$H_0$，即没有证据显示男女学生上网的平均时间有显著差异。

独立小样本的检验

为比较两家企业生产的同类产品的平均使用寿命是否有显著差异，质检人员对两家企业提供的各$20$个样品进行检测，得到的使用寿命数据。检验两家企业产品的平均使用寿命是否有显著差异($\alpha = 0.05$)。
现，假设两种情况，分别检验。

1. 假设两个总体方差相等
2. 假设两个总体方差不相等

用$\mu_1$表示甲企业产品的平均使用寿命，用$\mu_2$表示乙企业产品的平均使用寿命。依题意提出如下假设：

$$\begin{aligned} H_0 & : \mu_1 - \mu_2 = 0 \\ H_1 & : \mu_1 - \mu_2 \neq 0 \end{aligned}$$

假设总体方差相等，示例代码：

import pandas as pd
from statsmodels.stats.weightstats import ttest_ind

df = pd.read_csv('XXX.csv')

x1 = df['甲企业']
x2 = df['乙企业']

xbar1 = x1.mean()
xbar2 = x2.mean()

t, p_value, _ = ttest_ind(x1=x1, x2=x2, alternative='two-sided', usevar='pooled')

print(t, p_value)

运行结果：

-3.4942702671563377 0.001224733436714876

所以，拒绝原假设，表明两家企业产品的平均使用寿命有显著差异。

假设总体方差不相等，修改ttest_ind方法的usevar参数的值为unequal。示例代码：

import pandas as pd
from statsmodels.stats.weightstats import ttest_ind

df = pd.read_csv('XXX.csv')

x1 = df['甲企业']
x2 = df['乙企业']

xbar1 = x1.mean()
xbar2 = x2.mean()

t, p_value, _ = ttest_ind(x1=x1, x2=x2, alternative='two-sided', usevar='unequal')

print(t, p_value)

运行结果：

-3.4942702671563377 0.0013526838634792162

同样，拒绝原假设。

配对样本的检验

某饮料公司研制出一款新产品，为了比较消费者对新旧产品口感的满意程度，随机抽取$10$个消费者，让每个消费者先品尝一款饮料，再品尝另一款饮料，两款饮料的品尝顺序是随机的，然后每个消费者要对两款钦料分别进行评分($[0,10]$分)，记录评分结果。设显著性水平$\alpha=0.05$，检验消费者对两款饮料的评分是否有显著差异。

用$\mu_1$表示消费者对旧款饮料的平均评分，用$\mu_2$表示消费者对新款饮料的平均评分。依题意提出的原假设与备择假设为：

$$\begin{aligned} H_0 & : \mu_1 - \mu_2 = 0 \\ H_1 & : \mu_1 - \mu_2 \neq 0 \end{aligned}$$

示例代码：

import pandas as pd
from scipy.stats import ttest_rel

df = pd.read_csv('XXX.csv')

t, p_value = ttest_rel(a=df['旧款饮料'], b=df['新款饮料'])

print(t, p_value)

运行结果：

-2.750847901848533 0.022445658672013483

在该项检验中，$t=-2.750848$，$p=0.02245$，由于$p<0.05$，拒绝$H_0$，消费者对新旧两款饮料的评分有显著差异。

总体比例的检验

一个总体比例的检验

一家电视台的影视频道制作人认为，某电视连续剧如果在黄金时段播出，收视率将会达到$25\%$以上。经过一周的试播放后，该制作人随机抽取一个由$2000$人组成的样本，发现有$450$名观众观看了该电视连续剧。取显著性水平$\alpha=0.05$，检验收视率是否达到制作人的预期。

制作人想支持的观点是收视率达到$25\%$以上，因此提出的假设为：

$$\begin{aligned} H_0 & : \pi \leq 25\% \\ H_1 & : \pi > 25\% \end{aligned}$$

示例代码：

import numpy as np
from scipy.stats import norm

n = 2000
p = 450 / 2000
pi0 = 0.25
z = (p - pi0) / np.sqrt(pi0 * (1 - pi0) / n)
p_value = 1 - norm.cdf(z)

print(z, p_value)

运行结果：

-2.5819888974716108 0.9950883627462404

在该项检验中，$z=-2.581989$，$p=0.995088$，由于$p>0.05$，不拒绝$H_0$，没有证据表明收视率达到了制作人的预期。

两个总体比例差的检验

一所大学准备采取一项新的上网收费措施，为了解男女学生对这一措施的看法是否有差异，分别抽取$200$名男生和$200$名女生进行调查。其中的一个问题是"你是否赞成采取新的上网收费措施？"。其中，男生表示赞成的比例为$27\%$，女生表示赞成的比例为$35\%$。调查者认为，男生表示赞成的比例显著低于女生。取显著性水平$\alpha=0.05$，样本提供的证据是否支持调查者的看法？

用$\pi_1$表示男生表示赞成的比例，用$\pi_2$表示女生表示赞成的比例。
依题意提出如下假设：

$$\begin{aligned} H_0 & : \pi_1 - \pi_2 \geq 0 \\ H_1 & : \pi_1 - \pi_2 < 0 \end{aligned}$$

示例代码：

import numpy as np
from scipy.stats import norm

n1 = 200
n2 = 200
p1 = 0.27
p2 = 0.35

p = (p1 * n1 + p2 * n2) / (n1 + n2)
z = (p1 - p2) / np.sqrt(p * (1 - p) * (1 / n1 + 1 / n2))
p_value = norm.cdf(z)

print(z, p_value)

运行结果：

-1.7297550002576414 0.04183702872205522

在该项检验中，$z= -1.7298$，$p=0.041837$，由于$\pi<0.05$，拒绝$H_0$，样本提供的证据文持调查者的看法，即男生表示赞成的比例显著低于女生。

总体方差的检验

一个总体方差的检验

啤酒生产企业采用自动生产线灌装啤酒，每瓶的填装量为$640$ml，但受某些不可控因素的影响，每瓶的填装量会有差异。假定生产标准规定每瓶填装量的方差不应超过$16$。企业质检部门抽取了$10$瓶啤酒进行检验，得到样本数据。检验填装量的方差是否符合要求($\alpha = 0.05$)。

依题意提出如下假设：

$$\begin{aligned} H_0 & : \sigma^2 \leq 16 \\ H_1 & : \sigma > 16 \end{aligned}$$

示例代码：

import pandas as pd
from scipy.stats import chi2

data = pd.read_csv('XXX.csv')

x = data['填装量']
sigma0_2 = 16
s2 = x.var()
n = len(x)
df = n - 1

chi2_value = (n - 1) * s2 / sigma0_2

p_value = 1 - chi2.cdf(chi2_value, df=df)

print(chi2_value, p_value)

运行结果：

2.974062500000023 0.9653144162422501

在该项检验中，$\chi^2 = -2.9741$，$p=0.9653$，由于$p>0.05$，不拒绝$H_0$，没有证据显示啤酒填装量的方差不符合要求。

两个总体方差比的检验

沿用上文"Python计算-总体均值的检验-两个总体均值差的检验-独立小样本的检验"的数据。
现在检验两家企业产品使用寿命的方差是否有显著差异($\alpha=0.05$)。

令甲企业产品使用寿命的方差为$\sigma_1^2$，乙企业产品使用寿俞的方差为$\sigma_2^2$，依题意建立的原假设与备择假设为：

$$\begin{aligned} H_0 & : \frac{\sigma_1^2}{\sigma_2^2} = 1 \\ H_1 & : \frac{\sigma_1^2}{\sigma_2^2} \neq 1 \end{aligned}$$

示例代码：

import pandas as pd
from scipy.stats import f

df = pd.read_csv('XXX.csv')

x1 = df['甲企业']
x2 = df['乙企业']

s1_square = x1.var()
dfn = len(x1) - 1

s2_square = x2.var()
dfd = len(x2) - 1

f_value = s1_square / s2_square
p_value = (1 - (f.cdf(f_value, dfn=dfn, dfd=dfd))) * 2

print(f_value, p_value)

运行结果：

2.115367444040601 0.11103857279289997

在该项检验中，$f=2.1154$，$p=0.1110$，由于$p>0.05$，不拒绝$H_0$，没有证据表明两家企业产品使用寿命的方差有显著差异。

正态性检验

S-W 检验

沿用上文"Python计算-总体均值的检验-一个总体均值的检验"的数据。
用S-W方法检验PM2.5是否服从正态分布($\alpha=0.05$)。

提出假设：

$$\begin{aligned} H_0 & : \text{PM2.5服从正态分布} \\ H_1 & : \text{PM2.5不服从正态分布} \end{aligned}$$

示例代码：

import pandas as pd
from scipy.stats import shapiro

df = pd.read_csv('XXX.csv')

w, p_value = shapiro(df['PM2.5值'])

print(w, p_value)

运行结果：

0.9827210665767173 0.7888236849198136

在该项检验中，$w=0.9827$，$p=0.7888$，由于$p>0.05$，不拒绝原假设，即没有证据显示PM2.5不服从正态分布。

K-S 检验

沿用上文"Python计算-总体均值的检验-一个总体均值的检验"的数据。
用K-S检验方法检验该PM2.5是否服从正态分布($\alpha=0.05$)。

提出假设：

$$\begin{aligned} H_0 & : \text{PM2.5服从正态分布} \\ H_1 & : \text{PM2.5不服从正态分布} \end{aligned}$$

K-S检验要求正态总体是已知的，即参数$\mu$和$\sigma^2$已知。当$\mu$和$\sigma^2$未知，可以考虑分别用样本均值$\bar{x}$和样本方差$s^2$来代替。

示例代码：

import pandas as pd
from scipy.stats import kstest

df = pd.read_csv('XXX.csv')

x = df['PM2.5值']

d, p_value = kstest(x, 'norm', alternative='two-sided', mode='asymp', args=(x.mean(), x.std()))

print(d, p_value)

运行结果：

0.09033014922111654 0.8998565903483988

在该项检验中，$d=0.0903$，$p=0.8999$，由于$p>0.05$，不拒绝$H_0$，没有证据显示PM2.5不服从正态分布。