4.参数估计

基本概念

什么是参数估计

参数估计(parameter estimation)，用样本统计量去估计总体的参数。

例如，用样本均值$\bar{x}$估计总体均值$\mu$，用样本方差$s^2$估计总体方差$\sigma^2$，用样本比例$p$估计总体比例$\pi$，等等。

在参数估计中，总体参数笼统地用$\theta$来表示，用来估计总体参数的统计量称为估计量(estimator)，用符号$\hat{\theta}$表示，参数估计也就是如何用$\hat{\theta}$来估计$\theta$。样本均值、样本方差、样本比例等都可以是一个估计量，根据一个具体的样本计算出来的估计量的数值称为估计值(estimated value)。

点估计与区间估计

参数估计的方法有两种：

1. 点估计
2. 区间估计

点估计

点估计(point estimate)，用样本统计量$\hat{\theta}$的某个取值直接作为总体参数$\theta$的估计值。

点估计的局限性在于，无法给出，一个具体的点估计值的可靠性的度量。

点估计的方法包括矩估计法、顺序统计量法、最大似然法、最小二乘法等多种方法。这些都不是参数估计的主要方法，本文不讨论。
评价估计量的指标有三个：无偏性、有效性、一致性。我们也不会展开讨论，因为这三个评价的都是点估计的。

区间估计

区间估计(interval estimate)，在点估计的基础上，给出总体参数估计的一个区间范围，该区间范围通常由样本统计量加减估计误差得到。

与点估计不同，进行区间估计时，根据样本统计量的抽样分布可以对样本统计量与总体参数的接近程度给出一个概率度量。

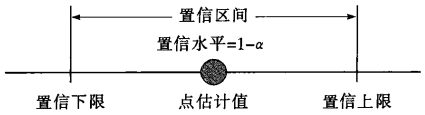
置信区间

置信区间(confidence interval)，由样本统计量所构造的总体参数的估计区间，其中区间的最小值为置信下限，最大值为置信上限。

通俗的说，用区间估计的方法，所得到的区间，被称为置信区间。

置信度

一般地，如果将构造置信区间的步骤重复很多次，置信区间中包含总体参数真值的次数所占的比例，这就是置信度(confidence coefficient)，也被称为置信水平(confidence level)或置信系数，表示为$1-\alpha$

$\alpha$是事先确定的一个概率值，也称风险值，是总体参数不在区间内的概率。

例如，置信水平值为$99\%$、$95\%$、$90\%$，相应的$\alpha$为$0.01$、$0.05$、$0.10$。

一种常见的错误，置信度是总体参数落在置信区间的概率。

我们借助套圈游戏来描述置信度。

先有总体参数，再有置信区间。就好比，先有已经摆放好的某个工艺品，再有套圈。置信度就好比套圈能套住某个工艺品的概率。假如以统计定义去描述置信度，进行N次套圈试验去套某个工艺品，M次套中，则置信度为M/N。

 
即，对于置信度：

1. 如果用某种方法构造的所有区间中有$95\%$的区间包含总体参数的真值，$5\%$的区间不包含总体参数的真值，那么，用该方法构造的区间称为置信水平为$95\%$的置信区间。
2. 总体参数的真值是固定的、未知的，而样本构造的区间则是不固定的。若抽取不同的样本，用该方法可以得到不同的区间，从这个意义上说，置信区间是一个随机区间，它会因样本的不同而不同，而且不是所有的区间都包含总体参数的真值。
3. 在实际问题中，进行估计时往往只抽取一个样本，此时所构造的是与样本相联系的一定置信水平下的置信区间。由于用该样本构造的区间是一个特定的区间，而不是随机区间，所以无法知道这个样本所产生的区间是否包含总体参数的真值。

一个总体参数的区间估计

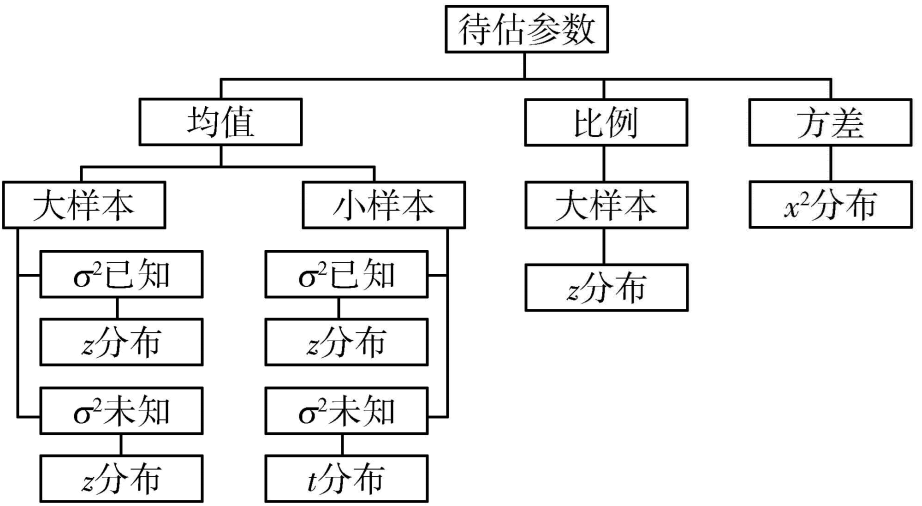
研究一个总体时，所关心的参数主要有：

1. 总体均值$\mu$
2. 总体比例$\pi$
3. 总体方差$\sigma^2$

总体均值的区间估计

在对总体均值进行区间估计时，需要考虑：

1. 总体是否为正态分布
2. 总体方差是否已知
3. 用于构造估计量的样本是大样本(通常要求$n \geq 30$)，还是小样本($n < 30$)

正态总体、方差已知，或非正态总体、大样本

方法

1. 假定条件，当总体服从正态分布且$\sigma^2$已知时，或者总体不是正态分布但为大样本时。
   样本均值$\bar{x}$的抽样分布均为正态分布，其数学期望为总体均值$\mu$，方差为$\frac{\sigma^2}{n}$。
2. 而样本均值经过标准化以后的随机变量服从标准正态分布。
   使用正态分布统计量

   $$z = \frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt{n}}} \sim N(0,1)$$

3. 根据正态分布的性质可以得出，总体均值$\mu$在$1-\alpha$置信水平下的置信区间为：

   $$\bar{x} \pm z_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}}$$

式中，$\bar{x} - z_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}}$称为置信下限，$\bar{x} + z_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}}$称为置信上限；$\alpha$是事先确定的一个概率值，也称为风险值，它是总体值不被包括在置信区间内的概率；$a-\alpha$称为置信水平；$z_{\frac{\alpha}{2}}$是标准正态分布右侧面积为$\frac{\alpha}{2}$时的$z$值；$z_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}}$是估计总体均值时的估计误差(estimate error)。

如果总体服从正态分布但$\sigma^2$未知，或总体并不服从正态分布，只要是在大样本条件下，总体方差$\sigma^2$就可以用样本方差$s^2$代替，这时总体均值$\mu$在$1-\alpha$置信水平下的置信区间可以写为：

$$\bar{x} \pm z_{\frac{\alpha}{2}} \frac{s}{\sqrt{n}}$$

案例

一家食品生产企业以生产袋装食品为主，每天的产量大约为8000袋。按规定每袋的重量应为100克。为对产品重量进行监测，企业质检部门经常要进行抽检，以分析每袋重量是否符合要求。
现从某天生产的一批食品中随机抽取25袋，测得每袋重量为：112.5、101.0、103.0、102.0、100.5、102.6、107.5、95.0、108.8、115.6、100.0、123.5、102.0、101.6、102.2、116.6、95.4、97.8、108.6、105.0、136.8、102.8、101.5、98.4、93.3。
已知产品重量服从正态分布，且总体标准差为10克。试估计该天产品平均重量的置信区间，置信水平为95%。

已知$X \sim N(\mu,10^2)$，$n=25$，$1-\alpha=95\%$，$Z_{\frac{\alpha}{2}}=1.96$。
由于是正态总体，且方差已知。总体均值在$1-\alpha$置信水平下的置信区间为：

$$\begin{aligned} \bar{x} \pm z_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}} & = 105.36 \pm 1.96 \times \frac{10}{\sqrt{25}} \\ & = (101.44,109.28) \end{aligned}$$

即，该食品平均重量的置信区间为$(101.44,109.28)$。

正态总体、方差未知、小样本

方法

1. 假定条件，总体方差$\sigma^2$未知，而且是在小样本的情况下
   需要用样本方差$s^2$代替$\sigma^2$，这时，样本均值经过标准化以后的随机变量服从自由度为$n-1$的t分布
2. 即，使用t分布统计量

   $$t = \frac{\bar{x}-\mu}{\frac{s}{\sqrt{n}}} \sim t(n-1)$$

3. 需要采用t分布来建立总体均值$\mu$的置信区间。根据t分布建立的总体均值$\mu$在$1-\alpha$置信水平下的置信区间为：

   $$\bar{x} \pm t_{\frac{\alpha}{2}}\frac{s}{\sqrt{n}}$$

式中，$t_\frac{\alpha}{2}$是自由度为$n-1$时，t分布中右侧面积为$\frac{\alpha}{2}$时的t值。

案例

已知某种灯泡的寿命服从正态分布。
现从一批灯泡中随机抽取16个，测得其使用寿命(单位：小时)如下：1510、1450、1480、1460、1520、1480、1490、1460、1480、1510、1530、1470、1500、1520、1510、1470。
试建立该批灯泡平均使用寿命的95%的置信区间。

根据抽样结果有：

$$\begin{aligned} \bar{x} & = \frac{1}{n} \sum_{i=1}^{n} x_i = \frac{23840}{16} = 1490 \\ s & = \sqrt{\frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2} = \sqrt{\frac{9200}{16-1}} = 24.77 \end{aligned}$$

根据$\alpha=0.05$，$n=16$，可知：

$$t_{\frac{\alpha}{2}}(n-1) = t_{0.025}(15) = 2.131$$

平均使用寿命的置信区间为：

$$\begin{aligned} \bar{x} \pm t_{\frac{\alpha}{2}}\frac{s}{\sqrt{n}} & = 1490 \pm 2.131 \times \frac{24.77}{\sqrt{16}} \\ & = (1476.8,1503.2) \end{aligned}$$

即1490±13 .2=(1476 .8,1503 .2),该种灯泡平均使用寿命的95%的置信区间为

总体比例的区间估计

方法

1. 假定条件，总体服从二项分布，可以由正态分布来近似。
   由样本比例$p$的抽样分布可知，当样本量足够大时，比例$p$的抽样分布可用正态分布近似。也就是说，我们讨论的，都是大样本情况下。
   $p$的数学期望为$E(p)=\pi$；$p$的方差为$\sigma_{p}^2=\frac{\pi(1-\pi)}{n}$，样本比例经标准化后的随机变量服从标准正态分布。
2. 即，使用正态分布统计量$z$

   $$z = \frac{p-\pi}{\sqrt{\frac{\pi(1-\pi)}{n}}} \sim N(0,1)$$

3. 总体比例$\pi$在$1-\alpha$置信水平下的置信区间为：

   $$p \pm z_{\frac{\alpha}{2}} \sqrt{\frac{p(1-p)}{n}}$$

式中，$\alpha$是显著性水平；$z_\frac{\alpha}{2}$是标准正态分布右侧面积为$\frac{\alpha}{2}$时的$z$值；$z_{\frac{\alpha}{2}}\sqrt{\frac{p(1-p)}{n}}$是估计总体比例时的估计误差。

解释一下，为什么是$p \pm z_{\frac{\alpha}{2}} \sqrt{\frac{p(1-p)}{n}}$，而不是$p \pm z_{\frac{\alpha}{2}} \sqrt{\frac{\pi(1-\pi)}{n}}$；总体比例$\pi$在$1-\alpha$置信水平下的置信区间为：$p \pm z_{\frac{\alpha}{2}} \sqrt{\frac{\pi(1-\pi)}{n}}$；但是，因为$\pi$值恰好是要估计的，所以，需要用样本比例$p$来代替$\pi$；所以，总体比例的置信区间表示为：$p \pm z_{\frac{\alpha}{2}} \sqrt{\frac{p(1-p)}{n}}$。

案例

某城市想要估计下岗职工中女性所占的比例，随机抽取了100个下岗职工，其中65人为女职工。试以95%的置信水平估计该城市下岗职工中女性比例的置信区间。

已知，$n=100$，$z_\frac{\alpha}{2} = 1.96$，根据抽样结果计算的样本比例为：

$$p = \frac{65}{100} = 65\%$$

根据置信区间公式得，

$$\begin{aligned} p \pm z_{\frac{\alpha}{2}} \sqrt{\frac{p(1-p)}{n}} & = 65\% \pm 1.96 \times \sqrt{\frac{65\% (1-65\%)}{100}} \\ & = (55.65\%,74.35\%) \end{aligned}$$

任意大小的样本

对于任意大小的样本，将试验次数(样本量)$n$加上$4$，即用$\widetilde{n}=n+4$代替$n$；将试验成功的次数$x$加上$2$，即用$\widetilde{p}=(x+2)/\widetilde{n}$代替$p$，可以改进置信区向。

由此得到的总体比例$\pi$在$(1-\alpha)$置信水平下的置信区间为：

$$\widetilde{p} \pm z_{\frac{\alpha}{2}} \sqrt{\frac{\widetilde{p}(1-\widetilde{p})}{n}}$$

总体方差的区间估计

方法

1. 假定条件，总体服从正态分布。
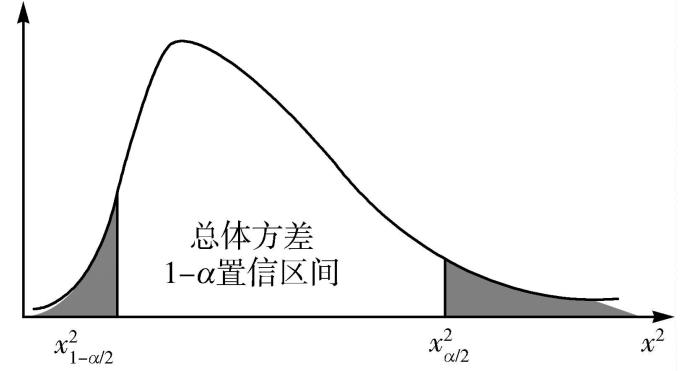
2. 根据在《3.抽样分布》所讨论的$\chi^2$分布的一个推论，我们知道

   $$\frac{(n-1)S^2}{\sigma^2} \sim \chi^2(n-1)$$

3. 总体方差$\sigma^2$对在$1-\alpha$置信水平下的置信区间为：

   $$\frac{(n-1)s^2}{\chi_{\frac{\alpha}{2}}^2} \leq \sigma^2 \leq \frac{(n-1)s^2}{\chi_{1-\frac{\alpha}{2}}^2}$$

根据样本方差的抽样分布可知，样本方差服从自由度为$n-1$的$\chi^2$分布。因此，用$\chi^2$分布构造总体方差的置信区间。

案例

一家食品生产企业以生产袋装食品为主，现从某天生产的一批食品中随机抽取25袋，测得每袋重量为：112.5、101.0、103.0、102.0、100.5、102.6、107.5、95.0、108.8、115.6、100.0、123.5、102.0、101.6、102.2、116.6、95.4、97.8、108.6、105.0、136.8、102.8、101.5、98.4、93.3。
已知产品重量服从正态分布。以95%的置信水平建立该种食品重量方差的置信区间。

已知$n=25$，$1-\alpha=95\%$，根据样本数据计算得$s^2=93.21$。

$$\begin{aligned} \chi_{\frac{\alpha}{2}}^2(n-1) & = \chi_{0.025}^2(24) = 39.3641 \\ \chi_{1-\frac{\alpha}{2}}^2(n-1) & = \chi_{0.975}^2(24) = 12.4011 \\ \end{aligned}$$

$\sigma^2$的置信度为$95\%$的置信区间为

$$\begin{aligned} \frac{(n-1)s^2}{\chi_{\frac{\alpha}{2}}^2} & \leq \sigma^2 \leq \frac{(n-1)s^2}{\chi_{1-\frac{\alpha}{2}}^2} \\ \frac{(25-1) \times 93.21}{39.3641} & \leq \sigma^2 \leq \frac{(25-1) \times 93.21}{12.4011} \\ 56.83 & \leq \sigma^2 \leq 180.39 \end{aligned}$$

小结

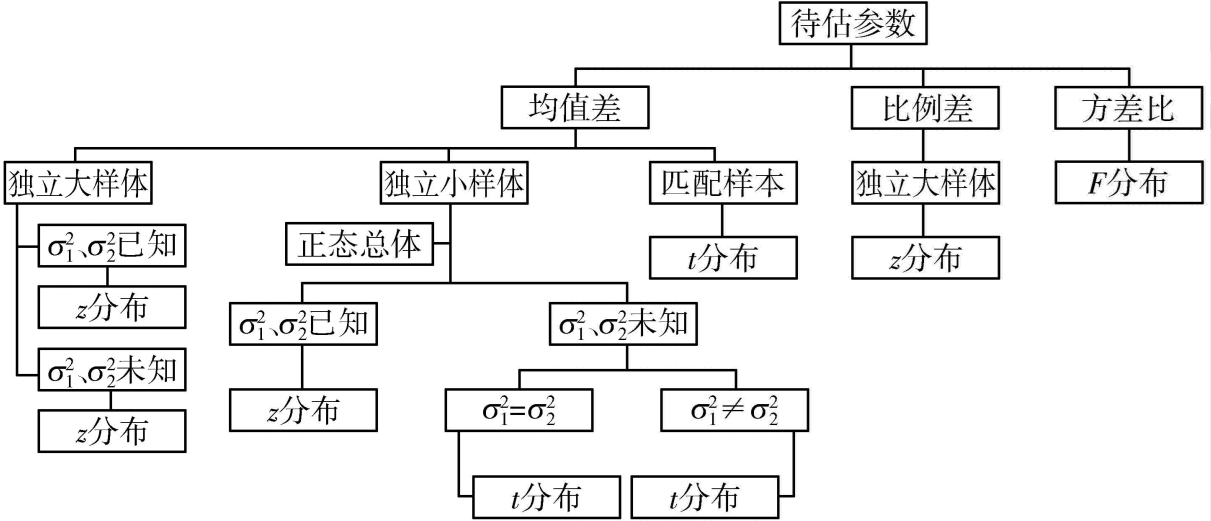
两个总体参数的区间估计

对于两个总体，所关心的参数主要有：

1. 两个总体的均值之差$\mu_1 - \mu_2$
2. 两个总体的比例之差$\pi_1 - \pi_2$
3. 两个总体的方差比于$\frac{\sigma_1^2}{\sigma_2^2}$

两个总体均值之差

独立样本 大样本

方法

假定条件：
两个总体都服从正态分布 $\sigma_1^2$、$\sigma_2^2$已知 或者 两个总体不服从正态分布但是样本都为大样本；
并且，两个样本为独立随机的样本。

使用正态分布统计量$z$

$$z = \frac{(\bar{x}_1 - \bar{x}_2) - (\mu_1 - \mu_2)}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}} \sim N(0,1)$$

当两个总体的方差$\sigma_1^2$和$\sigma_2^2$都已知时，两个总体均值之差$\mu_1 - \mu_2$在$1-\alpha$置信水平下的置信区间为：

$$(\bar{x}_1 - \bar{x}_2) \pm z_{\frac{\alpha}{2}}\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}$$

当两个总体的方差$\sigma_1^2$和$\sigma_2^2$未知时，可用两个样本方差$s_1^2$和$s_2^2$来代替，这时，两个总体均值之差$\mu_1 - \mu_2$在$1-\alpha$置信水平下的置信区间为：

$$(\bar{x}_1 - \bar{x}_2) \pm z_{\frac{\alpha}{2}}\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}$$

案例

某地区教育管理部门想估计两所中学的学生高考时的英语平均分数之差，为此在两所中学独立抽取两个随机样本。

中学一	中学二
$n_1=46$	$n_2=33$
$\bar{x_1} = 86$	$\bar{x_2}=78$
$s_1=5.8$	$s_2=7.2$

试建立两所中学高考英语平均分数之差的95%的置信区间。

$$\begin{aligned} (\bar{x}_1 - \bar{x}_2) \pm z_{\frac{\alpha}{2}}\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}} & = (86 - 78) \pm 1.96 \times \sqrt{\frac{5.8^2}{46}+\frac{7.2^2}{33}} \\ & = (5.03,10.97) \end{aligned}$$

独立样本 小样本 方差相等

方法

假设条件：
两个总体都服从正态分布，或者，两个总体方差未知但相等，即$\sigma_1^2 = \sigma_2^2$；
并且，两个独立的小样本。

此时，需要用两个样本的方差$s_1^2$和$s_2^2$来估计。这时，需要将两个样本的数据组合在一起，以给出总体方差的合并估计量$s_p^2$：

$$s_p^2 = \frac{(n_1 - s)s_1^2 + (n_2 - 1)s_2^2}{n_1 + n_2 - 2}$$

两个样本均值之差经标准化后服从自由度为$n_1 + n_2 - 2$的t分布，即

$$t = \frac{(\bar{x}_1 - \bar{x}_2) - (\mu_1 - \mu_2)}{s_p \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}} \sim t(n_1 + n_2 - 2)$$

因此，两个总体均值之差$\mu_1 - \mu_2$在$1-\alpha$置信水平下的置信区间为：

$$(\bar{x}_1 - \bar{x}_2) \pm t_{\frac{\alpha}{2}}(n_1 + n_2 - 2)\sqrt{s_p^2(\frac{1}{n_1} + \frac{1}{n_2})}$$

案例

为估计两种方法组装产品所需时间的差异，分别为两种不同的组装方法随机安排12个工人，每个工人组装一件产品所需的时间如下：
方法一：28.3、36.0、30.1、37.2、29.0、38.5、37.6、34.4、32.1、28.0、28.8、30.0
方法二：27.6、31.7、22.2、26.0、31.0、32.0、33.8、31.2、20.0、33.4、30.2、26.5
假定两种方法组装产品的时间服从正态分布，且方差相等，试以95%的置信水平建立两种方法组装产品所需平均时间之差的置信区间。

根据样本数据计算得

$$\begin{aligned} \bar{x}_1 & = 32.5 \\ s_1^2 & = 15.996 \\ \bar{x}_2 & = 28.8 \\ s_2^2 & = 19.358 \end{aligned}$$

合并估计量为：

$$s_p^2 = \frac{(12-1) \times 15.996 + (12-1) \times 19.358}{12+12-2} = 17.677$$

根据$\alpha=0.05$，自由度$12+12-2=22$，可知$t_{\frac{0.05}{2}}(22)=2.0739$。

两个总体均值之差在95%的置信水平下的置信区间为：

$$\begin{aligned} (\bar{x}_1 - \bar{x}_2) \pm t_{\frac{\alpha}{2}}(n_1 + n_2 - 2)\sqrt{s_p^2(\frac{1}{n_1} + \frac{1}{n_2})} & = (32.5 - 28.8) \pm 2.0739 \times \sqrt{17.677 \times (\frac{1}{12} + \frac{1}{12})} \\ & = 3.7 \pm 3.56 \end{aligned}$$

独立样本 小样本 方差不相等

方法

假设条件：
两个总体都服从正态分布，或者，两个总体方差未知但不相等，即$\sigma_1^2 \neq \sigma_2^2$；
并且，两个独立的小样本。

使用t统计量

$$t = \frac{(\bar{x}_1 - \bar{x}_2) - (\mu_1 - \mu_2)}{\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}} \sim t(v)$$

此时，两个样本均值之差经标准化后近似服从自由度为$v$的t分布。
自由度$v$的计算公式为：

$$v = \frac{(\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2})^2}{\frac{(\frac{s_1^2}{n_1})^2}{n_1 - 1} + \frac{(\frac{s_2^2}{n_2})^2}{n_2 - 1}}$$

两个总体均值之差在$1-\alpha$置信水平下的置信区间为：

$$(\bar{x}_1 - \bar{x}_2) \pm t_{\frac{\alpha}{2}}(v) \sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}$$

案例

沿用上文的例子。假定第一种方法随机安排12名工人，第二种方法随机安排8名工人，即$n_1=12$，$n_2=8$。
方法一：28.3、36.0、30.1、37.2、29.0、38.5、37.6、34.4、32.1、28.0、28.8、30.0
方法二：27.6、31.7、22.2、26.5、31.0、33.8、20.0、30.2
假定两种方法组装产品的时间服从正态分布，且方差不相等。以95%的置信水平建立两种方法组装产品所需平均时间差值的置信区间。

根据样本数据计算得：

$$\begin{aligned} \bar{x_1} & = 32.5 \\ s_1^2 & = 15.996 \\ \bar{x_2} & = 27.875 \\ s_2^2 & = 23.014 \end{aligned}$$

代入公式，自由度$v = 13.188 \approx 13$。

根据自由度=13，可知$t_\frac{0.05}{2}(13)=2.1604$。

两个总体均值之差在$1-\alpha$置信水平下的置信区间为:

$$\begin{aligned} (\bar{x}_1 - \bar{x}_2) \pm t_{\frac{\alpha}{2}}(v) \sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}} & = (32.5 - 27.875) \pm 2.1604 \times \sqrt{\frac{15.996}{12}+\frac{23.014}{8}} \\ & = 4.625 \pm 4.433 \end{aligned}$$

匹配样本

什么是匹配样本

上文使用的都是独立的样本，在使用独立样本来估计两个总体均值之差具有潜在的弊端。比如，在为每种方法随机指派12个工人时，偶尔可能会将技术比较差的12个工人指给方法一，而将技术较好的12个工人指给方法二，这种不公平的指派可能会掩盖两种方法组装产品所需时间的真正差异。

为解决这一问题，可以使用匹配样本(matched sample)，即一个样本中的数据与另一个样本中的数据相对应。

比如，先指定12个工人用第一种方法组装产品，然后再让这12个工人用第二种方法组装产品，这样得到的两种方法组装产品的数据就是匹配数据。基于匹配样本，可以消除由于样本指定的不公平造成的两种方法组装耗时上的差异。

大样本的方法

假定条件：
两个匹配的大样本($n_1 \geq 30$和$n_2 \geq 30$)；
并且，两个总体各观察值的配对差服从正态分布

两个总体均值之差$\mu_d=\mu_1 - \mu_2$在$1-\alpha$置信水平下的置信区间为：

$$\bar{d} \pm z_{\frac{\alpha}{2}} \frac{\sigma_d}{\sqrt{n}}$$

式中，$d$表示两个匹配样本对应数据的差值；$\bar{d}$表示各差值的均值；$\sigma_d$表示各差值的标准差。当总体的$\sigma_d$未知时，可用样本差值的标准差$s_d$来代替。

小样本的方法

假定条件：
两个匹配的大样本($n_1 < 30$和$n_2 < 30$)；
并且，两个总体各观察值的配对差服从正态分布。

两个总体均值之差$\mu_d = \mu_1 - \mu_2$在$1-\alpha$置信水平下的置信区间为：

$$\bar{d} \pm t_{\frac{\alpha}{2}}(n-1)\frac{s_d}{\sqrt{n}}$$

案例

由10名学生组成一个随机样本，让他们分别采用A、B两套试卷进行测试，结果如表所示。

学生编号	试卷 A	试卷 B	差值 d
1	78	71	7
2	63	44	19
3	72	61	11
4	89	84	5
5	91	74	17
6	49	51	-2
7	68	55	13
8	76	60	16
9	85	77	8
10	55	39	16

假定两套试卷分数之差服从正态分布，试建立两套试卷平均分数之差$\mu_d = \mu_1 - \mu_2$的95%的置信区间。

根据上表可以计算得到

$$\begin{aligned} \bar{d} & = 11 \\ s_d & = 6.53 \\ t_{\frac{0.05}{2}}(9) & = 2.2622 \end{aligned}$$

因此，得到两套试卷平均分之差的95%置信区间为：

$$\begin{aligned} \bar{d} \pm t_{\frac{\alpha}{2}}(n-1)\frac{s_d}{\sqrt{n}} & = 11 \pm 2.2622 \frac{6.53}{\sqrt{10}} \\ & = 11 \pm 4.67 \end{aligned}$$

两个总体比例之差的区间估计

方法

假定条件：
两个总体服从二项分布，可以用正态分布来近似；
并且，两个样本是独立的。

根据正态分布建立的两个总体比例之差在$1-\alpha$置信水平下的置信区间为：

$$(p_1 - p_2) \pm z_{\frac{\alpha}{2}} \sqrt{\frac{p_1(1-p_1)}{n_1} + \frac{p_2(1-p_2)}{n_2}}$$

案例

在某个电视节目的收视率调查中，从农村随机调查了400人，有32%的人收看了该节目；从城市随机调查了500人，有45%的人收看了该节目。试以95%的置信水平估计城市与农村收视率之差的置信区间。

城市收视率$p_1=45\%$
农村收视率$p_2=32\%$

当$\alpha=0.05$时，$z_\frac{\alpha}{2}=1.96$，因此，置信区间为：

$$\begin{aligned} (p_1 - p_2) \pm z_{\frac{\alpha}{2}} \sqrt{\frac{p_1(1-p_1)}{n_1} + \frac{p_2(1-p_2)}{n_2}} & = (45\% - 32\%) \pm 1.96 \times \sqrt{\frac{45\%(1-45\%)}{500} + \frac{32\%(1-32\%)}{400}} \\ & = 13\% \pm 6.32\% \end{aligned}$$

两个任意大小样本的估计方法

对于两个任意大小的样本，只要对$n_1$和$n_2$、$p_1$和$p_2$略加修正就可以改进估计区间。

具体做法是：

1. 将试验次数(样本量)$n_1$和$n_2$加上$2$，即用$\widetilde{n_1}=n_1+2$代替$n_1$，用$\widetilde{n_2}=n_2+2$代替$n_2$。
2. 将试验成功的次数$x_1$和$x_2$各加上$1$，即用$\widetilde{p_1}=\frac{(x_1 + 1)}{\widetilde{n_1}}$代替$p_1$，用$\widetilde{p_2}=\frac{(x_2 + 1)}{\widetilde{n_2}}$代替$p_2$。

由此得到的两个总体比例之差$(\pi_1 - \pi_2)$在$(1-\alpha)$置信水平下的置信区间为：

$$(\widetilde{p_1} - \widetilde{p_2}) \pm z_{\frac{\alpha}{2}} \sqrt{\frac{\widetilde{p_1}(1-\widetilde{p_1})}{n_1} + \frac{\widetilde{p_2}(1-\widetilde{p_2})}{n_2}}$$

两个总体方差比的区间估计

方法

该方法用于比较两个总体方差。
比如，比较用两种不同方法生产的产品性能的稳定性，比较不同测量工具的精度，等等。

比较两个总体的方差比，用两个样本的方差比来判断：

1. 如果$\frac{S_1^2}{S_2^2}$接近$1$，说明两个总体方差很接近。
2. 如果$\frac{S_1^2}{S_2^2}$远离$1$，说明两个总体方差之间存在差异。

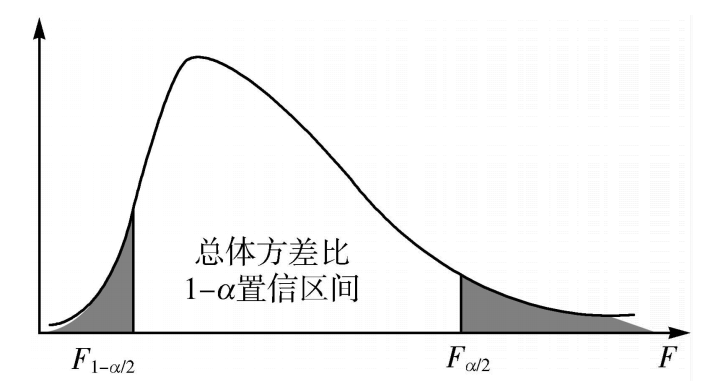
两个总体方差比$\frac{\sigma_1^2}{\sigma_2^2}$在$1-\alpha$置信水平下的置信区间为：

$$\frac{(\frac{s_1^2}{s_2^2})}{F_{\frac{\alpha}{2}}} \leq \frac{\sigma_1^2}{\sigma_2^2} \leq \frac{(\frac{s_1^2}{s_2^2})}{F_{1 - \frac{\alpha}{2}}}$$

                                             (7.26)

式中，$F_{\frac{\alpha}{2}}$和$F_{1-\frac{\alpha}{2}}$分别是分子自由度为$n_1-1$和分母自由度为$n_2-1$的F分布的右侧面积为$\frac{\alpha}{2}$和$1-\frac{\alpha}{2}$的分位数。由于F分布表中只给出面积较小的右分位数，此时可利用下面的关系求得$F_{1-\frac{\alpha}{2}}$的分位数值：

$$F_{1-\frac{\alpha}{2}}(n_1,n_2) = \frac{1}{F_{\frac{\alpha}{2}}(n_2,n_1)}$$

案例

为研究男女学生在生活费支出(单位：元)上的差异，在某大学随机抽取25名男学生和25名女学生，得到下面的结果：
男学生：$\bar{x_1}=520 \quad s_1^2=260$
女学生：$\bar{x_2}=480 \quad s_2^2=280$
试以90%的置信水平估计男女学生生活费支出方差比的置信区间。

$$\begin{aligned} n_1 & = 25 - 1 = 24 \\ n_2 & = 25 - 1 = 24 \\ F_{\frac{\alpha}{2}}(n_2,n_1) & = F_{0.05}(24,24) = 1.98 \\ F_{1-\frac{\alpha}{2}}(24,24) & = \frac{1}{F_{0.05}(24,24)} = \frac{1}{1.98} = 0.505 \end{aligned}$$

由此得到：

$$\begin{aligned} \frac{(\frac{260}{280})}{1.98} & \leq \frac{\sigma_1^2}{\sigma_2^2} \leq \frac{(\frac{260}{280})}{0.505} \\ 0.47 & \leq \frac{\sigma_1^2}{\sigma_2^2} \leq 1.84 \end{aligned}$$

小结

样本量的确定

在进行参数估计之前，首先应该确定一个适当的样本量，也就是应该抽取一个多大的样本来估计总体参数。

在进行估计时，总是希望提高估计的可靠程度。但在一定的样本量下，要提高估计的可靠程度(置信水平)，就应扩大置信区间，而过宽的置信区间在实际估计中往往是没有意义的。想要缩小置信区间，又不降低置信程度，就需要增加样本量。

但样本量的增加会受到许多限制，比如会增加调查的费用和工作量。通常，样本量的确定与可以容忍的置信区间的宽度以及对此区间设置的置信水平有一定关系。

因此，如何确定一个适当的样本量，是抽样估计中需要考虑的问题。

估计总体均值时样本量的确定

方法

在进行参数估计时，估计误差为$z_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}}$，由此可知，$z_{\frac{\alpha}{2}}$和样本容量$n$共同确定了估计误差的大小。对于给定的置信水平和总体标准差，就可以确定任一希望的估计误差所需要的样本量。
所希望达到的估计误差为：

$$E = z_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}}$$

可以推出需要的样本量为：

$$n = \frac{(z_{\frac{\alpha}{2}})^2 \sigma^2}{E^2}$$

从式中可以看出，样本量与置信水平成正比；与总体方差成正比；与估计误差的平方成反比；
与可靠性系数成正比。

当计算出的样本量不是整数时，通常进行向上取整，这个也被称为样本量的圆整法则。

案例

考虑总体均值的$95.44\%$置信度的置信区间，已知总体服从正态分布且标准差为$10$，要使得到
的置信区间的半径不超过$1$，需要的最小样本容量为多少？

置信区间的半径不超过$1$，即估计误差小于$1$，由题意可以构造不等式如下

$$\begin{aligned} z_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}} & \leq 1 \\ 1.96 \times \frac{\sigma}{\sqrt{n}} & \leq 1 \\ n \geq 400 \end{aligned}$$

估计总体比例时样本量的确定

方法

与估计总体均值时样本量的确定方法类似，在重复抽样或无限总体抽样条件下，估计总体比例置信区间的估计误差为$z_{\frac{\alpha}{2}}\sqrt{\frac{\pi(1-\pi)}{n}}$，$z_\frac{\alpha}{2}$的值、总体比例$\pi$和样本量$n$共同确定了估计误差的大小。一旦确定了置信水平$1-\alpha$，$z_{\frac{\alpha}{2}}$的值就确定了。由于总体比例的值是固定的，所以估计误差由样本量来确定，样本量越大，估计误差就越小，估计的精度也就越好。

所希望达到的估计误差为：

$$E = z_{\frac{\alpha}{2}}\sqrt{\frac{\pi(1-\pi)}{n}}$$

由此可以推导出重复抽样或无限总体抽样条件下确定样本量的公式：

$$n = \frac{(z_\frac{\alpha}{2})^2 \pi (1-\pi)}{E^2}$$

当$\pi$的值无法知道时，通常取使$\pi(1-\pi)$最大时的$0.5$。

案例

根据以往的生产统计，某种产品的合格率约为$90\%$，现要求估计误差为$5\%$，在$95\%$的置信
区间下，应抽取多少个产品作为样本？

已知：

$$\begin{aligned} \pi & = 90\% \\ E & = 5\% \\ z_{\frac{\alpha}{2}} & = 1.96 \\ n & = \frac{(z_\frac{\alpha}{2})^2 \pi (1-\pi)}{E^2} \\ & = \frac{1.96^2 \times 0.9 \times (1-0.9)}{0.05^2} \\ & = 138.3 \\ & \approx 139 \end{aligned}$$

Python计算

均值

一个总体均值的估计

大样本的估计

一家研究机构随机抽取40辆相同排气量的家用轿车，经测试得到每百公里的耗油量数据。构建该排气量轿车平均耗油量的90%的置信区间。

虽然总体方差未知，但为大样本，因此可用样本方差来代替，用正态分布构建置信区间。

示例代码：

import pandas as pd
import numpy as np
import scipy.stats as st

df = pd.read_csv('XXX.csv')
x = df['耗油量']

# confidence 为置信水平
int_arr = st.norm.interval(confidence=0.90, loc=np.mean(x), scale=st.sem(x))
print(int_arr)

运行结果：

(7.835886999819788, 8.099113000180214)

• scipy.stats包中的norm.interval，函数默认位置参数(均值)loc=0，尺度参数(标准差)scale=1，confidence为置信水平。

小样本的估计

从一批袋装食品中随机抽取25袋，测得每袋重量。假定食品重量服从正态分布，构建该批食品平均重量的置信区间，置信水平为95%。

总体服从正态分布但未知，由于是小样本，样本均值经标准化后服从自由度为$n-1$的t分布，

示例代码：

import pandas as pd
import numpy as np
import scipy.stats as st

df = pd.read_csv('XXX.csv')

# 置信水平
x = df['食品重量']

int_arr = st.t.interval(confidence=0.95, df=len(x) - 1, loc=np.mean(x), scale=st.sem(x))
print(int_arr)

运行结果：

(101.37482261947405, 109.34517738052598)

两个总体均值差的估计

独立大样本的估计

为研究男性和女性网上购物支出的差异，从某电商平台中随机抽取男女各50人，得到某个月的网购支出数据。构建男女平均支出差值的95%的置信区间。

示例代码：

import pandas as pd
import numpy as np
from scipy.stats import norm

df = pd.read_csv('XXX.csv')

x1 = df['女性支出']
x2 = df['男性支出']

xbar1 = x1.mean()
s1 = x1.std()
n1 = len(x1)

xbar2 = x2.mean()
s2 = x2.std()
n2 = len(x2)

interval = norm.interval(confidence=0.95, loc=(xbar1 - xbar2), scale=np.sqrt(s1 ** 2 / n1 + s2 ** 2 / n2))

print(interval)

运行结果：

(381.184439490999, 957.7155605090002)

独立小样本的估计

为估计两种方法组装产品所需时间的差异，分别对两种不同的组装方法各随机安排12名工人，统计每名工人组装一件产品所需的时间。假定两种方法组装产品的时间服从正态分布，以95%的置信水平构建两种方法组装产品所需平均时间差值的置信区间。

1. 假定$\sigma_1^2 = \sigma_2^2$
2. 假定$\sigma_1^2 \neq \sigma_2^2$

假定$\sigma_1^2 = \sigma_2^2$，示例代码：

import pandas as pd
from scipy.stats import t
from statsmodels.stats.weightstats import ttest_ind

data = pd.read_csv('XXX.csv')

x1 = data['方法一']
x2 = data['方法二']

xbar1 = x1.mean()
xbar2 = x2.mean()

# 计算方差的合并估计量
t_value, p_value, df = ttest_ind(x1=x1, x2=x2, alternative='two-sided', usevar='pooled')

interval = t.interval(confidence=0.95, df=df, loc=(xbar1 - xbar2), scale=(xbar1 - xbar2) / t_value)

print(interval)

运行结果：

(0.14029361395375695, 7.259706386046249)

假定$\sigma_1^2 \neq \sigma_2^2$，修改ttest_ind方法的usevar参数的值为unequal。示例代码：

import pandas as pd
from scipy.stats import t
from statsmodels.stats.weightstats import ttest_ind

data = pd.read_csv('XXX.csv')

x1 = data['方法一']
x2 = data['方法二']

xbar1 = x1.mean()
xbar2 = x2.mean()

# 计算方差的合并估计量
t_value, p_value, df = ttest_ind(x1=x1, x2=x2, alternative='two-sided', usevar='unequal')

interval = t.interval(confidence=0.95, df=df, loc=(xbar1 - xbar2), scale=(xbar1 - xbar2) / t_value)

print(interval)

运行结果：

(0.13842654466524218, 7.261573455334764)

配对样本的估计

由10名学生组成一个随机样本，让他们分别采用A和B两套试卷进行测试，统计所得分数。假定两套试卷的分数之差服从正态分布，构建两套试卷平均分数之差的95%的置信区间。

示例代码：

import pandas as pd
import numpy as np
from scipy.stats import t

df = pd.read_csv('XXX.csv')

x1 = df['试卷A']
x2 = df['试卷B']
d = x1 - x2

d_bar = d.mean()
sd = d.std()

interval = t.interval(confidence=0.95, df=len(d) - 1, loc=d_bar, scale=sd / np.sqrt(len(d)))

print(interval)

运行结果：

(6.327308257173503, 15.672691742826498)

比例

一个总体比例的估计

大样本的估计方法

某企业想要进行一项工作时间的改革，为征求员工对该项改革措施的意见，随机调查500人，其中325人赞成改革措施。用95%的置信水平估计赞成该项改革的人数比例的置信区间。

示例代码：

import numpy as np
from scipy.stats import norm

conf_level = 0.95
n = 500
x = 325
p = x / n

interval = norm.interval(confidence=conf_level, loc=p, scale=np.sqrt(p * (1 - p) / n))

print(interval)

运行结果：

(0.6081925393809212, 0.6918074606190788)

任意大小样本的估计方法

沿用上例，用95%的置信水平估计该企业员工中赞成该项改革的人数比例的置信区间。

示例代码：

import numpy as np
from scipy.stats import norm

conf_level = 0.95
n = 500 + 4
x = 325 + 2
p = x / n

interval = norm.interval(confidence=conf_level, loc=p, scale=np.sqrt(p * (1 - p) / n))

print(interval)

运行结果：

(0.6071357532950432, 0.6904832943240045)

两个总体比例差的估计

两个大样本的估计方法

在某档电视节目的收视率调查中随机调查500名女性观众，有225人收看了该节目；随机调查400名男性观众，有128人收看了该节目。用95%的置信水平估计女性与男性收视率差值的置信区间。

示例代码：

import numpy as np
from scipy.stats import norm

conf_level = 0.95
n1 = 500
n2 = 400
p1 = 225 / n1
p2 = 128 / n2

interval = norm.interval(confidence=conf_level, loc=(p1 - p2), scale=np.sqrt(p1 * (1 - p1) / n1 + p2 * (1 - p2) / n2))

print(interval)

运行结果：

(0.06682345597691185, 0.19317654402308815)

两个任意大小样本的估计方法

沿用上例，用95%的置信水平估计女性与男性收视率差值的置信区间。

示例代码：

import numpy as np
from scipy.stats import norm

conf_level = 0.95
n1 = 500 + 2
n2 = 400 + 2
p1 = (225 + 1) / n1
p2 = (128 + 1) / n2

interval = norm.interval(confidence=conf_level, loc=(p1 - p2), scale=np.sqrt(p1 * (1 - p1) / n1 + p2 * (1 - p2) / n2))

print(interval)

运行结果：

(0.0662439605945023, 0.1923634010038803)

方差

一个总体方差的估计

以95%的置信水平构建某种食品重量的方差和标准差的置信区间。

示例代码：

import pandas as pd
from scipy.stats import chi2

df = pd.read_csv('XXX.csv')
x = df['食品重量']

conf_level = 0.95
sigma2 = x.var()
n = len(x)

LCI = (n - 1) * sigma2 / chi2.ppf(q=(1 + conf_level) / 2, df=n - 1)
UCI = (n - 1) * sigma2 / chi2.ppf(q=(1 - conf_level) / 2, df=n - 1)

print(LCI, UCI)
print(pow(LCI, 1 / 2), pow(UCI, 1 / 2))

运行结果：

56.82897120865117 180.38810600433104
7.53849926766934 13.43086393365412

两个总体方差比的估计

以95%的置信水平构建两种方法组装产品所需时间方差比的置信区间。

示例代码：

import pandas as pd
from scipy.stats import f

df = pd.read_csv('XXX.csv')

x1 = df['方法一']
x2 = df['方法二']

conf_level = 0.95

var1 = x1.var()
var2 = x2.var()

n1 = len(x1)
n2 = len(x2)

LCI = (var1 / var2) / f.ppf(q=(1 + conf_level) / 2, dfn=n1 - 1, dfd=n2 - 1)
UCI = (var1 / var2) / f.ppf(q=(1 - conf_level) / 2, dfn=n1 - 1, dfd=n2 - 1)

print(LCI, UCI)

运行结果：

0.23788360619409207 2.8704427774446266