3.抽样分布

统计量

什么是统计量

统计量，我们在《1.概括性度量》就有提到过，只不过当时我们没说，这是统计量。

统计量的严格定义如下：
设$X_1,X_2,X_3,\cdots,X_n$是从总体$X$中抽取的容量为$n$的一个样本，如果由此样本构造一个函数$T(X_1,X_2,X_3,\cdots,X_n)$，不依赖于任何未知参数，则称函数$T(X_1,X_2,X_3,\cdots,X_n)$是一个统计量。

注意，上文的定义，有两个重点：

1. 由样本构造函数
2. 不依赖于任何未知参数

通常，$T(X_1,X_2,X_3,\cdots,X_n)$也被称为样本统计量。

统计量也是一个随机变量，只有通过抽样，获得样本的一组具体观测值$x_1,x_2,x_3,\cdots,x_n$时，代入$T$，计算得到$T(x_1,x_2,x_3,\cdots,x_n)$的数值，这时候，才会得到一个具体的统计量值。

例如，$X_1,X_2,X_3,\cdots,X_n$是从某总体$X$中抽取的一个样本，以下两个都是统计量。

$$\begin{aligned} \bar{X} & = \frac{1}{n} \sum_{i=1}^{n} X_i \\ S^2 & = \frac{1}{n-1} \sum_{i=1}^{n} (X_i - \bar{X})^2 \end{aligned}$$

但是，$\sum_{i=1}^{n}[X_i - E(X)]^2$，$[X_i - E(X)]/D(X)$都不是统计量，因为其中的$E(X)$和$D(X)$都是依赖于总体分布的未知参数。

常用统计量

通常，我们把数学期望及方差等概念用所谓"矩"的概念来描述。当$n$充分大时，有定理可以保证经验分布函数$F_n(x)$很靠近总体分布函数$F(X)$。因此，经验分布函数$F_n(x)$的各阶矩就反映了总体各阶矩的信息。

经验分布函数的各阶矩也被称为样本各阶矩。

常用的样本各阶矩及其函数就是实际应用中的具体统计量，例如：

1. $\bar{X} = \frac{1}{n}\sum_{i=1}^{n}X_i$，样本均值，反映总体$X$的数学期望的信息。
2. $S^2 = \frac{1}{n-1}\sum_{i=1}^{n}(X_i - \bar{X})^2$，样本方差，反映总体$X$的方差的信息。
3. $V=\frac{S}{\bar{X}}$，样本变异系数，反映总体变异系数$C$的信息，$C=\frac{\sqrt{D(X)}}{E(X)}$，反映出随机变量在以它的均值为单位时取值的离散程度。
   此统计量消除了均值不同对不同总体的离散程度的影响，常用来刻画均值不同时不同总体的离散程度。
4. $m_k = \frac{1}{n}\sum_{i=1}^n X_i^k$，$m_k$被称为样本的$k$阶矩，反映总体的$k$阶矩。
   对于$m_1$，有$m_1 = \frac{1}{n}\sum_{i=1}^n X_i$，即$m_1$就是样本均值。
5. $v_k = \frac{1}{n-1}\sum_{i=1}^n(X_i - \bar{X})^k$，$v_k$被称为样本的$k$阶中心矩，反映总体的$k$阶中心矩。
   对于$v_2$，有$v_2 = \frac{1}{n-1}\sum_{i=1}^n(X_i - \bar{X})^2$，即$v_2$就是样本方差。
6. 样本偏度，关于样本偏度的计算方法有三种，具体可以参考《1.概括性度量》。
   样本偏度反映总体的偏度。
   偏度描述了随机变量密度函数曲线在众数(密度函数在这一点达到最大值)两边的偏斜性。
   正态随机变量$X \sim N(\mu,\sigma^2)$的偏度等于$0$。
7. 样本峰度，关于样本峰度的计算方法有三种，具体可以参考《1.概括性度量》。
   样本峰度反映总体的峰度。
   峰度反映了密度函数曲线在众数附近的"峰"的尖峭程度。
   正态随机变量$X \sim N(\mu,\sigma^2)$的峰度等于$0$。

三个重要分布

卡方分布

什么是卡方分布

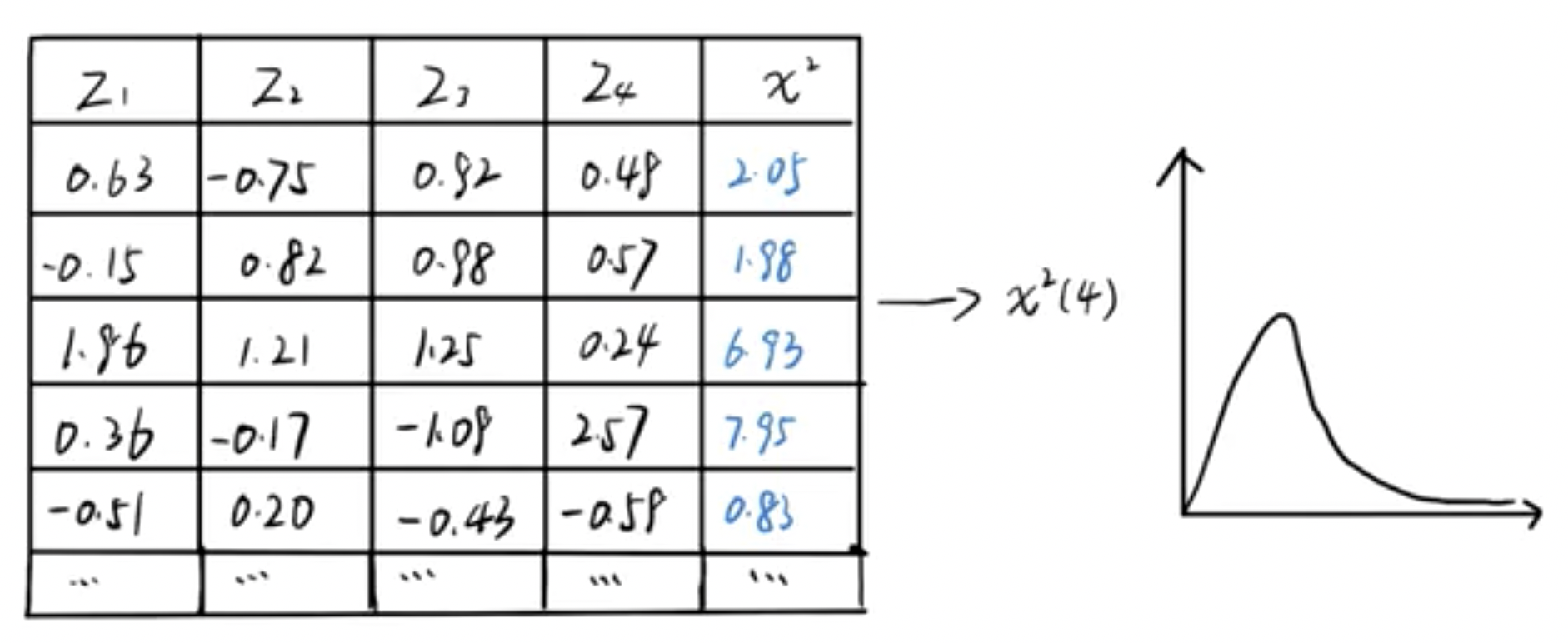
设随机变量$X_1,X_2,X_3,\cdots,X_n$相互独立，且$X(i=1,2,3,\cdots,n)$服从标准正态分布$N(0,1)$，则它们的平方和$\sum_{i=0}^{n}X_i^2$服从自由度为$n$的$\chi^2$分布(卡方分布)。

自由度，我们可以理解为独立变量的个数。

例如，如果我们认为$Z_1$、$Z_2$、$Z_3$、$Z_4$是4个独立的变量，则我们认为其构成的$chi^2$分布的自由度为$4$，即$chi^2(4)$。

关于$\chi^2$分布的密度函数较为复杂，本文不讨论。
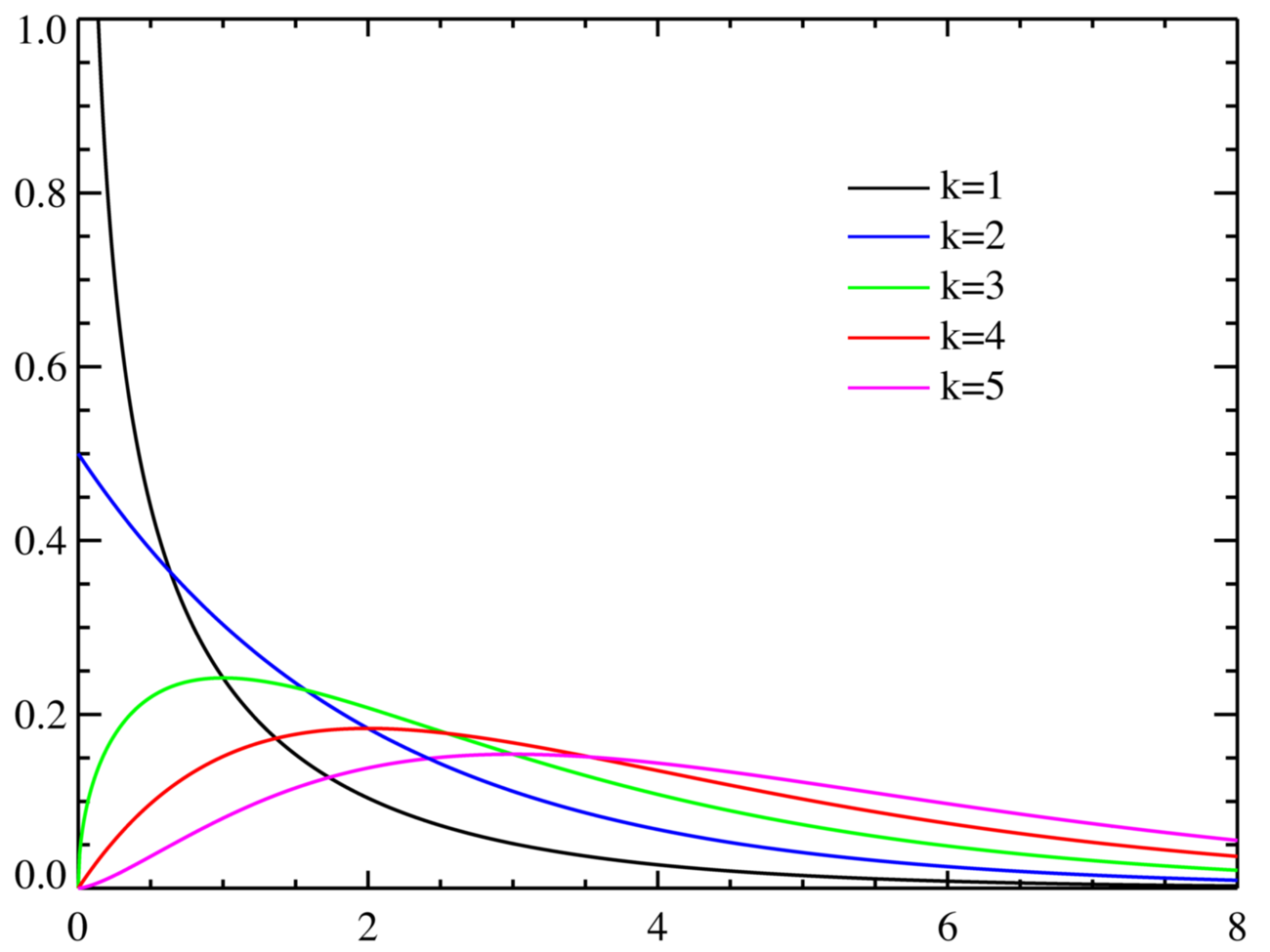
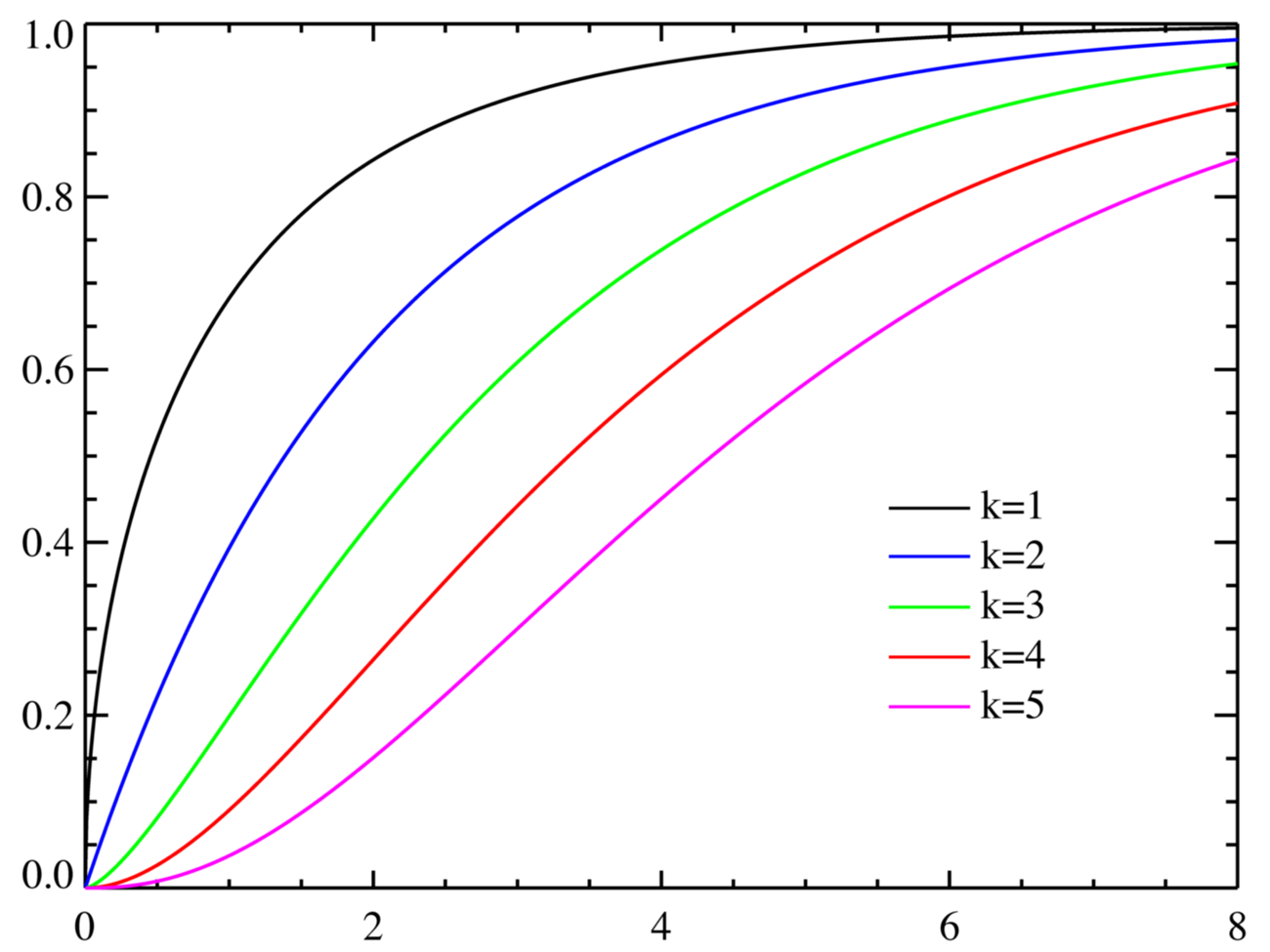
下面给出当$n=1$，$n=2$，$n=3$，$n=4$，$n=5$时，$\chi^2$分布的概率密度函数曲线和累积分布函数曲线。

概率密度函数曲线

累积分布函数曲线

性质

数学期望

$\chi^2$分布的数学期望：$E(\chi^2)=n$。

方差

$\chi^2$分布的方差：$D(\chi^2)=2n$。

可加性

$\chi^2$分布具有可加性，即若$\chi_{1}^{2}\sim\chi^2(n_1)$，$\chi_{2}^{2}\sim\chi^2(n_2)$，且独立，则有

$$\chi_{1}^{2} + \chi_{2}^{2} \sim \chi^2(n_1 + n_2)$$

自由度趋近于无穷时

当$n \rightarrow + \infty$时，$\chi^2$分布的极限分布是正态分布。

推论

设$X_1,X_2,X_3,\cdots,X_n$是来自正态总体$N(\mu,\sigma^2)$的一个样本，其样本均值和样本方差分别为

$$\begin{aligned} \bar{X} & = \frac{1}{n} \sum_{i=1}^{n} X_i \\ S^2 & = \frac{1}{n-1} \sum_{i=1}^{n} (X_1 - \bar{X})^2 \end{aligned}$$

则有：

1. $\bar{X}$与$S^2$相互独立
2. $\bar{X} \sim N(\mu,\frac{\sigma^2}{n})$
3. $\frac{(n-1)S^2}{\sigma^2} \sim \chi^2(n-1)$

t分布

什么是t分布

t分布(t distribution)，也被称为学生氏分布，是戈塞特(W.S.Gosset)于1908年在一篇以"Student"(学生)为笔名的论文中首次提出的。

设随机变量$X \sim N(0,1)$，$Y \sim \chi^2(n)$，且$X$与$Y$独立，则

$t=\frac{X}{\sqrt{\frac{Y}{n}}}$

该分布称为t分布，记为$t(n)$，其中，$n$为自由度。

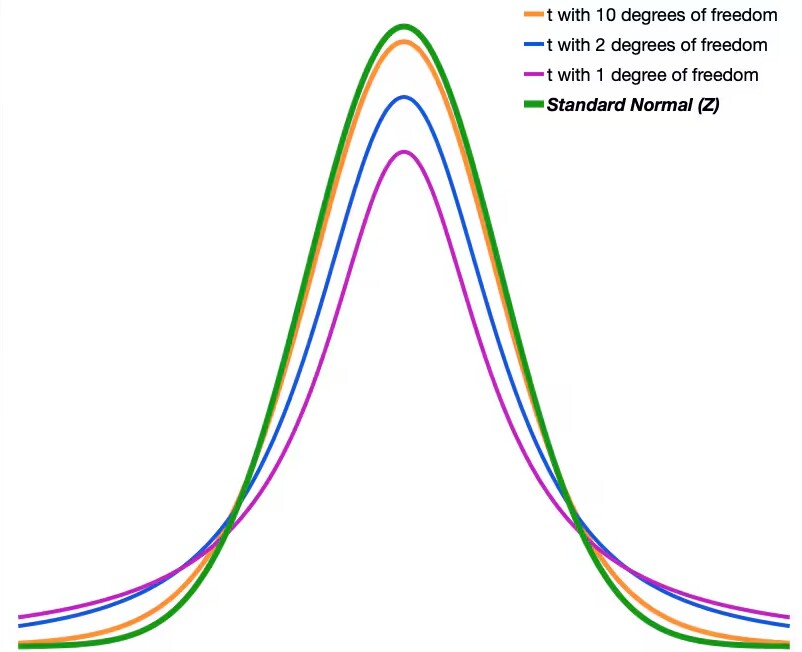
t分布的密度函数曲线如图。
与标准正态分布$N(0,1)$的密度函数曲线非常相似，都是单峰偶函数。只是$t(n)$的密度函数的两侧尾部要比$N(O,1)$的两侧尾部粗一些。$t(n)$的方差比$N(0,1)$的方差大一些。

性质

数学期望

当$n \geq 2$时，t分布的数学期望$E(t)=0$。

方差

当$n \geq 3$时，t分布的方差$D(t)=\frac{n}{n-2}$

自由度趋近于无穷时

随着自由度$n$的增加，t分布的密度函数越来越接近标准正态分布$N(0,1)$的密度函数。

在实际应用中，一般当$n \geq 30$时，t分布与标准正态分布$N(0,1)$就非常接近。

推论

设$X_1$，$X_2$，$X_3$，$\cdots$，$X_n$是来自正态分布$N(\mu,\sigma^2)$的一个样本，$\bar{X}$和$S^2$分别是该样本的样本均值与样本方差，
$\bar{X} = \frac{1}{n} \sum_{i=1}^{n}X_i$，
$S^2=\frac{1}{n-1}\sum_{i=1}^{n}(X_i-\bar{X})^2$，
则

$$\frac{\sqrt{n}(\bar{X}-\mu)}{S} \sim t(n-1)$$

称为服从自由度为$(n-1)$的t分布。

案例

设$X$和$Y$是两个相互独立的总体，$X \sim N(\mu_1,\sigma^2)$，$Y \sim N(\mu_2,\sigma^2)$，$X_1$，$X_2$，$X_3$，$\cdots$，$X_n$是来自$X$的一个样本，$Y_1$，$Y_2$，$Y_3$，$\cdots$，$Y_m$是来自$Y$的一个样本，记

$$\begin{aligned} \bar{X} & = \frac{1}{n}\sum_{i=1}^{n}X_i \\ \bar{Y} & = \frac{1}{m}\sum_{i=1}^{m}Y_i \\ S_x^2 & = \frac{1}{n-1}\sum_{i=1}^{n}(X_i - \bar{X})^2 \\ S_y^2 & = \frac{1}{m-1}\sum_{i=1}^{m}(Y_i - \bar{Y})^2 \\ S_{xy}^2 & = \frac{(n-1)S_x^2 + (m-1)S_y^2}{n+m-2} \end{aligned}$$

则

$$\frac{(\bar{X} - \bar{Y}) - (\mu_1 - \mu_2)}{S_{xy}}\sqrt{\frac{mn}{m+n}} \sim t(n+m-2)$$

F分布

什么是F分布

F分布(F distribution)是统计学家费希尔首先提出的。F分布有着广泛的应用，在方差分析、回归方程的显著性检验中有重要的地位。

设随机变量$Y$与$Z$相互独立，且$Y$和$Z$分别服从自由度为$m$和$n$的$\chi^2$分布，随机变量$X$有如下表达式：

$$X = \frac{(\frac{Y}{m})}{(\frac{Z}{n})} = \frac{nY}{mZ}$$

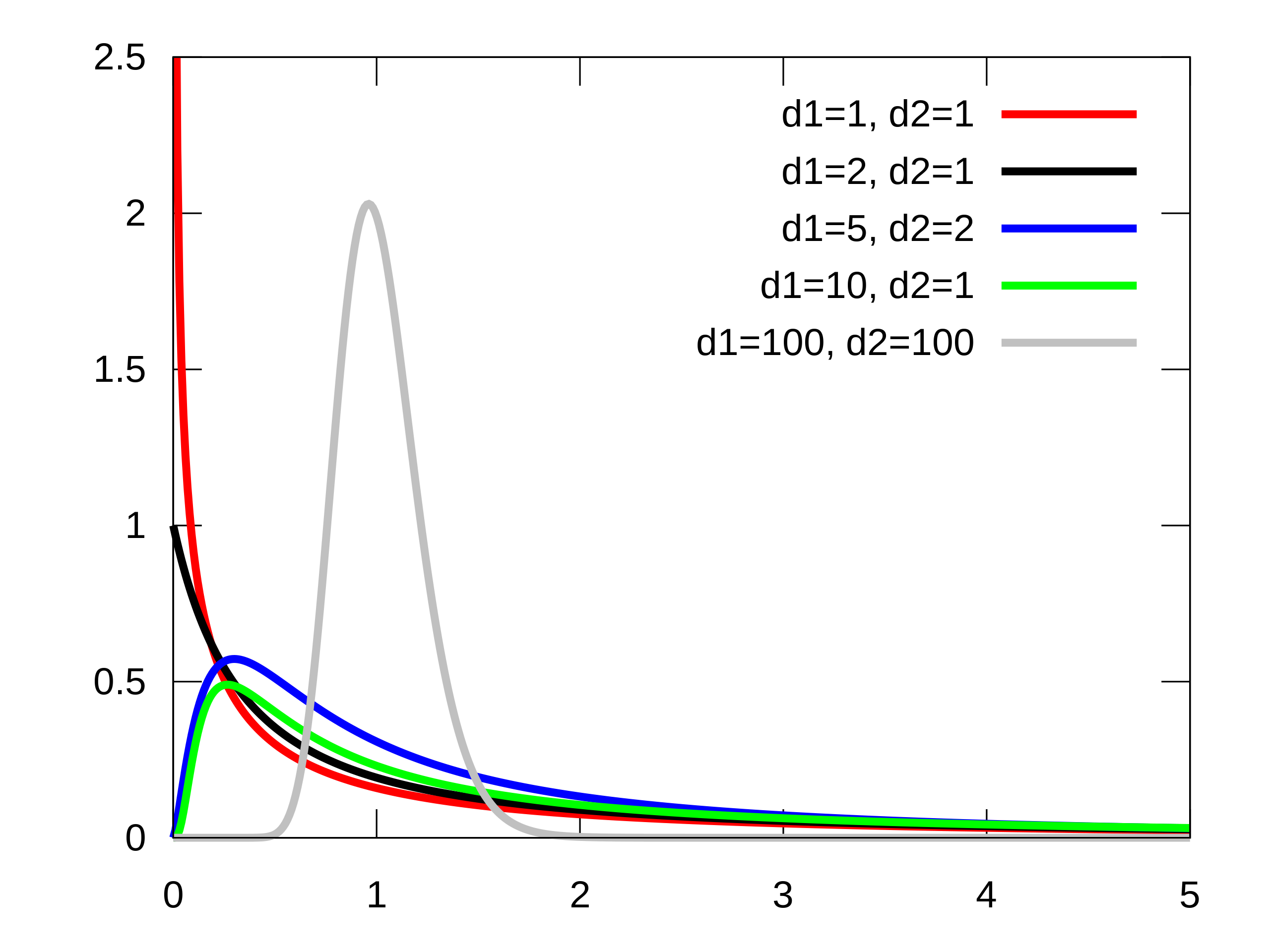
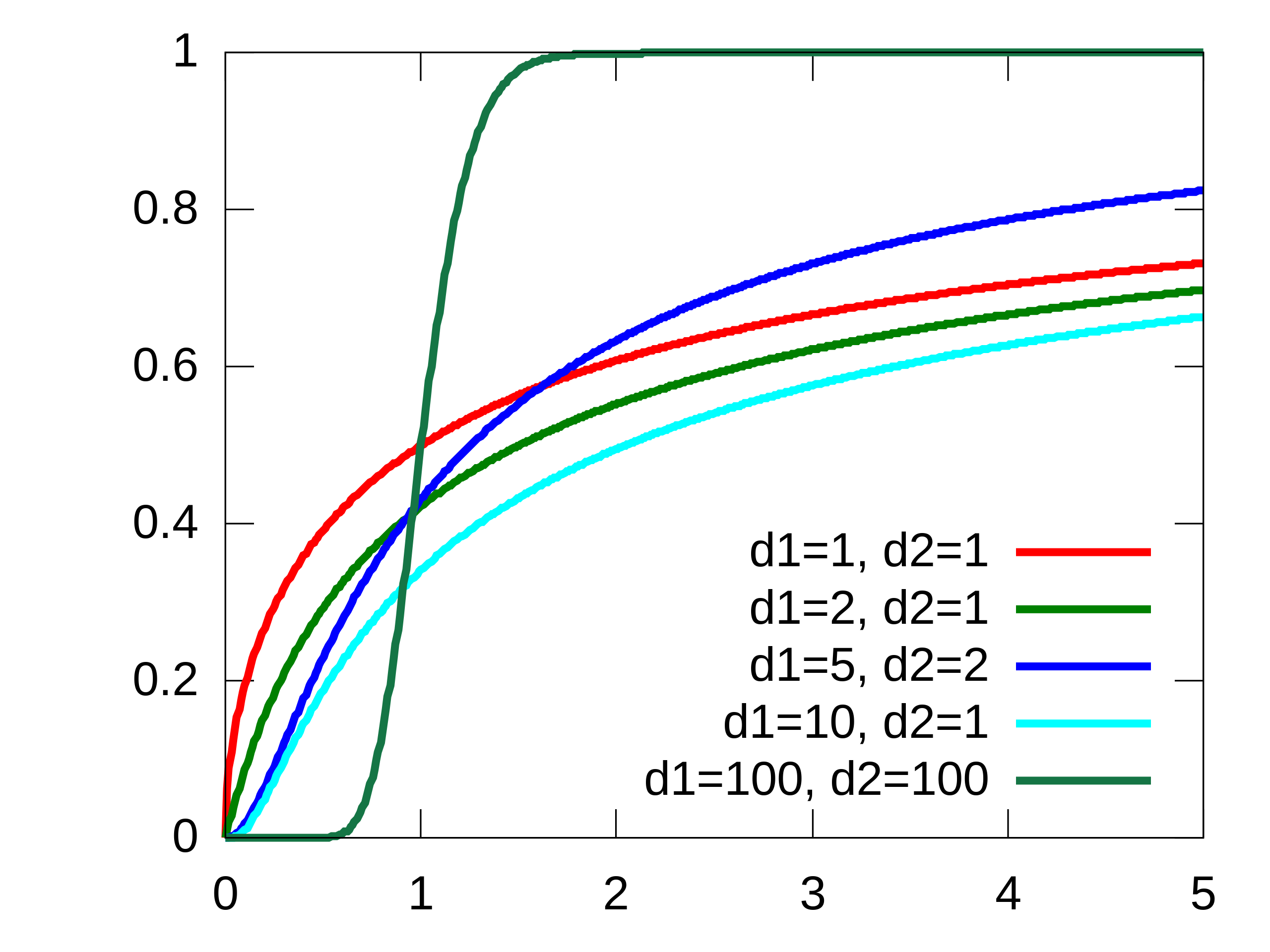
则称$X$服从第一自由度为$m$，第二自由度为$n$的F分布，记为$F(m,n)$，简记$X \sim F(m,n)$。F分布的密度函数的图形如图所示。

性质

期望和方差

设随机变量$X$服从$F(m,n)$分布，则数学期望和方差分别为：

$$\begin{aligned} E(X) & = \frac{n}{n-2},\quad n > 2 \\ D(X) & = \frac{2n^2(m+n-2)}{m(n-2)(n-4)},\quad n > 4 \end{aligned}$$

两个自由度的位置

若$X \sim F(m,n)$，则$\frac{1}{X} \sim F(n,m)$

和t分布的关系

F分布与t分布还存在如下关系：如果随机变量$X \sim t(n)$，则$X^2 \sim F(1,n)$。

推论

设$X_1$，$X_2$，$X_3$，$\cdots$，$X_m$是来自正态分布$N(\mu_1,\sigma_1^2)$的样本，$Y_1$，$Y_2$，$Y_3$，$\cdots$，$Y_n$是来自正态分布$N(\mu_2,\sigma_2^2)$的样本，且这两个样本相互独立，记

$$\begin{aligned} S_X^2 & = \frac{1}{m-1}\sum_{i=1}^{m}(X_i - \bar{X})^2 \\ S_Y^2 & = \frac{1}{n-1}\sum_{i=1}^{n}(Y_i - \bar{Y})^2 \end{aligned}$$

其中

$$\begin{aligned} \bar{X} & = \frac{1}{m}\sum_{i=1}^{m}X_i \\ \bar{Y} & = \frac{1}{n}\sum_{i=1}^{n}Y_i \end{aligned}$$

则有

$$F = \frac{(\frac{S_X^2}{\sigma_1^2})}{(\frac{S_Y^2}{\sigma_2^2})} \sim F(m-1,n-1)$$

特别的，若$\sigma_1^2=\sigma_2^2$，则

$$F = \frac{S_X^2}{S_Y^2} \sim F(m-1,n-1)$$

中心极限定理

抽样分布

1. 抽样分布
   抽样分布(sampling distribution)，重复抽样条件下，样本统计量的所有可能取值及概率分布。是样本统计自身的分布量的分布。
2. 精确的抽样分布
   在总体$X$的分布类型已知时，若对任一自然数$n$，都能导出统计量$T=T(X_1,X_2,X_3,\cdots,X_n)$的分布的数学表达式，这种分布称为精确的抽样分布。
   精确的抽样分布大多是在正态总体情况下得到的，例如上文我们讨论的$\chi^2$分布、t分布和F分布，都属于精确的抽样分布。
3. 浙近分布
   样本容量无限增大时，统计量$T(X_1,X_2,X_3,\cdots,X_n)$的极限分布。
   在实际应用中，是$n$较大时抽样分布的一种近似。
4. 随机模拟获得的近似分布
   针对复杂问题，利用计算机的随机模拟技术获得的近似抽样分布。
   (这个思路，我们在强化学习中有用到。关于强化学习，可以参考《强化学习浅谈及其Python实现》)。

总体分布为正态分布

设$X_1$，$X_2$，$X_3$，$\cdots$，$X_n$为从某一总体中抽出的随机样本，即$X_1$，$X_2$，$X_3$，$\cdots$，$X_n$为互相独立且与总体有相同分布的随机变量。

当总体分布为正态分布$N(\mu,\sigma^2)$时，可以得到下面的结果：

$\bar{X}$的抽样分布(sampling distribution)仍为正态分布，$\bar{X}$的数学期望为$\mu$，方差为$\frac{\sigma^2}{n}$，即

$$\bar{X} \sim N(\mu,\frac{\sigma^2}{n})$$

$\bar{X}$的期望值与总体均值相同，而方差则缩小为总体方差的$\frac{1}{n}$。也就是说当用样本均值$\bar{X}$去估计总体均值$\mu$时，平均来说没有偏差(这一点称为无偏性)；当$n$越来越大时，$\bar{X}$的离散程度越来越小，即用$\bar{X}$估计$\mu$越来越准确。

什么是中心极限定理

上文我们是假定总体的分布是正态分布，那么对于非正态分布呢？

中心极限定理(central limit theorem)：设从均值为$\mu$、方差为$\sigma^2$(有限)的任意一个总体中抽取样本量为$n$的样本，当$n$充分大时，样本均值$\bar{X}$的抽样分布近似服从均值为$\mu$，方差为$\frac{\sigma^2}{n}$的正态分布。

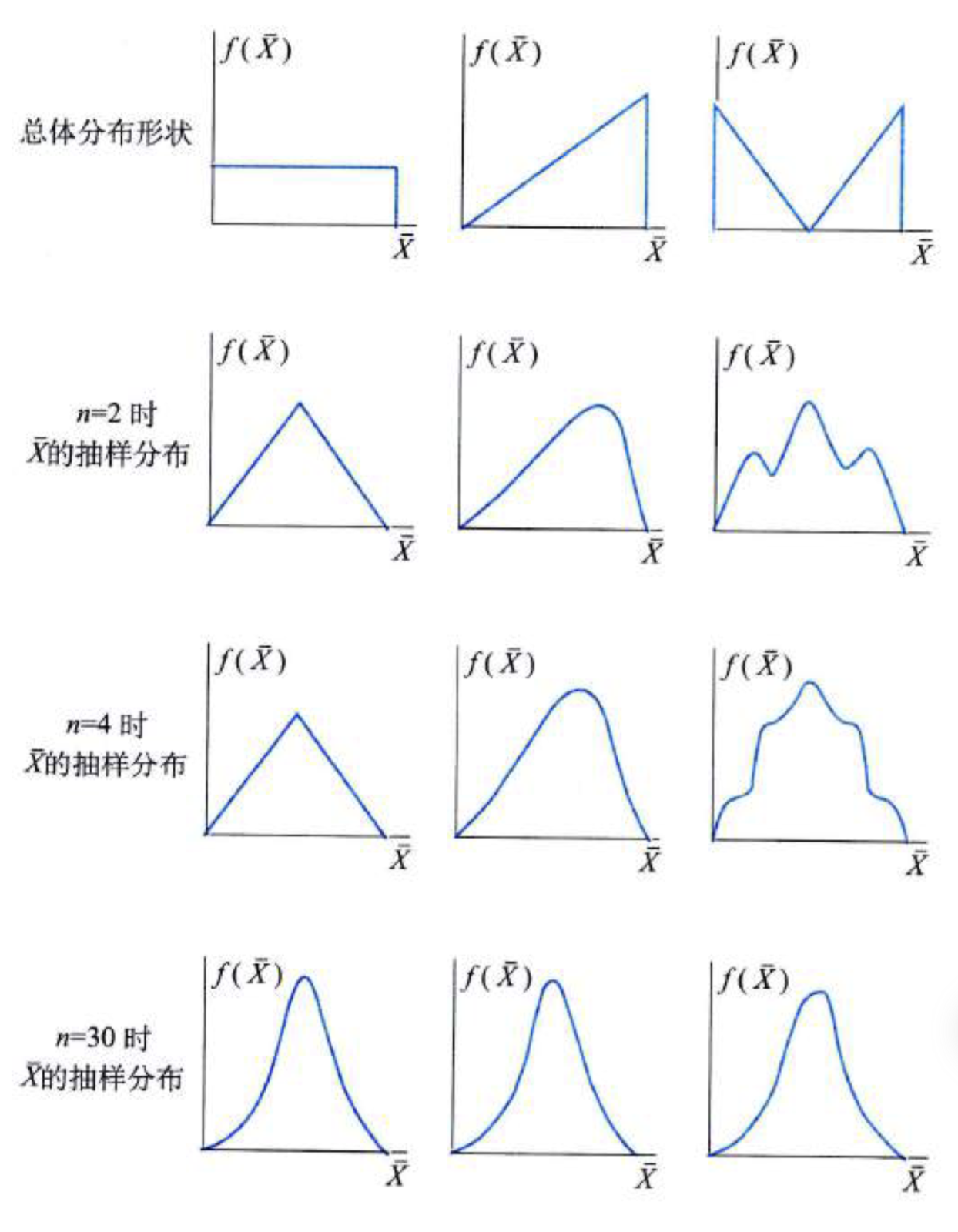
如图描述$\bar{X}$的抽样分布趋于正态分布的过程。

中心极限定理要求$n$必须充分大，那么多大才叫充分大呢？
这与总体的分布形状有关。总体偏离正态越远，则要求$n$越大。

然而在实际应用中，总体的分布未知。一般，我们常要求$n \geq 30$。需要注意的是，$30$只是一个经验值。

案例

案例一

设从一个均值$\mu=10$、标准差$\sigma=0.6$的总体中随机选取容量$n=36$的样本。假定该总体不是很偏，则有：

根据中心极限定理，不论总体的分布是什么形状，在假定总体分布不是很偏的情形下，当从总体中随机选取$n=36$的样本时，样本均值$\bar{X}$近似服从均值为$10$、方差为$\frac{\sigma^2}{n}=\frac{0.6^2}{36}=0.01$的正态分布，即$\bar{X} \sim N(10,0.01)$。

案例二

某汽车电瓶生产厂声称其生产的电瓶具有均值为$60$个月、标准差为$6$个月的寿命分布。现假设质检部门决定检验该厂的说法是否准确，为此随机抽取了$50$个该厂生产的电瓶进行寿命试验。

1. 假定厂方说法是正确的，试描述$50$个电瓶的平均寿命的抽样分布。
2. 假定厂方说法是正确的，则$50$个样品组成的样本的平均寿命不超过$57$个月的概率为多少？

根据中心极限定理可以推出，$50$个电瓶的平均寿命近似服从正态分布，其均值为$60$，方差为$\frac{\sigma^2}{n}=\frac{6^2}{n}=\frac{36}{50}=0.72$的正态分布。即$\bar{X} \sim N(60,0.72)$。

如果厂方说法是正确的，则观察到$50$个电瓶的平均寿命不超过57个月的概率为：

$$\begin{aligned} P(\bar{X} \leq 57) & = P(\frac{\bar{X} - 60}{\sqrt{0.72}} \leq \frac{57 - 60}{\sqrt{0.72}}) \\ & = P(Z \leq \frac{57-60}{\sqrt{0.72}}) \\ & = P(Z \leq -3.529) \\ & = 1 - P(Z \leq 3.529) \\ & = 1 - \Phi(3.529) \\ & = 1 - 0.9998 \\ & = 0.0002 \end{aligned}$$

其他抽样分布

样本比例的抽样分布

例如，我们假定总体中对具有某一产品的喜好比例为$pi$，在此条件下去研究从总体中随机抽取$n$个个体进行调查时，喜好某一产品的个体数$X$的概率。

例如，我们要估计在总体中，喜好某一产品的比例$\pi$。我们抽取了$n$个样本，即样本数为$n$，其中喜好某一产品的数量为$X$。所以，我们用样本比$\hat{p}=\frac{X}{n}$，来估计总体的比例$\pi$。

根据二项分布的原理和渐近分布的理论，我们知道，当$n$充分大时，$\hat{p}$的分布近似服从均值为$\pi$、方差为$\frac{\pi(1-\pi)}{n}$的正态分布，即

$$\hat{p} \sim N(\pi,\frac{\pi(1-\pi)}{n})$$

• 一般认为，当$np \geq 5$，并且$n(1-p) \geq 5$，认为$n$充分大。

两样本均值差的抽样分布

设$\bar{X}_1$是独立抽样自总体$X_1 \sim N(\mu_1,\sigma_1^2)$的一个样本容量为$n_1$的样本均值，$\bar{X}_2$是独立抽样自总体$X_2 \sim N(\mu_2,\sigma_2^2)$的一个样本容量为$n_2$的样本均值，则有

$$\begin{aligned} E(\bar{X}_1 - \bar{X}_2) & = E(\bar{X}_1) - E(\bar{X}_2) = \mu_1 - \mu_2 \\ D(\bar{X}_1 - \bar{X}_2) & = D(\bar{X}_1) + D(\bar{X}_2) = \frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2} \end{aligned}$$

如果两个样本均为正态分布，则$\bar{X}_1 - \bar{X}_2$也为正态分布，其均值和方差就符合上述均值和方差的计算公式，即

$$\bar{X}_1 - \bar{X}_2 \sim N(\mu_1 - \mu_2,\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2})$$

假设：甲、乙两所著名高校在某年录取新生时，甲校的平均分为$655$分，且服从正态分布，标准差为$20$分；乙校的平均分为$625$分，也是正态分布，标准差为$25$分。现从甲、乙两校各随机抽取$8$名新生计算其平均分数，出现甲校比乙校的平均分低的可能性有多大？

因为两个总体均为正态分布，所以$8$名新生的平均成绩$\bar{X}_1$和$\bar{X}_2$也分别为正态分布，$\bar{X}_1 - \bar{X}_2$也为正态分布，且

$$\bar{X}_1 - \bar{X}_2 \sim N(\mu_1 - \mu_2,\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2})$$

甲校比乙校的平均分低，即$\bar{X}_1 - \bar{X}_2 \leq 0$，即求$P((\bar{X}_1 - \bar{X}_2) \leq 0)$。

两样本比例差的抽样分布

设分别从具有参数为$\pi_1$和参数$\pi_2$的二项总体中抽取包含$n_1$个观测值和$n_2$个观测值的独立样本，则两个样本比例差的抽样分布为

$$\hat{p}_1 - \hat{p}_2 = \frac{X_1}{n_1} - \frac{X_2}{n_2}$$

具有以下性质：

1. $E(\hat{p}_1 - \hat{p}_2) = \pi_1 - \pi_2$
2. $D(\hat{p}_1 - \hat{p}_2) = \frac{\pi_1(1-\pi_1)}{n_1} + \frac{\pi_2(1 - \pi_2)}{n_2}$
3. 当$n_1$和$n_2$很大时，$(\hat{p}_1 - \hat{p}_2)$的抽样分布近似为正态分布，其均值与方差为上述计算公式，即：

$$p_1 - p_2 \sim N(\pi_1 - \pi_2,\frac{\pi_1(1-\pi_1)}{n_1} + \frac{\pi_2(1 - \pi_2)}{n_2})$$

样本方差的抽样分布

样本方差的抽样分布，也就是上文讨论的$\chi^2$分布的推论中的$\frac{(n-1)S^2}{\sigma^2} \sim \chi^2(n-1)$。

两样本方差比的抽样分布

两样本方差比的抽样分布，也就是上文讨论的F分布的推论。

Python计算

卡方分布

计算：

1. 自由度为$15$，$\chi^2$值小于等于$15$的概率
2. 自由度为$25$，$\chi^2$值大于$15$的概率
3. 自由度为$10$，$\chi^2$分布右尾概率为$0.05$时的分位数

示例代码：

from scipy.stats import chi2

# 自由度为15，卡方值小于等于10的概率
p1 = chi2.cdf(10, df=15)
# 自由度为25，卡方值大于15的概率
p2 = 1 - chi2.cdf(15, df=25)
# 自由度为10，卡方分布右尾概率为0.05时的分位数
q = chi2.ppf(0.95, df=10)

print(p1)
print(p2)
print(q)

运行结果：

0.18026008049639844
0.9413825679762463
18.307038053275146

t分布

计算：

1. 自由度为$10$，t值小于$-2$的概率
2. 自由度为$15$，t值大于$3$的概率
3. 自由度为$25$，t分布右尾概率$0.025$时的t值。

示例代码：

from scipy.stats import t

# 自由度为10，t值小于等于-2的概率
p1 = t.cdf(-2, df=10)
# 自由度为15，t值大于3的概率
p2 = 1 - t.cdf(3, df=15)
# 自由度为25,t分布右尾概率为0.025时的t值
q = t.ppf(0.975, df=25)

print(p1)
print(p2)
print(q)

运行结果：

0.036694017385370196
0.004486368738611635
2.059538552753294

F分布

计算：

1. 分子自由度为$10$，分母自由度为$8$，F值小于$3$的概率
2. 分子自由度为$18$，分母自由度为$15$，F值大于$2.5$的概率
3. 分子自由度为$25$，分母自由度为$20$，F分布累积概率为$0.95$时的F值

示例代码：

from scipy.stats import f

# df_1=10，df_2=8，F值小于等于3的概率
p1 = f.cdf(3, dfn=10, dfd=8)
# df_1=18，df_2=15，F值大于2.5的概率
p2 = 1 - f.cdf(2.5, dfn=18, dfd=15)
# df_1=25，df_2=20，F分布累积概率为0.95时的值
q = f.ppf(0.95, dfn=25, dfd=20)

print(p1)
print(p2)
print(q)

运行结果：

0.9335491372878875
0.03944962943005237
2.073920163193128