概括性度量，即数据的分布特征，可以从三个方面进行测度和描述：

中央趋势
离散程度
分布的形状

中央趋势

中央趋势，central tendency，有些资料译作"集中趋势"，我认为更好的翻译是中央趋势，“集中趋势"容易被误认为是"向某处集中的趋势”。

中央趋势描述的是数据的中心位置，测度中央趋势的统计量主要有

平均数
中位数
四分位数
众数

平均数

什么是平均数

平均数(mean)，也称均值，是一组数据相加后除以数据的个数得到的结果，平均数是度量数据集中趋势的常用统计量，在参数估计和假设检验中经常用到。

平均数容易收到极端值的影响。

平均数还具有两个数学性质：

各变量值与平均数的离差之和等于零。
各变量值与平均数的离差平方和最小。

样本平均数

假设存在一组样本数据， $x_1,x_2,x_3,\cdots,x_n$ ，样本量(样本数据的个数)为 $n$ ，样本平均数用 $\bar{x}$ 表示，则有：

$\begin{aligned} \bar{x} & = \frac{x_1 + x_2 + x_3 + \cdots + x_n}{n} \\ & = \frac{\sum_{i=1}^n x_i}{n} \end{aligned}$

总体平均数

什么是总体平均数

上文，我们专门强调了样本数据，如果存在的是总体数据，则该平均数被称为总体平均数。

假设存在总体的全部数据 $x_1,x_2,x_3,\cdots,x_N$ ，总体平均数用 $\mu$ 表示，其计算公式如下：

$\begin{aligned} \mu & = \frac{x_1 + x_2 + x_3 + \cdots + x_N}{N} \\ & = \frac{\sum_{i=1}^N x_i}{N} \end{aligned}$

和样本平均数的关系

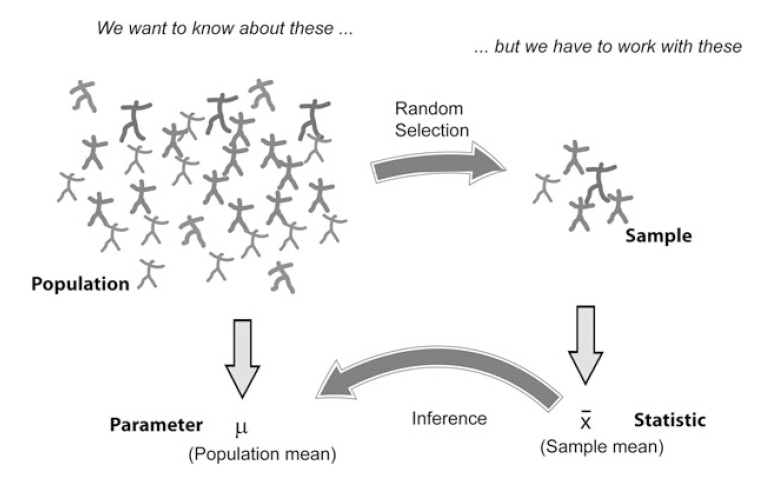
需要注意的是，无论是总体平均数，还是样本平均数，其实描述的都是总体的特征，样本平均数，不过是一个统计推断值，是从样本中获得信息以估计来自总体的参数。之间的关系如下

加权平均数

上述"样本平均数"和"总体平均数"的式子，都被称为简单平均数(simple mean)，与之对应的是加权平均数(weighted mean)。

在样本加权平均数中，样本中每一个数字都有一个权重，计算公式为：

$\begin{aligned} \bar{x} & = \frac{m_1 f_1 + m_2 f_2 + m_3 f_3 + \cdots + m_n f_n}{f_1 + f_2 + f_3 + \cdots + f_n} \\ & = \frac{\sum_{i=1}^n m_f f_i}{\sum_{i=1}^n f_i} \end{aligned}$

同样，存在总体的加权平均数，计算公式为：

$\begin{aligned} \mu & = \frac{m_1 f_1 + m_2 f_2 + m_3 f_3 + \cdots + m_N f_N}{f_1 + f_2 + f_3 + \cdots + f_N} \\ & = \frac{\sum_{i=1}^N m_f f_i}{\sum_{i=1}^N f_i} \end{aligned}$

其他几种平均数

几何平均数

几何平均数(geometric mean)是 $n$ 个变量值乘积的 $n$ 次方根，用 $G$ 表示，计算公式为：

$\begin{aligned} G & = \sqrt[n]{x_1 x_2 x_3 \cdots x_n} \\ & = \sqrt[n]{\prod_{i=1}^{n}x_i} \end{aligned}$

$\prod$ 是连乘符号
当数据中出现零值或负值时，不宜计算几何平均数。

几何平均数适用于计算平均比率，当我们确认变量值本身是比率形式时，采用几何平均法计算平均比率更为合理。在实践中，几何平均数主要用于计算现象的平均增长率。

例如，假设存在一个基金，该基金在连续三年的收益率分别为 $20\%$ ， $-10\%$ ，和 $30\%$ ，即比率分别为 $1.2$ ， $0.9$ ， $1.3$ 。如果我们用算术均值评估这三年投资的回报率，会因为没有考虑到复利的效应而出现失真，而几何平均数则更具有代表性。

当各比率数值差别不大时，算术平均和几何平均的结果较为接近；当各比率数值相差较大时，算术平均和几何平均结果的差别则很明显。

调和平均数

调和平均数(harmonic mean)，将所有数值取倒数并求其算术平均数后，再将此算术平均数取倒数而得，其结果等于数值的个数除以数值倒数的总和。

$\begin{aligned} H & = \frac{n}{\frac{1}{x_1} + \frac{1}{x_2} + \frac{1}{x_3} + \cdots + \frac{1}{x_n}} \\ H & = \frac{n}{\sum _{i=1}^{n}{\frac{1}{x_i}}} \end{aligned}$

分位数

一组数据从小到大排序后，找出排在某个位置上的数值，并用该数值代表数据水平的高低，则这些位置上的数值就是相应的分位数(quantile)，包括：中位数、四分位数等。

中位数

中位数(median)，一组数据排序后处在中间位置上的数值，一般用 $M_e$ 表示。

计算中位数时，先对数据从小到大进行排序，然后确定中位数的位置，最后确定中位数的具体数值。如果位置是整数值，中位数就是该位置所对应的数值；如果位置是整数加0.5的数值，中位数就是该位置两侧值的平均值。

中位数不容易受极端值的影响。

四分位数

四分位数(quartile)，一组数据排序后处于 $25\%$ 和 $75\%$ 位置上的数。

计算四分位数时，首先对数据进行排序，然后确定四分位数所在的位置，该位置上的数值就是四分位数。如果位置是整数，四分位数就是该位置对应的数值；如果是在整数加0.5的位置上，则取该位置两侧数值的平均数；如果是在整数加0.25或0.75的位置上，则四分位数等于该位置前面的数值加上按比例分摊的位置两侧数值的差值。

与中位数不同的是，在实践中，四分位数位置的确定方法有多种，每种方法得到的结果可能会有一定差异，例如：

$Q_{25\%}\text{位置} = \frac{n+1}{4}$ ， $Q_{75\%}\text{位置} = \frac{3(n+1)}{4}$
$Q_{25\%}\text{位置} = \frac{n+3}{4}$ ， $Q_{75\%}\text{位置} = \frac{3n+1}{4}$

四分位数不容易受极端值的影响。

众数

众数(mode)是一组数据中出现频数最多的数值，用 $M_o$ 表示。

从分布的角度看，众数是一组数据分布的峰值点所对应的数值。如果数据的分布没有明显的峰值，众数可能不存在；如果有两个或多个峰值，也可以有两个或多个众数。

众数的特点有：

不易受极端值的影响。
只有在数据量较大时众数才有意义。

比较

关系

从分布的角度看，平均数则是全部数据的算术平均，中位数是处于一组数据中间位置上的值，众数是一组数据分布的最高峰值。
因此，对于具有单峰分布的大多数数据而言，之间具有以下关系：

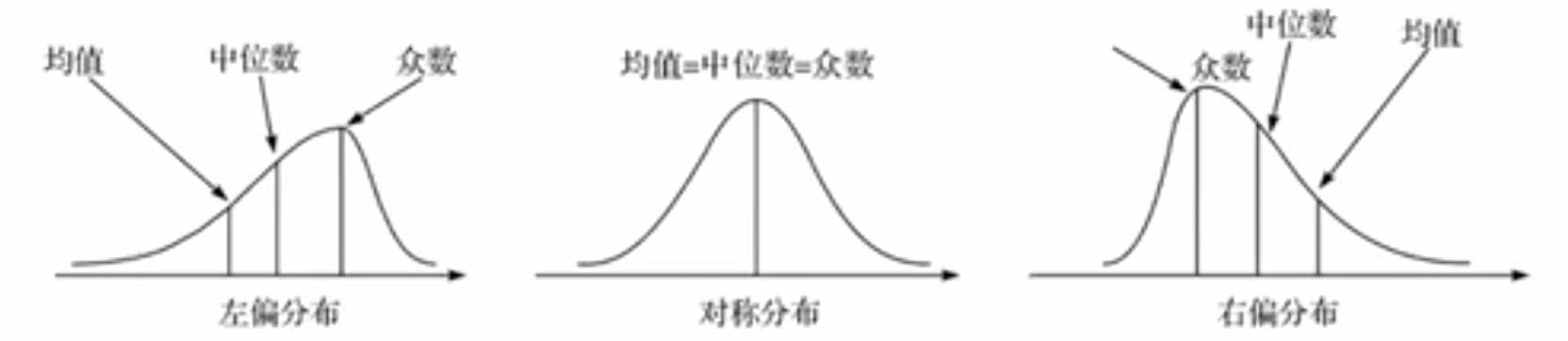
如果数据的分布是严格对称的，平均数 $\bar{x}$ 、中位数 $M_e$ 和众数 $M_o$ 必定相等，即 $\bar{x} = M_e = M_o$ 。
如果数据是左偏分布，说明数据存在极小值，必然拉动平均数向极小值一方靠，而众数和中位数由于是位置代表值，不受极值的影响，因此三者之间的关系表现为： $\bar{x} < M_e < M_o$ 。
如果数据是右偏分布，说明数据存在极大值，必然拉动平均数向极大值一方靠，因此 $M_o < M_e < \bar{x}$ 。

应用场景

在实践中，平均数是应用最广泛的集中趋势测度值，尤其是当数据呈对称分布或接近对称分布时，应选择平均数作为集中趋势的代表值。但是，平均数易受数据极端值的影响，对于偏态分布的数据，平均数的代表性较差。因此，当数据为偏态分布，特别是偏斜程度较大时，可以考虑选择中位数或众数，这时它们的代表性要比平均数好。

众数是一组数据分布的峰值，不受极端值的影响。其缺点是具有不唯一性，一组数据可能一个或多个众数，还可能没有众数。而且，众数只有在数据量较多时才有意义，当数据量较少时，不宜使用众数。一般，众数适合作为分类数据的集中趋势测度值。

中位数是一组数据中间位置上的值，不受数据极端值的影响。当一组数据的分布偏斜程度较大时，使用中位数也许是一个不错的选择。中位数适合作为顺序数据的集中趋势测度值。

离散程度

描述数据离散程度的统计量主要有：

全距
四分位距
方差
标准差
离散系数
异众比率

全距和四分位距

全距

全距(range)，一组数据的最大值与最小值之差，也称极差，用 $R$ 表示。计算公式为：

$R=\max(x)-\min(x)$

由于全距只是利用了一组数据两端的信息，容易受极端值的影响，不能全面反映数据的差异状况。

虽然全距是描述数据离散程度的一个参考值，但在实践中，全距很少单独使用。

四分位距

四分位距(inter-quartile range)，一组数据 $75\%$ 位置上的四分位数与 $25\%$ 位置上的四分位数之差，也被称四分位差，用 $IQR$ 表示。计算公式为：

$IQR = Q_{75\%} - Q_{25\%}$

四分位距反映了中间 $50\%$ 数据的离散程度：其数值越小，说明中间的数据越集中；数值越大，说明中间的数据越分散。
四分位距不受极值的影响。
此外，由于中位数处于数据的中间位置，因此，四分位距的大小在一定程度上也说明了中位数对一组数据的代表程度。

方差和标准差

什么是方差和标准差

我们还可以考虑每个数据 $x_i$ 与其平均数 $\bar{x}$ 之间的差异，即离差，将此作为一组数据离散程度的度量。但是，所有的离差 $(x_i - \bar{x})$ 之和一定等于 $0$ ，我们需要进行一定的处理，有两种方法：

对离差取绝对值，求和后再平均，这一结果被称为平均差(mean deviation)或平均绝对离差(mean absolute deviation)。
对离差平方后再求平均数，这一结果称为方差(variance)。方差开方后的结果称为标准差(standard deviation)。
在实践中，方差(或标准差)是应用最广泛的测度数据离散程度的统计量。

样本方差和样本标准差

我们用 $s^2$ 表示样本方差，其计算公式为：

$s^2 = \frac{\sum_{i=1}^n (x_i - \bar{x})^2}{n-1}$

用 $s$ 表示样本标准差，其计算公式为：

$s = \sqrt{\frac{\sum_{i=1}^n (x_i - \bar{x})^2}{n-1}}$

总体方差和总体标准差

什么是总体方差和总体标准差

与样本均值和总体均值类似，也有样本方差和总体方差。

总体方差(population variance)，用 $\sigma^2$ 表示，其计算公式为

$\sigma^2 = \frac{\sum_{i=1}^N (x_i - \mu)^2}{N}$

总体标准差，用 $\sigma$ 表示，其计算公式为

$\sigma = \sqrt{\frac{\sum_{i=1}^N (x_i - \mu)^2}{N}}$

贝塞尔修正

在样本均值和总体均值中，分母分别是样本数 $n$ 和总体数 $N$ 。在总体方差和总体标准差中，分母是 $N$ 。但是，在样本方差和样本标准差，分母却是 $n-1$ 。

因为，对于一个总体，我们进行抽样后，抽样得到的数据，通常会更集中，导致我们低估了总体的方差。
例如，假设总体数据服从如下的分布，我们进行抽样，天然的不容易抽到小于 $-2$ 和大于 $2$ 的值，从而导致数据更集中。

所以，对于样本方差，通常需要进行一个修正，具体就是除以 $n-1$ ，而不是 $n$ 。

$\begin{aligned} s^2 & = \frac{\sum_{i=1}^n (x_i - \bar{x})^2}{n-1} \\ s & = \sqrt{\frac{\sum_{i=1}^n (x_i - \bar{x})^2}{n-1}} \end{aligned}$

这个修正，就是贝塞尔修正，有严格的数学上的推导证明，本文略。

加权方差和加权标准差

样本加权方差的计算公式为：

$s^2 = \frac{\sum_{i=1}^n (x_i - \bar{x})^2 f_i}{n-1}$

样本加权标准差的计算公式为：

$s = \sqrt{\frac{\sum_{i=1}^n (x_i - \bar{x})^2 f_i}{n-1}}$

总体加权方差的计算公式为：

$\sigma^2 = \frac{\sum_{i=1}^N (x_i - \mu)^2 f_i}{N}$

总体加权标准差的计算公式为：

$\sigma = \sqrt{\frac{\sum_{i=1}^N (x_i - \mu)^2 f_i}{N}}$

比较

与方差相比，标准差具有量纲，与原始数据的计量单位相同，其实际意义要比方差清楚。因此，在实践中，更多的时候，使用标准差。

离散系数

标准差是反映数据离散程度的绝对值，其数值的大小受原始数据取值大小的影响，数据的观测值越大，标准差的值通常也就越大。此外，标准差与原始数据的计量单位相同，采用不同计量单位计量的数据，其标准差的值也就不同。因此，对于不同组别的数据，如果原始数据的观测值相差较大或计量单位不同，就不能用标准差直接比较其离散程度，这时需要计算离散系数。

离散系数(coefficient of variation,CV)，也被称为变异系数，是一组数据的标准差与其相应的平均数之比。其计算公式为：

$CV = \frac{s}{\bar{x}}$

离散系数消除了数据取值大小和计量单位对标准差的影响，因而可以反映一组数据的相对离散程度。离散系数大说明数据的相对离散程度也大，离散系数小说明数据的相对离散程度也小。

但是需要 $\bar{x}$ 接近于 $0$ 的情况，此时，微小的扰动也会对变异系数产生巨大影响，因此造成精确度不足，必须慎重解释。

异众比率

异众比率，一般用于分类数据中。

我们用 $V_r$ 表示非众数组的频数占总频数的比例，则有：

$V_r = \frac{(\sum f_i) - f_m}{\sum f_i} = 1 - \frac{f_m}{\sum f_i}$

$\sum f_i$ 变量值的总频数。
$f_m$ f为众数组的频数。

异众比率主要用于衡量众数对一组数据的代表程度，主要适用于测度分类数据的离散程度。

异众比率越大，说明非众数组的频数占总频数的比重越大，众数的代表性越差；异众比率越小，说明非众数组的频数占总频数的比重越小，众数的代表性越好。

一些容易混淆的概念

标准分数

标准分数(standard score)，是某个数据与其平均数的离差除以标准差后的值。我们用 $z$ 表示某个样本数据的标准分数，计算公式为：

$z_i = \frac{x_i - \bar{x}}{s}$

标准分数，就是我们在《机器学习实战方法(Python)：特征工程-1.特征预处理》讨论过的标准化(Z-Score标准化)，一种把原始数据映射到均值为0方差为1的范围内的数学方法。
标准分数是测度每个数值在该组数据中的相对位置。通过标准分数对原始数据进行线性变换后，没有改变某个数值在该组数据中的位置，也没有改变该组数据分布的形状。

标准误

标准差描述的是，分布中取值与均值间的平均差异，是数据的分布范围。
标准误描述的是，样本均值与其期望值的平均差异，是由样本推测总体的预期误差。

标准误的计算公式如下：

$sem = \frac{s}{\sqrt{n}}$

$s$ 是样本标准差
$n$ 是样本的个数

通过上述公式，我们还可以得到几个大小关系

在样本数 $n$ 不变的情况下，样本标准差 $s$ 越大，标准误 $sem$ 越大。
在样本标准差 $s$ 不变的情况下，样本数 $n$ 越大，标准误 $sem$ 越小。反之，标准误 $sem$ 越大。
所以，有时候为了标准误尽量小，我们应该让样本数尽量大。

离群点

经验法则

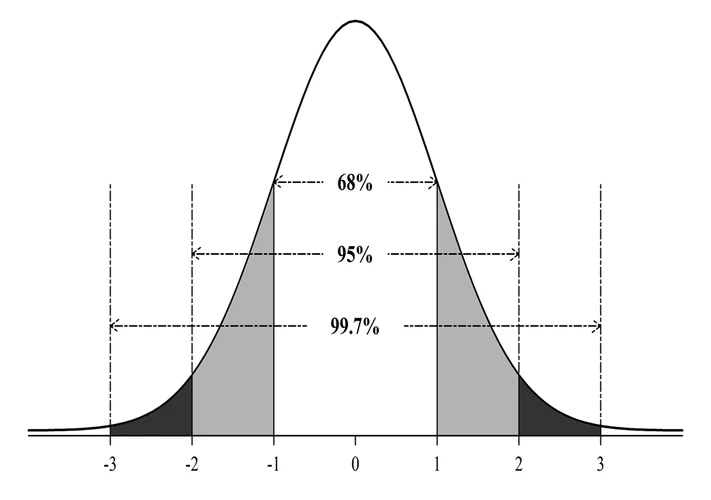
根据经验：当一组数据对称分布时，约有68%的数据在平均数加减1个标准差的范围之内；约有95%的数据在平均数加减2个标准差的范围之内；约有99%的数据在平均数加减3个标准差的范围之内。
也就是说，对于对称分布的数据，在平均数加减3个标准差的范围内几乎包含了全部数据，而在3个标准差之外的数据在统计上也称为离群点(outlier)。

即，离群点特指某些样本，而不是数据的离散程度。

切比雪夫不等式

需要注意的是，上文我们专门强调了对称分布的数据，如果一组数据不是对称分布，当然也会有离群点，只是判断方法不一样。
此时，基于切比雪夫不等式 (Chebyshev’s inequality)，这种方法对任何分布形态的数据都适用。
切比雪夫不等式提供的是"下界"，也就是"所占比例至少是多少"，对于任意分布形态的数据，根据切比雪夫不等式，至少有 $1-\frac{1}{k^2}$ 的数据落在 $\pm k$ 个标准差之内。其中 $k$ 是大于 $1$ 的任意值，不一定是整数。
例如，对于 $k=2,3,4$ ，该不等式的含义是：至少有 $75\%$ 的数据在平均数 $\pm 2$ 个标准差的范围之内；至少有 $89\%$ 的数据在平均数 $\pm 3$ 个标准差的范围之内；至少有 $94\%$ 的数据在平均数 $\pm 4$ 个标准差的范围之内。

分布的形状

我们可以把所有的数据画成一个直方图，这样我们可以直观的感觉数据的分布是否对称。但是，如果想量化对称程度(或不对称程度)，就需要计算相应的描述统计量。
偏度系数和峰度系数就是对分布不对称程度和峰值高低的一种度量。

偏度系数

什么是偏度系数

偏度(skewness)，描述数据分布的不对称性。测度数据分布不对称性的统计量称为偏度系数(coefficient of skewness)，一般用 $SK$ 表示。

三种计算方法

偏度系数的计算方法有三种。

我们令 $m_r = \frac{1}{n}\sum_i^n (x_i - \bar{x})^r$ 为样本的 $r$ 阶中心矩，三种方法分别为：

$SK = \frac{m_3}{m_2^{3/2}}$
$SK = \frac{m_3}{m_2^{3/2}} \times \frac{\sqrt{n(n-1)}}{n-2}$
$SK = \frac{m_3}{m_2^{3/2}} \times (\frac{n-1}{n})^{3/2}$

含义

当数据对称分布时，偏度系数等于0。
偏度系数越接近于0，偏斜程度越小，数据也就越接近于对称分布。
如果偏度系数明显不等于0，则表示分布是不对称的。
若偏度系数大于 $1$ 或小于 $-1$ ，则视为严重偏斜分布。
若偏度系数在$[0.5,1]或[-1,-0.5]之间，则视为中等偏斜分布。
若偏度系数小于 $0.5$ 或大于 $-0.5$ ，则视为轻微偏斜。
其中负值表示左偏分布(在分布的左侧有长尾)。
正值则表示右偏分布(在分布的右侧有长尾)。