2.概率与概率分布

随机事件

几个基本概念

1. 试验和事件，在同一组条件下，对某事物或现象所进行的观察或实验被称作试验，观察或试验的结果被称作事件。
2. 随机事件(random event)，在同一组条件下，每次试验可能出现也可能不出现的事件。
3. 必然事件(certain event)，在同一组条件下，每次试验一定出现的事件。
   例如，在掷骰子的活动中，点数小于7，是一个必然事件。
4. 不可能事件(impossible event)，在同一组条件下，每次试验一定不出现的事件。
   例如，在掷骰子的活动中，点数大于6，是一个必然事件。
5. 基本事件(elementary event)，如果一个事件不能分解成两个或多个事件，则称这个事件为基本事件。
   例如，在掷骰子的活动中，分别观察到点数为1、2、3、4、5、6，这是该试验中的6个基本事件。
6. 一个试验中所有的基本事件的全体被称为样本空间或基本空间。

随机事件的概率

什么是随机事件的概率

事件A的概率是对事件A在试验中出现的可能性大小的一种度量。

记事件A出现可能性大小的数值为$P(A)$，$P(A)$是事件A的概率(probability)。

基于对概率的不同解释，概率的定义有所不同，主要有：

1. 古典定义
2. 统计定义
3. 主观概率定义

古典定义

古典定义，起源于"掷硬币"、"掷骰子"等，这些活动有两个特点：

1. 结果有限，基本空间中只包含有限个元素。
   如掷硬币，只能出现"正面朝上"和"反面朝上"两种结果。
2. 各个结果出现的可能性被认为是相等的。
   如掷硬币，出现正面和反面的机会被认为是相等的。

具有上述两个特点的随机试验所研究的问题称为古典概型。

即，概率的古典定义是，如果某一随机试验的结果有限，而且各个结果出现的可能性相等，则某一事件A发生的概率为该事件所包含的基本事件个数$m$与样本空间中所包含的基本事件个数$n$的比值。

$$P(A) = \frac{\text{事件A所包含的基本事件个数}}{\text{样本空间所包含的基本事件个数}} = \frac{m}{n}$$

概率的统计定义

在相同条件下随机试验$n$次，某事件A出现$m$次$(m \leq n)$，则比值$\frac{m}{n}$称为事件A发生的频率。并且，随着$n$的增大，该频率围绕某一常数$p$上下波动，且波动的幅度逐渐减小，趋于稳定，这个频率的稳定值即为该事件的概率。

$$P(A) = \frac{m}{n} = p$$

概率的统计定义局限性在于，要求在相同的条件下进行大量重复试验，但很多现象并不能进行大量重复试验，特别是一些社会经济现象无法重复。此外，有些现象即使能重复试验，也很难保证试验条件完全一样。

主观概率定义

所谓主观概率，是指对一些无法重复的试验，只能根据以往的经验，人为确定这个事件的概率。

例如，某企业想投资一个新的项目，那么可能成功，也可能失败。这个无法在相同的条件下进行大量重复试验，只能在综合分析多方面信息的基础上，主观给出一个概率。比如投资成功的概率是$0.7$，投资失败的概率为$0.3$。

主观概率的定义是，决策者根据所掌握的信息对某个事件发生可能性作出的判断。

关于主观概率，不会是我们所讨论的重点。

随机变量

随机变量的定义

在同一组条件下，如果每次试验可能出现这样或那样的结果，并且所有的结果都能列举出来，即$X$的所有可能值$x_1,x_2,x_3,\cdots,x_n$都能列举出来，而且$X$的可能值$x_1,x_2,x_3,\cdots,x_n$具有确定概率$P(x_1),P(x_2),P(x_3),\cdots,P(x_n)$，其中$P(x_i)=P(X=x_i)$。
则：$P(x_i)=P(X=x_i)$是概率函数(probability function)；$X$是$P(X)$的随机变量；$P(X)$是随机变量$X$的概率函数。

两种类型的随机变量

按照随机变量的特性，通常可把随机变量分为两类：

1. 离散型随机变量(discrete random variable)
   如果随机变量$X$的所有取值都可以逐个列举出来，则称$X$为离散型随机变量。
   例如，在一批产品中取到次品的个数、单位时间内某交换台收到的呼叫次数等都是离散型随机变量。
2. 连续型随机变量(continuous random variable)
   如果随机变量$X$的所有取值无法逐个列举出来，而是取数轴上某一区间内的任一点，则称$X$为连续型随机变量。
   例如，一批电子元件的寿命、实际工作中常遇到的测量误差等都是连续型随机变量。

离散型随机变量

概率分布

设有一离散型随机变量$X$，可能取值$x_1,x_2,x_3,\cdots,x_n$，其相应的概率为$p_1,p_2,p_3,\cdots,p_n$，即$P(X=x_i)=p_i(i=1,2,3,\cdots,n)$，如下表所示

$X=x_i$	$x_1$	$x_2$	$x_3$	$\cdots$	$x_n$
$P(X=x_i)=p_i$	$p_1$	$p_2$	$p_3$	$\cdots$	$p_n$

称该表格形式为离散型随机变量X的概率分布(probability distribution), 其中，$P(X=x_i)=p_i$ 是$X$的概率函数。

因为$x_1,x_2,x_3,\cdots,x_n$构成一完备组，所以

$$\sum_{i=1}^{n}P_i = 1$$

概括性度量

期望值

在离散型随机变量$X$的一切可能值的完备组中，各可能值$x_i$与其对应概率$p_i$的乘积之和称为该随机变量$X$的期望值(expected value)，记作$E(X)$或$\mu$。

$$E(X) = x_1 p_1 + x_2 p_2 + x_3 p_3 + \cdots + x_n p_n = \sum_{i=1}^{n} x_i p_i$$

方差与标准差

随机变量的方差是用来反映随机变量取值的离散程度的，随机变量的方差定义为每一个随机变量取值与期望值的离差平方之期望值。

假设随机变量为$X$, 其方差用$D(X)$表示，则有

$$D(X) = E[X - E(X)]^2$$

即，方差实际上就是随机变量$X$的函数$[X-E(X)]^2$的数学期望。

我们将上式展开，则有：

$$D(X) = \sum_{i=1}^{n}[x_i - E(X)]^2 p_i$$

这个式子，也就是我们在《1.概括性度量》所讨论的加权方差。

在计算方差时，还有一个简化公式为：

$$D(X)=E(X^2)-[E(X)]^2$$

随机变量方差的平方根为标准差，记为：

$$\sigma = \sqrt{D(X)}$$

假设存在两批灯泡，两批灯泡的平均寿命相等，那么我们可以考察各个灯泡寿命$X$与平均寿命$E(X)$的离差的平均水平，若这个值较小，则认为质量比较稳定，属于质量较好；反之，认为质量较差。

离散系数

离散系数可用来比较不同期望值的总体之间的离散趋势。

计算公式为：

$$V = \frac{\sigma}{E(X)}$$

假设，存在两个投资项目，两个投资项目的预期回报率和方差标准差都不一样，这时候我们可以用离散系数进行比较。

例如，如果投资项目A的预期回报率为$7\%$，标准差为$5\%$，而投资项目B的预期回报率为$12\%$，标准差为$7\%$。
计算离散系数，项目A的离散系数为$0.714$，项目B的离散系数为$0.583$，投资项目A每单位回报率承受$0.714$单位的风险，投资项目B每单位回报率的风险为$0.583$单位；因此，认为A的风险较大。

二项分布

什么是二项分布

二项分布(binomial distribution)，离散型随机变量的概率分布的一种。

假如，我们现在n次掷硬币，这个活动具有以下特点

• 包含n个相同的试验。
• 每次试验只有两个可能的结果。
• 出现"成功"的概率$p$对每一次试验是相同的，"失败"的概率$q$也是如此，且$p+q=1$。
• 试验是互相独立的。
• 试验"成功"或"失败"可以计数，即试验结果对应于一个离散型随机变量。

具有上述特征的$n$次重复独立试验为$n$重贝努里试验，简称贝努里试验(Bernoulli trials)。

以$X$表示$n$次重复独立试验中事件A(成功)出现的次数，则有：

$$P\{X=x\} = C_n^x p^x q^{n-x} x=0,1,2,\cdots,n$$

其中：

• $P\{X=x\} \geq 0,\quad x=0,1,2,\cdots,n$
• $C_n^x$表示表示从$n$个元素中抽取$x$个元素的组合，计算公式为$C_n^x = \frac{n!}{x!(n-x)!}$
• $\sum_{x=0}^{n}C_n^x p^x q^{n-x} = (p+q)^n = 1$

其中$X$就是一个随机变量，所服从的概率分布就是二项分布，参数为$n,p$，记作$X \sim B(n,p)$。

二项分布的期望值：$E(X)=np$
二项分布的方差：$D(X)=npq$

特别地，当$n=1$时，即只进行一次试验时，二项分布化为

$$P(X=x)=p^x q^{1-x},\quad x=0,1$$

这种被称为0-1分布。

例子

已知100件产品中有5件次品，现从中任取1件，有放回地取3次，求在所取的3件中恰有2件次品的概率。

因为这是有放回地取3次，所以这3次试验的条件是完全相同的，由此可知是贝努里试验。

根据题意，每次试验取到次品的概率为$\frac{5}{100}$。设$X$为所取的3件产品中的次品数，则$X \sim B(3,0.05)$，于是有

$$P(X=2)=C_3^2(0.05)^2(0.95)=0.007125$$

特别的，如果我们将"有放回"改为"无放回"，那么每次试验条件就不同了，这时候不能用二项分布的概率公式来计算，而只能用古典概型求解，这种情况的概率分布被称为超几何分布。

假设存在N件产品，其中有M件次品，现从中任取n件$(n \leq N)$，则在这n件中所含的次品件数$X$是一个随机变量，$X$的概率函数为：

$$P\{X=m\}= \frac{C_M^m C_{N-M}^{n-m}}{C_N^n}$$

• $m$为任取$n$件中次品的件数。

泊松分布

什么是泊松分布

泊松分布(poisson distribution)，离散型随机变量的概率分布的一种。用来描述在一指定时间范围内或在指定的面积或体积之内某一事件出现的次数的分布。

下面是一些典型的服从泊松分布的随机变量的例子：

• 某企业每月发生事故的次数。
• 单位时间内到达某一服务柜台(服务站、诊所、超市收银台、电话总机等)需要服务的顾客人数。
• 人寿保险公司每天收到的死亡声明的份数。
• 某种仪器每月出现故障的次数。

泊松分布的公式为：

$$P(X) = \frac{\lambda^x e^{-x}}{x!},\quad x=0,1,2,3,\cdots$$

• $\lambda$为给定的时间间隔内事件的平均数。

泊松分布的期望值：$E(X)=\lambda$
泊松分布的方差：$D(X)=\lambda$

例子

假定某企业职工在周一请事假的人数$X$近似服从泊松分布，设周一请事假的平均数为2.5人，则有
$X$的均值与标准差均为$2.5$，标准差为$\sqrt{2.5}$。

某周一正好请事假是5人的概率为：

$$P(5) = \frac{2.5^5 e^{-2.5}}{5!} = 0.067$$

和二项分布的关系

在n重贝努里试验中，当成功的概率很小(即$p \rightarrow 0$)，试验次数很大时，二项分布近似等于泊松分布，即

$$C_n^x p^x q^{n-x} \approx \frac{\lambda^x e^{-x}}{x!}$$

在实际应用中，当$p \leq 0.25$，$n>20$，$np \leq 5$时，用泊松分布近似二项分布的效果良好。

例如，某批集成电路的次品率为$0.15\%$，随机抽取1000块集成电路，求次品数分别为0,1,2,3的概率。
我们可以把把"集成电路的次品数"看成随机变量$X$，显然$X$服从二项分布，$p=0.0015$，$n=1000$，我们可以用二项分布公式求解。
因为$p \leq 0.25$，$n > 20$，$np \leq 5$，所以我们也可以用泊松分布近似计算。其中$\lambda = np = 1.5$。

连续型随机变量

概率密度与分布函数

为了描述连续型随机变量，我们需要引入一个概念概率密度函数(probability density function)。

概率密度函数$f(x)$应满足以下两个条件：

1. $f(x) \geq 0$
2. $\int_{- \infty}^{+ \infty} f(x)dx=1$

需要强调的是，$f(x)$不是概率，即$f(x) \neq P(X=x)$，$f(x)$是概率密度函数，而$P(X=x)$在连续分布的条件下为零。

连续型随机变量的概率密度是其分布函数的导数。

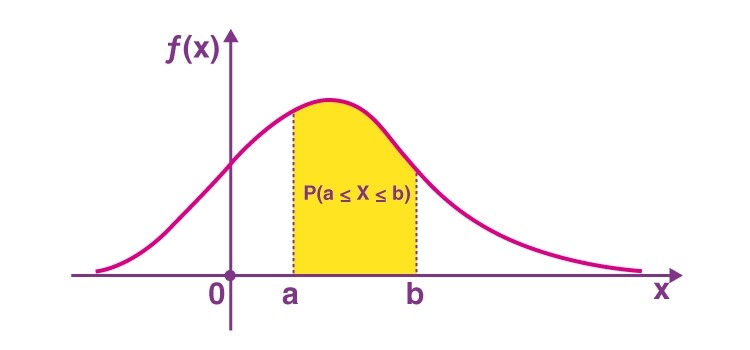
在连续分布的情况下，以曲线下面的面积表示概率，如随机变量$X$在$a$与$b$之间的概率可以写成：

$$P(a \leq X \leq b) = \int_a^b f(x) dx$$

$$P(X \leq t) = \int_{- \infty}^t f(x) dx,\quad - \infty < t < + \infty$$

连续型随机变量的期望值：

$$E(X) = \int_{- \infty}^{+ \infty} x f(x) dx = \mu$$

连续型随机变量的方差：

$$D(X) = \int_{- \infty}^{+ \infty} [x - E(x)]^2 f(x) dx = \sigma^2$$

正态分布

什么是正态分布

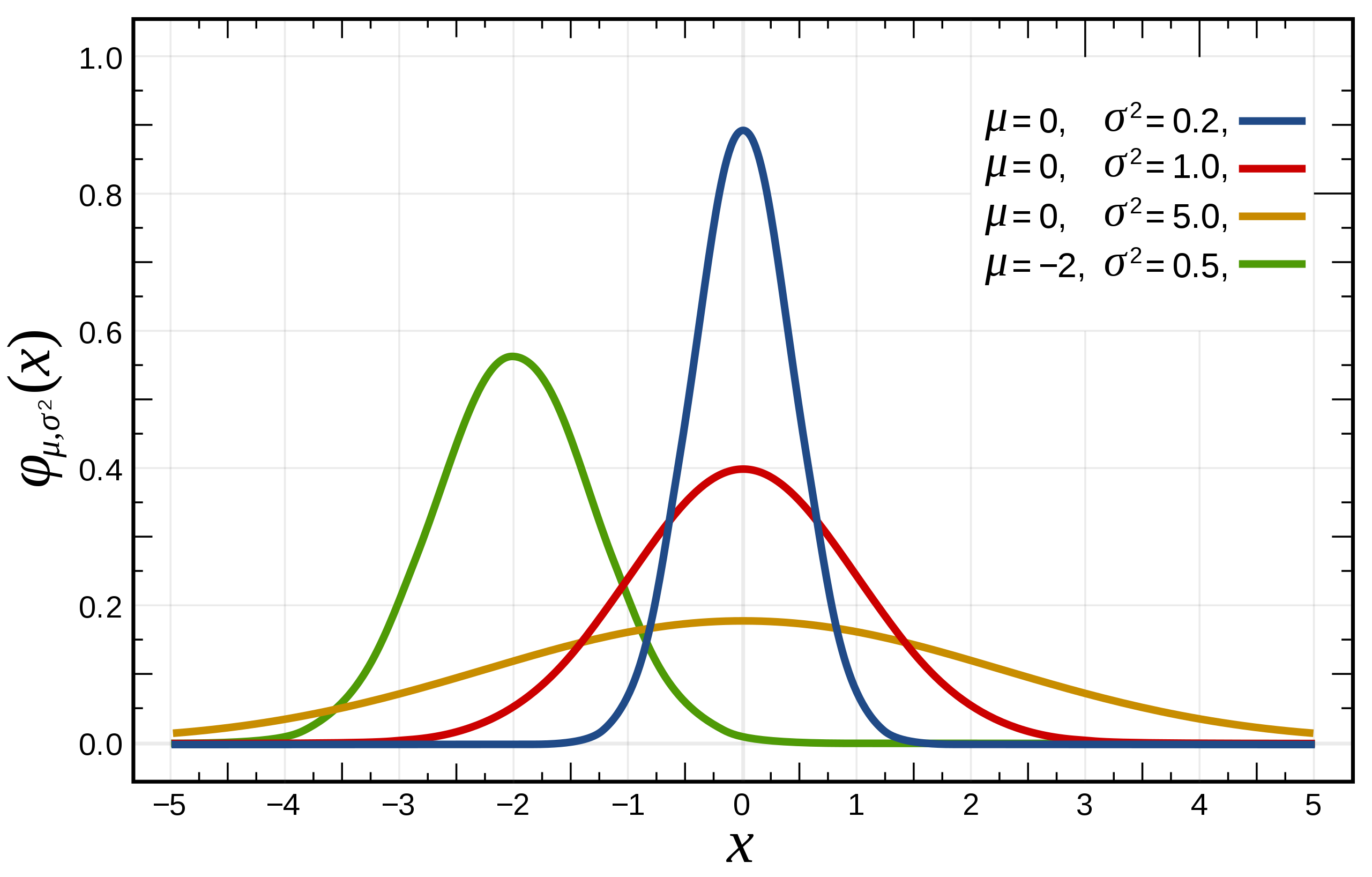
在连续型随机变量中，最重要的一种随机变量是具有钟形概率分布的随机变量，如图所示。我们称之为正态随机变量，相应的概率分布称为正态分布(normal distribution)。

概率密度函数及其特点

如果随机变量$X$的概率密度为：

$$f(x) = \frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{1}{2\sigma^2}(x-\mu)^2},\quad - \infty < x < + \infty$$

则称X服从正态分布，记作$X \sim N(\mu,\sigma^2)$，其中

• $- \infty < x < + \infty$，$\mu$为随机变量$X$的均值。
• $\sigma > 0$，$\sigma$为随机变量$X$的标准差。

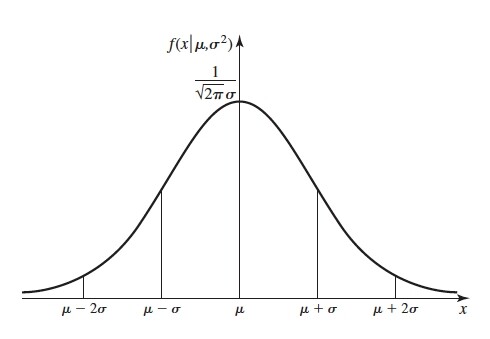
正态分布的概率密度$f(x)$，有以下特点：

1. $f(x) \geq 0$，即整个概率密度曲线都在x轴的上方。
2. 曲线$f(x)$相对于$x=\mu$对称，并在$x=\mu$处达到最大值，$f(\mu)=\frac{1}{\sqrt{2 \pi}\sigma}$
3. 函数曲线的陡缓程度由$\sigma$决定，$\sigma$越大，曲线越平缓；$\sigma$越小，曲线越陡峭。
4. 当$x$趋于无穷时，曲线以x轴为其渐近线。

标准正态分布

什么是标准正态分布

当$\mu=0$，$\sigma=1$时，概率密度函数为

$$f(x) = \frac{1}{\sqrt{2 \pi}}e^{- \frac{x^2}{2}},\quad - \infty < x < + \infty$$

相应的正态分布为$N(0,1)$，这就是标准正态分布(standard normal distribution)。

标准化

任何一个一般的正态分布都可以通过线性变换转化为标准正态分布。
假设$X \sim N(\mu,\sigma^2)$，则有

$$Z = \frac{X - \mu}{\sigma} \sim N(0,1)$$

这个也就是我们在《机器学习实战方法(Python)：特征工程-1.特征预处理》所讨论的"标准化(Z-Score标准化)"。

正态分布表

对于其他的正态分布，我们只需要将其转化为标准正态分布，就可以通过查表解决正态分布的概率计算问题。

对于负值，可采用以下公式：

$$\Phi(-x) = 1 - \Phi(x)$$

• $\Phi(x)$是标准正态分布的概率分布函数。

Python计算

二项分布

已知一批产品的不合格品率为$6\%$，从中有放回地抽取5个产品。求5个产品中：

1. 没有不合格品的概率
2. 恰好有1个不合格品的概率
3. 有3个及3个以下不合格品的概率。

抽取一个产品相当于一次试验，因此$n=5$。由于是有放回地抽取，所以每次试验都是独立的，每次抽取的不合格品率都是$6\%$。设$X$为抽取的不合格品数，显然$X \sim B(5,0.06)$。

示例代码：

from scipy.stats import binom

# 没有不合格品的概率
pO = binom.pmf(0, 5, 0.06)
# 恰好有1全不合格品的概率
p1 = binom.pmf(1, 5, 0.06)
# 有3个及3个以下不合格品的概率
p3 = binom.cdf(3, 5, 0.06)

print(pO)
print(p1)
print(p3)

运行结果：

0.7339040223999996
0.23422468800000015
0.9999383104

泊松分布

计算方法

可以使用scipy.stats中的poisson.pmf(k, mu)和poisson.cdf(k, mu)计算泊松分布相关的概率。

等于某值得概率

某商店每天平均有三位顾客，某天恰好有5人的概率。

示例代码：

from scipy.stats import poisson

p = poisson.pmf(k=5, mu=3)

print(p)

运行结果：

0.10081881344492458

小于某值的概率

某商店平均每天卖7个足球，那么某天卖出足球数量小于5的概率。

示例代码：

from scipy.stats import poisson

# 计算累积概率
p = poisson.cdf(k=4, mu=7)

print(p)

运行结果：

0.17299160788207146

大于某值的概率

某商店平均每天卖15个罐头，则某天卖出罐头超过20个的概率。

示例代码：

from scipy.stats import poisson

# 1减去累积概率
p = 1-poisson.cdf(k=20, mu=15)

print(p)

运行结果：

0.08297091003146029

正态分布

计算下列概率：

1. $X \sim N(50,10^2)$，求$P(X \leq 40)$和$P(30 \leq X \leq 40)$。
2. $Z \sim N(0,1)$，求$P(Z \leq 2.5)$和$P(-1.5 \leq Z \leq 2)$。
3. 标准正态分布累积概率为$0.025$时的分位数值$Z$。

示例代码：

from scipy.stats import norm

# P(X <= 40)的概率
p1 = norm.cdf(40, loc=50, scale=10)
# P(30 <= X <= 40)的概率
p2 = norm.cdf(40, 50, 10) - norm.cdf(30, 50, 10)
# (P(Z <= 2.5]的概率
p3 = norm.cdf(2.5, loc=0, scale=1)
# P(-1.5 <= Z <= 2)的概率，默认为标准正态分布
p4 = norm.cdf(2) - norm.cdf(-1.5)
# 累积概率为0.025时的分位数值
q = norm.ppf(0.025, loc=0, scale=1)

print(p1)
print(p2)
print(p3)
print(p4)
print(q)

运行结果：

0.15865525393145707
0.13590512198327787
0.9937903346742238
0.9104426667829627
-1.9599639845400545