Optiver-1.金融基础与赛题解析

比赛链接

Optiver Realized Volatility Prediction
https://www.kaggle.com/competitions/optiver-realized-volatility-prediction

交易

什么是订单簿

订单簿是指按价格水平组织的某个特定金融资产的买入和卖出订单的表格。
订单簿列出了每个价格点上竞价的股票数量。
如下，就是订单簿的快照，所有意图购买的订单都在显示为"bid"，在订单簿的左侧；而所有意图出售的订单都在显示为"ask"，在订单簿的右侧。

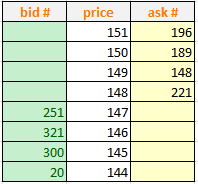
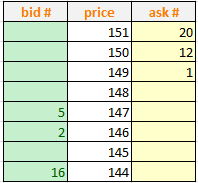
对于交易活跃的金融资产，其订单簿一般都是密集的，但是对于不活跃的金融资产，其订单簿是稀疏的，如下是一个稀疏的订单簿。

订单簿的衍生特征

订单簿是市场需求/供应的连续表示，我们可以从订单簿数据中衍生出许多特征，这些特征可以反映市场流动性和股票估值。
举两个例子：

1. 买卖价差(bid/ask spread)
2. 加权平均价(weighted averaged price)

除了上述两个，还可以基于订单簿衍生出许多其他特征。

买卖价差

买卖价差，bid/ask spread。
我们采用最佳买价(买一)和最佳卖价(卖一)的比率来衡量买卖差价。

$$\text{买卖价差} = \frac{\text{卖一}}{\text{买一}} - 1$$

加权平均价

加权平均价，weighted averaged price，计算瞬时股票估值。

$$\text{WAP} = \frac{\text{买价}\times\text{卖量} + \text{卖价}\times\text{买量}}{\text{买量} + \text{卖量}}$$

这个和我们直观的理解可能不太一样，我们直观的理解应该是买价乘以买量，卖价乘以卖量。
但是，如果买量比卖量大很多，通常认为价格会上涨，买量越多，WAP应该越接近卖价。
所以，是买价乘以卖量，卖价乘以买量。

(具体过程可以参考《金融产品和金融市场：沪深股票的交易规则》的"竞价与成交"部分。)

对数回报率

回报

如何比较股票在昨天和今天的价格？
最简单的方法是计算它们之间的价差，这绝对是最直观的方法，但是价差在所有股票中并不总是可比较的，特别贵的股票涨了10元与特别便宜的股票涨了1元，其意义是不一样的。

回报率(普通回报率)

我们应该用回报率。

$$\text{回报率} = \frac{\text{股票价格的变动}}{\text{股票的初始价格}}$$

对数回报率

但是在对金融问题建立数学模型的时候，我们更的时候，会采用对数回报率。

$$r_{t_1, t_2} = \log \left( \frac{S_{t_2}}{S_{t_1}} \right)$$

• $S_t$表示$t$时间时的股票$S$的价格。
• $r_{t_1, t_2}$表示$t_1$到$t_2$之间的对数回报率。
• 在有些情况下，我们根据固定的时间间隔来查看对数回报率。
  例如10分钟来查看对数回报率，这时候，可能会用$r_t$表示$r_{t - 10\text{分钟},t}$。

对数回报率的优点

与普通回报率相比，对数回报率的优点有：

1. 随时间累加(可加性)
   $r_{t_1, t_2} + r_{t_2, t_3} = r_{t_1, t_3}$
2. 一般普通回报率的值域是$[-1,1]$，对数回报率值域没有限制，可以覆盖全部实数域，不需要处理特别的边界。
3. 在一些传统的计量模型中，采用对数回报率的效果会更好。

波动率

波动率分类

波动率可以分为三类：

1. 真实波动率(也被称为实际波动率)
2. 实现波动率(也被称为历史波动率、回望型波动率)
3. 隐含波动率

他们之间的关系如下：

$$\text{真实波动率} \approx \text{实现波动率} \neq \text{隐含波动率}$$

• 真实波动率，也被称为实际波动率，这个永远是一个未知数。
• 隐含波动率，implied volatility，是把期权价格代入BS模型(Black-Scholes Model)里反推出来的波动率，代表市场对标的资产未来一段时间内波动率的预期。
  (关于期权和BS模型，可以参考《未分类【金融】：一种基于强化学习的期权定价方法》的"附录：期权概述"。)

我们主要讨论实现波动率。

什么是实现波动率

实现波动率，也被称为历史波动率、回望型波动率，衡量的是过去一段时间，某个资产价格的波动，是波动率的事后估计。

在《JPX-1.赛题解析》，我们讨论过夏普比率，在夏普比率的分母部分，用标准差来衡量风险，在这里也是如此，我们用标准差衡量波动率。
但，两者存在不同：

• 夏普比率，一般用标准差，很少用样本标准差的。
• 实现波动率，一般用样本标准差，很少用标准差的。

实现波动率的计算公式：

$$\text{实现波动率} = \sqrt{\frac{\sum_{i=1}^n (r_i - \mu)}{n-1}}$$

• $r_i$是对数回报率。
• $\mu$是对数回报率的平均

$$\mu=\frac{\sum_{i=1}^n r_i}{n}$$

Optiver比赛中的实现波动率

在Optiver的比赛中，Optiver是基于连续订单簿的对数回报率来计算实现波动率。

计算公式如下：

$$\sigma = \sqrt{\sum_t r_{t-1, t}^2}$$

其中，$r_{t-1, t}$依旧是对数回报率。不过，在计算其价格的时候，采用的不是某一时刻的成交价，而是某一时刻的加权平均价(WAP)。

这个实现波动率的特点还有：

1. 没有减去平均值
   Optiver官方的解释是，他们假设在赛题中的对数回报率的平均值为0。
2. 没有除以样本数，或除以样本数减一的差
   因为衡量的都是十分钟之类的波动率，在赛题的范围内，除以或不除以样本数，没有本质上的影响。

聚集效应

什么是聚集效应

波动率存在聚集效应，通俗的说，波动率喜欢窝在一起，高波动率的前后通常也是高波动率，低波动率的前后一般也都是低波动率。
这个在统计学上，叫做自相关性。

历史波动率模型

所以，可以利用这个特性，直接对波动率建模，不考虑对收益率分布的拟合。以此来实现一些模型，最典型的就是历史波动率模型：

1. 随机游走模型
2. 简单移动平均模型
3. 指数加权移动平均模型

随机游走模型

历史波动率模型中最简单的形式是随机游走模型：

$$\widehat{\sigma_t} = \sigma_{t-1}$$

即未来波动率最好的预测是前一天的波动率。

简单移动平均模型

简单移动平均模型：

$$\widehat{\sigma_t} = \frac{1}{t}(\sigma_{t-1} + \sigma_{t-2} + \cdots + \sigma_{t - \tau - 1})$$

指数加权移动平均模型

指数加权移动平均模型，一个变量在第n天的波动率由第n-1天波动率估计值和变量在最近一天变化百分比决定的。

$$\sigma_{n}^2=\lambda\sigma_{n-1}^2 + (1-\lambda)u_{n-1}^2$$

波动率的应用

VIX指数及其应用

芝加哥期权交易所(Chicago Board Options Exchange，CBOE)发布了一个波动率指数(Volatility Index，VIX)，这个指数也被称为"恐惧指数"，衡量的是标准普尔500指数(S&P 500 Index)期权的隐含波动率，代表市场对未来30天的市场波动率的预期。

VIX表达了期权投资者对未来股票市场波动性的预期，当指数越高时，显示投资者预期未来股价指数的波动性越剧烈；当VIX指数越低时，代表投资者认为未来的股价波动将趋于缓和。

VIX到达相对高点时，表示投资者对短期未来充满恐惧，市场通常接近或已在底部；反之，则代表投资者对市场现状失去戒心，此时应注意市场随时有变盘的可能。

指数与投资者情绪的关系如下表

VIX指数区间(%)	投资者情绪	VIX出现的频率
5-10	毫无警觉	0.15%
10-15	满足程度较高	27.5%
15-20	适度满意	29.19%
20-25	满意度较低	22.72%
25-30	开始忧虑	10.68%
30-35	忧虑较高	4.85%
35-40	忧虑很高	2.09%
40-45	忧虑极高	1.32%
45-50	接近恐慌	0.56%
50-55	温和恐慌	0.25%
55-60	恐慌	0.24%
60-65	强烈恐慌	0.15%
65以上	极度恐慌	0.31%

在中国也有类似的指数：iVIX和CIMV。

基于波动率的交易

期权的成交价受由市场供求关系来决定的，这一点与其他市场的价格决定机制是一样的，但是在期权的交易中，可以通过波动率来判断期权的成交价是否合理。

我们可以通过期权价格，反向计算出隐含波动率，然后可以将隐含波动率和实现波动率(或者我们预测的波动率)进行比较。

波动率交易的核心就是赚取隐含波动率与已实现波动率(或者我们预测的波动率)之间的价差。

• 当预期隐含波动率高于已实现波动率(或者我们预测的波动率)时则卖出期权
• 当预期隐含波动率低于已实现波动率(或者我们预测的波动率)时则买入期权

赛题解析

任务

在这个比赛中，我们需要是从一个固定的10分钟窗口的订单簿数据和成交数据中生成一系列短期信号，以预测下一个10分钟窗口的实现波动率。

数据

train.csv

查看train.csv中的数据，示例代码：

import pandas as pd
train = pd.read_csv('../input/optiver-realized-volatility-prediction/train.csv')
train.head()

运行结果：

   stock_id  time_id    target
0         0        5  0.004136
1         0       11  0.001445
2         0       16  0.002168
3         0       31  0.002195
4         0       62  0.001747

一个time_id表示一个20分钟的交易窗口，对于所有的股票而言是一致的。例如，假设time_id=1代表的是一个时间窗口，从"1900-01-01 12:00:00"到"1900-01-01 12:20:00"，所有股票在该time_id对应的交易窗口数据是一致的。
前10分钟窗口的数据是公开的，而后10分钟波动率是需要我们预测的。

即，结构如下：

需要注意的是，time_id乱序的，不包含任何信息，只作为不同数据集之间的桥梁。

(但是，我们确保测试数据集中的数据点是未来的，不存在数据泄漏。但训练数据集之间，time_id不会包含任何其他信息。)

以数据的第一行为例，它意味着时间id为5，股票id为0的目标桶的实现波动率为0.004136。
我们查看对应的订单簿数据和成交数据。

book_train.parquet

book_train.parquet，订单簿数据。

我们查看book_train.parquet中的内容，示例代码：

book_example = pd.read_parquet('../input/optiver-realized-volatility-prediction/book_train.parquet/stock_id=0')
book_example = book_example[book_example['time_id']==5]
book_example.loc[:,'stock_id'] = '0'
book_example.head()

运行结果：

   time_id  seconds_in_bucket  bid_price1  ask_price1  bid_price2  ask_price2  bid_size1  ask_size1  bid_size2  ask_size2 stock_id
0        5                  0    1.001422    1.002301     1.00137    1.002353          3        226          2        100        0
1        5                  1    1.001422    1.002301     1.00137    1.002353          3        100          2        100        0
2        5                  5    1.001422    1.002301     1.00137    1.002405          3        100          2        100        0
3        5                  6    1.001422    1.002301     1.00137    1.002405          3        126          2        100        0
4        5                  7    1.001422    1.002301     1.00137    1.002405          3        126          2        100        0

我没可以把订单簿数据想象成是一个连续的数据流。在比赛中，公开了每秒的最后一张订单簿快照。seconds_in_bucket=1表示第一秒的最后一张订单簿更新的快照。

trade_train.parquet

trade_train.parquet，成交数据，成交数据表示在一个秒内发生的所有个人订单的聚合。

示例代码：

trade_example =  pd.read_parquet('../input/optiver-realized-volatility-prediction/trade_train.parquet/stock_id=0')
trade_example = trade_example[trade_example['time_id']==5]
trade_example.loc[:,'stock_id'] = '0'
trade_example.head()

运行结果：

   time_id  seconds_in_bucket     price  size  order_count stock_id
0        5                 21  1.002301   326           12        0
1        5                 46  1.002778   128            4        0
2        5                 50  1.002818    55            1        0
3        5                 57  1.003155   121            5        0
4        5                 68  1.003646     4            1        0

缺失seconds_in_bucket

在有些情况下，会有缺失的"seconds_in_bucket"字段，表示在过去的一秒钟内，没有相关的市场活动。

• 对于订单簿数据，我们可以假设前两个记录的数据保持与在同一时间段前一个可用的订单簿更新相同，或者说可以用所有字段中的缺失数据点进行前向填充。
• 对于成交数据，这意味着该一秒内没有成交发生。
  一般成交数据与订单簿数据相比更为稀疏。

计算实现波动率

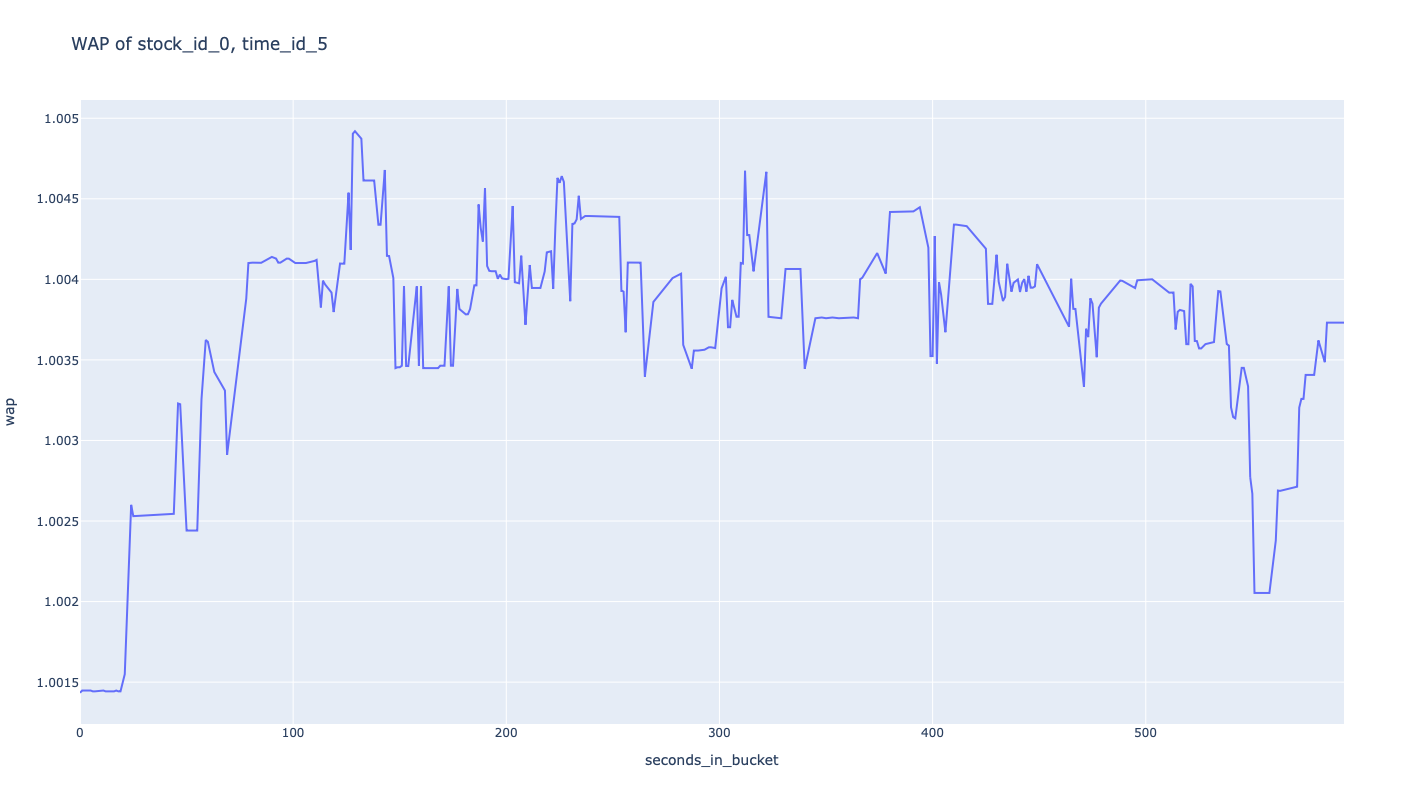
计算WAP

使用提供的订单簿数据，计算加权平均价格(WAP)，示例代码：

book_example['wap'] = (book_example['bid_price1'] * book_example['ask_size1'] + book_example['ask_price1'] * book_example['bid_size1']) / (book_example['bid_size1']+ book_example['ask_size1'])
book_example.head()

运行结果：

   time_id  seconds_in_bucket  bid_price1  ask_price1  bid_price2  ask_price2  bid_size1  ask_size1  bid_size2  ask_size2 stock_id       wap
0        5                  0    1.001422    1.002301     1.00137    1.002353          3        226          2        100        0  1.001434
1        5                  1    1.001422    1.002301     1.00137    1.002353          3        100          2        100        0  1.001448
2        5                  5    1.001422    1.002301     1.00137    1.002405          3        100          2        100        0  1.001448
3        5                  6    1.001422    1.002301     1.00137    1.002405          3        126          2        100        0  1.001443
4        5                  7    1.001422    1.002301     1.00137    1.002405          3        126          2        100        0  1.001443

我们可以将其绘制成图，示例代码：

import plotly.express as px

fig = px.line(book_example, x="seconds_in_bucket", y="wap", title='WAP of stock_id_0, time_id_5')
fig.show()

运行结果：

• 计算WAP

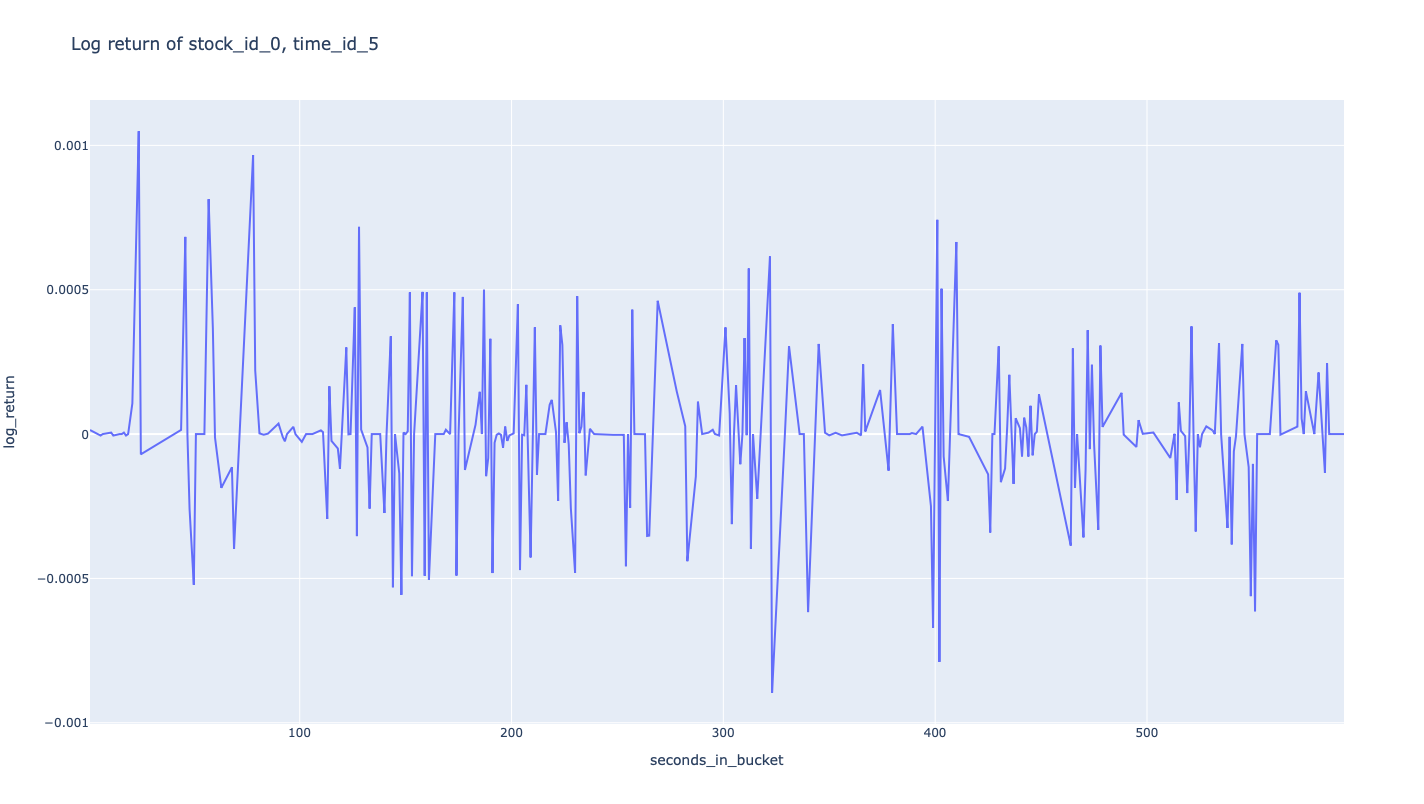
计算对数回报率

示例代码：

def log_return(list_stock_prices):
    return np.log(list_stock_prices).diff()

book_example.loc[:,'log_return'] = log_return(book_example['wap'])
book_example = book_example[~book_example['log_return'].isnull()]
book_example.head()

运行结果：

   time_id  seconds_in_bucket  bid_price1  ask_price1  bid_price2  ask_price2  bid_size1  ask_size1  bid_size2  ask_size2 stock_id       wap  log_return
1        5                  1    1.001422    1.002301     1.00137    1.002353          3        100          2        100        0  1.001448    0.000014
2        5                  5    1.001422    1.002301     1.00137    1.002405          3        100          2        100        0  1.001448    0.000000
3        5                  6    1.001422    1.002301     1.00137    1.002405          3        126          2        100        0  1.001443   -0.000005
4        5                  7    1.001422    1.002301     1.00137    1.002405          3        126          2        100        0  1.001443    0.000000
5        5                 11    1.001422    1.002301     1.00137    1.002405          3        100          2        100        0  1.001448    0.000005

解释说明，第一行将没有收益率，因为前面的订单簿更新是未知的，因此将放弃这个空白的返回数据点。

我们可以将其绘制成图，示例代码：

fig = px.line(book_example, x="seconds_in_bucket", y="log_return", title='Log return of stock_id_0, time_id_5')
fig.show()

• 计算对数回报率

计算实现波动率

示例代码：

def realized_volatility(series_log_return):
    return np.sqrt(np.sum(series_log_return**2))

realized_vol = realized_volatility(book_example['log_return'])
print(f'Realized volatility for stock_id 0 on time_id 5 is {realized_vol}')

运行结果：

Realized volatility for stock_id 0 on time_id 5 is 0.004499364172786558

随机游走模型的应用

最后，我们以随机游走模型为例，直接将前10分钟的波动率，作为后10分钟的波动率。

示例代码：

import pandas as pd
import numpy as np
import glob
from sklearn.metrics import r2_score

train = pd.read_csv('../input/optiver-realized-volatility-prediction/train.csv')
list_order_book_file_train = glob.glob('/kaggle/input/optiver-realized-volatility-prediction/book_train.parquet/*')

def log_return(list_stock_prices):
    return np.log(list_stock_prices).diff()

def realized_volatility(series_log_return):
    return np.sqrt(np.sum(series_log_return**2))

def realized_volatility_per_time_id(file_path, prediction_column_name):
    df_book_data = pd.read_parquet(file_path)
    df_book_data['wap'] =(df_book_data['bid_price1'] * df_book_data['ask_size1']+df_book_data['ask_price1'] * df_book_data['bid_size1'])  / (df_book_data['bid_size1']+ df_book_data['ask_size1'])
    df_book_data['log_return'] = df_book_data.groupby(['time_id'], group_keys=False)['wap'].apply(log_return)
    df_book_data = df_book_data[~df_book_data['log_return'].isnull()]
    df_realized_vol_per_stock =  pd.DataFrame(df_book_data.groupby(['time_id'], group_keys=False)['log_return'].agg(realized_volatility)).reset_index()
    df_realized_vol_per_stock = df_realized_vol_per_stock.rename(columns = {'log_return':prediction_column_name})
    stock_id = file_path.split('=')[1]
    df_realized_vol_per_stock['row_id'] = df_realized_vol_per_stock['time_id'].apply(lambda x:f'{stock_id}-{x}')
    return df_realized_vol_per_stock[['row_id',prediction_column_name]]

def past_realized_volatility_per_stock(list_file,prediction_column_name):
    df_past_realized = pd.DataFrame()
    for file in list_file:
        df_past_realized = pd.concat([df_past_realized, realized_volatility_per_time_id(file,prediction_column_name)])
    return df_past_realized

df_past_realized_train = past_realized_volatility_per_stock(list_file=list_order_book_file_train, prediction_column_name='pred')

train['row_id'] = train['stock_id'].astype(str) + '-' + train['time_id'].astype(str)
train = train[['row_id','target']]
df_joined = train.merge(df_past_realized_train[['row_id','pred']], on = ['row_id'], how = 'left')

from sklearn.metrics import r2_score
def rmspe(y_true, y_pred):
    return  (np.sqrt(np.mean(np.square((y_true - y_pred) / y_true))))
R2 = round(r2_score(y_true = df_joined['target'], y_pred = df_joined['pred']),3)
RMSPE = round(rmspe(y_true = df_joined['target'], y_pred = df_joined['pred']),3)
print(f'Performance of the naive prediction: R2 score: {R2}, RMSPE: {RMSPE}')

运行结果：

Performance of the naive prediction: R2 score: 0.628, RMSPE: 0.341

我们看到，均方误差根是0.341。

提交，示例代码：

list_order_book_file_test = glob.glob('/kaggle/input/optiver-realized-volatility-prediction/book_test.parquet/*')
df_naive_pred_test = past_realized_volatility_per_stock(list_file=list_order_book_file_test, prediction_column_name='target')
df_naive_pred_test.to_csv('submission.csv',index = False)

最终分数为0.3357。