avatar
主页
计算机
金融
数学
关于
本站文章数 :
175
本站总字数 :
1251.5K
已运行天数 :
Kaka Wan Yifan
主页
计算机
金融
数学
关于
7.方差分析
数学应用统计推断及其Python计算
字数总计:8.5K

基本概念

什么是方差分析

引例

假设，消费者协会在零售业、旅游业、航空公司、家电制造业分别抽取了不同的企业作为样本。其中，零售业抽取了77家，旅游业抽取了66家，航空公司抽取了55家，家电制造业抽取55家。每个行业中所抽取的这些企业，假定它们在服务对象、服务内容、企业规模等方面基本上是相同的。然后统计出最近一年中消费者对总共2323家企业投诉次数，结果如表所示：

样本 零售业 旅游业 航空公司 家电制造业
1 57 68 31 44
2 66 39 49 51
3 49 29 21 65
4 40 45 34 77
5 34 56 40 58
6 53 51
7 44

现在，我们想知道各行业之间的服务质量是否有显著差异。

所以，接下来我们比较各行业之间，被投诉次数的均值，来判断各行业之间的服务质量是否有显著差异。
也就是说，我们比较分类型的自变量对于数值型的因变量有没有一个显著的影响。

那么，这和方差有什么关系呢？
上述我们得到的是抽样数据，计算的是样本均值，不是总体均值，样本均值不一定能代表总体均值。

这似乎也没什么难度，在《5.假设检验》，我们就讨论过"两个总体参数的检验"。
上述例子，就属于"两个总体参数的检验-独立样本总体均值之差的检验-方差未知 小样本"。

但现在，我们有四个总体，理论上要做六次两两检验，这样就很繁琐了。
而且，如果α=0.05\alpha = 0.05，即每次检验犯第I类错误的概率都是0.050.05，作多次检验会使犯第I类错误的概率相应增加，连续作66次检验犯第I类错误的概率为1−(1−α)6=0.2651-(1-\alpha)^6 = 0.265，而置信水平则会降低到0.956=0.7350.95^6 = 0.735。

这就需要方差分析了。

定义

方差分析：通过对数据误差来源的分析检验各总体的均值是否相等来判断分类型自变量对数值型因变量是否有显著影响。

这也是为什么叫做分析，虽然我们关注的点是均值，但是在判断均值之间是否有差异时需要借助方差。

在方差分析中，所要检验的对象被称为因素或因子(factor)；因素的不同表现称为水平或处理(treatment)；在每个因子水平下得到的样本数据称为观测值。

在上文的例子中，要分析行业对被投诉次数是否有显著影响。这里的行业是要检验的对象，被称为因素或因子；零售业、旅游业、航空业、家电制造业是行业这一因素的具体表现，称为水平或处理；在每个行业下得到的样本数据(被投诉次数)称为观测值。

由于这里只涉及行业一个因素，因此称为单因素4水平的试验。也就是单因素方差分析，只有一个因素的方差分析，涉及分类型自变量和数值型自变量两个变量。
因素的每一个水平可以看作一个总体，如零售业、旅游业、航空业、家电制造业可以看作4个总体，上面的数据可以看作从这4个总体中抽取的样本数据。

如果涉及到多个因素，则被称为双因素方差分析。

思路

误差分解

组内误差

在同一行业(同一个总体)中，样本的各观测值是不同的。例如，在零售业中，所抽取的7家企业之间被投诉次数就是不同的。由于企业是随机抽取的，因此它们之间的差异可以看成是随机因素的影响造成的，或者说是由抽样的随机性造成的随机误差。
这种来自水平内部的数据误差也称为组内误差，组内误差只包含随机误差。

组间误差

不同行业(不同总体)的观测值也是不同的。不同水平之间的数据误差称为组间误差。这种差异可能是由抽样本身形成的随机误差，也可能是由行业本身的系统性因素造成的系统误差。
因此，组间误差是随机误差和系统误差的总和。

总误差

  • 反映全部数据误差大小的平方和称为总平方和，记为SSTSST。
    例如，所抽取的全部2323家企业被投诉次数之间的误差平方和就是总平方和，反映了全部观测值的离散状况。
  • 反映组内误差大小的平方和称为组内平方和，也称误差平方和或残差平方和，记为SSESSE。
    例如，每个样本内部的数据平方和加在一起就是组内平方和，反映了每个样本内各观测值的离散状况。
  • 反映组间误差大小的平方和称为组间平方和，也称因素平方和，记为SSASSA。
    例如，4个行业被投诉次数之组内误差(SSE)间的误差平方和就是组间平方和，它反映了样本均值之总误差(SST)间的差异程度。

三个误差(平方和)的关系

总平方和SST=组内平方和SSE+组间平方和SSA\text{总平方和}SST = \text{组内平方和}SSE + \text{组间平方和}SSA

误差分析

  • 如果不同行业对被投诉次数没有影响，那么在组间误差中只包含随机误差，而没有系统误差。
    这时，组间误差与组内误差经过平均后的数值(称为均方或方差)就应该很接近，它们的比值就会接近11。
  • 如果不同行业对被投诉次数有影响，则组间误差中除了包含随机误差，还会包含系统误差。
    这时组间误差平均后的数值就会大于组内误差平均后的数值，它们之间的比值就会大于11。
    当这个比值大到某种程度时，就认为因素的不同水平之间存在显著差异，也就是自变量对因变量有显著影响。

因此，判断行业对被投诉次数是否有显著影响这一问题，实际上也就是检验被投诉次数的差异主要是由什么原因引起的。如果这种差异主要是系统误差，就认为不同行业对被投诉次数有显著影响。

三个假定

方差分析也是按照我们之前的假设检验，设置原假设和备择假设，整个流程走。
需要注意的是，不是所有的情况，都可以方差分析。

有三个假定：

  1. 每个总体都应服从正态分布
    对于因素的每一个水平，其观察值是来自服从正态分布总体的简单随机样本。
    比如，每个行业被投诉的次数必须服从正态分布。
  2. 各个总体的方差必须相同
    各组观察数据是从具有相同方差的总体中抽取的。
    比如，4个行业被投诉次数的方差都相等。
  3. 观察值是独立的
    比如，要求每个被抽中的企业被投诉次数都与其他企业被投诉次数相互独立。

单因素方差分析

单因素方差分析：当方差分析中只涉及一个分类型自变量，研究的是一个分类型自变量对一个数值型因变量的影响。

分析步骤

与我们之前讨论假设检验和卡方检验一样，方差分析主要主要步骤包括：

  1. 提出假设
  2. 构造检验统计量
  3. 统计决策

提出假设

在方差分析中，原假设所描述的是在按照自变量的取值分成的类中，因变量的均值相等。

设因素有kk个水平，每个水平的均值分别用μ1,μ2,μ3,⋯ ,μk\mu_1,\mu_2,\mu_3,\cdots,\mu_k表示，要检验kk个水平(总体)的均值是否相等，需要提出如下假设：

H0:μ1=μ2=μ3=⋯=μk自变量对因变量没有显著影响H1:μ1,μ2,μ3,⋯ ,μk不全相等自变量对因变量有显著影响\begin{aligned} H_0 & : \mu_1 = \mu_2 = \mu_3 = \cdots = \mu_k \quad \text{自变量对因变量没有显著影响} \\ H_1 & : \mu_1,\mu_2,\mu_3,\cdots,\mu_k \text{不全相等} \quad \text{自变量对因变量有显著影响} \end{aligned}

如果拒绝原假设H0H_0，则意味着自变量对因变量有显著影响；如果不拒绝原假设H0H_0，则没有证据表明自变量对因变量有显著影响，不能认为自变量与因变量之间有显著关系。
注意：拒绝原假设，只表明至少有两个总体的均值不相等，并不意味着所有的均值都不相等。

构造检验的统计量

构造检验的统计量的步骤有：

  1. 计算各样本的均值
  2. 计算全部观测值的总均值
  3. 计算各误差平方和
  4. 计算统计量

计算各样本的均值

假定从第ii个总体中抽取一个容量为nin_i的简单随机样本，第ii个总体的样本均值为该样本的全部观测值总和除以观测值的个数，即

xˉi=∑j=1nixijni(i=1,2,3,⋯ ,k)\bar{x}_i = \frac{\sum_{j=1}^{n_i} x_{ij}}{n_i} \quad (i=1,2,3,\cdots,k)

式中：nin_i为第ii个总体的样本观察值个数，xijx_{ij}为第ii个总体的第jj个观察值

计算全部观测值的总均值

全部观测值的总和除以观测值的总个数

xˉ‾=∑i=1k∑j=1nixijn=∑i=1knixˉin\overline{\bar{x}} = \frac{\sum_{i=1}^{k} \sum_{j=1}^{n_i} x_{ij}}{n} = \frac{\sum_{i=1}^{k} n_i \bar{x}_i}{n}

式中，n=n1+n2+n3+⋯+nkn=n_1 + n_2 + n_3 + \cdots + n_k

在上例中

零售业 旅游业 航空公司 家电制造业
样本均值 xˉ1=49\bar{x}_1 = 49 xˉ2=48\bar{x}_2 = 48 xˉ3=35\bar{x}_3 = 35 xˉ4=59\bar{x}_4 = 59
样本容量(nn) 7 6 5 5

总均值：

xˉ‾=57+66+49+⋯+77+5823=47.869565\overline{\bar{x}} = \frac{57 + 66 + 49 + \cdots + 77 + 58}{23} = 47.869565

计算各误差平方和

计算总平方和

全部观测值xijx_{ij}与总平均值xˉ‾\overline{\bar{x}}的误差平方和。

SST=∑i=1k∑j=1r(xij−xˉ‾)2SST = \sum_{i=1}^{k} \sum_{j=1}^{r} (x_{ij} - \overline{\bar{x}})^2

在上例中

SST=(57−47.869565)2+⋯+(58−47.869565)2=4164.608696SST = (57 - 47.869565)^2 + \cdots + (58 - 47.869565)^2 = 4164.608696

计算组间平方和

各组平均值xˉi\bar{x}_i与总平均值xˉ‾\overline{\bar{x}}的误差平方和。

SSA=∑i=1kn1(xˉi−xˉ‾)2SSA = \sum_{i=1}^{k} n_1(\bar{x}_i - \overline{\bar{x}})^2

在上例中

SSA=7×(49−47.869565)2+⋯+5×(59−47.869565)2=1456.608696SSA = 7 \times (49 - 47.869565)^2 + \cdots + 5 \times (59 - 47.869565)^2 = 1456.608696

计算组内平方和

每个水平或组的各样本数据与其组平均值的误差平方和，该平方和反映的是随机误差的大小。

SSE=∑i=1k∑j=1ni(xij−xˉi)2SSE = \sum_{i=1}^{k} \sum_{j=1}^{n_i} (x_{ij} - \bar{x}_i)^2

在上例中，

零售业∑j=17(x1j−xˉ1)2=700⋯家电制造业∑j=15(x4j−xˉ4)2=650\begin{aligned} \text{零售业} & \quad \sum_{j=1}^{7} (x_1j - \bar{x}_1)^2 = 700 \\ & \cdots \\ \text{家电制造业} & \quad \sum_{j=1}^{5} (x_4j - \bar{x}_4)^2 = 650 \\ \end{aligned}

将其加总可以得到：

SSE=2708SSE = 2708

计算统计量

各误差平方和的大小与观测值的多少有关，为消除观测值多少对误差平方和大小的影响，需要将其平均，也就是用各平方和除以它们所对应的自由度，这就是均方，也称为方差。

三个平方和对应的自由度分别是：

  • SSTSST的自由度为n−1n-1，其中nn为全部观察值的个数。
  • SSASSA的自由度为k−1k-1，其中kk为因素水平(总体)的个数。
  • SSESSE的自由度为n−kn-k。

通常只计算SSA的均方和SSE的均方：

组间方差：SSASSA的均方，记为MSAMSA。

MSA=SSAk−1MSA = \frac{SSA}{k-1}

在本例中

MSA=1456.6086964−1=485.536232MSA = \frac{1456.608696}{4-1} = 485.536232

组内方差：SSESSE的均方，记为MSEMSE。

MSE=SSEn−kMSE = \frac{SSE}{n-k}

在本例中

MSE=270823−4=142.526316MSE = \frac{2708}{23 - 4} = 142.526316

将MSAMSA和MSEMSE进行对比，即得到所需要的检验统计量FF。当H0H_0为真时，二者的比值服从分子自由度为k−1k-1、分母自由度为n−kn-k的F分布，即

F=MSAMSE∼F(k−1,n−k)F = \frac{MSA}{MSE} \sim F(k - 1, n - k)

在本例中

F=485.536232142.526316=3.406643F = \frac{485.536232}{142.526316} = 3.406643

统计决策

将统计量的值FF与给定的显著性水平α\alpha的临界值FαF_{\alpha}进行比较，从而作出对原假设H0H_0的决策。

若F>FαF > F_{\alpha}，则拒绝原假设H0H_0，表明均值之间的差异是显著的，所检验的因素对观测值有显著影响。
若F<FαF < F_{\alpha}，则不拒绝原假设H0H_0，没有证据表明均值之间的差异是显著的，不能认为所检验的因素对观测值有显著影响。

当然，我们也可以计算PP值，将与显著性水平α\alpha进行比较。若P<αP<\alpha，则拒绝H0H_0；若P>αP>\alpha，则不拒绝H0H_0。

在上例中，F=3.406643F=3.406643，F0.05(3,19)=3.13F_{0.05}(3,19)=3.13。由于F>FαF>F_{\alpha}，因此拒绝原假设H0H_0，表明μ1,μ2,μ3,μ3\mu_1,\mu_2,\mu_3,\mu_3之间有显著差异，即行业对被投诉次数有显著影响。

关系强度的测量

变量间关系的强度用自变量平方和SSASSA占总平方和SSTSST的比例大小来反映，即

R2=SSASSTR^2 = \frac{SSA}{SST}

在上例中

R2=SSASST=1456.6086964146.608696=0.349759\begin{aligned} R^2 & = \frac{SSA}{SST} \\ & = \frac{1456.608696}{4146.608696} \\ & = 0.349759 \end{aligned}

这表明，行业(自变量)对被投诉次数(因变量)的影响效应占总效应的34.9759%34.9759\%，而残差效应则占65.0241%65.0241\%。

也有一些资料用R2R^2的根RR。

多重比较方法

什么是多重比较方法

通过上文的讨论，我们知道，不同行业被投诉次数的均值不完全相同。
但究竟哪些均值之间不相等？这种差异到底出现在哪些行业之间？
这就需要作进一步的分析，所使用的方法就是多重比较方法(multiple comparison procedures)，这种方法通过对总体均值之间的配对比较来进一步检验到底哪些均值之间存在差异。

多重比较方法有许多种，这里介绍由费希尔提出的最小显著差异方法(least significant difference)，简称LSD。

步骤

  1. 提出假设
  2. 计算检验的统计量
  3. 计算LSD
  4. 统计决策

提出假设

提出假设：H0:μi=μjH_0 : \mu_i = \mu_j，H1:μi≠μjH_1 : \mu_i \neq \mu_j。

计算检验的统计量

计算检验的统计量：xˉi−xˉj\bar{x}_i - \bar{x}_j

计算LSD

LSD=tα2MSE(1ni+1nj)LSD = t_{\frac{\alpha}{2}} \sqrt{MSE (\frac{1}{n_i} + \frac{1}{n_j})}

式中，tα2t_{\frac{\alpha}{2}}为t分布的临界值，其自由度为n−kn-k，这里的kk是因素中水平的个数；MSEMSE为组内方差；nin_i和njn_j分别是第ii个样本和第jj个样本的样本量。

作出决策

根据显著水平α\alpha决策：
若∣xˉi−xˉj∣>LSD|\bar{x}_i - \bar{x}_j| > LSD，拒绝H0H_0
若∣xˉi−xˉj∣<LSD|\bar{x}_i - \bar{x}_j| < LSD，不拒绝H0H_0

案例

提出假设

检验1：H0:μ1=μ2H_0 : \mu_1 = \mu_2 H1:μ1≠μ2H_1 : \mu_1 \neq \mu_2
检验2：H0:μ1=μ3H_0 : \mu_1 = \mu_3 H1:μ1≠μ3H_1 : \mu_1 \neq \mu_3
⋯\cdots
检验6：H0:μ3=μ4H_0 : \mu_3 = \mu_4 H1:μ3≠μ4H_1 : \mu_3 \neq \mu_4

计算检验统计量

检验1：∣xˉ1−xˉ2∣=∣49−48∣=1| \bar{x}_1 - \bar{x}_2| = |49 - 48| = 1
检验2：∣xˉ1−xˉ3∣=∣49−35∣=14| \bar{x}_1 - \bar{x}_3| = |49 - 35| = 14
⋯\cdots
检验6：∣xˉ3−xˉ4∣=∣35−59∣=24| \bar{x}_3 - \bar{x}_4| = |35 - 59| = 24

计算LSD

检验1：LSD1=2.093×142.526316×(17+16)=13.90LSD_1 = 2.093 \times \sqrt{142.526316 \times (\frac{1}{7} + \frac{1}{6})} = 13.90
检验2：LSD2=2.093×142.526316×(17+15)=14.63LSD_2 = 2.093 \times \sqrt{142.526316 \times (\frac{1}{7} + \frac{1}{5})} = 14.63
⋯\cdots
检验6：LSD6=2.093×142.526316×(15+15)=15.80LSD_6 = 2.093 \times \sqrt{142.526316 \times (\frac{1}{5} + \frac{1}{5})} = 15.80

作出决策

根据显著水平α\alpha决策：
若∣xˉi−xˉj∣>LSD|\bar{x}_i - \bar{x}_j| > LSD，拒绝H0H_0
若∣xˉi−xˉj∣<LSD|\bar{x}_i - \bar{x}_j| < LSD，不拒绝H0H_0

结论如下：
不能认为零售业与旅游业均值之间有显著差异
不能认为零售业与航空公司均值之间有显著差异
不能认为零售业与家电业均值之间有显著差异
不能认为旅游业与航空业均值之间有显著差异
不能认为旅游业与家电业均值之间有显著差异
航空业与家电业均值有显著差异

双因素方差分析

两种类型

双因素方差分析(two-way analysis of variance)：方差分析中涉及两个分类型自变量。
比如，分析影响彩电销售量的时候，需要考虑品牌、销售地区、价格、质量等多个因素的影响。

具体分为两种类型

  1. 无交互作用(non-interaction)或无重复双因素(two-factor without replication)方差分析
    如果两个因素对试验结果的影响是相互独立的，分别判断行因素和列因素对试验数据的影响。
  2. 有交互作用或可重复双因素(two-factor with replication)方差分析
    如果除了行因素和列因素对试验数据的单独影响外，两个因素的搭配还会对结果产生一种新的影响。

无交互作用的双因素分析

应用场景(例子)

举一个"无交互作用的双因素分析"的例子，来说明应用场景

有44个品牌的彩电在55个地区销售，每个品牌在各地区的销售量数据如下：

品牌因素地区因素
地区1地区2地区3地区4地区5
品牌1365350343340323
品牌2345368363330333
品牌3358323353343308
品牌4288280298260298

试分析品牌和地区对彩电的销售量是否有显著影响。α=0.05\alpha=0.05

在上述例子中，品牌和地区是两个分类型自变量，认为是两个没有交互作用的双因素。

同时分析品牌和地区对销售量的影响，分析究竟是一个因素在起作用，还是两个因素在起作用，这就是一个双因素方差分析问题。

分析步骤

提出假设

对行因素提出的假设为：

H0:μ1=μ2=μ3=⋯=μk行因素(自变量)对因变量没有显著影响H1:μi(i=1,2,3,⋯ ,k)不全相等行因素(自变量)对因变量有显著影响式\begin{aligned} H_0 & : \mu_1 = \mu_2 = \mu_3 = \cdots = \mu_k \quad \text{行因素(自变量)对因变量没有显著影响} \\ H_1 & : \mu_i(i=1,2,3,\cdots,k)\text{不全相等} \quad \text{行因素(自变量)对因变量有显著影响式} \end{aligned}

对列因素提出的假设为：

H0:μ1=μ2=μ3=⋯=μr列因素(自变量)对因变量没有显著影响H1:μi(i=1,2,3,⋯ ,r)不全相等列因素(自变量)对因变量有显著影响式\begin{aligned} H_0 & : \mu_1 = \mu_2 = \mu_3 = \cdots = \mu_r \quad \text{列因素(自变量)对因变量没有显著影响} \\ H_1 & : \mu_i(i=1,2,3,\cdots,r)\text{不全相等} \quad \text{列因素(自变量)对因变量有显著影响式} \end{aligned}

构造检验统计量

与单因素方差分析构造统计量的方法一样，也需要从总平方和的分解入手。
不同之处在于：

SST=SSR+SSC+SSESST = SSR + SSC + SSE

  • SST：全部样本观测值与总的样本均值的误差平方和。
  • SSR：行因素所产生的误差平方和。
    计算方法类似"单因素方差分析"的"SSA"，不赘述。
  • SSC：列因素所产生的误差平方和。
    计算方法类似"单因素方差分析"的"SSA"，不赘述。
  • SSE：除行因素和列因素之外的剩余因素所产生的误差平方和。

在上述误差平方和的基础上计算均方，也就是将各平方和除以相应的自由度。
与各误差平方和相对应的自由度分别是：

  • 总平方和SST的自由度为kr−1kr - 1
  • 行因素的误差平方和SSR的自由度为k−1k - 1
  • 列因素的误差平方和SSC的自由度为r−1r - 1
  • 随机误差平方和SSE的自由度为(k−1)(r−1)(k-1)(r-1)

为构造检验统计量，需要计算下列均方：

  • 行因素的均方，MSR，MSR=SSRk−1MSR = \frac{SSR}{k - 1}
  • 列因素的均方，MSC，MSC=SSCr−1MSC = \frac{SSC}{r - 1}
  • 随机误差项的均方，MSE，MSE=SSE(r−1)(k−1)MSE = \frac{SSE}{(r-1)(k-1)}

检验行因素对因变量的影响是否显著，采用统计量为：

FR=MSRMSE∼F((k−1),((k−1)(r−1)))F_R = \frac{MSR}{MSE} \sim F((k-1),((k-1)(r-1)))

检验列因素对因变量的影响是否显著，采用统计量为：

FC=MSRMSE∼F((r−1),((k−1)(r−1)))F_C = \frac{MSR}{MSE} \sim F((r-1),((k-1)(r-1)))

作出统计决策

计算出检验统计量后，根据给定的显著性水平α\alpha和两个自由度，得到相应的临界值FαF_{\alpha}，然后将FRF_R和FCF_C与F_{\alpha进行比较。

  • 若FR>FαF_R > F_{\alpha}，拒绝行的原假设H0H_0，说明所检验的行因素对观测值有显著影响。
  • 若FC>FαF_C > F_{\alpha}，拒绝列的原假设H0H_0，说明所检验的列因素对观测值有显著影响。

关系强度的测量

注意，这里测量的是两个自变量对因变量的联合效应。
行平方和SSR度量了自变量对因变量的影响效应，列平方和SSC度量了自变量对因变量的影响效应，这两个平方和加在一起则度量了两个自变量对因变量的联合效应，联合效应与总平方和的比值定义为：

R2=联合效应总效应=SSR+SSCSSTR^2 = \frac{\text{联合效应}}{\text{总效应}} = \frac{SSR + SSC}{SST}

需要需要分别测量行变量对因变量的效应，列变量对因变量的效应呢？
例如，我们想分别考察品牌和地区与销售量之间的关系，这就需要作每个自变量与销售量的单因素方差分析，并分别计算每个R2R^2。

有交互作用的双因素方差分析

应用场景(例子)

城市道路交通管理部门为研究不同的路段和不同的时间段对行车时间的影响，让一名交通警
察分别在两个路段和高峰期与非高峰期亲自驾车进行试验，通过试验共获得20个行车时间(单位：
min)的数据，得到如下数据：

路段(列变量)
路段1路段2
时段(行变量)高峰期2619
2420
2723
2522
2521
非高峰期2018
1717
2213
2116
1712

试分析路段、时段以及路段和时段的交互作用对行车时间的影响。

方法

与无交互作用的方差分析方法类似，有交互作用的方差分析也需要提出假设、构造检验统计量、统计决策等步骤。

假设行因素有kk个水平，列因素有rr个水平，且每个处理组合下的观察数相等为mm，则总样本量n=k×r×mn = k \times r \times m。

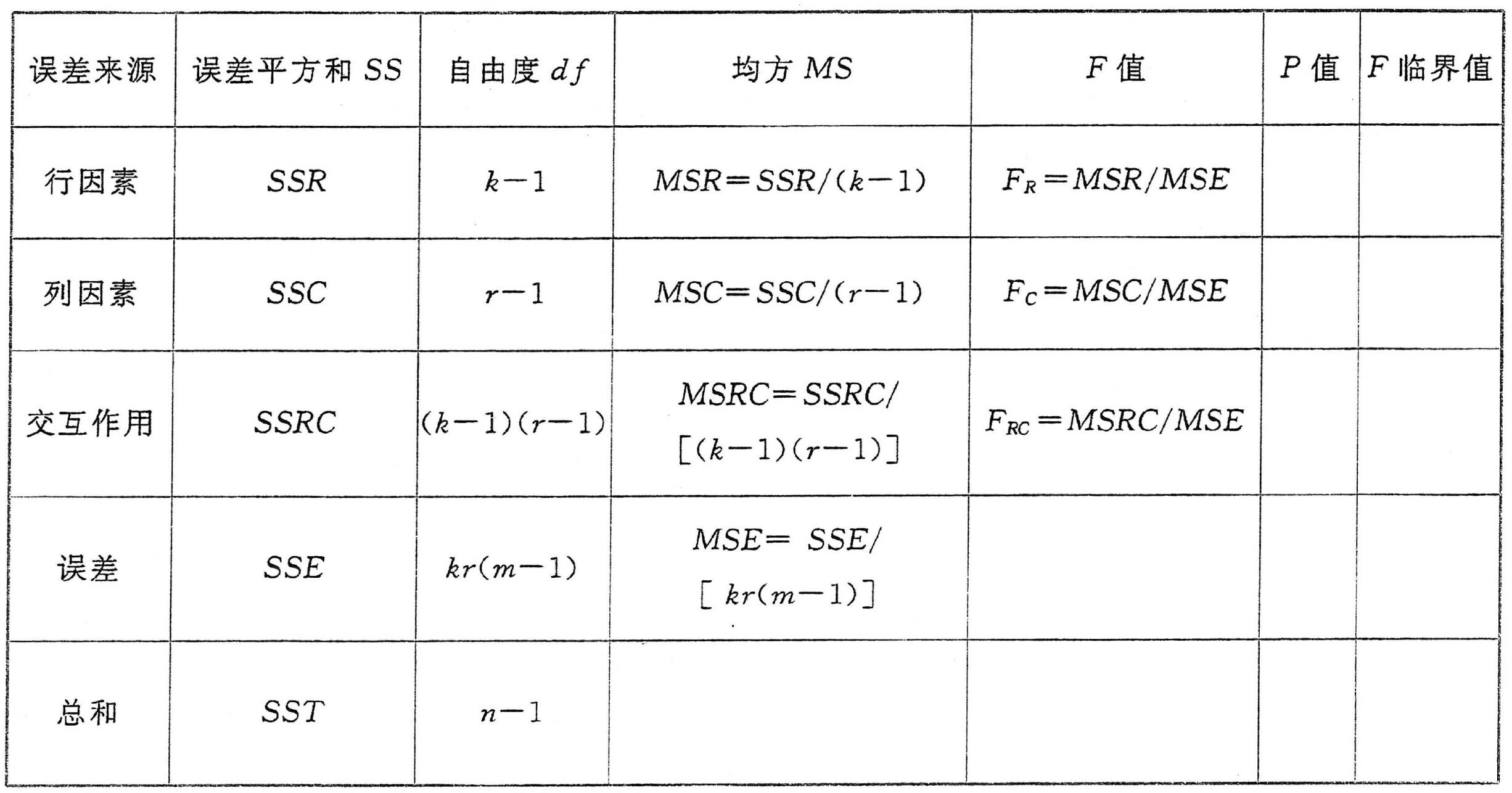
有交互作用的方差分析表如下所示

有交互作用的方差分析表

  • 对于F检验自由度，分子是主效应自由度，分母是误差项的自由度。
    例如，对于行因素的F检验自由度：分子是行因素的主效应自由度，即(k−1k-1)；分母是误差项的自由度，即kr(m−1)kr(m-1)。

方差齐性检验

方差齐性，即方差分析的假定中的"各个总体的方差必须相同"。

方差齐性检验的方法有很多，例如Levene检验(译作"列文检验")，该检验既可用于正态总体，也可用于非正态总体。

对于因素的II个水平，方差齐性检验的假设是：

H0:σ1=σ2=σ3=⋯=σI2H1:σ1,σ2,σ3,⋯ ,σI2至少有两个不等\begin{aligned} H_0 & : \sigma^1 = \sigma^2 = \sigma^3 = \cdots = \sigma_I^2 \\ H_1 & : \sigma^1 , \sigma^2 , \sigma^3 , \cdots , \sigma_I^2 \text{至少有两个不等} \end{aligned}

检验统计量为：

F=MSAMSE∼F(I−1,n−I)F = \frac{MSA}{MSE} \sim F(I-1,n-I)

  • MSA和MSE是对因变量实施yi′=∣yi−Medi∣y_i^{'}=|y_i - Med_i|的变换后进行方差分析得到的处理均方和残差均方。
  • MediMed_i是第ii个水平的yy的中位数。

如果p<αp<\alpha，则拒绝H0H_0，表示各总体的方差不相等。

Python计算

单因素方差分析

为了分析小麦品种对产量的影响，一家研究机构挑选了3个小麦品种，品种1、品种2、品种3，然后选择条件和面积相同的30个地块，每个品种在10个地块上试种，实验获得的产量数据。

品种1 品种2 品种3
729 639 684
738 648 711
711 648 693
729 594 684
702 648 702
801 693 801
828 729 783
783 693 756
765 657 783
774 711 783

检验小麦品种对产量的影响是否显著(α=0.05\alpha=0.05)。

提出如下假设：

H0:μ1=μ2=μ3自变量对因变量没有显著影响H1:μ1,μ2,μ3不全相等自变量对因变量有显著影响\begin{aligned} H_0 & : \mu_1 = \mu_2 = \mu_3 \quad \text{自变量对因变量没有显著影响} \\ H_1 & : \mu_1,\mu_2,\mu_3 \text{不全相等} \quad \text{自变量对因变量有显著影响} \end{aligned}

示例代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
# coding:utf-8

import pandas as pd
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm

df = pd.read_csv('XXX.csv')
# 调整数据格式
df = pd.melt(df, value_vars=['品种1', '品种2', '品种3'], var_name='品种', value_name='产量')

# 拟合方差分析模型
model = ols(formula='产量~品种', data=df).fit()
print(anova_lm(model, type=1))

运行结果：

1
2
3
            df   sum_sq  mean_sq          F    PR(>F)
品种         2.0  45360.0  22680.0  12.312704  0.000158
Residual  27.0  49734.0   1842.0        NaN       NaN

由于p=0.000158<0.05p=0.000158<0.05，拒绝H0H_0。

双因素方差分析

无交互作用的双因素分析

假定在"单因素方差分析"的基础上，除了考虑品种对产量的影响外，还考虑施肥方式对产量的影响。设有甲、乙两种施肥方式，此时，33个品种和22种施肥方式的搭配共有66种组合。如果选择3030个地块进行实验，每一种搭配可以做55次实验，也就是每个品种的样本量为55，这相当于每个品种重复做了55次实验。记录实验取得的数据。
检验品种和施肥方式对产量的影响是否显著(α=0.05\alpha=0.05)。

对行因素提出的假设为：

H0:μ1=μ2=μ3行因素(自变量)对因变量没有显著影响H1:μi(i=1,2,3)不全相等行因素(自变量)对因变量有显著影响式\begin{aligned} H_0 & : \mu_1 = \mu_2 = \mu_3 \text{行因素(自变量)对因变量没有显著影响} \\ H_1 & : \mu_i(i=1,2,3)\text{不全相等} \quad \text{行因素(自变量)对因变量有显著影响式} \end{aligned}

对列因素提出的假设为：

H0:μ1=μ2=μ3列因素(自变量)对因变量没有显著影响H1:μi(i=1,2,3)不全相等列因素(自变量)对因变量有显著影响式\begin{aligned} H_0 & : \mu_1 = \mu_2 = \mu_3 \text{列因素(自变量)对因变量没有显著影响} \\ H_1 & : \mu_i(i=1,2,3)\text{不全相等} \quad \text{列因素(自变量)对因变量有显著影响式} \end{aligned}

示例代码：

1
2
3
4
5
6
7
8
9
10
11
import pandas as pd
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm

df = pd.read_csv('XXX.csv')
df = pd.melt(df, id_vars=['施肥方式'], value_vars=['品种1', '品种2', '品种3'], var_name='品种', value_name='产量')

# 拟合主效应模型
model = ols(formula='产量~品种+施肥方式', data=df).fit()
# 输出方差分析表
print(anova_lm(model, type=1))

运行结果：

1
2
3
4
            df   sum_sq       mean_sq          F        PR(>F)
品种         2.0  45360.0  22680.000000  54.328358  5.184290e-10
施肥方式       1.0  38880.0  38880.000000  93.134328  4.422633e-10
Residual  26.0  10854.0    417.461538        NaN           NaN

检验品种和施肥方式两个因素的pp值(PR(>F))，均小于0.050.05，均拒绝H0H_0。

有交互作用的双因素方差分析

提出三组假设，分别是

  1. 检验品种效应的假设
  2. 检验施肥方式效应的假设
  3. 检验交互效应的假设

示例代码：

1
2
3
4
5
6
7
8
9
10
import pandas as pd
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm

df = pd.read_csv('XXX.csv')
df = pd.melt(df, id_vars=['施肥方式'], value_vars=['品种1', '品种2', '品种3'], var_name='品种', value_name='产量')

model = ols(formula='产量~品种+施肥方式+品种:施肥方式', data=df).fit()
# 输出方差分析表
print(anova_lm(model, type=1))

运行结果：

1
2
3
4
5
            df   sum_sq   mean_sq          F        PR(>F)
品种         2.0  45360.0  22680.00  54.368932  1.220666e-09
施肥方式       1.0  38880.0  38880.00  93.203883  9.729467e-10
品种:施肥方式    2.0    842.4    421.20   1.009709  3.792836e-01
Residual  24.0  10011.6    417.15        NaN           NaN

检验品种和施肥方式的pp值均小于0.050.05，拒绝H0H_0，即两个因素对产量的影响均显著；而检验交互效应的p=0.379p=0.379，大于0.050.05，不拒绝H0H_0，认为交互效应对产量的影响不显著。

方差齐性检验

用Levene方法检验不同品种的产量和不同施肥方式的产量是否满足方差齐性(α=0.05\alpha=0.05)。

不同品种产量的Levene检验，示例代码：

1
2
3
4
5
6
7
8
9
10
11
import pandas as pd
from scipy.stats import levene

df = pd.read_csv('XXX.csv')

sample1 = df.loc[df['品种'] == '品种1', '产量'].values
sample2 = df.loc[df['品种'] == '品种2', '产量'].values
sample3 = df.loc[df['品种'] == '品种3', '产量'].values

F, p_value = levene(sample1, sample2, sample3)
print(F, p_value)

运行结果：

1
0.9291859695565853 0.4071375497000196

由于pp值均大于0.050.05，不拒绝H0H_0。

  • 对于不同施肥方式产量的Levene检验，类似。
  • 读取的CSV文件内容如下： 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    施肥方式,品种,产量
    甲,品种1,729
    甲,品种1,738
    甲,品种1,711

    【部分内容略】

    乙,品种3,756
    乙,品种3,783
    乙,品种3,783

参考资料：

统计学 - 贾俊平 何晓群 金勇进 - 中国人民大学出版社

应用统计考研通关宝典 - 索瑜 - 北京理工大学出版社

https://www.bilibili.com/video/BV17h411G767

统计学 基于Python - 贾俊平 吴翌琳 - 中国人民大学出版社

https://cloud.tencent.com/developer/news/175814

文章作者: Kaka Wan Yifan
文章链接: https://kakawanyifan.com/30107
版权声明: 本博客所有文章版权为文章作者所有，未经书面许可，任何机构和个人不得以任何形式转载、摘编或复制。
留言板