16.总结

引言和附录部分，我们不做总结。

核心理论

2.神经网络基础

原文连接：https://kakawanyifan.com/10402

全连接层

全连接层的定义：
每一个结点都与上一层的所有结点相连。

神经网络

神经网络的定义：
由神经元相互连接而成的网络叫做神经网络。

神经网络的结构：

1. 输入层
2. 隐藏层
3. 输出层

输出层

不同的应用场景有不同的输出层。

输出值属于实数空间：
$o_i \in R^d$
常见的应有场景：回归。

输出值在[0,1]的区间：
$o_i \in [0,1]$
常见的应有场景：二分类。
激活函数：：sigmoid。

$$sigmoid(x) = \frac{1}{1 + e^{-x}}$$

实现方法：

tf.sigmoid()

输出值在[0,1]的区间，并且所有输出值之和为1：
$o_i \in [0,1] \text{且} \sum o_i = 1$
常见的应有场景：二分类和多分类。
激活函数：SoftMax。

$$softmax(z_i) = \frac{e^{z_i}}{\sum_{1}^{j}{e^{z_j}}}$$

• 其中$e$是自然对数

实现方法：

tf.nn.softmax()

输出值在[-1,1]之间：
$o_i \in [-1,1]$
激活函数：$\tanh$。

$$tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$$

实现方法：

tf.tanh()

损失函数

常见的损失函数有两中：

1. 均方误差(MSE)
2. 交叉熵损失(Cross Entropy Loss)

均方误差：

$$MSE(\bold{y},\bold{o}) = \frac{1}{d_{out}}\sum_{i=1}^{d_{out}}(y_i - o_i)^2$$

有时候，为了计算方便，会有非标的均方误差。

两种实现方法：

tf.losses.MSE()

tf.keras.losses.mean_squared_error()

交叉熵损失：
交叉熵的公式

$$H(\bold{p}||\bold{q}) = - \sum_i p_i \log_2 q_i$$

和KL散度的关系
$D_{KL}(\bold{p}||\bold{q})$代表$\bold{p}$和$\bold{q}$的KL散度：

$$D_{KL}(\bold{p}||\bold{q}) = \sum p_i \log\Big( \frac{p_i}{q_i} \Big)$$

$$H(\bold{p}||\bold{q}) = H(\bold{p}) + D_{KL}(\bold{p}||\bold{q})$$

即

$$H(\bold{p}||\bold{q}) = \text{p的熵} + \text{p和q的KL散度}$$

KL散度和交叉熵的不对称性

• $D_{KL}(\bold{p}||\bold{q}) \neq D_{KL}(\bold{q}||\bold{p})$
• $H(\bold{p}||\bold{q}) \neq H(\bold{q}||\bold{p})$

当$\bold{p}$采用One-Hot编码时

$$H(\bold{p}||\bold{q}) = - \log{o_j}$$

其中$j$为One-Hot编码中1所在的索引号。

实现方法

tf.losses.categorical_crossentropy()

3.梯度下降

原文连接：https://kakawanyifan.com/10403

梯度

整体框架：

$$\text{导数} \ \longrightarrow \ \text{偏导数} \ \longrightarrow \ \text{方向导数} \ \longrightarrow \ \text{梯度}$$

导数：

$$f'(x_0) = \lim_{\Delta x \rightarrow 0}\frac{\Delta y}{\Delta x} = \frac{f(x+\Delta x) - f(x)}{\Delta x}$$

即，随着自变量$x$的变化，$y$的变化。是$y$在$x$上的变化率。

偏导数：

$$\frac{\partial f(x,y)}{\partial x} = \lim_{\Delta x \rightarrow 0}\frac{f(x_0 + \Delta x,y_0) - f(x_0,y_0)}{\Delta x}$$

即，$f(x,y)$在点$(x_0,y_0)$处对$x$的偏导数。同理，我们可以知道$f(x,y)$在点$(x_0,y_0)$处对$y$的偏导数。
函数在不同的坐标轴上的变化率就是偏导数。

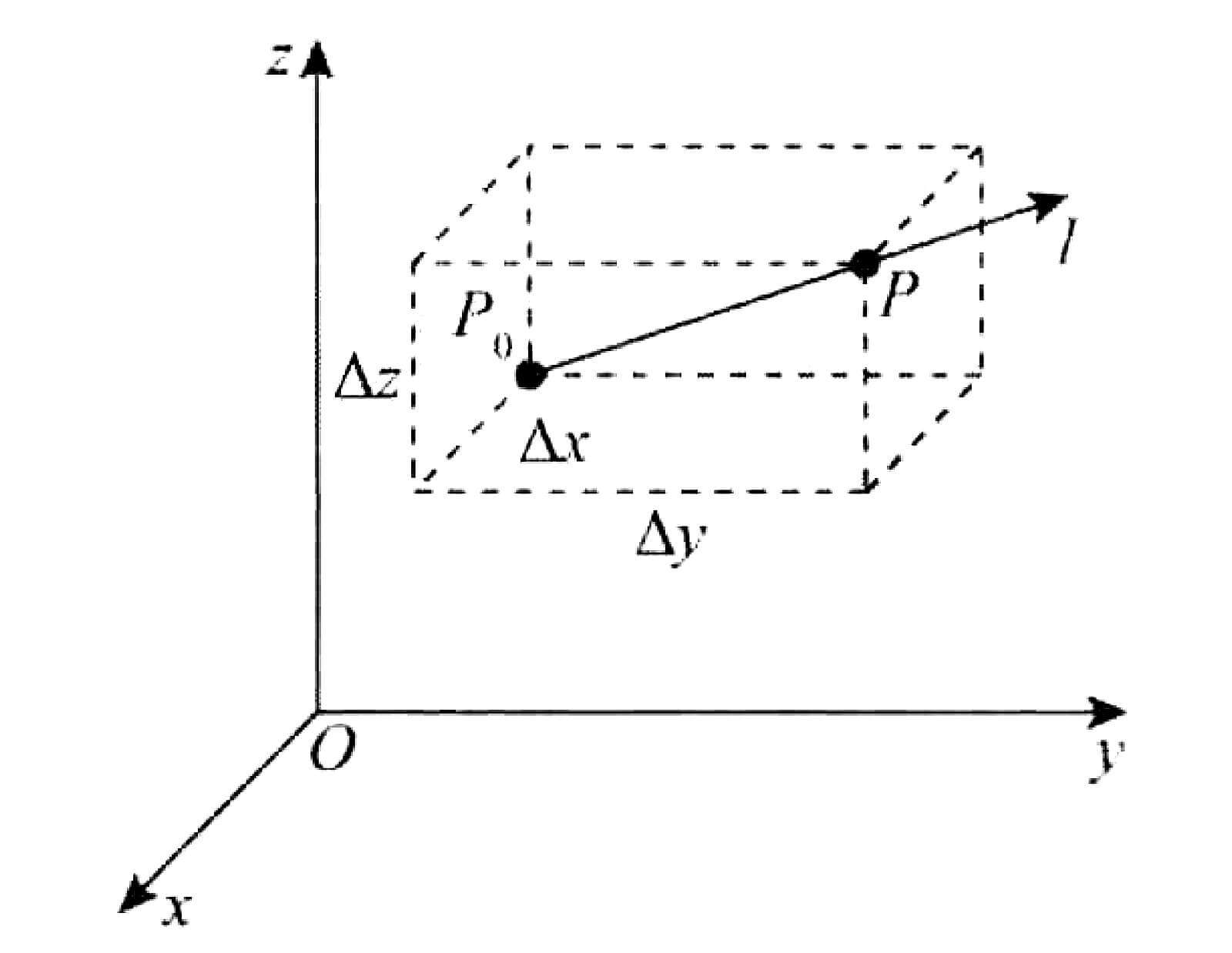
方向导数：
方向导数的定义
函数在某点，沿着某特定方向（不一定是坐标轴）的变化率就是方向导数。

假设存在一个三元函数$u=u(x,y,z)$在点$P_0(x_0,y_0,z_0)$的某空间领域$U\subset\bold{R}^3$内有定义，$l$为从点$P_0$出发的射线，$P(x,y,z)$为$l$上的且$U$内的任一点。则有：

$$\begin{cases} x - x_0 = \Delta x = t \cos \alpha \\ y - y_0 = \Delta y = t \cos \beta \\ z - z_0 = \Delta z = t \cos \gamma \end{cases}$$

其中$t$表示$P$到$P_0$之间的距离，$t=\sqrt{(\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2}$。

$$\lim_{t \rightarrow 0^+}\frac{u(P) - u(P_0)}{t} = \lim_{t \rightarrow 0^+}\frac{u(x_0 + t\cos\alpha,y_0 + t\cos\beta,z_0 + t\cos\gamma) - u(x_0,y_0,z_0)}{t}$$

这个极限，就是函数$u=u(x,y,z)$在$P_0$处，沿方向$l$的方向导数，记作$\frac{\partial u}{\partial l}\Big|_{p_{0}}$

方向导数的计算公式：
假设存在一个三元函数$u=u(x,y,z)$在$P_0(x_0,y_0,z_0)$处可微，则有：

$$\frac{\partial u}{\partial l}\bigg|_{p_{0}} = u'_{x}(P_0)\cos\alpha + u'_{y}(P_0)\cos\beta + u'_{z}(P_0)\cos\gamma$$

其中，$\cos\alpha$、$\cos\beta$、$\cos\gamma$是方向$l$的方向余弦。

梯度：
把方向导数的计算公式，写成这种形式：

$$\frac{\partial u}{\partial l}\bigg|_{p_{0}} = \left[ \begin{matrix} u'_{x}(P_0) \quad u'_{y}(P_0) \quad u'_{z}(P_0) \end{matrix} \right] \cdot \left[ \begin{matrix} \cos\alpha \\ \cos\beta \\ \cos\gamma \\ \end{matrix} \right]$$

其中，$[u'_{x}(P_0),u'_{y}(P_0),u'_{z}(P_0)]$就是$\bold{grad}\ u$，梯度。

方向导数和梯度的关系：
为什么梯度是方向导数最大的方向？

$$\begin{aligned} \frac{\partial u}{\partial l}\bigg|_{p_{0}} &= \left[ \begin{matrix} u'_{x}(P_0) \quad u'_{y}(P_0) \quad u'_{z}(P_0) \end{matrix} \right] \cdot \left[ \begin{matrix} \cos\alpha \\ \cos\beta \\ \cos\gamma \\ \end{matrix} \right] \\ &= \bold{grad}\ u|_{P_0} \cdot \overrightarrow{l} \\ &= \bold{|}\bold{grad}\ u|_{P_0}\bold{|} * \bold{|}\overrightarrow{l}\bold{|} * \cos\theta \end{aligned}$$

其中，$\theta$是$\bold{grad}\ u|_{P_0}$和$\overrightarrow{l}$的夹角。而且，$\bold{|}\overrightarrow{l}\bold{|} = 1$，则有

$$\frac{\partial u}{\partial l}\bigg|_{p_{0}} = \bold{|}\bold{grad}\ u|_{P_0}\bold{|} * \cos\theta$$

显然，当$\theta = 0$时候，$\cos\theta$取得最大值，$\frac{\partial u}{\partial l}|_{p_{0}}$也取得最大值。

函数在某点的梯度是一个向量，它的方向与取得最大方向导数的方向一致，而它的模为方向导数的最大值。

求解梯度的实现方法

1. 首先，我们需要用with tf.GradientTape() as tape:把函数表达式包进去。
2. 用[w_grad] = tape.gradient(func,[w])求解梯度，传入函数和需要求解的参数。返回参数的梯度。

示例代码：

import tensorflow as tf

with tf.GradientTape() as tape:
    x = tf.Variable(1.0)
    y = tf.Variable(2.0)
    tape.watch([x,y])
    z = tf.math.pow(x,2) + tf.math.pow(y,2)

print(tape.gradient(z,[x,y]))

运行结果：

[<tf.Tensor: shape=(), dtype=float32, numpy=2.0>, <tf.Tensor: shape=(), dtype=float32, numpy=4.0>]

损失函数的梯度

均方误差：
均方误差的公式：

$$MSE(\bold{y},\bold{o}) = \frac{1}{d_{out}}\sum_{i=1}^{d_{out}}(y_i - o_i)^2$$

均方误差的梯度：

$$\frac{\partial L}{\partial o_i} = (o_i - y_i)$$

交叉熵
交叉熵的公式：

$$L = - \sum_{k=1}^{K} y_k \log(p_k)$$

交叉熵的梯度，非One-Hot编码：

$$\frac{\partial L}{\partial z_i} = p_i\Big( y_i + \sum_{k \neq i}^{K} y_k) - y_i \Big)$$

交叉熵的梯度，One-Hot编码：

$$\frac{\partial L}{\partial z_i} = p_i - y_i$$

4.反向传播

原文链接：https://kakawanyifan.com/10404

链式法则

假设存在函数$f(u)$，而$u$也是一个函数，$u = g(x)$，则有

$$\frac{\partial f(g(x))}{\partial x} = \frac{\partial f(u)}{\partial u} \frac{\partial g(x)}{\partial x} = f'(u) g'(x)$$

反向传播算法

反向传播算法的定义：
误差以某种形式在各层的表现，并以此来修正各层的权重。

对于输出层节点，$k \in K$，有：

$$\frac{\partial loss}{\partial w_{jk}} = o_j\delta_k^{K}$$

$$\delta_k^{K} = (o_k - t_k)(o_k - o_k^2)$$

对于输出层的前一个隐藏层，$j \in J$，有：

$$\frac{\partial loss}{\partial w_{ij}} = o_i\delta_j^J$$

$$\delta_j^J = (o_j - o_j^2)\sum_{k = 1}^{K}\delta_k^{K} w_{jk}$$

对于再前一个隐藏层，$i \in I$，有

$$\frac{\partial loss}{\partial w_{ni}} = o_n\delta_i^{I}$$

$$\delta_i^I = (o_i - o_i^2)\sum_{j = 1}^{J}\delta_j^{I} w_{ij}$$

其中，$o_n$是输入。

依照此规律，只需要循环迭代计算每一层每个节点的$\delta_k^{(K)}$、$\delta_j^{(J)}$、$\delta_i^{(I)}$的值即可求得当前层的偏导数，从而得到每一层每一个节点的权值的梯度。

反向传播的梯度下降方法：

1. 网络初始化：对各连接权重赋一个初始值，设定误差函数，设定学习率和最大学习次数。
2. 随机选取：随机选取第n个训练样本以及对应的期望输出。
3. 隐藏层计算：计算隐藏层各神经元的输入和输出。
4. 求偏导数：利用网络期望输出和实际输出，计算误差函数对输出层的各神经元的偏导数。
5. 修正输出层权值：利用输出层各神经元的偏导数和隐藏层各神经元的输出来修正输出层的权值。
6. 修正隐藏层权值：利用当前隐藏层各神经元的偏导数和输入层各神经元的输入修正当前隐藏层的权值。
7. 计算误差：用修正后的权重，计算新模型的误差。
8. 如此迭代更新。

5.过拟合

原文链接：https://kakawanyifan.com/10405

什么是过拟合

过拟合：
过于复杂的模型，在训练集上表现非常好，但在测试集上表现不如人意。这种现象就是过拟合。

模型的复杂程度：
模型的复杂程度用模型的容量来衡量，模型的容量就是模型假设空间的大小，模型假设空间的大小就是模型可以表示的函数集的大小。

泛化能力：
通过训练集所训练出的模型在测试集上也能表现良好，这个就叫泛化能力较好。反之，则称为泛化能力较差。

交叉验证

例如：4折交叉验证。

第一份	第二份	第三份	第四份	结果
验证集	训练集	训练集	训练集	当前情况下，模型的准确率
训练集	验证集	训练集	训练集	当前情况下，模型的准确率
训练集	训练集	验证集	训练集	当前情况下，模型的准确率
训练集	训练集	训练集	验证集	当前情况下，模型的准确率

在每一种的训练集和验证集下，我们都可以一个得到模型的准确率，对准确率求平均。通过这种方法让模型的评估结果更加准确可信，看看到底是不是过拟合。

1. 过拟合：
   一个假设在训练数据上能获得比较好的拟合， 但是在训练数据外的数据集上却不能很好地拟合数据，此时认为这个假设出现了过拟合的现象。

2. 欠拟合：
   一个假设在训练数据上不能获得更好的拟合， 但是在训练数据外的数据集上也不能很好地拟合数据，此时认为这个假设出现了欠拟合的现象。

实现方法：在model.fit()中传入validation_split的参数。

model.fit(x_train, y_train, epochs=5,validation_split=validation_split, verbose=1)

重新设计模型

如果真的是过拟合了，可以重新设计模型。

提前停止

间隔一定数量的epoch或者一定数量的step，做交叉验证，如果模型的效果持续一定的次数没有提升，就提前停止。

实现方法：

early_stopping=tf.keras.callbacks.EarlyStopping(monitor='val_loss', min_delta=0,
                              patience=0, verbose=0, mode='auto',
                              baseline=None, restore_best_weights=False)

model.fit(callbacks = [early_stopping])

参数介绍：

1. monitor：被监测的数据。
2. min_delta：在被监测的数据中被认为是提升的最小变化， 例如，小于min_delta的绝对变化会被认为没有提升。
3. patience：没有进步的训练轮数，在这之后训练就会被停止。
4. verbose：详细信息模式。
5. mode：{auto,min,max} 其中之一。 在min模式中， 当被监测的数据停止下降，训练就会停止；在max模式中，当被监测的数据停止上升，训练就会停止；在 auto 模式中，方向会自动从被监测的数据的名字中判断出来。
6. baseline：要监控的数量的基准值。 如果模型没有显示基准的改善，训练将停止。
7. restore_best_weights：是否从具有监测数量的最佳值的时期恢复模型权重。 如果为False，则使用在训练的最后一步获得的模型权重。

Dropout

Dropout通过随机断开神经网络的连接，减少每次训练时实际参与的参数量；需要注意的是，在测试的时候，Dropout会恢复所有的连接，保证模型测试时获得最好的性能。

两种实现方法：

tf.nn.dropout(x, rate)

model.add(layers.Dropout())

正则化

在损失函数中加入模型复杂度的惩罚。

$$L(f_\theta(\bold{x},y)) + \lambda \cdot \Omega(\theta)$$

$$\Omega(\theta) = \sum||\theta_i||_l$$

其中

• $\lambda$是正则化力度，这是一个超参数。
• $||\theta_i||_l$表示参数$\theta_i$的$l$范数。

常见的有

1. $L0$正则化：$\Omega(\theta) = \sum||\theta_i||_0$，表示$\theta_i$中非零元素的个数。
2. $L1$正则化：$\Omega(\theta) = \sum||\theta_i||_1$，表示$\theta_i$中非所有元素的绝对值之和。
3. $L2$正则化：$\Omega(\theta) = \sum||\theta_i||_2$，表示$\theta_i$中非所有元素的平方和。

两种实现方法：

# L1 Regularization Penalty
tf.keras.regularizers.L1(0.3)
# L2 Regularization Penalty
tf.keras.regularizers.L2(0.1)
# L1 + L2 penalties
tf.keras.regularizers.L1L2(l1=0.01, l2=0.01)

layer = tf.keras.layers.Dense(
    5, input_dim=5,
    kernel_initializer='ones',
    kernel_regularizer=tf.keras.regularizers.L1(0.01),
    activity_regularizer=tf.keras.regularizers.L2(0.01))

动量

添加动量后的修改梯度下降：

$$\bold{z}^{k+1} = \beta\bold{z}^{k} + f'(\bold{w}^k)$$

$$\bold{w}^{k+1} = \bold{w}^{k} - lr * \bold{z}^{k+1}$$

实现方法：通过设置momentum参数实现。

optimizers.SGD(learning_rate=0.02,momentum=0.9)

optimizers.RMSprop(learning_rate=0.01,momentum=0.02)

学习率衰减

学习效率从大到小，逐步衰减。

实现方法：每迭代一定的epoch或者一定的step后，为优化器设置新的学习率。

optimizer = optimizers.SGD(learning_rate=0.2)

for epoch in range(100):
    
    # 部分代码略

    optimizer.learning_rate = 0.2 * (100-epoch)/100
    
    # 部分代码略

数据增强

人为添加脏数据或噪音数据等。

常见模型

6.卷积神经网络

原文链接：https://kakawanyifan.com/10406

卷积

卷积的两个特点：

1. 局部连接
2. 权值共享

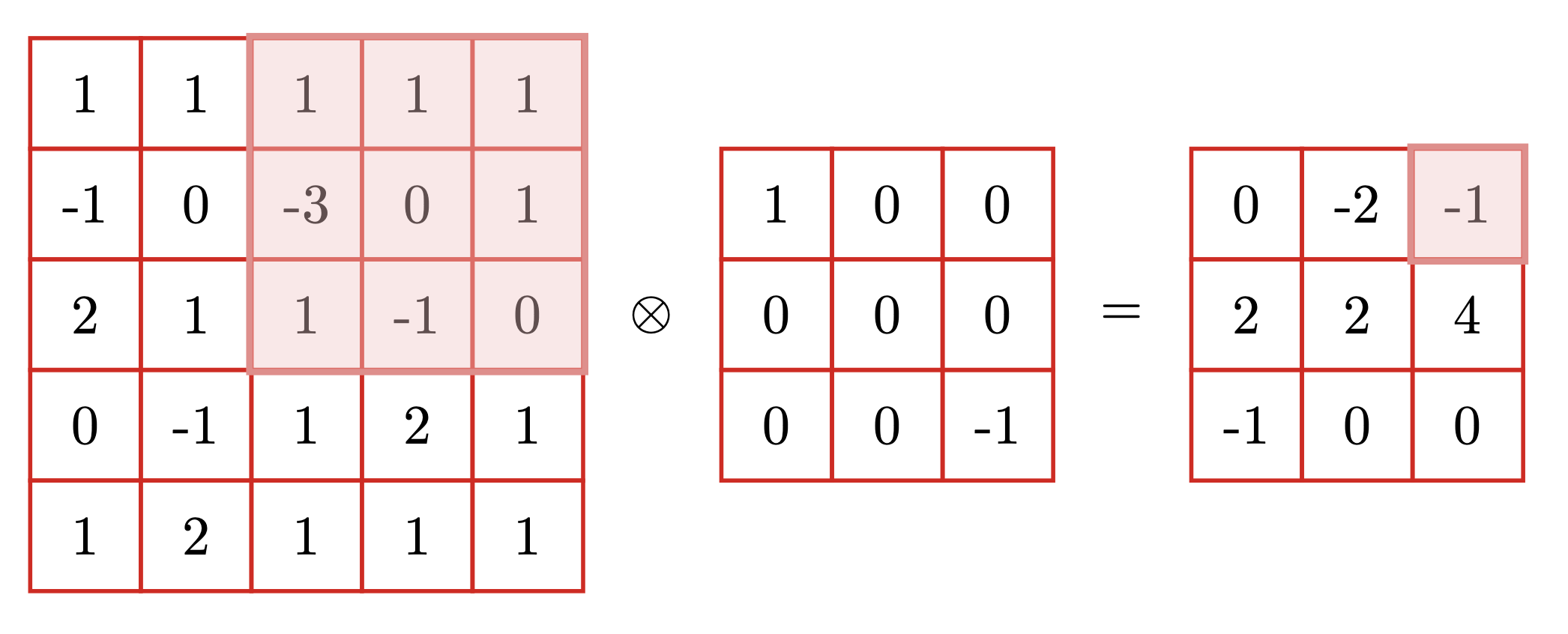
卷积的运算法则：
翻转卷积

$$y = \sum_{u=1}^{m} \sum_{v=1}^{n} = w_{u,v} \cdot x_{m-u+1,n-v+1}$$

不翻转卷积：

$$y = \sum_{u=1}^{m} \sum_{v=1}^{n} = w_{u,v} \cdot x_{u,v}$$

通常，在神经网络中，我们所指的的卷积，都是不翻转卷积。

输出和步长、填充的关系：
卷积层的输出尺寸$[h',w']$由卷积核的大小$k$，步长$s$，上下填充数量$p_h$，左右填充数量$p_w$以及输入$\bold{X}$的高宽$[h,w]$共同决定：

$$h' = \frac{h + 2 \cdot p_h - k}{s} + 1$$

$$w' = \frac{w + 2 \cdot p_w - k}{s} + 1$$

• 特别注意：这里只考虑上下填充数量$p_h$，左右填充数量$p_w$相同的情况。

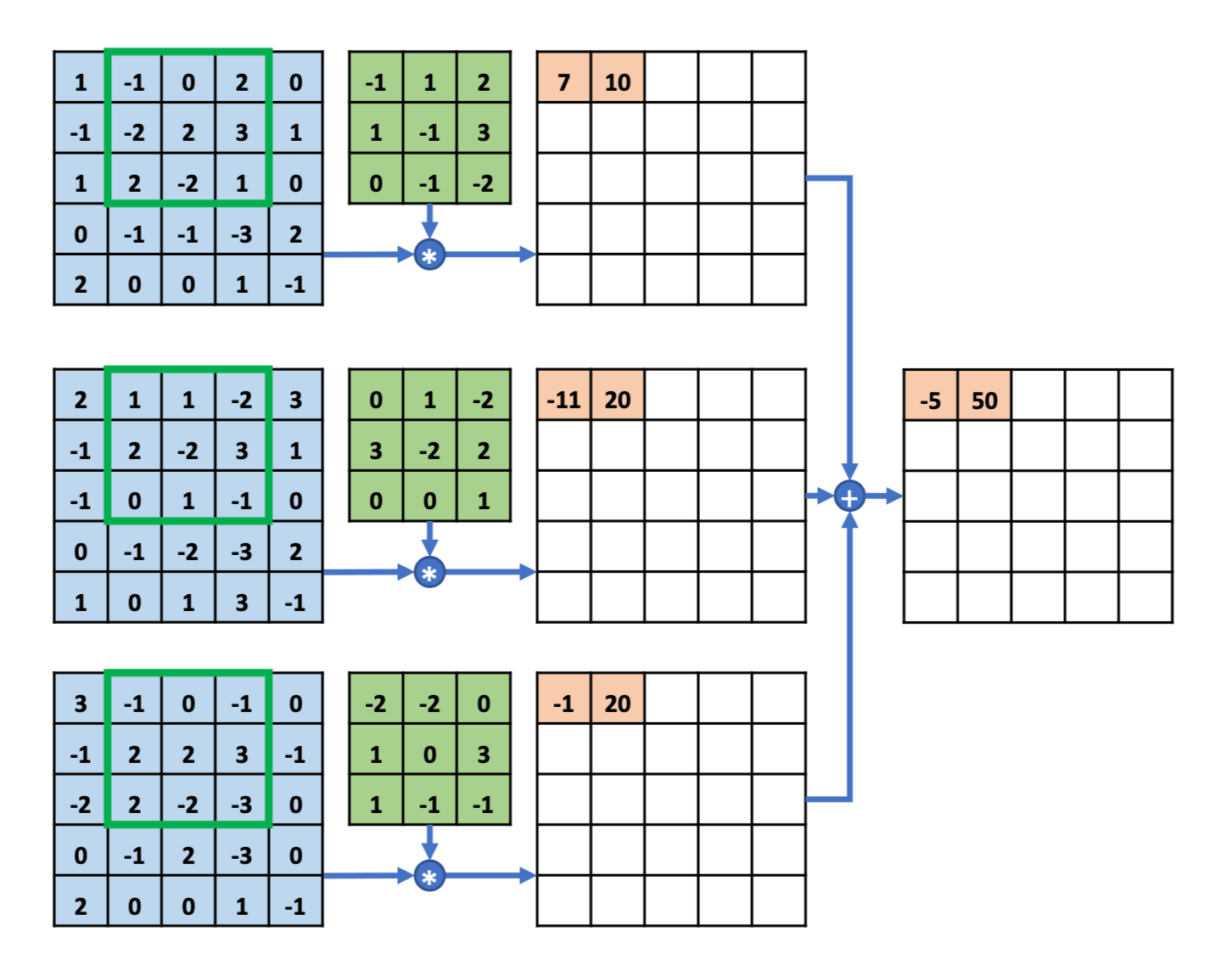
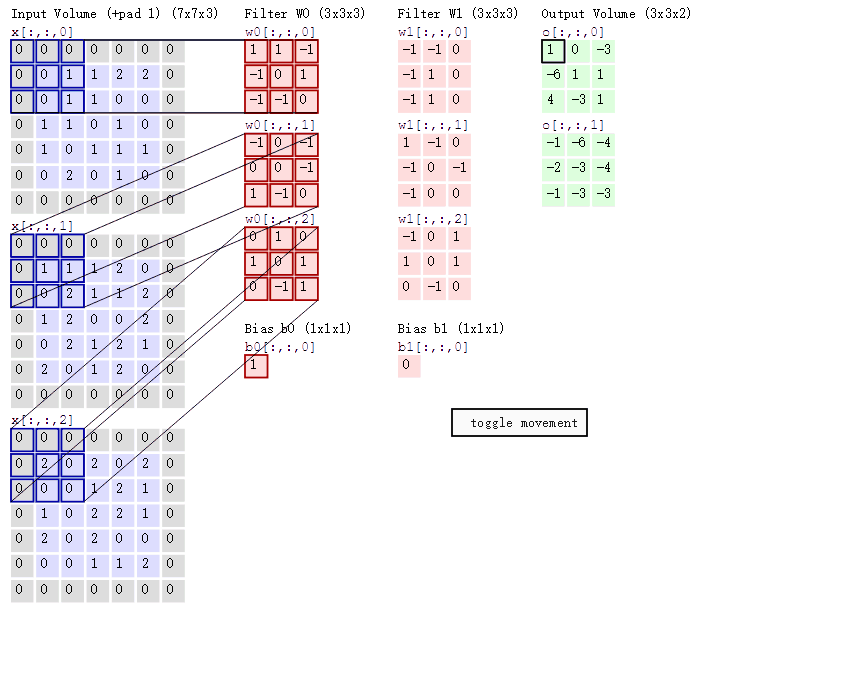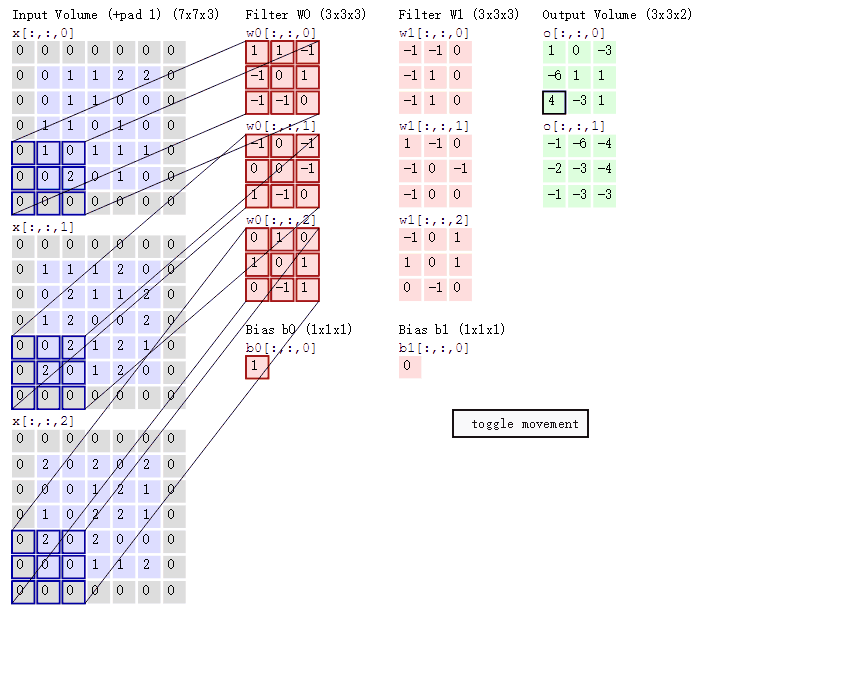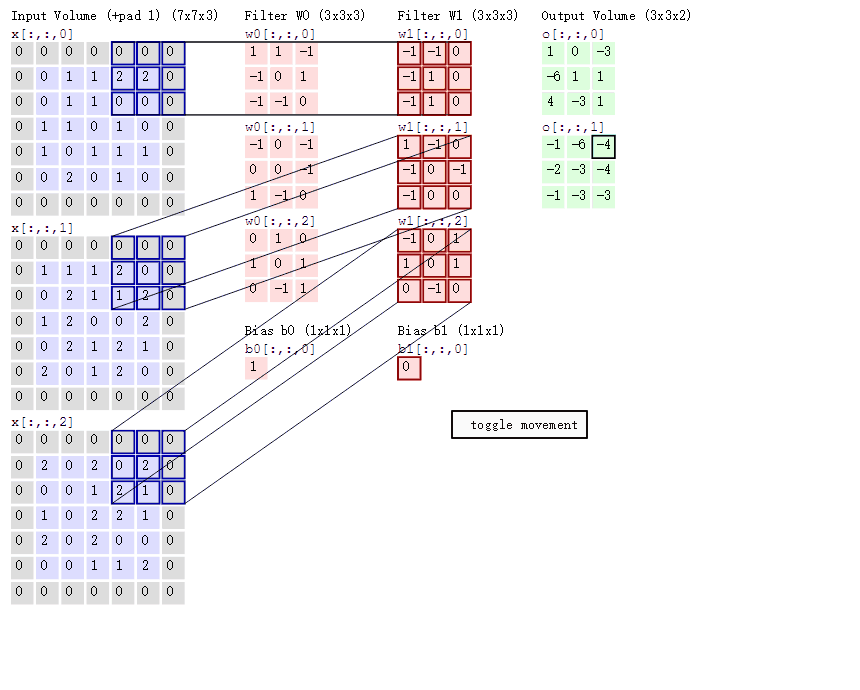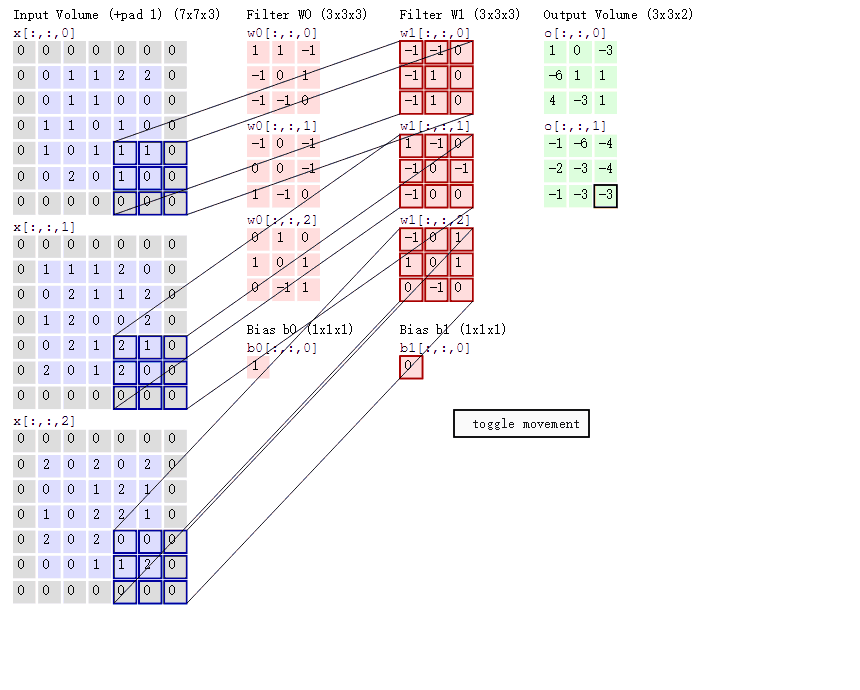
多通道输入的计算：
多通道输入，单卷积核

多通道输入，多卷积核

有几个卷积核，结果就有几个通道。

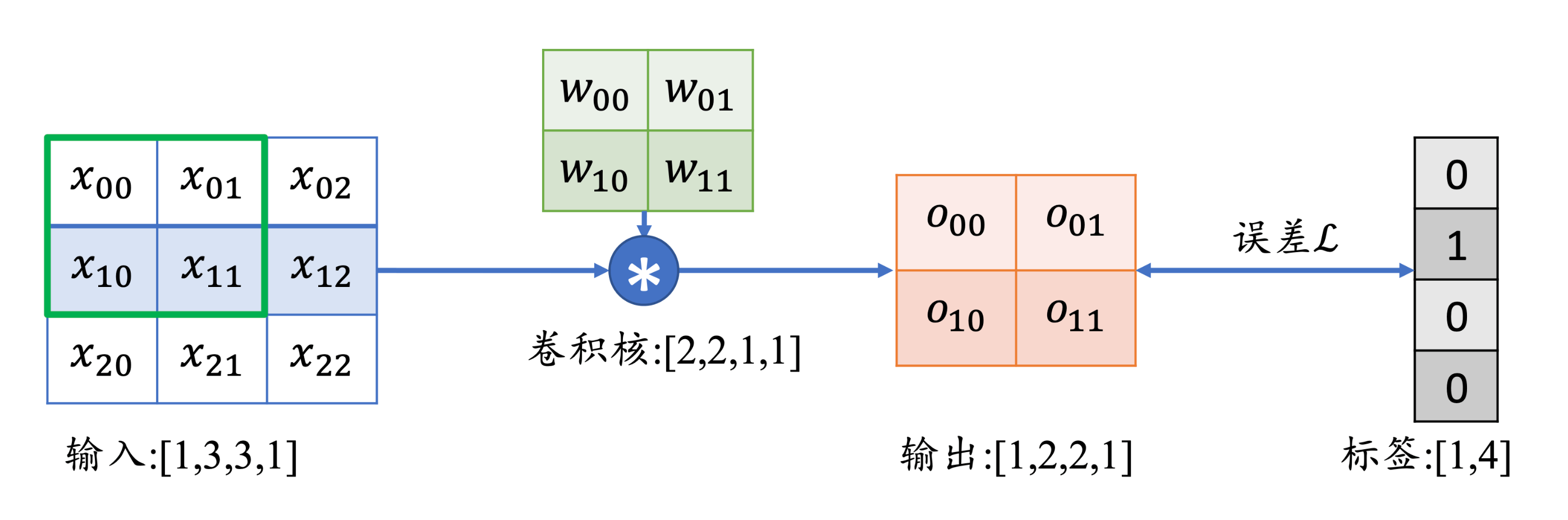
卷积的梯度：

$$\frac{\partial L}{\partial w_{00}} = \sum_{i \in \{00,01,10,11\}} \frac{\partial L}{\partial o_i} \frac{\partial o_i}{\partial w_{00}}$$

卷积层的两种实现方法：

tf.nn.conv2d(input=x,filters=w,strides=1,padding=[[0,0],[0,0],[0,0],[0,0]])

layer = layers.Conv2D()

池化

池化的一个特点：
局部连接

常见的两种池化：

1. 最大池化层(Max Pooling)从局部相关元素集中选取最大的一个元素值。
2. 平均池化层(Average Pooling)从局部相关元素集中计算平均值并返回。

池化层的两种实现方法：

tf.nn.max_pool2d()

layers.MaxPooling2D()

BatchNorm

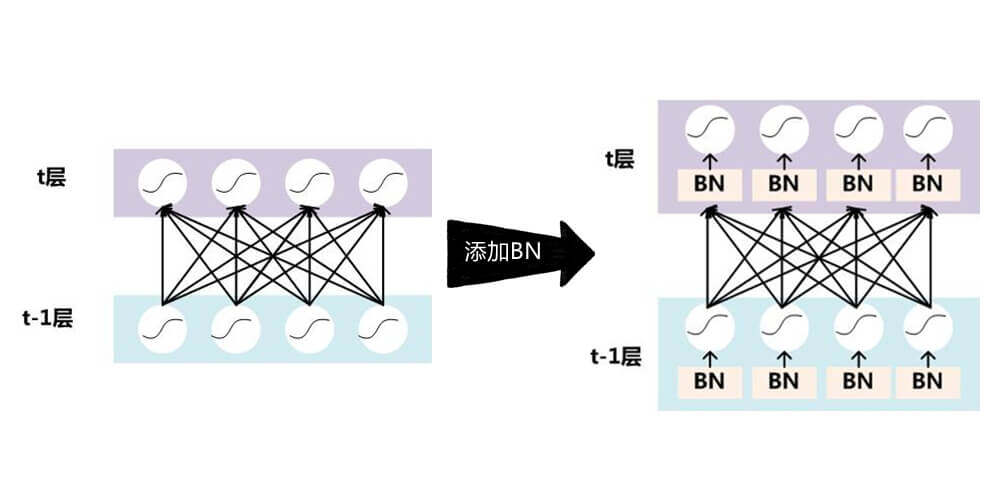
BatchNorm层所处的位置

BatchNorm的计算公式
训练阶段

$$\tilde{x}_{train} = \frac{x_{train} - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}} \cdot \gamma + \beta$$

• $\mu_B$和$\sigma_B^2$是当前Batch的均值和方差。
• $\epsilon$是为防止出现除0错误而设置的较小数字，如$10^{-9}$。
• $\gamma$和$\beta$，将由反向传播算法进行优化。
  同时按照

$$\mu_r \leftarrow momentum \cdot \mu_r + (1 - momentum) \cdot \mu_B$$

$$\sigma_r^2 \leftarrow momentum \cdot \sigma_r^2 + (1 - momentum) \cdot \sigma_B^2$$

迭代更新全局训练数据的统计值$\mu_r$和$\sigma_r^2$。

所以，Batch_Size也是一个超参数了，但在大样本的情况下，影响有限。

测试阶段

$$\tilde{x}_{test} = \frac{x_{test} - \mu_r}{\sqrt{\sigma_r^2 + \epsilon}} \cdot \gamma + \beta$$

测试阶段的$\mu_r$和$\sigma_r^2$是之前训练阶段所得到的$\mu_r$和$\sigma_r^2$。

BatchNorm的实现方法：

layer = layers.BatchNormalization()

7.经典卷积神经网络

原文链接：https://kakawanyifan.com/10407

这一章我们讨论了5个经典的卷积网络：

1. AlexNet
2. VGG
3. GoogLeNet
4. ResNet
5. DenseNet

但对于这5个经典卷积神经网络，我们都不总结，因为他们都是网络结构不同的卷积神经网络。但是，有一些网络有一些小技巧。
比如：

1. GoogLeNet的Inception
2. ResNet的Skip Connection

Inception

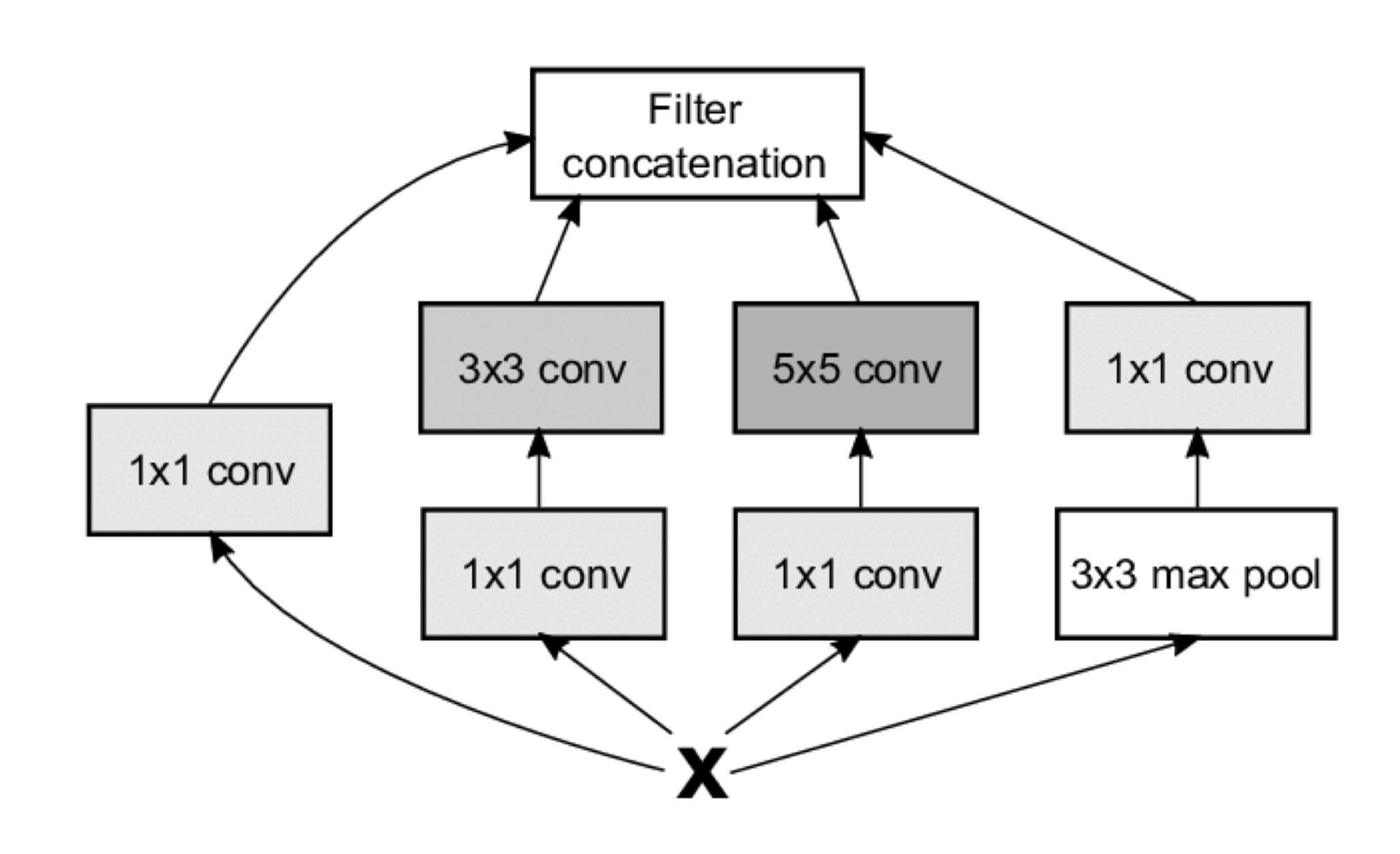
Inception的结构如图所示：

由4个子网络组成，从左到右依次是：

1. 1*1卷积层
2. 1*1卷积层 + 3*3卷积层
3. 1*1卷积层 + 5*5卷积层
4. 3*3最大池化层 + 1*1卷积层

这里每一个卷积层和池化层的步长都是1，padding都是'same'。所以最后的四个子网络的输出和一开始的输入，h相同，w也相同。
四个子网络的输出，会通过Filter concatenation进行合并。

concatenated_tensor = tf.concat(3, [branch1, branch2, branch3, branch4])

即，如果存在4个[10*10*3]的数据，会按照深度拼接成[10*10*12]的数据。

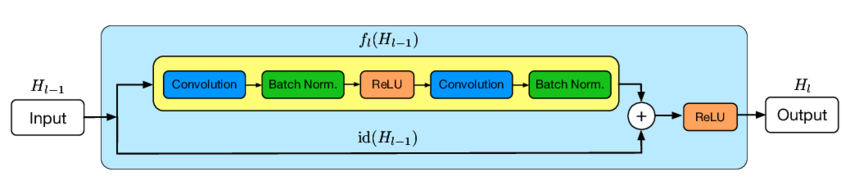
Skip Connection

Skip Connection的机制如下：

$\bold{H}(x) = x + \bold{F}(x)$。
为了保证$x$和$\bold{F}(x)$的Shape相同，可以在Skip Connection中添加额外的卷积运算，比如$identity(x)$。其中$identity(x)$以1*1的卷积运算居多，主要用于调整输入的通道数。

8.循环神经网络

原文链接：https://kakawanyifan.com/10408

序列

序列的定义：
序列(Sequence)是具有先后顺序的数据。

One-Hot的缺点：
无法表达词语之间的相似性

Word Embedding：

$$\begin{pmatrix}1 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 \end{pmatrix}\begin{pmatrix}w_{11} & w_{12} & w_{13}\\ w_{21} & w_{22} & w_{23}\\ w_{31} & w_{32} & w_{33}\\ w_{41} & w_{42} & w_{43}\\ w_{51} & w_{52} & w_{53}\\ w_{61} & w_{62} & w_{63}\end{pmatrix}=\begin{pmatrix}w_{11} & w_{12} & w_{13}\\ w_{21} & w_{22} & w_{23}\end{pmatrix}$$

输入是One-Hot的全连接层，参数是"字向量表"。

循环神经网络

全连接层的缺点：
不能感知序列顺序，导致句子整体语义的缺失。

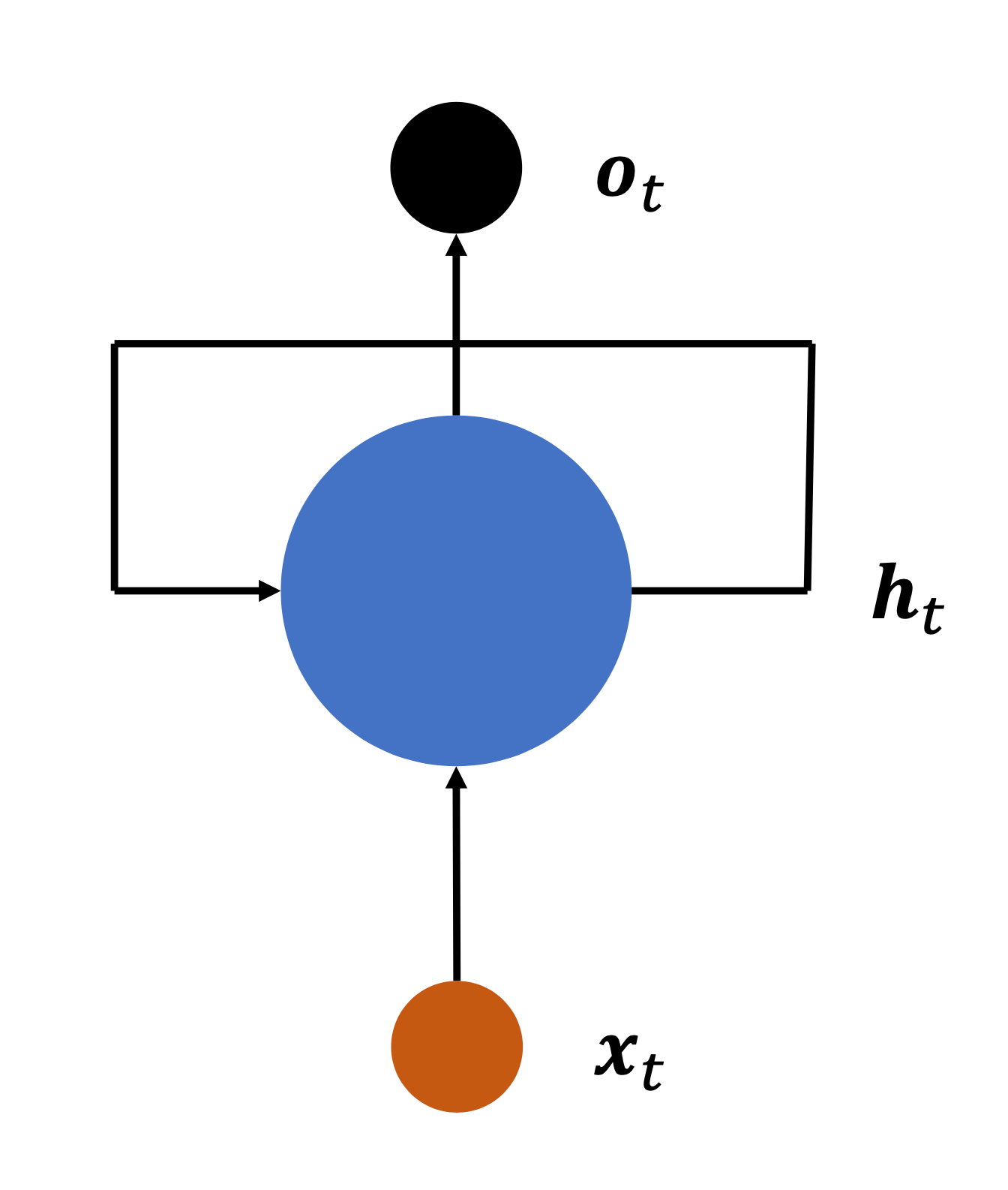
循环神经网络的结构：

$$\bold{h}_t = \tanh(\bold{W}_{xh}\bold{x}_t + \bold{W}_{hh}\bold{h}_{t-1} + b)$$

$\bold{o}_t$可以等于$\bold{h}_t$，也可以在$\bold{h}_t$的基础上再乘一个东西，$\bold{W}_{ho}\bold{h}_t$。

循环神经网络的循环是指：网络循环接受序列的每个特征向量$\bold{x}_t$，并刷新内部状态向量$\bold{h}_t$，同时形成输出$\bold{o}_t$。

循环神经网络的梯度弥散和梯度爆炸：
循环神经网络的梯度有$\bold{W}_{hh}$的连乘，容易导致梯度爆炸和梯度爆炸

梯度爆炸的解决方法：
1、直接对张量进行限幅
实现方法：

tf.clip_by_value(a,0.4,0.6)

2、通过限制张量$\bold{W}$的范数进行梯度裁剪
实现方法：

tf.clip_by_norm(a,0.5)

3、全局范数裁剪
神经网络的更新方向是由所有参数的梯度张量$\bold{W}$共同决定的，前两种方式只考虑单个梯度张量的限幅，会出现网络更新方向发生变动的情况。
实现方法：

tf.clip_by_global_norm([w1,w2],2)

梯度弥散的解决方法：

1. 增大学习率。
2. 减少网络深度。
3. skip connection

RNN层的两种实现方法：
1、基于SimpleRNNCell

layers.SimpleRNNCell(5)

我们可以在RNN层的Call方法中，循环调用RNNCell的前向计算，这样能最便捷的实现权值共享。这也是循环神经网络的循环。

2、基于SimpleRNN

layers.SimpleRNN()

循环神经网络的缺点：
长程依赖，或者说"RNN会遗忘"。

9.LSTM和GRU

原文链接：https://kakawanyifan.com/10409

LSTM

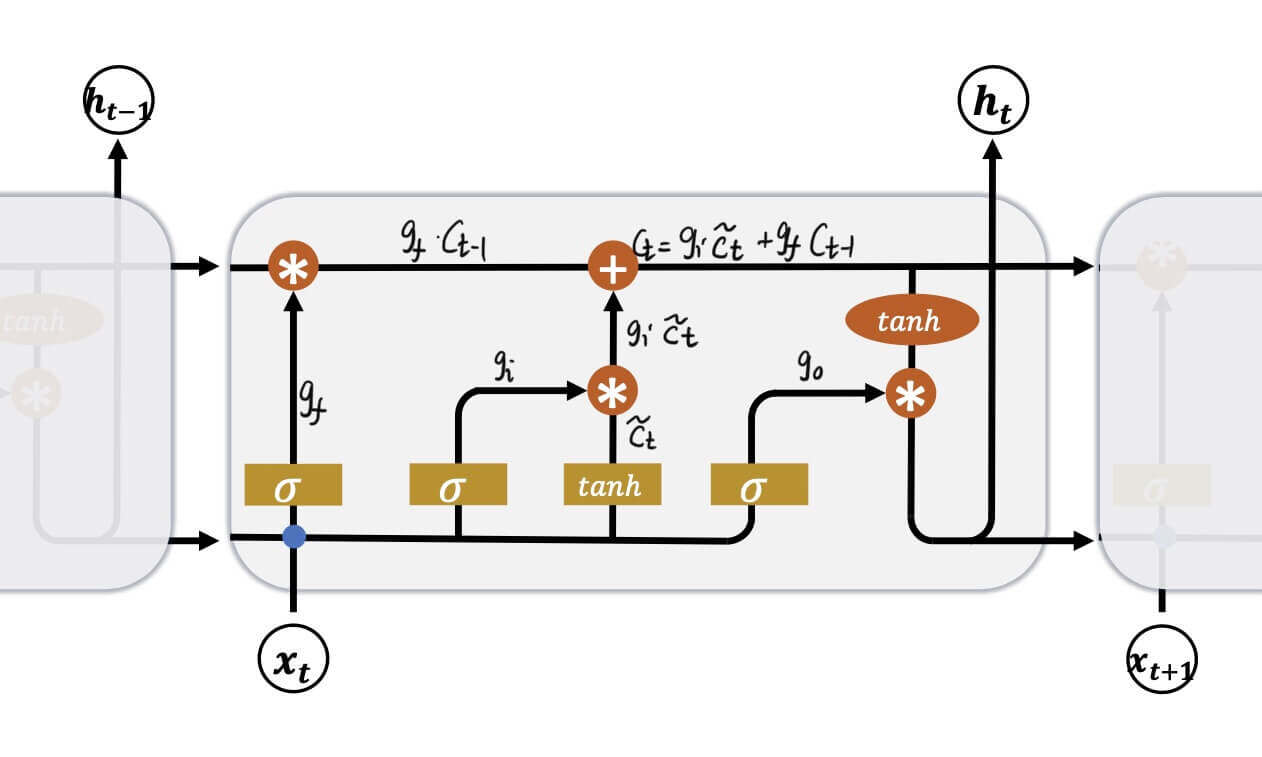
LSTM的结构：

三扇门：

$$\begin{aligned} \text{遗忘门：}\bold{g}_f &= \sigma(\bold{W}_f \cdot [ \bold{h}_{t-1},\bold{x}_t ] + \bold{b}_f) \\ \text{输入门：}\bold{g}_i &= \sigma(\bold{W}_i \cdot [ \bold{h}_{t-1},\bold{x}_t ] + \bold{b}_i) \\ \text{输出门：}\bold{g}_o &= \sigma(\bold{W}_o \cdot [ \bold{h}_{t-1},\bold{x}_t ] + \bold{b}_o) \end{aligned}$$

这三扇门都是由$\bold{h}_{t-1}$和$\bold{x}_t$控制的。

一个中间状态

$$\bold{\tilde{c}}_t = \tanh(\bold{W}_c \cdot [ \bold{h}_{t-1},\bold{x}_t ] + \bold{b}_c)$$

两个输出

$$\begin{aligned} \bold{c}_t &= \bold{g}_i \bold{\tilde{c}}_t + \bold{g}_f \bold{c}_{t-1} \\ \bold{h}_t &= \bold{g}_o * \tanh(\bold{c}_t) \end{aligned}$$

LSTM克服了梯度弥散：
只要没有忘记，或者几乎没有忘记。即遗忘门控$\bold{g}_f = 1$或遗忘门控$\bold{g}_f \approx 1$，就不会梯度弥散。

两种LSTM层的实现方法：
1、基于LSTMCell

keras.layers.LSTMCell

2、基于LSTM

layers.LSTM()

和RNN相比，LSTM的优缺点：
优点：

1. 具有更长的记忆能力
2. 不容易出现梯度弥散现象

缺点：

1. LSTM结构相对复杂，计算代价较高，模型参数量较大。

GRU

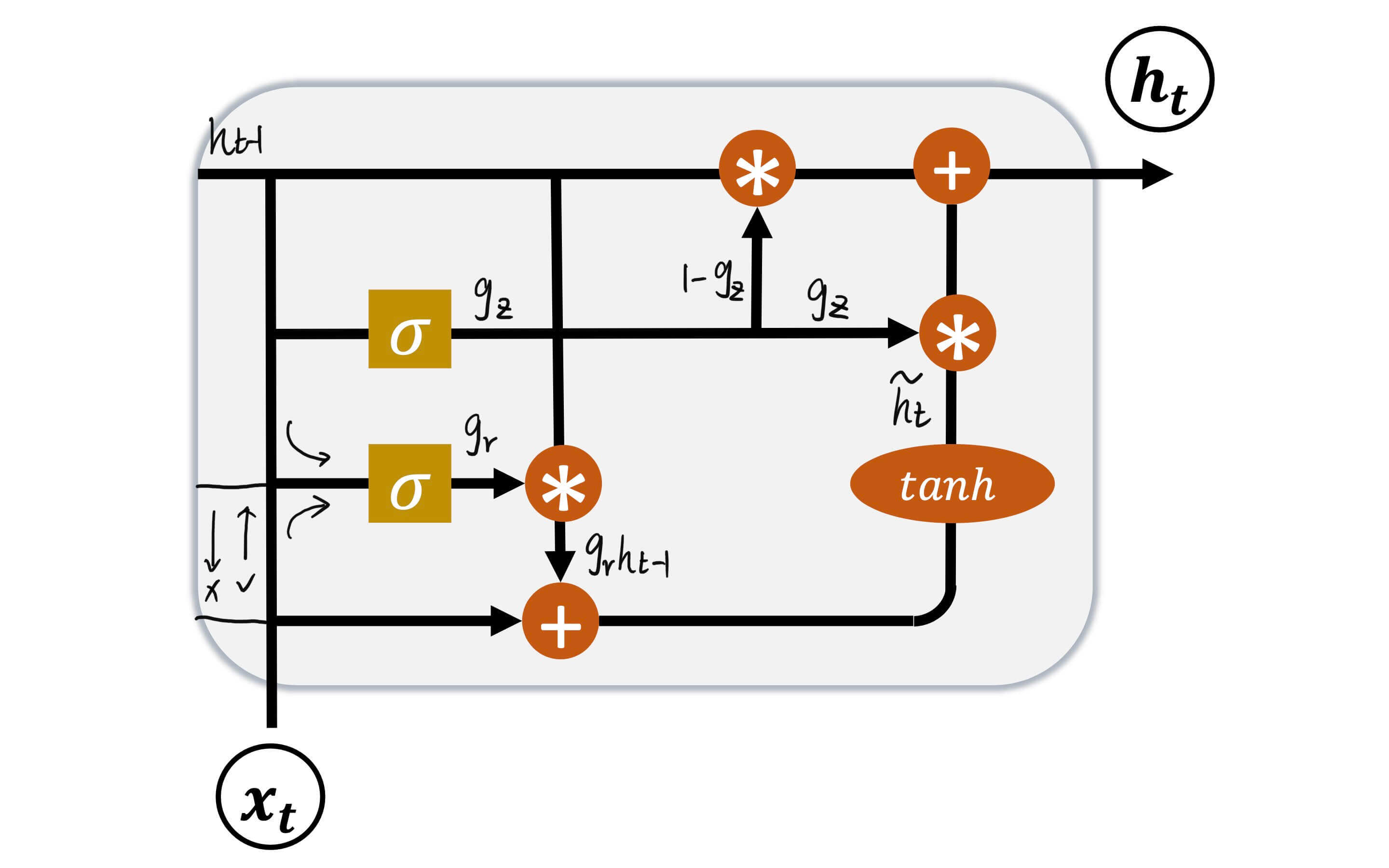
GRU的结构：

两扇门：

$$\begin{aligned} \text{复位门：}\bold{g}_r = \sigma(\bold{W}_r[\bold{h}_{t-1},\bold{x}_t] + \bold{b}_r) \\ \text{更新门：}\bold{g}_z = \sigma(\bold{W}_z[\bold{h}_{t-1},\bold{x}_t] + \bold{b}_z) \end{aligned}$$

这两扇门都是由$\bold{h}_{t-1}$和$\bold{x}_t$控制的。

一个中间状态：

$$\bold{\tilde{h}}_t = \tanh(\bold{W}_h \cdot [ \bold{g}_r \bold{h}_{t-1},\bold{x}_t] + \bold{b}_h)$$

一个输出：

$$\bold{h}_t = (1-\bold{g}_z) \bold{h}_{t-1} + \bold{g}_z \bold{\tilde{h}}_t$$

10.自编码器

原文链接：https://kakawanyifan.com/10410

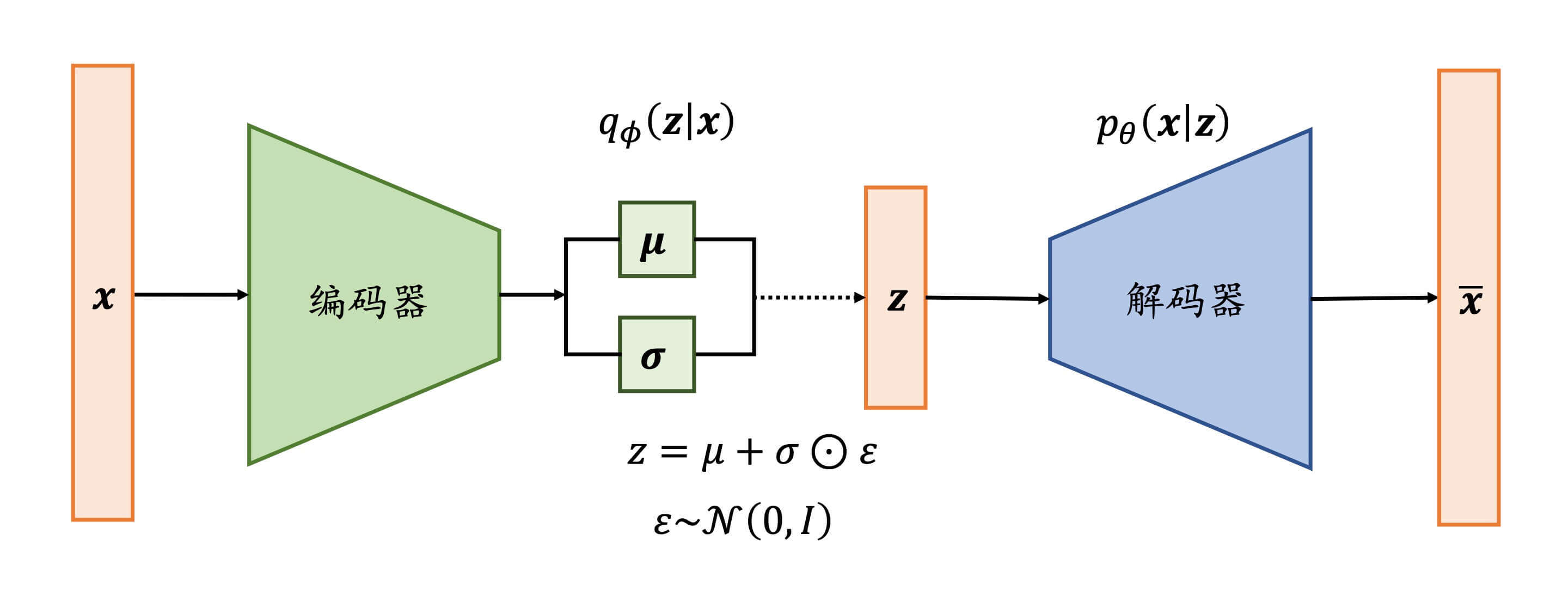
编码器

编码器的结构：

• 函数$f()$是编码器，$\bold{z} = f(\bold{x})$。
• 函数$g()$是解码器，$\bold{\widehat{x}} = g(\bold{z}) = g(f(\bold{x}))$。
• 损失函数$loss = dist(\bold{x},\bold{\widehat{x}})$，通常用欧式距离(两点间的距离)。

模型评估：
一般依赖于人工主观评价图片生成的质量，也有一些图片逼真度计算方法。

KL散度

（这一章我们再讨论了KL散度，但是总体和第二章类似，所以不再重复总结。）

变分自编码器

变分自编码器的结构：

• 用一个分布$q_{\phi}(\bold{z}|\bold{x})$去逼近$p(\bold{z}|\bold{x})$。
• 通常解码器网络层输出的是$\log \sigma^2$，而不是$\sigma$，这么做的原因是$\log \sigma^2$$(-\infty,+\infty)$，而$\sigma^2$的值域是$[0,+\infty)$。相当于自带激活函数。后面再把$\log \sigma^2$还原回$\sigma$。

损失函数：
损失函数的推导过程：

$$\min_{\phi} D_{KL}(q_{\phi}(\bold{z}|\bold{x})||p(\bold{z}|\bold{x})) \ \longrightarrow \ \max L(\phi,\theta) \quad \longrightarrow \quad \begin{cases} \min D_{KL}(q_{\phi}(\bold{z}|\bold{x})||p(\bold{z})) \\ \max \mathbf{E}_{z \sim q}[ \log p_{\theta}(\bold{x}|\bold{z})] \end{cases}$$

Reparameterization Trick
通过$z = \mu + \sigma \odot \varepsilon$进行采样，这样同时保证梯度传播是连续的。

11.生成对抗网络

原文链接：https://kakawanyifan.com/10411

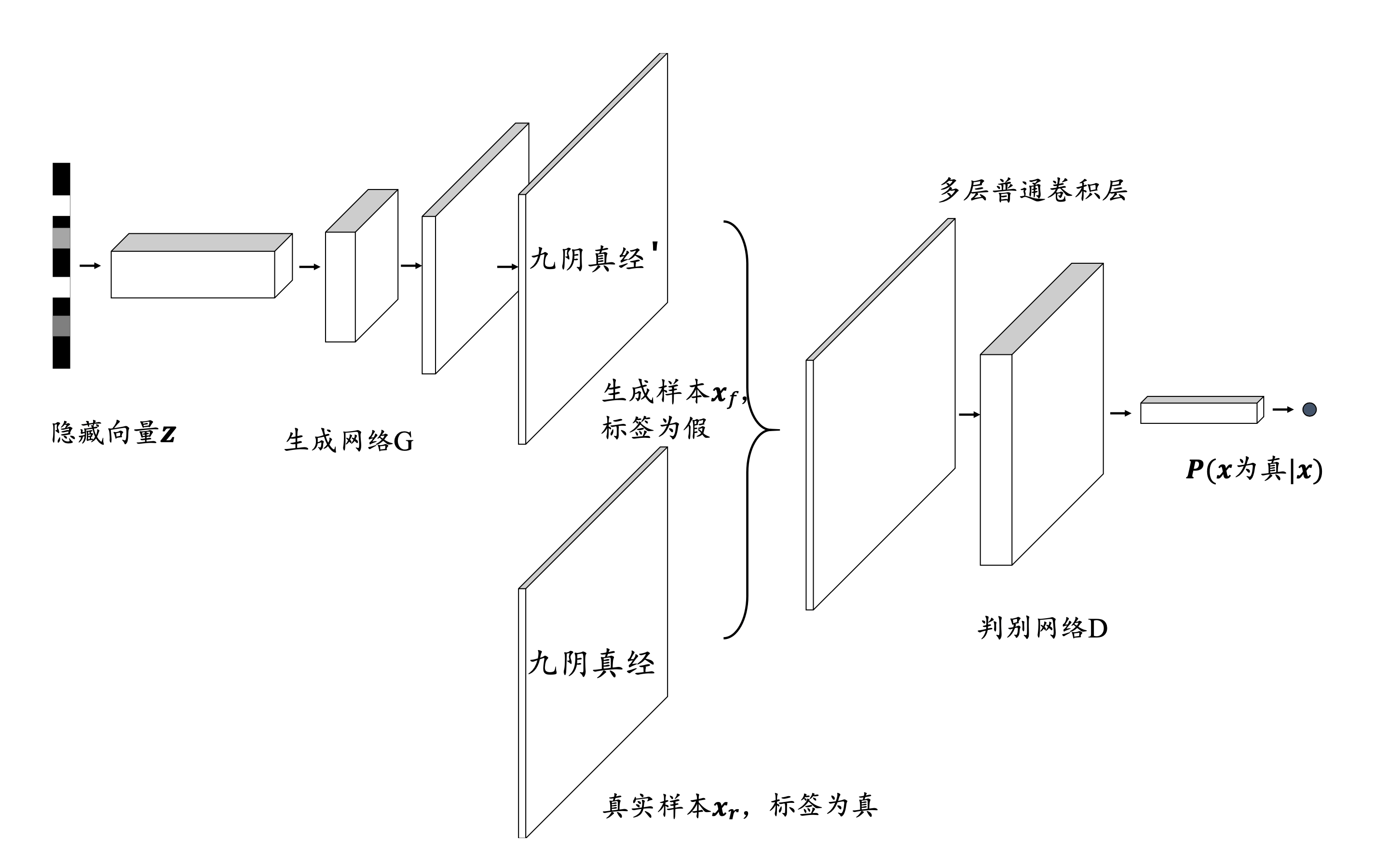
生成对抗网络的解释

生成对抗网络的结构：

目标函数：
对于鉴别器：

$$\max_D \ \mathbf{E}_{(x \sim p_data)}[\log(D(\bold{x}))] + \mathbf{E}_{\bold{z} \sim p_z}[\log(1 - D(G(\bold{z})))]$$

对于生成器：

$$\min_G \ \mathbf{E}_{\bold{z} \sim p_z}[\log(1 - D(G(\bold{z})))]$$

总目标：
先实现鉴别器，再成就生成器。先$\max$，再$\min$。

$$\min_G \max_D \ \mathbf{E}_{(x \sim p_data)}[\log(D(\bold{x}))] + \mathbf{E}_{\bold{z} \sim p_z}[\log(1 - D(G(\bold{z})))]$$

算法流程：
随机初始化参数$\theta$和$\phi$
repeat
  for step = 1,2,…,N do
    随机采样 $\bold{z} \sim p_z$
    随机采样真实样本$\bold{x_r} \sim p_r$
    根据梯度上升算法更新鉴别器D网络：

$$\nabla_{\theta}\ \mathbf{E}_{\bold{x_r} \sim p_r} \log D_{\theta}(\bold{x_r}) + \mathbf{E}_{\bold{x_f} \sim p_g} \log(1 - D_{\theta}(\bold{x}_f))$$

  随机采样隐向量$\bold{z} \sim p_z$
  根据梯度下降算法更新生成器G网络：

$$\nabla_{\phi}\ \mathbf{E}_{\bold{z} \sim p_z} \log (1 - D_{\theta}(G_{\phi}(\bold{z})))$$

  end
until 训练达到最大回合数 Epoch 或者达到要求
输出：训练之后的生成器$G_{\phi}$

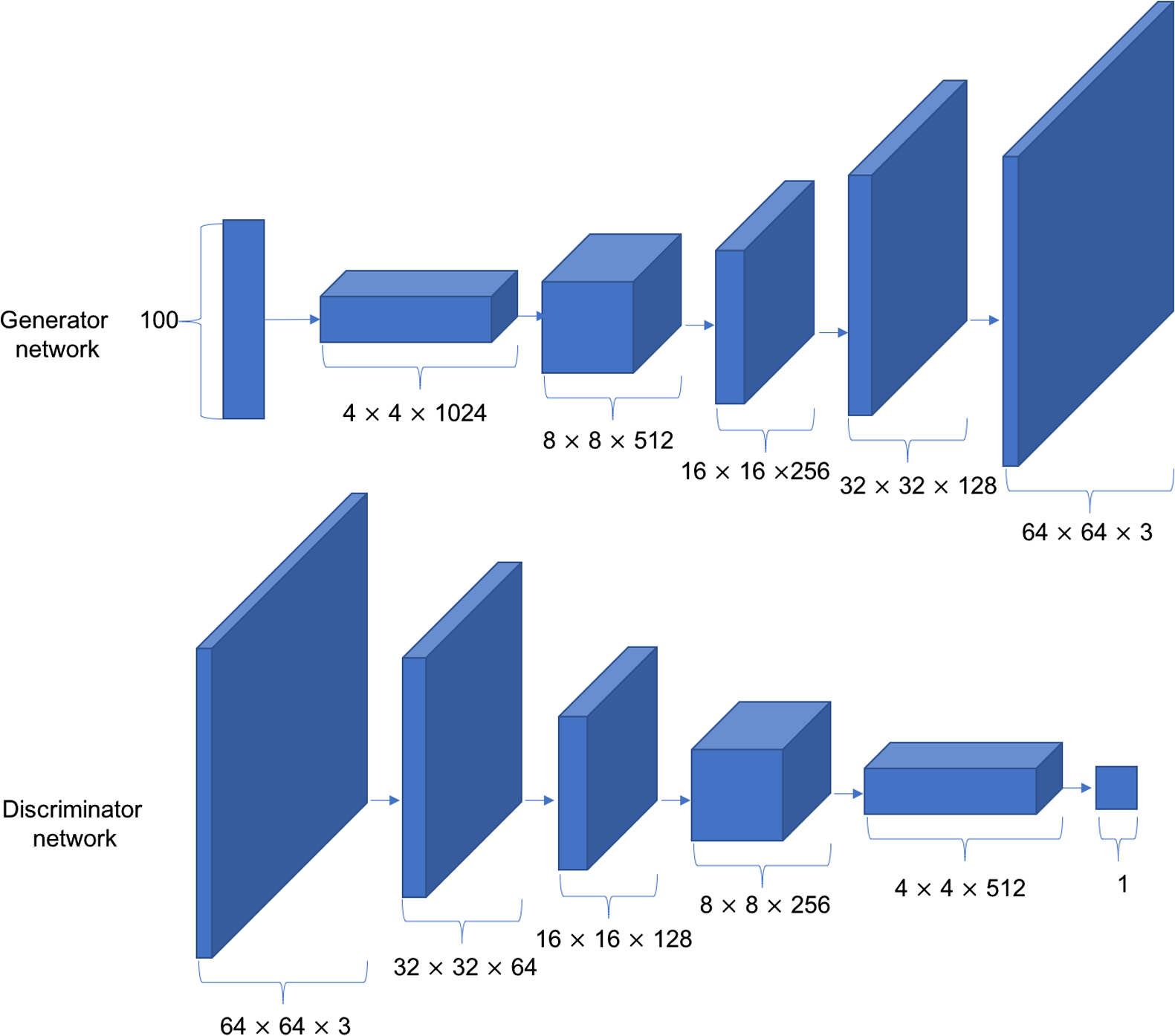
DCGAN的结构

生成器内部结构和鉴别器内部结构，可以多种多样，完全可以自定义的。其中，最经典的是深度卷积生成对抗网络(Deep Convolution Generative Adversarial Networks，简称DCGAN)。

GAN的不稳定性

两个不稳定性：

1. 超参数敏感
   网络结构、学习率、初始化状态等这些都是超参数。这些超参数的一个微小的调整可能导致网络的训练结果截然不同。
2. 模式崩塌
   生成模型倾向于生成真实分布的部分区间中的少量高质量样本，以此来在鉴别器中获得较高的概率值，而不会学习到全部的真实分布。导致生成器生成的样本单一，多样性很差。

原因：
JS散度在不重叠的分布$p$和$q$上的梯度曲面是恒为0的。

WGAN-GP

WANG-GP克服了不稳定性。和GAN相比有三个主要区别。

1. 梯度惩罚项
2. 鉴别器的损失函数
   直接最大化真实样本的输出值，最小化生成样本的输出值，没有交叉熵计算的过程。
3. 生成器的损失函数
   只需要最大化生成样本在判别器D的输出值即可，同样没有交叉熵的计算过程。

12.强化学习初探

原文链接：https://kakawanyifan.com/10412

强化学习

强化学习的定义：
智能体(agent)在和环境(environment)的交互中学习，根据环境的状态(state)，执行动作(action)，并根据环境的反馈(reward)来指导更好的动作。
两个主体：

1. 智能体(agent)
2. 环境(environment)

三个要素：

1. 状态(state)
2. 动作(action)
3. 反馈(reward)

和监督学习，无监督学习的区别：

• 监督学习是寻找输入到输出之间的映射
• 无监督学习是寻找数据之间的隐藏关系
• 强化学习是在与环境的交互中学习和寻找最佳决策

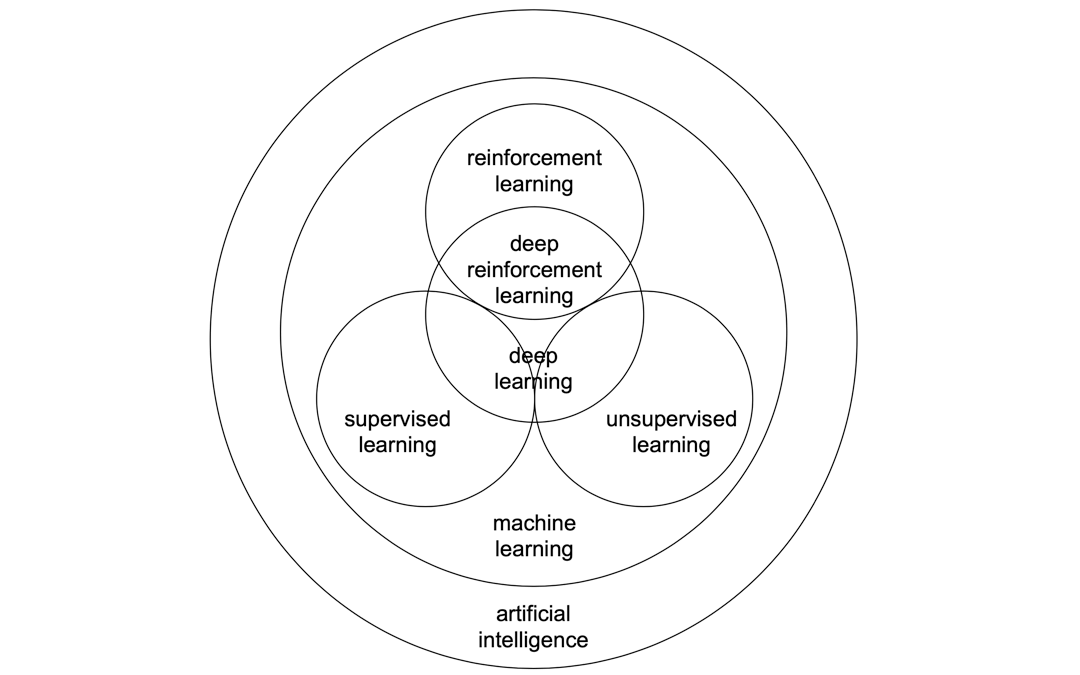
强化学习、监督学习、无监督学习、机器学习、深度学习之间的关系可以用下面的图表示。

强化学习的分类：
按照环境是否已知，强化学习可以分为两类：

1. Model-Based，环境已知，代表算法是动态规划。
2. Model-Free，环境未知，在这种情况下，只有一种办法，探索与利用。

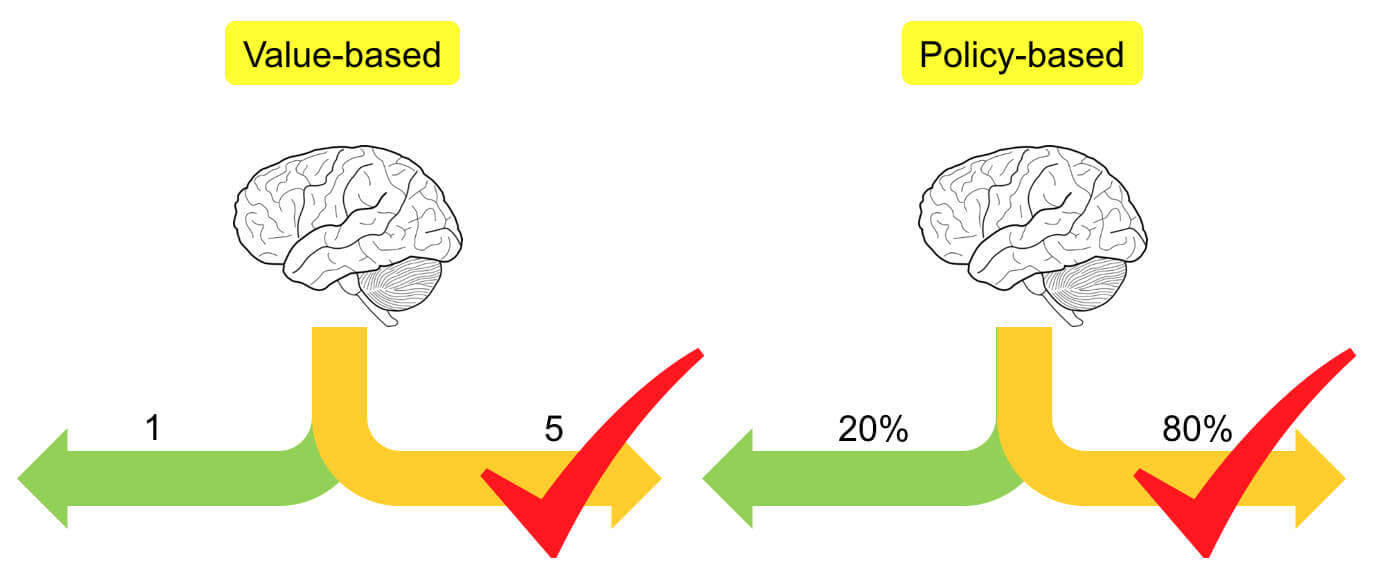
而Model-Free又可以分为两类：

1. Value-Based：基于价值
2. Policy-Based：基于策略

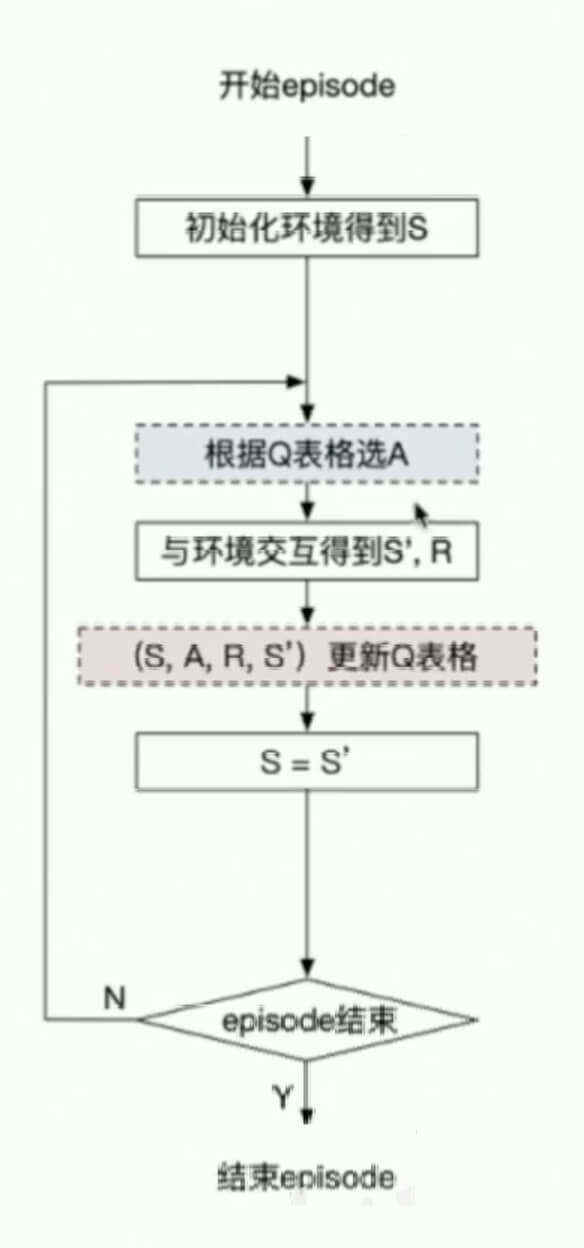
基于表格型方法求解RL

Q表格：
在不同的$S$下采取不同的$A$，分别有多少价值。

目标：

$$\max \ \text{总收益}G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdot\cdot\cdot$$

• $\gamma$被称为衰减率

Q表格的更新：
“巴普洛夫的狗”，下一个状态的价值，会强化去影响当前状态的价值。

$$Q(S_t,A_t) \leftarrow Q(S_t,A_t) + \alpha[R_{t+1} + \gamma Q(S_{t+1},A_{t+1}) - Q(S_t,A_t)]$$

两个代表算法：

1. SARSA
2. Q-Learning

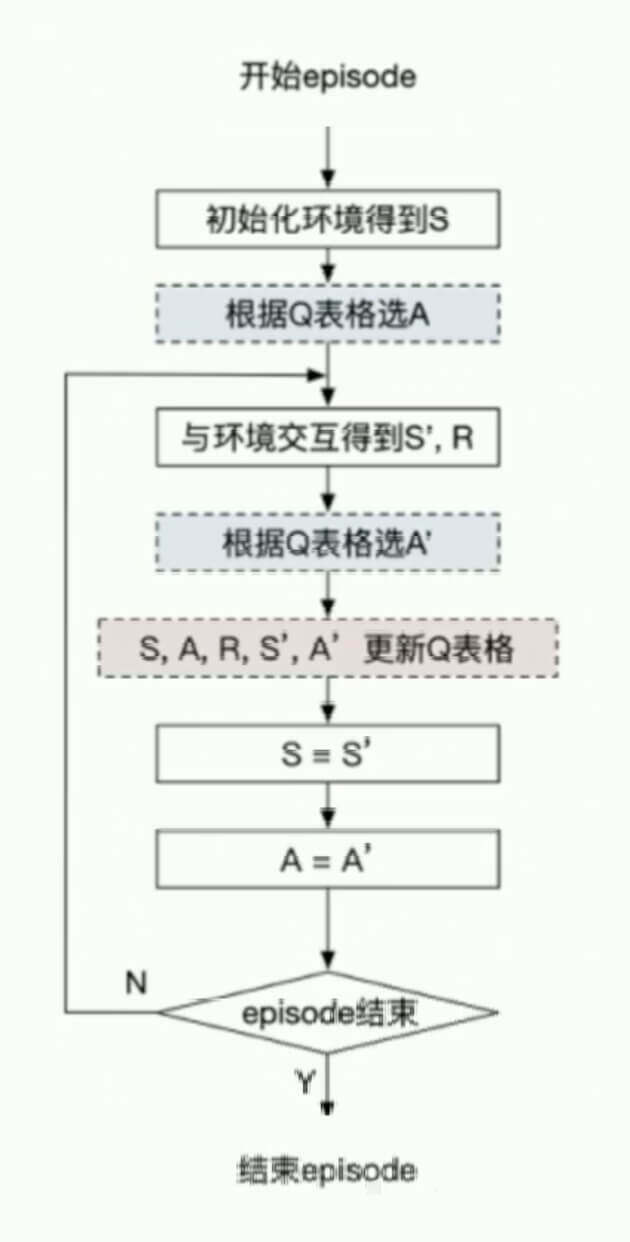
SARSA：

更新策略：

$$Q(S_t,A_t) \leftarrow Q(S_t,A_t) + \alpha[R_{t+1} + \gamma Q(S_{t+1},A_{t+1}) - Q(S_t,A_t)]$$

Q-Learning：

更新策略：

$$Q(S_t,A_t) \leftarrow Q(S_t,A_t) + \alpha[R_{t+1} + \gamma \max_a Q(S_{t+1},a) - Q(S_t,A_t)]$$

基于神经网络方法求解RL

构造一个值函数$\hat{q}(s,a,\bold{w}) \approx Q(s,a)$

基于策略梯度求解RL

目标：

$$\max \overline{R}_{\theta} = \sum_{\tau}R(\tau)p_{\theta}(\tau)$$

求R的方法：
蒙特卡洛法（抽样调查）